
-
论文标题:Excess Description Length of Learning Generalizable Predictors -
论文链接:https://arxiv.org/pdf/2601.04728
TL;DR
如何区分大模型微调是在“激发”(Elicitation)潜在能力,还是在“教授”(Teaching)全新能力?这是一个关乎模型评估与安全的核心问题。Anthropic 与 UC Berkeley 的研究团队提出了一种基于信息论的形式化框架——超额描述长度 (Excess Description Length, EDL) 。
EDL 通过前序编码 (Prequential Coding) 定义,量化了微调过程中模型从训练数据中提取并写入参数的“预测性结构”信息量。该框架不仅在理论上建立了 EDL 与泛化增益的界限,还通过一系列玩具模型(Toy Models)阐明了关于学习过程中信息流动的常见误区。
核心发现包括:
-
EDL 是衡量可泛化信息的指标:对于随机标签,EDL 趋近于零; -
区分激发与教授的信号:能力激发表现为 EDL/样本 的单调递减,且对参数容量要求极低;能力教授则表现为 EDL/样本 的先升后降(倒 U 型),且对参数容量有较高阈值。
1. 引言
大型语言模型(LLM)在预训练阶段获得了广泛的能力,其中许多能力在零样本(Zero-shot)行为中并不明显。微调(Fine-tuning)作为一种后训练干预手段,可以显著提升特定任务的性能。然而,这种提升的本质在不同场景下存在根本差异:
-
激发 (Elicitation) :微调似乎只是唤醒了模型中已有的潜在能力,使原本存在但难以访问的结构浮出水面。 -
教授 (Teaching) :微调必须注入模型此前缺乏的全新预测结构。
这种区分在安全性和实用性上至关重要。如果一项能力是潜在的(例如某些有害知识),它可能仅需极少的数据和算力就能被“激发”出来;如果一项能力必须被“教授”,则其信息壁垒更高。
然而,现有的评估指标(如准确率、损失曲线、样本复杂度)无法清晰区分这两种机制。两者在更多数据下都能提升准确率,且起始性能可能相同。
论文提出了一种基于最小描述长度 (MDL) 原理的度量框架——超额描述长度 (EDL)。不同于通常定义在无限数据极限下的渐进 MDL,EDL 关注有限数据下的信息压缩效率,旨在回答一个务实的问题:有限的信息(高质量样本或权重更新)在多大程度上足以解锁广泛的能力?
2. 信息论基础与形式化定义
为了定义 EDL,我们需要引入前序编码(Prequential Coding)的概念,并将交叉熵损失解释为编码长度。
2.1 交叉熵作为压缩
根据 Shannon 的信源编码定理,如果我们使用分布 来编码来自分布 的符号,每个符号的预期编码长度为交叉熵 。
在监督学习中,给定输入 和标签 ,模型参数 定义了条件分布 。观察到 的交叉熵损失为:
这不仅是优化的目标函数,更是使用模型预测分布作为编码方案时,编码标签 所需的纳特 (nats) 或 比特 (bits) 数。
2.2 前序编码与 MDL
前序编码 (Prequential Coding) 提供了一种在不显式传输模型参数的情况下编码序列数据的框架。考虑一个通信协议:Alice 想要将训练数据集 中的标签发送给 Bob。Bob 已知输入 和初始模型 ,以及双方商定的训练算法 。
过程如下:
-
对于第 个样本,双方使用当前模型 的预测分布 来编码 。 -
Alice 发送编码,Bob 解码得到 。 -
双方同步运行训练算法更新参数:。
整个数据集的总编码长度即为前序最小描述长度 (Prequential MDL) :
这里, 表示在处理前 个样本后更新的参数。MDL 衡量了在学习过程中,利用不断进化的模型对训练数据进行编码所需的总比特数。
2.3 超额描述长度 (EDL) 的定义
训练通常不仅限于对数据的一次遍历(Epoch),模型最终会收敛到参数 。最终模型的测试损失(Test Loss)为:
超额描述长度 (EDL) 定义为前序 MDL 与使用最终模型编码同样数量样本所需编码长度之差:
直观解释:
-
MDL 是在学习过程中,模型对数据的“初次见面”时的惊讶程度累积。 -
是假如我们一开始就拥有了最终训练好的模型 ,对数据进行编码所需的长度。这代表了数据中剩余的、即使是最终模型也无法解释的随机性或噪声(即不可压缩的残差)。 -
EDL 差值代表了模型在训练过程中吸收并存储在参数中的预测性信息。它是从训练数据中提取的、使得模型能够比初始状态更好地预测数据的结构化信息。
通过分解 MDL,我们可以更清晰地看到这一点:
EDL 累积了每一步当前模型相对于最终模型的“超额”损失。
3. EDL 的理论性质
论文证明了 EDL 作为信息度量的几个基本性质,确保其在操作上的合理性。
3.1 期望非负性
如果训练过程是有效的,那么“吸收的信息”应该是非负的。论文定义了总体单调算法 (Population-Monotonic Algorithm) ,即每一步更新在期望上不增加总体损失:
其中 是总体分布上的期望损失。
定理:对于从分布 独立同分布(i.i.d.)采样的 和 ,如果算法 是总体单调的,则:
这表明,平均而言,训练应当从数据中提取信息而非破坏信息。虽然对于单个数据集实现,由于方差存在,EDL 可能略小于零,但在期望上它保证了非负性。
3.2 与在线学习遗憾 (Regret) 的关系
在线学习理论中的遗憾 (Regret) 定义为在线算法累积损失与某个固定比较器 的累积损失之差:
EDL 可以重写为:
这里揭示了 EDL 的两个来源:
-
泛化差距 (Generalization Gap) :。如果模型过拟合,这项可能为负。 -
遗憾 (Regret) :学习过程中的代价。
在渐进无限数据极限下,如果模型完美泛化()且遗憾是次线性的(),则平均每样本 EDL 趋向于 0。这符合直觉:在无限数据下,任何有限的结构信息平均分摊到每个样本上都变得微不足道。因此,EDL 是一个针对有限数据体制的度量。
3.3 与剩余描述长度 (SDL) 的收敛
Whitney et al. (2021) 提出了剩余描述长度 (SDL),即累积损失减去理论最优损失 。EDL 是 SDL 的可计算版本(用 代替不可知的 )。
论文证明,在一致性(Consistency)假设下,随着 ,EDL 收敛于 SDL。EDL 的优势在于它不需要知道理论最优损失,也不需要无限数据假设,完全可从训练日志中计算。
3.4 泛化增益界限
EDL 为期望泛化误差的改善提供了上界。期望 EDL 满足:
其中 是训练轨迹上的平均预期损失。
这意味着 EDL/n 衡量了最终模型相对于训练过程中平均模型的性能提升。
4.解析学习动力学
为了消除关于学习信息的常见困惑,并解释为何“激发”与“教授”表现不同,论文引入了一系列精巧的玩具模型。
4.1 随机标签:EDL 为零
场景:标签 与输入 独立,且在训练集和测试集间独立。
分析:在这种情况下, 恒定(等于标签熵)。MDL 会随着 线性增加(因为无法预测),且 也线性增加。
结果:。
意义:这验证了 EDL 测量的是可泛化的结构,而非单纯的记忆或计算工作量。即使模型强行记住了随机标签(过拟合),测试损失不会下降,EDL 依然接近零。
4.2 假设坍缩 (Hypothesis Collapse):单样本的高信息量
困惑:一个二进制标签只有 1 bit 熵,怎么可能提供超过 1 bit 的信息?
场景:贝叶斯学习者,假设空间 。只有一个正确假设。
分析:
-
在观察数据前,不确定性(熵)为 。 -
假设存在一个诊断性样本 (Diagnostic Example) ,它能排除除 以外的所有假设。 -
观察到该样本后,不确定性降为 0。 -
EDL 贡献:虽然编码该标签的瞬时损失可能仅为 (例如 1 bit),但模型获得的关于“哪个规则支配数据”的信息量是 。 -
这解释了激发 (Elicitation) :如果预训练模型已经包含了 个潜在的技能(假设),只需要极少量的样本来“指向”正确的那个技能,就能消除巨大的不确定性,从而获得巨大的泛化增益。
结论:在激发场景下,单个样本消除的不仅仅是标签的不确定性,而是关于任务身份的不确定性。
4.3 不相交子分布:泛化与覆盖率
场景:数据分布 是 个不相交子分布的混合 。
分析:在一个子分布上学习到的规则无法泛化到其他子分布。期望泛化增益与该子分布的权重 成正比。
结果:
意义:稀有子分布上的学习对全局 EDL 贡献甚微。如果训练数据集中在某些狭窄领域,即使局部学习效果很好,全局 EDL 也可能很低。
4.4 赠券收集者动力学 (Coupon Collector):教授的特征
场景:任务包含 个独立的概念(Coupons),模型必须见过每个概念至少一次才能泛化。
分析:
-
这是一个典型的教授 (Teaching) 场景。模型不具备先验知识。 -
在初期(收集概念少),新样本大概率是新概念,MDL 累积快,测试损失下降慢(因为还有很多未见概念)。 -
随着收集的概念接近 ,模型开始能预测大部分数据。 -
EDL 轨迹:呈现倒 U 型(或先升后降)。 -
Phase 1 (低覆盖) :EDL/sample 增加。每多一个样本,模型不仅学到了该样本,还增加了对未来可能出现的同类样本的预测能力。 -
Phase 2 (高覆盖) :EDL/sample 达到峰值。 -
Phase 3 (冗余) :随着 ,新样本提供的信息减少,EDL/sample 随 衰减。
-
结论:先升后降的 EDL 曲线是“教授”或从头学习复杂结构任务的特征信号。 这反映了从部分覆盖到完全覆盖的相变。
4.5 格式学习与瞬态
场景:任务需要学习格式(Format,如“答案是X”)和能力(Capability,实际的推理)。
分析:格式通常熵低、易学;能力熵高、难学。
结果:
-
训练初期,格式迅速被掌握,导致 MDL 和测试损失急剧下降。这会在 EDL 曲线早期产生一个瞬态峰值。 -
随后,随着能力缓慢提升,EDL 可能再次上升或趋于平稳。
建议:在计算 EDL 时,应仅对答案 Token 进行评分,或对输出进行归一化,以剥离格式学习的干扰,专注于能力的获取。
5. 区分激发与教授:实证预测与应用
基于上述理论框架和玩具模型,论文提出了区分 LLM 微调机制的关键签名。这些预测在配套的实证论文中得到了验证。
5.1 EDL 缩放签名 (Scaling Signatures)
-
激发 (Elicitation) :
-
表现为 EDL/token 随数据集大小单调递减。 -
类似于“假设坍缩”模型。模型已有潜能,样本只是用来消除不确定性。每增加一个样本,其边际信息贡献迅速下降。 -
总 EDL 相对于能力提升来说较小。
-
-
教授 (Teaching) :
-
表现为 EDL/token 在初期有上升阶段(或平顶)。 -
类似于“赠券收集者”模型。模型需要积累多个组件才能形成完整能力。在达到临界覆盖率之前,额外样本的边际价值是递增的。 -
总 EDL 较大,说明写入了大量新结构。
-
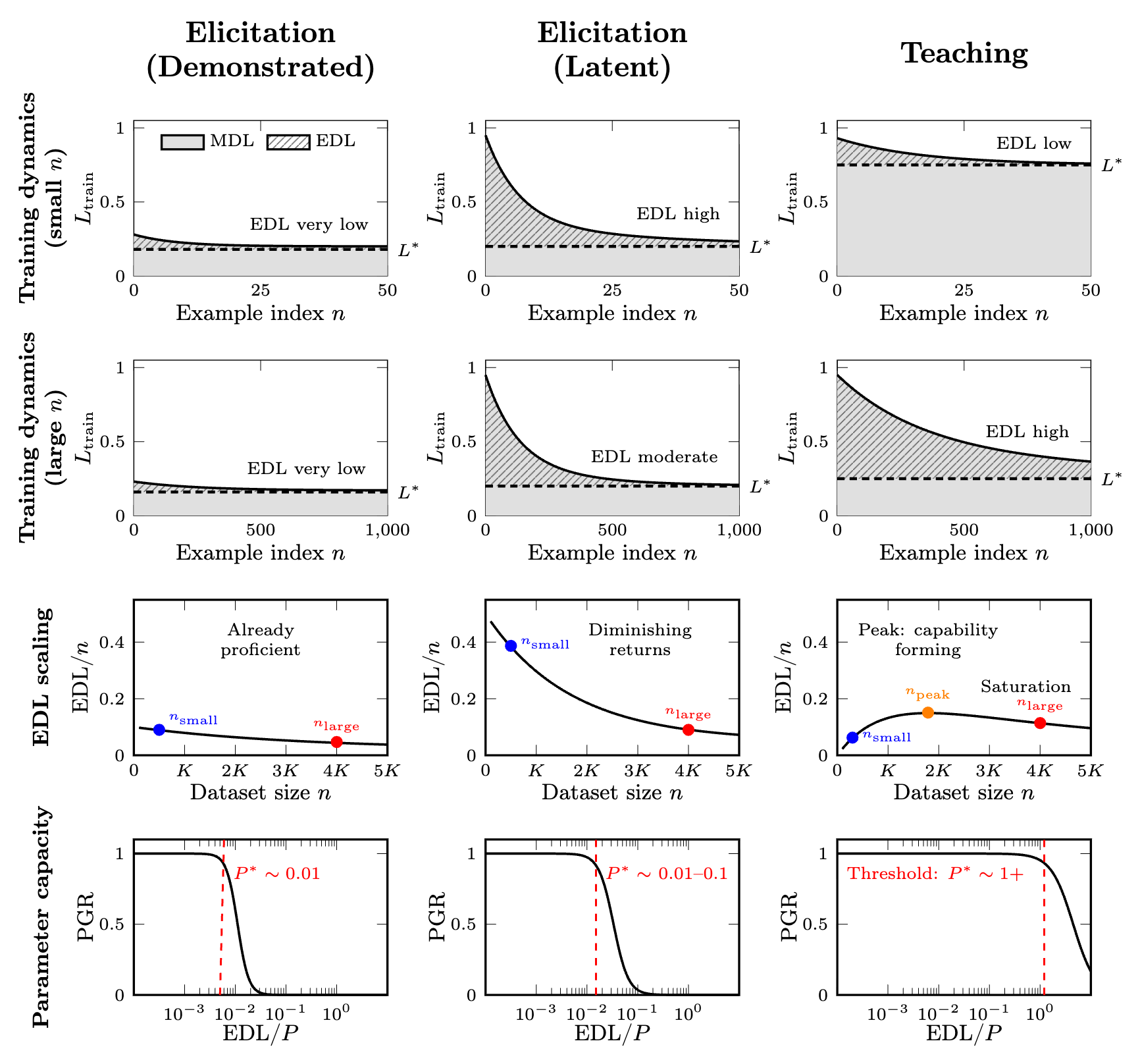
5.2 参数容量阈值 (Parameter Capacity)
EDL 还可以通过 每参数 EDL (EDL per parameter) 进行归一化。这对于参数高效微调(如 LoRA)尤为重要。
-
激发:对参数容量要求极低(例如 ~0.01 bits/param)。因为只需要少量的位来选择潜在的假设。 -
教授:对参数容量要求较高(例如 >1 bits/param)。因为必须存储大量全新的预测链路。
实证推论:如果一个任务可以通过极低秩的 LoRA(如 rank=8)完美解决,且性能不输于全量微调,这强有力地暗示了该任务是在进行“激发”。反之,如果 LoRA 性能随着秩的降低而急剧恶化,且 EDL/param 很高,则属于“教授”。
6. 概念澄清
为了避免误解,论文特意澄清了几个关键点:
6.1 计算量 vs. 分布期望
计算出的 EDL 是针对特定训练序列的统计量。它是一个随机变量。严格的信息论解释需要对数据集分布求期望。但在实践中,对于大数据集,计算值是期望值的良好估计。
6.2 为什么单标签能提供多比特信息?
再次强调,这不是关于标签本身的熵(Label Entropy),而是关于标签提供的关于学习问题(Learning Problem)的信息。在假设空间巨大的情况下,排除错误的假设所带来的信息收益远超标签本身的比特数。
6.3 EDL 不是语义信息
EDL 是预测性压缩 (Predictive Compression) 的度量。
-
高 EDL 意味着模型更能预测测试数据。 -
这可能源于真正的“理解”,也可能源于死记硬背的统计规律。EDL 对此是不可知的(Agnostic)。 -
低 EDL 可能意味着没有学到东西,也可能意味着早就学会了(在零样本时就已经掌握)。
6.4 算法依赖性
EDL 依赖于训练算法 。不同的优化器、学习率调度会产生不同的 MDL 轨迹,从而产生不同的 EDL。这并非缺陷,而是特性:EDL 衡量的是特定算法从数据中提取信息的效率。在比较模型或任务时,必须固定训练算法。
更多细节请阅读原文。
往期文章:




