• 论文标题：GDPO: Group reward-Decoupled Normalization Policy Optimization for Multi-reward RL Optimization
• 论文链接：https://arxiv.org/pdf/2601.05242

TL;DR

今天解读一篇来自 NVIDIA 团队的一篇论文《GDPO: Group reward-Decoupled Normalization Policy Optimization for Multi-reward RL Optimization》，论文指出当前业界常用的 Group Relative Policy Optimization (GRPO) 在处理多奖励（Multi-reward）场景时存在理论缺陷：直接对加和后的总奖励进行组内归一化（Group-wise Normalization），会导致不同奖励组合在归一化后坍缩为相同的优势值（Advantage），从而丢失训练信号的粒度，导致收敛次优甚至训练失败。

为此，论文提出了 GDPO（Group reward-Decoupled Normalization Policy Optimization）。该方法的核心在于“先归一化，后聚合”，即对每个独立的奖励分量分别进行组内归一化，然后再求和，最后辅以 Batch-wise 的归一化以稳定数值范围。实验表明，GDPO 在工具调用、数学推理和代码生成等任务上，无论是在正确率还是约束满足度上，均一致优于 GRPO。

1. 引言

在当前的后训练（Post-training）阶段，强化学习（RL）已成为对齐人类偏好的标准范式。早期的 RLHF 主要关注单一维度的偏好（如有用性或准确性），但随着模型部署场景的复杂化，我们需要模型同时满足多个异构目标，例如：

• 准确性（Correctness）： 答案是否正确。
• 格式（Format）： 是否遵循特定的 JSON 或 XML 结构。
• 长度（Length）： 回答是否简洁，避免啰嗦。
• 安全性（Safety）： 是否拒绝有害指令。

在多奖励 RL（Multi-reward RL）的实践中，最直观的方法是将各个目标的奖励 加权求和，得到总奖励 ，然后直接套用现有的 RL 算法。

GRPO（Group Relative Policy Optimization）因其去除了 Value Model 的高效性，成为了近期（尤其是 DeepSeek-R1 等工作之后）的主流选择。然而，NVIDIA 的这项研究重新审视了 GRPO 在多奖励设定下的适用性，揭示了一个被长期忽视的“奖励信号坍缩”（Reward Signal Collapse）问题，并提出了相应的解决方案 GDPO。

2. GRPO 在多奖励场景下的“信号坍缩”

2.1 GRPO 的标准计算流程

回顾 GRPO 的核心机制：对于同一个问题 ，策略模型 采样一组输出 ，其中 是组大小（Group size）。假设有 个优化目标，第 个输出的总奖励为各分量之和：

GRPO 通过组内归一化来计算优势函数（Advantage），公式如下：

这种方法在单目标优化中表现稳定，但在多目标优化中，先求和再归一化的操作会造成严重的信息丢失。

2.2 信号坍缩的数学示例

为了直观展示这一问题，论文构建了一个极简的理论模型。

假设：

• 场景： 针对每个问题生成 2 个回答（）。
• 奖励： 有两个二元奖励 。
• 总分： 单个回答的总奖励取值范围为 。

我们列举所有可能的奖励组合（不考虑顺序），可以发现尽管原始的奖励组合有多种情况，但在 GRPO 处理后，优势值出现了坍缩。

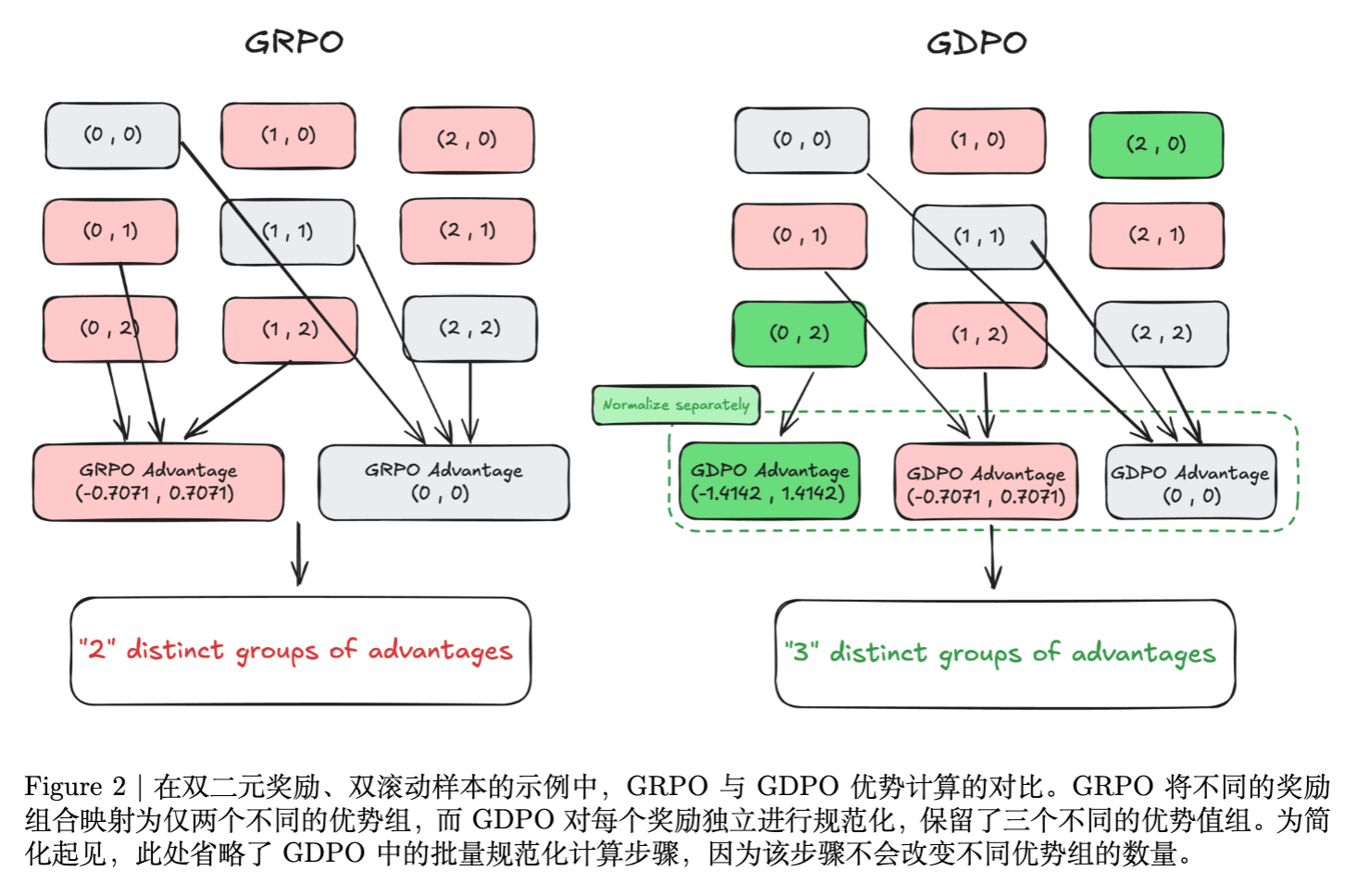
如上图所示，考虑以下两种截然不同的情况：

1. 情况 A：

   • Rollout 1 得分： （总分 1）
   • Rollout 2 得分： （总分 0）
   • 组内奖励集合为 。
   • GRPO 归一化后的优势为：。

2. 情况 B：

   • Rollout 1 得分： （总分 2）
   • Rollout 2 得分： （总分 0）
   • 组内奖励集合为 。
   • GRPO 归一化后的优势为：。

问题所在：
在情况 B 中，Rollout 1 同时满足了两个目标（总分 2），理应比情况 A 中只满足一个目标（总分 1）获得更大的正向优势信号。然而，经过 GRPO 的组内标准化（减均值除方差）后，两者的优势值完全相同。

这意味着，模型无法区分“表现完美”和“表现平庸”，只要它们相对于组内最差样本的“相对差距”在统计学上分布一致。这种分辨率的降低直接导致了训练信号的模糊，使得模型难以快速收敛到同时满足所有最优目标的状态。

2.3 为什么去除标准差归一化无法解决问题？

近期有一些工作（如 DeepSeek-v3/R1 的部分变体）提出在 GRPO 中去除标准差归一化项，仅做减均值处理（Center-only）：

论文指出，虽然这在一定程度上缓解了上述特例中的数值相同问题（情况 A 变为 ，情况 B 变为 ），但在 rollout 数量增加或奖励维度增加的更一般场景下，优势值的“组数”（Distinct Advantage Groups）并没有显著增加。实验证明，单纯去除标准差项并不能带来下游任务性能的实质性提升，甚至在某些格式约束任务上会导致无法收敛（参见后文实验分析）。

3. GDPO 方法详解

为了解决上述问题，论文提出了 GDPO。其核心思想是将归一化操作解耦（Decouple）到每个独立的奖励分量上。

3.1 算法步骤

GDPO 的计算流程包含三个关键步骤：

第一步：组内解耦归一化（Group-wise Decoupled Normalization）

对于第 个奖励目标，单独计算其在组内的归一化优势：

这一步确保了每个奖励维度的相对分布信息被完整保留，不会因为与其他奖励相加而被掩盖。

第二步：优势聚合（Aggregation）

将各分量的归一化优势求和：

第三步：Batch-wise 优势归一化（Batch-wise Advantage Normalization）

这是 GDPO 引入的一个重要工程细节。由于 是多个标准正态分布变量的和，随着奖励数量 的增加，其数值范围会扩大（方差叠加）。为了保证训练的稳定性，并在引入新奖励时不破坏原有的超参数敏感度，GDPO 在整个 Batch 层面（包含所有问题 和所有采样 ）对聚合后的优势再次进行归一化：

3.2 GDPO 的优势解析

1. 信息保真度： 回到 2.2 节的例子。

   • 对于情况 A（奖励 1, 0），GDPO 计算出的优势（归一化后）依然对应较小的数值。
   • 对于情况 B（奖励 2, 0），由于每个分量分别贡献了正向优势，聚合后的数值会显著大于情况 A。
   • 结论： GDPO 能够区分“满足所有目标”和“满足部分目标”的样本，提供更精细的梯度信号。

2. 数值稳定性： Batch-wise 归一化确保了最终输入给 Policy Gradient 的优势值分布稳定在 附近，使得学习率等超参数对奖励数量的变化不敏感。

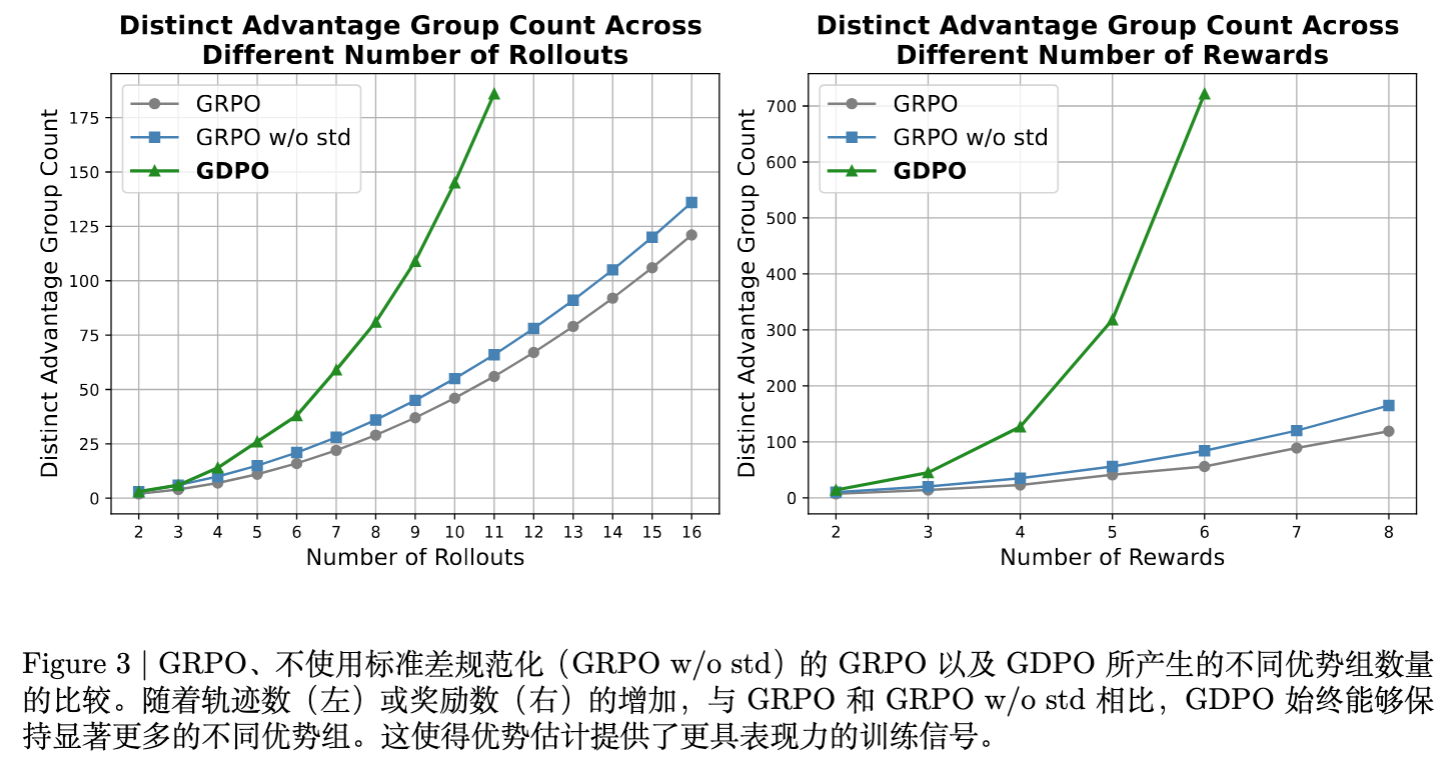
如图 3 所示，随着采样数量（Rollout）或奖励目标数量的增加，GDPO 产生的“不同优势值组”的数量显著多于 GRPO。这意味着 GDPO 能够利用更丰富的信息来更新策略。

4. 如何防止“Reward Hacking”？

在实际应用中，不同目标的重要性往往不同。例如，我们可能认为“答案正确”比“格式完美”更重要。论文对此进行了深入的探讨，指出了传统加权方法的局限性，并推荐了条件奖励（Conditioned Reward）策略。

4.1 传统加权法的局限

最常见的做法是加权求和：

然而，研究发现，当不同任务的难度差异巨大时，单纯调整权重往往失效。
例如，在数学推理任务中，“长度惩罚”（让回复变短）通常比“做对难题”容易得多。如果模型发现缩短长度能轻松获得 ，而做对题目很难获得 ，即使 设得很高，模型也可能倾向于坍缩到生成极短但错误的回答，以稳拿长度分。

4.2 解决方案：条件奖励（Conditioned Reward）

为了解决难度不平衡导致的 Reward Hacking 问题，论文建议使用条件奖励机制。即：简单任务的奖励，只有在困难任务达成时才发放。

以数学题为例，定义长度奖励 为：

效果分析：

• 强制优先级： 模型被强制必须先攻克核心任务（正确率），才能享受到辅助任务（长度）的奖励红利。
• 避免局部最优： 防止模型陷入“生成空字符串”这种满足长度约束但毫无意义的局部最优解。
• 实验支持： 在后文实验中，使用条件奖励的 GDPO 在 AIME 等高难度数学基准上，不仅减少了长度违规，还实现了比单纯加权更高的准确率。

5. 实验结果与分析

论文在三个具有代表性的任务上对比了 GDPO 和 GRPO：工具调用（Tool Calling）、数学推理（Math Reasoning）和代码推理（Coding Reasoning）。

5.1 任务一：工具调用 (Tool Calling)

• 目标：

  1. 格式（Format）： 严格遵循 XML 标签 <think>, <tool_call> 等。
  2. 准确性（Correctness）： 调用的函数名、参数名、参数值必须与 Ground Truth 匹配。

• 模型： Qwen2.5-Instruct (1.5B/3B)。

• 结果：

  

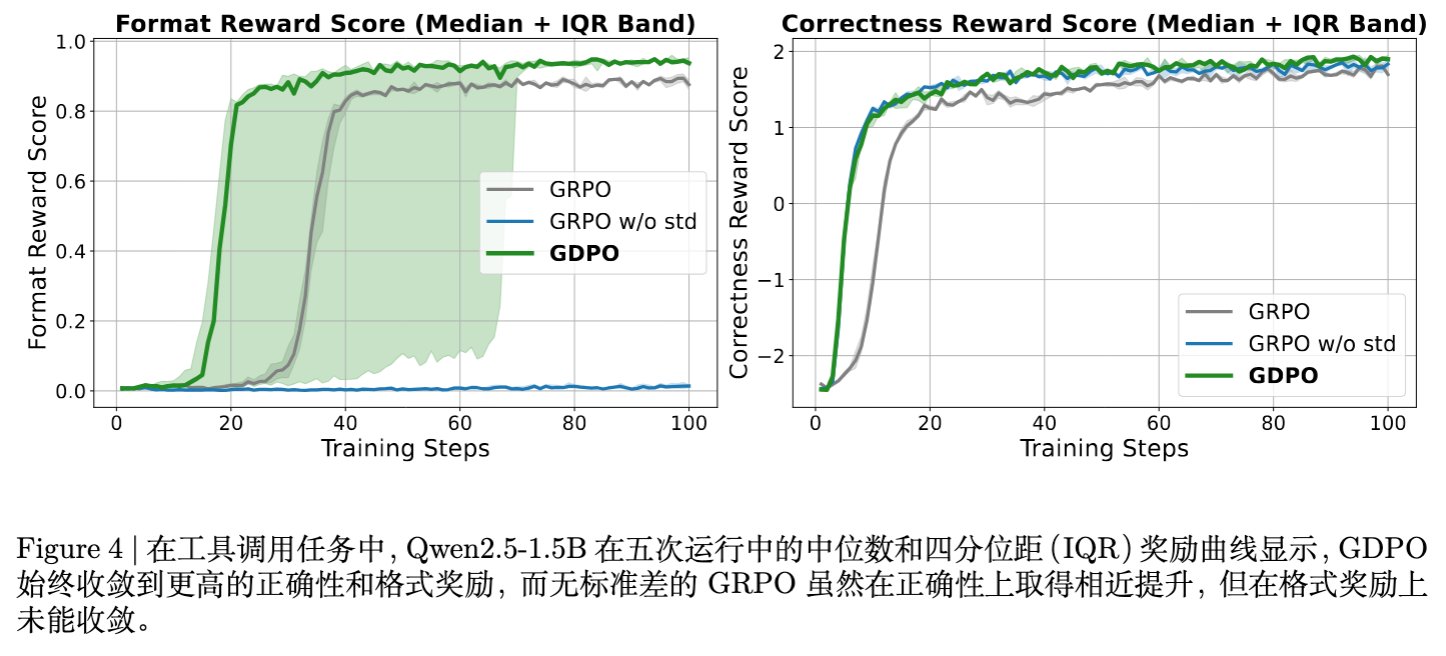
  • GRPO 的问题： 在格式奖励上收敛缓慢，且最终上限较低。
  • GDPO 的表现： 格式和准确性双重提升。特别是在 Format 准确率上，GDPO 达到了 ~82%，而 GRPO 仅为 ~81%（3B 模型）。
  • 消融实验： 仅去除标准差归一化的 GRPO (GRPO w/o std) 在此任务中彻底失败，格式奖励为 0，说明简单的修改不足以处理严格的格式约束。

5.2 任务二：数学推理 (Math Reasoning)

• 目标：

  1. 准确性（Accuracy）： 答案正确。
  2. 长度约束（Length Constraint）： 鼓励回复长度小于 4000 token。

• 模型： DeepSeek-R1-1.5B/7B, Qwen3-4B-Instruct。

• 现象：

  

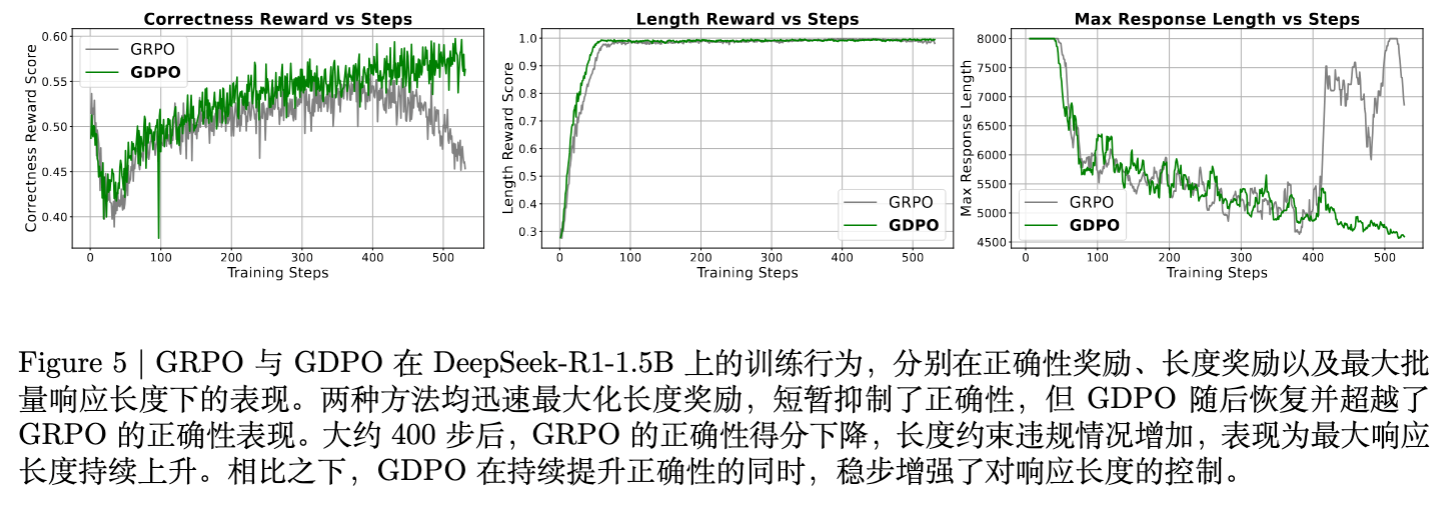
  • GRPO 的训练坍缩： GRPO 在训练约 400 步后，正确率奖励开始下降，同时长度开始失控（变长）。这表明模型在权衡两个冲突目标时失败。
  • GDPO 的鲁棒性： 即使在长度奖励极易获取的情况下，GDPO 依然能保持正确率的稳步上升，同时有效地控制最大响应长度。

• 基准测试（MATH, AIME, AMC）：

  • 在 DeepSeek-R1-7B 上，GDPO 在 AIME 上的准确率比 GRPO 高出 2.9% ，同时长度违规率从 2.1% 降至 0.2% 。
  • 这证明了 GDPO 实现了更好的“准确率-效率”权衡。

5.3 任务三：代码推理 (Coding Reasoning)

• 目标（3 个奖励）：

  1. 通过率（Pass Rate）： 通过测试用例。
  2. 长度（Length）： 简明代码。
  3. 无 Bug（Bug Ratio）： 无运行时/编译错误。
• 模型： DeepSeek-R1-7B。
• 结果：

  • 在三目标联合优化中，GDPO 在保持与 GRPO 相似的 Pass Rate 的同时，显著降低了 Bug 率和长度违规率。
  • 例如在 Taco 数据集上，GDPO 将 Bug 率从 30.0% 降至 28.0% ，同时长度违规从 14.7% 降至 10.6% 。

6. 消融实验

6.1 Batch-wise 归一化的必要性

论文在附录 A 中展示了去除 Batch-wise 归一化后的训练曲线。结果显示，如果不进行这一步，训练过程偶尔会出现不收敛的情况（Loss 震荡或奖励无法提升）。这是因为不同奖励分量求和后，数值波动范围可能过大，甚至导致梯度爆炸或消失。Batch-wise 归一化将输入分布拉回标准范围，增强了优化器的稳定性。

6.2 奖励权重的敏感度分析

作者在数学任务上测试了不同的长度奖励权重 。

• GRPO 的表现： 权重调整效果混乱。降低长度权重并不一定能显著增加长度违规率（意味着模型并没有听从权重的指挥），控制力较弱。
• GDPO 的表现： 表现出更强的可控性。随着 降低，模型逐渐放宽长度限制以换取准确率。
• 配合条件奖励： 当结合条件奖励（Conditioned Reward）时，GDPO 展现出最佳的帕累托前沿（Pareto Frontier），在大幅压缩长度的同时几乎不损失（甚至提升）准确率。

更多细节请阅读原文。

往期文章：

• DeepSeek-R1 v2 发布：新增技术细节与训练流程全解读

• WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题