• 论文标题：WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?
• 论文链接：https://arxiv.org/pdf/2512.12895

TL;DR

推理模型（如 DeepSeek-R1, QwQ 等）通过生成长思维链（CoT）来解决复杂问题，但在低温度采样或贪婪解码时，这些模型极易陷入无限重复文本的“死循环”现象。今天解读一篇来自 MIT、Microsoft Research 和 UW-Madison 的最新研究 《Wait, Wait, Wait... Why Do Reasoning Models Loop? 》。该研究通过对开源推理模型的系统性评测及构建合成图推理任务，揭示了导致循环的三个核心机制：

1. 学习误差（Errors in Learning）与风险规避：当“推进推理的正确动作”难以学习（难以与错误选项区分），而“循环动作”（如复述已知条件）容易学习时，模型倾向于将概率质量分配给容易的循环动作，表现为风险规避。
2. 时间相关的误差（Temporally Correlated Errors）：即便没有学习难度，Transformer 架构存在一种归纳偏置，即在重复出现的决策点上产生的预测误差是时间相关的。这导致模型在遇到相似状态时倾向于重复相同的错误选择，从而形成闭环。
3. 自信度累积（Confidence Buildup）：一旦模型开始重复，这种重复行为会自我强化，模型对重复内容的置信度会迅速趋近于 1，使其难以逃脱循环。
   研究指出，虽然提高采样温度（Temperature）可以缓解循环，但这主要归功于强制探索，而非修正了底层的学习误差，因此高温下的思维链往往由于过度探索而比理想长度冗余得多。

1. 引言

随着大语言模型（LLM）的发展，通过延长推理时间计算（Inference-time compute）来解决复杂问题已成为新的扩展范式。从 DeepSeek-R1 到 OpenAI o1，这些推理模型通过生成数千甚至上万 tokens 的长思维链（Chain of Thought, CoT），在数学竞赛（如 AIME）和复杂代码任务上取得了显著进展。

然而，这一范式面临一个普遍且棘手的问题：循环（Looping）。
在贪婪解码（Greedy Decoding）或低温度设置下，模型经常会陷入死循环，不断重复同一段推理步骤或文本，导致生成失败。为了规避这一问题，模型提供商（如 DeepSeek, Qwen Team）通常建议用户使用较高的采样温度（例如 0.6 或更高）。

这引发了一系列深层次的研究问题：

• 为什么推理模型会循环？是数据问题、架构问题还是优化问题？
• 温度到底起到了什么作用？它是否解决了根本原因，还是仅仅是一个掩盖问题的权宜之计（Stopgap）？
• 为什么经过蒸馏（Distillation）的学生模型比教师模型更容易循环？

2. 开源推理模型中的循环行为

研究团队首先对现有的开源推理模型进行了大规模的实证研究。

2.1 实验对象与设置

研究涵盖了多种规模和类型的模型：

• Qwen 系列：DeepSeek-R1 Distilled Qwen (1.5B, 7B, 32B)。
• OpenThinker 系列：OpenThinker3 (1.5B, 7B) 及其教师模型 QwQ-32B。
• Phi-4 系列：Phi-4-reasoning 及其 RL 微调版本。
• Llama 系列：DeepSeek-R1 Distilled Llama 8B。

评测数据集主要使用 AIME（美国数学邀请赛）的 2024 和 2025 年题目，以及 GPQA 数据集。
循环的定义：如果在响应中，任意长度为 的 n-gram 出现了至少 次，则判定该响应发生了循环。

2.2 核心观测结论

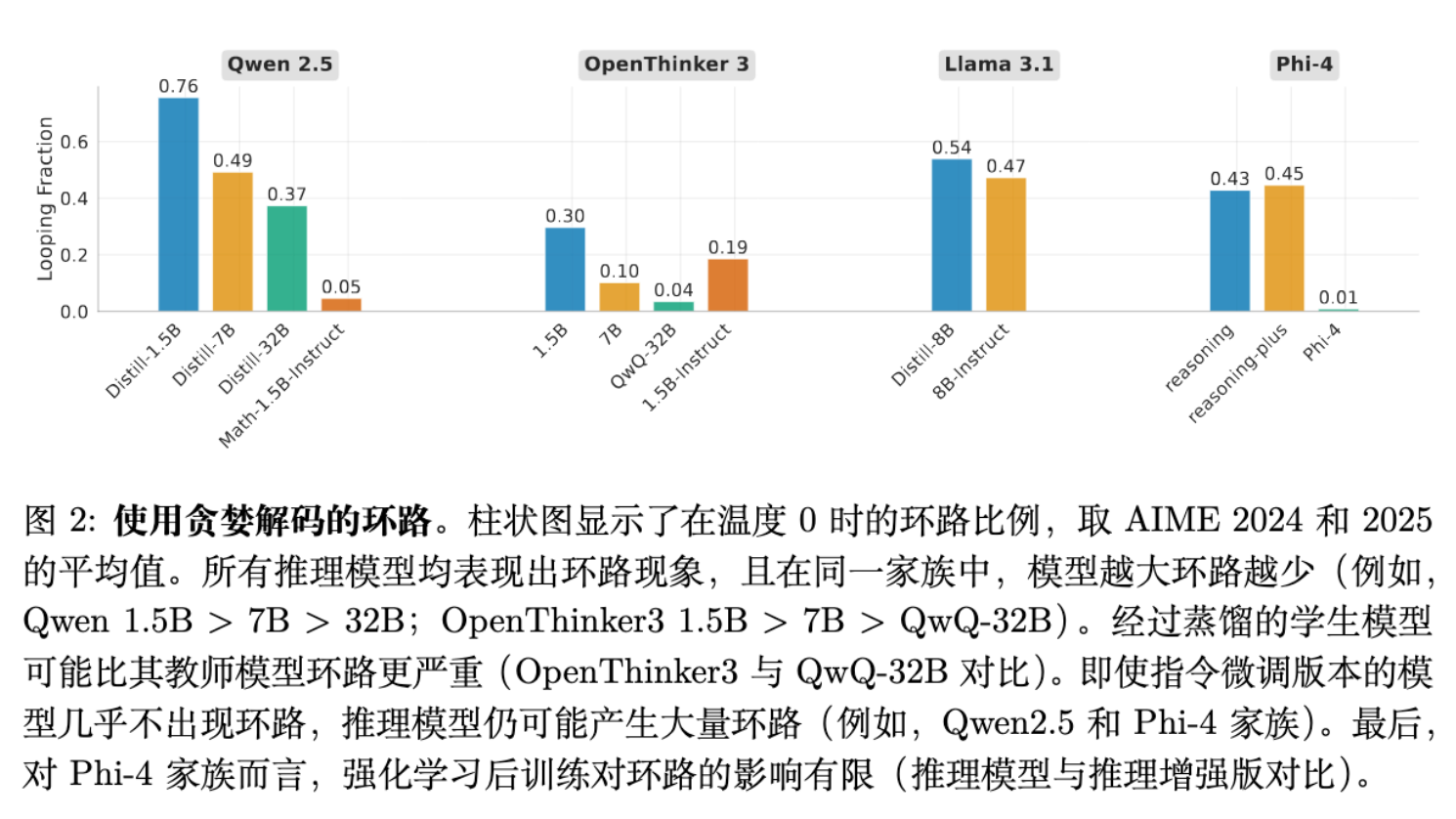
通过在不同温度（0 到 1.0）下对模型进行测试，研究得出了以下关键结论（见图 2）：

1. 低温下普遍循环：所有测试的推理模型在温度为 0（贪婪解码）或低温度时，都表现出高频率的循环行为。随着温度升高，循环比例显著下降。
2. 模型越大，循环越少：在同一家族中，参数量大的模型循环概率更低。例如 Qwen 32B 的循环率远低于 Qwen 1.5B。
3. 蒸馏带来的“退化”：这是一个非常关键的发现。学生模型（Student）的循环频率显著高于其教师模型（Teacher）。

   • 例如，OpenThinker3-1.5B 在贪婪解码下的循环率约为 30%，而其教师模型 QwQ-32B 几乎不循环。
   • 如果学生完美学习了教师的分布，两者行为应一致。这种巨大的差异指向了学习误差（Errors in Learning）——学生模型未能完美拟合教师的概率分布。
4. 难题更易引发循环：对于模型而言较难的问题（高温度下准确率低的问题），在低温度下更容易诱发循环。
5. 指令微调模型（Instruct Models）循环较少：相比于专门的推理模型，普通的指令微调模型（如 Qwen2.5-Instruct）循环现象较轻。这可能是因为推理数据（CoT）中本身包含了更多的“循环动作”（如回溯、反思、复述条件），为模型提供了陷入循环的素材。

2.3 模型是如何陷入循环的？

论文详细展示了 OpenThinker-3 1.5B 在解决 AIME 2025 题目时的循环轨迹（Trace）。

• 风险规避行为（Risk Aversion）：模型在推导过程中，往往会停下来反复确认题意、复述公式或检查基本事实（例如“单词是由两个字母按字母顺序排列组成的”）。

  • 在轨迹中，模型甚至能够意识到自己在重复（“Wait, no...”），但紧接着又回到了相同的逻辑路径上。
  • 这种行为表明，模型认为执行“复述/检查”（Cyclic Action）的风险比执行“下一步推导”（Progress-making Action）的风险更低。
• 对比教师模型：在相同的上下文中，如果让教师模型（QwQ-32B）接续生成，教师模型能够迅速识别错误并推进推理，而不会陷入循环。GPT-5 的评估显示，教师模型在后续生成的 token 中包含更多实质性的推理进展。

这表明，学生模型在面对选择时，给“容易生成的循环废话”分配了过高的概率，而给“难生成的推理步骤”分配了过低的概率。

3. 理论机制一：学习难度导致的风险规避

为了剥离语言模型的复杂性，从数学原理上解释上述现象，作者设计了一个合成图推理任务（Synthetic Graph Reasoning Task）。

3.1 实验设计：星型图上的随机游走

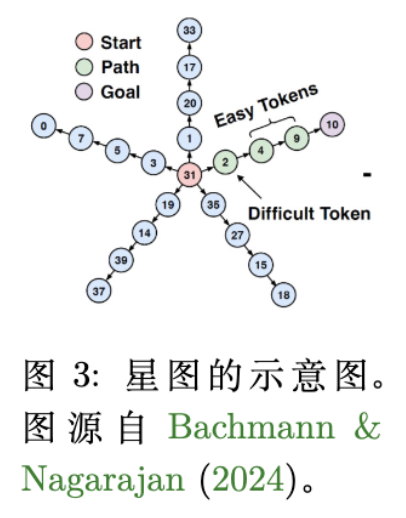
作者构建了一个基于星型图（Star Graph） 的任务：

• 结构：一个根节点（Root），连接着 个分支（Spokes），每个分支长度为 。
• 目标：从起点（Start）出发，寻找通往目标叶节点（Goal）的路径。
• 训练数据生成：模拟推理过程中的“回溯”。

  • 在任意节点，模型以概率 选择向目标前进的正确边（Progress-making action）。
  • 以概率 选择“重置”回起点（Cyclic action/Reset）。
  • 这种设置模拟了思维链中“尝试推进”与“推倒重来/反思”的动态过程。
  • 为了引入学习难度（Hardness），除根节点外，所有节点只有一条出边（容易学习）；而根节点有 条出边，只有一条通向目标。

3.2 命题 1：概率的稀释与风险规避

作者提出了一个核心命题来解释为什么学习难度会导致循环。

命题 1 (Proposition 1) ：
假设存在 个难以区分的上下文（Contexts），每个上下文对应一个正确的“困难动作” （概率为 ）和一个通用的“简单动作” （概率为 ）。
如果学习器（模型）无法区分这 个上下文（即它对这 种情况只能输出同一个概率分布），那么最大化对数似然（MLE）的最优解是：

• 分配给简单动作 的概率为 。
• 分配给每个困难动作 的概率被稀释为 。

证明直觉：
由于模型无法区分正确的具体分支（例如，不知道该选 个分支中的哪一个），它只能采取“对冲”策略，将概率平均分配给所有可能的困难动作。
然而，简单动作（如“重置回起点”）在所有情况下都是一样的，模型可以轻易学会并分配 的概率。

结果：
当 足够大时， 将远小于 。
在贪婪解码时，模型会选择概率最大的动作。由于 ，模型将总是选择简单动作 （重置/循环），而不是尝试去猜某一个具体的困难动作。

3.3 实验验证：Transformer 的行为

作者从头训练了一个 Transformer 来学习上述随机游走任务。

• 训练分布：在根节点，正确向前的概率是 0.7，重置的概率是 0.3。
• 测试表现：

  • 在低温度下，模型陷入了 Start -> Root -> Start -> Root 的死循环。
  • 模型学会了重置动作（容易学），但在根节点无法确定哪条边是通往目标的（难学），于是将 0.7 的概率分散到了 条边上。
  • 因为 （当 较大时），贪婪解码导致模型不断选择重置。
• 温度的作用：提高温度引入了随机性，使模型有机会采样到概率较低的正确路径，从而打破循环。但模型的底层概率分布依然是错误的。

这一机制完美解释了为什么学生模型比教师模型更易循环：教师模型容量大、训练充分，能区分 个困难选项；学生模型容量小或未训练充分，无法区分，只能退而求其次选择容易的“废话”或“回溯”。

4. 理论机制二：时间相关的误差与归纳偏置

除了学习难度（Hardness），论文还发现了另一种更为隐蔽的机制。即使没有“难学”的动作，Transformer 的架构本身也存在导致循环的偏置。

4.1 实验设置：无偏随机游走

在这一设置中，训练数据的生成方式改为：

• 在根节点，均匀随机选择一条出边（概率均等）。
• 没有“正确路径”之分，所有路径都是平等的。
• 理论上，完美的学习器应该在根节点学到均匀分布 。

4.2 时间相关的误差（Temporally Correlated Errors）

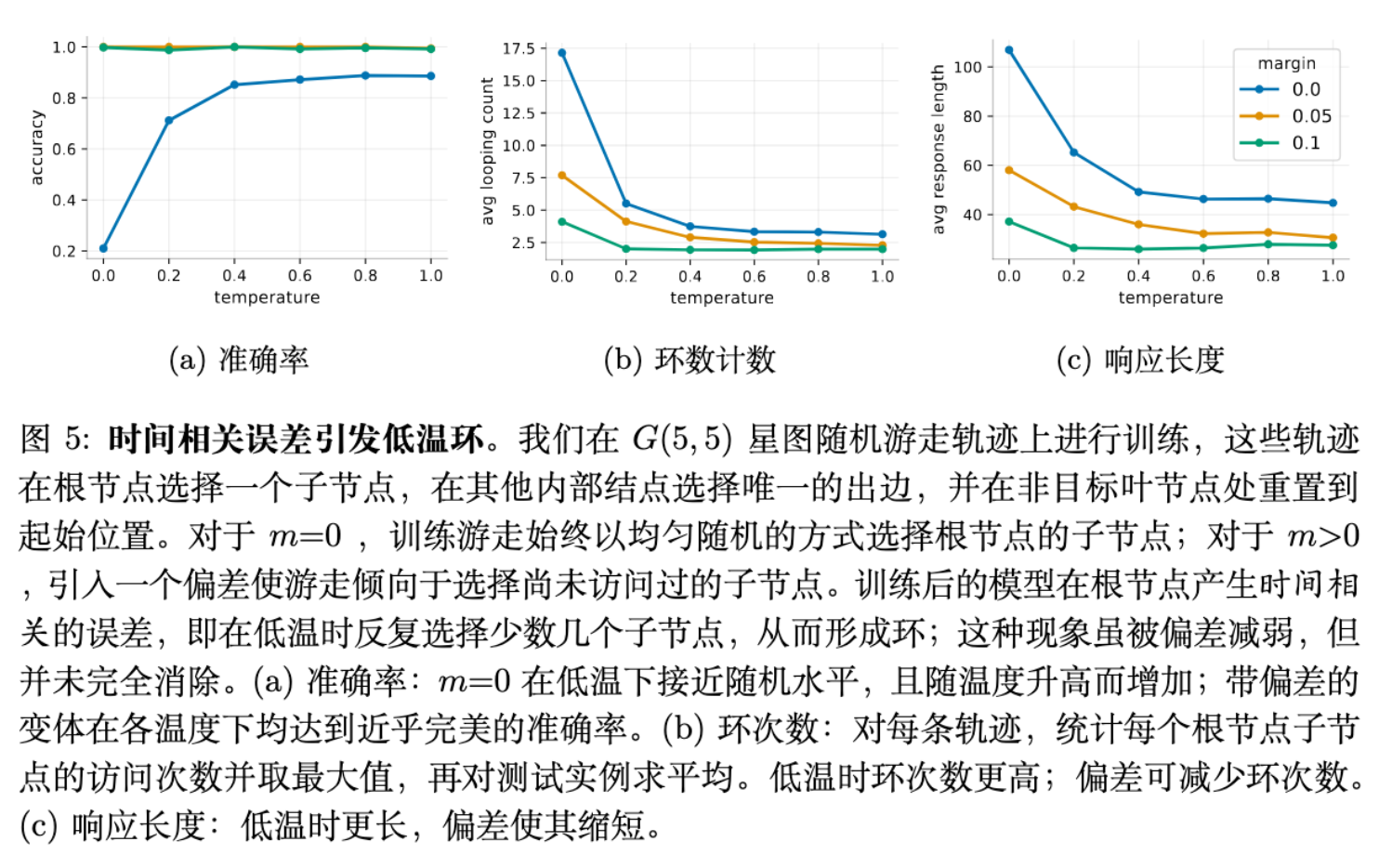
实验发现，即使在这种完全随机、无难度的设置下，训练好的 Transformer 在低温下依然会循环。

• 现象：模型并不是每次随机选择一条路，而是倾向于反复选择同一条（或某几条）特定的路。
• 原因分析：

  • 模型无法学到完美的 分布，总会存在微小的估计误差（Estimation Errors）。例如，它可能给分支 A 分配了 ，给分支 B 分配了 （理论值皆为 ）。
  • 关键在于，这些误差在时间上是相关的（Temporally Correlated）。当模型从叶节点回到根节点时，历史上下文发生了变化（变长了），但 Transformer 对于相似的输入状态（都在根节点）往往会产生相似的误差偏向。
  • 如果模型第一次偏向了分支 A，那么当它转了一圈回到根节点时，它大概率依然偏向分支 A。
  • 这种偏好的一致性导致了贪婪解码下的重复路径选择，进而形成循环。

4.3 Margin 机制的影响

作者尝试了一种干预手段：Margin（边际）。
在生成训练数据时，如果在一次游走中已经访问过某个分支，下次再访问根节点时，强制降低该分支的采样概率。

• 结果：在含有 Margin 的数据上训练的模型，循环现象显著减少。
• 启示：这解释了为什么 Inference-time 的惩罚措施（如 Repetition Penalty）有效，同时也暗示在训练阶段引入对重复行为的惩罚（Negative Constraints）可能是一种解决方案。

5. 自信度累积

在附录 E 中，作者进一步探讨了循环一旦开始，为何难以停止。

自信度累积（Confidence Buildup）：

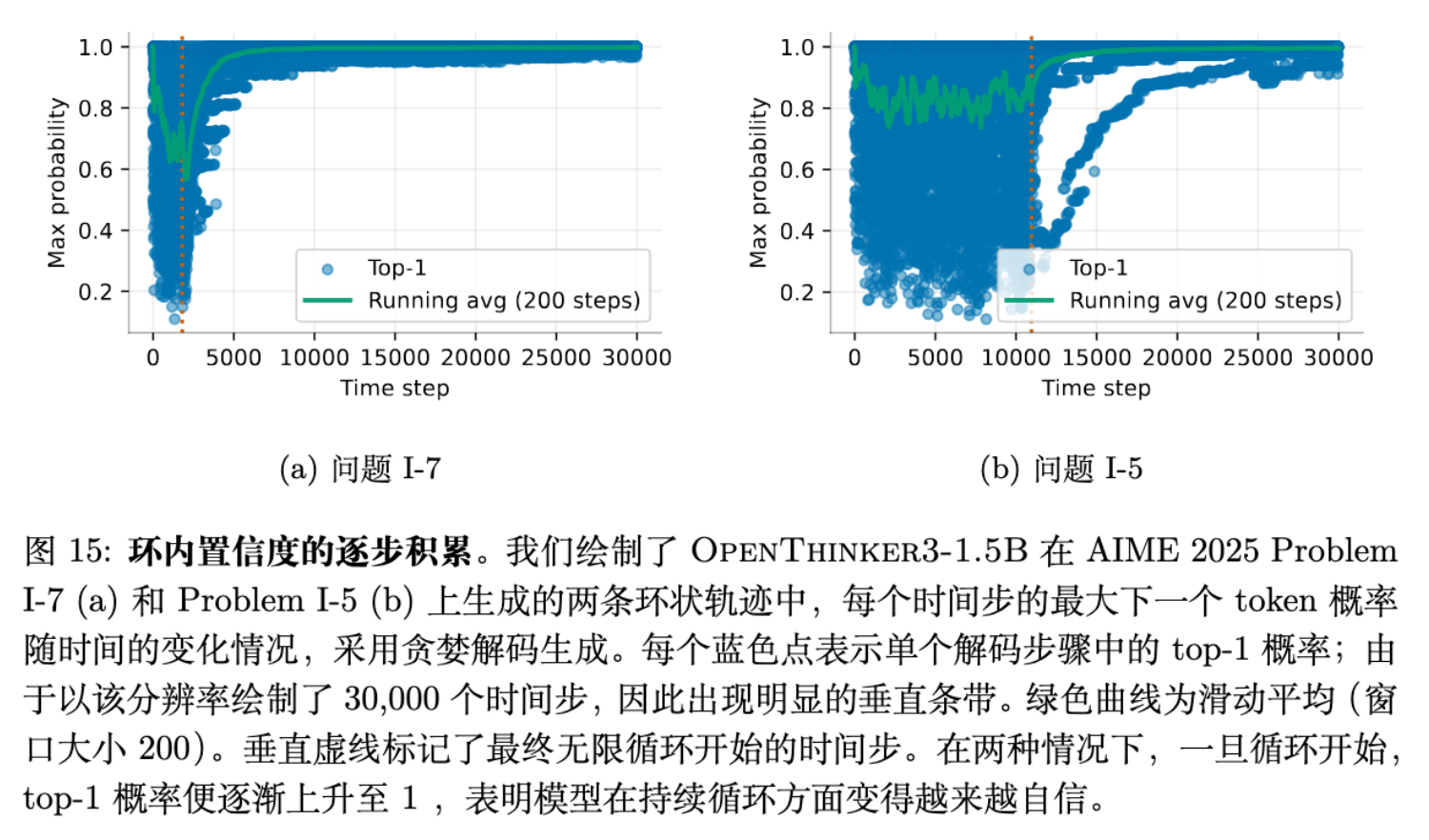
• 观察发现，在循环开始的初期，模型对下一个 token 的预测概率分布还相对正常。
• 然而，随着重复次数的增加，模型对重复内容的预测概率（Top-1 Probability）会迅速上升，最终接近 1.0。
• 原因：这可能源于预训练数据中的归纳偏置。在自然语言中，如果一段文本已经重复了多次（例如 "Again and again and again..."），它继续重复下去的概率在统计上确实会变大。
• 后果：这种机制充当了催化剂。无论是由“风险规避”还是“相关误差”触发了初始的循环，一旦进入循环轨道，自信度累积机制就像黑洞一样，通过自我强化让模型彻底“锁死”在循环中，即便提高温度也难以逃脱（因为概率质量高度集中）。

6. 温度的作用

回到最初的问题：为什么模型提供商建议调高温度？

根据上述分析：

1. 低温（Low Temp）：模型受制于学习误差（倾向于选容易的循环动作）或归纳偏置（重复偏好），导致死循环。
2. 高温（High Temp）：强制平滑概率分布，使模型有机会“跳出”概率最高的错误选项（循环动作），探索其他路径（正确动作）。

结论：温度主要起到了掩盖（Masking）底层问题的作用，而非修复。

• 证据：在合成实验和真实模型评测中，高温虽然消除了显式的循环，但生成的响应长度（Response Length）依然远超理想值。
• 解释：模型依然给循环动作分配了过高的概率。高温采样只是让模型在“循环”和“前进”之间随机游走，最终跌跌撞撞地找到终点。这导致推理链中充斥着无效的尝试和回溯，虽然没有死循环，但效率极低。

因此，温度是一个Stopgap（权宜之计）。真正的解决之道在于修正模型学到的概率分布。

7. 讨论与展望

既然温度不能治本，那我们应该关注哪些方向？

7.1 减少学习误差（Reducing Errors in Learning）

论文的核心观点是：循环源于学生模型未能学好困难的推进动作。

• 数据增强：针对教师模型轨迹中学生认为“困难”的节点（即 Loss 高的地方），进行定向的数据增强或添加提示（Hints），降低学习难度。
• 改进架构：采用更能处理长程依赖或能够更好区分相似上下文的架构（如近期的一些非 Transformer 架构或改进的 Attention 机制）。

7.2 打破相关误差（Breaking Correlated Errors）

• 训练时干预：借鉴 Margin 的实验结果，在训练数据构造或 Loss 设计中，明确惩罚重复路径。让模型学会“如果这条路走不通，下次回来时应该换条路”，而不是“因为上次走了这条路，所以这次还走”。
• 多样性训练：在 RL 阶段（如 PPO/GRPO），不仅仅奖励最终答案，还可以奖励路径的多样性，抑制这种时间相关的坍缩。

7.3 更好的蒸馏策略

简单的 Behavior Cloning（SFT）显然是不够的。学生模型需要理解教师模型在决策点的分布，而不仅仅是复制最高概率的路径。也许需要更复杂的蒸馏损失函数（如最小化分布间的距离，而非简单的 Next Token Prediction）。

更多细节请阅读原文。

往期文章：

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题