• 论文标题：The Surprising Effectiveness of Negative Reinforcement in LLM Reasoning
• 论文链接：https://arxiv.org/pdf/2506.01347v2

TL;DR

今天分享一篇 NeurIPS 2025 的论文《The Surprising Effectiveness of Negative Reinforcement in LLM Reasoning》。该研究针对具有可验证奖励的强化学习（RLVR）在提升大语言模型（LLM）推理能力时的机制进行了剖析。

核心结论如下：

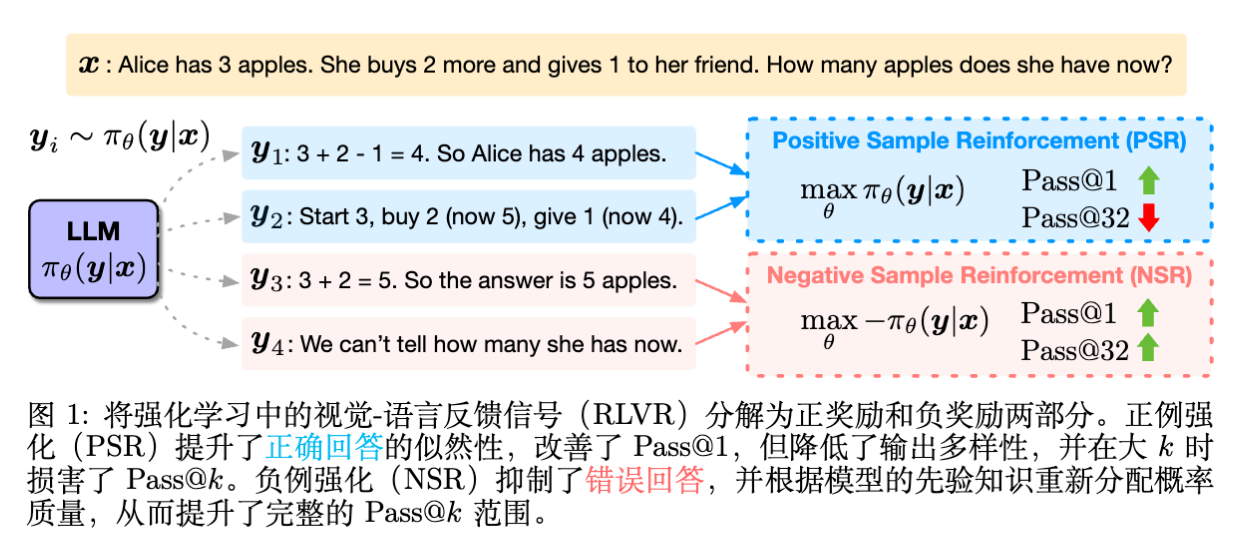
1. 分解视角：作者将 RLVR 的学习信号分解为正样本强化（PSR，即奖励正确答案）和负样本强化（NSR，即惩罚错误答案）。
2. NSR 的有效性：实验发现，仅使用负样本进行训练（NSR）就能在 Pass@ 指标上取得与 PPO 和 GRPO 相当甚至更好的效果，尤其是在 值较大时。这意味着模型在不被显式告知“什么是对的”的情况下，仅通过“什么是错的”就能显著提升推理能力。
3. PSR 的局限性：仅使用正样本训练（PSR）虽然能快速提升 Pass@1（贪婪解码准确率），但会导致模型输出分布坍缩，多样性下降，从而损害 inference-time scaling（推理时扩展）的能力。
4. 梯度机制：通过 Token 级别的梯度分析揭示，PSR 倾向于强化已生成的正确路径并抑制所有其他路径（包括潜在的正确路径），导致过拟合；而 NSR 通过抑制错误路径，利用模型自身的先验知识将概率质量重新分配给其他合理的候选者，从而保留了探索能力。
5. Weighted-REINFORCE：基于上述发现，论文提出了一种加权 REINFORCE 算法，降低正样本的权重，在 MATH、AIME 2025 和 AMC23 等基准测试中取得了一致的性能提升。

1. 引言

近期，大语言模型在数学、代码和科学推理等复杂任务上展示了显著的能力。这一进步背后的关键技术之一是基于可验证奖励的强化学习（Reinforcement Learning with Verifiable Rewards, RLVR）。与传统的基于人类反馈的强化学习（RLHF）不同，RLVR 应用于结果客观可验证的领域（如数学题答案、代码通过测试用例）。DeepSeek-R1、Kimi k1.5 等近期工作的成功，进一步证实了 RLVR 诱发长思维链（Long CoT）和自我修正行为的潜力。

RLVR 通常采用二元奖励机制：由于结果只有对错之分，模型获得的奖励通常是 或 。这种机制简单且有效，避免了复杂的奖励模型训练，也减少了对人类标注的依赖。尽管 RLVR 在提升样本效率和推理时扩展（Inference-time Scaling）方面表现出色，但社区对于其内在运作机制的理解尚不充分。

核心问题在于：在只有二元信号的情况下，模型究竟是如何通过正向和负向反馈来更新其行为的？

为了回答这个问题，作者在本文中提出了一种解构分析方法。他们将 RLVR 的目标函数拆解为两个独立的学习范式：

• 正样本强化（Positive Sample Reinforcement, PSR）：仅从获得正奖励的样本中学习。
• 负样本强化（Negative Sample Reinforcement, NSR）：仅从获得负奖励的样本中学习。

这项研究通过对比实验和梯度分析，揭示了一个反直觉的现象：仅依赖负向信号（NSR）在提升模型推理的综合能力（特别是多样性生成能力）上，可能比正向信号更为稳健。

2. RLVR 目标函数及其分解

在深入探讨机制之前，我们需要先建立数学框架。

2.1 RLVR 的标准定义

给定参数为 的语言模型，提示词集合 ，以及可验证的奖励函数 。RLVR 的目标是学习一个策略 ，使得期望奖励最大化。在实际操作中，通常最小化以下损失函数：

其中，对于数学推理任务，奖励 。 表示答案正确， 表示答案错误。在 PPO 或 GRPO 等算法中，通常会对奖励进行归一化处理（例如减去基线），但在本文的分析中，为了隔离正负信号的物理意义，作者直接使用了原始的二元奖励。

2.2 正负样本强化的分解

为了理解模型在面对“成功”和“失败”时的不同学习动力学，作者将上述目标函数根据奖励的正负性进行了分解：

基于此，定义两个子目标：

1. PSR 目标（Positive Sample Reinforcement）：

   这本质上类似于监督微调（SFT），即最大化正确路径的似然概率。

2. NSR 目标（Negative Sample Reinforcement）：

   注意，最小化 等价于最小化错误路径的似然概率。

这两种范式都是 On-policy 的，即样本 是从当前模型 中采样生成的。这种分解使得我们可以单独训练 PSR 或 NSR，观察它们对模型行为的独立影响。

3. 实验设置与评估体系

为了验证不同强化方式的效果，作者进行了大规模的实验。

3.1 模型与数据

• 模型：选择了三个不同规模和架构的模型：

  • Qwen2.5-Math-7B
  • Qwen3-4B (使用了其 non-thinking 模式进行训练)
  • Llama-3.1-8B-Instruct
• 训练集：MATH 数据集，包含 7,500 个问题。
• 框架：使用 verl 框架进行训练。Prompt batch size 设为 1024，每个 prompt 采样 8 个 rollout。
• 基线算法：对比了 PPO 和 GRPO。注意，PSR 和 NSR 的实现方式是选择性地仅使用正确或错误的样本更新模型，因此其每个 batch 的有效样本数少于 PPO/GRPO。

3.2 评估指标：Pass@ 的重要性

传统的评估往往关注贪婪解码的准确率（即 Pass@1）。然而，最近的研究（如 DeepSeek-R1 和 OpenAI o1 的相关分析）表明，推理模型的上限往往取决于其在多次尝试中找到正确答案的能力，即 Inference-time Scaling。

因此，本文采用了全谱系的 Pass@ 作为核心评估指标。

• Pass@1：反映了模型的 Exploitation（利用） 能力，即模型有多大信心直接输出正确答案。
• Pass@ (Large ) ：反映了模型的 Exploration（探索） 能力和推理边界。如果模型能生成多样化的正确路径，Pass@ 会随着 的增加而显著上升。

Pass@ 的无偏估计公式为：

其中 是总采样次数， 是正确样本数。实验中， 取 256（Qwen2.5/Llama）或 64（Qwen3）。

4. 实验结果

实验结果展示了不同训练目标对模型推理能力产生的显著差异。

4.1 NSR 展现出惊人的 Pass@ 扩展性

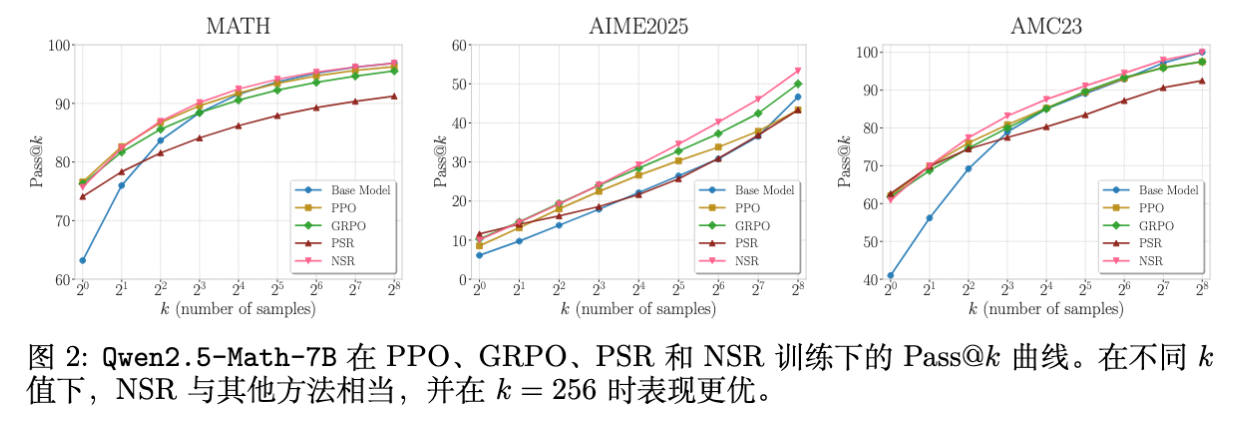
如上图所示，这是本文最核心的实验发现：

1. PSR 的短视：PSR（红线）在 Pass@1 上表现尚可，但在 之后，其性能增长明显放缓，甚至低于 Base Model（蓝线）。这表明仅奖励正样本损害了模型的多样性。
2. NSR 的强劲：NSR（粉线）虽然从未见过被强化的“正确答案”，但其性能曲线在整个 值谱系上都表现出色。在 时，NSR 甚至超过了 PPO 和 GRPO。
3. Pass@1 的对比：令人惊讶的是，NSR 的 Pass@1 并没有因为缺乏正向引导而崩塌，而是达到了与 Base Model 相当甚至略高的水平。

4.2 Qwen3-4B 与潜在能力的激发

对于 Qwen3-4B，作者在一个特殊设置下进行了测试：使用 non-thinking 模式（不触发 <think> 标签）进行训练和推理。这是一个模型潜在能力很强但未被激活的场景。

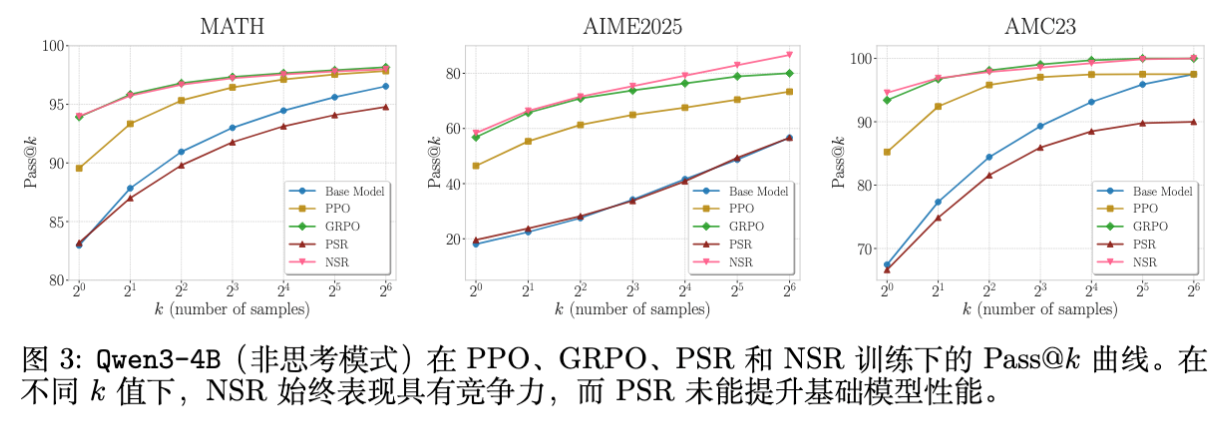
结果显示：

• PSR 无法激活潜能：PSR 在此场景下表现糟糕，未能有效利用模型潜在的推理能力。
• NSR 与 GRPO 有效：NSR 表现出了与 GRPO 相似的强劲性能，成功激活了模型的推理能力。这暗示 NSR 有助于模型跳出当前的局部最优，探索更复杂的推理路径。

4.3 Llama-3.1 的退化现象

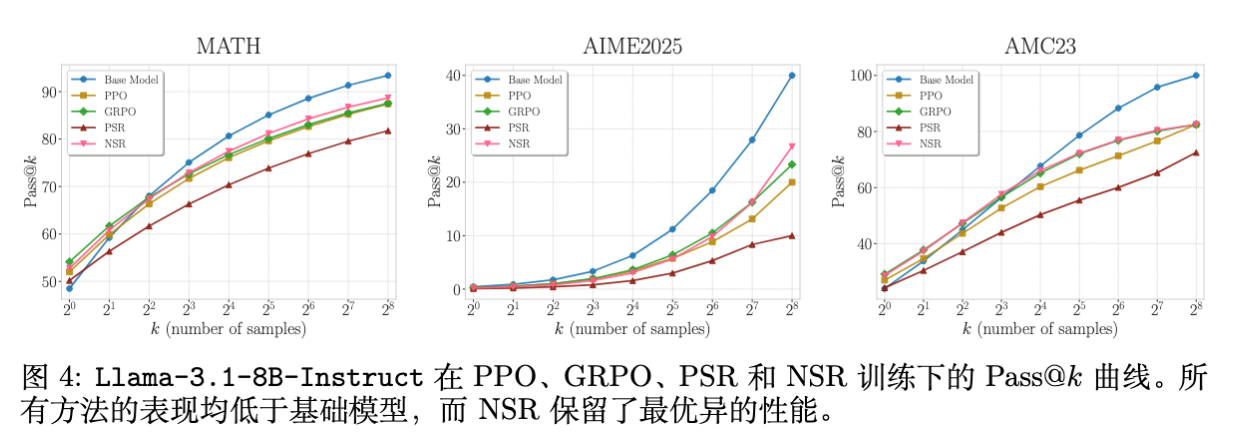
在 Llama-3.1 上，所有 RL 方法相对于 Base Model 都有所退化（特别是在高 处）。这与近期一些关于 RL 在某些 Base Model 上可能导致 Inference scaling 性能下降的研究一致（如 RLOO 等论文的观察）。但在所有 RL 方法中，NSR 导致的退化是最小的，再次证明了其在保持分布多样性方面的优势。

4.4 训练动态分析：熵与过拟合

为了解释上述现象，作者监控了训练过程中的几个关键指标。

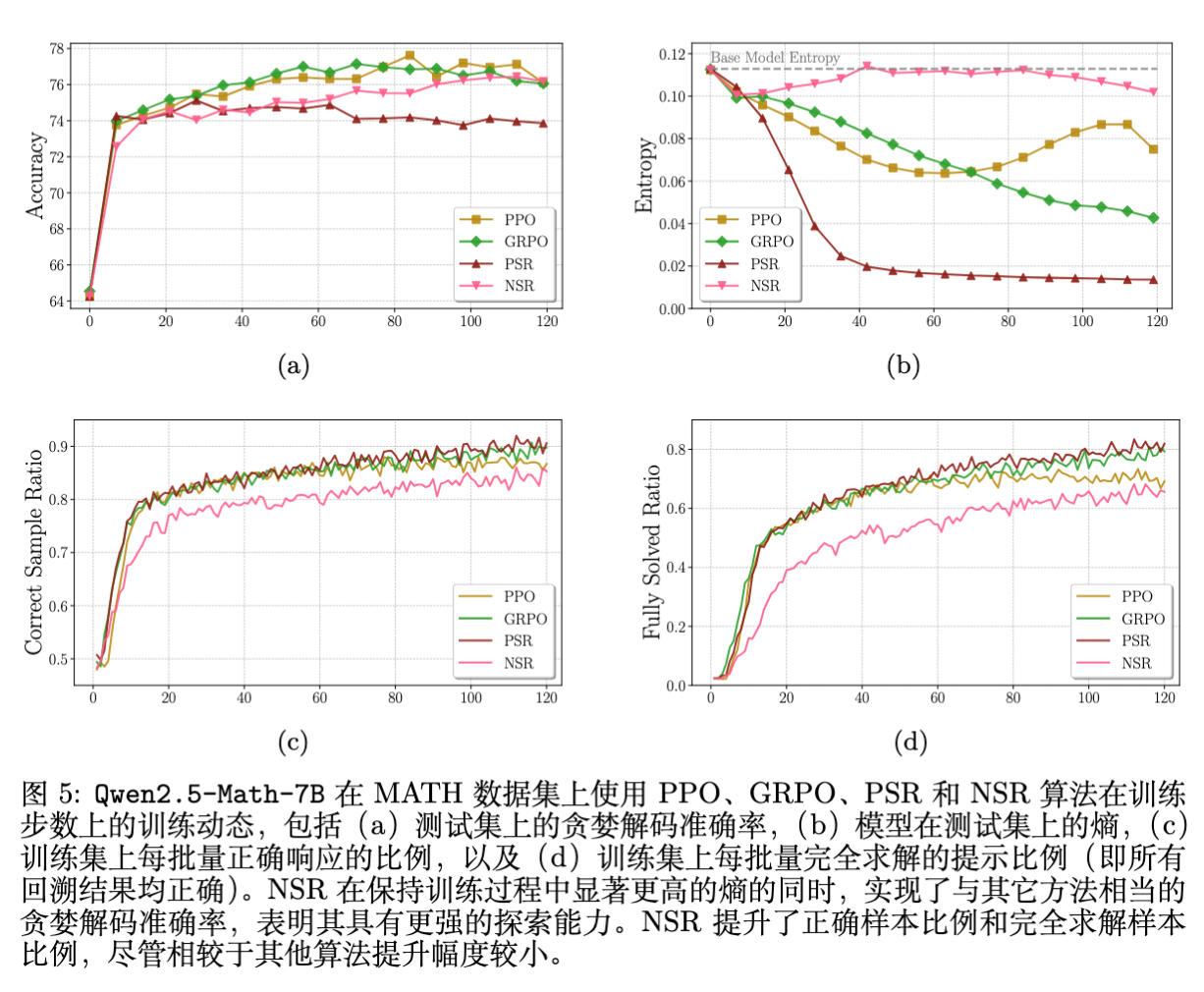
1. 熵（Entropy）的变化：

   • PSR（红线）：在训练初期，测试集上的熵迅速下降。这意味着模型对其输出变得非常自信，分布急剧尖峰化。
   • NSR（粉线）：熵在整个训练过程中保持在较高水平，几乎与 Base Model 持平。这说明 NSR 保留了模型的探索能力。
   • PPO/GRPO：介于两者之间。

2. 正确样本比例（Correct Sample Ratio）：

   • PSR 的正确样本比例上升最快，这解释了其 Pass@1 的提升，但也预示了过拟合。
   • NSR 的正确样本比例上升较慢，且始终低于 PSR，说明它没有过度拟合特定的正确路径。

结论是：PSR 通过牺牲多样性换取了准确率（Exploitation），而 NSR 在提升准确率的同时保留了多样性（Exploration）。

5. 为什么 NSR 有效？

这一部分是论文的精华，通过 Token 级别的梯度分析，揭示了 NSR 和 PSR 本质的运作机制。

5.1 梯度推导基础

考虑单步 Token 的生成。对于一个训练实例 ，损失函数对 Logits 的梯度决定了参数更新的方向。
令 为当前时间步 模型预测 token 的概率。 为实际采样的 token。

损失函数的梯度通用形式推导如下（详见论文附录 A）：

其中 。

5.2 PSR 的梯度动力学 ()

当 时，梯度变为：

• 采样 Token ()：。梯度为负，增加 的 Logit。
• 未采样 Token ()：。梯度为正，减小 其他所有 token 的 Logit。

解读：
PSR 的机制非常直接且霸道。它不仅提升被采样到的正确 token 的概率，还会无差别地抑制所有其他 token。

• 后果：即使词表中还有其他合理的 token（例如同义词，或者另一条正确推理路径的起始词），只要它们没被采样到，就会受到抑制。随着训练进行，分布会迅速向采样到的路径坍缩，导致“赢家通吃”。这就是为什么 PSR 会导致熵急剧下降，损害 Pass@。

5.3 NSR 的梯度动力学 ()

当 时，梯度变为：

• 采样 Token ()：。梯度为正，减小 错误 token 的 Logit。
• 未采样 Token ()：。梯度为负，增加 其他所有 token 的 Logit。

解读：
这是 NSR 展现魔力的地方。

1. 惩罚错误：它明确地降低了导致错误的 token 的概率。
2. 基于先验的重分配（Prior-guided Redistribution）：注意未采样 token 的更新量 与 成正比。这意味着，模型在抑制错误 token 后，释放出来的概率质量并不是均匀分配给其他 token，而是按照模型当前的信念分布（Prior Beliefs） 进行分配。

   • 原本概率高的合理 token（High-confidence tokens）会获得更多的概率提升。
   • 原本概率低的无关 token 获得的提升微乎其微。

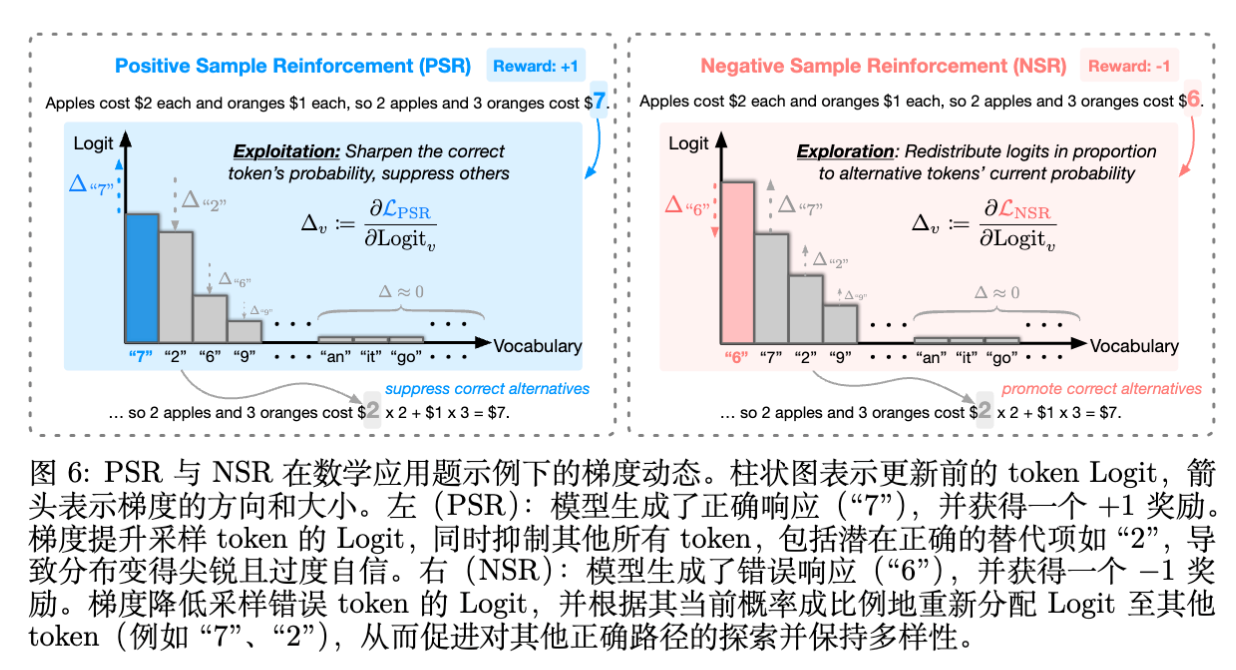
NSR 的三大特性：

1. 保护高置信度先验：对于错误路径中出现的语法性高频词（如 "the", "is"），即使 ，由于其 ，梯度中的 项会使得惩罚力度很小。这防止了模型遗忘基本的语言能力。
2. 软性重排序（Soft Reranking）：NSR 执行的是一种软性的概率重排序，它仅仅剔除了被验证为错误的选项，而保留了其他候选者的相对顺序。
3. 隐式正则化：一旦模型不再生成该错误答案（），NSR 的梯度更新就会停止。这提供了一种自然的停止机制，防止过拟合。

5.4 与其他方法的对比

• 与熵正则化（Entropy Regularization）对比：
  单纯增加熵正则项（）虽然能提升多样性，但其梯度倾向于压制高概率 token 并提升低概率 token，这违背了模型的先验知识（即强行让模型说胡话）。而 NSR 是在保留先验结构的前提下提升相对多样性。

• 与 Unlikelihood Training 对比：
  Unlikelihood Training 最小化 。其梯度在 很大时非常剧烈，容易破坏模型已有的知识。而 NSR 的梯度包含 因子，具有阻尼效应，更加温和。

6. Weighted-REINFORCE

基于上述分析，我们面临一个权衡：

• PSR：提升 Pass@1，但损害多样性。
• NSR：保持多样性，提升 Pass@，但对 Pass@1 的直接引导较弱。

作者提出了一个简单而有效的变体：Weighted-REINFORCE (W-REINFORCE) 。其核心思想是降低正样本的权重，或者说相对提升负样本的权重。

目标函数如下：

其中 是调节系数。

• 当 时，退化为标准的 REINFORCE。
• 当 时，退化为 NSR。

6.1 实验效果

作者发现，将 设为较小的值（如 0.1）效果最佳。

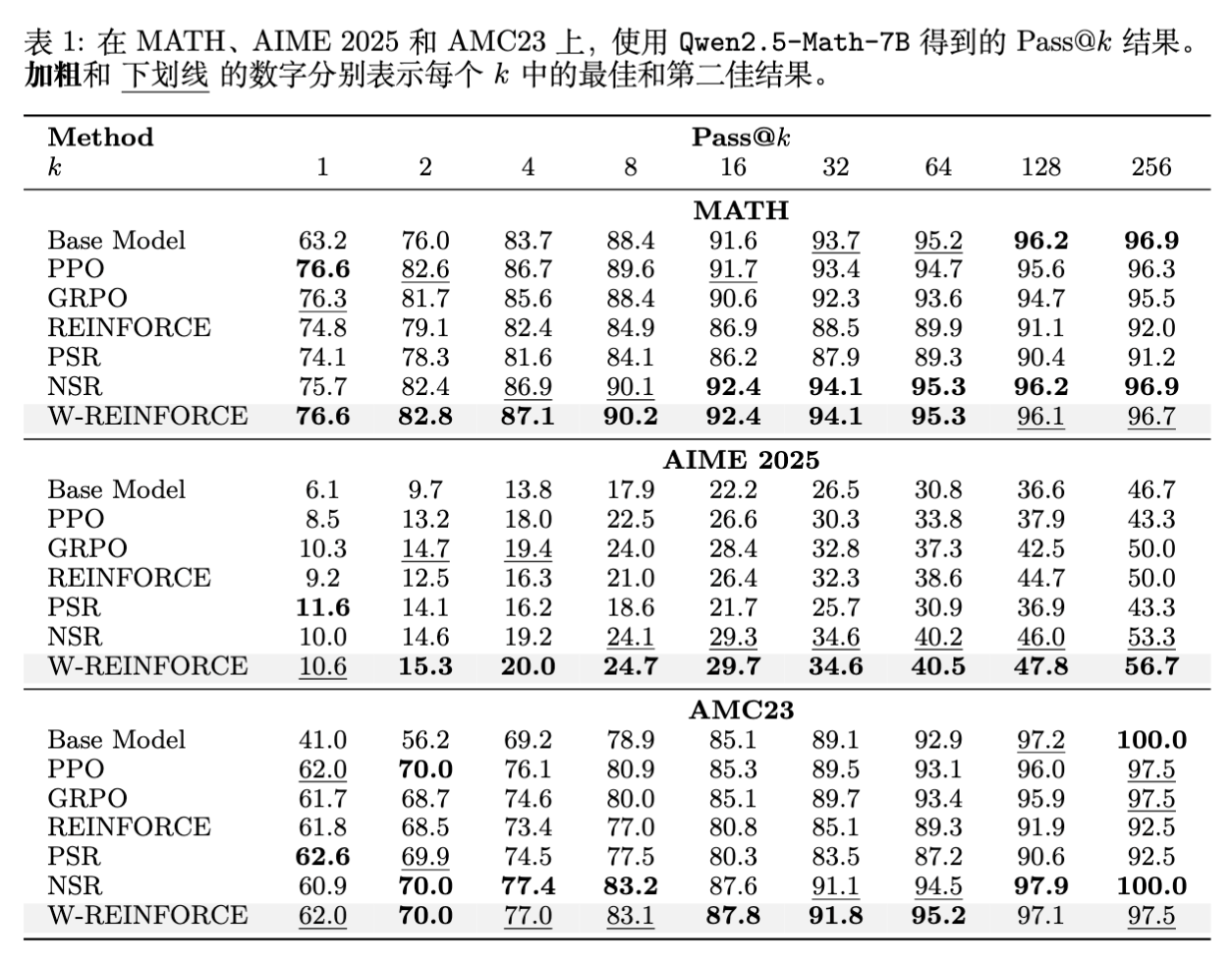
实验数据表明，W-REINFORCE () 结合了 PSR 和 NSR 的优点：

• Pass@1：在 MATH 上达到了 76.6，匹配了 PPO 的最佳性能，超过了单纯的 NSR。
• Pass@256：达到了 96.7，接近 NSR 的 96.9，远超 PPO (96.3) 和 GRPO (95.5)。
• 在 AIME 2025 和 AMC23 上，W-REINFORCE 展现了更强的一致性优势，特别是在 AIME 上，Pass@256 达到了 56.7，显著优于其他所有方法。

6.2 的消融实验

实验显示 的选择具有一定的鲁棒性，只要 ，模型就能保持良好的多样性。一旦 接近 1，Pass@256 性能就会显著下降，验证了正样本信号过强是导致多样性丧失的根本原因。

7. 讨论与相关工作

7.1 与推理时扩展（Inference-time Scaling）的关系

这篇论文的发现与近期关于 Test-time Compute 的研究紧密相关。文献指出，SFT 或强 RL 往往会损害模型的 Pass@ 扩展能力。本文从梯度的角度给出了具体的解释：正向强化导致的分布尖峰化（Sharpening）限制了模型生成多样化候选答案的能力，而多样性正是 Majority Voting 或 Verifier 机制生效的基础。

7.2 与 PPO/GRPO 的对比

PPO 和 GRPO 引入了 Critic 模型和 KL 散度约束等机制来稳定训练。然而，本文的分析表明，即便有 KL 约束，正向奖励信号本身带来的“抑制未采样路径”的梯度特性，依然会导致熵的降低。相比之下，调整正负样本的权重（W-REINFORCE）可能是一种更本质、更简洁的解决方法。

7.3 局限性

虽然 NSR 和 W-REINFORCE 表现出色，但也存在局限性：

1. 长期训练的不稳定性：如同其他 RL 算法，长时间训练后性能可能会震荡或下降。
2. 稀疏奖励问题：本文主要处理二元稀疏奖励。对于更密集的奖励（如过程奖励 Process Reward），正负信号的定义可能变得模糊，NSR 的应用方式需要进一步探索。

更多细节请阅读原文：arXiv:2506.01347v2 [cs.CL] 25 Oct 2025 版本。代码已开源于：https://github.com/TianHongZXY/RLVR-Decomposed

往期文章：

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题