祝大家新年快乐～

• 论文标题：Coupling Experts and Routers in Mixture-of-Experts via an Auxiliary Loss
• 论文链接：https://arxiv.org/pdf/2512.23447

TL;DR

Mixture-of-Experts (MoE) 模型在扩展大语言模型参数规模的同时保持了推理效率。然而，现有的 MoE 架构存在一个根本性的设计缺陷：路由器（Router）的决策与专家（Expert）的真实能力之间缺乏显式的关联。路由器往往仅凭输入的梯度进行试错学习，而无法直接感知专家的参数特征或激活状态。

为了解决这一问题，字节 Seed 与人大提出了一种名为 专家-路由耦合损失（Expert-Router Coupling Loss, ERC Loss） 的轻量级辅助损失函数。

该方法的核心思想是将路由器的权重向量视为专家的“聚类中心”，通过向这些中心添加有界随机噪声生成“代理 token（proxy token）”，并将这些代理 token 输入给所有专家。ERC Loss 通过强制要求每个专家对其对应的代理 token 产生最强的激活，从而在数学上建立了路由器参数与专家能力之间的强耦合。

主要贡献与结论：

1. 方法创新：提出 ERC Loss，利用代理 token 探测专家能力，无需在该环节引入真实数据。
2. 计算高效：计算复杂度仅为 （ 为专家数量），与 batch size 无关。相比于 Autonomy-of-Experts (AoE) 等方法，ERC Loss 的训练开销几乎可以忽略不计（额外开销 < 1%），且推理阶段零开销。
3. 性能提升：在 3B 和 15B 参数规模的模型上，ERC Loss 显著提升了下游任务性能，并缩小了 MoE 与高计算成本变体（如 AoE）之间的差距。
4. 可解释性工具：ERC Loss 提供了一种定量追踪专家专业化程度（Specialization）的方法，揭示了专家专业化与模型性能之间的权衡关系。

1. 背景

1.1 标准 MoE 的路由机制

在主流的 MoE 架构（如 Switch Transformer, Mixtral, Qwen-MoE, DeepSeek-MoE）中，通常采用 SwiGLU 结构的专家层。对于输入 token ，MoE 层包含 个专家，每个专家 由三个矩阵参数化： 和 。

路由决策由一个线性分类器（路由器）决定，其权重矩阵为 。路由器计算出的专家权重向量 为：

通常选择权重最高的 Top-K 个专家处理 token。专家 的处理逻辑为：

1.2 存在的问题：解耦的决策与能力

在理想情况下，路由器应该准确掌握每个专家的“能力边界”，将 token 分配给最擅长处理它的专家。然而，传统的 MoE 架构中不存在这种显式的约束。

• 盲目路由：路由器无法直接访问专家的参数（即专家的真实能力）。它只能通过最终的 loss 反传梯度来调整 。
• 相互干扰：这种试错学习（trial-and-error）导致许多 token 被错误路由。错误路由产生的梯度会更新专家参数，这反而干扰了专家向特定方向的专业化（Specialization）。

1.3 现有解决方案的局限性

• Autonomy-of-Experts (AoE) ：AoE 方法将路由决策权下放给专家自身，通过计算 token 在专家内部的中间激活范数来决定是否选择该专家。虽然有效，但其计算成本随着 token 数量 线性增长，且需要在所有专家上进行部分前向计算，训练和推理开销巨大。
• 辅助损失（Load Balancing Loss）：传统的负载均衡损失仅关注 token 分配的均匀性，而不关注分配的准确性或专家能力的匹配度。
• 专家正交化：部分工作尝试强制专家输出正交，但这并不等同于专家能力的专业化，且可能限制模型的表达能力。

ERC Loss 的动机在于寻找一种既能保留标准 MoE 路由的高效性，又能建立路由器与专家之间深层联系的轻量级方法。

2. 专家-路由耦合损失 (ERC Loss)

ERC Loss 的设计基于一个核心视角：将路由器的权重向量 视为分配给专家 的 token 集合 的聚类中心（Cluster Center）。

基于此视角，ERC Loss 通过三个步骤构建：生成代理 token、计算专家激活、施加双重约束。

2.1 步骤一：生成有界噪声的代理 token

为了评估专家 的能力，我们不需要将真实的 dataset token 输入给所有专家（这太慢了）。相反，我们利用路由向量 作为“代理”。但 只是一个点，为了让它代表整个聚类簇 ，我们需要引入随机性。

对于每个专家 ，我们构建一个扰动的代理 token ：

其中 是有界的乘性随机噪声。

噪声的边界设计（关键推导）：
噪声必须足够大以模拟簇内变化，但又不能过大导致 越过决策边界进入另一个专家 的聚类区域。
根据附录 A 的推导，为了保证 仍然属于专家 的聚类（即距离 比距离任何其他 更近），噪声水平 必须满足：

其中 是距离 最近的聚类中心。这确保了代理 token 的有效性。在实际操作中，噪声 服从均匀分布 。

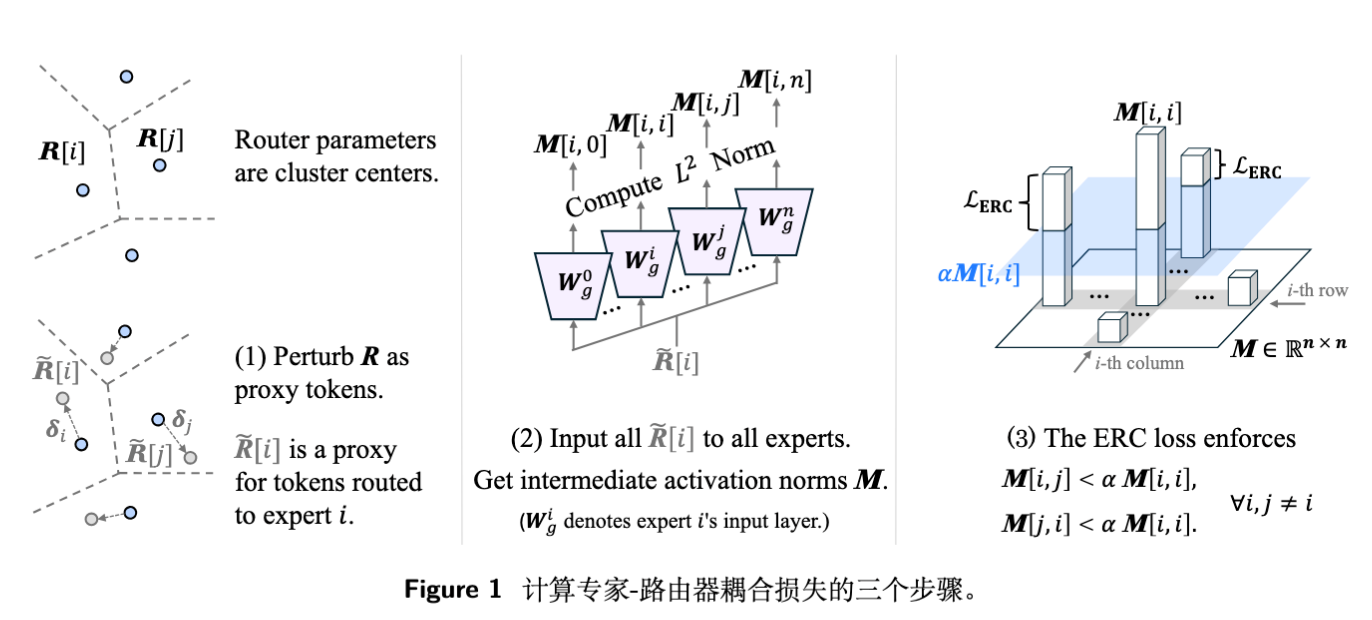
2.2 步骤二：计算中间激活矩阵 M

利用生成的 个代理 token，将其输入到所有 个专家的输入投影层 中。我们利用激活范数（L2 Norm）作为衡量专家对输入响应强度的指标。

构建矩阵 ，其中 表示第 个专家对第 个代理 token 的响应强度：

这里选择 而非完整的专家输出，是因为先前的研究（如 AoE）表明 MLP 的中间激活范数能很好地反映其能力匹配度。

2.3 步骤三：施加双重耦合约束

为了实现专家与路由的耦合，ERC Loss 对矩阵 施加两个约束。对于所有 和 ：

1. 专家专业化约束（Expert Specialization）：

   含义：代理 token 应当最强烈地激活其对应的专家 。如果其他专家 对该 token 的激活更强，说明专家 并没有针对其负责的 token 簇进行最优的专业化学习。

2. 精确路由约束（Precise Token Routing）：

   含义：专家 应当对它自己的代理 token 产生比对其他代理 token 更强的响应。这确保了路由器 能够准确代表专家 的偏好。

其中 是一个超参数，用于控制耦合的强度。 越小，要求越严格。

最终的 ERC Loss 定义为：

2.4 效率分析：为什么 ERC 极度高效？

这是该方法最大的亮点。

• 标准 MoE 开销：，其中 是 token 数（通常为数百万）。
• AoE 开销：，与 token 数 线性相关。
• ERC Loss 开销：。

注意，ERC Loss 的计算仅涉及 个代理 token（ 通常为 64, 128, 256），完全独立于 batch size 中的 token 数量 。
在 15B 参数模型训练中，ERC Loss 引入的额外 FLOPs 仅占总计算量的 0.2% - 0.8% 。相比之下，AoE 的额外开销可能高达 20-30% 甚至更多（取决于 和 的比例）。

3. 实验设置

为了验证 ERC Loss 的有效性，研究团队进行了从 3B 到 15B 参数规模的从头预训练（Pre-training from scratch）。

• 基础架构：OLMoE (基于 Llama 架构)，SwiGLU 激活。
• 模型配置：

  • 3B 模型：12 层，Model Dim 1536，64 个专家（Top-8），激活参数 500M。
  • 15B 模型：24 层，Model Dim 2048，256 个专家（Top-8），激活参数 700M。
• 训练数据：Dolma 数据集的一个子集，约 500B tokens。
• 对比基线：

  • Vanilla MoE：仅使用标准负载均衡损失。
  • AoE (Autonomy-of-Experts) ：一种高成本的强基线。
• 评估基准：MMLU, GSM8K, MATH, BoolQ, HellaSwag 等。

4. 实验结果分析

4.1 下游任务性能

实验结果表明，ERC Loss 在几乎所有测试基准上都优于 Vanilla MoE，并且逼近甚至超越了计算昂贵的 AoE。

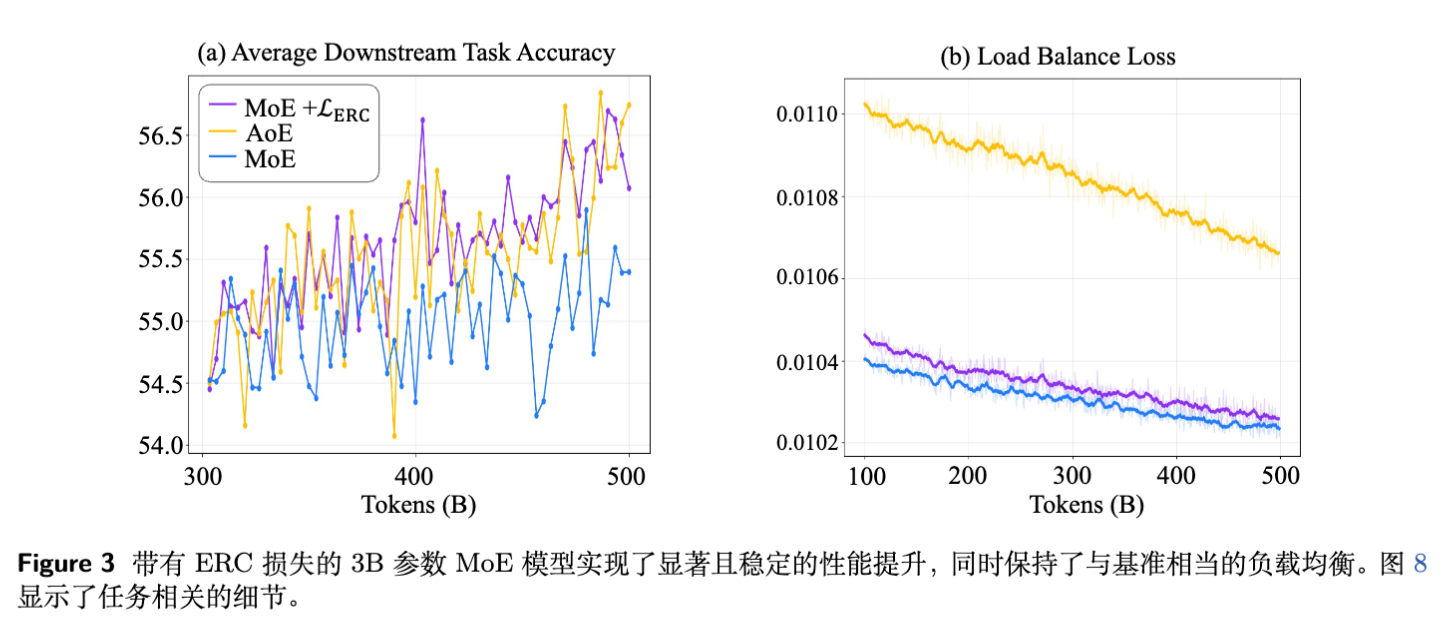
• 3B 模型结果：ERC Loss 显著提升了平均准确率，尤其是在数理逻辑任务（GSM8K, MATH）上提升明显。
• 15B 模型结果：随着模型规模扩大（专家数量从 64 增加到 256），ERC Loss 的优势依然稳固。

  • MMLU：从 63.2 (MoE) 提升至 64.6 (ERC)。
  • GSM8K：从 45.2 (MoE) 提升至 45.8 (ERC)。
  • MATH：从 25.7 (MoE) 提升至 26.1 (ERC)。

值得注意的是，15B 规模下，由于计算成本过高，AoE 甚至无法在有限资源下完成训练，而 ERC Loss 模型仅需增加 <1% 的时间即可完成训练。

4.2 负载均衡与训练稳定性

虽然 ERC Loss 的目标不是负载均衡，但实验发现它与负载均衡辅助损失（Load Balancing Loss）兼容性良好。

• 添加 ERC Loss 后，负载均衡损失并没有显著恶化，仅有 量级的微小差异。
• 在大规模训练中，未观察到 Loss 尖峰或梯度异常，表明该方法具有良好的数值稳定性。

4.3 专家专业化的可视化 (t-SNE)

为了直观展示 ERC Loss 如何影响专家参数，研究者对专家权重 进行了 t-SNE 投影。

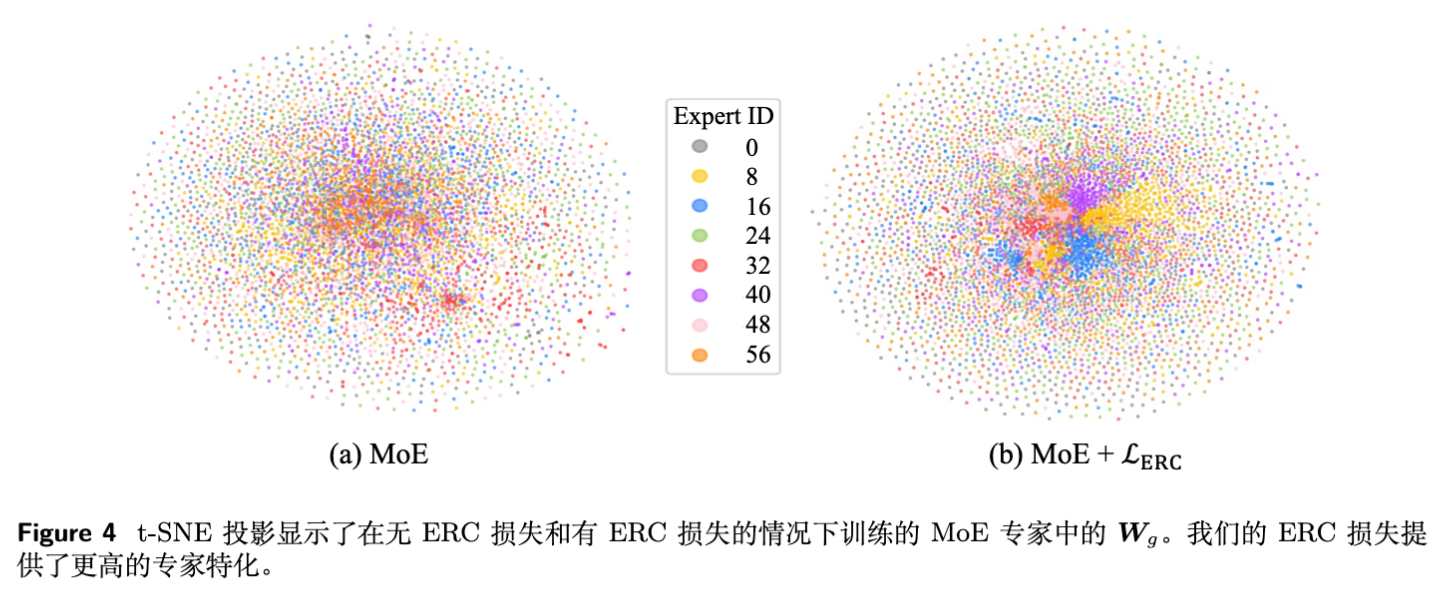
• Vanilla MoE：专家的参数特征混杂在一起，缺乏明显的聚类结构。这证实了标准 MoE 中专家专业化程度较低。
• MoE + ERC Loss：呈现出清晰的簇状结构。不同的颜色（代表不同专家）在空间中被推开，形成了各自的“领地”。这表明专家确实在参数空间上实现了专业化。

5. 专家专业化与 的权衡

ERC Loss 提供了一个独特的视角来研究 MoE 的行为。

5.1 作为专业化程度的度量

前文提到的噪声边界 取决于路由向量 之间的距离。

• 当专家趋于同质化时， 之间的距离变小，导致 变小。
• 当专家高度专业化时， 分布更稀疏， 变大。
  因此， 可以作为训练过程中专家专业化程度的动态监控指标。

5.2 对性能的影响

参数 显式控制了耦合的紧密程度。

• ：强制极端的专业化（正交）。
• ：允许一定程度的重叠。

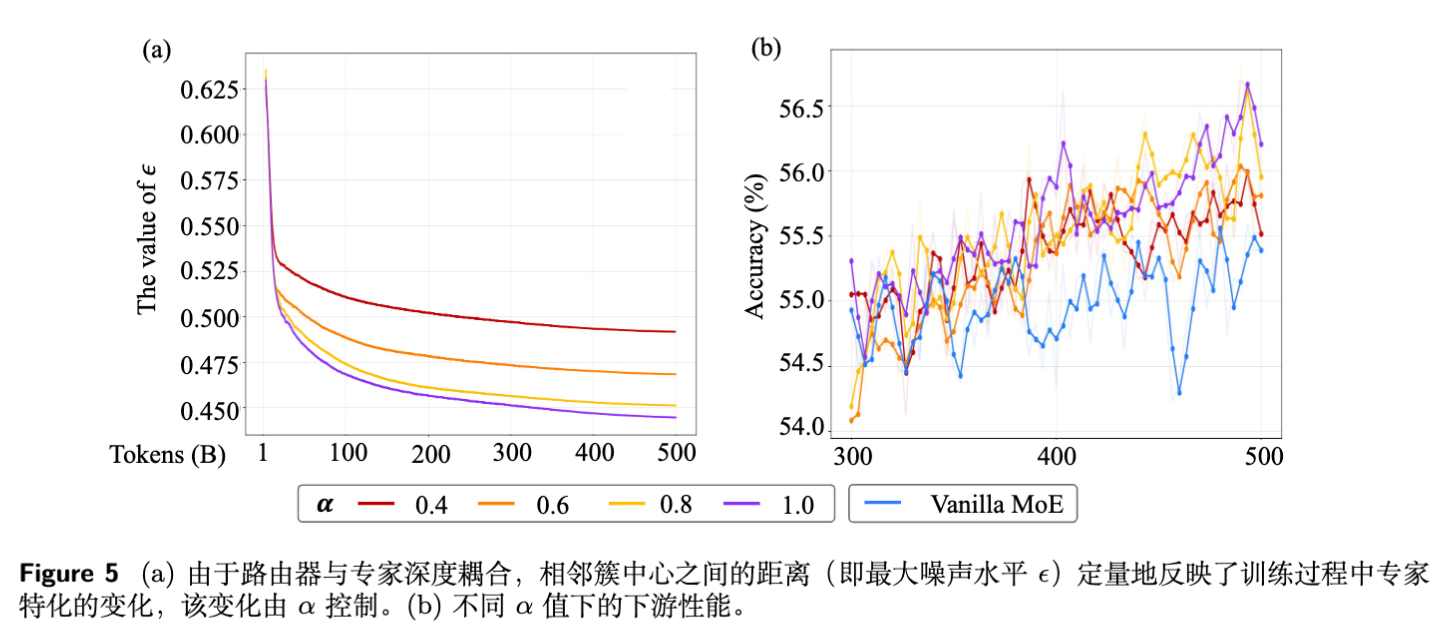
实验发现：

1. 并非越专业越好：极端的专业化（ 过小）反而会导致性能下降。这揭示了 MoE 中“专家专业化”与“专家协作”之间的权衡。过度的专业化可能破坏了专家间的知识共享或互补性。
2. 最佳实践：在 3B 模型（）中， 效果最好；在 15B 模型（）中， 更优。这暗示随着专家数量增加，模型可以容忍（或需要）更高程度的专业化。

6. 消融实验与讨论

为了证明 ERC Loss 设计的合理性，论文进行了详尽的消融研究（主要在附录 C 中）。

6.1 激活度量 的选择

计算 时，可以使用不同的激活值：

• (默认)
• SwiGLU 后的输出
• 专家最终输出

结果显示，使用第一层投影 的效果最好且计算最高效。这与 AoE 的发现一致，即 包含了主要的特征筛选能力。

6.2 随机噪声 的必要性

如果去掉噪声，直接使用 计算 Loss，效果会大打折扣。
原因：没有噪声，模型会过拟合于 这一个点，而无法泛化到 代表的整个 token 簇 。噪声 强制模型在 的邻域内保持一致的响应，从而实现了真正的耦合。

6.3 为什么不直接对路由器进行正交化？

有观点认为，只需让路由器输出正交即可实现专业化。论文对比了 Router Orthogonality Loss。
结果表明，单纯的正交化带来的提升有限。分析发现，Vanilla MoE 的路由器向量在训练后本身就已经接近正交（平均余弦相似度仅 0.15）。因此，问题的瓶颈不在于路由器是否正交，而在于路由器与专家能力是否对齐。ERC Loss 解决的是对齐问题，而非单纯的几何分布问题。

6.4 模型是否通过“作弊”来降低 Loss？

有人可能会担心，模型是否会通过简单地缩放参数模长（例如把 变小）来降低 ERC Loss，而不是真正学习耦合关系。
数学推导（附录 C.5）证明，单纯改变模长无法同时满足 ERC 的所有约束项。实验数据也证实，使用 ERC Loss 训练的模型的参数范数与基线模型相当，说明 Loss 的下降确实源于学到了更好的路由-专家映射。

7. 代码实现详解

论文在 Figure 7 中提供了 PyTorch 风格的伪代码。以下是核心逻辑的解读：

# 核心代码逻辑解析

class MoE(nn.Module):
    # ... 初始化 ...
    
    def erc_loss(self, M):
        # 约束 1: Expert Specialization
        # M[i, j] < alpha * M[i, i]
        # 计算 M 的对角线元素（即 M[i, i]），并扩展维度以便广播
        row_diff = (M - self.alpha * torch.diag(M).unsqueeze(1))
        # 只取违反约束的部分（大于0的部分），clamp(min=0) 实现 ReLU 逻辑
        row_diff_clamped = torch.clamp(row_diff, min=0.0)

        # 约束 2: Precise Routing
        # M[j, i] < alpha * M[i, i]
        col_diff = (M - self.alpha * torch.diag(M).unsqueeze(0))
        col_diff_clamped = torch.clamp(col_diff, min=0.0)

        # 掩码 mask：忽略对角线元素（自己对自己无需惩罚）
        mask = torch.ones_like(M) - torch.eye(M.size(0), device=M.device)
        
        # 总 Loss 是两个方向违约项之和
        total_diff = (row_diff_clamped + col_diff_clamped) * mask
        return total_diff.mean()

    def get_noisy_router(self, R):
        with torch.no_grad(): # 噪声生成不需要梯度
            # 1. 计算所有 R[i] 之间的欧氏距离
            distances = torch.cdist(R, R, p=2)
            # 将对角线设为无穷大，以便找最近邻
            distances.fill_diagonal_(float('inf'))
            # 找到最近邻距离
            min_dist, _ = torch.min(distances, dim=1)
            
            # 2. 计算最大噪声边界 epsilon (公式 4)
            norm_R = torch.norm(R, dim=1)
            eps = min_dist / 2 / norm_R
            
            # 3. 生成均匀分布噪声
            low = (1 - eps).unsqueeze(1)
            high = (1 + eps).unsqueeze(1)
            noise = torch.rand_like(R) # [0, 1]
            
            # 缩放噪声到 [1-eps, 1+eps] 并乘到 R 上
            # 注意：这里返回的是 R * noise，即 Hadamard 积
            return (low + noise * (high - low)) * R

    def forward(self, x):
        # ... 标准 MoE 前向 ...
        
        if self.training:
            # 1. 获取带噪声的代理 token
            R_noisy = self.get_noisy_router(self.R)
            
            # 2. 计算激活矩阵 M
            # einsum 计算: R_noisy (n, d) * W_g (n, d, D) -> M (n, n, D) -> norm -> (n, n)
            # 注意：这里实现需要技巧，实际上是把 R_noisy[i] 广播给所有 Expert[j]
            # M[i, j] = || R_noisy[i] @ W_g[j].T ||
            # 具体实现取决于 W_g 的存储格式
            M = torch.norm(
                torch.einsum('jDd, id -> ijD', self.experts.Wg, R_noisy), 
                dim=-1
            )
            
            # 3. 计算 Loss
            loss = self.erc_loss(M)
            return output, loss
            
        return output, 0.0

实现细节注意事项：

1. 梯度截断：生成 R_noisy 时使用了 torch.no_grad()，这意味着我们不希望通过优化噪声边界来降低 Loss，而是希望在给定的噪声下优化 和 。
2. 并行策略：在实际的大规模训练（如 Megatron-LM 框架）中，专家通常分布在不同的 GPU 上（Expert Parallelism, EP）。计算矩阵 需要收集所有专家的 或将 广播。由于 较小，这部分通信开销极低。论文附录 B.2 详细分析了 EP 模式下的吞吐量，证实仅下降不到 1%。

更多细节请阅读原文。

往期文章：

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题