
-
论文标题:Bottom-up Policy Optimization: Your Language Model Policy Secretly Contains Internal Policies -
论文链接:https://arxiv.org/pdf/2512.19673
TL;DR
今天解读一篇来着中科院的一篇论文《Bottom-up Policy Optimization: Your Language Model Policy Secretly Contains Internal Policies》。该研究并未将大型语言模型(LLM)视为一个单一的黑盒策略,而是利用 Transformer 的残差流特性,将其分解为层级内部策略(Internal Layer Policies)和模块内部策略(Internal Modular Policies)。
通过分析内部策略的熵动力学(Entropy Dynamics),作者发现:
-
分层推理结构:所有模型均表现出“早期层高熵探索,晚期层低熵收敛”的通用结构。 -
架构差异:Llama 系列在最后几层才突然收敛;而 Qwen 系列(特别是 Qwen3)展示了类似人类的渐进式推理模式(探索-整合-收敛)。 -
BuPO 方法:基于上述发现,作者提出了自下而上的策略优化(BuPO)。该方法在训练早期优先优化中间层的内部策略,通过对齐底层特征来构建更稳固的推理基础,随后再优化整体模型策略。实验证明,BuPO 在 MATH、AIME 等复杂推理基准上优于 GRPO 和 PPO 等基线方法。
1. 引言
随着 DeepSeek-R1 等工作的出现,基于可验证奖励的强化学习(RLVR)已成为提升大语言模型复杂推理能力的关键范式。目前的 RLVR 研究(如 GRPO、Reinforce++)主要关注如何设计更好的奖励函数或正则化项,但在优化过程中,往往将 LLM 视为一个整体策略 ,忽略了其内部复杂的运作机制。
可解释性研究(Interpretability)已经表明,Transformer 的残差流(Residual Stream)中蕴含着丰富的信息,且随着层数加深不断演化。Logit Lens 等工具揭示了我们可以将中间层状态映射到词表空间进行解码。然而,现有的 RL 算法很少利用这些内部信息来指导优化过程。
本文提出一个核心观点:语言模型并非单一策略,而是由一系列隐含的“内部策略”组成的集合。
作者通过系统性地分解和分析这些内部策略,揭示了不同模型家族(Llama vs Qwen)在推理模式上的本质差异,并据此提出了一种新的训练范式——Bottom-up Policy Optimization (BuPO)。
2. 语言模型策略的分解
要理解 BuPO,首先需要建立对 Transformer 内部信息流的数学描述,并定义什么是“内部策略”。
2.1 Transformer 的残差流视角
对于一个包含 层的 Transformer 解码器,输入序列 经过嵌入层得到 。每一层的处理过程可以形式化为:
其中, 和 分别代表第 层的自注意力(Attention)和前馈网络(FFN)的输出(不包含残差连接前的输入)。由于残差连接的存在,第 层的输出隐藏状态 (在论文中也记为 )可以表示为所有之前模块输出的累加:
最终,模型的输出概率分布(即语言模型策略)通过将最后一层状态 投影到词表空间获得:
其中 是解嵌入(unembedding)矩阵。
2.2 定义内部策略
基于残差流的线性叠加性质,作者提出任何中间层的隐藏状态 都可以被视为某种程度上的“潜在预测”。如果我们将这些中间状态直接与解嵌入矩阵 结合,就能得到一个可采样的概率分布。
作者定义了两种粒度的内部策略:
-
内部层策略 (Internal Layer Policy) :
利用第 层的累积隐藏状态 生成的策略:
-
内部模块策略 (Internal Modular Policy) :
单独利用某个模块(Attention 或 FFN)的输出与 结合:
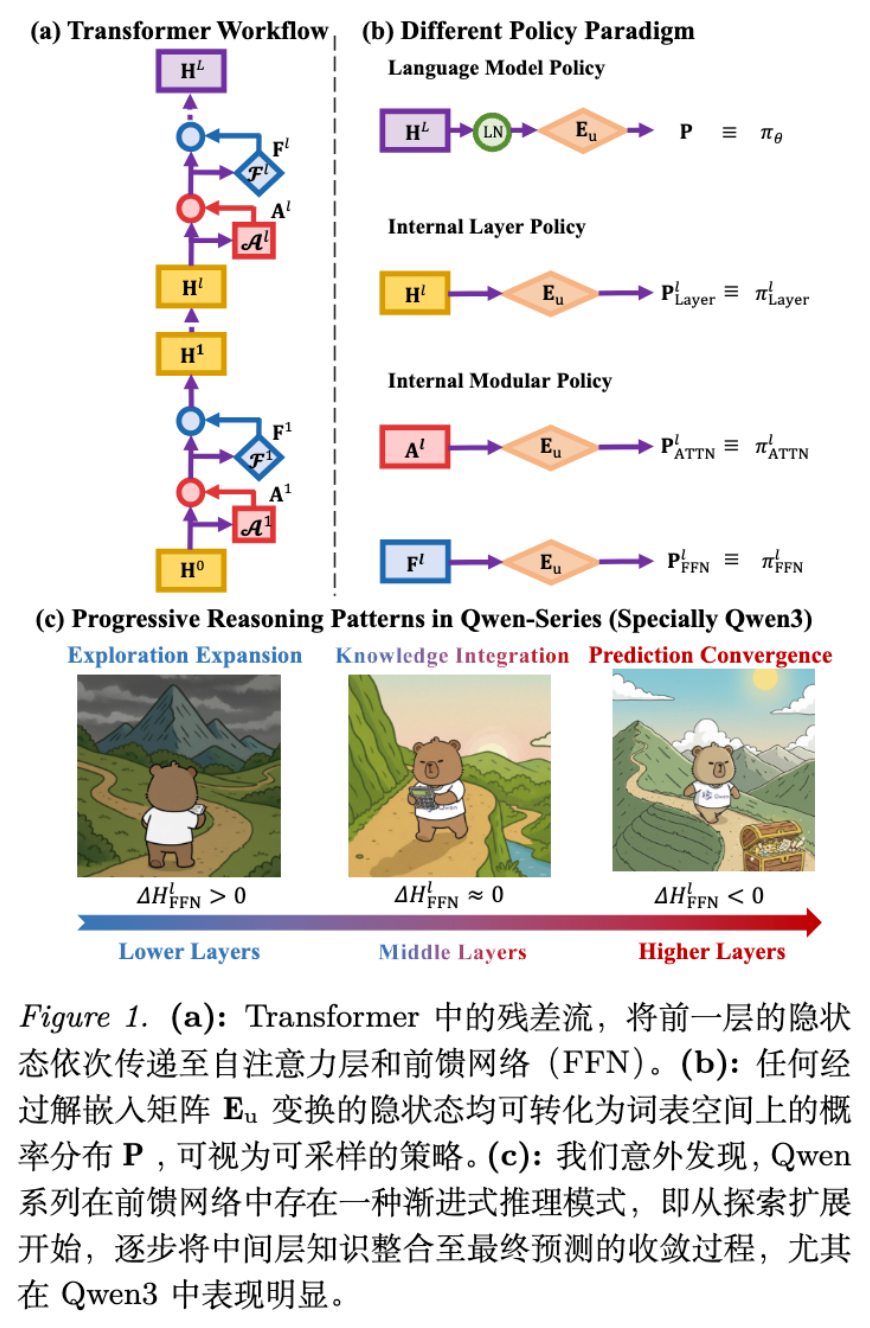
注意与 Logit Lens 的区别:
Logit Lens 通常在应用 之前会对隐藏状态应用层归一化(Layer Normalization, LN),即 。
本文作者通过实验发现,在定义内部策略时,去除 LN 能获得更稳定的熵动力学特性,并且在数学上更符合残差流的直接分解特性(因为 LN 是非线性的,会破坏纯粹的加性分解)。因此,本文的内部策略定义中不包含中间层的 LN。
3. 分析工具:内部策略熵
为了量化推理过程在层级间的演变,作者采用了熵 (Entropy) 作为核心指标。熵能够反映策略对当前预测的不确定性。
对于第 层的内部层策略,其熵定义为:
同样地,可以计算 和 。
3.1 熵变 (Entropy Change)
单一的熵值只反映了状态,为了观察信息在流经某个模块时的动态变化,作者定义了 熵变 ():
这个指标的物理含义非常直观:
-
:探索 (Exploration) 。模块增加了不确定性,扩大了搜索空间。 -
:知识整合 (Knowledge Integration) 。不确定性保持稳定,主要进行信息的搬运或整合。 -
:收敛 (Convergence) 。模块减少了不确定性,使得预测聚焦于特定 token。
4. 深度分析:推理是如何在模型内部涌现的?
作者利用上述工具,对 Qwen 系列(Qwen2.5, Qwen3)和 Llama 系列(Llama-3.1, Llama-3.2, Llama-OctoThinker)进行了详尽的分析。
4.1 通用结构:从探索到收敛
所有被测试的模型都遵循一个通用的宏观趋势:
-
浅层 (Early Layers) :保持高熵。这是模型在语义空间中进行广泛探索的阶段,此时模型尚未确定具体的输出词汇。 -
深层 (Top Layers) :熵值迅速下降至接近零。这对应于决策的确定和最终输出的生成。
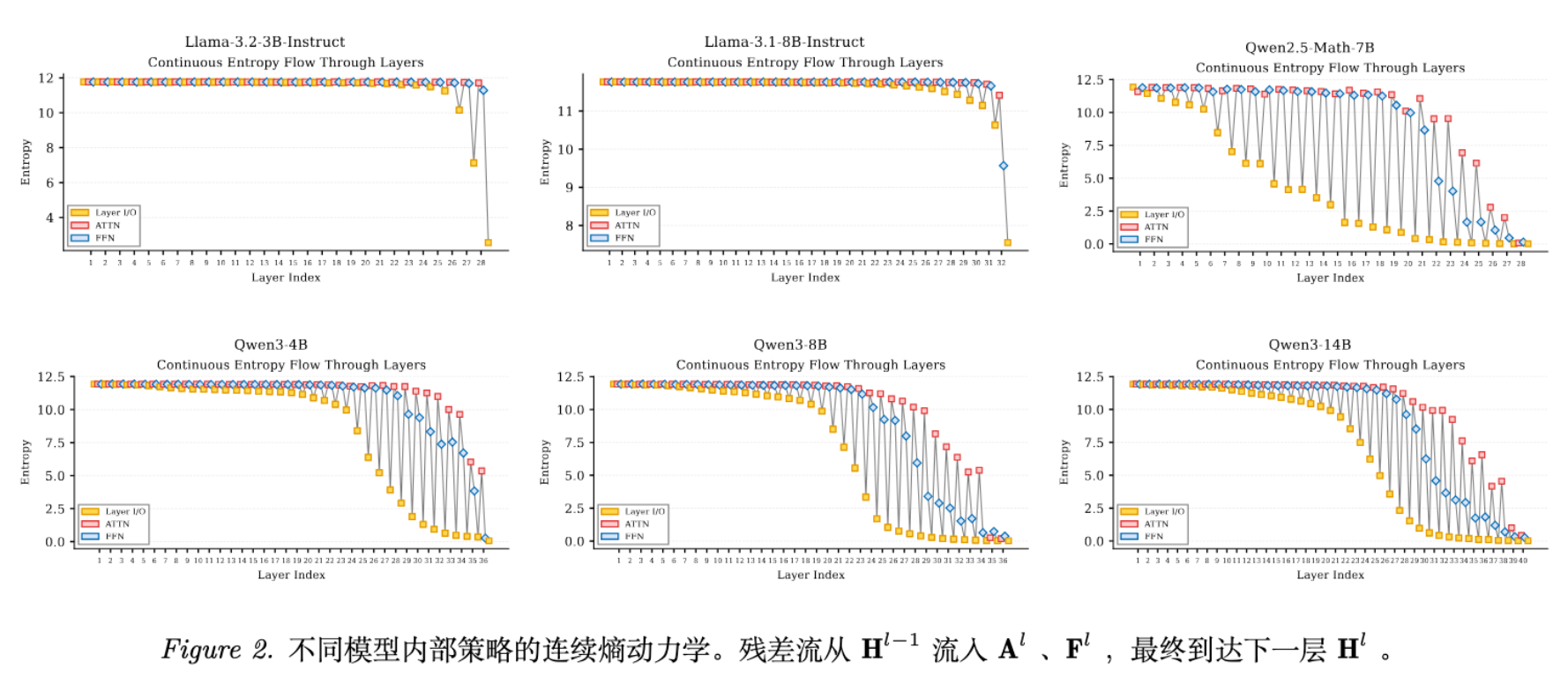
4.2 关键差异:Qwen 的渐进式推理 vs Llama 的突变式收敛
尽管宏观趋势一致,但在收敛的节奏上,不同模型家族表现出显著的架构性差异。
Llama 系列:突变式收敛 (Sudden Convergence)
Llama 模型的内部策略熵在绝大多数层中保持较高水平,仅在最后 3 层左右发生剧烈的塌缩(Collapse)。这意味着 Llama 在大部分计算过程中并没有逐步缩小预测范围,而是将决策压力集中在最后。
-
FFN 的表现:在 Llama 中,FFN 的 在几乎所有层都保持正值(),直到最后一层。这表明其 FFN 一直在进行发散性的特征扩展。
Qwen 系列(特别是 Qwen3):渐进式推理 (Progressive Reasoning)
Qwen 模型展示了一种分阶段的、逐步降低不确定性的过程。这种模式在 Qwen3 上尤为明显,被作者总结为 "探索-整合-收敛" (EIC) 模式:
-
探索阶段 (Exploration) :底层 FFN 显示 ,扩大搜索空间。 -
整合阶段 (Integration) :中间层 FFN 显示 ,利用知识神经元(Knowledge Neurons)检索并整合参数化知识。 -
收敛阶段 (Convergence) :高层 FFN 显示 ,逐步排除干扰选项,聚焦最终答案。
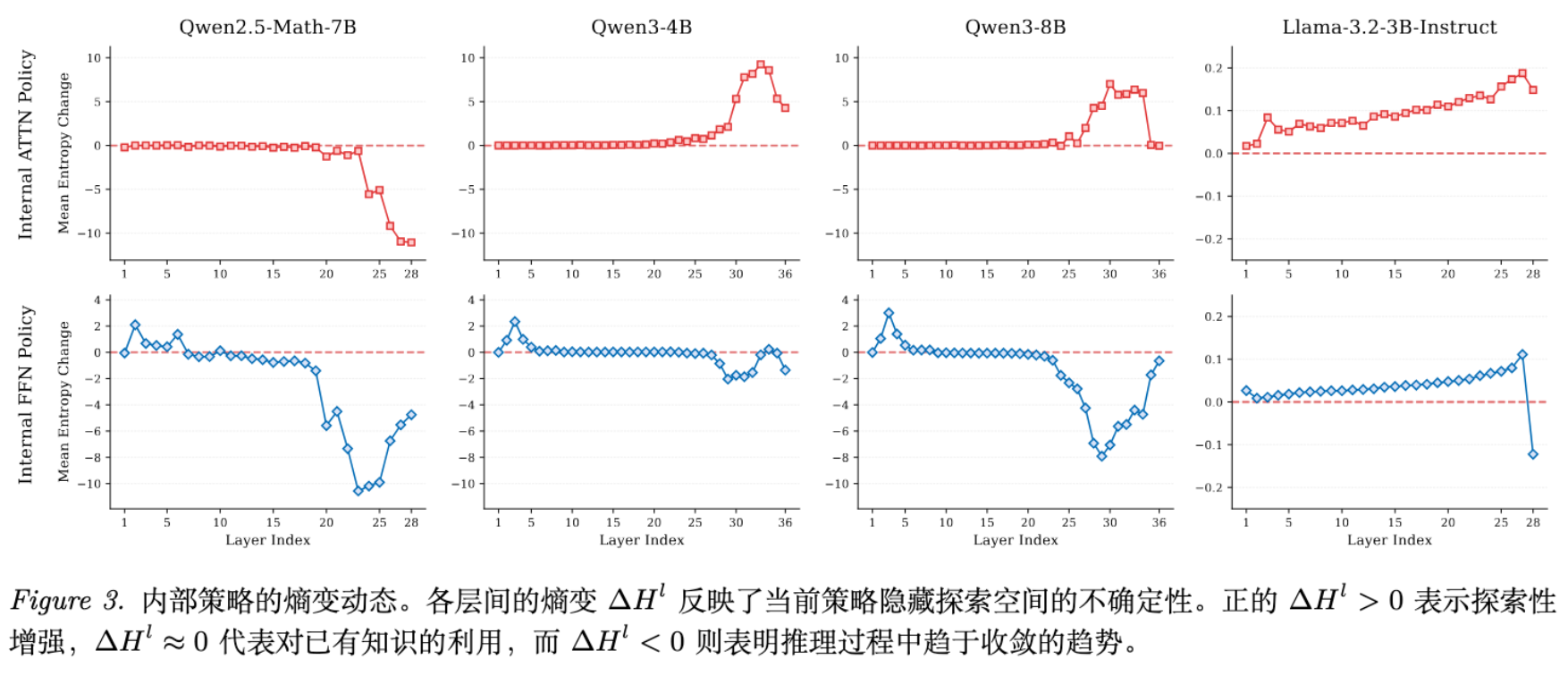
这种渐进式的结构与人类的认知过程(从发散思维到聚合思维)更为相似。作者推测,Qwen3 这种更结构化的推理模式,可能是其在后训练(Post-training)阶段表现出更高数据吸收效率的原因之一。
4.3 Attention 与 FFN 的分工
通过分析 和 ,作者还发现:
-
Attention:在 Qwen3 中,Self-Attention 持续表现出正的熵变(),说明注意力机制主要负责引入上下文信息,扩大可能性的边界。 -
FFN:如前所述,FFN 承担了更复杂的调节作用,负责处理这些信息并逐步收敛。
4.4 残差流的余弦相似度分析
为了验证上述熵分析的结论,作者还计算了模块输出与残差流的余弦相似度。
-
Qwen3 的 Attention 模块持续向残差流写入正向增强的特征(高相似度)。 -
Qwen3 的 FFN 模块在底层写入正交特征(探索),在中层抑制模糊信号,在高层放大特征以驱动收敛。
这一物理层面的分析与熵层面的统计分析高度吻合。
5. 初步实验:直接优化内部策略会发生什么?
基于“推理是分层涌现的”这一发现,一个自然的问题产生了:如果我们在 RL 训练中直接优化中间层的内部策略,会发生什么?
作者设计了一个实验,使用 InterGRPO(内部 GRPO,即用中间层的策略 计算梯度并更新 层的参数)来训练 Qwen3-4B。
5.1 现象一:特征精炼
实验发现,当优化底层(例如第 6 层)的内部策略时,该层的隐藏状态 与模型最终层 的相似度随着训练显著增加。
这表明,内部策略优化迫使底层网络“抢跑”,即尽早地捕获高层的推理特征。这为后续的层提供了更稳固、更高级的语义基础。
5.2 现象二:过度优化的崩溃
然而,如果持续仅优化内部策略,模型最终会崩溃。
-
PPL 上升:语言模型整体的困惑度(Perplexity)剧增。 -
熵过低:内部策略迅速收敛到极低熵,导致生成重复、无意义的内容。

结论:内部策略优化是一把双刃剑。它能有效地提炼底层特征,但不能完全替代整体策略的优化。它更适合作为一个早期的引导阶段。
6. 方法:Bottom-up Policy Optimization (BuPO)
基于上述分析,作者提出了 BuPO。其核心思想是:利用内部策略优化作为一种“预热”或“课程学习”,在训练早期对齐底层表征,然后再进行全模型的 RL 训练。
6.1 算法流程
BuPO 的训练过程分为两个阶段,由参数 (内部优化步数)控制:
-
阶段一:内部策略优化 (Phase 1)
-
当训练步数 时。 -
选择一个目标层 (通常选择 FFN 开始收敛前的最后一层,即 的边界)。 -
构建内部策略 。 -
计算奖励 和优势 。 -
使用 InterGRPO 目标函数更新参数。
-
-
阶段二:语言模型策略优化 (Phase 2)
-
当训练步数 时。 -
切换回标准的 GRPO,优化最终层策略 。
-
6.2 InterGRPO 目标函数
InterGRPO 的形式与 GRPO 类似,但作用于内部策略:
其中重要性采样比率 基于内部策略计算:
6.3 梯度流分析
BuPO 的一个关键特性是梯度的截断效应。在阶段一优化 时,梯度为:
这意味着,在早期阶段,只有 到 层(以及解嵌入矩阵 )被更新,而 层之上的参数保持不变。这种机制强迫底层网络独立地承担起预测任务,从而在底层建立起更强的推理表征能力。
7. 实验结果
7.1 实验设置
-
模型:Qwen3-4B/8B, Llama-OctoThinker-3B/8B。 -
数据集:MATH500, AMC23, AIME24, AIME25。 -
基线:GRPO, PPO, Reinforce++, RLOO。 -
评估指标:Pass@K (K=1 到 256),报告 Avg@K 以减少方差。 -
层选择:根据熵分析,对于 Qwen3-4B 选择第 6 层;对于 Llama 则选择更靠后的层(如 27 层),遵循 的原则。
7.2 主实验结果
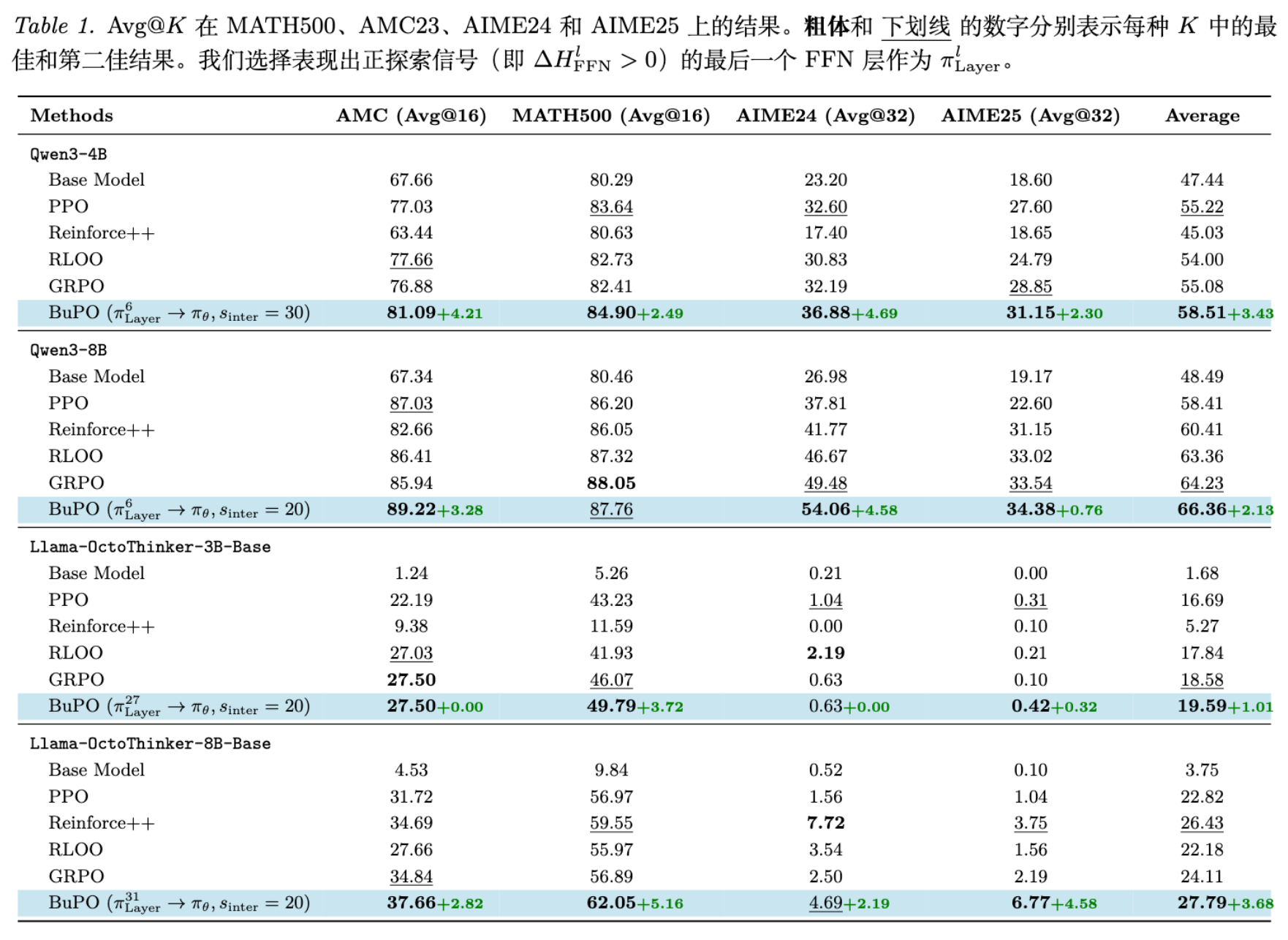
实验结果表明,BuPO 在绝大多数情况下都优于基线方法:
-
Qwen3-4B:BuPO 在 AIME24 上比 GRPO 提升了 4.69 分,在平均分上提升了 3.43 分。 -
Qwen3-8B:在 AIME24 上提升了 4.58 分,平均提升 2.13 分。 -
Llama 系列:同样观察到了显著提升,Llama-OctoThinker-8B 在平均分上提升了 3.68 分。
值得注意的是,BuPO 不仅提升了 Pass@1,在 Pass@K (K=1~256) 的整个曲线上都保持了优势。这说明模型生成的每一个样本的质量普遍提高了,而不是仅依靠运气。
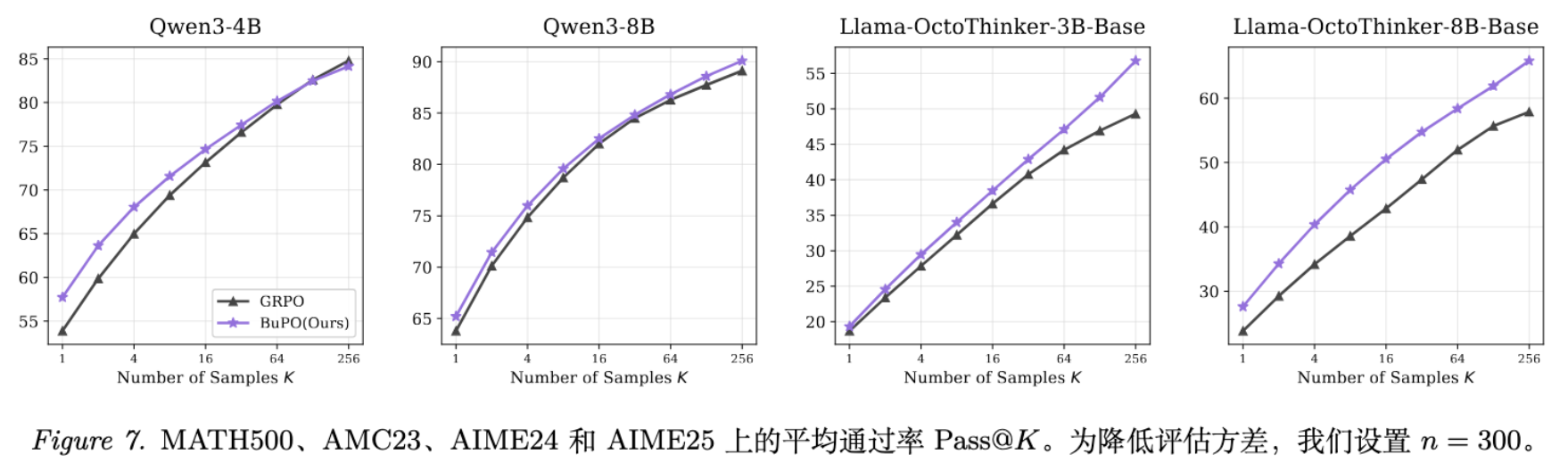
7.3 消融实验
内部优化步数 () 的影响
作者对比了不同的 (30, 50, 70)。
-
适度最佳: 时效果最好。 -
过度有害:当 增加到 70 时,性能急剧下降至个位数。这验证了“内部策略优化应作为引导而非主力”的假设。
优化层的选择 ()
作者对比了优化第 6 层、第 26 层和第 35 层(倒数第二层)。
-
底层/中层更优:优化第 6 层或第 26 层(对应 Qwen3 的探索/整合阶段边界)效果显著好于 GRPO。 -
高层无效:优化第 35 层效果与 GRPO 持平或略差,因为这几乎等同于优化最终策略,失去了“自下而上”构建基础的意义。
8. 讨论与展望
8.1 为什么 BuPO 有效?
BuPO 的成功可以归结为对齐的层次化。传统的 RL 就像是在教学生解题时,只看最后的答案(Final Logits)给分。学生可能会死记硬背(过拟合高层参数)。
而 BuPO 类似于在教学初期,先检查学生的中间步骤(Internal Layers),要求学生在思维的早期阶段就形成正确的直觉(Feature Alignment)。这种抢先式(Preemptive)的特征学习,使得底层网络能够输出包含更多推理信息的表示,从而减轻了高层网络的负担,使其能专注于最终的收敛和决策。
8.2 对模型架构设计的启示
论文对 Llama 和 Qwen 的对比分析极具启发性。Qwen3 展现出的类似人类的“探索-整合-收敛”模式,似乎与更强的推理能力和后训练潜力相关。这暗示了未来的模型架构设计可能需要显式地引入这种分阶段的模块化结构,或者通过特定的初始化/正则化手段来诱导这种结构的形成。
8.3 局限性
-
超参数敏感: 和目标层 的选择需要依赖熵分析,且对结果影响较大。 -
计算开销:虽然 BuPO 并没有显著增加推理开销,但在训练时需要额外的计算来构建内部策略和反向传播(尽管使用了截断梯度,实际开销增加有限)。
更多细节请阅读原文。
往期文章:




