
-
博客标题:Who is Adam? SGD Might Be All We Need For RLVR In LLMs -
博客链接:https://www.notion.so/sagnikm/Who-is-Adam-SGD-Might-Be-All-We-Need-For-RLVR-In-LLMs-1cd2c74770c080de9cbbf74db14286b6
TL;DR
今天来看一篇有趣的工作《Who is Adam? SGD Might Be All We Need For RLVR In LLMs》。该研究针对大语言模型(LLM)在具有可验证奖励的强化学习(RLVR)阶段的优化器选择提出了反直觉的发现。主要结论如下:
-
SGD 足矣: 在 Transformer 基模型的 RLVR 训练中,不带动量的简单随机梯度下降(SGD)在性能上能够匹配甚至在某些指标上略优于行业标准的 AdamW 优化器。 -
内存效率: 由于 SGD 不需要维护一阶矩(动量)和二阶矩(方差)的优化器状态,其显存占用显著低于 AdamW,类似于“免费的午餐”。 -
极度稀疏的更新: 研究发现 SGD 在训练过程中表现出极高的权重更新稀疏性(约 99.99% 的参数更新几乎为零),这表明 RLVR 过程本质上是在微调一个极小的子网络。 -
优于 Rank-1 LoRA: 尽管更新量极小,但全参数 SGD 的表现优于 Rank-1 LoRA。这表明 SGD 能够自动定位到模型中关键的“有效参数”子空间,而不受 LoRA 预定义低秩结构的几何约束。 -
学习率是关键: SGD 需要比 AdamW 大得多的学习率(例如 1e-1 对比 1e-6)才能达到相当的收敛效果。
1. 引言
在过去几年的大语言模型(LLM)研究中,AdamW(Adam with Decoupled Weight Decay)几乎成为了训练 Transformer 架构的默认选择。无论是在预训练(Pre-training)、监督微调(SFT)还是基于人类反馈的强化学习(RLHF)阶段,研究人员往往习惯性地使用 AdamW,默认其自适应学习率机制能够处理非凸优化问题中的复杂曲率。
然而,随着 LLM 后训练(Post-training)技术的发展,特别是针对数学推理、代码生成等具有明确正误判断的任务——即具有可验证奖励的强化学习(RLVR, Reinforcement Learning with Verifiable Rewards)——训练的动态特性可能与预训练阶段存在显著差异。
Mukherjee 等人的这项工作《Who is Adam? SGD Might Be All We Need For RLVR In LLMs》挑战了“AdamW 优于 SGD”这一既定认知。作者通过实验论证,在 RLVR 场景下,复杂的自适应优化器可能并非必要,甚至可能引入不必要的计算和内存开销。这一发现不仅具有工程上的价值(节省显存),更从理论层面揭示了 LLM 在特定任务微调阶段的参数更新机制。
2. 背景知识与理论基础
2.1 从 SGD 到 AdamW
在深度学习优化中,我们主要关注参数 的更新。
2.1.1 随机梯度下降(SGD)
最基础的 SGD 更新规则如下,其中 是 时刻的梯度, 是学习率:
在本文讨论的上下文中,作者使用的是不带动量(Momentum)的纯 SGD。这意味着优化器是无状态的(Stateless),它不需要存储任何关于梯度的历史信息。对于一个参数量为 的模型,SGD 仅需存储 个参数本身(以及计算过程中的梯度),其优化器状态内存占用为 (相对于模型参数量而言的额外状态)。
2.1.2 带动量的 SGD
为了加速收敛并减少震荡,通常会引入动量项 :
其中 是动量系数。这种方法需要维护一个与参数量相同的动量向量,内存开销增加 。
2.1.3 AdamW
Adam(Adaptive Moment Estimation)引入了对一阶矩(均值)和二阶矩(未中心化的方差)的估计,以实现对每个参数的自适应学习率调整。AdamW 在此基础上解耦了权重衰减(Weight Decay)。其更新规则较为复杂:
-
更新一阶矩估计:
-
更新二阶矩估计:
-
偏差修正:
-
参数更新:
其中 是指数衰减率, 是数值稳定常数, 是权重衰减系数。
关键区别: AdamW 需要为每个参数存储 和 两个状态变量。这意味着对于一个 参数的模型,AdamW 的优化器状态需要占用 的显存(通常使用 FP32 存储)。相比之下,本文研究的 SGD 不需要这些额外显存,这在显存受限的大模型训练中是一个巨大的优势。
2.2 RLVR:具有可验证奖励的强化学习
RLVR 指的是在强化学习框架下,奖励信号(Reward Signal)并非来自一个黑盒的奖励模型(Reward Model),而是来自确定的、可验证的结果。
-
典型场景: 数学题求解(答案对错分明)、代码生成(能否通过单元测试)。 -
特性: 与依赖人类反馈偏好模型(RLHF)相比,RLVR 的信号更加稀疏但更加准确(Ground Truth)。
论文建立在 Mukherjee 等人先前的发现之上,即 RLVR 过程倾向于更新 LLM 中的一个“小子网络”(Small Subnetwork)。这种稀疏性假设是尝试使用 SGD 的主要动机。
3. 实验设置
为了验证 SGD 在 RLVR 中的有效性,作者设计了严格的对比实验。
3.1 模型与算法
-
基础模型: Qwen-3-8B。这是一个具有代表性的开源大模型,参数量适中,便于进行多次消融实验。 -
训练算法: GRPO (Group Relative Policy Optimization)。这是一种在 RLHF/RLVR 中常用的策略优化算法,通过从群体采样中计算相对优势来稳定训练。 -
硬件: 所有实验均在 GPU 上进行。
3.2 数据集
-
训练集: 从 NuminaMath 语料库中随机采样的 35,000 个实例。NuminaMath 包含了大量数学推理题目,适合 Chain-of-Thought (CoT) 训练。 -
验证集: MATH 数据集。这是衡量模型数学推理能力的标准基准。
3.3 评估指标
-
训练指标: KL 散度(KL Divergence)、Actor 熵(Actor Entropy)、平均回复长度(Mean Response Length)、训练奖励(Training Rewards)。 -
下游基准测试: 除了 MATH,还包括 AIME, AMC, OlympiadBench 等数学竞赛级基准。 -
比较对象: -
Baseline: AdamW (学习率 1e-6 或 5e-6)。 -
Experimental: SGD (无动量,学习率 1e-1)。
-
注意: 这里的对比是“苹果对苹果”(Apples-to-Apples)的,即除了优化器和学习率外,其他所有超参数(如 Batch Size, Context Length 等)保持一致。
4. 核心发现一:SGD 在 RLVR 中匹配 AdamW 的性能
论文最直观的结论展示在训练曲线和验证结果中。
4.1 训练动态分析
作者展示了 SGD 和 AdamW 在训练过程中的动态变化。
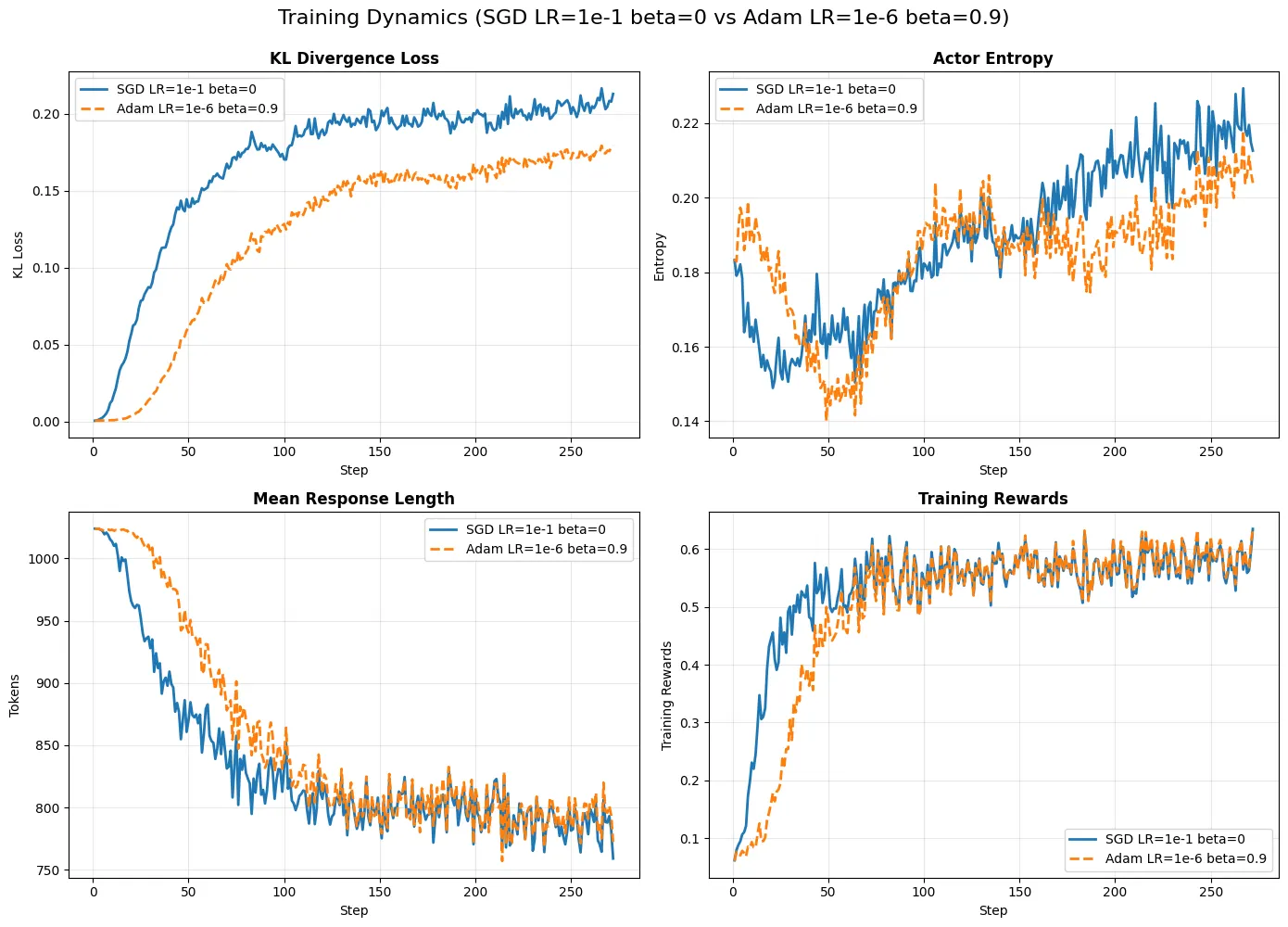
-
初始阶段差异: 从图中可以观察到,SGD 在训练初期的奖励增长(Training Rewards)甚至略高于 AdamW。 -
最终收敛: 尽管轨迹不同,两者最终收敛到了相当的性能水平。 -
学习率的决定性作用: -
AdamW 使用的学习率通常在 到 之间。 -
SGD 必须使用 的学习率才能达到类似效果。 -
这是一个高达 5 个数量级的差异。这反映了 AdamW 通过二阶矩归一化放大了更新步长,而 SGD 需要通过增大全局 来补偿缺乏自适应缩放的问题。
-
4.2 验证集表现
在 MATH 和 AMC 等验证集上,SGD 的表现同样稳健。
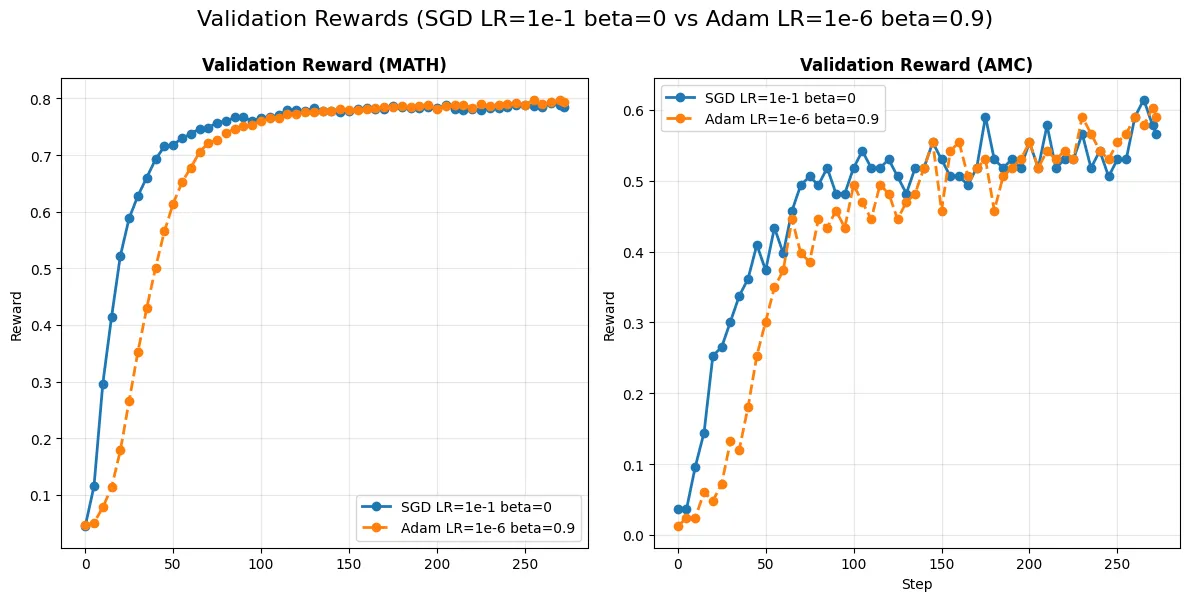
曲线显示,SGD(蓝色线)和 AdamW(橙色线)的验证奖励上升趋势高度重合,且 SGD 并未表现出明显的训练不稳定性或发散迹象。
4.3 广泛的基准测试
为了证明结果的普适性,作者在两种不同的上下文长度设置(max seq len = 1024 和 8192)下进行了评估。
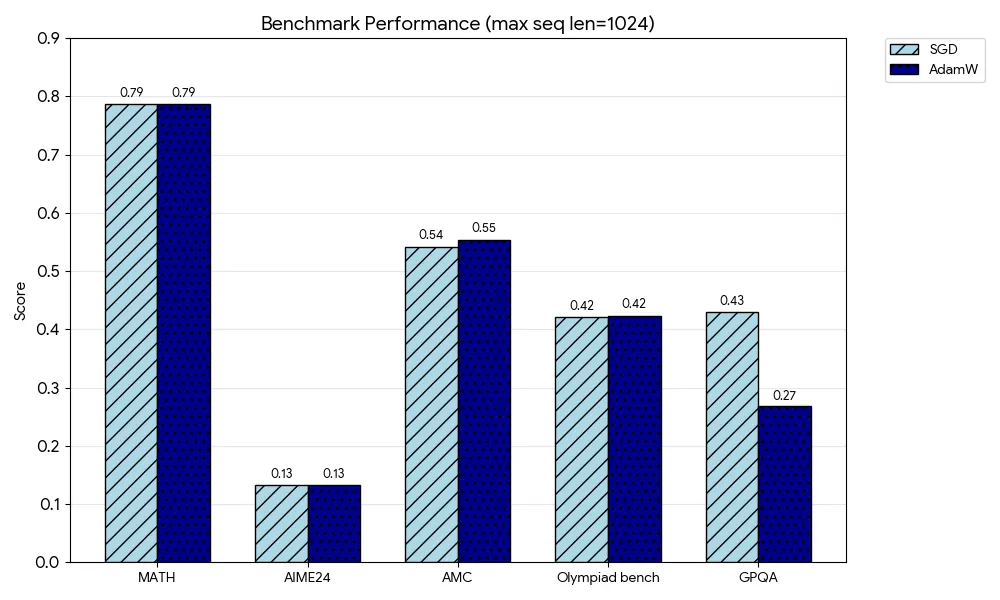
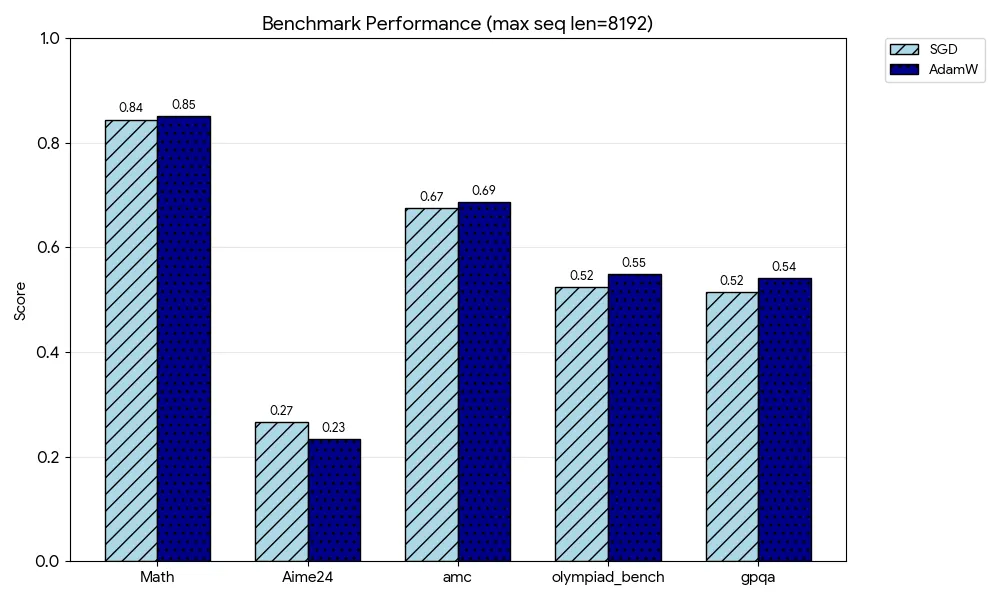
在 MATH, AIME24, AMC, OlympiadBench, GPQA 等多个数据集上,SGD 取得的分数与 AdamW 互有胜负,差异处于统计误差范围内。例如,在序列长度 8192 的设置下,SGD 在 MATH 上得分 0.84,AdamW 得分 0.86;而在 AIME24 上,SGD 得分 0.67,AdamW 得分 0.69。考虑到 SGD 在显存上的巨大优势,这种微小的性能差异通常是可以接受的。
5. 核心发现二:SGD 导致极度的局部更新
如果说第一个发现是工程上的胜利,那么第二个发现则提供了深刻的理论洞察。
5.1 稀疏性分析
作者深入研究了模型权重在训练前后的变化量。这里定义的“更新”是指权重 。
-
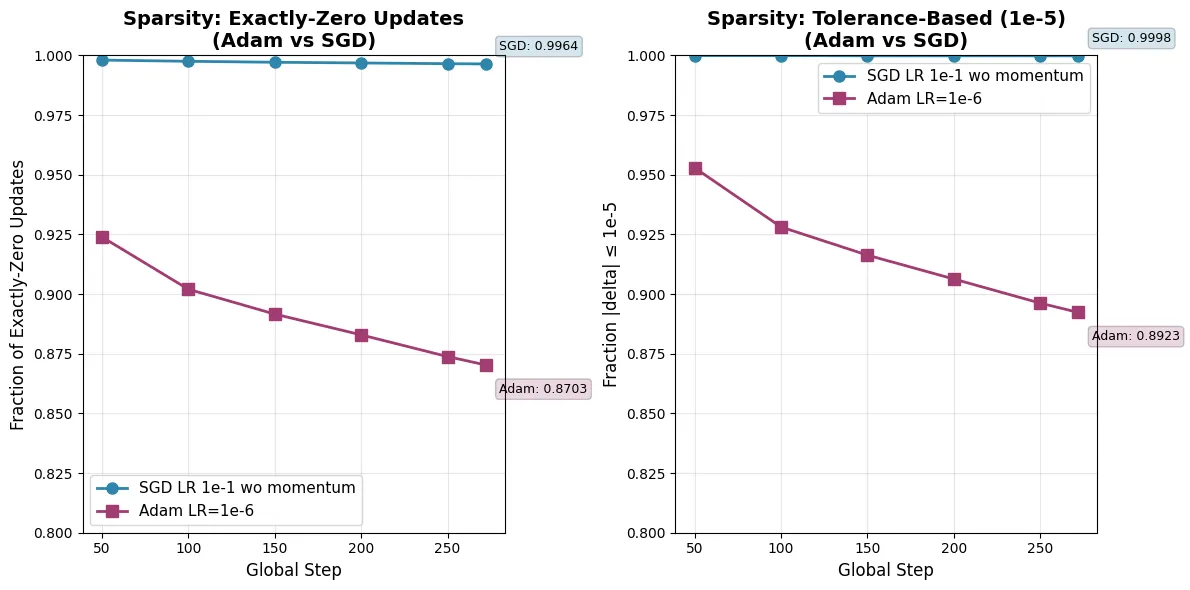
AdamW 的更新分布: AdamW 的更新相对稠密,大约 80% 的参数发生了显著变化(即便变化量很小,由于动量的存在,很少有参数完全不动)。 -
SGD 的更新分布: SGD 表现出惊人的稀疏性。 -
基于阈值的稀疏性(Tolerance-Based): 如果将变化量小于 视为未更新,SGD 的更新稀疏性极高。 -
完全零更新(Exactly-Zero Updates): 作者观察到,在相同的训练检查点,SGD 的更新表现出 的稀疏度。
-
这意味着,在使用 SGD 进行 RLVR 训练时,模型中绝大多数参数实际上并没有移动,或者移动量微乎其微。只有极少数(约 0.01%)的参数承担了适应新任务的主要责任。
5.2 物理直觉:为什么会这样?
为了解释这一现象,论文提出了关于损失景观(Loss Landscape)的几何解释。
-
曲率与学习率:
-
AdamW 的设计初衷是应对不同参数方向上曲率(Hessian 矩阵的特征值)差异巨大的情况。它通过除以 来“拉平”损失景观,使得各个方向的更新步长归一化。 -
SGD 使用单一的全局学习率 。按照传统优化理论,如果 设得很大(如 0.1),在曲率大的方向上会导致震荡甚至发散。 -
然而,SGD 在此任务中表现良好,且主要更新了极少部分参数。这暗示了 RLVR 任务所对应的损失景观中,关键的下降路径位于一个曲率相对一致的子空间中。
-
-
“免费午餐”:
-
作者认为 SGD 能够自动识别出那些需要改变的、对损失敏感的参数。 -
对于那些梯度接近于零的参数,由于没有动量项的历史累积,SGD 此时 。 -
相比之下,AdamW 即使当前梯度微小,只要历史动量 不为零,或者 很小导致分母很小,仍可能产生非零更新(虽然 Weight Decay 会起到一定约束作用,但机制不同)。
-
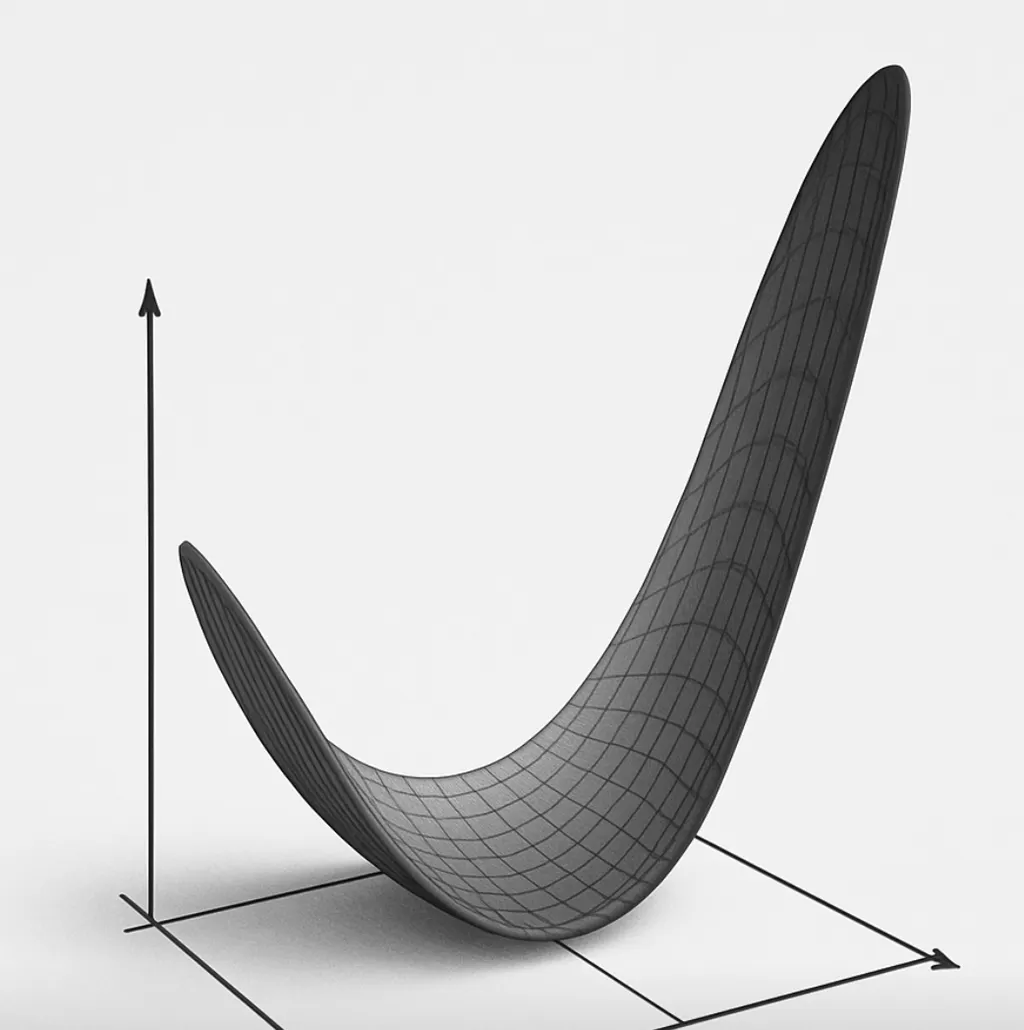
上图形象地展示了这一点:损失函数可能呈现为一个狭长的山谷。在山谷底部(平坦区域),SGD 几乎不移动;而在陡峭的下降方向,SGD 能够有效下降。
6. 为何 SGD 优于/等于 Rank-1 LoRA
这一发现自然引出了与低秩适应(LoRA, Low-Rank Adaptation)的对比。
6.1 LoRA 的局限性
LoRA 假设权重的改变量 可以分解为两个低秩矩阵的乘积:,其中 ,且 。
-
几何约束: LoRA 强制将参数更新限制在一个预定义的秩为 的子空间内。 -
子空间选择: 虽然 LoRA 能够学习这个子空间的方向,但它受到 大小的严格限制。
6.2 SGD 的自适应稀疏性
论文指出,SGD 更新的有效参数量(0.01%)大约相当于 Rank-1 LoRA 的活跃参数量。然而,SGD 的表现通常优于 Rank-1 LoRA。
-
无约束选择: SGD 没有施加硬性的几何约束。它可以在全参数空间的任何维度上进行更新。 -
自动特征选择: SGD 实际上执行了一种“隐式”的子网络搜索。它仅更新那些梯度显著的参数,这些参数构成了特定任务所需的“最佳子网络”。 -
结论: 论文提出,Vanilla SGD(普通 SGD)实际上比 Rank-1 LoRA 更具参数效率(Parameter-Efficient)。因为它不需要引入额外的适配器参数,而是利用了模型本身的高维空间中自然的稀疏性。LoRA 虽然减少了存储量,但在极低秩(如 Rank-1)时可能无法覆盖包含最优解的子空间,而 SGD 总是能访问全空间,只是选择只在少数维度上移动。
7. 讨论
论文在结尾处引用了 Ilya Sutskever 的名言:“we are back to the age of research”(我们回到了研究的时代)。这一部分讨论了研究心态的转变。
7.1 挑战“默认设置”
在“GPU-Rich”(算力充裕)的时代,研究人员倾向于使用最保险的配置(如 AdamW),因为即使付出 2 倍甚至 3 倍的显存代价,只要能保证收敛且不需要调参,就是值得的。
然而,随着模型规模不断扩大(从 8B 到 70B 再到 405B+),优化器状态占用的显存成为了巨大的瓶颈。
-
AdamW State: 假设模型参数为 ,AdamW 需要 字节(如果用 FP32 存储状态)。对于 405B 模型,仅优化器状态就需要 ~3TB 显存(未经量化优化前)。 -
SGD State: 需要 字节(无状态)。
这种差异对于“GPU-Poor”(算力受限)的研究实验室来说是决定性的。SGD 的回归意味着可以在有限的硬件上微调更大的模型,或者在相同的硬件上使用更大的 Batch Size。
7.2 学习率敏感性与调参策略
虽然 SGD 省显存,但作者也诚实地指出了其代价:对学习率更敏感。
-
AdamW 的自适应特性使其对学习率的选择相对宽容(通常在 1e-6 到 1e-4 之间都有一定效果)。 -
SGD 没有二阶矩归一化,梯度的尺度直接影响更新幅度。如果梯度范数在不同层之间差异很大,单一的全局学习率 可能会导致某些层更新过慢,而某些层更新过快(尽管在 Transformer 中 LayerNorm 缓解了部分问题)。
研究人员在使用 SGD 替代 AdamW 时,必须重新进行学习率扫描(Learning Rate Sweep)。论文建议从较大的学习率(如 0.1)开始尝试。
更多细节请阅读原文。
往期文章:




