• 论文标题：Differential Smoothing Mitigates Sharpening and Improves LLM Reasoning
• 论文链接：https://arxiv.org/pdf/2511.19942

TL;DR

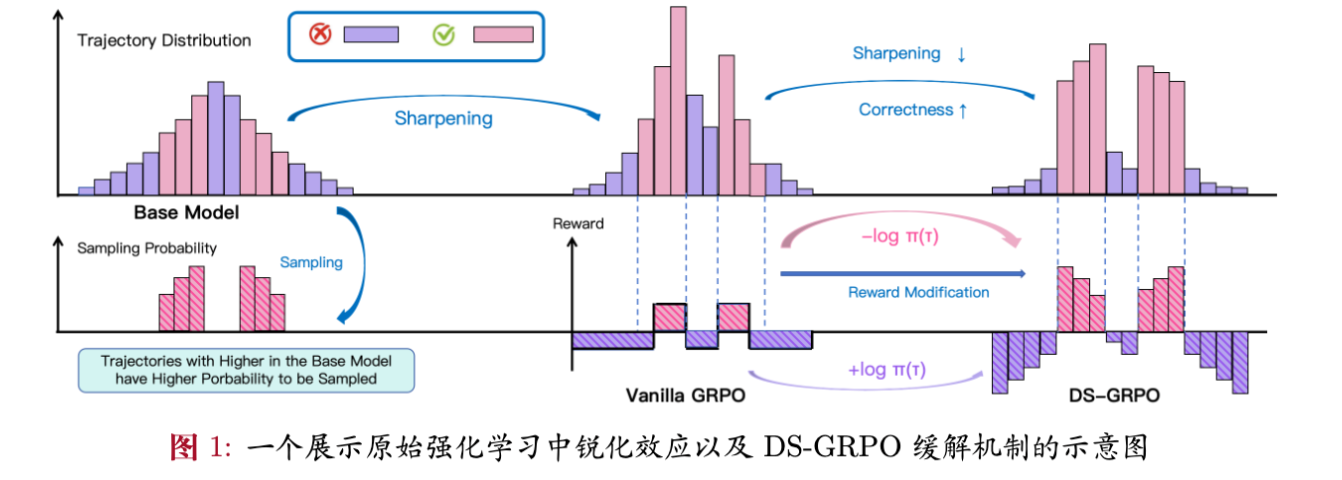
在大语言模型（LLM）的强化学习（RL）微调过程中，普遍存在“多样性坍缩”（Diversity Collapse）现象，即模型倾向于反复生成少数高概率的正确路径，导致输出分布“尖锐化”（Sharpening）。这虽然能提升 Pass@1 指标，但往往损害 Pass@K 性能，限制了模型在多次采样下的推理潜力。现有的解决方法（如熵正则化）通常难以兼顾正确性（Correctness）和多样性（Diversity）。

本文介绍卡内基梅隆大学与清华大学合作的一项工作：《Differential Smoothing Mitigates Sharpening and Improves LLM Reasoning》。该工作从理论上剖析了 RL 微调中选择偏差（Selection Bias）和强化偏差（Reinforcement Bias）是导致坍缩的根本原因。基于此，作者提出了一种名为 Differential Smoothing (DS) 的方法，其核心思想是对正确和错误的轨迹施加差异化的平滑策略：对正确的高概率轨迹进行惩罚以鼓励多样性，对错误的高概率轨迹进行惩罚以提升正确性。结合 GRPO 算法，作者提出了 DS-GRPO。实验表明，DS-GRPO 在从 1B 到 8B 的多个模型及数学推理任务（如 MATH, AIME）上，均能同时提升 Pass@1 和 Pass@K，且性能优于现有的熵控制方法。

1. 引言

强化学习（RL）已成为提升大语言模型复杂推理能力（如数学求解、代码生成）的标准范式。通过如 PPO 或 GRPO 等算法，模型在生成正确答案时获得正向奖励，从而强化其推理能力。然而，随着 RL 训练的进行，研究人员观察到一个显著的副作用：生成多样性的坍缩。

具体表现为，模型倾向于收敛到少数几条特定的解题路径，导致策略分布变得极度“尖锐”（Sharpening）。虽然这种尖锐化通常有助于提高贪婪解码（Greedy Decoding）下的 Pass@1 准确率，但在需要进行多次采样（Repeated Sampling）的场景下，模型的 Pass@K 指标提升往往呈现边际递减，甚至低于基座模型。这对于依赖 Test-time Compute（测试时计算）来扩展推理能力的场景是一个巨大的阻碍。

现有的缓解策略主要包括：

1. 早停（Early Stopping）或高温度解码：这些是简单的启发式方法，往往以牺牲 Pass@1 为代价来换取 Pass@K。
2. 熵正则化（Entropy Regularization）：这是一个充满争议的领域。部分工作主张最大化熵（Entropy Bonus）以鼓励探索，而另一部分工作则发现最小化熵（Entropy Penalty）反而能提升正确率。这种矛盾的现象表明，全局统一的熵控制策略缺乏鲁棒性。

2. 理论视角：为何 RL 会导致多样性坍缩？

为了深入理解多样性坍缩，论文首先将 LLM 的生成过程建模为一个标记级（Token-level）的马尔可夫决策过程（MDP）。

2.1 理论设定

• 状态与动作：状态 包含提示词 和已生成的 token，动作 为下一个 token。
• 轨迹： 表示一条完整的生成轨迹。
• 奖励：二值奖励 ，其中 是正确轨迹的集合。
• 目标函数：标准的 RL 微调目标通常包含 KL 散度约束：

  
  其中 是估计后的奖励。

2.2 两大偏差驱动坍缩

论文通过理论分析指出，RL 微调过程中存在两种偏差，共同导致了正确轨迹内部的多样性坍缩。

偏差一：选择偏差 (Selection Bias)

选择偏差指的是，在基座模型（Base Model）下概率较高的正确轨迹，更容易被采样出来并获得奖励。

命题 3.1 (Selection Bias) ：
对于任意两条正确轨迹 ，如果在基座模型下 ，那么 相比 更有可能在微调后的策略 中获得概率提升。

这意味着，模型倾向于“发现”并奖励那些原本概率就高的解法，而忽略了那些原本概率低但同样正确的解法。

偏差二：强化偏差 (Reinforcement Bias)

强化偏差进一步指出，即使所有正确轨迹都被发现，原本概率较高的轨迹获得的提升幅度也更大。

命题 3.2 (Reinforcement Bias) ：
对于任意正确轨迹 ，其概率增益的幅度直接正比于其在基座策略下的概率：

这两个偏差共同作用，形成了一个“富者愈富”的反馈循环：高概率的正确路径被选中的概率大，且更新后的概率增幅也大。结果就是概率质量迅速向少数几条路径集中，导致分布尖锐化和多样性丧失。

值得注意的是，对于错误轨迹，情况恰恰相反：高概率的错误轨迹会受到更强的惩罚，导致其概率分布趋于平坦而非尖锐。

3. 重新审视：正确性与多样性的权衡

在提出新方法之前，我们先分析现有的缓解手段为何无法从根本上解决问题。

3.1 熵奖励（Entropy Bonus）的局限性

为了对抗坍缩，一种直观的方法是修改奖励函数，加入熵奖励项：

这里的 鼓励策略去探索那些在基座模型下概率较低的轨迹。

然而，这种全局性的熵奖励存在明显的副作用：它不仅增加了正确轨迹的多样性，也增加了错误轨迹的多样性，往往导致 Pass@1 性能下降。论文在实验中证实，虽然熵奖励在 Countdown 任务上有效，但在 MATH500 任务上却损害了性能。

3.2 熵惩罚（Entropy Penalty）的矛盾

与之相对，另一派研究主张使用熵惩罚（即 ），意在让分布更加尖锐，提升 Pass@1。这在某些任务上确实有效，但显然会加剧多样性坍缩，损害 Pass@K。

3.3 任务依赖性：解的多样性 (Solution Multiplicity)

论文提出了一个关键洞察：熵控制的最佳策略高度依赖于任务本身的特性，具体而言是“解的多样性”（Solution Multiplicity）。

其中 是问题 的正确解的数量。

• 高解多样性任务（如 Countdown）：存在大量且分布广泛的正确解。此时，熵奖励带来的多样性收益超过了其对正确率的损害，因此熵奖励有效。
• 低解多样性任务（如特定数学题）：正确解的路径较少。此时，盲目增加熵只会引入更多错误，熵惩罚反而更优。

这一分析解释了为何现有文献中关于熵控制的结论存在矛盾。

4. Differential Smoothing：差异化平滑策略

基于上述分析，作者提出了 Differential Smoothing (DS)。该方法的核心逻辑是：我们不需要在全局范围内统一增加或减少熵，而是应该根据轨迹的正确性采取差异化的策略。

4.1 核心理念

1. 针对正确轨迹（Correct Trajectories）：我们需要对抗选择偏差和强化偏差，防止分布过早收敛到少数路径。因此，应增加熵（Entropy Bonus），即惩罚高概率的正确样本，奖励低概率的正确样本。
2. 针对错误轨迹（Incorrect Trajectories）：我们希望模型尽快远离错误，且不要在错误路径上发散。理论分析显示错误轨迹的分布趋于平坦，这不利于模型识别主要错误模式。因此，应减少熵（Entropy Penalty），即加大对高概率错误的惩罚力度，或者理解为让模型更“确定”地认为这是错的。

4.2 奖励函数设计

基于此，DS 定义了如下的修正奖励函数 ：

这里， 是原始奖励（如 0 或 1）。对于正确轨迹，减去 （即加上 ）相当于给予一个与自身概率成反比的额外奖励，鼓励探索低概率的正确解。

更进一步，在实际算法实现中（见下文 DS-GRPO），作者对错误轨迹引入了对称的 项来显式地减少熵。

4.3 理论保证

论文在定理 3.4 中给出了严格的证明，表明 DS 方法在满足 KL 散度约束的前提下，能够在正确性（Correctness, ）和正确解的多样性（Correct-Solution Diversity, ）上同时优于全局熵最大化策略（）。

定理 3.4 (理论优势) ：
假设模型能正确估计奖励。对于任意满足接近度约束 的熵正则化策略 ，总是存在对应的参数配置，使得 DS 策略 也满足同样的约束，且成立：

其中：

• 表示正确性（生成正确答案的总概率）。
• 使用正确轨迹上的归一化方差来衡量多样性（方差越小，分布越均匀，多样性越高）。

该定理的证明（详见论文附录）利用了 KL 散度和 散度的性质，证明了差异化处理可以比全局统一处理更有效地利用“概率预算”。

5. 算法实现：DS-GRPO

作者将 Differential Smoothing 的思想集成到了 GRPO (Group Relative Policy Optimization) 算法中，提出了 DS-GRPO。

5.1 GRPO 基础回顾

GRPO 是一种去除了 Critic 模型的 PPO 变体。它对每个输入 采样一组输出 ，并基于组内的相对优势来更新策略。
原始优势函数为：

5.2 DS-GRPO 的改进

为了实现 Differential Smoothing，DS-GRPO 直接在优势函数 上引入修正项。具体的修正公式如下：

这里的修改项具有直观的物理意义：

• 对于正确样本 ()： 是一个正数（因为 ）。这意味着，样本生成的概率 越低， 越大，获得的额外奖励越多。这直接对抗了选择偏差，鼓励模型去挖掘那些“冷门”的正确解。
• 对于错误样本 ()： 是一个负数。这意味着，样本生成的概率 越高， 越大（绝对值越小），惩罚越小；反之概率越低，惩罚越大（负得越多）。（注：此处需仔细辨析论文公式含义。根据论文公式(6)，错误样本加的是 。由于 是负数，这实际上是一个惩罚项。如果 很小，这个惩罚很大；如果 很大，这个惩罚较小。这似乎与“惩罚高概率错误”的直觉稍有出入，或者是论文中的符号定义需要结合 Implementation Detail 理解。让我们回顾论文 Section 4.2 的描述）

勘误与深入理解：
查阅论文原文公式 (4) 和 (6)：
对于错误轨迹，论文使用的是 。
在 Section 3.5 中提到："decreasing entropy for negative samples reinforces correctness"。
在 Section 4.2 中描述："conversely, for unsuccessful completions, we add the term "。
由于 是负值，加上这一项相当于降低总奖励。
让我们看 Log 项的性质：当 ，；当 ，。
如果加上 ：

• 高概率错误（ 大）：惩罚项接近 0。
• 低概率错误（ 小）：惩罚项是非常大的负数。

这里似乎存在一个与直觉的冲突。通常我们要压制高概率错误。但论文 Section 3.5 明确指出 "entropy penalty on negative trajectories does not impact the policy's diversity over correct responses... can improve correctness"。
实际上，DS-GRPO 的目标函数对于错误样本引入熵惩罚（Entropy Penalty），即最小化熵。这意味着让分布更尖锐。对于错误样本集，让分布尖锐意味着什么？意味着模型会更集中地识别出某些“典型错误”并避免之，或者说是让模型对“什么是错的”有更确定性的认知，从而把概率质量挤压给正确样本。
关键点在于： 这一项主要作用于区分正确和错误的边界，通过压低错误样本的熵，实际上是为了让模型更“自信”地将其识别为错误，从而提升整体的 Correctness ()。

5.3 实践细节

在实际实现中，DS-GRPO 使用 （当前采样策略）来代替 （基座策略）计算对数概率。这被证明在经验上更稳定，且在数学上通过重新参数化是等价的（附录 B.3）。

6. 实验评估：全方位的性能提升

论文在多个模型（Qwen2.5, Ministral）和数据集上进行了广泛的实验。

6.1 实验设置

• 模型：Qwen2.5-Math-1.5B, Qwen3-1.7B, Qwen2.5-Math-7B, Ministral-8B-Instruct。
• 数据集：

  • Countdown：算术游戏，目标是用给定的数字构造等式等于目标值。这是一个高解多样性的任务。
  • Math Reasoning：包含 MATH500, AIME24, OlympiadBench 等高难度数学竞赛题。
• 评价指标：Pass@1（衡量正确性）和 Pass@K（衡量多样性与鲁棒性）。

6.2 主要结果：打破 Trade-off

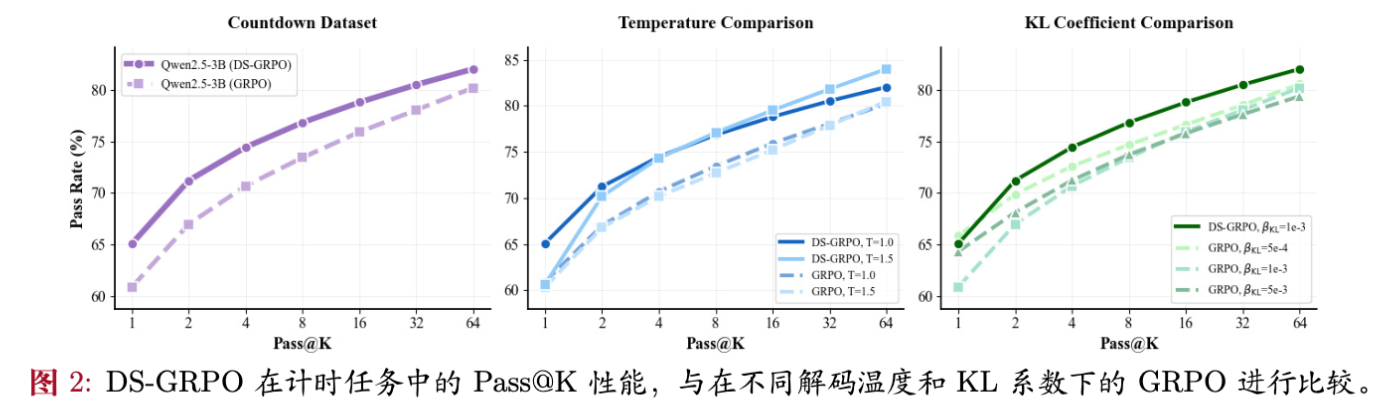
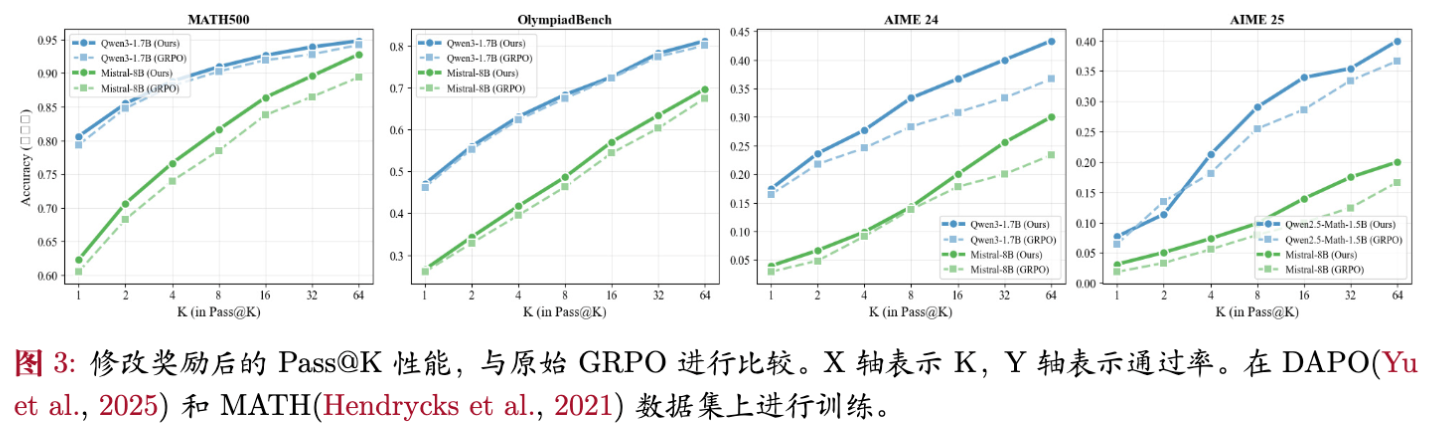
实验结果显示了 DS-GRPO 的一致优越性：

1. Pass@1 与 Pass@K 双提升：与 Vanilla GRPO 相比，DS-GRPO 几乎在所有测试的 值上都取得了提升。例如在 Mistral-8B 上，Pass@1 提升了 0.2%~2.9%，而 Pass@64 提升了 0.5%~6.7%。
2. 推理效率提升：为了达到相同的 Pass 准确率，DS-GRPO 所需的采样次数更少。例如，DS-GRPO 在 时的性能即可匹敌 Vanilla GRPO 在 时的性能，相当于4倍的推理加速。

6.3 与其他方法的对比

论文将 DS-GRPO 与多种现有的多样性增强方法进行了对比：

• Outcome Reward (Vanilla GRPO) ：基线。
• Pass@K Reward (Tang et al., 2025)：直接将 Pass@K 作为奖励信号。这种方法训练不稳定，且往往牺牲 Pass@1。
• Unlikeliness Reward (He et al., 2025a)：对高概率序列进行惩罚。DS-GRPO 在各个 K 值下均优于此方法。
• Entropy Regularization（全局熵奖励/惩罚）：

  • 在 Countdown 任务（高解多样性）中，全局熵奖励有效，但 DS-GRPO 更好。
  • 在 MATH 任务（低解多样性）中，全局熵奖励失效甚至有害，而 DS-GRPO 依然稳健提升。

这一对比有力地证明了差异化平滑比全局策略更具普适性。

6.4 消融实验：

为了验证 DS 策略中两部分的必要性，作者进行了消融研究：

• DS-GRPO-Positive：仅对正确轨迹应用熵奖励（）。

  • 结果：能提升 Pass@K（多样性），但在 Pass@1 上提升有限。
• DS-GRPO-Negative：仅对错误轨迹应用熵惩罚（）。

  • 结果：能提升 Pass@1（正确性），但在 Pass@K 上不如完整版。
• 完整版 DS-GRPO：结合两者，实现了最佳平衡。

这验证了论文的核心假设：在正确轨迹上通过增加熵来提升多样性，在错误轨迹上通过减少熵来巩固正确性，两者是互补的。

7. 深入讨论：熵控制的原则

论文通过实验数据进一步阐释了任务特性与熵控制策略的关系。

通过定义并测量“解的多样性”（Solution Multiplicity），作者发现：

• Countdown（解多样性 ~15.7）：熵奖励带来的收益高达 +3.4%。
• Math（解多样性 ~3.7）：熵奖励导致性能下降 -6.0%。
• Knight and Knaves（逻辑题，解唯一，解多样性 1.5）：熵奖励严重损害性能 -9.0%。

这一发现具有重要的指导意义：在实际应用中，如果任务允许开放式解答（如创意写作、复杂代码），全局熵奖励可能是安全的；但在答案唯一或路径收敛的逻辑推理任务中，必须谨慎使用熵奖励，或者直接转向 DS-GRPO 这种更精细的控制方法。

可视化图解：

更多细节请阅读原论文。

往期文章：

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题