• 论文标题：Scaling Embeddings Outperforms Scaling Experts in Language Models
• 论文链接：https://arxiv.org/pdf/2601.21204

TL;DR

今天解读一篇来自美团 LongCat 团队近期发布的技术报告。报告探讨了在混合专家模型（MoE）面临稀疏性扩展瓶颈时，如何利用 Embedding 层作为正交的扩展维度。报告通过系统性的实验分析，对比了扩展专家数量（Expert Scaling）与扩展 Embedding 参数（Embedding Scaling）的效能，发现了 Embedding Scaling 具备更优 Pareto 前沿的特定区间。

基于 N-gram Embedding 技术，研究团队从零训练了 LongCat-Flash-Lite 模型（68.5B 总参数，约 3B 激活参数），其中 Embedding 参数占比超过 30B（约 46%）。评估结果显示，该模型在保持推理效率的同时，在同等参数规模下优于单纯扩展专家的 MoE 基线，并在 Agent 和代码任务上展现出竞争力。

1. 引言

1.1 MoE 的收益递减与系统瓶颈

混合专家（MoE）架构已成为大语言模型（LLM）稀疏扩展的主流范式。通过动态路由机制，MoE 能够在增加模型总容量的同时保持较低的计算成本（FLOPs）。然而，随着模型规模和稀疏度的增加，MoE 面临两个主要问题：

1. 性能收益递减：随着专家数量增加，性能提升的边际效应逐渐降低，最终趋近于效率饱和点。
2. 系统级瓶颈：在分布式训练中，扩展专家数量带来了巨大的通信开销（All-to-All 通信）和内存带宽压力。

1.2 Embedding

相比于 FFN 层的专家扩展，Embedding 层提供了一个具有 查找复杂度的稀疏维度。理论上，Embedding 层的参数扩展不会引入路由开销，且 lookup 操作天然稀疏。

现有的 Scaling Laws 研究指出，为了最大化计算效率，更大的模型应当配备更大的词表（Vocabulary）。目前利用这一潜力的策略主要分为两类：

• 结构性扩展：如 Per-Layer Embedding (PLE)，在每一层分配独立的 Embedding 参数。
• 词表扩展：利用 N-gram 技术增加每个 Token 的信息密度。

本文的核心贡献在于系统地量化了 Embedding 参数与专家参数之间的缩放效率对比，确立了 Embedding Scaling 的有效边界和最佳实践。

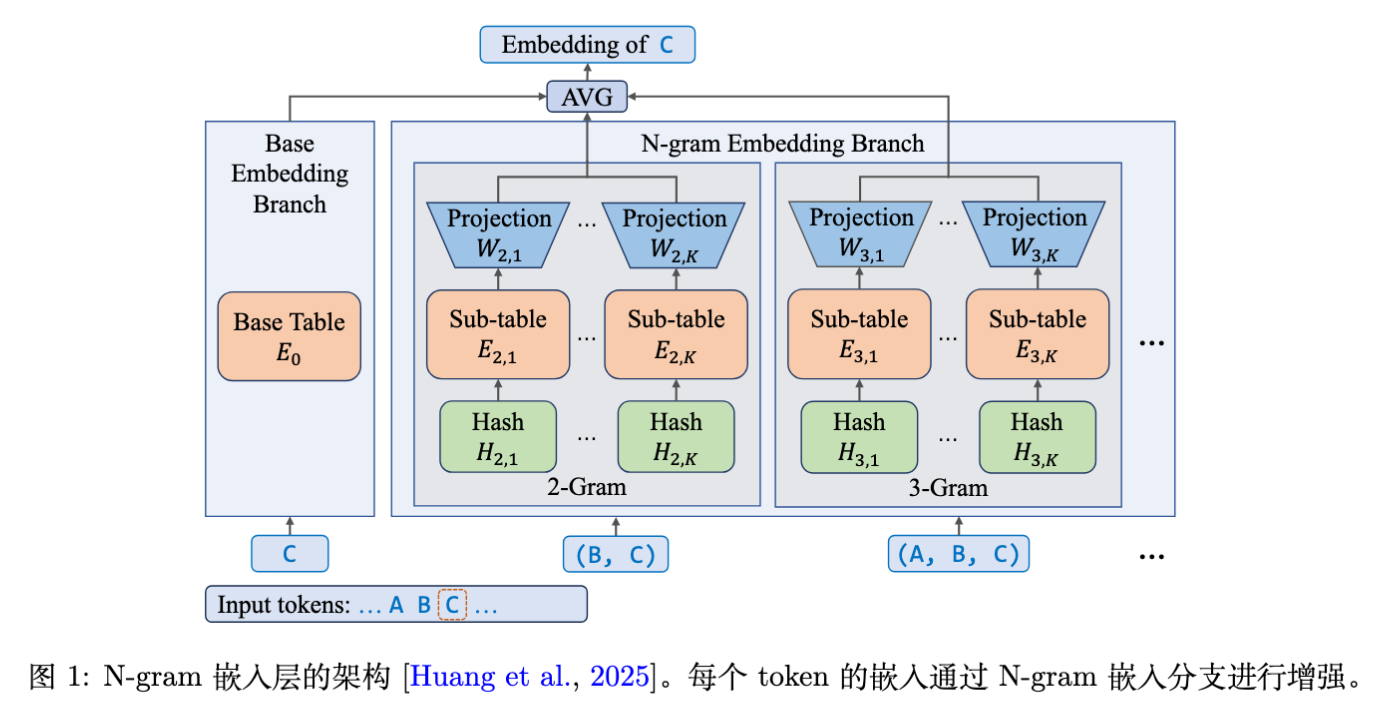
2. N-gram Embedding 层

为了在不因词表爆炸导致训练困难的前提下扩展 Embedding 参数，论文采用了 N-gram Embedding 方法（基于 Clark et al., 2022; Huang et al., 2025 等工作）。

2.1 基础定义

对于序列中的第 个 Token ，其增强后的 Embedding 计算方式如下：

其中：

• 是基础 Embedding 表。
• 是扩展的 N-gram Embedding 表。
• 是最大 N-gram 阶数。
• 是哈希映射函数。

哈希函数采用多项式滚动哈希（Polynomial Rolling Hash）：

2.2 进阶实现：子表分解（Sub-tables）

为了增强表达能力并减少哈希冲突，模型将每个 N-gram Embedding 表分解为 个具有不同词表大小的子表，并引入线性投影。最终形式如下：

• 是子表，维度为 。
• 是线性投影矩阵。
• 通过调整子表维度，确保参数总量对 和 不敏感。

架构示意图如下：

3. Embedding Scaling 与 Expert Scaling 的对比分析

这是论文最核心的章节。研究团队构建了严格的对比实验：在相同的激活参数预算（280M, 790M, 1.3B）下，通过从头预训练（From-scratch Pre-training）来对比两种扩展策略。

• 基线（MoE Baseline）：通过增加专家数量来达到目标总参数量。
• 实验组（N-gram Embedding）：在固定专家数量的基础上，通过 N-gram Embedding 增加参数至与基线相同。

3.1 最佳切入时机：稀疏度阈值

实验发现，N-gram Embedding 的缩放动力学主要取决于基础模型的稀疏度（定义为总参数量与激活参数量之比）。

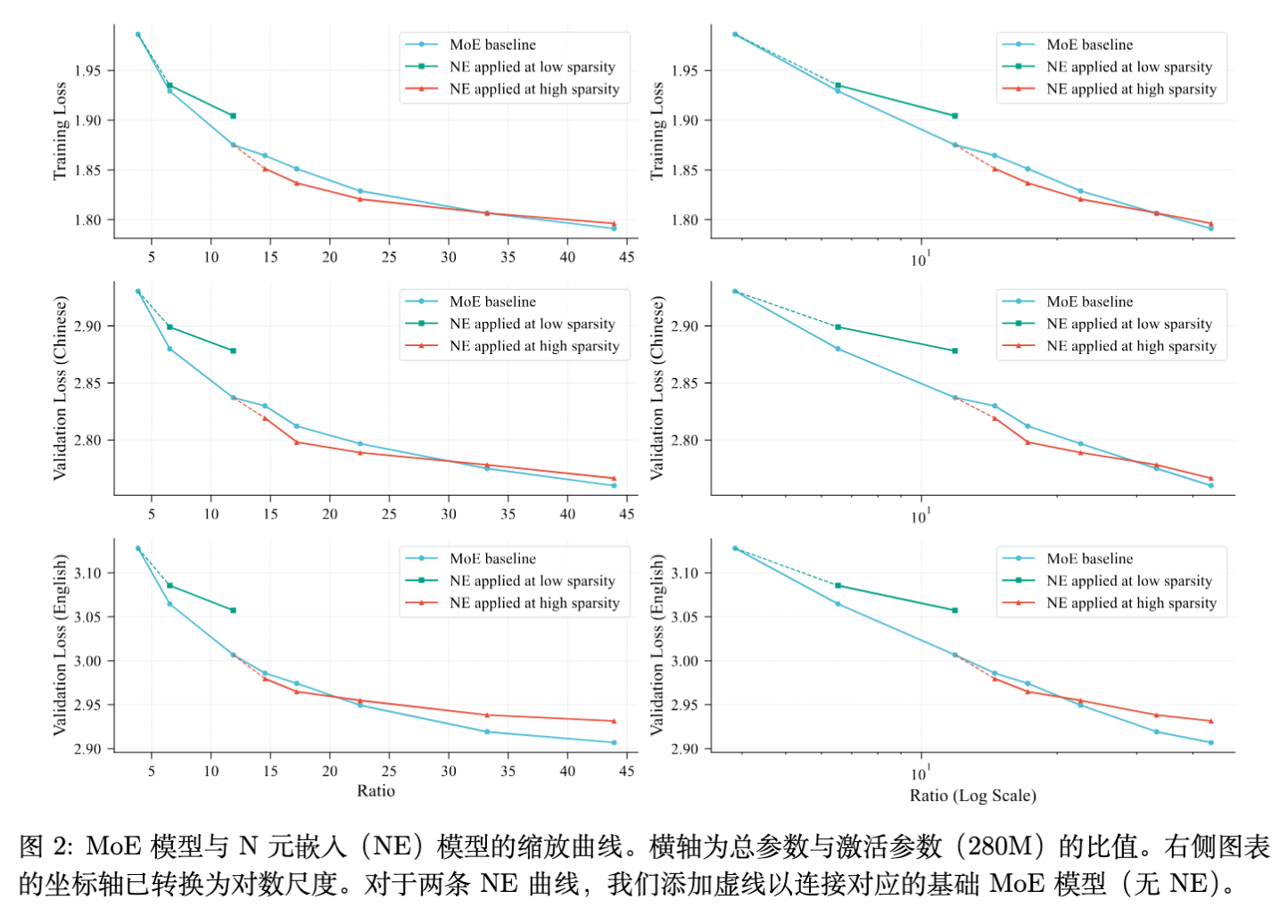
现象分析：

1. MoE 的对数线性关系：MoE 的 Loss 随专家数量增加呈现对数线性下降。在低倍率（Ratio）区间，少量增加专家就能显著降低 Loss。
2. 高倍率区间的收益反转：随着倍率增加，MoE 需要极其庞大的专家数量才能获得同等的 Loss 下降。
3. 结论：在低参数倍率下，Embedding Scaling 不如直接增加专家有效；但在高稀疏度水平（高倍率）下，Embedding Scaling 的收益显著超过 Expert Scaling。

设计原则：应在专家数量扩充至超过其“甜点（Sweet Spot）”区，即边际收益开始明显下降后，再引入 N-gram Embedding。

3.2 参数预算分配策略

观察图 2 中的曲线交叉点，研究发现当 N-gram Embedding 占据过多参数预算时，性能会被 MoE 基线反超。Loss 随 N-gram Embedding 比例呈现 U 型曲线。

设计原则：分配给 N-gram Embedding 的参数预算不应超过模型总参数预算的 50% 。

3.3 缓解哈希冲突：词表大小的选择

哈希冲突会导致不同 N-gram 的语义叠加在同一个 Embedding 向量上，阻碍学习效率。研究团队分析了“词表命中率（Vocabulary Hit Rate）”和“哈希冲突数（Hash Collisions）”。

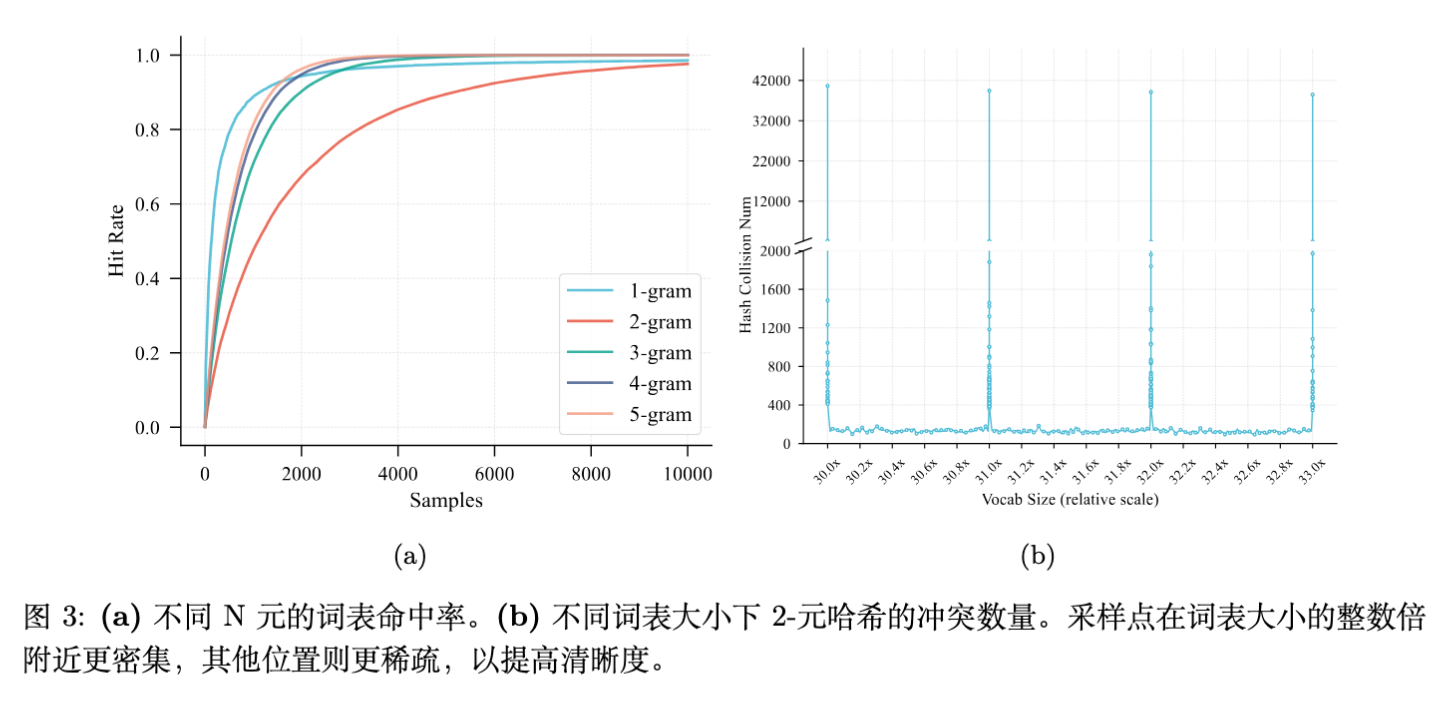
关键发现：

• 2-gram 的哈希冲突数与词表大小呈现强非线性相关。
• 当 N-gram 词表大小接近基础词表大小的整数倍时，冲突数会剧烈飙升。

设计原则：N-gram Embedding 的词表大小应避免设为基础词表大小的整数倍。

3.4 超参数敏感性分析

针对 N-gram 阶数 和子表数量 的消融实验（基于 790M 激活参数模型）：

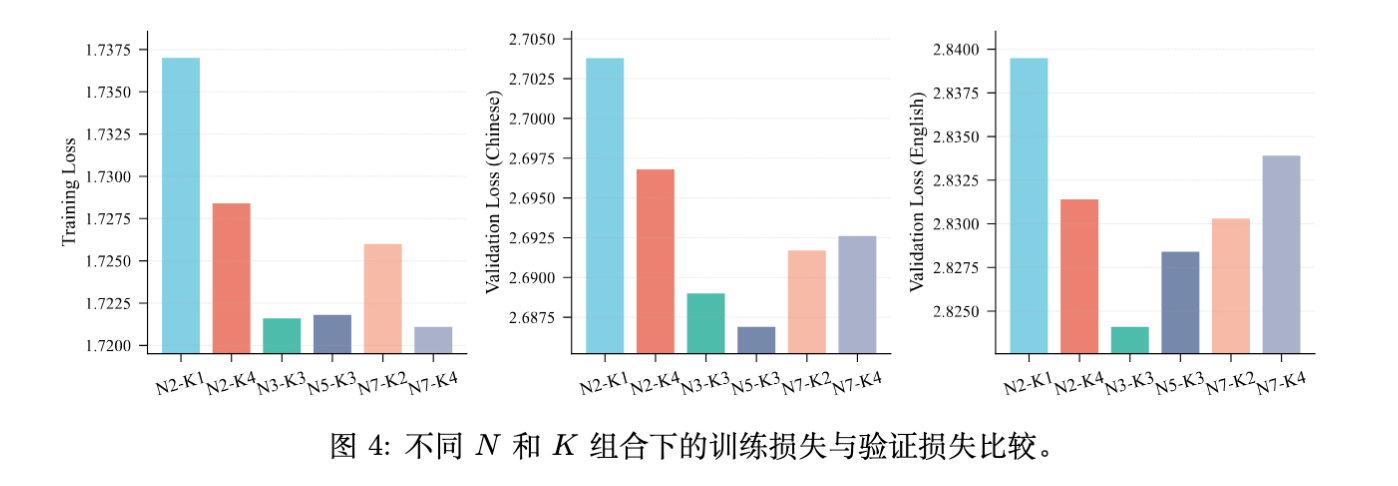
• 低配表现差： 时模型性能最差。
• 鲁棒区间：当 且 时，性能差异较小。
• 经验法则：将 设定在 3 到 5 之间通常能获得近乎最优的性能。

3.5 训练稳定性：Embedding 放大

早期实验发现，N-gram Embedding 模型在训练初期面临信号被淹没的问题。

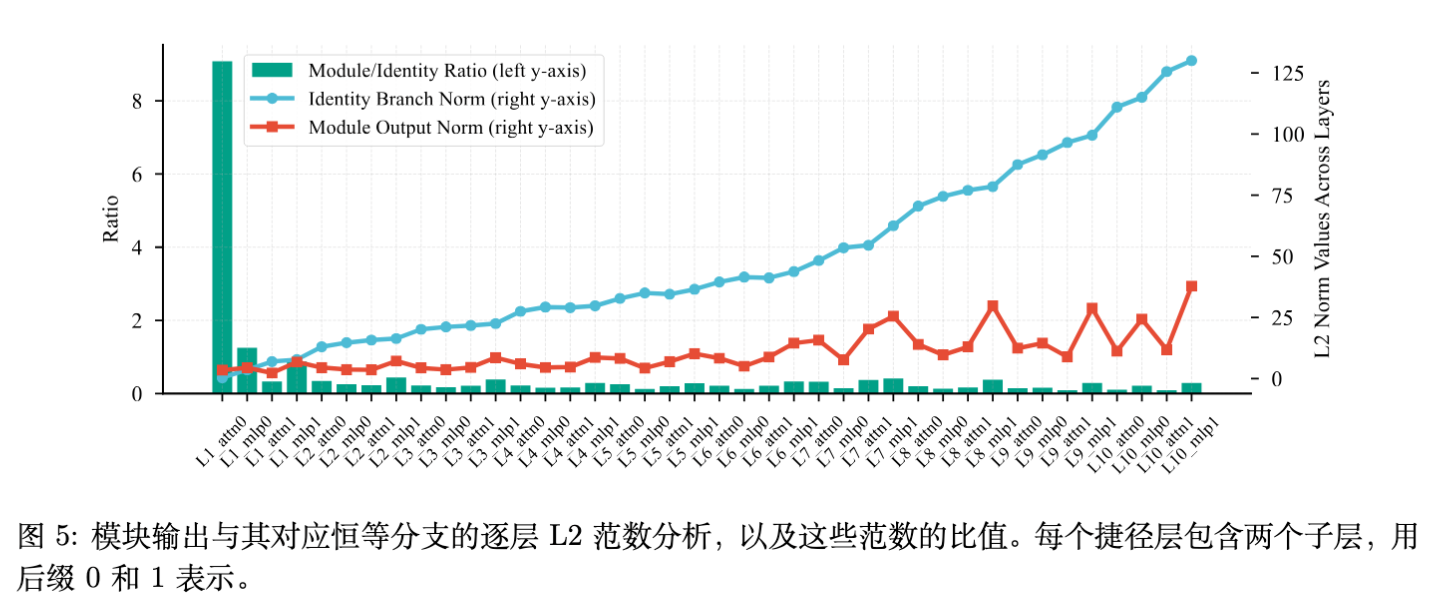
问题：首个 Attention 模块输出的 L2 范数比 Embedding 输出（Identity 分支）高出一个数量级（约 10 倍）。在残差连接求和时，Embedding 信号实际上被“淹没”了，导致训练困难。

解决方案：

1. 缩放因子（Scaling Factor）：引入 对 Embedding 输出进行缩放。
2. 归一化（Normalization）：在合并到残差流之前应用 LayerNorm。

实验表明，应用上述 Embedding Amplification 技术后，Training Loss 和 Validation Loss 均有一致性的降低（约 0.02），这在预训练中是显著的提升。

3.6 模型宽度与深度的影响

这是影响 Embedding Scaling 效能的两个关键架构因素。

3.6.1 模型宽度的影响（Width）

在固定层数（10层）的情况下，分别在 790M 和 1.3B 激活参数规模下进行实验。

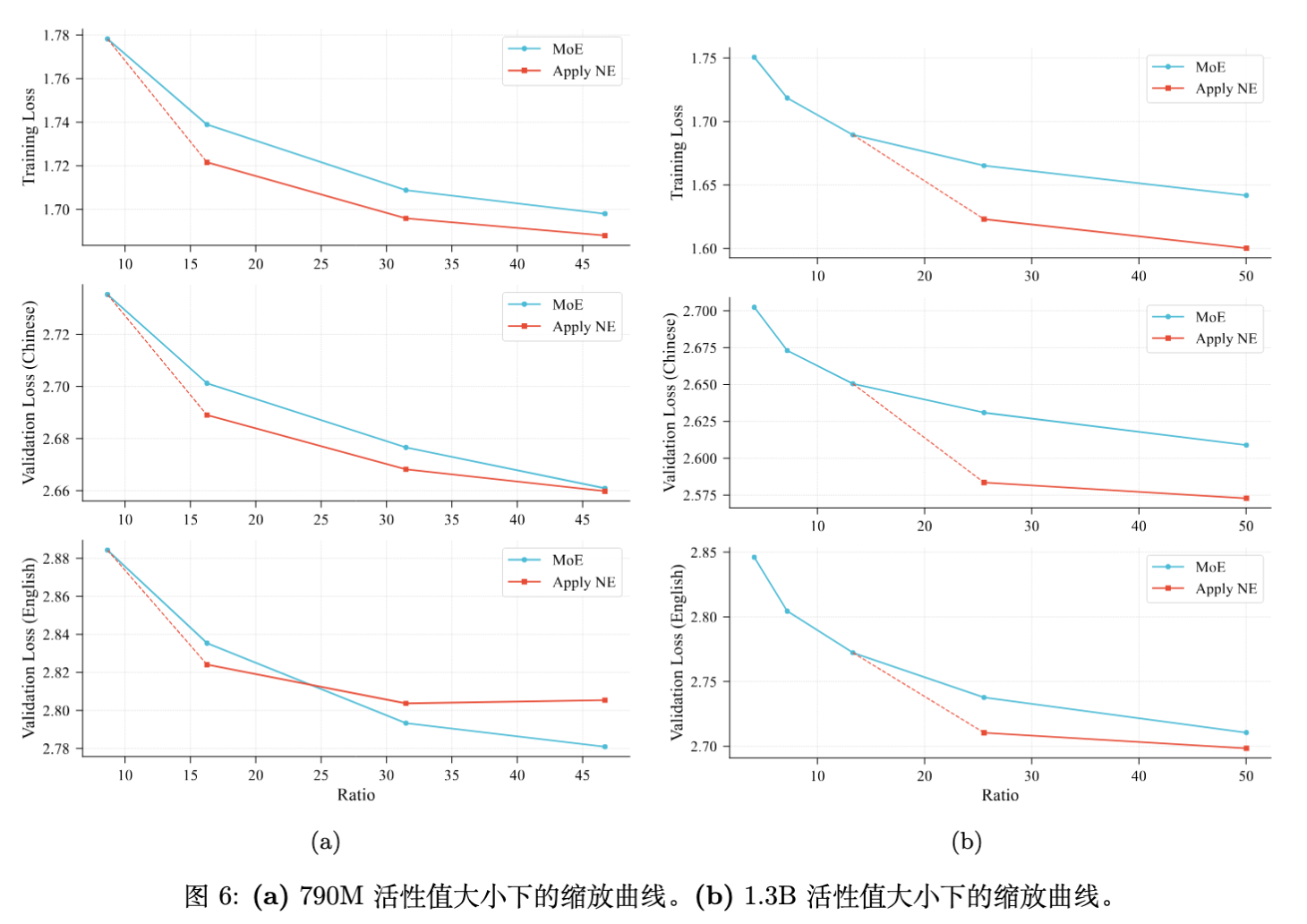
发现：

• 更宽的模型优势更大：随着模型宽度增加，N-gram Embedding 曲线与 MoE 曲线的交叉点向更高的倍率（Ratio）移动。
• 在 1.3B 激活规模下，即使 Ratio 高达 50，N-gram Embedding 依然保持优势。

结论：增加模型宽度（Hidden Size）能够显著扩大 N-gram Embedding 的有效利用窗口。

3.6.2 模型深度的影响（Depth）

在 Pre-Norm 架构中，随着网络深度增加，通过 Skip Connection 传递的原始 Embedding 信号会被逐渐稀释。

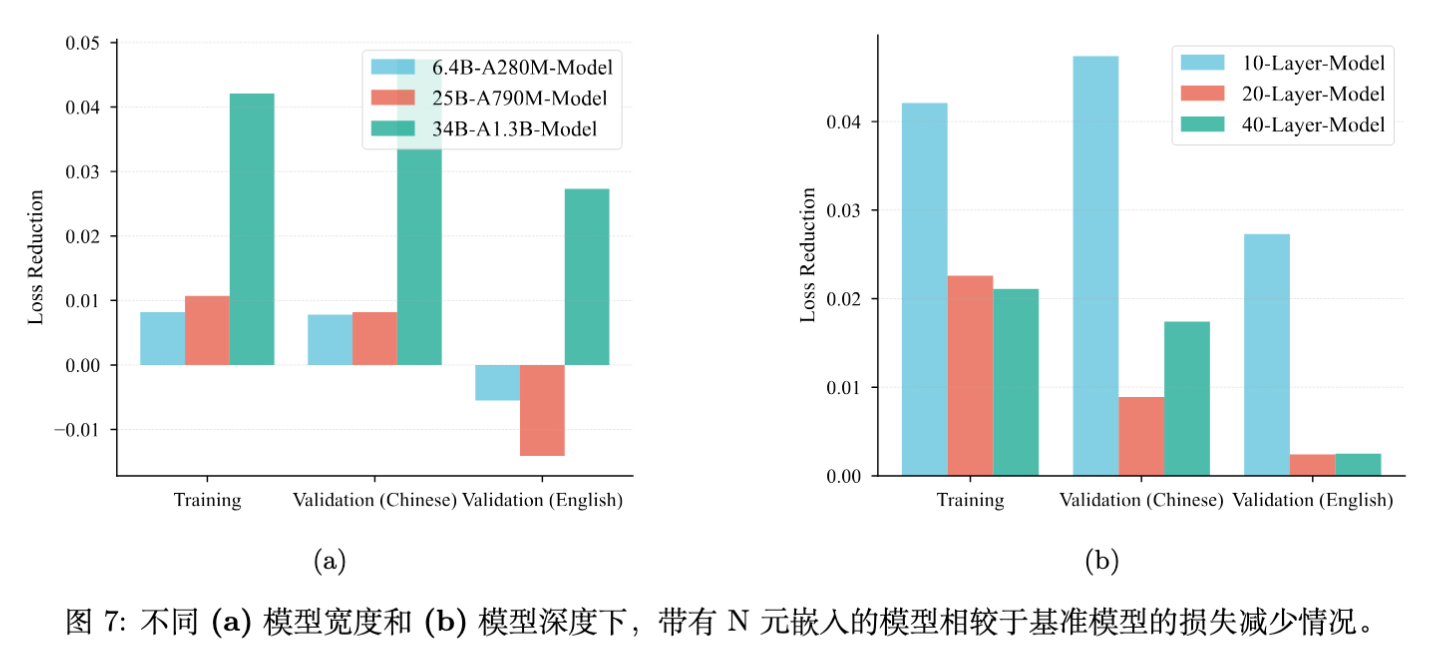
发现：

• 当模型深度超过 20 层时，N-gram Embedding 相对于 MoE 基线的性能优势显著收缩。
• 这与宽度的影响截然相反（宽度增加扩大优势）。

结论：增加模型深度会削弱 N-gram Embedding 的相对优势。

讨论：虽然深度有负面影响，但在常规深度（如 40 层以内）下，结合足够的宽度，N-gram Embedding 依然能带来显著增益。

4. 推理效率与系统优化

虽然 N-gram Embedding 减少了 MoE 层的激活参数，降低了内存 I/O 压力，但也引入了新的计算和通信开销。

4.1 激活参数的重新分配

N-gram Embedding 本质上是将参数从 MoE 层（需加载但计算稀疏）转移到了 Embedding 层（需查找）。对于 I/O 受限（I/O-bound）的大 Batch 解码场景，减少 MoE 层的激活参数至关重要。

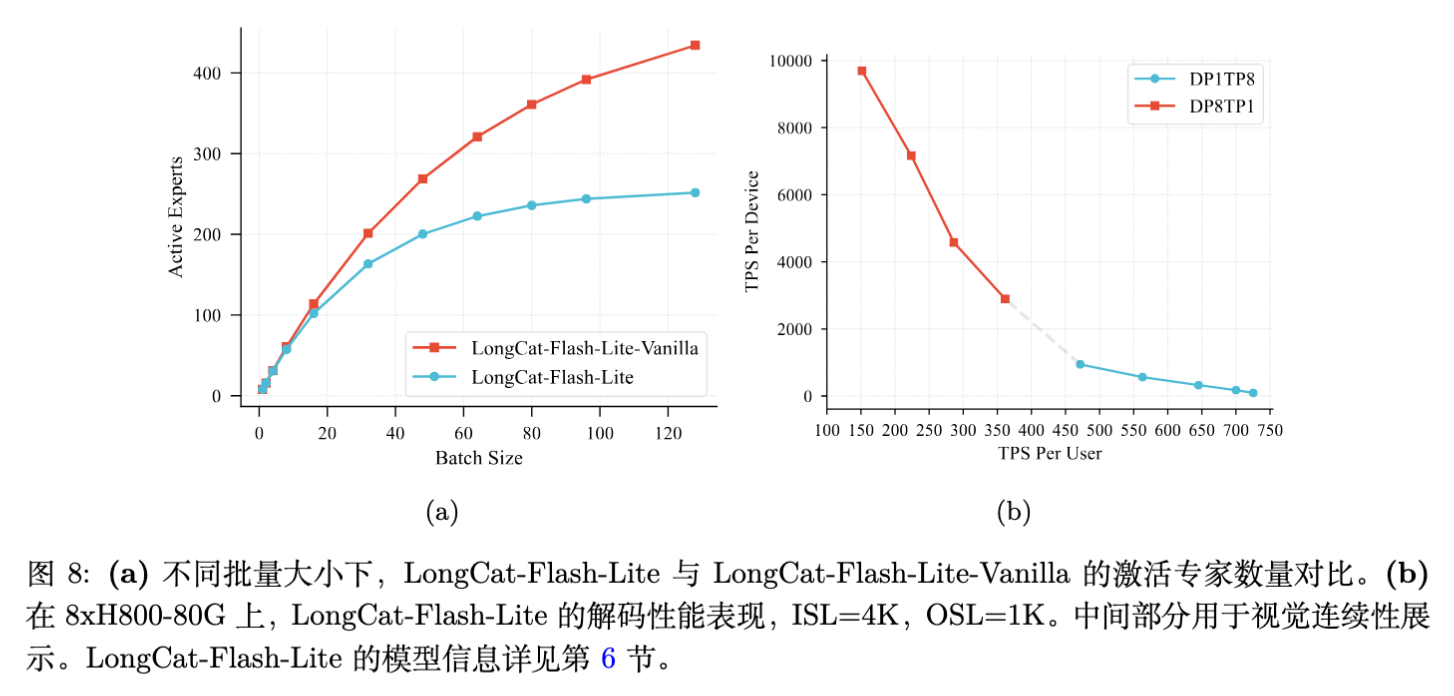
4.2 优化的 Embedding Lookup

挑战：

1. 动态调度：推理框架的复杂调度使得预先确定 Token 序列变得困难。
2. 计算开销：N-gram 哈希和查找引入额外延迟。

解决方案：N-gram Cache
受 KV Cache 启发，团队设计了 N-gram Cache。

• 机制：利用定制 CUDA Kernel 在设备端直接管理 N-gram ID。
• 优势：实现了与推理调度逻辑的低开销同步，避免了重复计算。

4.3 投机采样（Speculative Decoding）的协同

由于模型极高的稀疏性，必须使用大 Batch Size 才能饱和 GPU 内存带宽。这天然契合投机采样（Speculative Decoding）。

优化策略：

1. Draft Model 优化：Draft Model 通常层数少，N-gram 开销占比大。策略是让 Draft Model 使用常规 Embedding，跳过 N-gram 查找。
2. 缓存复用：在 Drafting 阶段缓存 N-gram Embedding，供 Verification 阶段复用，消除冗余计算。

前瞻性思考：
论文提出 N-gram Embedding 本身蕴含了丰富的局部上下文信息，未来可能直接用于构建超轻量级的 Draft Model（如 Early Rejection 机制）。

5. 与 Per-Layer Embedding (PLE) 的对比

PLE 是另一种扩展策略（如 Google DeepMind 的 Gemma 3n）。论文提出了 PLNE (Per-Layer N-gram Embedding) 进行对比。

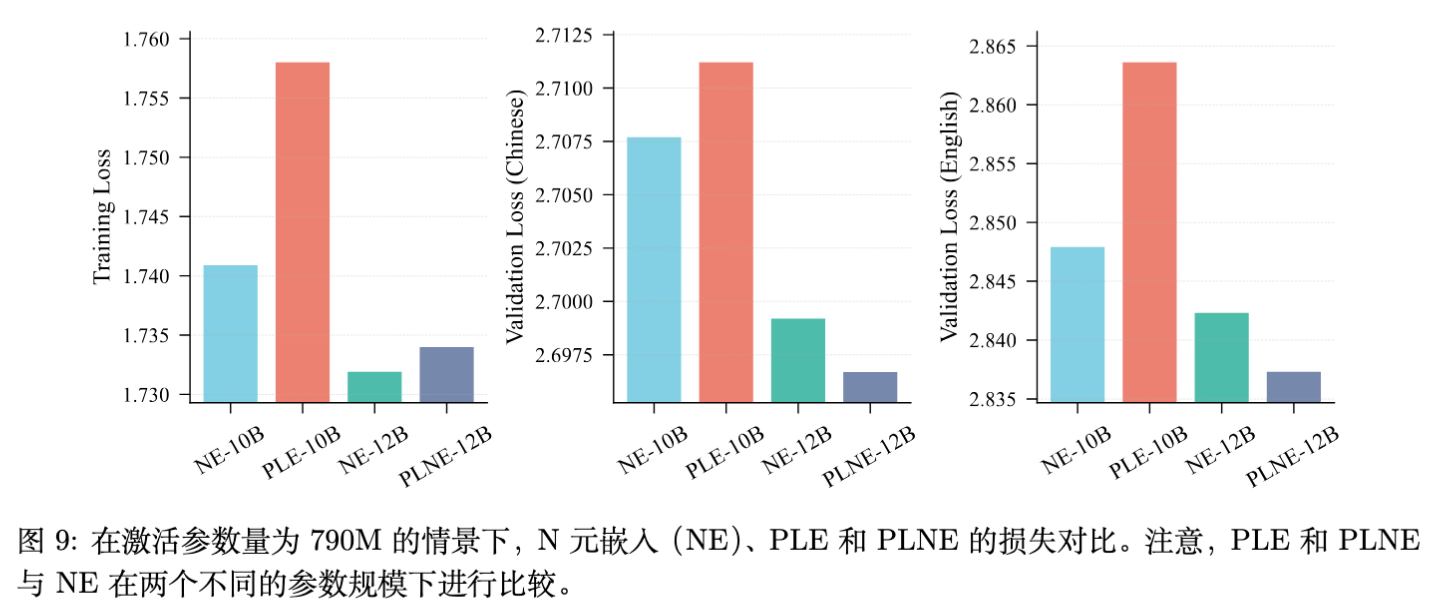
实验结论：

• PLE vs NE：PLE 表现不如 N-gram Embedding (NE)。原因是 NE 的学习效率更高。
• PLNE vs NE：PLNE 相比 NE 仅有边缘提升，但引入了更多参数（每层的投影矩阵）。在更大规模实验中，PLNE 未能展现持续优势。
• 决策：考虑到 PLNE 增加了激活参数量，团队最终选择了标准的 N-gram Embedding 方案。

6. LongCat-Flash-Lite 模型报告

基于上述研究，团队发布了 LongCat-Flash-Lite。

6.1 模型规格

• 总参数量：68.5B
• 激活参数量：2.9B ~ 4.5B (动态变化)
• Embedding 参数：31.4B (N-gram Embedding)，占比 46%。
• 结构：14 个 Shortcut Layers，每层 256 FFN Experts + 128 Zero-Experts，Top-12 Routing。
• 训练数据：11T Token 预训练 (8k context) -> 1.5T Token Mid-training (128k context) -> SFT。使用 YARN 支持长文。

6.2 基础模型评估 (Base Model)

对比基线 LongCat-Flash-Lite-Vanilla（同参数量，无 N-gram Embedding，全部参数用于扩展专家）。

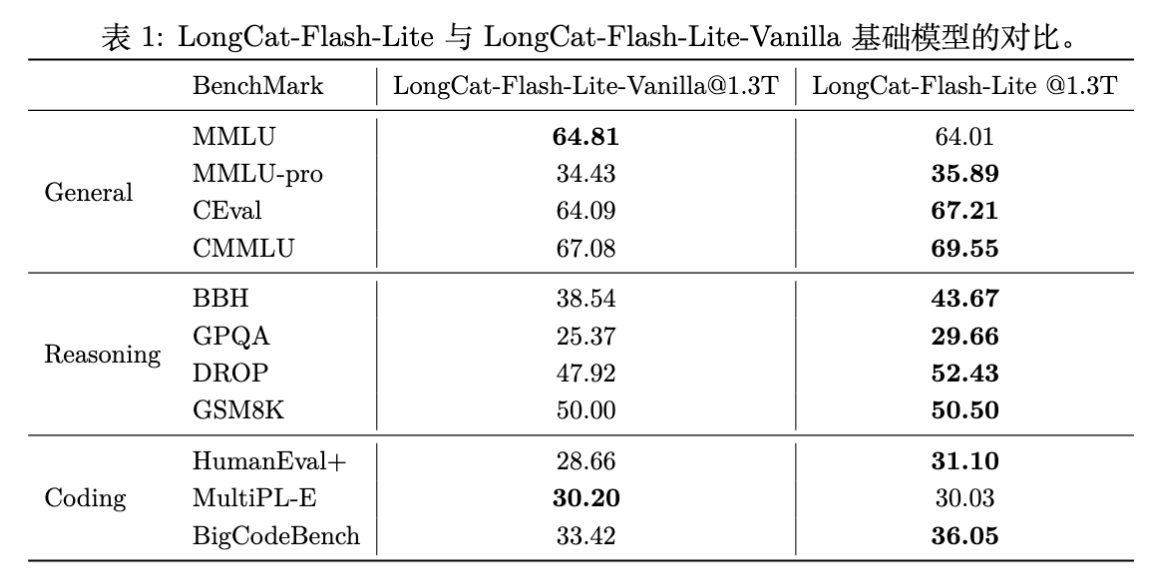
结果：

• 全面超越：在 MMLU, CMMLU, BBH, GSM8K, HumanEval+ 等绝大多数榜单上，LongCat-Flash-Lite 均优于 Vanilla 版本。
• 验证结论：在稀疏度足够高时，将参数预算分配给 Embedding 比分配给专家更有效。

6.3 Chat 模型评估

对比模型包括：Qwen3-Next-80B-A3B-Instruct, Gemini 2.5 Flash-Lite, Kimi-Linear-48B-A3B。

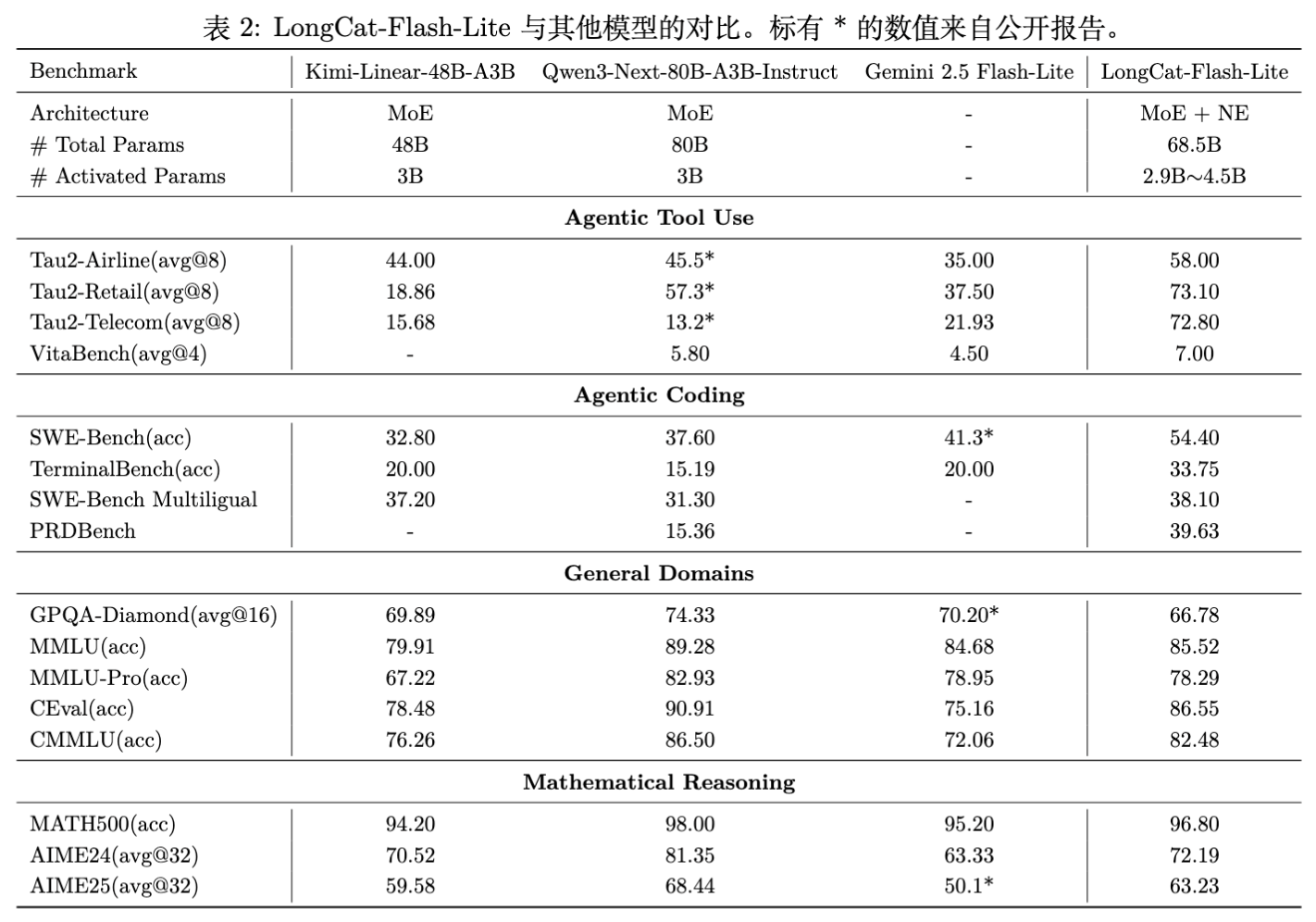
亮点：

• Agentic Tool Use：在 -Bench 的 Telecom 场景得分 72.8，大幅领先竞品（Gemini 2.5 为 21.93）。VitaBench 得分 7.00，位居第一。
• Coding：SWE-Bench 准确率 54.4%，优于 Qwen3-Next (37.6%) 和 Gemini 2.5 (41.3%)。
• Math：MATH500 得分 96.80，接近 Qwen3-Next (98.00)，优于 Gemini 2.5。

6.4 推理性能优化细节

为了解决“小激活参数、大总参数”带来的 Kernel Launch 瓶颈，采用了以下底层优化：

1. Eagle3 投机采样：采用 3-step speculative decoding。
2. Kernel Fusion：

   • 融合通信与计算（AllReduce + Residual + RMSNorm）。
   • 量化融合：将激活量化嵌入到 SwiGLU 和通信算子中。
   • Router Logits 处理融合（Softmax + TopK + Scaling）。
3. Split-KV Combine 优化：针对解码阶段 KV split 数较多的情况，优化 combine kernel，延迟降低 50%。
4. PDL (Programmatic Dependent Launch) ：利用 NVIDIA PDL 技术，允许依赖 Kernel 提前触发，消除 Kernel 间隙，提升 SM 利用率。

最终实测在 8xH800 上，随着 Batch Size 增加，吞吐量（TPS）表现优异。

7. 结论与展望

主要贡献

1. Scaling Law 的修正：证明了在特定的高稀疏度区间（High Sparsity Regimes），Scaling Embeddings 的 Pareto 前沿优于 Scaling Experts。
2. 架构设计指南：

   • Embedding 参数占比不超 50%。
   • 词表避开整数倍以防碰撞。
   • 更宽的模型更适合 Embedding Scaling。
   • 必须使用 Embedding Amplification 解决信号衰减。
3. 工程落地：通过 N-gram Cache 和投机采样解决了 I/O 瓶颈，并开源了 LongCat-Flash-Lite。

局限性与未来工作

• 深度扩展瓶颈：深层模型中 Embedding 信号稀释问题仍需探索更优解（如由残差连接改为 Dense 连接等）。
• PLNE 的分配：虽然 PLNE 整体优势不明显，但非均匀分配（集中在特定层）可能是一个方向。
• N-gram 的语义利用：利用 N-gram 蕴含的共现信息直接辅助投机采样的 Draft 阶段。
  更多细节请阅读原文。

往期文章：

• 阿里云提出 DASD 分布对齐的序列蒸馏：实现更优的长链思维推理

• DeepSeek-OCR 2: Visual Causal Flow 技术报告解读

• 美团 LongCat-Flash-Thinking-2601 技术报告解读

• Agentic Reasoning for Large Language Models 综述：基础、进化与协作

• 小米推出 JudgeRLVR：先判断后生成——打破推理模型“长思维链”的效率悖论

• 你的 GRPO 的优势估计是有偏差的：GRPO 中的统计陷阱与 HA-DW 修正方案

• Meta 提出 Dr.Zero：零数据训练的自进化 Search Agent

• 深度解析 Ministral 3：基于级联蒸馏的参数高效密集模型训练方法论

• Sparse-RL：通过稳定稀疏 Rollout 突破 LLM 强化学习的显存墙

• Qwen 发布 ArenaRL：解决开放域 Agent 的奖励建模难题

• NTU & 通义提出 AgentOCR：基于光学自压缩的智能体历史重构

• DeepSeek 新论文 Engram 深度解读

• Anthropic 提出 EDL 来量化大模型的泛化能力

• 小米 MiMo-V2-Flash 技术报告：MoE 架构、混合注意力机制与多教师在线蒸馏

• DeepSeek-R1 v2 发布：新增技术细节与训练流程全解读

• WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南