• 论文标题：How to Correctly Report LLM-as-a-Judge Evaluations
• 论文链接：https://arxiv.org/pdf/2511.21140

TL;DR

在大语言模型（LLM）评估领域，使用 LLM 作为评判者（LLM-as-a-Judge）已成为一种通过替代人工评估来降低成本的可扩展方案。然而，由于 LLM 评判者本身存在噪声（即其灵敏度和特异度不完美），直接使用其输出的原始准确率（raw accuracy）会导致对模型真实能力的估计产生偏差。

今天介绍一篇来自延世大学、威斯康星大学麦迪逊分校及 KRAFTON 的研究工作《How to Correctly Report LLM-as-a-Judge Evaluations》。该研究针对 LLM-as-a-Judge 的评估偏差问题，提出了一套完整的统计学修正框架。主要贡献包括：

1. 偏差修正（Bias Correction）：推导了一个基于“即插即用”的估计量，利用校准数据集（Calibration Dataset）中的混淆矩阵信息，修正了原始评估中的系统性偏差。
2. 置信区间构建（Confidence Intervals）：构建了包含测试集不确定性和校准集不确定性的置信区间，解决了以往研究仅关注点估计而忽略评估可靠性的问题。
3. 自适应采样分配（Adaptive Allocation）：提出了一种自适应算法，用于在给定校准预算下，最优分配正负样本的比例，以最小化置信区间的长度。

1. 引言

随着大语言模型（LLM）能力的提升，我们越来越多地依赖 LLM 来评估其他模型在各种任务上的表现，例如事实核查、代码生成质量评估以及有害内容检测。这种被称为 "LLM-as-a-Judge" 的范式提供了一种廉价且可扩展的评估手段，能够在缺乏大规模人工标注的情况下快速迭代模型。

通常，研究人员会报告 LLM 评判者认为“正确”的样本比例，记为 ，并将其作为被评估模型质量的代理指标。然而，这种做法存在一个根本性的统计学缺陷。

如下图所示，LLM 在评判过程中会犯两类错误：

1. 将错误的答案误判为正确（假阳性）。
2. 将正确的答案误判为错误（假阴性）。

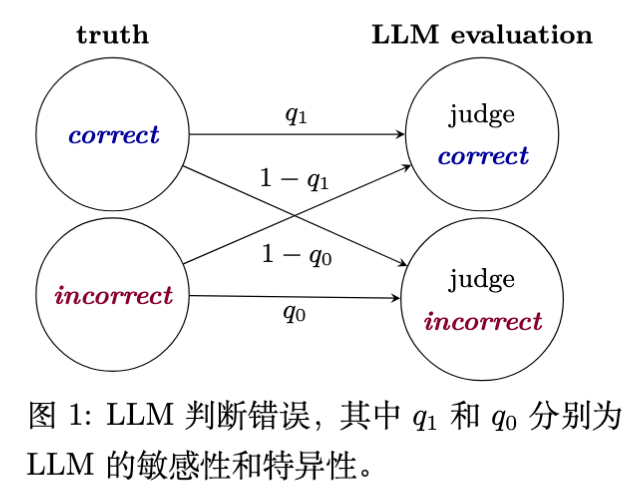
由于这种内在噪声的存在，直接观测到的判断比例 往往不是真实准确率 的无偏估计。现有的文献通常忽略了这一偏差，或者虽然意识到偏差存在但缺乏修正的统一标准。更关键的是，目前的评估报告往往只给出一个点估计值，而缺乏置信区间（Confidence Interval），这使得我们难以判断评估结果的统计显著性。

本文旨在解决上述问题，提供一套在 LLM-as-a-Judge 设置下正确报告评估结果的方法论。

2. 偏差的来源

为了深入理解偏差的成因，我们需要对评估过程进行严格的数学形式化。

考虑所有可能的测试实例集合 。对于每一个实例 （例如一个“问题-模型回答”对），假设存在一个人类定义的真实正确性标签。我们定义一个真实标签函数 ，其中：

• 表示人类判定该回答是“正确”的。
• 表示人类判定该回答是“错误”的。

当我们将此函数应用于随机抽取的测试变量 时，我们得到一个二元随机变量 。我们的最终目标是估计被评估模型相对于人类标准的真实准确率 ：

在实际操作中，我们使用一个 LLM 评判者 来替代人类。令 表示 LLM 的评判结果。在一个包含 个实例的测试集 上，LLM 产生的标签为 。研究人员通常报告的“朴素准确率”（Naive Accuracy） 定义为：

这个 实际上是在估计总体概率 ，即 LLM 将一个随机实例判定为正确的概率。

2.1 灵敏度与特异度

问题在于，LLM 的判定 与真实标签 并不总是通过恒等映射关联。我们需要引入两个参数来描述 LLM 评判者的性能：

1. 灵敏度（Sensitivity, ）：当真实标签为“正确”时，LLM 判定为“正确”的概率（即真阳性率）。

   
   

2. 特异度（Specificity, ）：当真实标签为“错误”时，LLM 判定为“错误”的概率（即真阴性率）。

   
   

2.2 偏差的定量分析

利用全概率公式，我们可以推导出观测概率 与真实准确率 之间的关系：

整理上述公式，我们得到期望观测值的表达式：

或者写作更能体现偏差的形式：

这个公式揭示了几个关键结论：

1. 仅当 LLM 评判者完美（）时，，此时没有偏差。
2. 只要评判者不完美（）， 就是有偏的。
3. 偏差的方向取决于 的值：

   • 当真实准确率较低（）时，LLM 倾向于高估模型性能（正偏差）。
   • 当真实准确率较高（）时，LLM 倾向于低估模型性能（负偏差）。

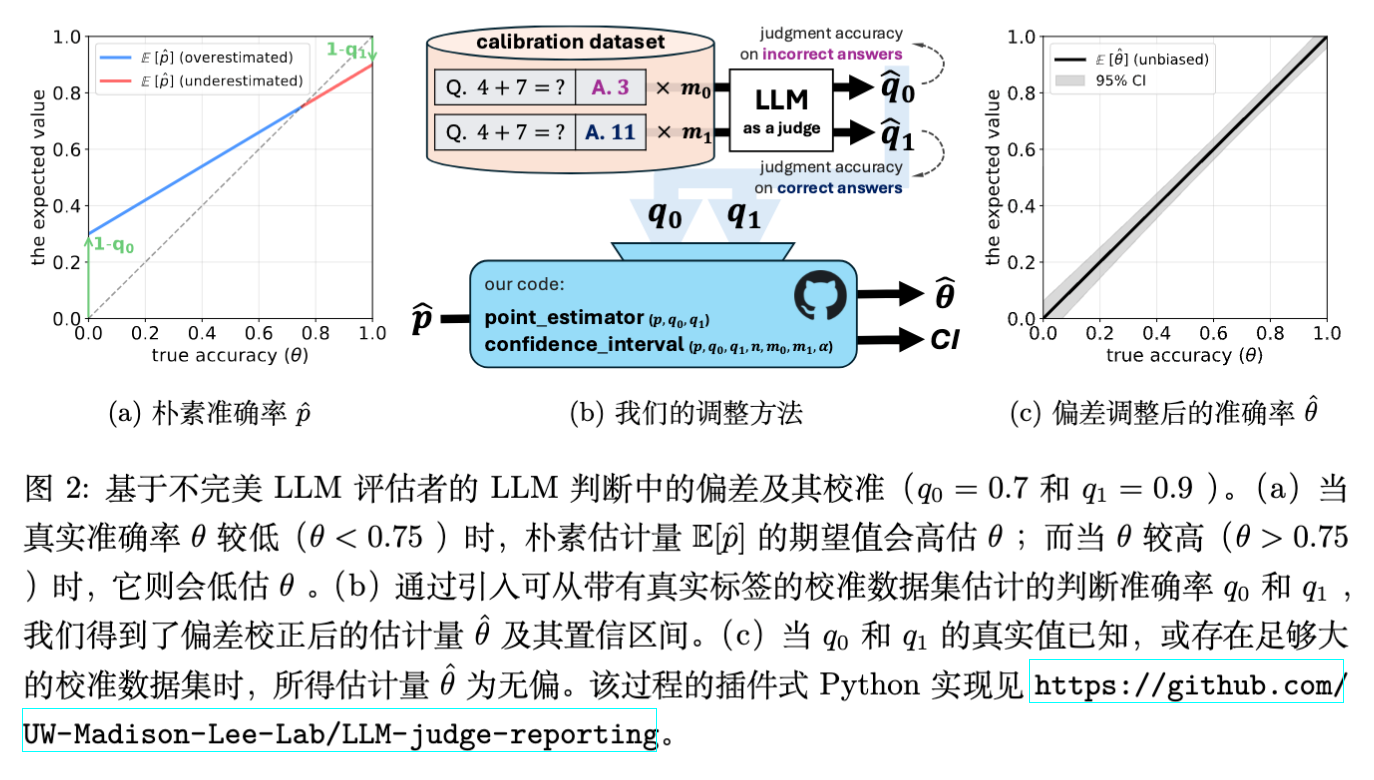
这种偏差的存在意味着，如果不进行修正，不同模型之间的比较可能是无效的。例如，一个实际性能提升的模型，可能因为处于偏差曲线的特定位置，导致被 LLM 评判为性能下降。

3. 偏差修正方法

既然我们已经量化了偏差的来源，接下来的任务就是构建一个无偏估计量。这一方法基于流行病学中经典的患病率估计（Prevalence Estimation）理论（Rogan and Gladen, 1978）。

3.1 点估计量的修正

假设我们已知 LLM 评判者的灵敏度 和特异度 ，且满足 （即 LLM 的表现优于随机猜测）。我们可以通过反解前文的线性方程来得到 的表达式：

在现实场景中，我们不知道真实的 。因此，我们需要使用估计值：

1. 从测试集估计 ：使用朴素准确率 。
2. 从校准集估计 ：构建一个包含人工标注标签的小型“校准数据集”（Calibration Dataset）。

假设校准集中有 个真实标签为“错误”（）的样本，和 个真实标签为“正确”（）的样本。我们统计 LLM 在这些样本上的预测结果，得到：

将这些经验估计值代入 的公式，我们得到偏差修正估计量（Bias-Adjusted Estimator） ：

理论保证：论文中的 Proposition 1 证明，只要校准集样本量 足够大（具体取决于 LLM 的噪声水平），修正后的估计量 的绝对偏差总是小于朴素估计量 的偏差。当 LLM 越接近随机猜测，所需的校准样本量就越大；反之，若 LLM 较为准确，少量的校准样本即可有效去除偏差。

4. 不确定性量化：构建置信区间

仅给出一个修正后的点估计值 是不够的。科学的报告必须包含不确定性范围。在 LLM-as-a-Judge 的场景下，不确定性来源于两个独立的部分：

1. 测试集随机性：用于估计 的样本量 有限。
2. 校准集随机性：用于估计 和 的样本量 有限。

以往的许多讨论往往忽略了第二点，导致置信区间过窄，从而产生盲目的自信。本文利用 Delta 方法（Delta Method）推导了 的渐近方差，并据此构建了有效的置信区间。

4.1 渐近方差的推导

根据 Delta 方法， 的方差可以通过对 的一阶泰勒展开近似得到。由于测试集和校准集是独立的，协方差项为零。 对各变量的偏导数分别为：

其中 。

结合二项分布的方差公式 等，我们可以得到 的渐近方差表达式：

这个公式清晰地展示了各项因素对总方差的贡献：

• 分子第一项来自测试集的不确定性。当测试集 时，此项消失。
• 分子后两项来自校准集的不确定性。这说明即使测试集无限大，如果不增加校准集大小，估计的不确定性依然存在。

4.2 改进的 Wald 置信区间

为了在小样本下获得更好的覆盖率（Coverage Probability），论文采用了 Agresti-Coull 的“加二成功、加二失败”（Add-two-successes and two-failures）调整方法。具体来说，在计算置信区间时，我们将各估计值替换为平滑后的版本：

最终的 置信区间为：

其中 是使用平滑参数计算出的修正准确率， 是标准正态分布的分位数（如 95% 置信度对应 1.96）。

5. 自适应校准样本分配算法

在实际应用中，人工标注校准数据是昂贵的。给定固定的校准预算 ，如何分配 （真实为负的样本）和 （真实为正的样本）的比例，使得最终的置信区间长度最短？

直觉上，如果 LLM 在某一类样本上的判断方差较大（即准确率接近 0.5），或者该类样本对最终 的计算权重较大，我们就应该在该类上分配更多的标注预算。

5.1 最优分配比例

论文中的 Proposition 2 给出了理论上的最优分配指导。假设 接近 1，定义误差率之比 。使得置信区间长度最小的分配满足：

这意味着：

1. 如果 LLM 在识别“错误”答案时更困难（误差率 大，即 大），则应增加 。
2. 如果测试集中观测到的正例比例 较小，这会放大 的影响，因此也应增加 。

5.2 自适应分配算法（Algorithm 1）

基于上述理论，论文提出了一种两阶段的自适应算法：

1. 试点校准（Pilot Calibration）：首先收集少量的校准样本（例如每类 10 个），获得 和 的初步估计。
2. 计算比例：利用测试集的 和初步估计的 ，计算最优样本量 。
3. 最终分配：根据计算出的比例，分配剩余的校准预算。

这一算法确保了数据标注资源被用在“刀刃”上，即最能降低估计不确定性的地方。

6. 实验验证

为了验证所提出方法的有效性，研究团队进行了大规模的蒙特卡洛模拟。实验设置如下：

• LLM 参数：设定 （代表一个有一定能力但不完美的评判者）。
• 真实准确率： 从 0 到 1 变化。
• 数据量：测试集 ，校准集总量 。

6.1 偏差修正效果

实验结果表明，朴素估计量 确实存在显著偏差。当真实准确率 较低时， 严重高估了模型性能；反之则低估。相比之下，修正后的估计量 在所有 取值下都紧密地围绕真实值波动，证明了修正方法的有效性。

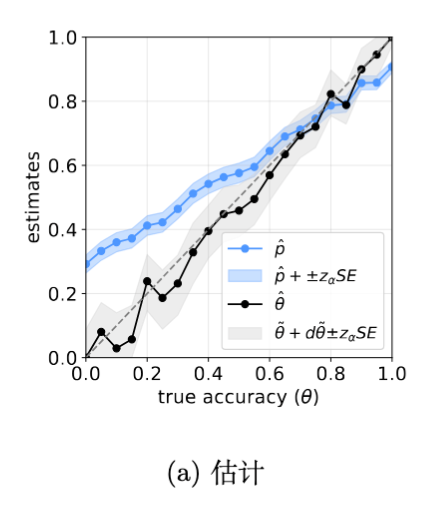
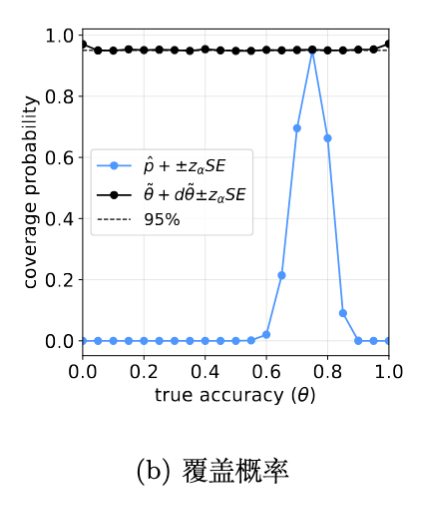
6.2 置信区间覆盖率

对于一个标称 95% 的置信区间，理想情况下，它应该在 95% 的实验中包含真实值 。实验显示，基于 构建的置信区间在所有 范围内都保持了接近 95% 的覆盖率。相反，基于朴素估计 的置信区间覆盖率极差，在许多情况下接近 0，这意味着它几乎总是给出一个错误的范围。

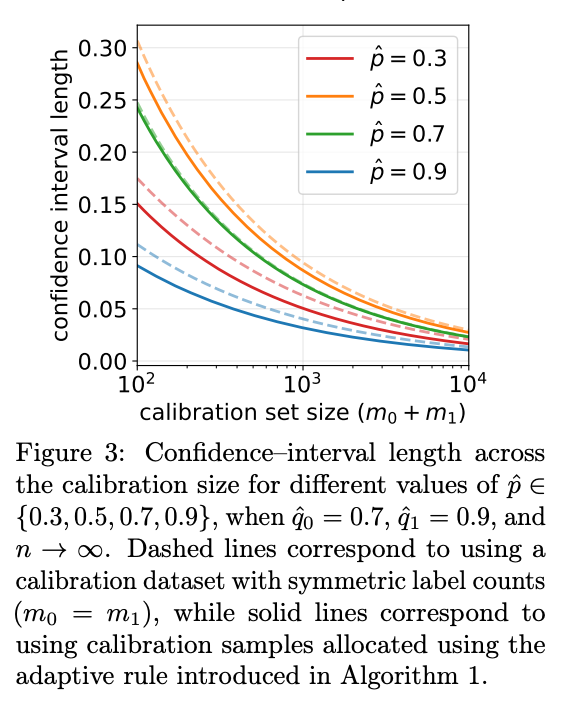
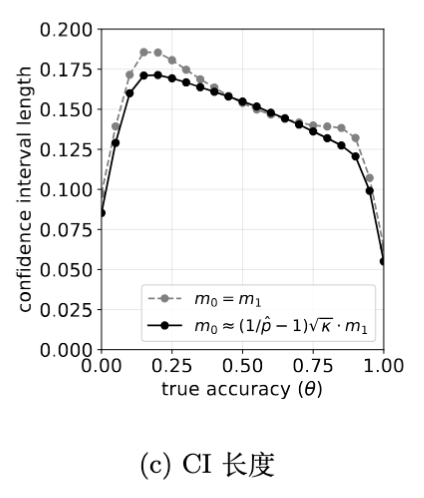
6.3 自适应分配的优势

对比“平均分配校准样本”（）和“自适应分配”，结果显示自适应分配始终能产生更短的置信区间。特别是在 远离 0.5 或 差异较大时，自适应分配带来的精度收益更为明显。

7. 代码实现详解

为了方便社区使用，论文在附录中提供了 Python 实现代码。以下是对核心函数的详细解读：

from math import sqrt
from scipy.stats import norm

def clip(x, low=0.0, high=1.0):
    """
    辅助函数：将数值截断在 [low, high] 范围内。
    用于确保概率值始终在 0 到 1 之间。
    """
    return max(low, min(high, x))

def point_estimator(p, q0, q1):
    """
    计算偏差修正后的点估计值 (Point Estimate)。
    对应论文中的公式 (4)。
    
    参数:
        p  : 朴素准确率 (Naive Accuracy, 对应论文中的 p_hat)
        q0 : LLM 的特异度/真阴性率 (Specificity, 对应论文中的 q0_hat)
        q1 : LLM 的灵敏度/真阳性率 (Sensitivity, 对应论文中的 q1_hat)
    """
    # 核心公式：利用 Rogan-Gladen 估计量反解真实准确率
    # 原理：E[p] = theta * q1 + (1-theta) * (1-q0)，反解出 theta
    th = (p + q0 - 1) / (q0 + q1 - 1)
    return clip(th)

def confidence_interval(p, q0, q1, n, m0, m1, alpha=0.05):
    """
    计算修正后的 (1 - alpha) 置信区间。
    同时考虑了测试集 (n) 和校准集 (m0, m1) 的不确定性。
    对应论文中的公式 (5), (6), (7)。
    
    参数:
        n  : 测试集样本量 (Test set size)
        m0 : 校准集中真实标签为负(错误)的样本量 (Calibration size for z=0)
        m1 : 校准集中真实标签为正(正确)的样本量 (Calibration size for z=1)
        alpha : 显著性水平 (默认 0.05，即 95% 置信区间)
    """
    # 1. 获取标准正态分布的分位数 z (例如 95% 置信度对应 1.96)
    z = norm.ppf(1 - alpha / 2)
    
    # 2. 平滑处理 (Smoothing) - 对应论文公式 (6)
    # 目的：使用 Agresti-Coull 或 Wilson 方法调整样本计数，
    # 防止因样本量过小或概率为 0/1 导致方差计算失效。
    # 注意：这里对 p 使用了 Wilson 类型的中心调整，对 q 使用了加1/加2 平滑
    p = (n * p + z2 / 2) / (n + z2)
    q0 = (m0 * q0 + 1) / (m0 + 2)
    q1 = (m1 * q1 + 1) / (m1 + 2)
    
    # 3. 更新有效样本量 (Effective Sample Sizes)
    n = n + z2
    m0 = m0 + 2
    m1 = m1 + 2
    
    # 4. 计算平滑后的中心估计量 (Smoothed Point Estimate)
    # 使用平滑后的 p, q0, q1 计算 theta_tilde
    th = (p + q0 - 1) / (q0 + q1 - 1)
    
    # 5. 计算中心偏移项 (Bias Shift Term) - 对应论文公式 (7) 中的 d_theta
    # 由于分母 (q0+q1-1) 也是随机变量，这会引入微小的二阶偏差，此处进行修正
    dth = 2 * z2 * (-(1 - th) * q0 * (1 - q0) / m0 + th * q1 * (1 - q1) / m1)
    
    # 6. 计算标准误 (Standard Error) - 基于 Delta Method 推导的渐近方差
    # 对应论文公式 (5) 的分母和根号部分
    # 第一项 p*(1-p)/n : 来自测试集的不确定性
    # 第二项 .../m0    : 来自校准集(特异度估计)的不确定性
    # 第三项 .../m1    : 来自校准集(灵敏度估计)的不确定性
    variance_term = (p * (1 - p) / n + 
                     (1 - th)2 * q0 * (1 - q0) / m0 + 
                     th2 * q1 * (1 - q1) / m1)
    
    se = sqrt(variance_term) / (q0 + q1 - 1)
    
    # 7. 构建 Wald 置信区间并截断
    lower_bound = th + dth - z * se
    upper_bound = th + dth + z * se
    
    return clip(lower_bound), clip(upper_bound)

这段代码简洁明了，我们可以轻松将其集成到现有的评估流水线中。只需额外维护一个小规模的校准集，即可大幅提升评估报告的科学性。

8. 结论与建议

LLM-as-a-Judge 的广泛应用带来便利的同时，也引入了不可忽视的统计偏差。如果我们继续仅报告朴素的准确率，可能会导致领域内出现错误的结论累积，甚至误导模型优化的方向。

一些建议：

1. 停止使用朴素准确率：意识到直接使用 LLM 判断结果作为度量的局限性。
2. 建立校准集：为评估任务构建一个小型的、高质量的人工标注数据集（例如 100-500 条）。
3. 报告修正后的指标：使用本文提供的公式或代码计算 ，并总是附带置信区间。
4. 关注校准集分配：如果不确定如何分配标注资源，优先标注那些 LLM 容易出错的类别，或者使用本文的自适应算法。

往期文章：

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题