-
论文标题:Soft Adaptive Policy Optimization -
论文链接:https://arxiv.org/pdf/2511.20347v1
TL;DR
今天解读一篇来自 Qwen 团队近期发布的论文 Soft Adaptive Policy Optimization (SAPO) 。针对大语言模型(LLM)强化学习(RL)训练中,策略重要性比率(Importance Ratios)方差大导致训练不稳定的问题,SAPO 提出了一种平滑且自适应的策略优化方法。该方法包含两个核心设计:
-
软门控机制(Soft Gating):利用以温度系数控制的 Sigmoid 函数替代传统的硬截断(Hard Clipping,如 PPO/GRPO),构建连续的信任区域,在偏离策略时平滑衰减梯度而非直接置零。 -
非对称温度控制(Asymmetric Temperatures):针对正负优势(Advantage)样本对训练稳定性的不同影响,对负样本采用更高的温度系数使其梯度衰减更快,从而抑制大词表下的噪声扩散。
理论分析表明,SAPO 在特定条件下可退化为序列级更新(类似 GSPO),但保留了 Token 级的自适应能力。实验显示,在 Qwen3-30B 及 Qwen3-VL 的训练中,SAPO 在数学推理和多模态任务上的训练稳定性与最终性能均优于 GRPO 和 GSPO。
1. 背景
在进入 SAPO 之前,我们需要回顾一下当前 LLM RL 的主流范式。
1.1 Group-based Policy Optimization
传统的 PPO 算法依赖于一个价值网络来计算优势函数(Advantage),但在大模型训练中,维护一个与策略网络同等规模的价值网络开销巨大。因此,GRPO (Group Relative Policy Optimization) 应运而生。其核心思想是:对于同一个查询 ,从旧策略 中采样一组回复 ,计算其奖励 ,并通过组内标准化来估计优势:
1.2 核心挑战:方差与截断
在策略更新时,我们通常最大化如下目标:
其中 是重要性比率。
硬截断(Hard Clipping) 的引入是为了防止策略更新步幅过大(即 偏离 1 太多)。然而,这种分段常数式的处理方式带来了两个问题:
-
非黑即白的梯度处理:当 超出 范围时,梯度直接被置为 0。这意味着稍稍“越界”的高价值样本将完全失去学习信号,降低了样本效率。 -
噪声与稳定性的博弈:如果放宽 ,虽然保留了更多样本,但引入了更多偏离策略分布(Off-policy)的噪声梯度,容易导致训练崩溃(Collapse)。
特别是在 MoE(Mixture-of-Experts) 模型中,由于专家路由的异质性,Token 之间的概率分布差异被放大,导致 的方差显著增加。Qwen 团队在论文中指出,MoE 模型的 Log-ratio 方差明显高于稠密(Dense)模型,这使得硬截断策略在 MoE 上的鲁棒性更差。
GSPO (Group Sequence Policy Optimization) 尝试在序列级别进行截断,即基于序列整体的概率比率 进行 Clip。虽然这保证了序列层面的一致性,但它缺乏 Token 级的细粒度控制:如果一个序列中仅有几个 Token 严重偏离,GSPO 会丢弃整个序列的梯度,造成极大的浪费。
2. SAPO 方法详解
SAPO 的核心动机是:用平滑的衰减替代硬性的截断,用自适应的权重平衡探索与利用。
2.1 总体目标函数
SAPO 提出的优化目标如下:
这里最关键的组件是门控函数(Gating Function)。
2.2 软门控机制(Soft Gating)
SAPO 定义 为:
其中 是 Sigmoid 函数。
为了理解这个公式的含义,我们需要观察其导数,即梯度更新时的加权系数。对目标函数求导后,我们得到加权对数策略梯度:
其中的权重 具有非常特殊的形态:
这个权重函数是一个以 为中心的钟形曲线(类似于高斯分布,但基于 Sigmoid 导数构建):
-
当 (On-policy)时:。此时梯度保持原样,鼓励正常的策略更新。 -
当 偏离 1 时: 平滑且指数级衰减。
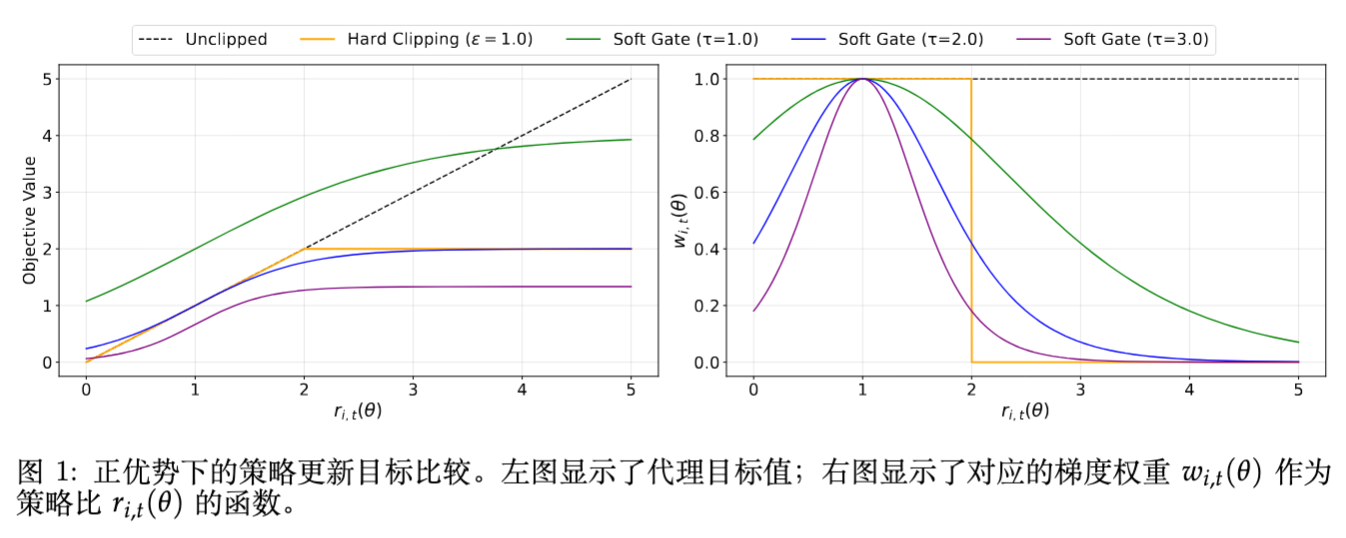
相较于硬截断的优势:
SAPO 实现了一个连续的信任区域(Continuous Trust Region)。它不会在某一个阈值突然切断梯度,而是根据偏离程度“软性”地降低权重。即使样本稍微 Off-policy,只要包含有价值的信息,模型依然能以较小的步长进行学习。这种机制在保留学习信号的同时,抑制了过大更新带来的不稳定性。
2.3 非对称温度控制(Asymmetric Temperatures)
SAPO 的另一个重要创新是针对正负优势(Advantage)使用了不同的温度参数 :
论文中设置 。由于 的衰减速度由 控制( 越大,钟形曲线越窄,衰减越快),这意味着负优势样本的梯度权重会比正优势样本衰减得更快。
为什么要这样设计?
论文提供了一个基于 Logit 梯度的深入分析。考虑 Softmax 输出概率 ,对于 Token 的梯度如下:
-
当 (正向更新):增加采样 Token 的 Logit,降低所有未采样 Token 的 Logit。 -
当 (负向更新):降低采样 Token 的 Logit,提升所有未采样 Token 的 Logit。
在 LLM 的大词表(通常 > 100k)场景下,负向更新具有极大的破坏力。因为它会盲目地提升成千上万个未采样 Token 的概率。虽然这能在一定程度上增加熵(探索),但在训练初期或 Off-policy 严重时,这种更新会迅速引入大量噪声,导致 Logit 分布混乱,引发训练崩溃。
通过设置 ,SAPO 更加激进地抑制那些 Off-policy 的负样本更新,从而显著提升了训练的稳定性。
3. SAPO 与 GRPO/GSPO 的统一
论文不仅在直觉上构建了 SAPO,还通过理论推导展示了 SAPO、GSPO 和 GRPO 可以在一个统一的框架下理解。
3.1 统一形式
定义统一的 Surrogate Objective:
-
GRPO 使用分段常数函数作为 (导数),即在 内为 1,否则为 0。 -
GSPO 使用序列级比率 进行截断,其 在同一序列内是常数。 -
SAPO 使用 形式的软门控。
3.2 理论推导
论文不仅提出了 SAPO 算法,还通过严谨的数学推导揭示了其与现有方法(GRPO、GSPO)的内在联系。核心结论是:在满足特定假设的条件下,SAPO 的 Token 级更新在数学期望上退化为类似于 GSPO 的序列级更新;而在假设失效(高方差)时,它又保留了 Token 级的细粒度控制能力。
以下是该推导的详细过程。
3.2.1 两个基础假设
为了建立 Token 级比率 与序列级比率 之间的联系,论文引入了两个在 RL 微调阶段通常成立的假设:
-
假设 A1 (Small-step / On-policy) :策略更新步幅较小,重要性比率接近 1,即 。根据泰勒展开,这意味着 。 -
假设 A2 (Low Intra-sequence Dispersion) :同一序列内不同 Token 的变化幅度较为一致。定义 为 Token 的对数比率, 为序列的平均对数比率(注: 为 的几何平均)。假设序列内的方差 较小。
3.2.2 软门控函数的泰勒展开
SAPO 的梯度权重函数(即软门控)可以写作关于对数比率 的函数:
利用假设 A1,我们将变量替换为 。接着,我们在序列均值 处对 进行二阶泰勒展开:
其中 是介于 和 之间的某个值。
3.2.3 序列平均后的结果
当我们对整个序列的所有 Token 求平均门控值时,线性项 由于 的定义而自然为 0。因此,平均 Token 门控 可以表示为:
论文进一步证明,由于 是有界的(),且根据假设 A2 序列方差 很小,因此误差项可以被忽略。
最终,我们得到如下近似关系:
这意味着,SAPO 的梯度更新在宏观上等效于根据整个序列的平均表现()来调整更新幅度。这解释了为什么 SAPO 能像 GSPO 一样具备序列一致性(Sequence Coherence)。
3.2.4 物理意义:自适应的 fallback 机制
这一推导的价值在于不仅展示了统一性,还揭示了 SAPO 优于 GSPO 的机制:
-
当假设成立时(大多数情况):Token 间差异小,SAPO 自动退化为序列级方法,利用序列整体信息进行稳定的梯度缩放,避免局部噪声干扰。 -
当假设失效时(离群情况):如果序列中包含个别极端 Off-policy 的 Token(导致方差 变大),上述近似不再成立。此时,GSPO 的硬截断策略会因为序列整体比率受影响而可能丢弃整个序列。而 SAPO 会退回到原始的 Token 级门控,精准地抑制那些离群 Token 的权重,同时保留序列中其他正常 Token 的有效梯度。
这种机制赋予了 SAPO 一种“平滑切换”的能力:在稳定时关注整体,在动荡时关注局部。
3.2.5 实证验证
论文通过统计 Qwen3 模型在训练过程中的数据分布,验证了上述假设的合理性。

图 2 是 MoE 模型(Qwen3-30B-A3B)上的假设验证。左图:Token 比率 高度集中在 1 附近(验证 A1)。中图:序列内对数比率方差 绝大多数小于 0.02(验证 A2)。右图:平均 Token 门控 与方差的关系。
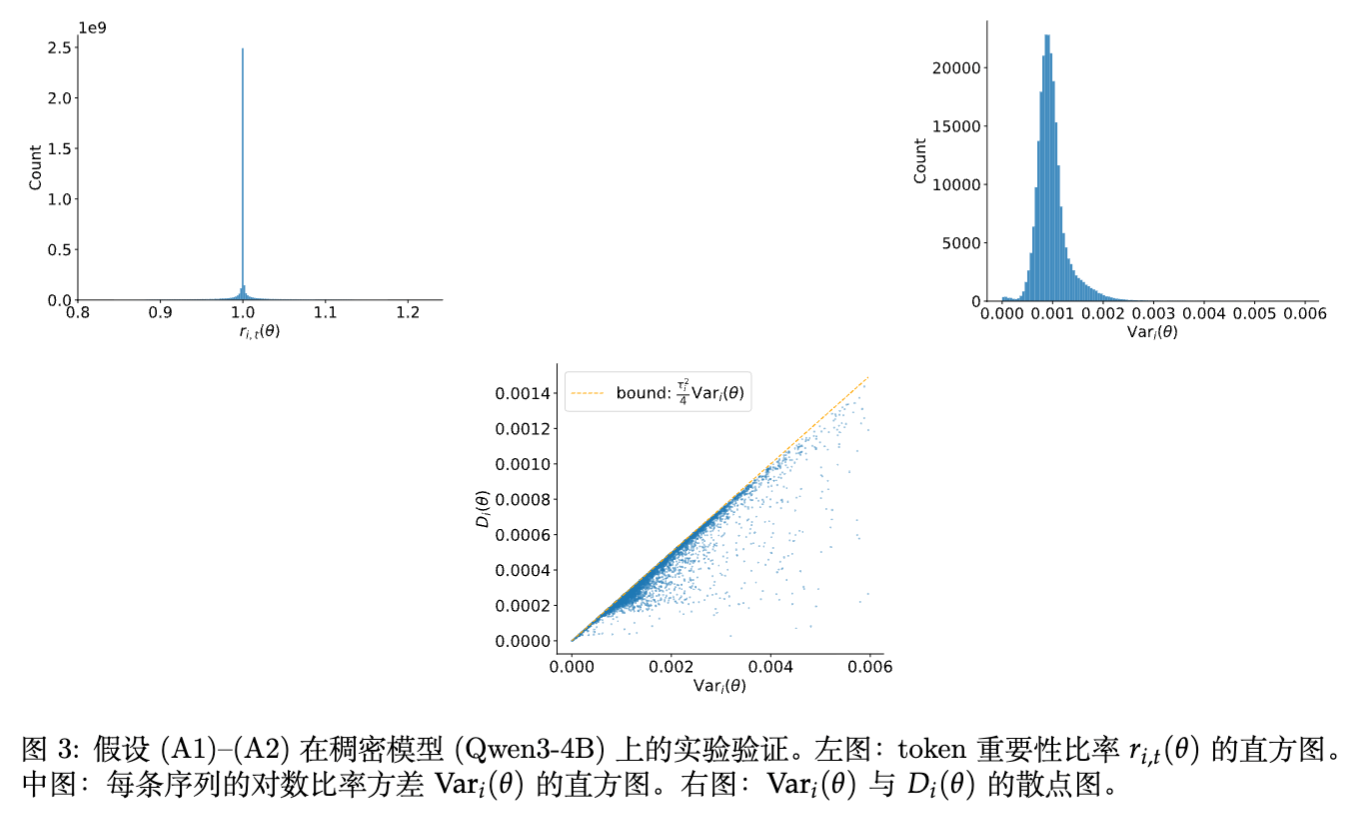
图 3 是Dense 模型(Qwen3-4B)上的假设验证。相比 MoE 模型,Dense 模型的序列内方差更小,数据分布更紧凑,进一步支持了 SAPO 在稠密模型上近似序列级方法的结论。
从图中可以看出,虽然 MoE 由于专家路由的引入导致方差略大于 Dense 模型,但整体依然满足低方差假设。这表明 SAPO 的理论推导在实际的大模型训练场景中是站得住脚的。
4. 实验结果分析
论文在受控环境(Math Benchmarks)和大规模生产环境(Qwen3-VL)中进行了详尽的实验。
4.1 受控实验:数学推理
-
模型:Qwen3-30B-A3B-Base (Cold-start)。 -
基准:AIME25, HMMT25, BeyondAIME。 -
对比方法:GSPO, GRPO-R2 (带 Routing Replay 的 GRPO), SAPO。
主要发现:
-
稳定性:如图 4 所示,GSPO 和 GRPO-R2 在训练初期均表现出了明显的 Training Collapse(训练崩溃,奖励骤降)。相比之下,SAPO 的曲线平滑上升,全程保持稳定。 -
最终性能:SAPO 不仅收敛更稳,而且最终的 Pass@1 准确率也超过了基线方法。 -
无需 Routing Replay:GRPO 通常需要 Routing Replay 来稳定 MoE 的训练,这增加了工程复杂度。SAPO 在不使用该技术的情况下依然胜出,显示了其自身的鲁棒性。

上图是 Qwen3-30B-A3B 在不同 RL 算法下的训练奖励曲线与验证集准确率。SAPO 展现了极佳的稳定性,而基线方法在早期出现崩溃。
4.2 消融实验:温度设置的重要性
为了验证非对称温度设计的必要性,论文对比了三种设置:
-
(1.05 > 1.0) -
(1.0 = 1.0) -
(0.95 < 1.0)
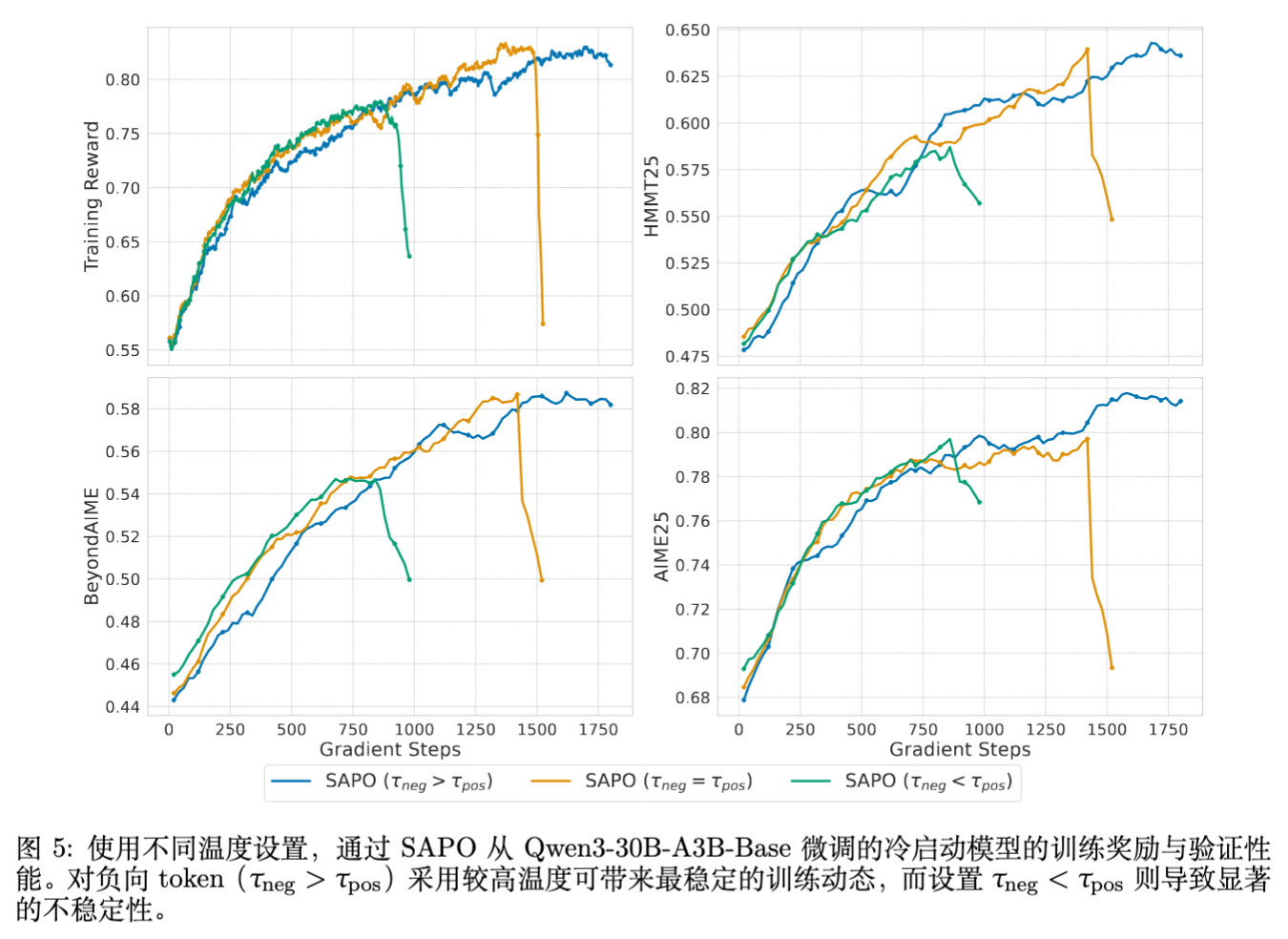
结果(如图 5 所示):
当 时,训练极不稳定,甚至比对称设置更差。而 带来了最稳定的训练动态。这强有力地支持了“负样本梯度更具破坏性,需要更强抑制”的假设。
4.3 大规模实战:Qwen3-VL
论文还将 SAPO 应用于 Qwen3-VL 系列模型的训练,涵盖了不同尺寸(Dense 和 MoE)以及多模态任务(MathVision, LiveCodeBench 等)。
结果:
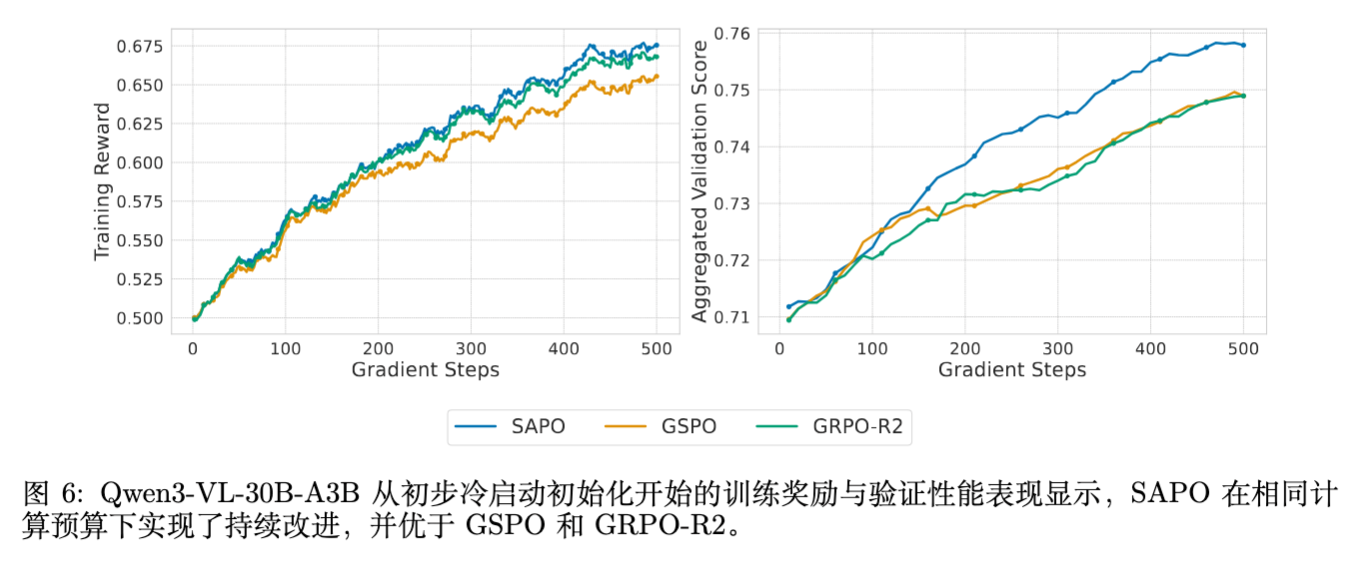
在相同的计算预算下,SAPO 在所有任务上均取得了一致的性能提升(如图 6 所示)。这证明了 SAPO 不仅是一个理论上优雅的算法,更是一个能经受住大规模工业级训练考验的实用方案。
5. 讨论与总结
5.1 为什么 SAPO 有效?
SAPO 的有效性可以归结为对 RL 训练中信号与噪声更精细的处理:
-
保留信号:硬截断丢弃了处于边界之外的梯度,而这些梯度往往包含最有价值的“修正”信号(即模型稍微犯错的地方)。SAPO 通过软门控挽回了这部分损失。 -
抑制噪声:在大词表生成中,负样本的更新具有高度的随机性和扩散性。SAPO 通过非对称温度,精准地遏制了负向更新带来的 Logit 空间扰动。
5.2 对 MoE 模型的意义
MoE 模型由于其稀疏激活特性,天然具有更高的输出方差。传统的 PPO/GRPO 在 MoE 上往往很难调参,容易发散。SAPO 的软门控本质上是一种自适应的方差缩减技术,它允许模型在路由波动较大的情况下,依然能安全地进行梯度更新。这对于未来更大规模的 MoE 模型训练具有重要意义。
5.3 结论
Qwen 团队提出的 SAPO 算法,通过引入 Sigmoid 形式的软门控和非对称温度机制,解决了大模型 RL 训练中硬截断带来的不稳定性与低效问题。它在理论上统一了 Token 级与序列级的方法,在实践中展现了优越的性能与鲁棒性。
往期文章: