DeepSeekMath-V2发布了，主打可自验证的数学推理。

• 论文标题：DeepSeekMath-V2: Towards Self-Verifiable Mathematical Reasoning
• 论文链接：https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf

TL;DR

DeepSeek-AI 团队发布了 DeepSeekMath-V2，这是一项旨在提升大语言模型（LLM）数学推理能力的研究，特别是针对自然语言定理证明任务。该研究的核心动机在于解决传统结果奖励（Outcome Reward）在复杂推理中的局限性，即答案正确但过程错误（假阳性）以及定理证明缺乏明确数值答案的问题。

该论文提出了一套包含证明生成器（Generator）、证明验证器（Verifier）和元验证器（Meta-Verifier）的完整框架。通过强化学习（RL），模型不仅学会了生成证明，还具备了自我验证和自我修正的能力。关键创新包括：

1. 验证器训练：训练模型识别证明中的逻辑漏洞并打分。
2. 元验证机制：引入元验证器来评估验证者提出的批评是否合理，从而减少验证者的幻觉（即对正确步骤的错误批评）。
3. 自验证强化：在生成器的训练中加入自省环节，若模型能诚实地指出自身证明的缺陷，将获得奖励。
4. 推理时计算扩展：利用训练好的验证器指导推理阶段的搜索（Sequential Refinement 和 High-Compute Search）。

实验结果显示，DeepSeekMath-V2 在 IMO 2025、CMO 2024 等高难度竞赛题目上达到了金牌水平，并在 Putnam 2024 中获得了 118/120 的高分。

1. 引言：从结果监督到过程验证

1.1 现有范式的局限性

当前，针对数学推理的强化学习（RL）主流方法主要依赖于最终答案的正确性作为奖励信号（Outcome Reward）。这种方法在 AIME 或 HMMT 等以数值计算为主的竞赛中取得了显著成效。然而，论文作者指出这种机制存在两个根本性的局限：

1. 代理指标的不可靠性：模型可能通过错误的逻辑或巧合得出正确的最终答案。这种“过程错误，答案正确”的现象使得结果奖励无法精确指导模型的推理过程。
2. 任务适用性受限：许多高级数学任务，特别是定理证明，并不要求输出一个简单的数值，而是要求严谨的逻辑推导过程。在这种情况下，基于最终答案的奖励机制完全失效。

1.2 自然语言定理证明的挑战

在自然语言定理证明任务中，模型不仅需要生成证明，还面临着“验证”的难题。现有的经过定量推理训练的模型，往往难以区分证明的有效性，经常出现误报（False Positive），即声称一个包含逻辑漏洞的证明是正确的。缺乏有效的验证反馈循环，阻碍了模型在复杂推理任务上的进一步扩展。

1.3 核心假设与方法论

DeepSeekMath-V2 的研究基于以下观察：

• 即便是对于未解决的问题，人类专家通常也能在没有标准答案的情况下识别出证明中的逻辑漏洞。
• 如果在投入大量计算资源进行验证后仍未发现漏洞，该证明为真的概率较高。
• 识别有效漏洞所需的计算量可以作为评估证明质量的代理指标。

基于此，研究团队提出训练一个LLM 验证器，使其能够在没有参考答案的情况下识别证明中的问题。该验证器随后被用作奖励模型来优化证明生成器。为了防止生成器通过通过“欺骗”验证器来获取高分，研究引入了元验证（Meta-Verification）机制，并构建了一个自动化的数据迭代飞轮，利用计算换取数据质量的提升。

2. 方法论：构建自验证系统

该研究的方法论部分详细描述了如何从零开始构建一个可靠的验证系统，并将其反哺给生成模型。整个流程可以分为三个主要阶段：验证器训练、元验证机制引入、以及生成器的自验证训练。

2.1 证明验证（Proof Verification）

验证器的目标是模拟人类专家评估数学证明的过程。给定一个数学问题 和一个候选证明 ，验证器 需要输出一段证明分析，并最终给出一个评分。

2.1.1 评分标准与数据构建

研究团队制定了一套高层级的评分量表 （详见附录 A.2），将证明质量量化为三个等级：

• 1分：完全正确，逻辑严密，所有步骤均有正当理由。
• 0.5分：整体逻辑成立，但存在细节遗漏或轻微错误。
• 0分：存在根本性缺陷，包含致命逻辑错误或关键缺失。

为了启动训练（Cold Start），团队构建了初始数据集 ：

1. 数据来源：从 Art of Problem Solving (AoPS) 抓取了 17,503 个问题，优先选择数学奥林匹克、选拔赛以及 2010 年后明确要求证明的问题。
2. 样本生成：使用 DeepSeek-V3.2-Exp-Thinking 的变体生成候选证明。由于该基座模型未针对定理证明优化，生成的证明往往简略且易错，因此通过多轮提示（Iterative Prompting）来提升其完整性。
3. 专家标注：随机采样证明，由数学专家根据评分量表进行打分。

由此得到的数据集表示为 ，其中 为专家评分。

2.1.2 强化学习目标

验证器的训练使用了两个奖励分量：

1. 格式奖励（Format Reward, ）：一个指示函数，强制模型按照特定格式输出。具体要求模型包含“Here is my evaluation of the solution:”以及在“Based on my evaluation, the final overall score should be:”后输出 \boxed{} 包裹的分数。
2. 分数奖励（Score Reward, ）：基于模型预测分数 与专家标注分数 的接近程度：

   
   

验证器的训练目标最大化以下期望：

其中 是验证器生成的分析文本， 是从中提取的分数。

2.2 引入元验证

2.2.1 验证者的幻觉问题

在初步训练中，验证器仅通过与专家分数对齐来获得奖励。这导致了一个严重的问题：当处理有缺陷的证明（）时，验证器可能会通过虚构不存在的问题来凑出正确的低分。这种“为了扣分而扣分”的行为虽然能满足分数奖励，但生成的分析文本在逻辑上是错误的，降低了验证器的可信度。

2.2.2 元验证器的训练

为了解决这一问题，研究引入了元验证器。这是一个二级评估过程，用于判断验证器指出的问题是否真实存在，以及这些问题是否足以支撑其给出的评分。

元验证的训练流程如下：

1. 使用初始验证器生成分析 。
2. 专家根据元验证量表 （详见附录 A.3）对 的质量进行打分，得到元验证分数 。
3. 构建元验证数据集 。
4. 训练元验证器 ，使其能对验证分析进行评价。

2.2.3 增强验证器训练

利用训练好的元验证器 ，研究团队改进了验证器的奖励函数，加入了元验证反馈：

其中 是元验证器给出的质量评分。通过在验证数据集 和元验证数据集 上的联合训练，验证器生成的分析质量显著提高。实验表明，在 的验证集上，验证分析的平均质量得分从 0.85 提升到了 0.96。

2.3 证明生成与自验证

2.3.1 生成器训练

以训练好的验证器 作为生成式奖励模型（Generative Reward Model），研究团队对证明生成器 进行训练。目标函数为：

其中 是验证器对生成证明 给出的分数。

2.3.2 通过自验证增强推理

单纯的生成训练存在一个局限：当模型一次性生成（One-shot）失败时，它往往缺乏自我纠错的能力。尽管模型可以根据外部反馈修正证明，但在没有外部输入时，生成器倾向于盲目自信地认为自己的证明是正确的。

为了赋予生成器内在的验证能力，训练过程被设计为要求生成器输出两部分内容：

1. 证明本身 () 。
2. 自我分析 () ：遵循与验证器相同的量表 对 进行评估。

此时的奖励函数设计需要兼顾证明质量和自我评估的诚实度。设验证器对 的评分为 ，对自我分析 的元验证评分为 。自我分析中预测的分数记为 。总奖励函数如下：

其中 ，。

这种奖励结构创造了以下激励导向：

• 诚实优于盲目自信：如果证明有错，承认错误（使 接近真实的低分 ）比坚持错误能获得更高的 。
• 完美证明收益最高：最高的奖励依然来自生成正确的证明并正确地识别其为正确。
• 审慎推理：为了最大化奖励，生成器的最佳策略是在最终确定答案前，尽可能在内部识别并解决所有问题。

2.4 Automated Labeling

随着生成器的变强，它生成的证明越来越复杂，初始的验证器可能难以发现其中的微妙错误。为了持续提升验证器，需要新的高质量标注数据。手动标注效率低下，因此研究团队提出了一套完全自动化的标注流程：

1. 大规模采样：对于每个新生成的证明，让验证器生成 个独立的验证分析。
2. 元验证过滤：对于报告了问题（0分或0.5分）的分析，生成 个元验证评估。只有当大多数元验证评估确认问题存在时，该分析才被视为有效。
3. 保守聚合：检查所有被视为有效的分析。如果至少有 个有效分析给出了最低分，则该证明被标记为该最低分。如果在所有验证尝试中均未发现合法问题，则标记为 1 分。

在训练的最后两个迭代周期中，该全自动管道完全替代了人工标注。质量检查证实，自动标注的标签与专家判断高度一致。

3. 实验设置

3.1 训练配置

• 基座模型：DeepSeek-V3.2-Exp-Base。
• RL 算法：采用 Group Relative Policy Optimization (GRPO)。
• 迭代策略：交替优化验证器和生成器。每一轮迭代先优化验证器，然后用验证器的 checkpoint 初始化生成器进行训练。从第二轮开始，验证器会通过 Rejection Fine-tuning 初始化，融合上一轮的生成和验证能力。

3.2 评估基准

评估涵盖了不同难度的定理证明任务：

• In-House CNML-Level Problems：91 个涵盖代数、几何、数论、组合和不等式的内部题目，难度对标中国高中数学联赛（CNML）。
• IMO 2025：6 道国际数学奥林匹克竞赛题。
• CMO 2024：6 道中国数学奥林匹克竞赛题。
• Putnam 2024：12 道威廉·洛厄尔·普特南数学竞赛题（北美顶级本科生竞赛）。
• ISL 2024：31 道 IMO 预选题目。
• IMO-ProofBench：包含 60 道题目的基准测试，分为基础版和高级版。

4. 实验结果

4.1 单次生成表现

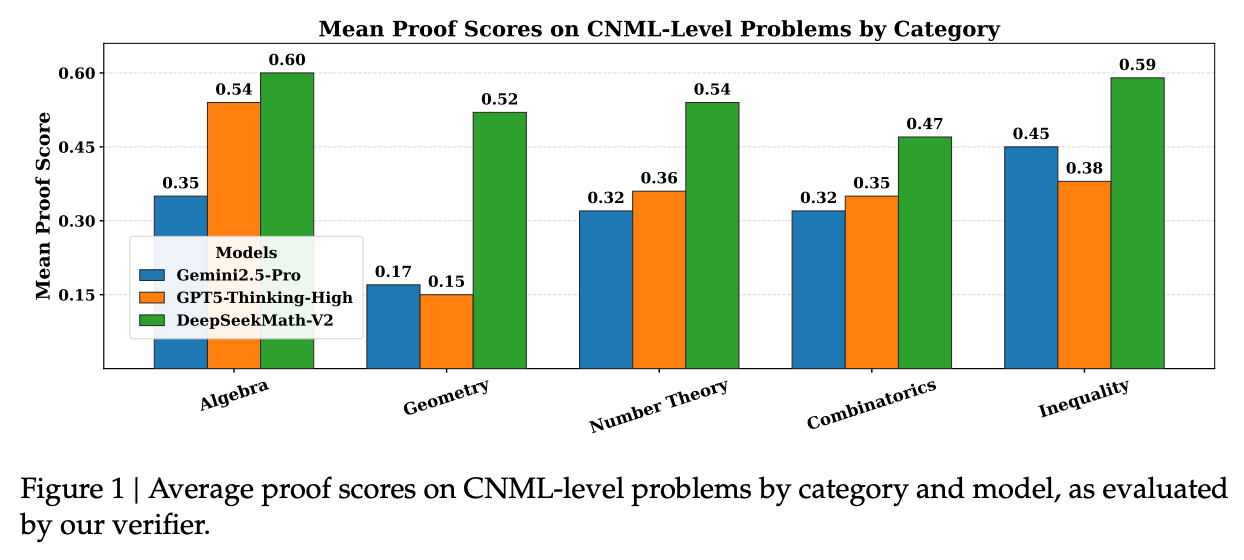
在内部 CNML 级别的问题集上，DeepSeekMath-V2 与 GPT-5-Thinking-High (OpenAI) 和 Gemini 2.5-Pro (DeepMind) 进行了对比。每个模型对每个问题生成 8 个样本，通过多数投票确定正确性。结果显示，DeepSeekMath-V2 在所有数学领域（代数、几何、数论、组合、不等式）均展现出优异的性能，证明了其在定理证明任务上的广泛适用性。

4.2 基于自验证的顺序精炼

对于 IMO 和 CMO 级别的难题，受限于上下文长度（128K token）和单次推理的深度，模型很难一次生成完美的证明。然而，DeepSeekMath-V2 具备识别自身证明无效的能力。

研究评估了“顺序精炼”策略：

1. 生成器生成证明及自我分析。
2. 将上一轮的输出作为提示，要求生成器基于自我识别的问题进行修正（Prompt 见附录 A.4）。
3. 重复此过程，直到生成器给自己打满分或达到最大迭代次数。

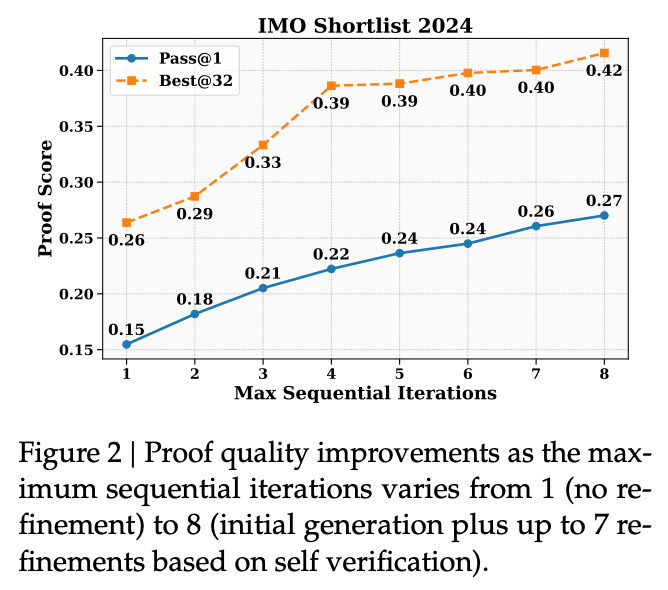
实验表明（见图 2），随着精炼次数的增加，Pass@1 指标显著上升。此外，Best@32（即从 32 个线程中根据自评通过的证明中选出最好的一个）的分数远高于平均水平。这证明了模型能够可靠地利用自我意识来区分高质量证明和有缺陷的证明，并指导自身的迭代改进。

4.3 高算力搜索

为了攻克最难的竞赛题，研究团队采用了大规模的推理时计算策略（Test-time Compute Scaling）。

具体策略：

• 维护一个候选证明池，初始包含 64 个样本。
• 对每个样本生成 64 个验证分析。
• 根据平均验证分选择得分最高的 64 个证明。
• 将每个选中的证明与 8 个随机抽取的验证分析（优先选择指出问题的分析）配对，生成修正后的证明，更新候选池。
• 该过程持续 16 轮，或直到某个证明通过所有 64 次验证尝试。

竞赛成绩：

• IMO 2025：解决了 6 题中的 5 题（P1, P2, P3, P4, P5），获得 83.3% 的分数，达到金牌水平。
• CMO 2024：解决了 4 题并获得另一题的部分分，总分 73.8%，同样达到金牌水平。
• Putnam 2024：解决了 12 题中的 11 题，另一题仅有细微错误，总分 118/120。相比之下，人类参赛者的最高分仅为 90 分。

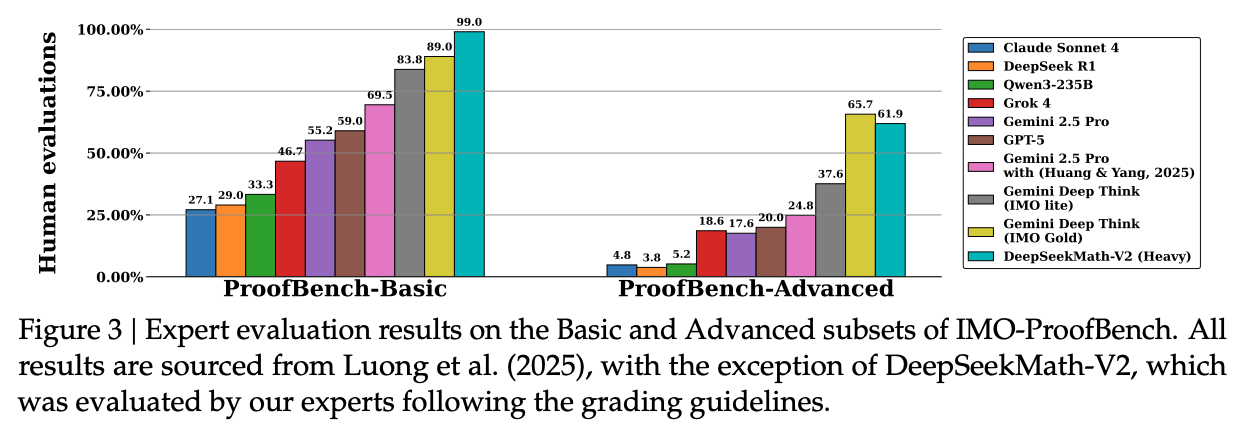
在 IMO-ProofBench 上，DeepSeekMath-V2 在基础集上超过了 DeepMind 的 DeepThink (IMO-Gold)，在高级集上也保持了极具竞争力的表现。

5. 相关工作与讨论

5.1 与形式化证明的对比

目前数学推理的另一条路线是利用 Lean 或 Isabelle 等证明辅助工具（如 AlphaProof, DeepSeek-Prover-V2）。形式化证明的优势在于一旦编译通过，正确性即由系统保证。然而，这要求模型掌握形式化语言。

DeepSeekMath-V2 专注于自然语言证明（Informal Proof）。尽管自然语言存在歧义，难以像代码那样严格验证，但该研究表明，通过训练强大的验证器，模型可以达到极高的自我评估准确率。此外，提升自然语言推理能力本身也能辅助形式化证明的生成（例如作为指导思路）。

5.2 自动验证的可行性

该研究证实了 LLM 可以被训练来评估以前被认为难以自动验证的复杂证明。特别是对于那些未能完全解决的问题，生成器通常能准确指出其中的真实问题；而对于被判定为完全解决的问题，其通过了所有 64 次验证。这种一致性表明自验证是通向更强 AI 数学系统的可行路径。

6. 附录深度解析：提示工程

论文的附录部分公开了关键的 Prompt 模板，这对于理解模型行为至关重要。

6.1 Proof Generation Prompt

该提示明确要求模型不仅要解决问题，还要进行自我评估。

• 双重任务：Solve + Rate。
• 评分指令：明确给出了 1/0.5/0 的判定标准。特别强调了“引用论文结论”必须提供证明，否则不得分。
• 思维链引导：In fact, you already have the ability to rate your solution yourself... 这段话由其强调了自省的重要性，要求模型在最终输出前进行内部的 "careful reasoning"。
• 防欺骗机制：提示中明确警告 If you cheat, we will know, and you will be penalized!，试图通过指令约束模型的奖励黑客（Reward Hacking）行为。

6.2 Proof Verification Prompt

验证提示要求模型模拟专家的评估过程。

• 结构化输出：强制模型按照

  Self Evaluation 开头，并在最后使用 \boxed{} 输出分数。

• 详细分析：要求明确指出哪些步骤是正确的，哪些是存疑的。对于错误步骤，必须解释原因及影响。

6.3 Meta-Verification Prompt

这是该系统的“法官”。它的任务不是解决原问题，而是评估“解决方案评价”是否合理。

• 三大分析维度：

  1. 步骤重述（Step Restatement）：检查评价中引用的内容是否真的出现在原解答中。
  2. 缺陷分析（Defect Analysis）：这是核心。需要同时判断“缺陷是否存在”以及“评价对缺陷的分析是否准确”。
  3. 表达分析（Expression Analysis）：检查评价本身的表述是否准确。
• 评分逻辑：

  • 如果发现至少一个不合理的缺陷指控，元验证评分为 0。
  • 如果部分指控合理，部分不合理，评分为 0.5。
  • 如果所有指控均合理（或者没有发现缺陷且评价也没找出缺陷），且分数匹配，评分为 1。

7. 结论

DeepSeekMath-V2 展示了一种通过自验证（Self-Verification）提升大模型数学推理能力的有效范式。通过摆脱单一的最终答案奖励，转向对推理过程的深度评估和自我修正，模型在处理开放式、高难度的定理证明任务时表现出了前所未有的鲁棒性。

该研究的贡献不仅在于刷榜（虽然 Putnam 118/120 的成绩很强），更在于提出了一套自我进化的训练框架：

1. Verifier 提供信号。
2. Generator 利用信号进行自省。
3. Meta-Verifier 保证信号的诚实性。
4. Auto-Labeling 实现数据的自动化扩展。

这一闭环为未来开发能够解决研究级数学问题的 AI 系统奠定了基础。随着测试时计算（Test-time Compute）的进一步扩展，基于自验证的推理系统有望发挥更大的作用。

往期文章：

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题