Group Relative Policy Optimization (GRPO) 作为一种面向大型语言模型(LLMs)训练后阶段的强化学习算法,在学术界和工业界都获得了关注。 传统观点认为,GRPO 需要较大的组规模 (group size) 来保证训练过程的稳定性,但这带来了巨大的计算开销。 来自蒙特利尔大学、麦吉尔大学、Mila 等机构的研究者们发表了一篇名为《IT TAKES TWO: YOUR GRPO IS SECRETLY DPO》的论文,对这一传统观念发起了挑战。

-
论文标题:IT TAKES TWO: YOUR GRPO IS SECRETLY DPO -
论文链接:https://arxiv.org/pdf/2510.00977
该论文的核心贡献在于,它从对比学习 (contrastive learning) 的视角重新审视了 GRPO,并揭示了其与直接偏好优化 (Direct Preference Optimization, DPO) 之间深层的理论联系。 基于 DPO 在成对偏好数据上的成功实践,研究者们提出了一个极简的 GRPO 变体——2-GRPO,即组规模仅为 2。通过严谨的理论分析和充分的实证检验,论文证明了 2-GRPO 不仅在性能上可以媲美传统的 16-GRPO,还能大幅减少计算资源消耗,将训练时间缩短超过 70%。
这项工作为设计资源高效的 LLM 训练后 RL 算法开辟了新的道路,并加深了我们对 GRPO 和 DPO 这两种主流对齐算法内在机制的理解。
1. 背景
强化学习 (Reinforcement Learning, RL) 已成为大型语言模型 (LLMs) 训练后阶段的核心技术范式。它主要用于两个方面:一是通过人类反馈强化学习 (RLHF) 来对齐模型与人类的偏好和价值观;二是通过可验证奖励强化学习 (RLVR) 来激发模型的推理能力。 在众多 RL 算法中,GRPO 作为近端策略优化 (Proximal Policy Optimization, PPO) 的一个变体,因其出色的性能和效率而备受瞩目。
1.1 主流的 LLM 训练后 RL 算法
在深入探讨本文的核心内容之前,我们先简要回顾一下几种关键的 RL 算法。
1.1.1 Vanilla Policy Gradient (VPG)
VPG,又名 REINFORCE,是策略梯度方法的基础。它的目标是通过梯度上升来最大化期望奖励。其学习目标函数为:
其中, 是从提示集合 中采样的一个提示 (prompt), 是模型 根据提示 生成的回复 (response), 是一个轨迹 (trajectory), 是该轨迹的奖励 (reward)。VPG 的梯度更新公式为:
其中 是轨迹 的奖励。VPG 的一个主要问题是梯度估计的方差很高,导致训练不稳定。
1.1.2 Proximal Policy Optimization (PPO)
为了解决 VPG 的高方差和不稳定性问题,Schulman 等人提出了 PPO。PPO 引入了重要性采样 (importance sampling)、裁剪 (clipping) 和一个价值函数 (value function) 来计算优势 (advantage)。其目标函数通常写作:
其中, 是生成序列的旧策略, 是待更新的策略, 是裁剪超参数, 是优势,通过从奖励 中减去一个基线 (baseline) 计算得到。这个基线通常由一个价值函数提供,该价值函数也需要作为另一个 LLM 进行参数化和训练,这带来了额外的计算和内存开销。
1.1.3 Direct Preference Optimization (DPO)
DPO 是为 RLHF 设计的一种新算法,它通常在离线的人类标注偏好数据 上进行训练,其中 是比 更受偏好的回复。 DPO 的损失函数为:
其中, 是一个基础的参考策略, 是一个控制与参考策略偏差程度的参数。DPO 的巧妙之处在于它避免了显式地训练一个奖励模型,而是直接通过一个简单的分类损失来优化语言模型,使其符合人类偏好。
1.1.4 Group Relative Policy Optimization (GRPO)
GRPO 是 PPO 的一个强大变种,尤其在 DeepSeek-R1 等模型的成功中扮演了关键角色。 与 PPO 不同,GRPO 不依赖价值网络来稳定奖励,而是为每个提示采样多个回复(称为 rollouts),并在每个组内对奖励进行归一化,从而计算优势。 GRPO 的目标函数与 PPO 类似,但其优势计算方式不同:
其中, 是组大小(每个 prompt 生成的 rollout 数量), 是对应的优势。这个 token 级别的优势由组内归一化给出:
其中, 是第 个 rollout 的奖励, 是该组所有 rollout 的奖励向量, 是一个为了避免除零而加入的小常数。在实践中,为了进行准确的归一化, 通常被设置为一个较大的值,例如 16。
1.2 GRPO 的计算瓶颈
尽管 GRPO 经验性能强大,但它也存在一个固有的问题:对大组规模的依赖。 生成大量的 rollouts 是一件计算和时间成本都极高的事情。事实上,生成阶段是主要的计算瓶颈,可能占到总训练时间的 70% 以上。这种低效率限制了 GRPO 的应用,并促使研究者寻找更高效的替代方案。
2. 对比学习
这篇论文的核心洞见在于,它没有将 GRPO 仅仅看作一种方差缩减技术,而是从一个全新的角度——对比学习 (Contrastive Learning)——来重新诠释它。
2.1 对比学习的核心思想
对比学习是一种自监督学习方法,其核心思想是“拉近相似的,推开不相似的”。在对比学习的框架中,通常有一个“锚点”(anchor),一些“正样本”(positive examples) 和一些“负样本”(negative examples)。学习的目标是让锚点在表示空间中与正样本的表示更接近,同时与负样本的表示更疏远。
2.2 将 GRPO 重新诠释为对比学习
论文指出,GRPO 中的优势值 是有符号的:它们要么为正,要么为负。这个观察自然地引出了一个对比学习的解释:
-
具有正优势的轨迹 可以被视为 “正样本”。 -
具有负优势的轨迹 可以被视为 “负样本”。
GRPO 的目标函数本质上是在增加正样本(高奖励回复)的概率,同时抑制负样本(低奖励回复)的概率。这与对比学习的核心原则完全一致。
为了从理论上形式化这个联系,论文首先定义了一个通用的对比损失函数 (General contrastive loss) 。
定义 3.1 (通用对比损失)
令 为一个概率模型, 为一个任意的数据分布, 为一个锚点, 和 分别为给定 的正样本和负样本分布。我们称一个可微的损失函数 是对比性的,如果它的梯度具有以下形式:
其中 和 是任意的系数函数,用于加权正负样本的贡献。
接下来,论文推导了 GRPO 目标函数的梯度,并证明了它完全符合上述对比损失的梯度形式。
在可验证奖励 (RLVR) 的设定下,奖励是二元的(例如,正确为 1,错误为 0)。 在这种情况下,一个大小为 的样本组中,假设有 个正确轨迹和 个错误轨迹。给定提示 ,正确回复的概率为 。那么组内奖励的均值近似为 ,标准差的平方(方差)为 。
论文忽略了裁剪 (clipping) 的影响(因为在裁剪范围之外梯度为零),经过一系列推导(详见原论文附录 A.1),GRPO 的目标函数可以近似为:
其中 是经验标准差。当 时,这个经验目标函数收敛到其真实的目标函数:
其中 是真实的方差, 和 分别代表正负(正确/错误)回复的子分布。
对这个真实目标函数求梯度,我们得到:
其中, 是论文中为了简化表达而定义的一个项,代表了轨迹 的 token 概率之和。
这个梯度形式清晰地展示了 GRPO 的对比本质:它在期望上增加了正样本的概率,减少了负样本的概率。通过选择 ,它完全符合定义 3.1。因此,论文得出了第一个关键结论:
命题 3.2:GRPO 目标是一个对比损失。
2.3 GRPO 与 DPO 的内在联系
有了 GRPO 是对比损失的认识,下一步自然是将其与另一个基于偏好的对比方法——DPO——进行比较。论文同样分析了 DPO 目标的梯度形式。DPO 的损失函数梯度为:
可以改写为:
这同样符合定义 3.1 中对比损失的梯度形式。因此,论文得出了第二个关键结论:
命题 3.3:DPO 目标是一个对比损失。
这两个命题共同揭示了一个深刻的联系:GRPO 和 DPO 都可以被理解为对比学习。它们都通过对比正负样本来优化策略。它们的主要区别在于如何定义和加权这些正负样本。DPO 使用的是成对的偏好数据,而 GRPO 是在一个组内通过奖励归一化来隐式地定义正负样本。
3. 2-GRPO
既然 GRPO 和 DPO 在本质上都是对比学习,而 DPO 仅使用一对正负样本就能成功,这自然引出一个问题:GRPO 是否真的需要一个大的组规模?GRPO 能否在只有一对样本的情况下有效学习?
为了探究这个问题,论文提出了 2-GRPO,即将 GRPO 的组规模 设置为最小值 2。
乍一看,这似乎违背了 GRPO 的设计初衷。一个只有两个样本的组,其统计估计(均值和标准差)会非常不稳定,甚至可能无法提供有效的学习信号。然而,论文通过深入分析,消除了这些顾虑。
当 时,对于一个给定的提示,我们生成两个 rollouts, 和 。在 RLVR 设定下,奖励是 0 或 1。会出现三种情况:
-
一正一负 (One positive, one negative): e.g., 。此时,均值为 0.5,标准差为 0.5。归一化后的优势为 ,。 -
两个都是正 (Both positive): 。此时,均值为 1,标准差为 0。优势 。 -
两个都是负 (Both negative): 。此时,均值为 0,标准差为 0。优势 。
可以看到,只有在采样到一正一负样本对时,2-GRPO 才会产生非零的梯度信号,此时它就等价于一个 DPO 式的更新:增加正样本的概率,降低负样本的概率。
2-GRPO 的目标函数可以简化为:
这个表达式是通过将原 GRPO 目标函数 (Eq. 9) 中的 替换为常数 1/2 得到的。
3.1 对 2-GRPO 的理论分析
论文从三个方面论证了 2-GRPO 的可行性,回应了可能的担忧。
3.1.1 优势估计 (Advantage Estimate)
担忧:2-GRPO 中简单计算出的优势值(-1, 0, 1)是否缺乏足够的归一化效果来稳定奖励?
分析:论文通过一个命题证明,2-GRPO 隐式地进行了有效的归一化。
命题 4.1
考虑两种情况,其中样本 服从伯努利分布 Bernoulli():
-
情况 1 (对应标准 GRPO): 从 中采样,进行标准化 。当 时,。 -
情况 2 (对应 2-GRPO): 考虑 N 对样本 ,对每对进行标准化 。在这种情况下,。
结论:这个命题表明,2-GRPO (情况 2) 计算出的期望优势与真实概率 之间是线性关系 (),这是一个无偏的估计。而标准 GRPO (情况 1) 的期望优势则被一个与 相关的因子 缩放了。这意味着,尽管 2-GRPO 的优势值看起来很简单(-1, 0, 1),但它们在期望上仍然与策略的正确率成正比,保留了优化的基本原理。两种方法计算出的优势估计仅仅相差一个缩放因子。
3.1.2 梯度方差 (Gradient Variance)
担忧:减小组规模 会不会增加梯度估计的方差,从而损害训练稳定性?
分析:表面上看,根据中心极限定理,减小组规模 确实会增大方差。然而,论文指出,在实践中,我们关注的是整个 mini-batch 的梯度。一个 mini-batch 的总样本数 (rollouts) 是 ,其中 是 mini-batch 中的提示数量。
当我们减小组规模 时(例如从 16 减到 2),我们可以通过增加提示数量 来补偿,以保持总样本数 不变(或相近)。例如,16-GRPO 使用 (Q=32, G=16) 的配置,总 rollouts 为 512。而 2-GRPO 可以使用 (Q=256, G=2) 的配置,总 rollouts 同样为 512。
由于总的训练数据集(提示的总数)是固定的,增加每个 mini-batch 的提示数量 并不会增加总体的计算负担。因此,通过调整 ,2-GRPO 可以在不牺牲(甚至可能改善)梯度估计稳定性的前提下,大幅提高计算效率。
3.1.3 对难题的探索能力 (Exploration on Hard Questions)
担忧:对于难题(即单次 rollout 成功率很低的 prompt),较小的组规模是否意味着更难采样到正确的答案,从而减慢学习速度?
分析:这个担忧是合理的,但它忽略了训练是在一个固定的计算预算下进行的。在相同的总 rollouts 数量下,2-GRPO 和 16-GRPO 探索的轨迹总数是近似相等的。
命题 4.4
令 为策略 单次 rollout 产生正确答案的概率。
-
在 次独立 rollouts 中,获得至少一个正确答案的概率是 。 -
进行 次试验,每次试验包含 2 次独立 rollouts(策略分别为 ),获得至少一个正确答案的概率是 。
如果策略在训练中不断改进 (),那么 。
结论:这个命题表明,在总 rollouts 数量相同的情况下,2-GRPO(对应情况 2)找到正确答案的概率甚至可能高于 16-GRPO(对应情况 1)。这是因为 2-GRPO 的更新频率更高。对于 16-GRPO,模型需要生成 16 个 rollouts 才能进行一次策略更新;而 2-GRPO 每生成 2 个 rollouts 就可以更新一次策略。这种更频繁的更新使得策略能够更快地改进,从而在后续的 rollouts 中以更高的概率 采样到正确答案。
综上所述,理论分析表明,2-GRPO 在优势估计、梯度方差控制和探索能力方面都是一个可行的、高效的算法。
4. 实验
为了验证理论分析的正确性,论文进行了一系列实验。
4.1 实验设置
-
模型: 实验采用了 Qwen-2.5-Math-1.5B (Qwen-1.5B), Qwen-2.5-Math-7B (Qwen-7B) 和 DeepSeek-R1-Distill-Qwen-1.5B (DS-1.5B) 作为基础模型。 -
数据集: 模型在 MATH 和 DAPO-Math-Sub 数据集上进行训练,并在五个广泛使用的数学推理基准上进行评估:MATH-500, AMC 2023, Minerva Math, AIME 2025, 和 Olympiad Bench。 -
对比方法: 主要对比了 2-GRPO 和 16-GRPO (基线)。 -
超参数: 为了公平比较,两种方法的每个 mini-batch 总 rollouts 数量保持一致 (512)。 -
16-GRPO: batch size = 32 (32 prompts 16 rollouts/prompt), learning rate = 。 -
2-GRPO: batch size = 256 (256 prompts 2 rollouts/prompt), learning rate = (根据线性缩放规则调整)。
-
-
评估指标: Mean@32 和 Pass@32。
4.2 主要实验结果
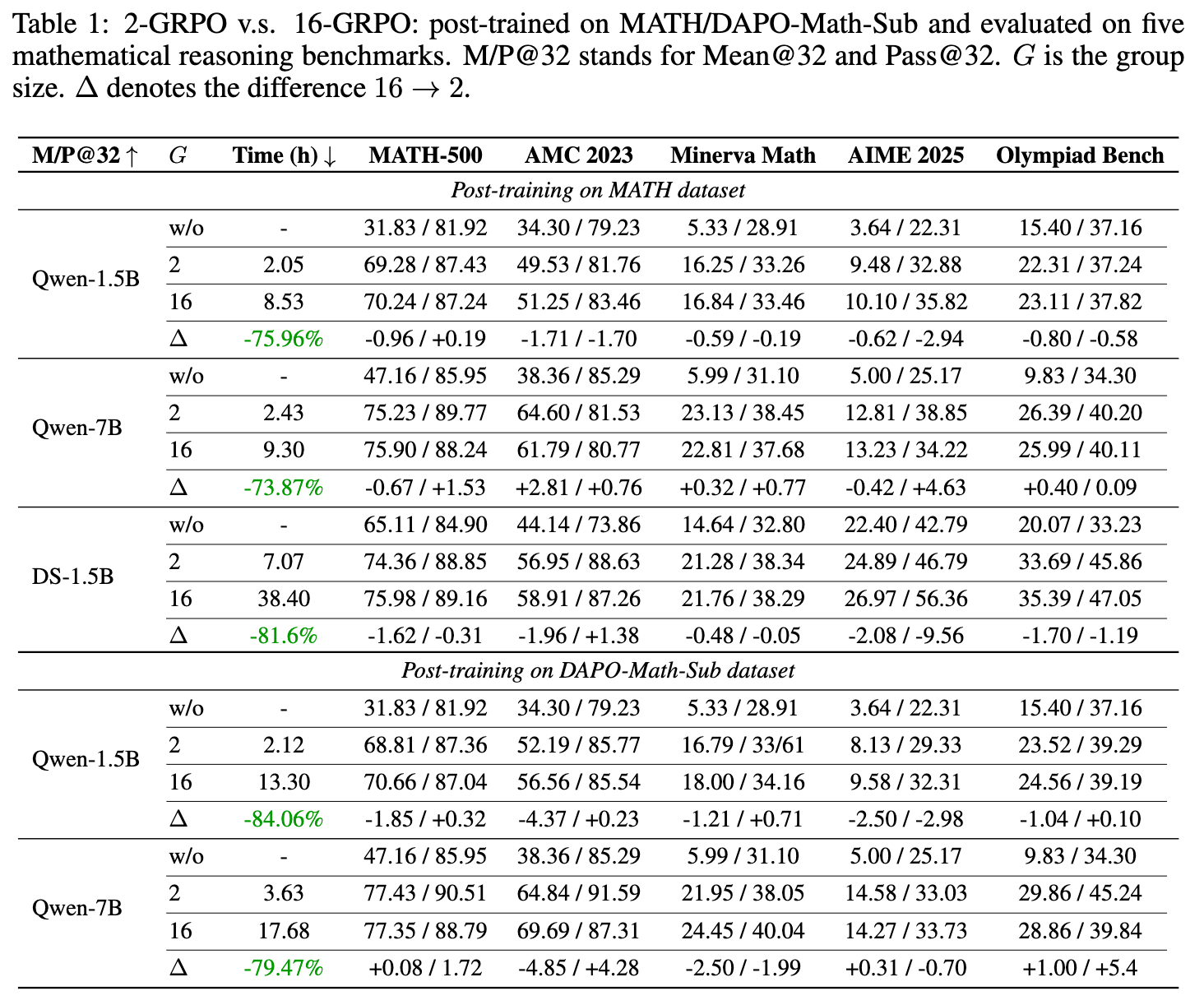
实验结果(如上表所示)清晰地表明:
-
性能相当: 在所有的模型、数据集和评估基准上,2-GRPO 的性能都与 16-GRPO 相当,有时甚至略有超出。两者之间的性能差异基本在统计误差范围内。 -
效率提升: 2-GRPO 实现了巨大的效率提升。与 16-GRPO 相比,2-GRPO 将训练墙钟时间 (wall-clock time) 减少了 70% 以上。例如,在 MATH 数据集上训练 Qwen-1.5B,16-GRPO 需要 8.53 小时,而 2-GRPO 仅需 2.05 小时。 -
样本效率: 2-GRPO 使用的生成 rollouts 总数仅为 16-GRPO 的 12.5%(1/8)。这意味着 2-GRPO 以低得多的样本成本达到了同等的性能。
这些结果为论文的理论发现提供了强有力的经验支持:减小组规模并不会损害性能,反而能带来显著的效率增益。
4.3 可视化分析
为了更直观地展示训练动态,论文还可视化了模型在 MATH 数据集上的奖励曲线和评估分数曲线。
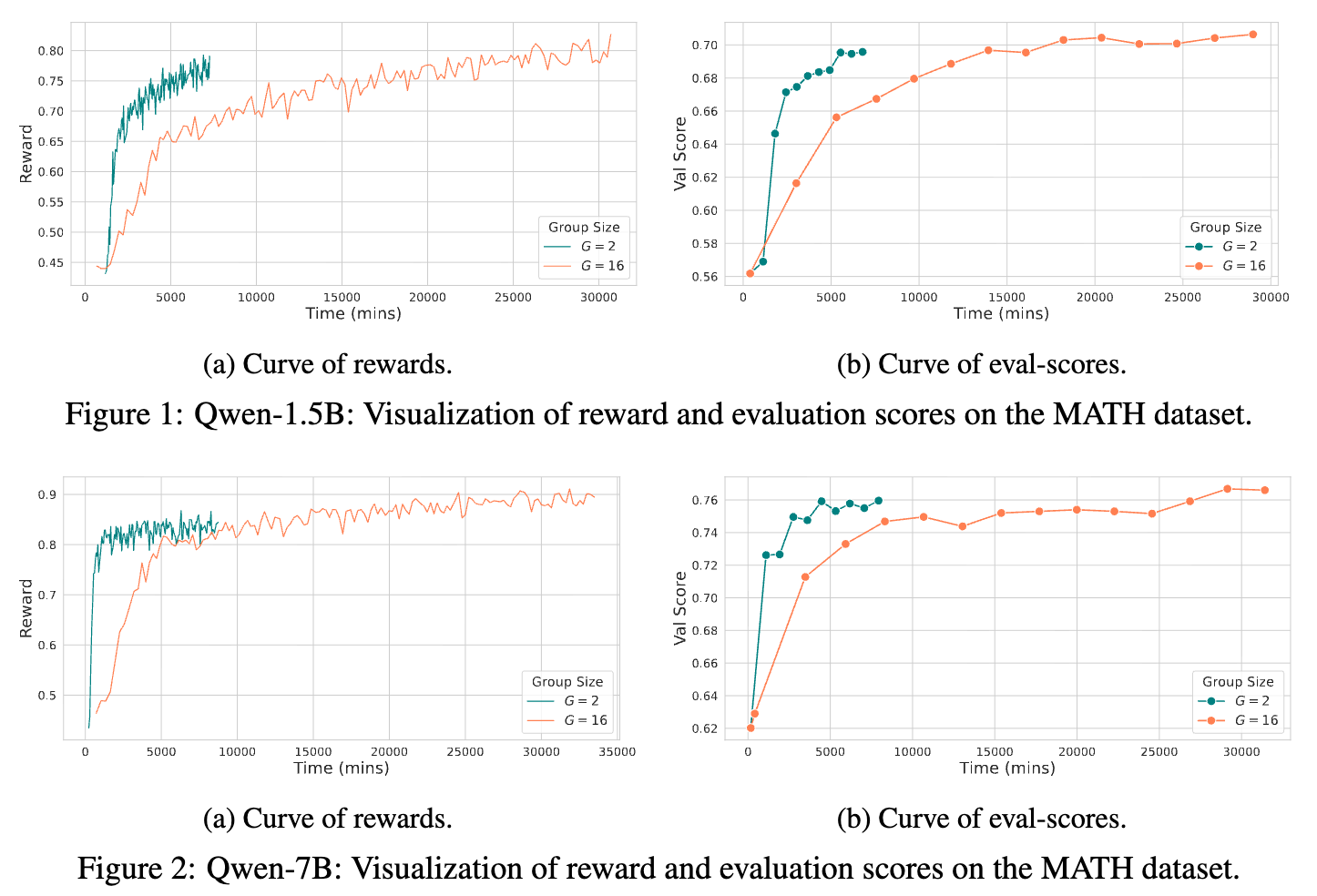
从图中可以看出,2-GRPO 和 16-GRPO 的学习曲线几乎重合。这表明,2-GRPO 不仅在最终性能上,而且在整个训练过程的动态上,都与 16-GRPO 表现出高度的一致性。这进一步证明了 2-GRPO 在分布内泛化能力上与 16-GRPO 是相当的。
5. 点评
这项工作对 GRPO 的理解和应用带来了新的启发。
-
更强的效率: 论文指出 2-GRPO 仍有提升效率的潜力。在 2-GRPO 中,当两个 rollouts 的奖励相同时(同为正或同为负),优势为零,不会产生梯度。未来的实现可以优化这一步,跳过对这些零优势样本的梯度计算,从而进一步加速训练。
-
2-GRPO 作为 GRPO 的一种量化: 从另一个角度看,2-GRPO 可以被视为标准 GRPO 的一种“量化”版本。在标准 GRPO 中,优势值是连续的;而在 2-GRPO 中,优势值被离散化为三个值:-1, 0, 1。尽管优势值被量化,但由于神经网络优化的随机性,以及足够多的训练步骤,2-GRPO 仍然能够有效地逼近连续优势值的优化效果。
-
数据效率的权衡: 2-GRPO 增强了计算效率,但在某种程度上牺牲了数据效率。当策略已经表现得很好(大部分 rollouts 都正确)或很差(大部分都错误)时,2-GRPO 采样到一正一负对的概率会降低,导致很多生成的 rollouts 被赋予零优势而被“浪费”。这可能会限制模型达到接近最优性能的能力。未来的工作可以探索自适应地调整组规模,以在计算效率和数据效率之间取得平衡。
结论
总而言之,这篇论文通过将 GRPO 重新框架为一种对比学习方法,成功地在 GRPO 和 DPO 之间建立了一座理论的桥梁。 这一新颖的视角不仅加深了我们对这两种重要算法的理解,还直接催生了 2-GRPO 这一 DPO 启发的、高效的 GRPO 变体。通过严谨的理论证明和扎实的实验结果,论文挑战了“GRPO 需要大组规模”的传统认知,证明了 2-GRPO 可以在保持与 16-GRPO 相当性能的同时,实现超过 70% 的训练时间缩减和 8 倍的样本效率提升。
往期文章:




