
-
论文标题:Retaining by Doing: The Role of On-Policy Data in Mitigating Forgetting -
论文链接:https://arxiv.org/pdf/2510.18874
TL;DR
今天分享一篇陈丹琦团队的新作《Retaining by Doing: The Role of On-Policy Data in Mitigating Forgetting》。尽管业界已基本达成共识——强化学习(RL)在微调阶段比监督微调(SFT)更能缓解灾难性遗忘——但其背后的深层机制尚未被完全解析。
本论文通过理论推导与合成实验,挑战了传统的直觉认知:通常认为 SFT 对应的 Forward KL(模式覆盖)比 RL 对应的 Reverse KL(模式寻找)更能保留分布信息。然而,作者提出并在多模态(Multi-modal)分布假设下证明,RL 的模式寻找(Mode-seeking)特性实际上允许模型在学习新任务(新模态)时,保持代表旧知识的旧模态不动,从而减少遗忘。 进一步的消融实验表明,RL 抵抗遗忘的鲁棒性主要来源于其使用 On-Policy 数据,而非 KL 正则化项或优势函数估计(Advantage Estimation)。基于此,论文提出了 Iterative-SFT 等近似 On-Policy 的方法,在无需完整 RL 流程的情况下有效缓解了遗忘。
1. 引言
将预训练语言模型(LMs)通过后训练(Post-training)适配到特定任务时,往往会引发灾难性遗忘(Catastrophic Forgetting),导致模型丧失已有的通用能力(如指令遵循、通用知识、推理能力等)。这种现象在 SFT 和 RLHF 阶段均有报道。
虽然现有观察表明 RL 在保持模型原有能力方面优于 SFT,但对于“为什么 SFT 比 RL 更容易导致遗忘”这一问题,社区缺乏系统性的理论解释。传统的观点可能认为 RL 的 KL 正则化起到了关键作用。
本文旨在通过系统性的实验和简化的理论模型,回答以下问题:
-
SFT 和 RL 的遗忘模式有何本质区别? -
从 KL 散度的角度,如何解释这种区别? -
是 RL 算法中的哪个组件(KL 正则、优势估计、数据采样策略)主导了对遗忘的缓解? -
能否利用这一发现改进 SFT,使其具备类似 RL 的抗遗忘能力?
2. RL 与 SFT 的遗忘对比
为了确保研究的前提立得住,作者首先在 Llama 3 和 Qwen 2.5 系列模型上,针对指令遵循(IFEval)、通用知识(MMLU)和数学推理(Countdown)任务进行了广泛的实验。
2.1 实验设置
-
模型: Llama-3.2-1B-Instruct, Llama-3.1-8B-Instruct, Qwen-2.5-1.5B-Instruct, Qwen-2.5-7B-Instruct。 -
基线方法: -
SFT: 使用 Llama-3.3-70B-Instruct 生成的高质量响应作为 Ground Truth。 -
Self-SFT: 使用初始模型(Initial Model)生成的响应,并经过奖励模型过滤,仅保留正确答案。这代表了无人类标注时的典型 SFT 起点。 -
RL (GRPO): 采用 Group Relative Policy Optimization (GRPO) 算法。
-
-
评价指标: -
Gain (): 目标任务上的准确率提升。 -
Drop (): 非目标任务(Non-target tasks)上的平均准确率下降。非目标任务包括 MATH、WildJailbreak、WildGuardTest 等。
-
2.2 实验结果分析
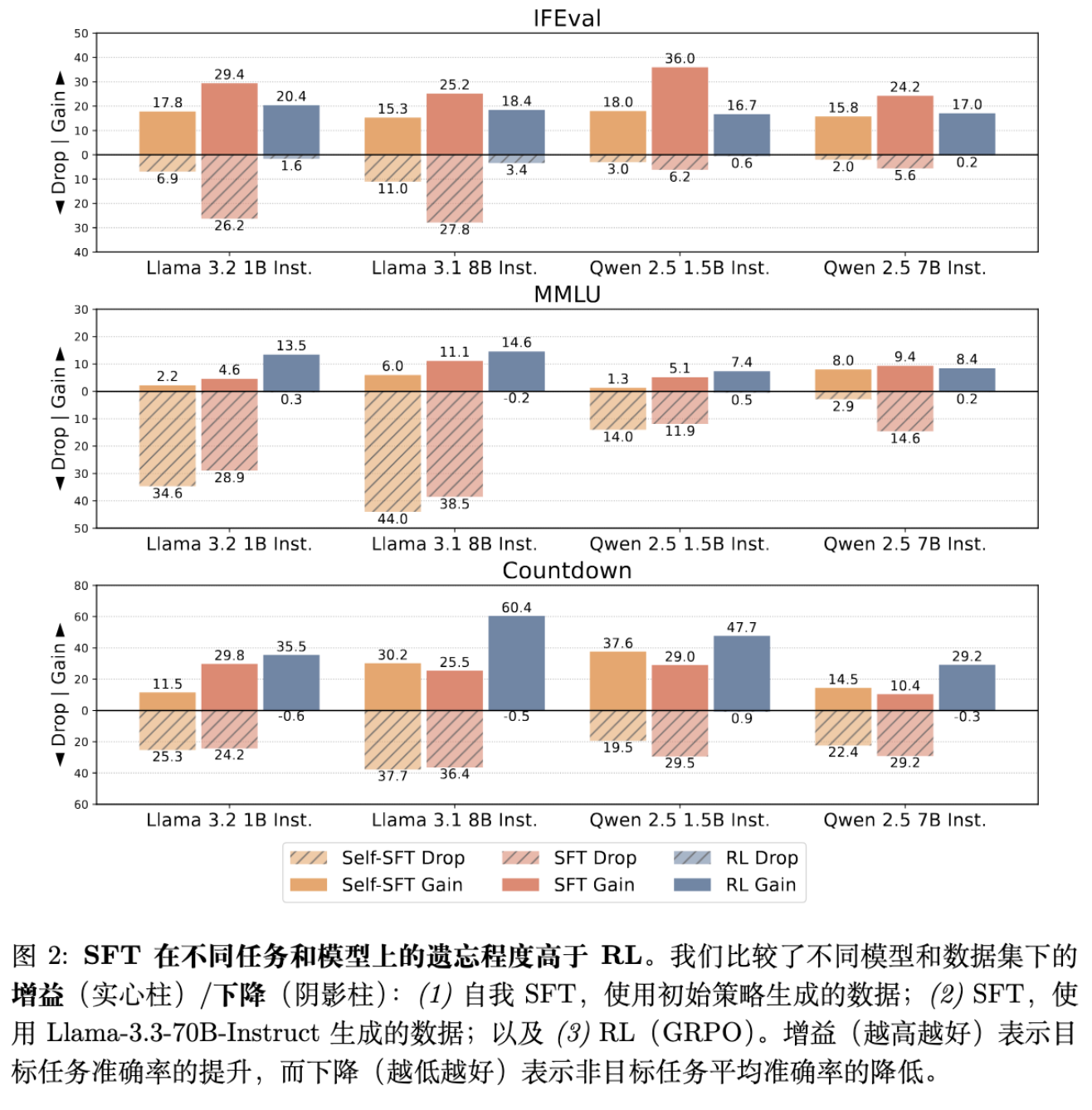
实验结果揭示了一个一致的趋势:
-
Self-SFT 的遗忘显著: 即使只利用自身生成的正确数据进行训练,Self-SFT 在获得与 RL 相似的目标任务增益时,会引发大幅度的非目标任务性能下降。 -
SFT 的权衡更差: 虽然 SFT 能够通过蒸馏强模型数据获得更高的目标任务分数,但其造成的遗忘往往比 Self-SFT 更严重。 -
RL 的鲁棒性: RL 能够在显著提升目标任务性能的同时,保持非目标任务的性能基本不下降,甚至在某些情况下微涨。
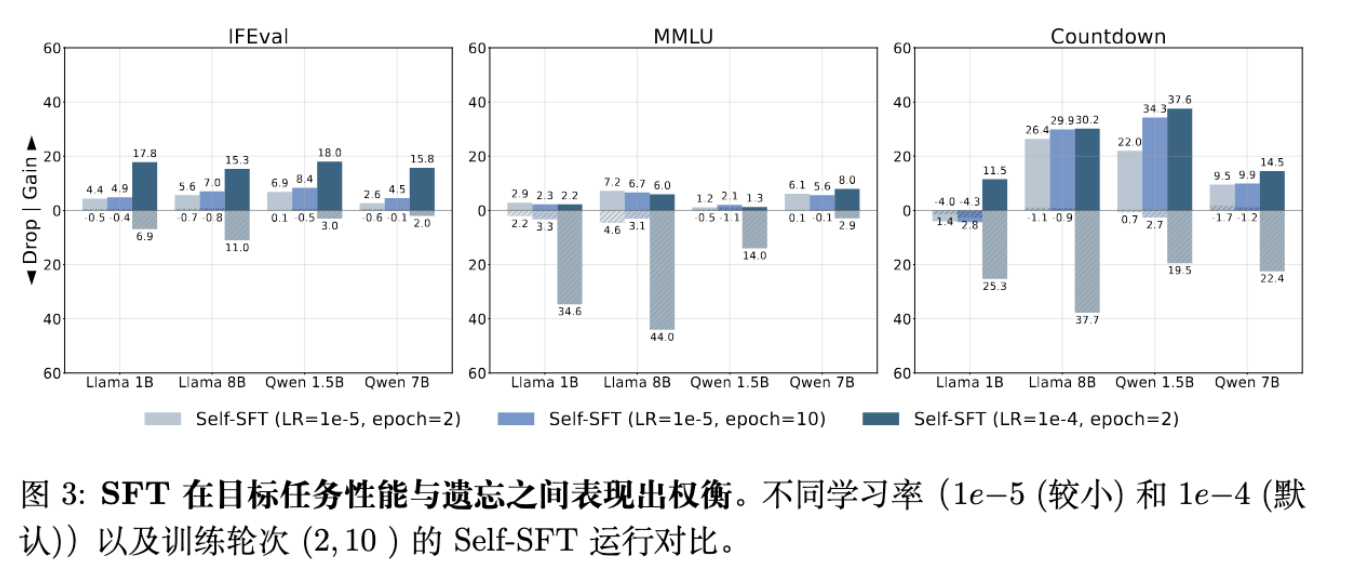
如上图所示,SFT 存在明显的“学习率-遗忘”权衡。高学习率能达到高性能但遗忘严重;低学习率虽减少遗忘但无法有效学习目标任务。相比之下,RL 打破了这种严格的权衡。
3. 通过 KL 散度理解遗忘动力学
这是论文最核心的理论贡献部分。作者试图通过分析目标函数(Objective Function)对应的 KL 散度方向来解释遗忘现象。
3.1 SFT 与 RL 的 KL 视角
-
SFT 对应 Forward KL (Mode-covering):
SFT 最小化交叉熵损失,等价于最小化最优策略 和当前策略 之间的 Forward KL 散度:Forward KL 具有 Mode-covering(模式覆盖)的特性,即 倾向于覆盖 的所有高概率区域。
-
RL 对应 Reverse KL (Mode-seeking):
最大化带 KL 正则的奖励函数,等价于最小化 Reverse KL 散度:其中最优策略 。Reverse KL 具有 Mode-seeking(模式寻找)的特性,即 倾向于集中在 的某一个高概率峰值(Mode)上,而忽略其他区域。
常规直觉的矛盾:
按照常规理解,Mode-seeking 的 Reverse KL 应该更容易导致遗忘,因为它会迅速将概率质量集中到新任务的最优解上,从而丢弃旧的模式(Prior Knowledge)。相反,Mode-covering 的 Forward KL 理论上应该试图保持整个分布的形状,从而保留旧知识。
然而,实验事实是 SFT(Forward KL)遗忘更严重。为了解决这个矛盾,作者引入了 多模态(Multi-modal)分布 的假设。
3.2 简化设定:单模态 vs 多模态
作者构建了一个合成实验,将最优策略 建模为两个高斯分布的混合:
-
代表先验知识(旧能力)。 -
代表目标任务(新能力)。
情况 A:初始策略是单模态(Uni-modal)
如果我们将训练策略 初始化为一个单模态高斯分布,并让它去拟合 的 部分。
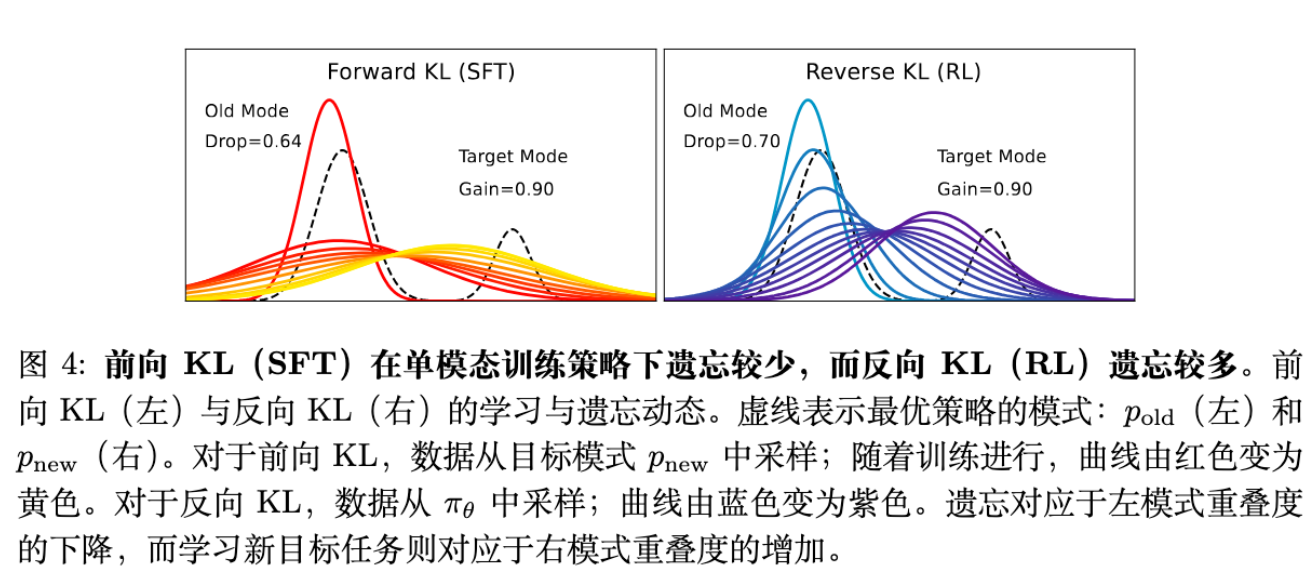
-
Forward KL: 为了覆盖新的模式 , 被迫拉伸(Stretch)其分布,虽然重心移向了新任务,但为了“覆盖”全程,它必须保留一部分质量在旧区域。 -
Reverse KL: 由于是 Mode-seeking, 会迅速移动并收缩到 上,完全放弃 区域。
结论: 在单模态假设下,Forward KL (SFT) 确实比 Reverse KL (RL) 遗忘得少。这符合传统直觉,但与大模型的实际表现不符。
情况 B:初始策略是双模态(Bi-modal)——更符合 LLM 实际
大模型通常具有极高的容量,能够通过 In-context learning 或微调展现出多种模式。因此,将初始策略建模为双模态分布更为合理:
初始化时, 覆盖了真实分布的 ,而 需要学习以匹配 。
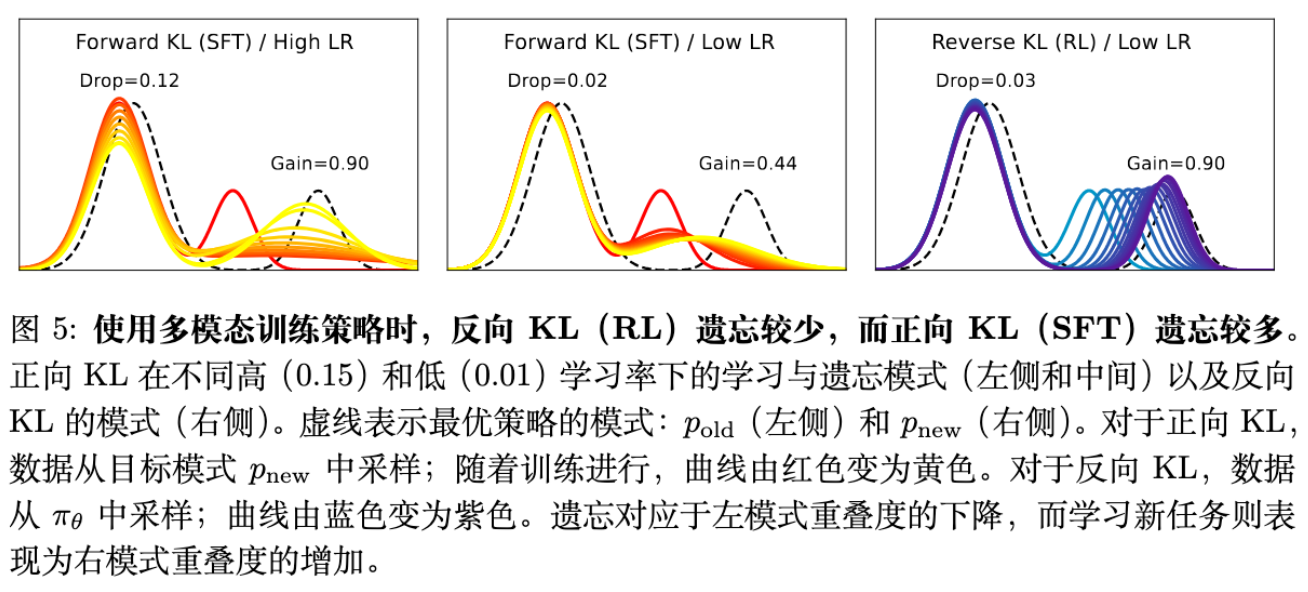
-
Forward KL (SFT): 当试图最小化 Forward KL 时,模型试图让整体分布去匹配目标。如果在高学习率下,为了快速拟合 ,优化器会倾向于不仅移动 ,还会扭曲 或者改变混合系数 ,导致在 上的重叠面积(Overlap Area)显著下降。即,为了覆盖新数据,SFT 牺牲了旧模式的完整性。 -
Reverse KL (RL): 由于 Reverse KL 关注的是 有概率的地方 必须也有概率()。优化过程中, 会被吸引向 (这是 概率高且 概率也高的地方)。关键在于,由于 已经很好地覆盖了 ,这部分产生的 Reverse KL 散度很小。Reverse KL 的 Mode-seeking 特性使得模型可以在调整 拟合新任务的同时,保持 几乎不动,因为它已经是局部最优的一个 Mode。
结论: 在多模态假设下,Reverse KL (RL) 能够在学习新 Mode 的同时,更好地保持旧 Mode 不变,从而实现更少的遗忘。这解释了 SFT 与 RL 在大模型后训练中的表现差异。
4. On-Policy 数据的主导作用
确立了 Reverse KL 在多模态设定下的优势后,接下来的问题是:在实际算法(如 PPO, GRPO)中,是什么因素导致了这种 Reverse KL 的行为?
通常 RL 与 SFT 有三个主要区别:
-
数据来源: RL 使用 On-Policy 数据(当前策略生成),SFT 使用 Off-Policy 数据(固定数据集)。 -
正则化: RL 通常包含 KL 惩罚项(),SFT 没有。 -
梯度加权: RL 使用优势函数(Advantage)或奖励对梯度进行加权,SFT 等价于权重为 1。
作者通过消融实验逐一排查。
4.1 KL 正则化不是关键
作者对比了带有 KL 惩罚()和不带 KL 惩罚()的 GRPO 算法。
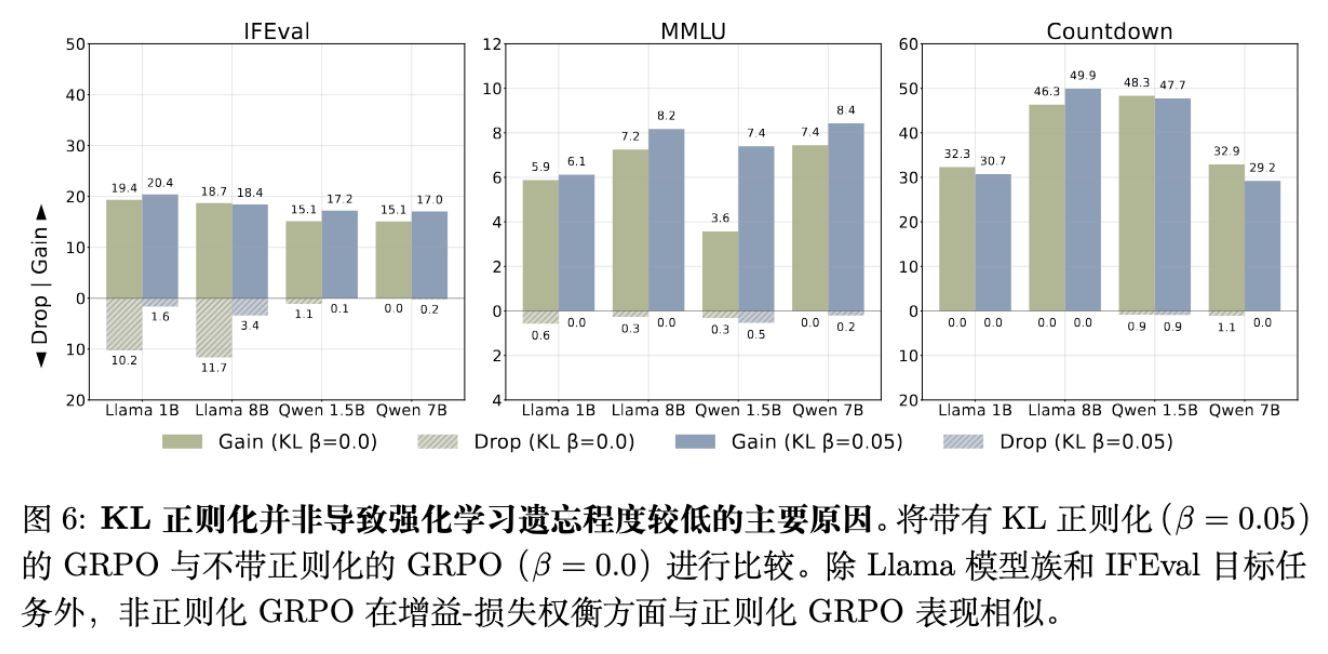
实验结果显示,除了 Llama 模型在 IFEval 任务上的特例,无论是否有 KL 正则化,GRPO 在 Gain-Drop 权衡曲线上的表现几乎一致。这意味着 KL 正则化并不是阻止遗忘的主要因素。
4.2 优势估计(Advantage)不是关键
最近有同期工作(Lai et al., 2025)提出假设,认为 RL 中的优势估计器(Advantage Estimator)提供的隐式正则化是缓解遗忘的原因。为了验证这一点,作者比较了 GRPO 和最基础的 REINFORCE 算法(没有优势减基线操作,直接用奖励作为权重)。
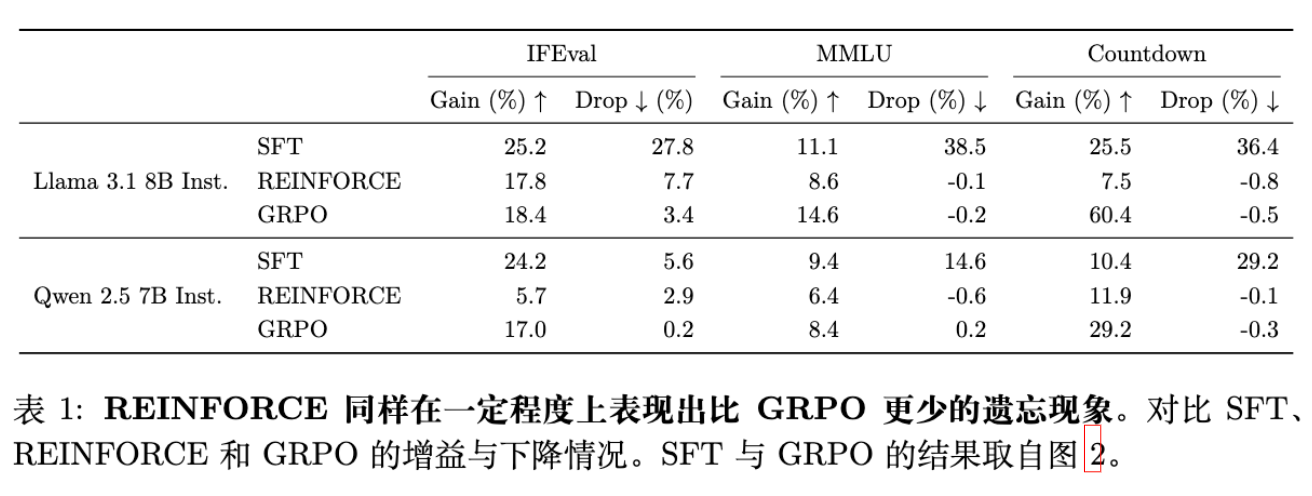
结果表明,虽然 REINFORCE 在目标任务上的学习效率不如 GRPO(Gain 较低),但它同样保持了极低的遗忘率(Drop 极低),与 GRPO 处于同一水平,且显著优于 SFT。这说明优势函数的具体形式并非缓解遗忘的根本原因。
4.3 结论:On-Policy 数据是核心
排除上述因素后,剩下的核心区别在于 On-Policy 数据。
-
SFT 即使是 Self-SFT,使用的数据也是从初始策略 采样的(对于后续训练步而言是 Off-Policy 的)。 -
RL 在每一步更新时,使用的数据均来自当前策略 。
这种实时采样机制确保了模型始终在优化 Reverse KL 方向(即调整当前策略的概率密度去匹配高奖励区域),从而展现出 Mode-seeking 的行为,保护了旧的 Mode。
5. 使用近似 On-Policy 数据缓解遗忘
如果 On-Policy 数据是关键,那么我们是否必须运行昂贵的 RL 流程?能否在 SFT 框架下通过更新数据分布来模拟这一效果?
5.1 Iterative-SFT
作者测试了一种名为 Iterative-SFT 的方法:
-
将训练分为多个 Round(或 Epoch)。 -
在每个 Round 开始时,使用当前模型重新生成数据,并用奖励函数过滤。 -
在这些新生成的数据上进行 SFT。
这种方法是“近似 On-Policy”的,因为它比只用初始数据更接近当前策略,但比全量 RL 的更新频率低。
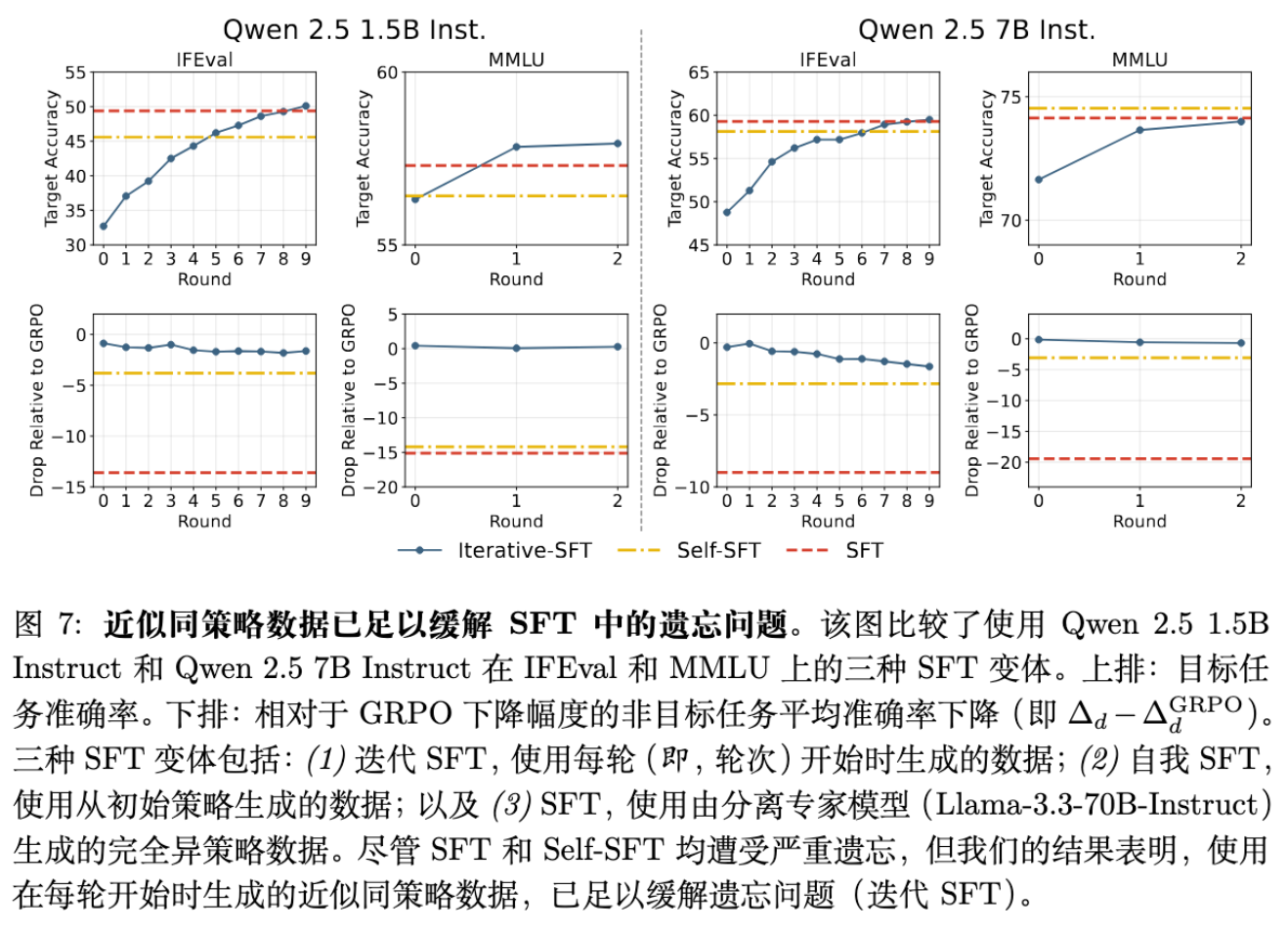
实验结果令人振奋:
-
Iterative-SFT 在目标任务准确率上达到甚至超过了标准 SFT。 -
更重要的是,Iterative-SFT 的遗忘程度显著降低,其 Gain-Drop 曲线大幅优于 Self-SFT 和 SFT,逼近 RL 的表现。
5.2 SFT on RL Traces
为了进一步验证“数据分布决定遗忘”的假设,作者直接拿 RL 训练过程中产生的 On-Policy 数据轨迹(Traces),用 SFT 的损失函数(Cross-Entropy)去训练模型。
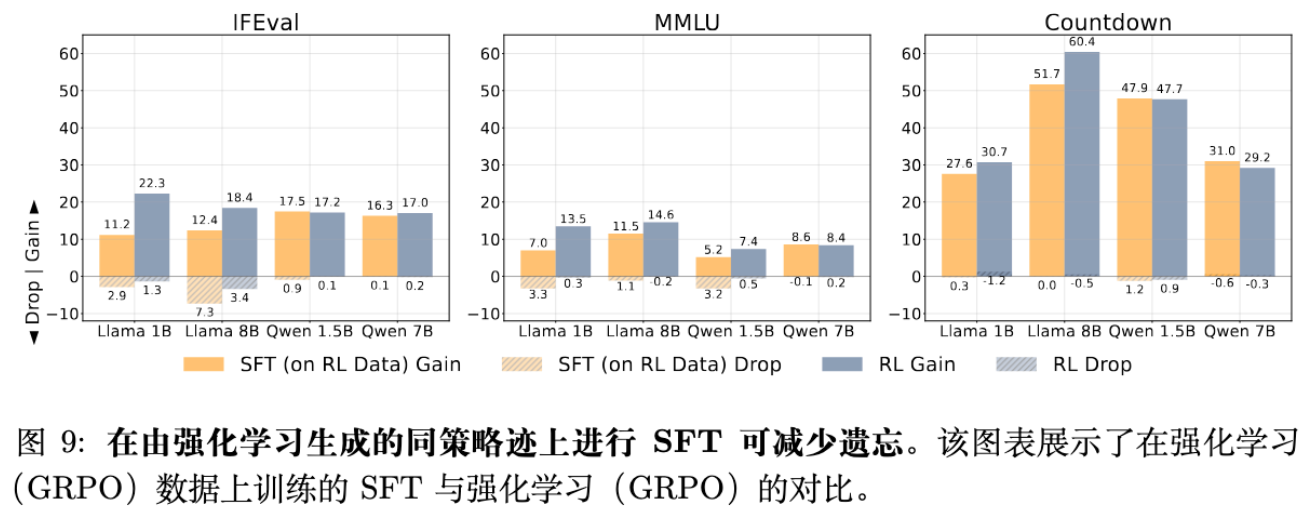
结果显示,使用 RL 产生的 On-Policy 数据进行 SFT 训练,其遗忘模式与原生 RL 高度一致。这进一步证实了:算法本身(Loss Function)不是最重要的,喂给模型的数据分布(是否 On-Policy)才是决定遗忘程度的关键。
6. 讨论与相关工作
6.1 与同期工作的对比
本文的发现与 Lai et al. (2025) 和 Shenfeld et al. (2025) 等同期工作存在对话关系。
-
Lai et al. 认为优势估计是关键。本文通过 REINFORCE 实验反驳了这一点,证明即使没有复杂的优势估计,只要是 On-Policy 采样,遗忘就很低。 -
Shenfeld et al. 同样发现了 RL 遗忘少,并将其归因于 RL 隐式地保持了与初始策略的低 KL 散度。本文在附录 A.5 中计算了 KL 散度与遗忘的相关性(Pearson correlation 0.52),认为相关性存在但并非完全单调对应(SFT 有时 KL 更大但遗忘不一定线性增加)。本文提供了更底层的解释:多模态下的 Reverse KL 动力学。
6.2 局限性与未来方向
-
计算成本: 生成 On-Policy 数据(即使是 Iterative)需要大量的推理计算。如何在计算效率和抗遗忘之间找到更优的平衡点(例如 Replay Buffer 的使用策略)是未来的方向。 -
理论假设: 高斯混合模型虽然直观,但毕竟是对高维 LLM 概率分布的极度简化。 -
数据多样性: 实验主要集中在指令遵循和推理任务,对于更开放的创意写作等任务,Mode-seeking 可能会导致多样性下降(Mode Collapse),这在某些场景下可能是不希望看到的。
7. 结论
这篇论文通过严谨的实证研究和直观的理论建模,解开了“RL 为何比 SFT 更能抗遗忘”的谜题。
核心结论如下:
-
机制: 在多模态分布假设下,RL 对应的 Reverse KL 目标函数具有 Mode-seeking 特性,能够独立地偏移新任务对应的 Mode,而不破坏代表旧知识的 Mode。相比之下,SFT 的 Forward KL 倾向于拉伸整个分布,导致旧知识的概率质量流失。 -
归因: 这种鲁棒性主要源于 On-Policy 数据 的使用,而非 KL 正则化项或特定的优势估计算法。 -
应用: 通过 Iterative-SFT(周期性更新训练数据)可以近似 On-Policy 的效果,从而在 SFT 框架下显著缓解灾难性遗忘。
这一发现为大模型后训练(Post-training)提供了重要的指导原则:如果希望保留模型原有的能力,请尽量避免使用静态的 Off-Policy 数据进行多 Epoch 训练;让模型“边做边学”(Retaining by Doing),通过实时反馈更新数据分布,是更安全的选择。
附录:技术细节深挖
这里补充论文中的部分数学推导细节。
附录 A:面积重叠(Area Overlap)与全变分距离(Total Variation Distance)的联系
在第 3 节的理论分析中,作者使用了“面积重叠”作为衡量遗忘和学习的指标。这并非随意选择,而是与全变分距离(Total Variation, TV)有严格的数学联系。
设 为定义在域 上的概率密度函数(可能未归一化)。它们之间的 TV 距离定义为:
作者定义的重叠面积为:
利用恒等式 ,我们可以推导出:
在论文的设定中,旧知识的保留程度 被定义为训练策略 与最优策略旧模态分量 的归一化重叠。
代入上述关系,遗忘指标(非目标任务下降 )本质上就是训练策略与最优策略旧分量之间 全变分距离的归一化增量。这从测度论的角度严格保证了 metric 的有效性。
附录 B:实验超参数细节
为了复现论文结果,以下是关键的超参数设置:
-
优化器: AdamW。 -
学习率: -
Llama-3.2-1B / Qwen-2.5-1.5B: 初始化为 。 -
Llama-3.1-8B / Qwen-2.5-7B: 初始化为 。
-
-
Scheduler: Cosine scheduler,3% warmup。 -
Batch Size: IFEval/MMLU 为 128,Countdown 为 64。 -
RL设置: -
算法: GRPO。 -
KL 系数: 0.05。 -
Group Size: 5。 -
优势计算: 无 Advantage Clipping。
-
-
Prompt 格式: -
MMLU 采用标准选择题格式。 -
Countdown 采用 Chain-of-Thought 提示:"Think and return the final answer in ."
-
通过这些详实的设置,我们可以在自己的环境中验证“On-Policy Data Mitigation”这一现象。
往期文章:




