思维链（Chain-of-Thought, CoT）通过引导模型生成一长串推理步骤，显著提升了模型在这些任务上的准确率。这种方法的直觉在于，更长的推理轨迹（即更多的“思考”）能够让模型更充分地探索解题策略、进行自我检查和修正，从而逼近正确答案。

然而，这种“长链思维”（Long CoT）并非没有代价。它带来了几个相互交织的挑战：

  • 计算与延迟的膨胀：生成更长的推理链条，直接意味着更多的 token 生成，这不仅增加了推理时的计算成本，也延长了用户等待最终答案的延迟时间。在许多实际应用场景中，这种高昂的成本和延迟是难以接受的。
  • 上下文长度的瓶颈：长链推理将推理深度与序列长度紧密耦合。随着推理步骤的增加，上下文窗口被迅速填满，这不仅带来了更高的计算开销，还可能触发长上下文相关的失败模式，例如模型“忘记”对话早期的关键信息。
  • 帕累托边界的困境：模型的性能表现似乎被一条“帕累托边界”所限制，即我们很难在不牺牲计算成本或延迟的情况下，单方面地提升准确率。长链思维虽然将这条边界向外推进，但它提供的通常是“高成本、高准确率”的选项。研究界一直在探索：在这条效率与效果的权衡曲线上，是否存在其他更优的组合点？例如，我们能否在保持甚至降低延迟的同时，获得比长链思维更高的准确率？

这些挑战共同构成了一个关键的研究问题：我们能否解耦模型的“思考总量”与“单次调用上下文长度”，从而在推理的帕累托边界上，找到成本更低、延迟更少、但准确率更高的解决方案？

来自 Meta Superintelligence Labs 的论文《Rethinking Thinking Tokens: LLMs as Improvement Operators》，为此提供了一个全新的视角。他们不再将 LLM 简单视为一个单向的“思考者”，而是将其重新定义为一个能够作用于自身“想法”的“改进算子”（Improvement Operator）。基于这一理念，他们提出了一套新的推理框架，旨在通过迭代和并行的策略，打破长链思维的固有束缚，探索推理效率与效果的全新可能性。

  • 论文标题：Rethinking Thinking Tokens: LLMs as Improvement Operators
  • 论文链接：https://arxiv.org/pdf/2510.01123

1. 将大语言模型视为“改进算子”

传统上，我们使用 LLM 的方式是“一次性”的：输入一个问题，模型生成一个包含推理过程和最终答案的长序列。这好比要求一位解题者必须从头到尾、一气呵成地写下所有思路，中间不能停顿或修改。

而该论文的核心思想是，将这个过程分解为多个“思考-改进”的循环。在这个视角下，LLM 扮演的角色不再是简单的答案生成器，而是一个可以接收现有“想法”（一个或多个解题草稿），并在此基础上进行优化和提炼的“改进算子”。这个改进过程可以有多种策略，形成一个连续的光谱。

这篇工作重点研究了一个名为“并行-蒸馏-精炼”（Parallel-Distill-Refine, PDR）的推理家族。PDR 的流程可以概括为以下三个核心步骤：

  1. 并行（Parallel）：针对同一个问题，并行生成多个不同（diverse）的解题草案。
  2. 蒸馏（Distill）：将这些并行的草案“蒸馏”成一个有界的、紧凑的文本工作区（workspace）。这个工作区可以看作是对当前所有思路的总结，包含了共识、矛盾、中间结果和待解决的子问题。
  3. 精炼（Refine）：模型以这个紧凑的工作区为条件，生成一个更优的、经过精炼的答案。这个新答案可以作为下一轮改进的起点。
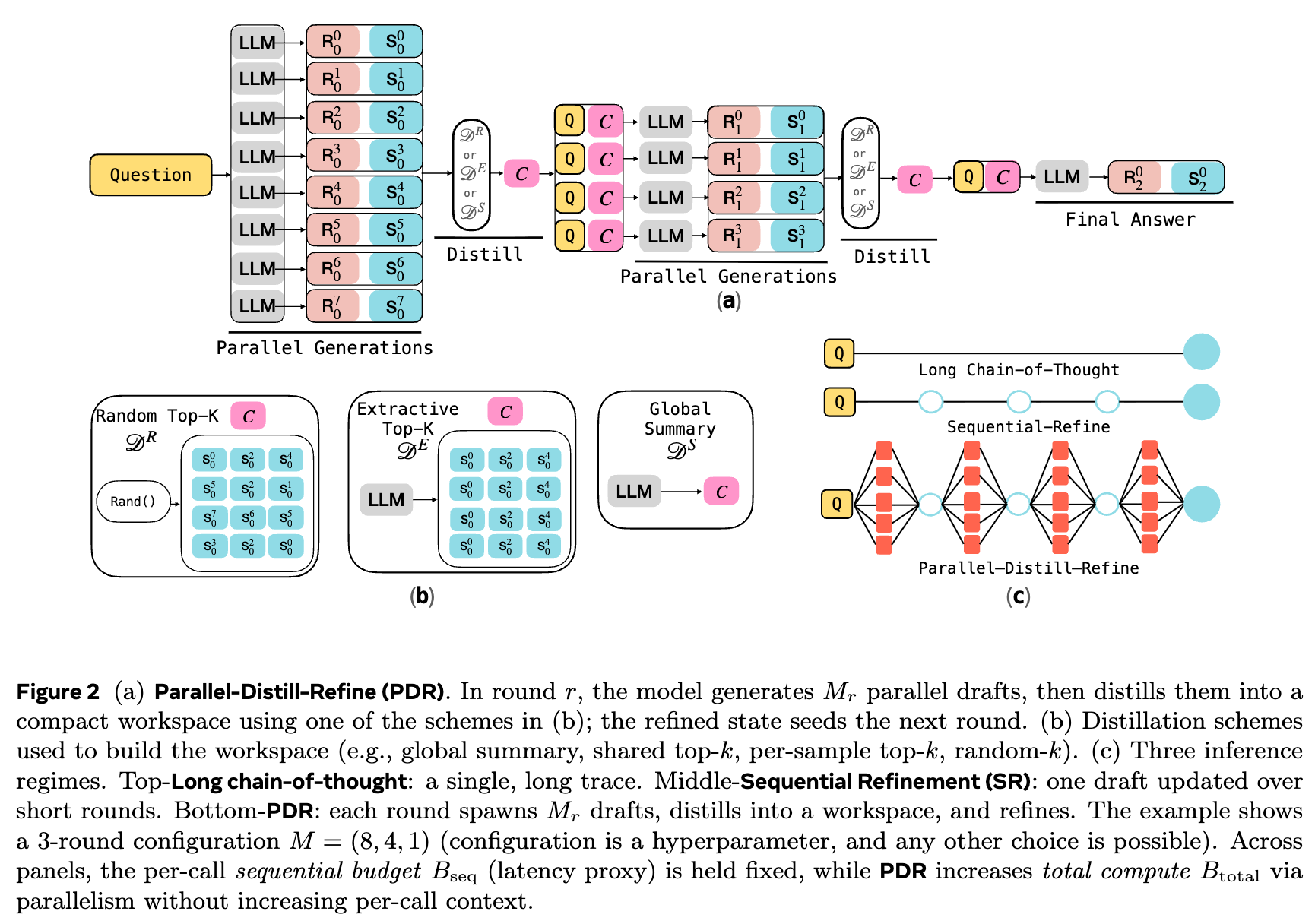
并行-蒸馏-精炼（PDR）流程图
并行-蒸馏-精炼（PDR）流程图

这个框架的关键优势在于，它有效地控制了上下文长度（以及计算成本）。模型的每次调用都只处理一个紧凑的工作区和问题本身，而不是一个不断增长的、包含所有历史尝试的冗长文本。总的“思考量”（即生成的总 token 数）可以通过并行度来控制，而不再与单次调用的上下文长度相混淆。

通过这种方式，PDR 框架旨在将更多的总计算量（通过并行实现）转化为更高的准确率，同时保持较低的单次调用延迟。

2. SR 与 PDR

论文详细研究了两种具体的“改进算子”实现，它们分别代表了迭代改进在深度和广度两个维度上的应用。

2.1 顺序精炼（Sequential Refinement, SR）：深度的迭代

SR 是 PDR 框架在并行度为 1 时的特例，也是最简单的迭代改进形式。它的工作流程如下：

  1. 模型首先针对问题生成一个初步的解决方案。
  2. 在下一轮中，模型接收自己上一轮生成的方案，并被要求“在不从头开始的情况下，提出一个更好的答案”。
  3. 这个过程可以重复进行 R 轮，最后一轮的输出即为最终答案。

SR 的本质是深度优先的探索。它让模型有机会反复审视和修正单一的解题思路，从而逐步提升答案质量。论文还探讨了一种 SR 的变体，即带有局部工作区（local workspace）的 SR。在这种模式下，模型在两轮之间会增加一个“错误分析”步骤：首先识别并解释当前方案中的缺陷，然后基于这些分析笔记生成一个修正后的方案。这些分析笔记就构成了一个临时的、局部的“工作区”。

SR 的优势在于其概念简单且实现直接。然而，它的一个潜在风险是可能会陷入局部最优，或者对最初的错误产生“锚定效应”，难以跳出错误的框架。

2.2 并行-蒸馏-精炼（Parallel-Distill-Refine, PDR）：广度的探索

PDR 是本文的核心贡献，它通过引入并行化来克服 SR 可能存在的局限性。PDR 采用的是广度优先的探索策略，它在每一轮都生成多个多样的草稿，然后汇总信息，再进行下一步。

一个典型的 PDR 流程如下（以一个 3 轮配置 M = (8, 4, 1) 为例）：

  • 第 1 轮：并行生成 个独立的解题草案。
  • 蒸馏：将这 8 个草案的关键信息（如共识、矛盾点、不同方法得出的中间结果）“蒸馏”成一个紧凑的摘要 。
  • 第 2 轮：以 为上下文，并行生成 个新的、更优的解题草案。
  • 蒸馏：再次将这 4 个新草案蒸馏成一个新的摘要 。
  • 第 3 轮：以 为上下文，生成 个最终的精炼答案。

PDR 的核心挑战在于信息蒸馏这一步。如何有效地将多个（可能包含正确、错误和部分正确信息的）草案压缩成一个简洁而信息丰富的“工作区”至关重要。研究者们探索了多种蒸馏策略（即蒸馏算子 的实现）：

  • 全局摘要（Global summary）：让 LLM 读取所有草案，然后生成一段自由格式的文本，总结其中的共识、矛盾、已证实的结论、未解决的子问题以及下一步的建议。
  • 提取式 Top-k 证据（Extractive top-k evidence）：不生成新的文本，而是直接从所有草案中挑选出质量最高的 k 个作为下一轮的上下文。这牺牲了一定的压缩率，但保留了原始证据的保真度。
  • 随机-k/自助采样工作区（Random-k/bootstrapped workspaces）：为下一轮的每个并行生成任务，都从上一轮的草案中随机采样 k 个来构建其独立的工作区。这种方法旨在注入多样性，防止模型过早地达成共识。

通过这种“并行生成-蒸馏摘要-条件精炼”的循环，PDR 能够在一个固定的、较短的上下文长度限制下，模拟出远超这个长度的深度思考过程。

3. 实验

为了验证 SR 和 PDR 的有效性，研究者们进行了一系列严谨的实验。

实验设置：

  • 模型：gpt-o3-mini（被描述为具有中等推理能力）和 gemini-2.5-flash。
  • 任务：使用 AIME（美国数学邀请赛）2024 和 2025 年的数学竞赛题作为基准测试。这类任务需要复杂的、多步骤的推理能力。
  • 评估指标：

    • 准确率：mean@16，即对每个问题独立生成 16 次答案，计算最终答案正确的比例。
    • 计算预算：为了公平比较不同方法的成本，论文定义了两个关键的 token 预算：

      1. 顺序预算（Sequential Budget, ）：沿着最终采纳的路径所消耗的 token 总和（包括 prompt 和生成内容）。这个指标可以被视为延迟的代理（latency proxy），因为它反映了用户需要等待的、不可并行的总生成长度。其计算公式为：


        其中 是最终被采纳的生成路径上的所有模型调用集合。

      2. 总预算（Total Budget, ）：所有模型调用（包括被丢弃的并行分支）消耗的 token 总和。这个指标是总计算成本的代理（compute/cost proxy）。其计算公式为：


        其中 是所有的模型调用。

核心研究问题（RQ）与发现：

RQ1：在匹配的延迟（）下，短上下文迭代能否超越长链思维？

发现：能。

实验结果明确表明，在相同的顺序预算（即相似的延迟）下，SR 和 PDR 的准确率都超过了传统的长链 CoT 基线。

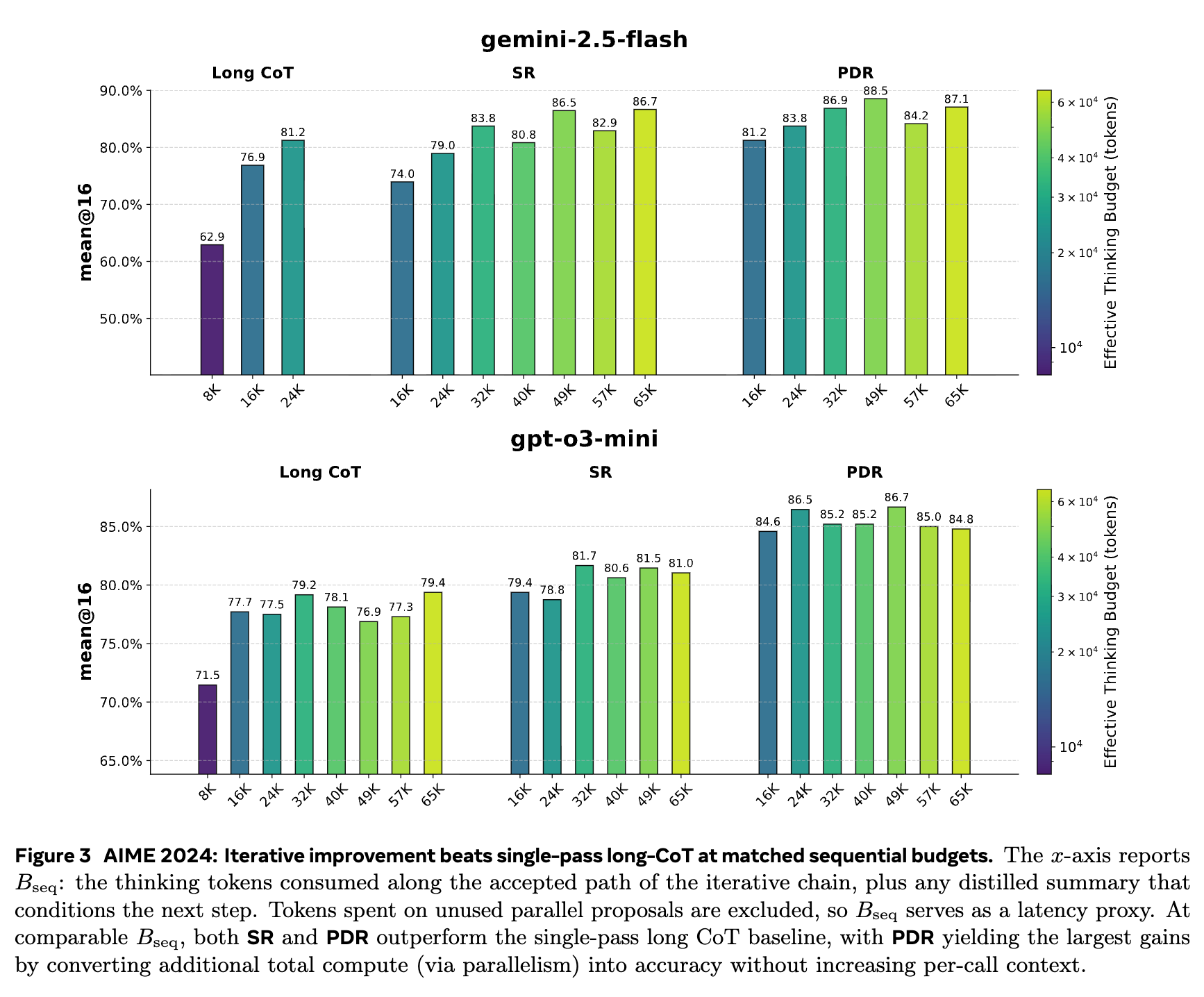
AIME 2024：在匹配的顺序预算下，迭代改进方法优于单次长 CoT
AIME 2024：在匹配的顺序预算下，迭代改进方法优于单次长 CoT

如上图所示，无论是 gemini-2.5-flash 还是 gpt-o3-mini，在 AIME 2024 数据集上，橙色（SR）和绿色（PDR）的柱状图在可比较的 （x 轴）下，其准确率（y 轴）普遍高于蓝色（Long CoT）。

PDR 表现尤为突出。它通过将额外的总计算量（）转化为并行草案，在不增加顺序预算（延迟）的情况下，获得了最大的准确率提升。例如，对于 gpt-o3-mini，在一个约 49k tokens 的顺序预算下，Long CoT 的准确率为 76.9%，SR 提升至 81.5%，而 PDR 则达到了 86.7%，相比基线提升了近 10 个百分点。

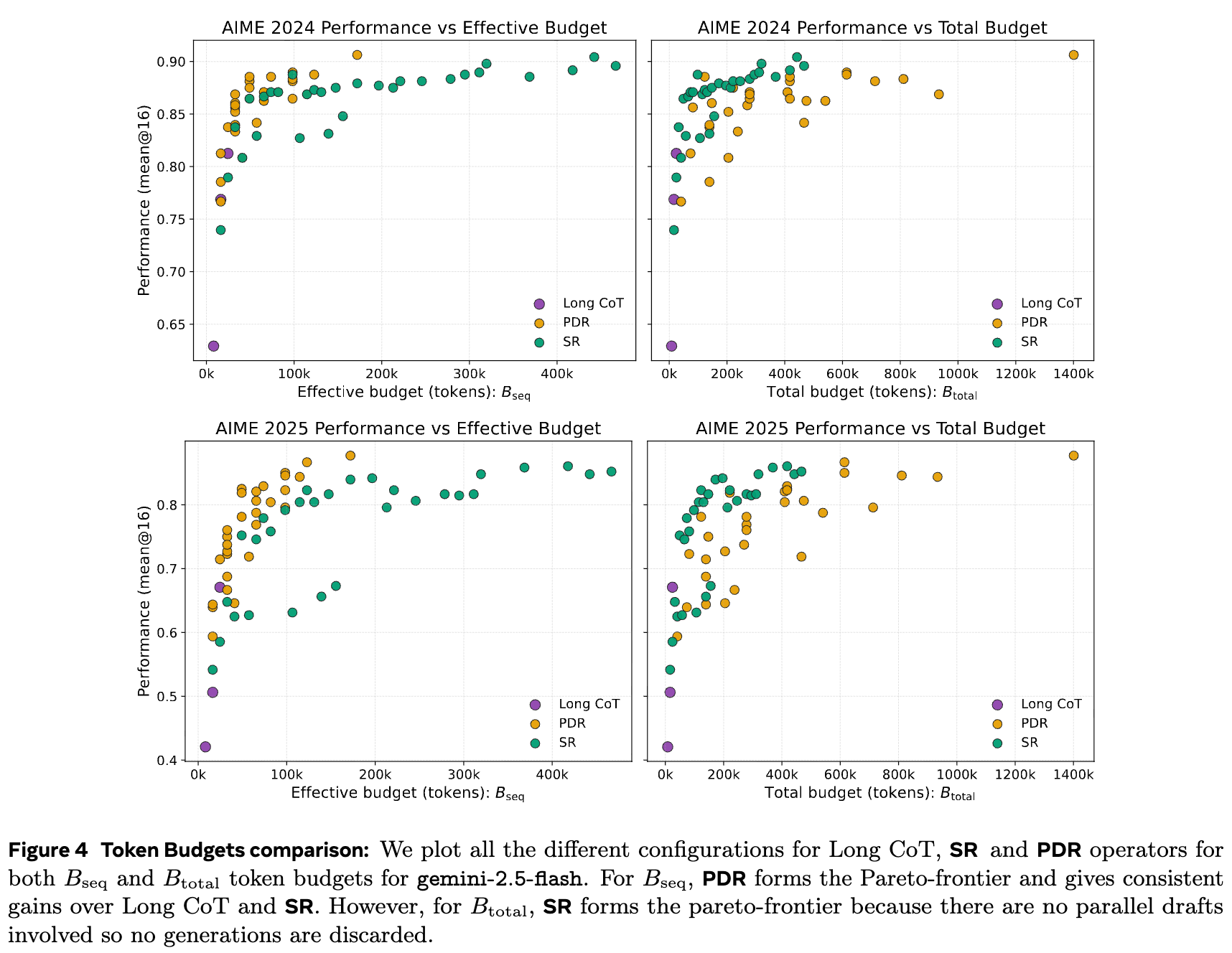
gemini-2.5-flash 在不同预算下的性能帕累托边界
gemini-2.5-flash 在不同预算下的性能帕累托边界
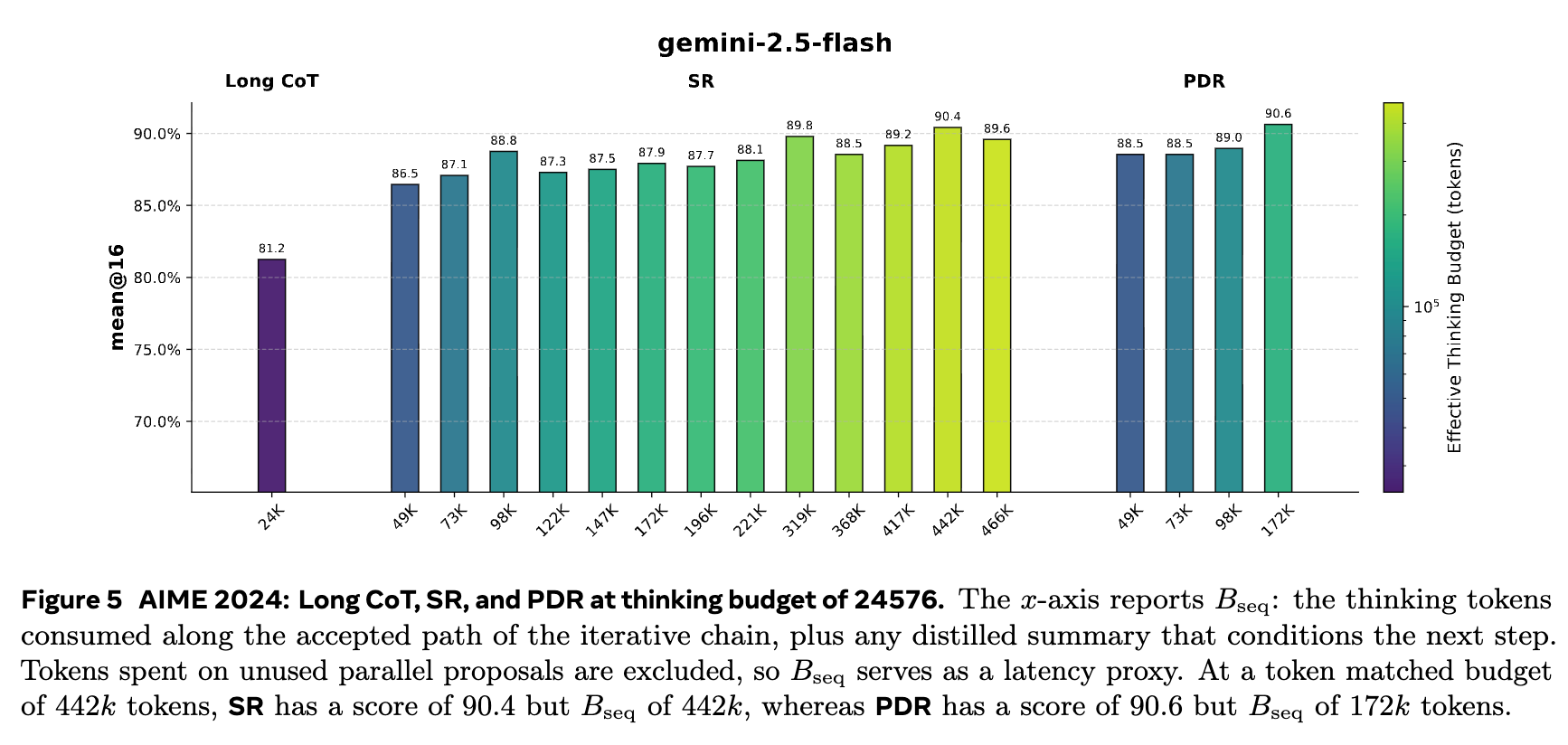
AIME 2024: 在 thinking budget 为 24576 时，Long CoT, SR 和 PDR 的性能对比
AIME 2024: 在 thinking budget 为 24576 时，Long CoT, SR 和 PDR 的性能对比

图 4 和图 5 进一步从帕累托边界的角度展示了这一点。在 （延迟）- 准确率的二维平面上（图 4 左侧），PDR（紫色点）形成了一条新的、更优的帕累托边界，压倒了 Long CoT（绿色点）和 SR（橙色点）。这意味着对于任何给定的延迟要求，PDR 都能提供更高的准确率。而在 （总计算成本）- 准确率的平面上（图 4 右侧），SR 由于没有并行开销（），形成了最优的边界。

这揭示了一个核心权衡：

  • 如果你最关心延迟，PDR 是最佳选择，因为它能用并行计算换取准确率，而无需等待更长的单序列生成。
  • 如果你最关心总计算成本，SR 是更经济的选择，因为它在不引入任何并行开销的情况下提升了性能。

RQ2：哪种蒸馏策略（Distillation Strategy）效果最好？

发现：全局摘要（Global summary）和每个样本的 Top-k（Per-sample top-k）表现突出。

研究者比较了四种蒸馏算子 的性能。

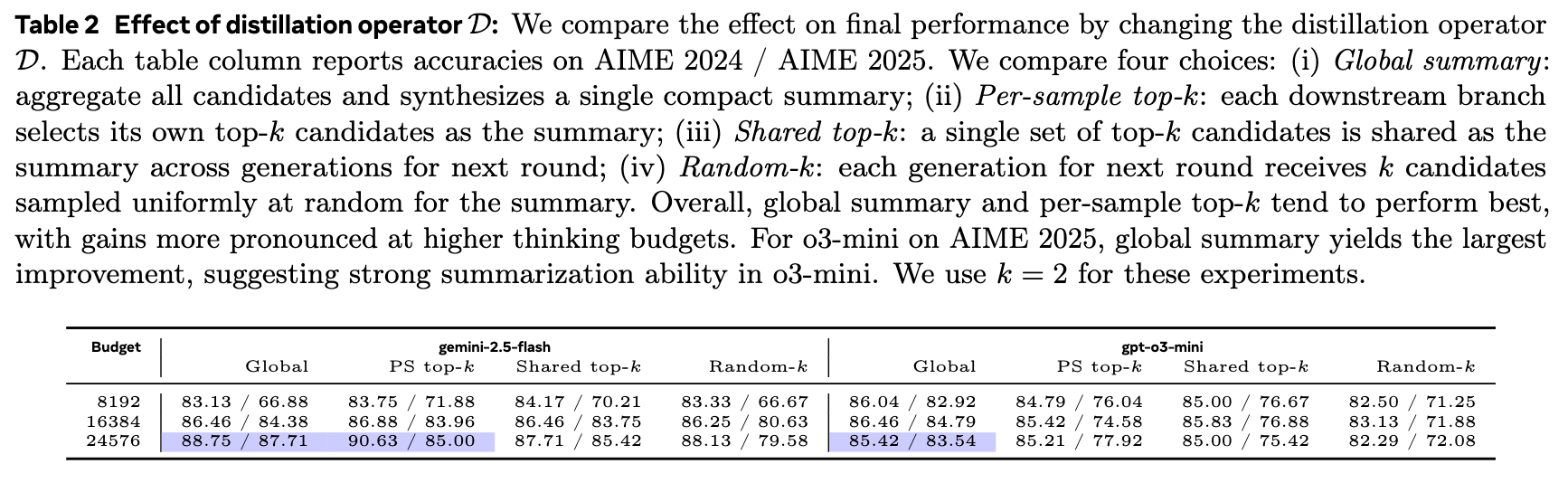
蒸馏算子 D 的效果对比
蒸馏算子 D 的效果对比

如表 2 所示，在 AIME 2024 和 2025 数据集上，Global summary 和 PS top-k（即 Per-sample top-k）两种策略在大多数情况下都优于 Shared top-k 和 Random-k。随着 thinking budget 的增加，这种优势更加明显。

这表明，一个高质量的“工作区”需要对信息进行有效的综合（Global summary）或者忠实地呈现最优的几个思路（PS top-k）。随机选择（Random-k）的效果最差，说明信息的质量而非随机性在迭代改进中更为关键。一个有趣的发现是，在 AIME 2025 数据集上，gpt-o3-mini 模型使用 Global summary 策略时效果提升最大，这可能暗示该模型具备较强的摘要和信息整合能力，能从正确和错误的草稿中提取出有价值的线索。

RQ3：模型的验证能力（Verification Ability）如何影响最终性能？

发现：模型存在明显的锚定偏见，验证能力是 PDR 成功的关键。

为了探究模型自身的验证能力在 PDR 框架中的作用，研究者们进行了一项“神谕”（Oracle）实验。他们人为地控制进入蒸馏环节的草案质量，构造了三种情况：

  1. Random-k：默认情况，随机选择 k 个草案。
  2. Oracle (Correct)：只将正确的草案送入工作区。
  3. Oracle (Incorrect)：只将错误的草案送入工作区。
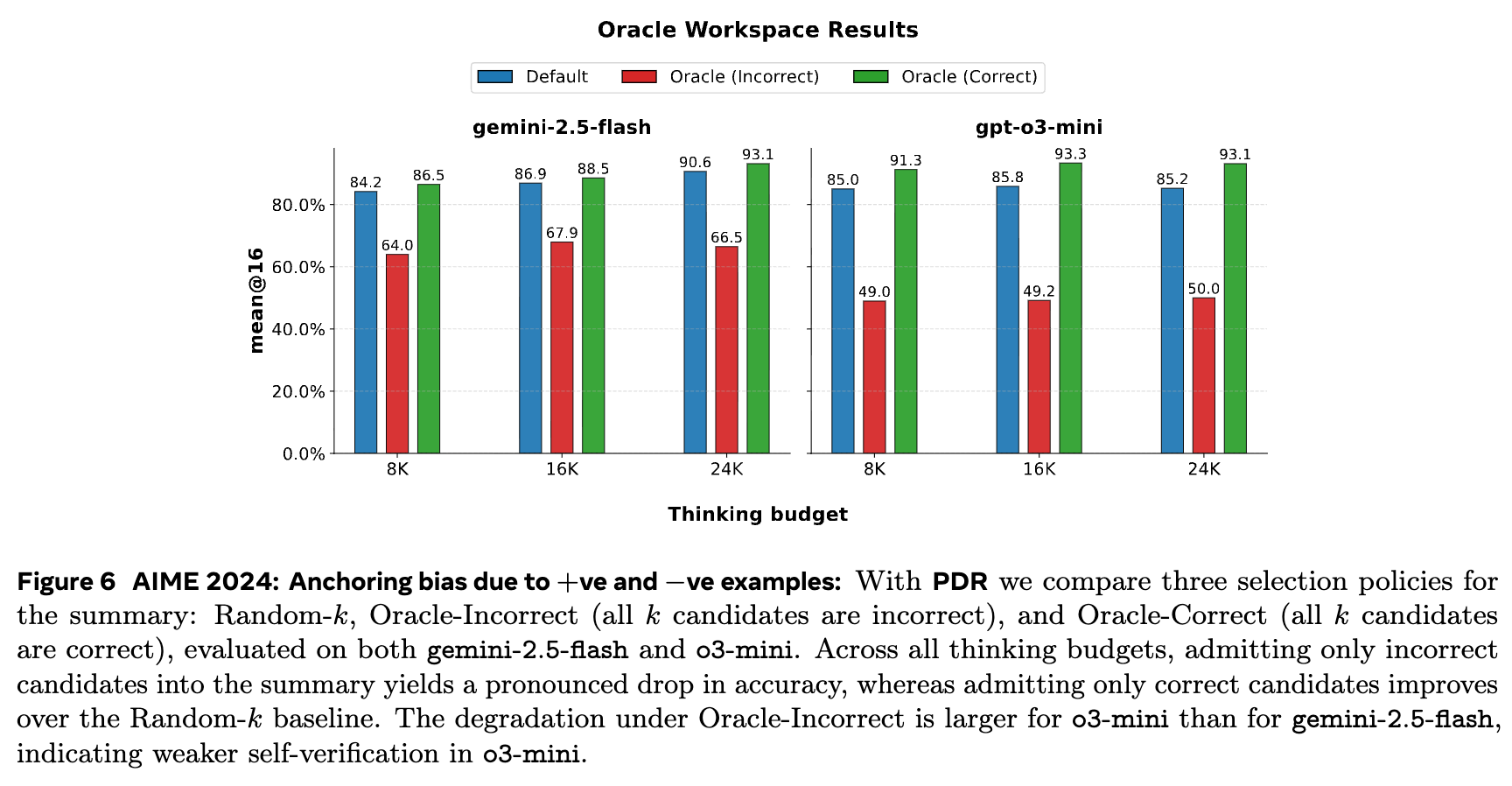
AIME 2024：因正负样本导致的锚定偏见
AIME 2024：因正负样本导致的锚定偏见
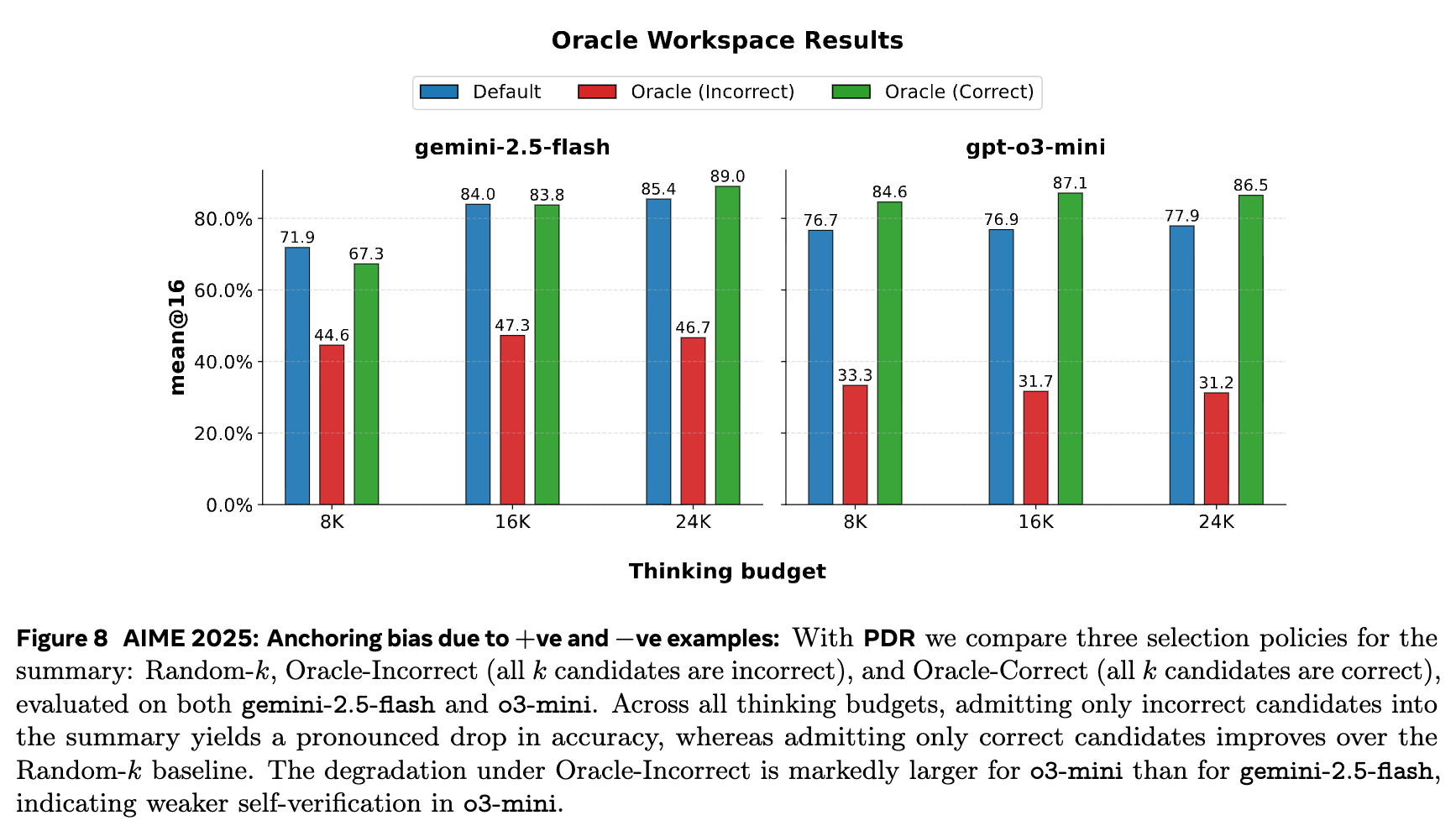
AIME 2025：因正负样本导致的锚定偏见
AIME 2025：因正负样本导致的锚定偏见

结果（如图 6 和图 8）是富有启发性的：

  • 当工作区中只包含错误的候选答案时（Oracle Incorrect），模型的最终准确率出现断崖式下跌，远低于默认的随机选择。这表明模型很容易被错误的中间结果“锚定”，并在其基础上继续进行错误的推理，而难以自我纠正。
  • 当工作区中只包含正确的候选答案时（Oracle Correct），模型的最终准确率得到了显著提升，超过了默认设置。这说明只要能识别并保留正确的“思想火花”，模型就能有效地将其发扬光大。

这个实验有力地证明了验证（Verification）是 PDR 框架成功的四大元技能（验证、精炼、压缩、多样化）中的核心环节。PDR 的蒸馏步骤必须扮演一个“具备验证意识的聚合器”的角色。同时，gpt-o3-mini 在“Oracle Incorrect”条件下的性能下降幅度比 gemini-2.5-flash 更大，这暗示后者的内在自我验证和纠错能力可能更强。

4. 算子一致性训练（Operator-Consistent Training）

上述实验都是在“推理时编排”（inference-time orchestration）的框架下进行的，即模型本身是冻结的。一个自然的问题是：我们能否通过训练，让模型更适应这种迭代式的、基于紧凑工作区的推理模式？

标准的大模型强化学习（RL）训练通常是优化一个单一的、长链条的轨迹。而 PDR 的推理模式是多条短轨迹+蒸馏+精炼。这种训练与测试的不匹配（train-test mismatch），可能会限制 PDR 性能的进一步发挥。

为此，研究者提出了一种算子一致性强化学习（Operator-Consistent RL）的训练策略。其核心思想是在训练数据中混合两种模式：

  • 模式 A（标准长轨迹优化）：常规的 RL 训练，优化一条完整的长链思维轨迹。这保留了模型在需要时进行长程推理的能力。
  • 模式 B（模拟 PDR 的算子 rollout）：在训练中模拟一个单轮的 PDR 过程。具体来说：

    1. 并行生成 M 个草案。
    2. 蒸馏出一个紧凑的工作区 C。
    3. 模型以 C 为条件，生成一个精炼的答案。
    4. 最后，基于这个精炼答案的最终奖励信号（例如，数学题是否解对）来优化整个过程。

通过在训练中引入模式 B，模型被显式地训练去学习如何在给定一个浓缩的“思路摘要”后进行有效的推理。这有助于模型学习 PDR 所需的核心元技能。

发现：算子一致性训练能够进一步推动帕累托边界。

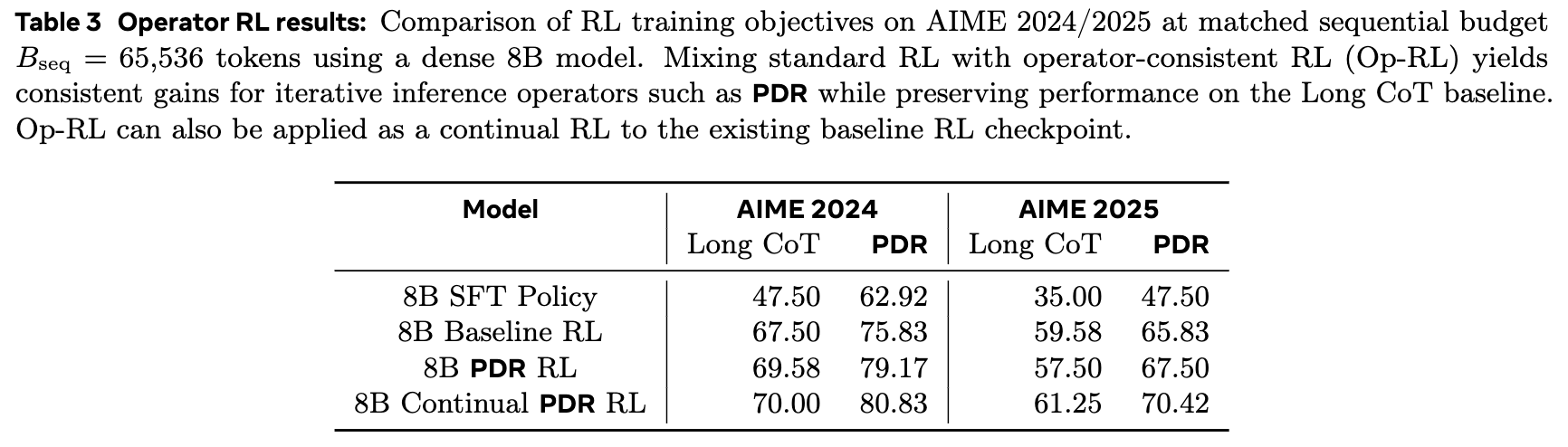
算子 RL 结果
算子 RL 结果

实验在一个 8B 参数的稠密模型上进行。如表 3 所示，与基线 RL 模型（Baseline RL）相比，混合了算子一致性训练的 PDR RL 模型在 PDR 推理模式下的性能得到了进一步提升（AIME 2024 从 75.83% 提升至 79.17%，AIME 2025 从 65.83% 提升至 67.50%）。如果从基线 RL checkpoint 出发进行持续的 PDR RL 训练（Continual PDR RL），性能提升更为显著。

这一结果表明，让训练过程与推理部署方式保持一致，可以有效缩小“训推差距”，使模型更好地掌握迭代式推理所需的元技能，从而将更多的计算量转化为实实在在的性能增益。

5. 结论

这篇论文通过将 LLM 重新概念化为“改进算子”，为提升复杂推理任务的性能和效率开辟了一条新的路径。它系统地研究了两种迭代式推理流程——顺序精炼（SR）和并行-蒸馏-精炼（PDR），并得出了几个关键结论：

  1. 迭代优于单次生成：在匹配延迟（顺序预算 ）的情况下，通过短上下文迭代的 SR 和 PDR 方法，其准确率优于传统的单次长链思维（Long CoT）。
  2. PDR 定义了新的效率边界：PDR 框架通过并行计算，在不增加延迟的情况下显著提升了准确率，从而在“延迟-准确率”的帕累托边界上取得了新的最优解。论文报告了在 AIME 2024 和 2025 数据集上高达 +11% 和 +9% 的性能提升。这表明，通过有界摘要积累证据，可以有效替代长链推理，同时保持延迟可控。
  3. 验证是核心元技能：模型的性能受到“锚定偏见”的显著影响。PDR 的成功在很大程度上依赖于其“蒸馏”步骤能否有效识别和筛选高质量的中间思想。
  4. 训推一致性可进一步提升性能：通过“算子一致性 RL 训练”，让模型在训练阶段就接触和学习 PDR 这种迭代推理模式，可以进一步提升模型性能，将在 AIME 2024 和 2025 上带来约 5% 的额外提升。

这项工作也为未来的研究指明了多个有前景的方向：

  • 可学习的蒸馏算子：当前的蒸馏过程（如全局摘要）仍然依赖于固定的 prompt。未来的工作可以探索如何通过训练来学习一个更高效的、可训练的摘要网络（synthesis operator ）。
  • 自适应的计算资源分配：可以设计一个控制器，根据当前问题的不确定性，动态地决定下一轮的并行数量（fan-out）和迭代深度，实现更智能的计算资源分配。
  • 与外部工具的深度融合：将迭代框架与外部验证器（如代码解释器、计算器）更紧密地结合，可以为模型提供更可靠的反馈，从而提高验证环节的准确性。
  • 跨领域的泛化能力：将 SR 和 PDR 的应用从数学推理扩展到代码生成、规划、创意写作等更广泛的领域，探索在不同任务上短上下文迭代的适用性和最优策略。

往期文章：