我们知道 RLVR 的核心思想很简单:让模型生成多个解题思路(轨迹),然后用一个确定的、可验证的奖励信号(比如答案是否正确)来告诉模型哪些思路是好的,哪些是坏的。通过这种方式,模型可以逐渐学会产出更高质量的推理过程。这种方法在提升模型单次回答的准确率(即 指标)方面表现出色,似乎为攻克复杂推理任务铺平了道路。
然而,一项近期发表的研究论文《BEYOND PASS@1: SELF-PLAY WITH VARIATIONAL PROBLEM SYNTHESIS SUSTAINS RLVR》发现了这条道路上一个不易察觉的陷阱。研究者发现,标准的 RLVR 训练虽然能有效提升 ,但这是以牺牲模型生成多样性为代价的。模型为了追求奖励,会倾向于“固化”到少数几条它认为最有效的推理路径上,导致其策略熵(policy entropy)持续下降。这种现象被称为“熵坍塌”(entropy collapse)。

-
论文标题:BEYOND PASS@1: SELF-PLAY WITH VARIATIONAL PROBLEM SYNTHESIS SUSTAINS RLVR -
论文链接:https://arxiv.org/pdf/2508.14029
熵坍塌的直接后果是,模型的潜在推理能力上限(通常用 指标衡量,即在 k 个采样中至少有一个正确答案的概率)停滞不前。更糟糕的是,当模型的探索能力因熵坍塌而耗尽时,连 的提升最终也会陷入瓶颈。这就好比一个学生,通过反复练习同一套题库,虽然对这些题目的解法了如指掌,但在面对新题型时却束手无策,其综合解题能力并未得到根本提升。
为了解决这一困境,该论文提出了一种新颖的训练策略,名为自博弈变分问题合成(Self-play with Variational problem Synthesis, SvS)。该策略的核心是让模型在训练过程中扮演学生和老师的双重角色:它不仅要解决问题,还要基于自己正确的解题过程,创造出新的、形式不同但答案相同的“变分问题”,从而为自己生成一个动态更新、源源不断的训练数据流。
1. 熵坍塌与性能瓶颈
在深入了解 SvS 之前,我们必须首先理解它试图解决的核心问题:标准 RLVR 训练中普遍存在的熵与性能的权衡。
1.1 与 :衡量推理能力的两种尺度
在评估模型的推理能力时,我们通常使用两个关键指标:
-
:这是最直观的指标,衡量的是模型在“贪婪采样”(即选择最有可能的token)下生成的单个答案的正确率。它反映了模型在最自信的情况下,给出正确答案的能力。 -
:该指标衡量的是,模型通过多次(k次)独立采样生成 k 个不同的答案,其中至少有一个是正确的概率。 通常被认为是模型真实推理能力的上限。一个高 值意味着正确答案存在于模型的可能输出中,即使它不是最自信的那个。
标准 RLVR 训练的目标函数通常直接或间接地优化 。然而,论文指出,一个真正强大的推理模型,不仅应该在 上表现出色,更应该拥有一个不断增长的 ,这代表了其探索更广阔、更高级推理空间的潜力。
1.2 策略熵:生成多样性的量化
策略熵(Policy Entropy)是信息论中的一个概念,在这里用来衡量模型输出的不确定性或多样性。一个高熵的策略会生成多种多样的答案,而一个低熵的策略则会倾向于生成非常相似甚至完全相同的答案。
在 RLVR 的初始阶段,模型的策略熵较高,它会探索各种各样的解题路径。随着训练的进行,模型会发现某些路径能够更稳定地获得奖励,于是它会增加选择这些路径的概率,同时降低探索其他路径的概率。这个过程会导致策略熵的不断下降。
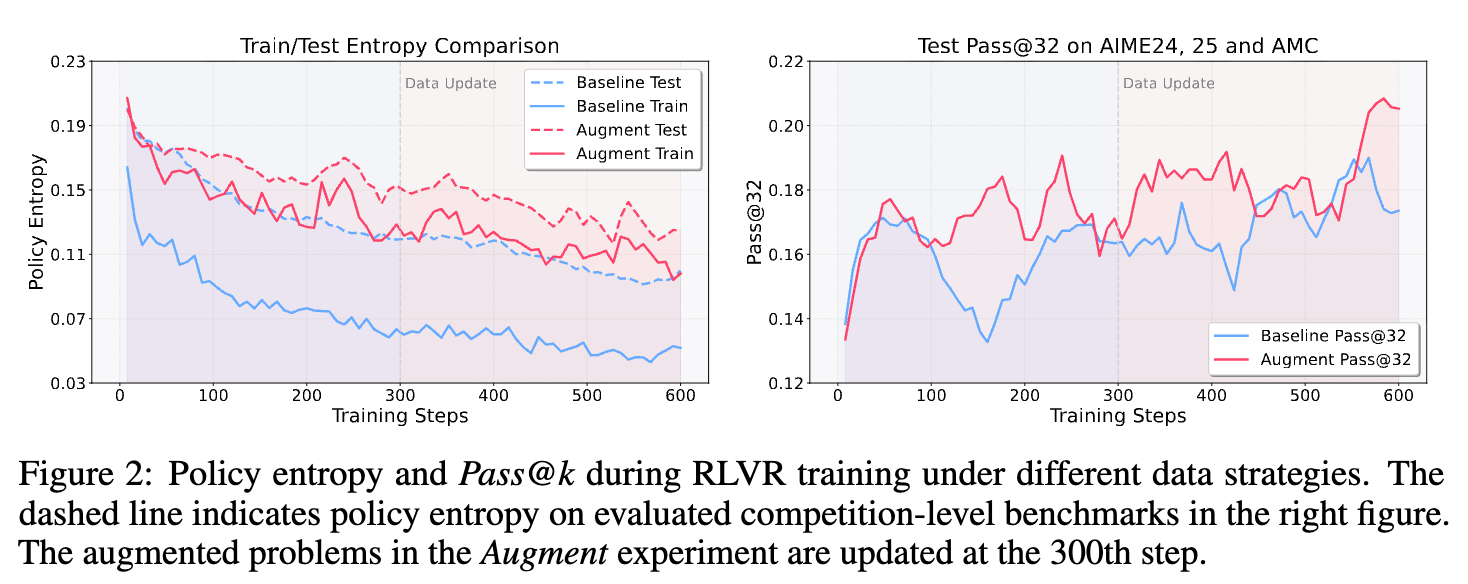
正如论文中图 2 所示的实验,在标准的 RLVR 训练下(图中的蓝色曲线),模型的策略熵随着训练步数的增加而稳步下降。这正是“熵坍塌”现象。
1.3 熵坍塌的恶性循环
熵坍塌并非无害。它引发了一系列连锁反应,最终限制了模型的性能。
-
探索能力减弱:熵的降低意味着模型不再愿意尝试新的、可能有风险但或许更优的解题思路。它满足于已经掌握的“套路”。 -
停滞:由于探索的减少,模型很难发现新的正确解法。因此, 的增长很快就会停滞。模型知识的边界被锁定了。 -
到达瓶颈: 的提升本质上是从 所代表的潜在能力池中“提炼”出最可靠的解法。当这个池子不再扩大时, 的提升也就成了无源之水,最终也会达到平台期。
这个问题的根源在于训练数据的静态性。当模型在同一个固定的、有限的问题集上反复训练时,它最终会从“学习推理”退化为“记忆解法”,这是一种“过拟合”到训练集上的表现。
1.4 现有解决方案的局限
一个自然的想法是增加训练数据的多样性。例如,使用另一个强大的 LLM 对现有问题进行“改写”或“复述”(rephrasing)。
然而,这种方法存在几个问题:
-
语义一致性风险:外部模型在改写过程中可能会引入与原问题不符的语义偏差,从而污染训练数据。 -
多样性有限:改写通常依赖于原问题的文本,其结构和核心逻辑很难有根本性的改变。 -
能力不匹配:外部模型生成的问题可能与当前正在训练的模型的“能力边界”不匹配,导致问题要么太难要么太简单。
因此,理想的数据增强方法应该满足几个条件:它是迭代的,能够根据模型当前状态动态生成;它能保证新问题的答案是精确的;它生成的问题难度应该与模型的能力相匹配。这正是 SvS 设计的核心出发点。
2. 自博弈变分问题合成 (SvS)
面对 RLVR 的困境,论文作者从 AlphaGo 的“自博弈”中汲取灵感,设计了 SvS 框架。在 SvS 中,模型不再是一个被动的信息接收者,而是一个主动的知识创造者。它通过与“自己”的互动,不断产生新的学习材料,从而打破静态数据集的束缚。
SvS 的核心工作流可以分解为以下几个步骤,形成一个优雅的自提升闭环:
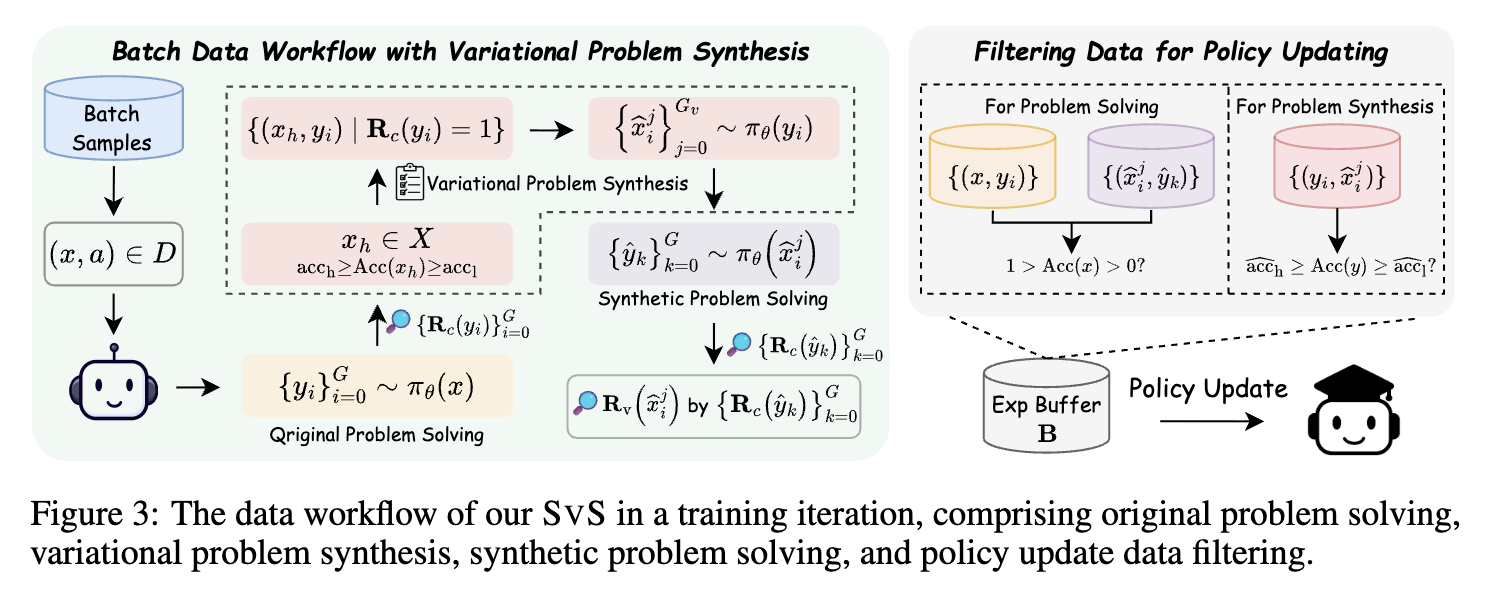
2.1 步骤一:原始问题求解(Original Problem Solving)
训练的每一步都从一个批次的原始训练问题(例如,MATH-12k 数据集中的问题)开始。模型(我们称之为“策略模型”)会像一个学生一样,尝试解决这些问题。对于每个问题 ,模型会生成 个不同的解法 。
然后,系统会根据预先知道的真实答案 来判断每个解法的正确性,并给予奖励 。如果一个解法得出的答案与 一致,,否则 。
2.2 步骤二:筛选挑战性问题(Filtering Challenging Problems)
接下来,模型扮演“教练”的角色。它不会对所有问题都一视同仁,而是会筛选出那些对它当前能力水平来说最具挑战性的问题。
“挑战性”的定义是:模型对这个问题的求解正确率(Group Average Accuracy, Acc(x))既不是 0%(太难,完全不会),也不是 100%(太简单,已经掌握),而是落在一个预设的中间区间内,例如 [12.5%, 50.0%]。
这个筛选步骤至关重要,因为它将模型的注意力集中在了其能力的“学习区”(Zone of Proximal Development),确保后续的问题合成是高效且有针对性的。
2.3 步骤三:变分问题合成(Variational Problem Synthesis)
这是 SvS 最具创新性的一步。对于上一步筛选出的挑战性问题,模型会利用它自己给出的正确解法 ()作为上下文,来生成一个新的、变分的问题 。
此时,模型扮演的是“出题老师”的角色。它的任务是,看着一个详细的解题步骤(),反向工程出一个新的问题描述()。这个新问题在措辞、结构、数值上可能与原问题 大相径庭,但其核心语义和最终答案必须与原问题保持一致。
例如,原问题可能是:
"求方程 的解。"
一个正确的解法 可能会写道:
"该方程是一个一元二次方程。根据求根公式... 我们得到两个根是 和 。所以解是 2 和 3。"
模型在看到这个解法后,可能会合成一个变分问题 :
"如果两个数的和是 5,积是 6,请问这两个数是多少?"
这个新问题显然与原问题形式不同,但它考察的是相同的数学关系,并且答案也是一样的。这个过程强迫模型去理解问题和解法之间更深层次的语义联系,而不仅仅是表面模式匹配。
2.4 步骤四:合成问题求解与学习(Synthetic Problem Solving & Learning)
生成了新的变分问题 后,模型再次切换回“学生”角色,去解决这些自己刚刚创造出来的问题。由于我们设计的目标是让 和 共享同一个答案 ,因此我们可以直接用原始的答案 来验证模型对 的解答是否正确,并计算奖励。
最后,在一个训练步中收集到的所有“经验”——包括求解原始问题的经验、合成变分问题的经验,以及求解合成问题的经验——都会被放入一个经验缓冲池中,用于共同更新策略模型的参数。
通过这个循环,模型不断地:
-
评估自己的能力边界。 -
在能力边界上创造新的挑战。 -
通过解决这些新挑战来扩展自己的能力边界。
这个过程是完全端到端和自包含的,不需要任何外部模型或额外的人工标注,真正实现了“自我进化”。
3. SvS的算法实现
为了更好地理解 SvS 的工作原理,我们需要深入其算法细节,特别是其底层的强化学习算法以及为问题合成任务量身定制的奖励机制。
3.1 基础:GRPO 算法
论文选择 Group Relative Policy Optimization (GRPO) 作为其底层的 RL 优化算法。GRPO 是为 LLM 设计的一种高效算法,其主要优点是不需要一个额外的“评论家”(Critic)模型来估计状态价值,而是通过比较在同一提示(prompt)下生成的一组(Group)解法的好坏来计算优势(Advantage)。
对于一个输入问题 ,模型生成 个解法 ,其对应的奖励为 。对于第 个解法中的第 个词元(token),其优势 被定义为该解法的总奖励相对于这组解法平均奖励的标准化值:
其中 是一个很小的常数以保证数值稳定性。这个公式的直观含义是:如果解法 的奖励高于平均水平,那么它内部所有词元的优势都是正的,模型会增加生成这些词元的概率;反之亦然。
GRPO 的最终优化目标 如下:
这个目标函数包含两部分:
-
策略梯度项:通过重要性采样比率 和优势 来更新策略。 函数用于限制单步更新的幅度,防止策略剧烈变化,这是 PPO(Proximal Policy Optimization)算法中的经典设计。 -
KL 散度正则化项: 用来惩罚当前策略 与某个参考策略 (通常是预训练模型)之间的偏差过大,有助于维持模型的语言能力和生成质量。
3.2 SvS 的核心创新:面向合成任务的奖励塑造(Reward Shaping)
现在我们来讨论 SvS 中最精妙的设计之一:如何为“问题合成”这个行为本身定义一个有效的奖励 。
一个最直接的想法是:如果模型为一个合成问题 找到了正确答案(即 ),那么就认为这次合成是成功的,给予正奖励。其奖励函数可以表示为:
其中 是指示函数。
然而,论文作者发现,这种简单的奖励机制很容易被模型“钻空子”(exploit)。模型会很快学会生成那些极其简单或者包含过多提示的“退化”问题,从而轻易地获得奖励。

例如,在论文的图 4 中,对于一个复杂的原始问题,模型可能会合成一个这样的问题 :
"......问题的答案是 2+22i,请用规范格式写出这个答案。"
模型解决这个问题易如反掌,但这个合成过程对提升其推理能力毫无帮助。这会导致整个自博弈流程陷入一种低水平的循环,无法收敛到有意义的能力提升上。
为了解决这个问题,作者设计了一种更复杂的奖励塑造策略。其核心思想是:一个好的合成问题,应该对当前的模型来说,具有适中的难度。 它不应该简单到模型可以 100% 解决,也不应该难到模型完全无法解决。
因此,他们将合成奖励 定义为:
这个公式意味着,只有当模型对合成问题 的求解正确率 落在一个预设的“中等难度”区间 (例如 )内时,这次问题合成才会被判定为成功,并获得正奖励。
这种奖励设计极大地提高了模型“钻空子”的难度。它激励模型去探索和创造那些真正位于其能力前沿、能够有效促进学习的新问题,确保了自博弈过程的可持续性和有效性。
3.3 完整的训练数据
总结一下,在每个训练步中,SvS 框架会向经验缓冲池 中添加三种类型的训练样本(prompt-response-reward 元组):
-
原始问题求解: -
Prompt 是原始问题 。 -
Response 是模型对 的解法 。 -
Reward 是基于标准答案 的正确性奖励 。
-
-
变分问题合成: -
Prompt 是模型对 的一个正确解法 。 -
Response 是模型合成的变分问题 。 -
Reward 是基于难度区间的塑造后奖励 。
-
-
合成问题求解: -
Prompt 是合成的变分问题 。 -
Response 是模型对 的解法 。 -
Reward 是基于原始标准答案 的正确性奖励 。
-
通过联合优化这三种任务,模型不仅学会了“如何解题”,还学会了“如何出题”以及“如何解自己出的题”,形成了一个强大而全面的自提升循环。
4. 实验分析
理论上的优雅设计最终需要通过严谨的实验来验证。论文在多个模型、多个数据集和多个评测基准上对 SvS 策略进行了全面的评估。
4.1 实验设置
-
模型:涵盖了从 3B 到 32B 参数量的多种模型,包括 LLaMA-3.1-8B,Qwen2.5-3B 和 Qwen2.5-32B。 -
训练数据:主要在两个数学推理数据集上进行训练:MATH-12k 和一个更具挑战性的竞赛级数据集 DAPO-17k。 -
评估基准:评估范围广泛,包括 GSM8K, MATH-500 等标准基准,以及 AIME, Beyond-AIME, OlymMATH 等一系列高难度竞赛级基准。 -
对比基线:主要的对比对象是使用相同 GRPO 算法的标准 RLVR 训练方法。
4.2 核心发现一:SvS 显著且持续地提升 和
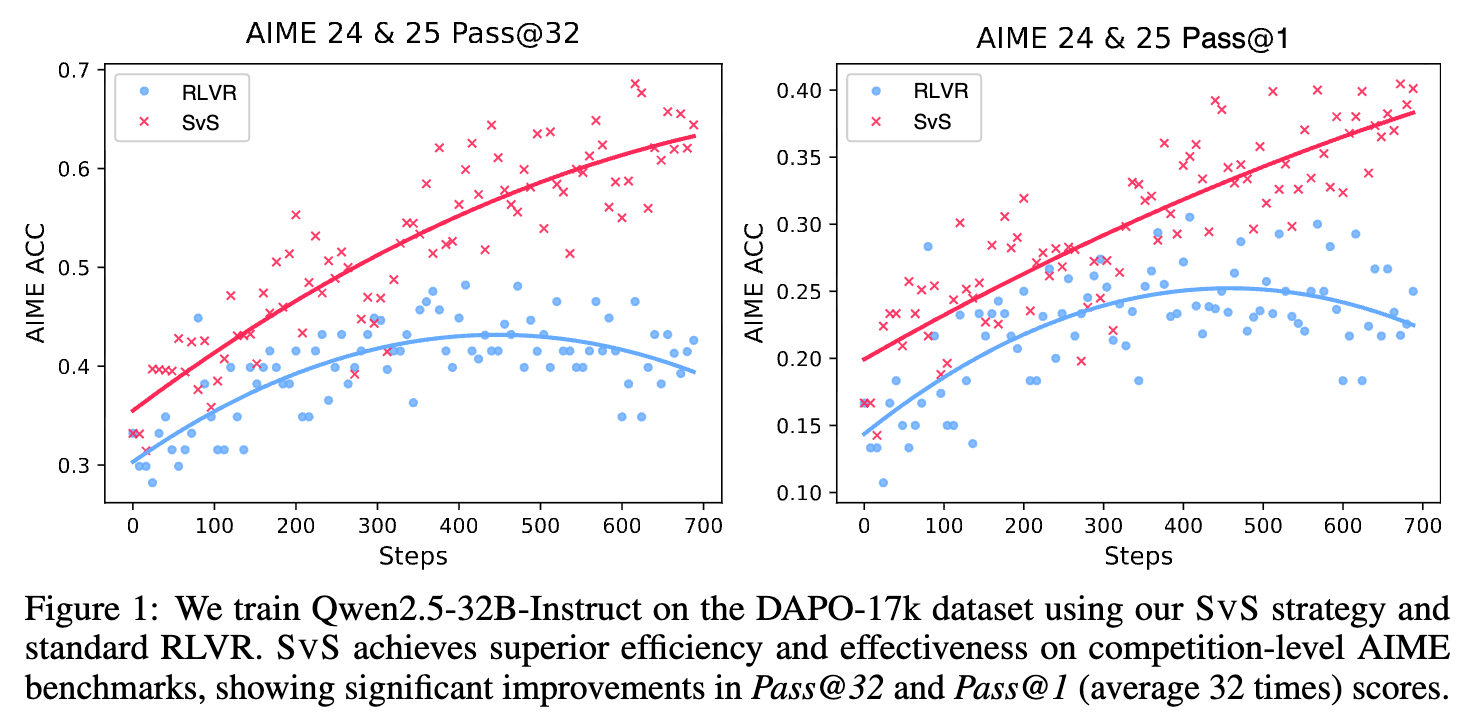
论文的图 1 直观地展示了 SvS 的核心优势。在极具挑战性的 AIME 竞赛基准上:
-
标准 RLVR(蓝色曲线)的性能在训练大约 450 步后就迅速进入平台期, 和 都不再有明显提升。 -
SvS(红色曲线)则展现了截然不同的行为。它的性能在整个训练过程中(700步)都保持着持续、稳定的增长,无论是 还是 。
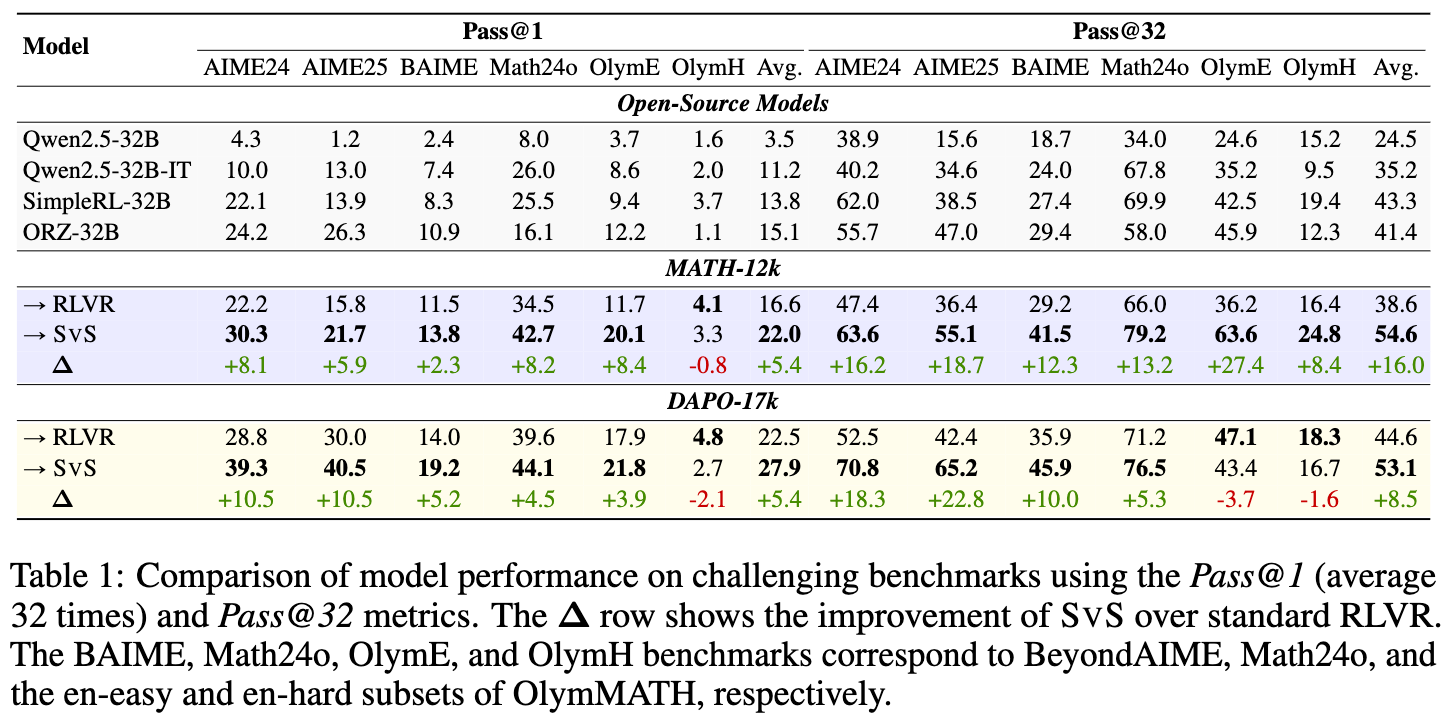
表1提供了更全面的数据。在 DAPO-17k 数据集上训练后,与标准 RLVR 基线相比,SvS 在 指标上取得了巨大的绝对提升:
-
在 AIME24 上,提升了 18.3% 。 -
在 AIME25 上,提升了 22.8% 。
这些结果有力地证明,SvS 成功地克服了标准 RLVR 的性能瓶颈问题,能够驱动模型实现更持久、更深入的学习。
4.3 核心发现二:SvS 有效地维持了策略熵
SvS 的性能优势从何而来?答案就在于它对策略熵的有效管理。
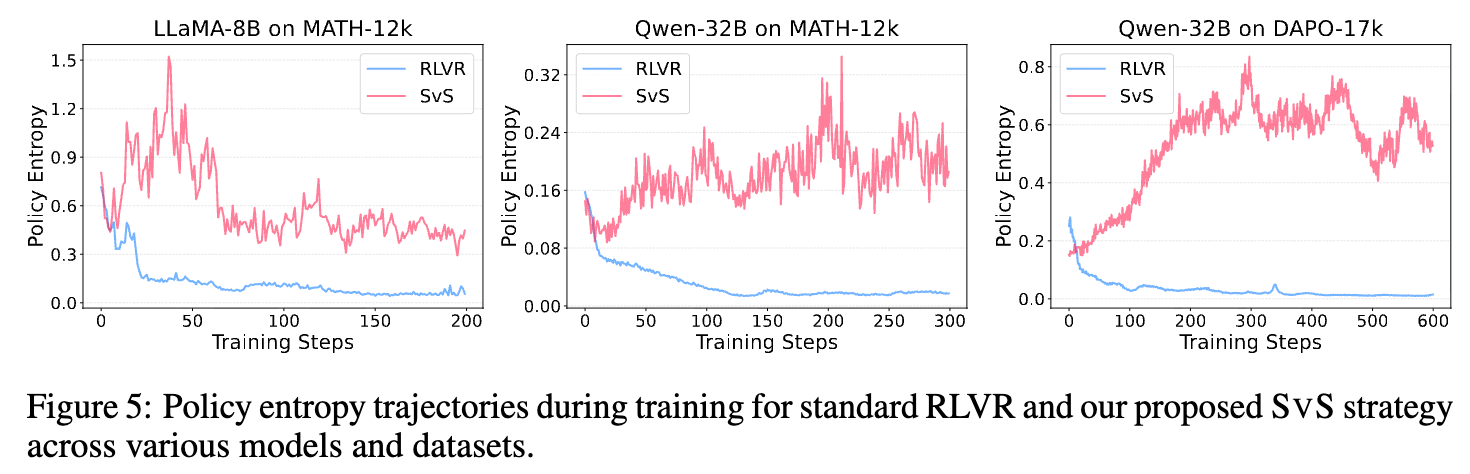
图 5 展示了训练过程中策略熵的变化轨迹。可以清晰地看到:
-
标准 RLVR 的策略熵(蓝色曲线)在所有实验设置下都呈现出单调下降的趋势,这正是熵坍塌的直接证据。 -
SvS 的策略熵(红色曲线)则在整个训练过程中都维持在一个相对稳定的范围内,没有出现明显的持续下降。
这种稳定的熵水平意味着模型始终保持着旺盛的探索能力。它不会过早地收敛到局部最优解,而是持续地在广阔的解题空间中进行探索和学习。这正是 SvS 能够实现持续性能提升的根本原因。
4.4 核心发现三:SvS 真正地拓展了模型的推理边界
随着 的增大而变化的情况,可以揭示一个训练方法是否真正增强了模型的内在能力。
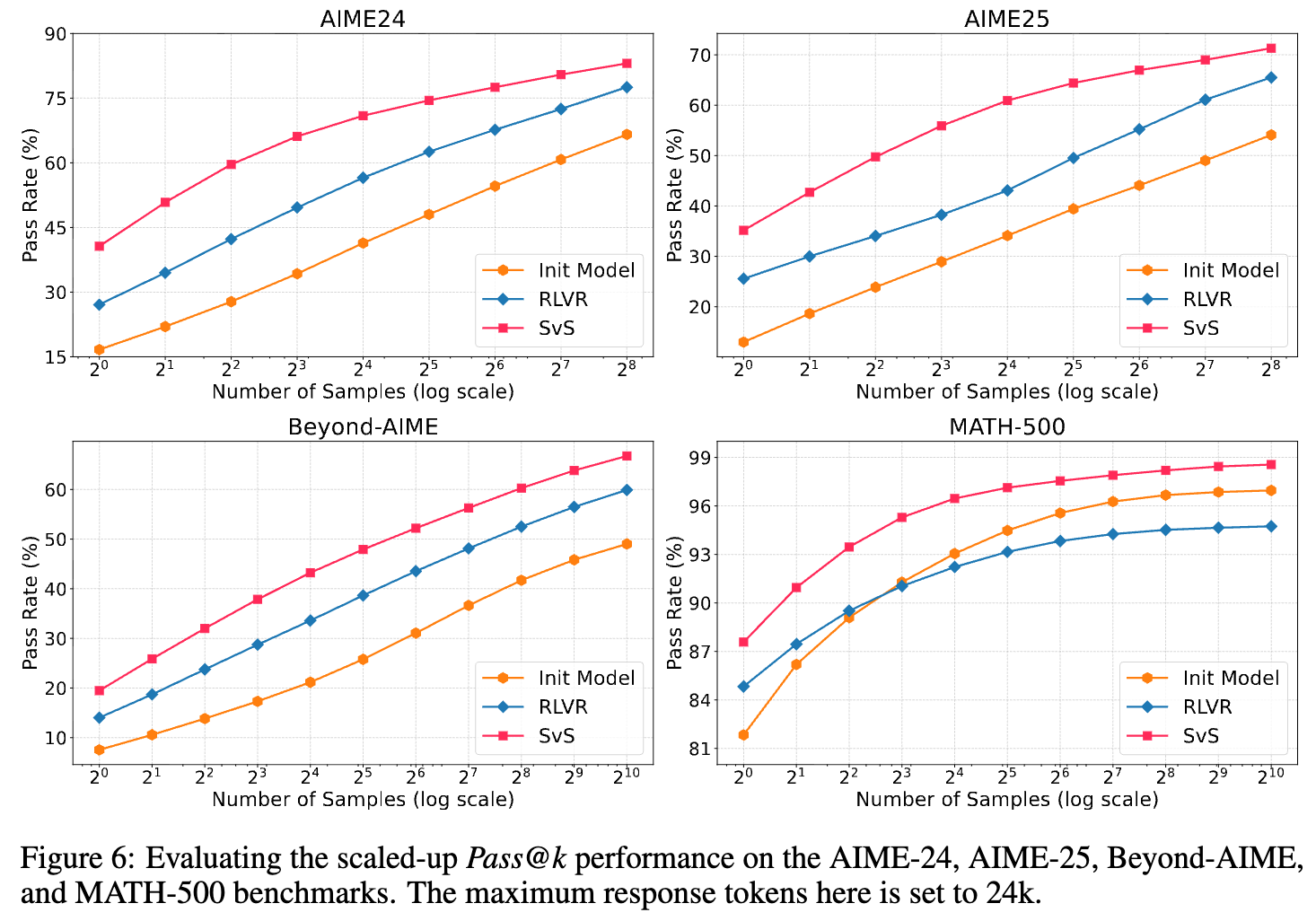
图 6 在 AIME、Beyond-AIME 和 MATH-500 等多个基准上,评估了 从 到 的变化情况。
-
在 MATH-500 基准上,标准 RLVR 在 较小时优于初始模型,但在 增大后,其性能甚至被初始模型反超。这说明标准 RLVR 只是让模型对已知的解法更加“自信”,而没有教给它新的解法。 -
相比之下,SvS 在所有的 值上都稳定地优于初始模型和标准 RLVR。这表明 SvS 不仅提升了模型对最优解的置信度,更重要的是,它扩展了模型能够触及的正确解法的集合,实实在在地推动了其推理能力的边界。
4.5 核心发现四:SvS 具备优秀的泛化能力,避免任务过拟合
一个潜在的担忧是,SvS 引入了问题合成任务,是否会导致模型在通用的问答和语言能力上出现性能下降(即所谓的“能力遗忘”)?
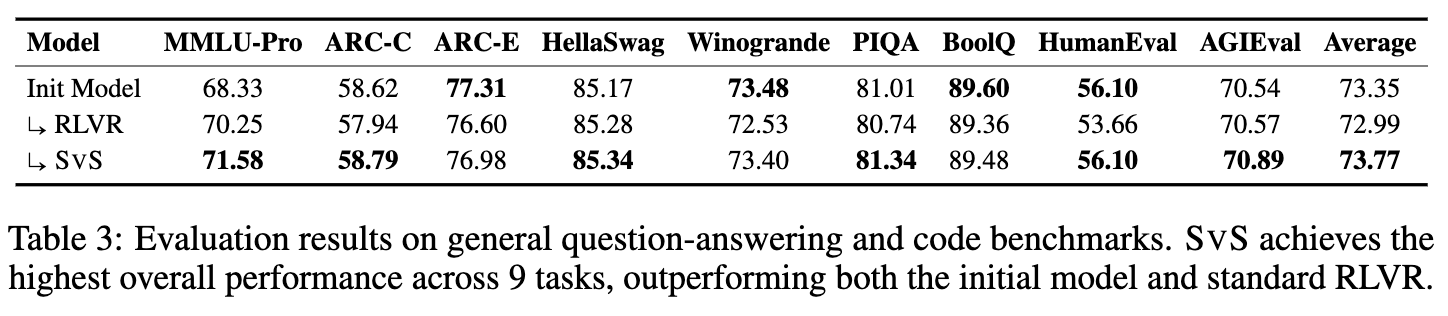
表3的结果打消了这一疑虑。实验评估了模型在 MMLU-Pro、ARC、HellaSwag 等 9 个通用 QA 和代码基准上的表现。
-
标准 RLVR 在这些通用任务上的平均分略低于初始模型,显示出了一定程度的过拟合,即模型过度专注于数学推理,牺牲了部分通用能力。 -
SvS 的平均分不仅没有下降,反而超越了初始模型和标准 RLVR,取得了三者中的最高分。
这个结果表明,问题合成任务本身是一种更通用的、需要深度语义理解的任务。训练模型进行问题合成,不仅没有损害其通用能力,反而通过防止其在单一问题求解任务上过拟合,增强了模型的通用指令遵循能力和泛化性。
点评
“熵坍塌”一直以来是RLVR中存在的问题,该论文从数据合成上下功夫可以说是一个新思路。论文对问题合成任务的奖励塑造 (Reward Shaping) 机制的设计是其技术上的一大亮点,引入了基于“中等难度”区间的奖励标准,避免模型学会生成过于简单或带提示的问题来“钻空子”。
SvS 在数学推理领域表现出色,因为数学问题通常是信息自洽的——一个完整的解题过程已经包含了重构一个等价问题所需的所有信息。然而,对于其它领域的数据,模型能否仅从一个“正确答案文本”中有效地合成出高质量、语义一致的新问题,是一个开放性问题。该方法的有效性可能存在一定的领域局限性。
最后,“吐槽”一下“变分问题”这个名字,它完美诠释了学术界的“黑话内卷”:
普通人会说:“我们让大模型自己出点题,答案得跟原来的一样。”
初级研究员会说:“我们提出一种基于约束的数据增强方法,叫‘同答案问题生成’。”
而这篇论文的作者则说:“我们引入了一个全新的范式,名为‘自博弈变分问题合成 (Self-play with Variational Problem Synthesis)’!”
往期文章:




