将 RL 应用于 LLM 的推理任务并非一帆风顺,一个普遍存在且棘手的问题是 “策略熵崩溃”(Collapse of Policy Entropy)。在 RL 训练的极早期阶段,模型的策略熵会急剧下降,导致模型对其决策变得“过度自信”。这种探索能力的减弱,往往伴随着模型性能的饱和,即无论再投入多少计算资源进行训练,模型表现也难以寸进。这构成了一个严峻的“熵瓶颈”,极大地限制了通过扩展计算来提升 LLM 推理能力的潜力。
面对这一挑战,来自上海人工智能实验室、清华大学等机构的研究者们发表了一篇题为《The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models》的论文。

-
论文标题:The Entropy Mechanism of Reinforcement Learning for Reasoning Language Models -
论文链接:https://arxiv.org/pdf/2505.22617 -
代码链接:https://github.com/volcengine/verl/tree/main/recipe/entropy
该研究深入剖析了 LLM 在 RL 训练中策略熵的动态机制,旨在回答以下几个核心问题:
-
策略熵与模型性能之间是否存在可预测的关系? -
策略熵为何会在训练中单调递减,其背后的数学原理是什么? -
我们能否设计出比传统方法更有效的熵控制策略,从而打破性能天花板?
我们将首先探讨作者发现的、可精确描述熵与性能关系的经验定律;接着,我们将深入其理论核心,揭示熵变背后的协方差驱动机制;最后,我们将介绍作者基于该机制提出的两种新颖且有效的熵控制技术——Clip-Cov 和 KL-Cov。希望通过本文的介绍,能帮助您对大模型强化学习中的熵管理问题有一个更全面、更深刻的理解。
第一部分:可预测的策略熵“崩溃”现象
在深入理论分析之前,我们首先需要直观地认识到问题的严重性和普遍性。研究者们通过大量的实验,观察到了一个在不同模型、不同任务上都高度一致的现象:策略熵的快速崩溃和随之而来的性能饱和。
1.1 问题的提出:熵崩溃与性能饱和
策略熵(Policy Entropy)是信息论中的一个概念,在强化学习中,它衡量了模型策略(即在给定状态下选择动作的概率分布)的不确定性。一个高熵的策略意味着模型在决策时更具探索性,愿意尝试多种不同的可能性;相反,一个低熵的策略则表示模型对其选择非常确定,倾向于反复执行少数几个它认为最优的动作。
研究者们发现,在没有进行任何熵干预的 RL 训练中,LLM 的策略熵会在训练开始后的极短时间内(例如,前几百个梯度步)急剧下降至接近于零的水平。与此同时,模型的性能(如下游任务的准确率)也呈现出类似的趋势:在早期快速提升,然后迅速进入一个几乎不再增长的“平台期”。
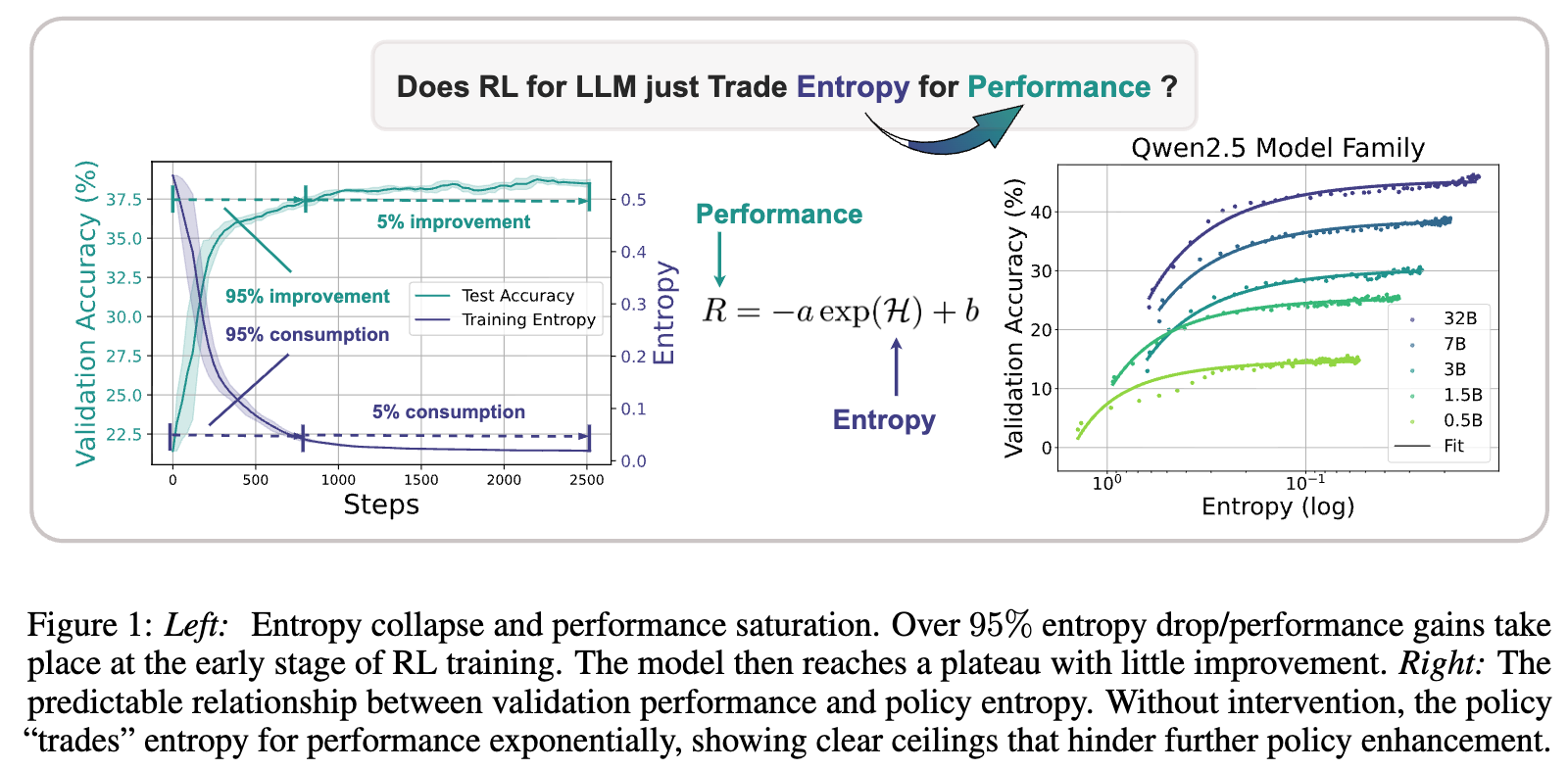
上图直观地展示了这一现象。蓝线代表训练过程中的策略熵,橙线代表验证集上的准确率。我们可以清晰地看到,超过95%的熵消耗和性能增益都发生在训练的极早期阶段。在此之后,漫长的训练过程只带来了微不足道的改进。
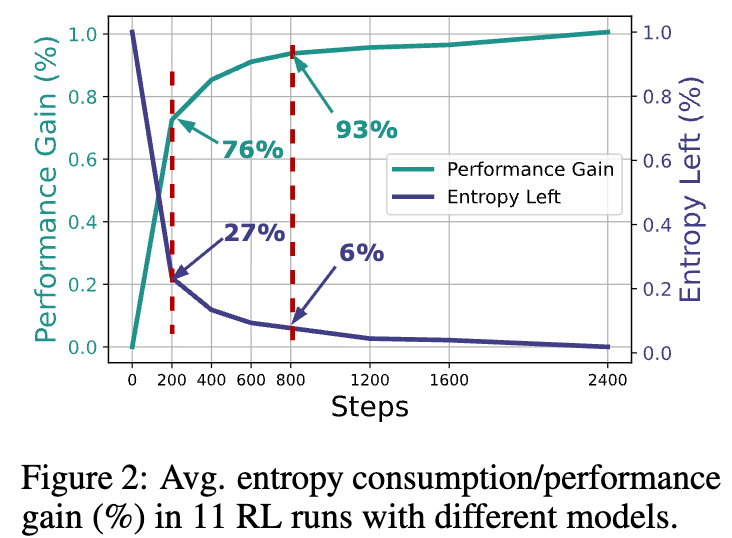
图 2 从另一个角度量化了这个问题。在对11个不同模型的 RL 运行进行平均后发现,大约76%的性能增益是在消耗了73%的策略熵后获得的,而这仅仅发生在训练前200步(占总训练步数的1/12)。整个训练过程超过三分之二的时间都处于一种低效的“边际收益递减”状态。
这种“交易”关系——即用熵(探索能力)来换取性能(奖励)——本身是 RL 的核心。但问题在于,这种交易似乎过早地、过快地耗尽了所有的熵,使得模型丧失了进一步探索和提升的可能性。这就引出了一个核心问题:这种熵与性能之间的“交易”是随机的、混乱的,还是遵循某种内在的、可预测的规律?
1.2 经验定律:熵与性能的指数关系
通过对跨越4个模型家族、11个开源基础模型(参数量从5亿到320亿)、多种数学和代码任务以及4种不同 RL 算法的广泛实验数据进行分析,研究者们发现了一个惊人的一致性规律。他们提出,下游任务的验证性能 和策略熵 之间的关系可以用一个简洁的指数函数来精确拟合:
其中, 和 是两个拟合系数。这个公式虽然形式简单,却深刻地揭示了 RL for LLM 中探索与利用的内在权衡。
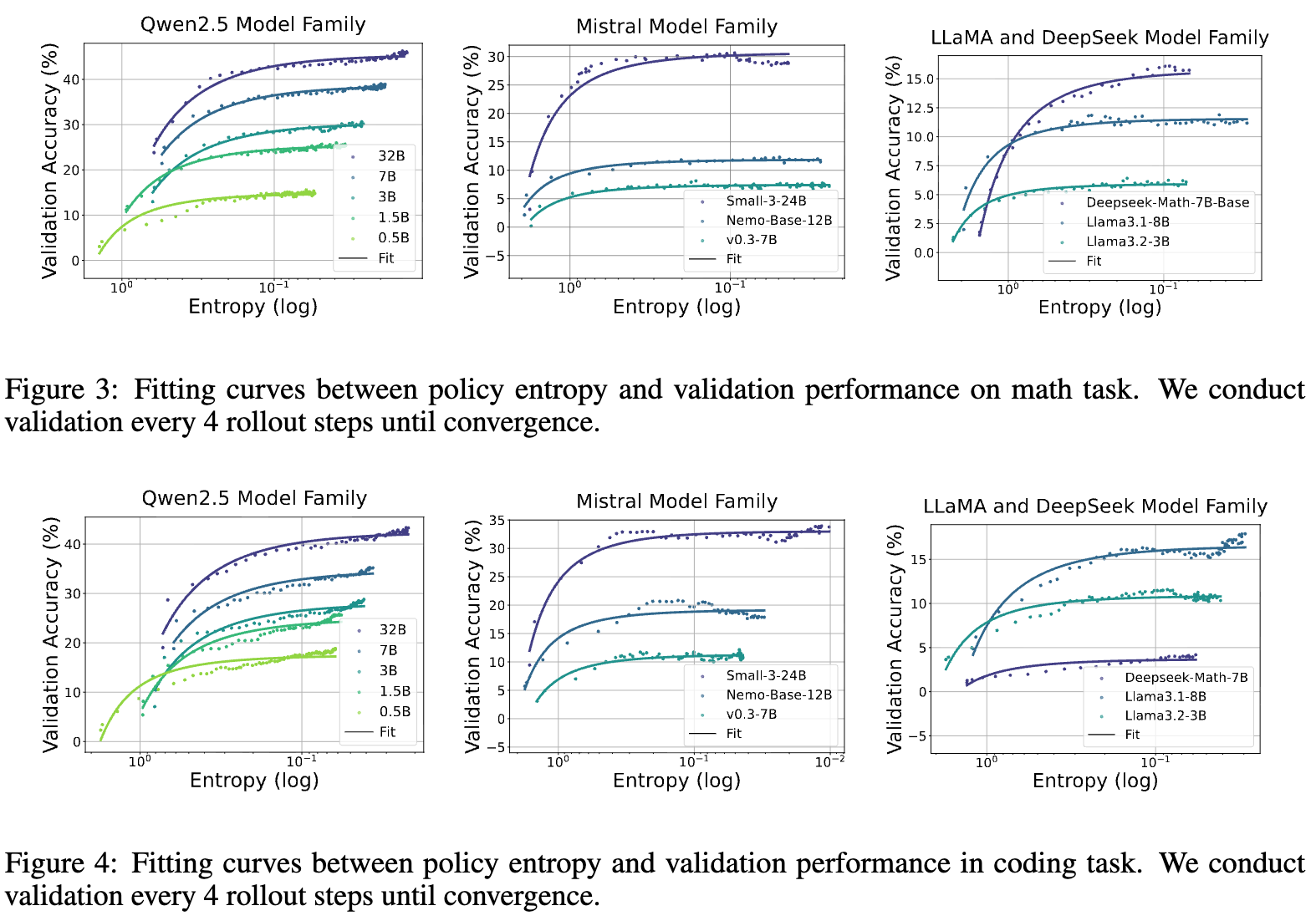
上面两张图展示了在数学和代码任务上,不同模型家族(Qwen2.5、Mistral、LLaMA & DeepSeek)的实验数据点(彩色散点)和使用上述指数函数拟合出的曲线(虚线)。我们可以看到,拟合曲线与实际数据点的吻合度非常高。这意味着,无论模型的具体架构或大小如何,其在 RL 训练中的性能轨迹似乎都受到这个统一规律的制约。仅仅用两个系数, 和 ,就能高度精确地描述包含超过200个数据点的整个训练动态,这本身就体现了其背后规律的强大。
1.3 定律的推论与启示
这个经验定律不仅是一个优美的数据拟合,更带来了两个关键的、具有实践意义的推论。
推论一:性能的可预测性
既然性能与熵的关系是确定的,那么我们就有可能在训练的早期阶段预测其最终性能。这与深度学习领域中著名的“缩放定律”(Scaling Laws)思想异曲同工。缩放定律告诉我们,模型的性能与其大小、数据量和计算量之间存在可预测的幂律关系。而这里的发现则揭示了 RL 过程中的一种“内在缩放定律”。
研究者们进行了验证实验。以 Qwen2.5 模型家族为例,他们仅使用前36个训练步(约占总训练量的15%)的数据来拟合系数 和 ,然后用得到的函数来预测后续200多个训练步的性能。
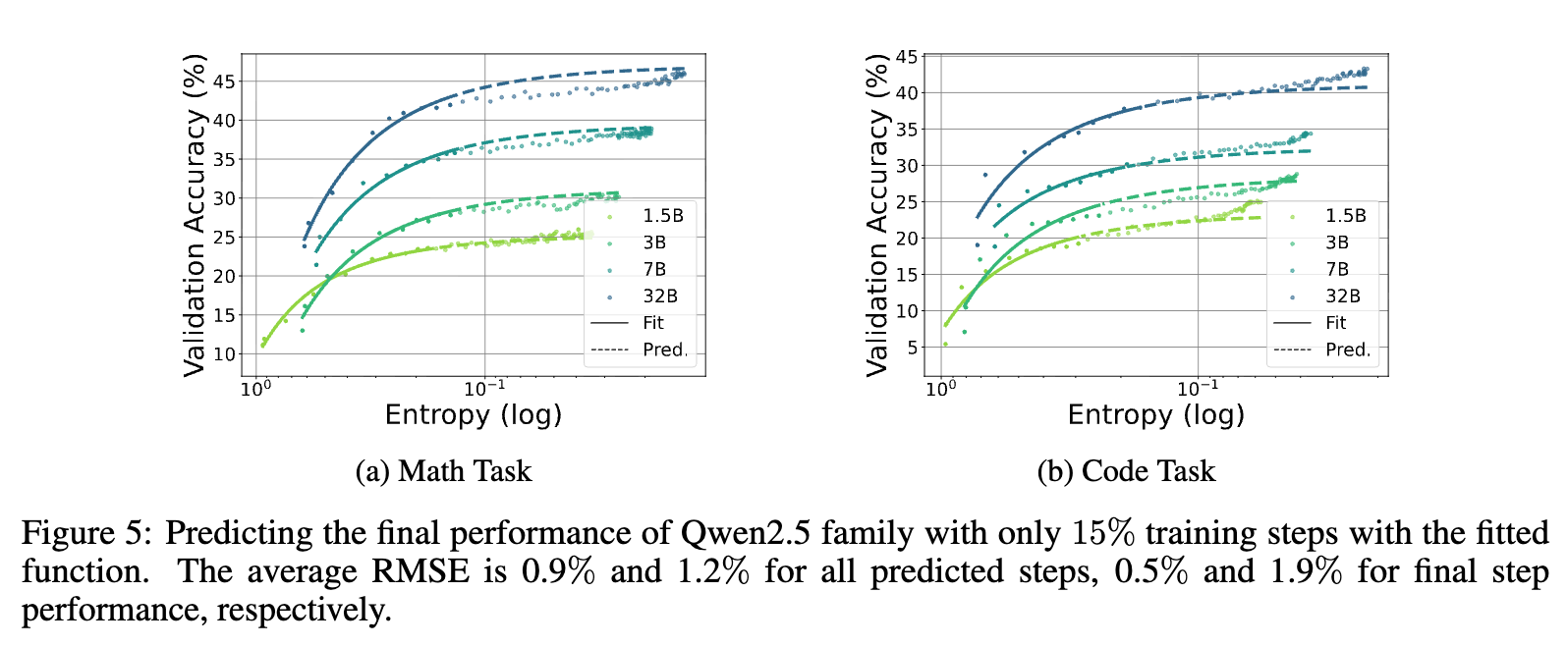
结果如上图所示,预测曲线(Pred.)与真实性能曲线(Fit)高度重合。对于数学和代码任务,所有预测步骤的平均均方根误差(RMSE)分别仅为0.9%和1.2%。这表明,我们不再需要完整地运行整个耗时耗力的 RL 训练过程,就可以提前预知模型的性能演进轨迹。
推论二:性能天花板的存在
这个定律更重要的一个启示,是它明确指出了模型性能的理论上限。当策略熵 被完全耗尽,即 时,。此时,模型的性能 将趋近于一个极限值:
这个 就是在当前模型和训练数据下,通过这种“熵换性能”模式所能达到的性能天花板。它意味着,一旦熵这个“燃料”耗尽,无论再增加多少训练步数,性能也无法突破这个由系数 和 内在决定的上限。这为我们开头观察到的性能饱和现象提供了数学解释,并深刻揭示了“熵瓶颈”的本质。
1.4 系数 和 的内在含义
那么,决定这个天花板的系数 和 究竟代表什么呢?
1. 算法无关性
研究者们首先验证了这些系数是否与具体的 RL 算法有关。他们使用 GRPO、RLOO、PRIME 和 REINFORCE++ 等具有不同优势函数估计方法的算法来训练同一个模型(Qwen2.5-7B)。
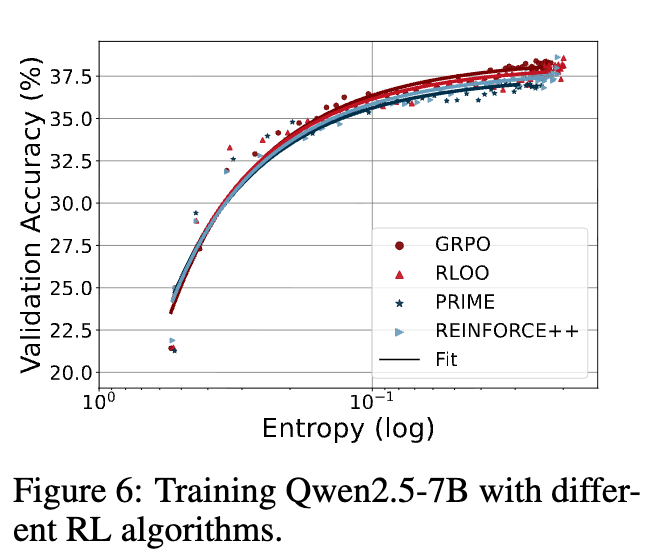
结果显示,尽管这些算法在实现细节上有所不同,但它们最终都收敛到了同一条熵-性能曲线上。这有力地证明了系数 和 并非由 RL 算法决定,而是反映了模型和训练数据本身更深层次的内在属性。
2. 对系数的理解
我们可以对这两个系数的含义做一个直观的解读。对经验定律公式求导,我们得到:
这个导数表示性能随熵变化的速率。系数 在其中扮演了关键角色,可以被理解为模型将“熵”转化为“性能”的效率。 越大,意味着熵的微小降低能带来更大的性能提升。而 则代表了模型在熵完全耗尽时的极限性能。
3. 与模型规模的缩放关系
研究者们进一步探究了这些系数是否像预训练中的缩放定律一样,与模型的大小存在可预测的关系。他们在 Qwen2.5 模型家族上(参数量从0.5B到32B)进行了实验,并绘制了系数 与模型参数量(不含嵌入层)的关系图。
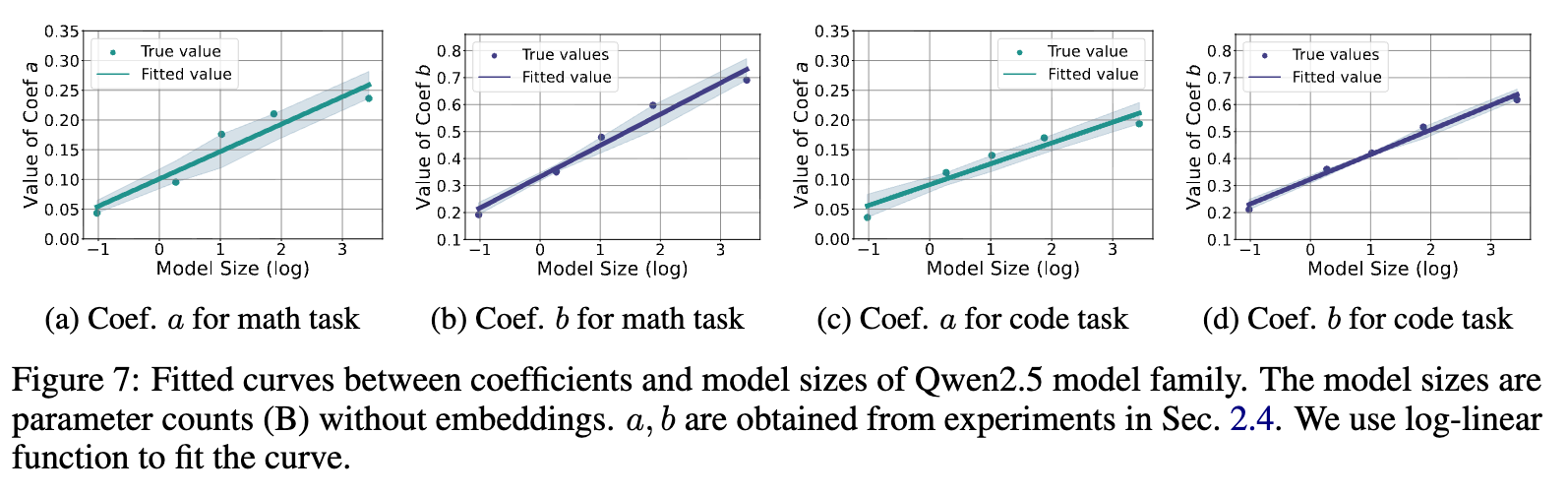
结果显示,在对数坐标系下,系数 和 都与模型大小呈现出近似线性的关系。这意味着,我们可以通过训练一系列小模型,拟合出系数与模型大小的缩放关系,然后外推出更大模型(甚至是尚未训练的更大模型)的系数 和 ,从而预测其在 RL 训练中的性能天花板。这为评估和选择大模型进行 RL 优化提供了极具价值的指导。
至此,我们已经系统地了解了论文的第一部分内容。它通过大量实验,建立了一个描述熵与性能关系的经验定律,并揭示了其在性能预测和天花板分析上的重要价值。然而,这只是“知其然”。为了真正解决问题,我们还必须“知其所以然”——策略熵为何会如此稳定且单调地下降?这便是我们下一部分将要探讨的核心问题。
第二部分:策略熵的动态学分析:为何熵会单调递减?
第一部分的经验定律为我们描绘了熵崩溃的宏观景象,但要从根本上解决问题,必须深入其微观机制。这一部分,我们将跟随论文的脚步,从理论层面推导策略熵在单步更新中的动态变化,从而揭示其单调递减的内在原因。
2.1 Softmax 策略的熵变
LLM 本质上是一个自回归的生成模型,其在每个时间步的输出都是一个基于 Softmax 函数的概率分布。因此,理解 Softmax 策略的熵变是分析问题的关键。
一个策略 在给定状态 下的熵定义为 。我们关心的是,在模型参数进行一次梯度更新后,这个熵值会如何变化。也就是研究 的值。
论文引用并改编了 Liu (2025) 的一个关键引理(Lemma 1),该引理指出,对于一个 Softmax 策略,在单步更新后,其熵的改变量可以近似表示为:
这里的 是模型对于状态-动作对 输出的 logit 值(即输入 Softmax 函数前的值)。 代表了一次更新中 logit 的变化量。Cov 表示协方差。
这个公式是理论分析的基石。它告诉我们,熵的变化由两个关键项的协方差决定:
-
动作的对数概率 :一个动作的概率越高,这个值就越大。 -
动作的 logit 变化量 :代表了模型在一次更新中对这个动作的“倾向”变化。
直观理解:
-
如果协方差为正:这意味着高概率的动作,其 logit 也倾向于增加();而低概率的动作,其 logit 倾向于减小。这会使得原先的概率分布变得更加“尖锐”(peaky),强的地方更强,弱的地方更弱。因此,策略的不确定性降低,熵减小(公式前的负号使得结果为负)。 -
如果协方差为负:这意味着高概率的动作,其 logit 反而减小了;而某些低概率的动作,其 logit 却增加了。这会使得概率分布变得更加“平坦”(flat),不确定性增加,熵增大。
所以,熵是增是减,关键取决于 logit 的变化方向与当前概率分布的关系。
2.2 策略梯度算法下的熵变
上一步分析了熵与 logit 变化量的关系。而 logit 具体如何变化,则是由我们所使用的 RL 算法决定的。论文接着分析了在经典的策略梯度(Policy Gradient, PG)类算法下 logit 的变化。
对于标准的 REINFORCE 算法(一种 vanilla PG 算法),其参数更新依赖于梯度 。论文推导(Proposition 1)得出,在单步更新中,一个动作的 logit 变化量满足:
其中 是学习率, 是该动作的优势函数(Advantage),它衡量了选择动作 相对于当前策略的平均表现有多好。
现在,我们将这个结果代入上一节的熵变公式。经过推导,可以得到在 vanilla PG 算法下,熵变的最终形式(Theorem 1):
论文还进一步指出,对于更先进的自然策略梯度(Natural Policy Gradient, NPG)算法,其 logit 变化更直接,为 。这使得熵变的形式也更简洁(Theorem 2):
尽管具体形式略有差异,但这两个结论共同指向了一个核心洞察:策略熵的变化,最终由动作的对数概率和其优势值之间的协方差决定。
核心洞察与直观解释:
让我们聚焦于 NPG 的简洁形式。熵减小的主要驱动力是 为正。这意味着:
-
高概率、高优势的动作:当模型认为一个动作很好()并且已经很倾向于选择它( 很高)时,PG 算法会进一步增强这个倾向。这种“强者愈强”的马太效应,正是导致策略分布变得更尖锐、熵减小的主要原因。 -
低概率、高优势的动作:如果一个动作优势很高(),但模型当前选择它的概率很低( 很低),那么 会是一个很大的负数。这种情况对协方差的贡献是负的,理论上可以增加熵,促进探索。 -
高概率、低优势的动作:如果一个常选的动作被发现效果不好(),这会产生一个负的协方差贡献,同样有助于增加熵。
那么,在 LLM 的 RL 训练中,实际情况是怎样的呢?在训练初期,LLM 作为一个强大的预训练模型,其本身已经具备了很强的先验知识。对于很多推理问题,它生成的高概率答案往往就是正确的,或者至少是部分正确的,因此能获得较高的优势值。这就造成了在训练数据上,高概率和高优势之间存在着强烈的正相关性。模型只是在“确认”并“强化”它已有的认知,而不是在探索全新的解法。
因此, 在训练初期乃至整个过程中,都持续保持为正值。这就从理论上完美解释了我们在第一部分观察到的宏观现象:策略熵为何会持续、单调地下降。
2.3 经验验证
为了验证上述理论推导的正确性,研究者们设计了实验。他们使用 GRPO 算法(一种 PG 类算法)在 Qwen2.5-7B 模型上进行训练,并在训练过程中实时记录了两个关键指标:
-
熵的实际变化率:,通过相邻步骤的熵差值来近似。 -
理论协方差项:,根据理论公式计算。
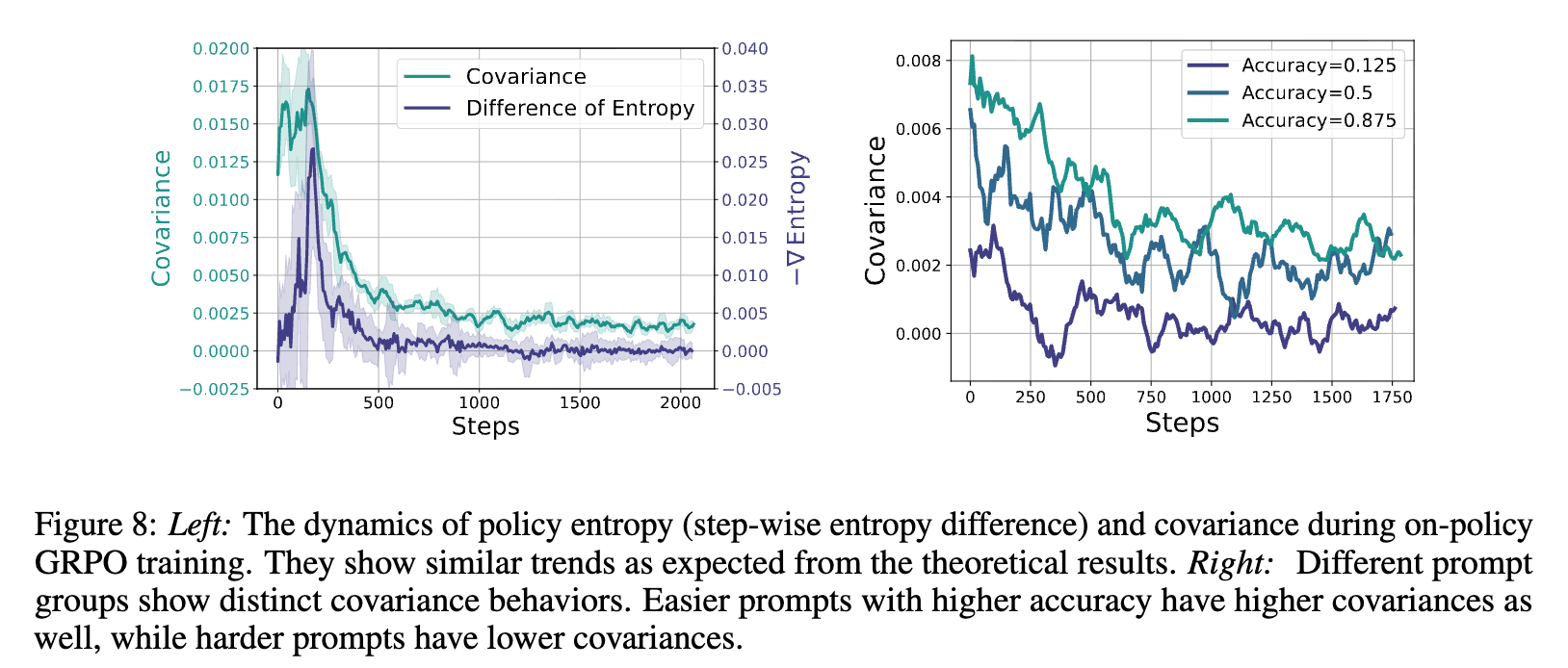
实验结果如上图左侧所示。蓝线代表协方差项,绿线代表熵的负变化率。可以看到,两条曲线的动态趋势高度相似,几乎重叠在一起,这为理论的正确性提供了强有力的经验支持。特别值得注意的是,协方差曲线在整个训练过程中始终保持在零以上,这正是熵持续减少的直接原因。
研究者们还利用其分组采样(group-wise sampling)的策略,进一步分析了不同难度样本的协方差动态。他们根据样本的平均回答正确率将样本分为“简单”(高正确率)、“中等”和“困难”(低正确率)三组。
上图右侧展示了三组样本的协方差曲线。结果非常符合直觉:
-
对于简单样本(绿色曲线,正确率0.875),模型更有信心,其高概率的回答也更容易获得高奖励,因此协方差值最高。 -
对于困难样本(蓝色曲线,正确率0.125),模型本身就很挣扎,其动作的概率和最终的优势之间没有稳定的正相关,因此协方差值最低。
这表明,熵的崩溃主要由模型在“能力圈内”的简单、中等难度样本上的利用(exploitation)行为所驱动。
总结第二部分,我们通过理论推导和实验验证,成功地揭示了策略熵单调递减的微观机制。其根源在于,在策略梯度类算法的驱动下,模型倾向于强化那些它已经认为不错(高概率、高优势)的动作,导致协方差项持续为正,从而不断消耗熵。理解了这一点,我们就为设计更具针对性的熵控制策略奠定了坚实的基础。
第三部分:基于协方差正则化的熵控制方法
在揭示了熵崩溃的根源——由高协方差驱动的过度利用——之后,一个自然的想法是:我们能否直接对这个协方差项进行干预,从而控制熵的下降速度?这就是本部分将要探讨的核心内容。
3.1 传统熵正则化方法的局限性
在提出新方法之前,研究者们首先考察了两种在传统 RL 中常用的熵控制技术在 LLM 任务上的表现。
1. 熵损失(Entropy Loss)
这是一种最直接的方法,即在原有的损失函数 中加入一个熵的正则项,鼓励模型保持高熵:
其中 是控制熵奖励权重的超参数。
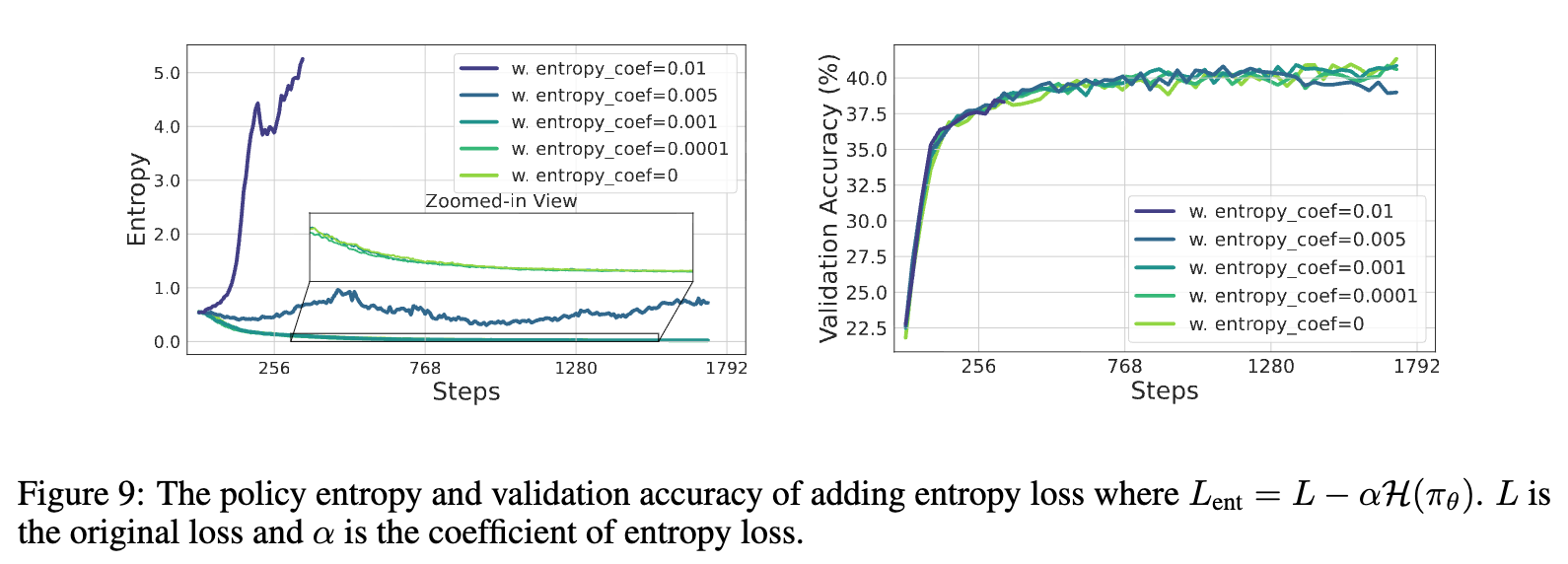
实验结果如上图所示。可以发现,这种方法对超参数 极其敏感。
-
当 很小(如 0.0001, 0.001)时,对熵的影响微乎其微,无法阻止熵崩溃。 -
当 很大(如 0.01)时,又会导致“熵爆炸”,策略变得过于随机,损害了性能。 -
即使选择了一个看似合适的中间值(如 0.005),虽然成功地稳定了熵,但其最终性能并没有超过不加熵损失的基线(baseline)。
2. KL 散度惩罚(KL Penalty)
另一种常见方法是使用 KL 散度来约束当前策略 不要偏离一个固定的参考模型 (通常是训练开始前的初始模型)太远。损失函数变为:
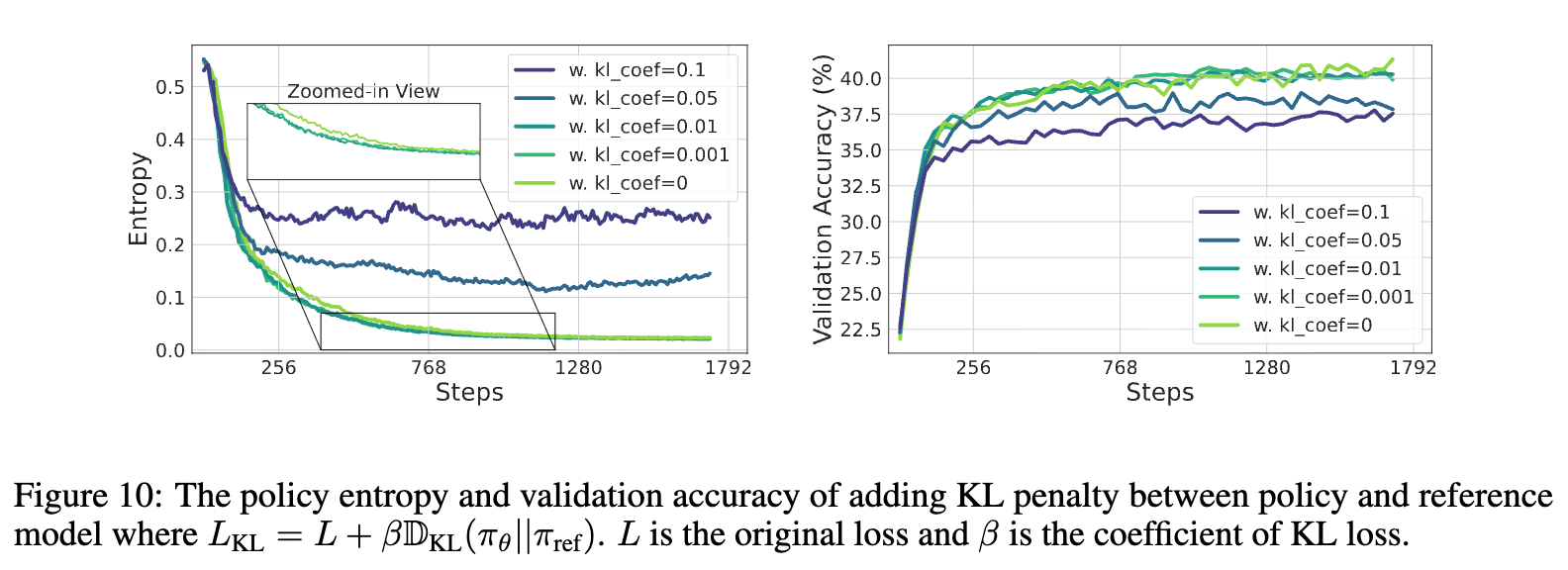
这种方法虽然能够有效地将策略熵维持在一个稳定的水平(因为策略无法偏离高熵的初始模型太远),但从上图右侧的性能曲线可以看出,它反而导致了性能的下降。这可能是因为它过度地限制了模型的学习,使其无法充分利用 RL 带来的信号。
综上所述,这些“全局性”的、简单粗暴的熵正则化方法,在 LLM 推理这个精细的任务上显得力不从心。它们要么难以调参,要么会损害性能,无法从根本上解决熵瓶颈问题。
3.2 新思路:抑制高协方差词元(Token)
既然全局正则化无效,那么就需要更“外科手术式”的精准干预。第二部分的分析告诉我们,熵的下降是由协方差驱动的。研究者们进一步分析了协方差在所有词元(token)中的分布情况。
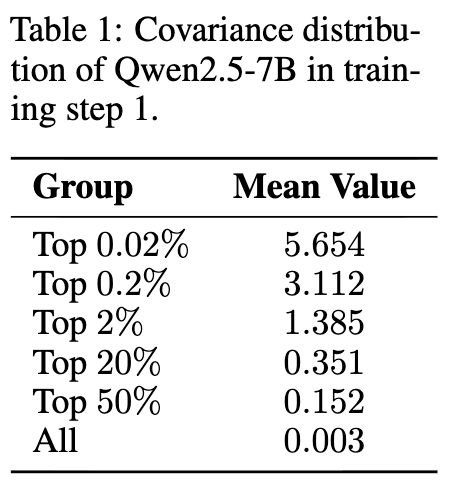
从上表可以看出,协方差的分布是极度不均衡的(呈现长尾分布)。仅仅 top 0.02% 的词元,其平均协方差值(5.654)就远超全体词元的平均值(0.003)。这意味着,熵的崩溃主要是由一小撮“害群之马”——那些具有极高协方差的“离群”词元——所主导的。
核心思想:我们不应该对所有词元都施加相同的正则化,而应该精准地识别出这些高协方差的词元,并专门限制它们对模型更新的贡献。
这个思想借鉴了 PPO 算法中通过裁剪(clipping)或 KL 惩罚来限制策略更新步长的思路,但将其应用得更加精细和有针对性——从全局限制,变成了“协方差感知的”局部限制。
3.3 两种具体技术:Clip-Cov 与 KL-Cov
基于上述思想,研究者们提出了两种简单而有效的技术。首先,他们定义了逐词元(token-wise)的协方差的近似计算方式。在一个包含 个词元的 rollout batch 中,对于第 个词元 ,其协方差可以计算为:
这个值衡量了单个词元的 和优势 相对于整个 batch 均值的偏离程度的乘积。
1. Clip-Cov (Clipping Covariance)
Clip-Cov 的做法是“忽略”掉这些高协方差的词元。
-
步骤1:计算 batch 中每个词元的 。 -
步骤2:随机从协方差值处于一个预设高位区间(例如,远大于平均值的区间)的词元中,选取一小部分(比例为 )出来。 -
步骤3:在进行策略梯度更新时,将这些被选中的词元的梯度直接“分离”(detach),即它们不参与损失计算和反向传播。
这种做法相当于直接裁剪掉了那些最可能导致熵下降的梯度信号,但又通过随机采样和小比例选择,避免了对整体学习过程的过度干扰。
2. KL-Cov (KL on Covariance)
KL-Cov 的做法则是对高协方差词元进行“惩罚”。
-
步骤1:计算 batch 中每个词元的 。 -
步骤2:对所有词元的协方差进行排序,选出协方差最高的 top-k 比例的词元。 -
步骤3:在计算损失时,只对这些被选中的词元额外施加一个 KL 散度惩罚项,迫使模型在更新这些词元的概率时保持谨慎,不要离 rollout 时的策略太远。

伪代码清晰地展示了这两种方法如何被整合进策略损失的计算中,实现起来非常简单,只需修改几行代码。
3.4 实验结果与分析
研究者们在 Qwen2.5-7B 和 Qwen2.5-32B 模型上,使用数学推理任务对所提出的方法进行了验证。他们将 Clip-Cov 和 KL-Cov 与基线方法 GRPO 以及一个改进的基线 Clip-higher(一种通过调整 PPO 裁剪上界来间接影响熵的方法)进行了比较。
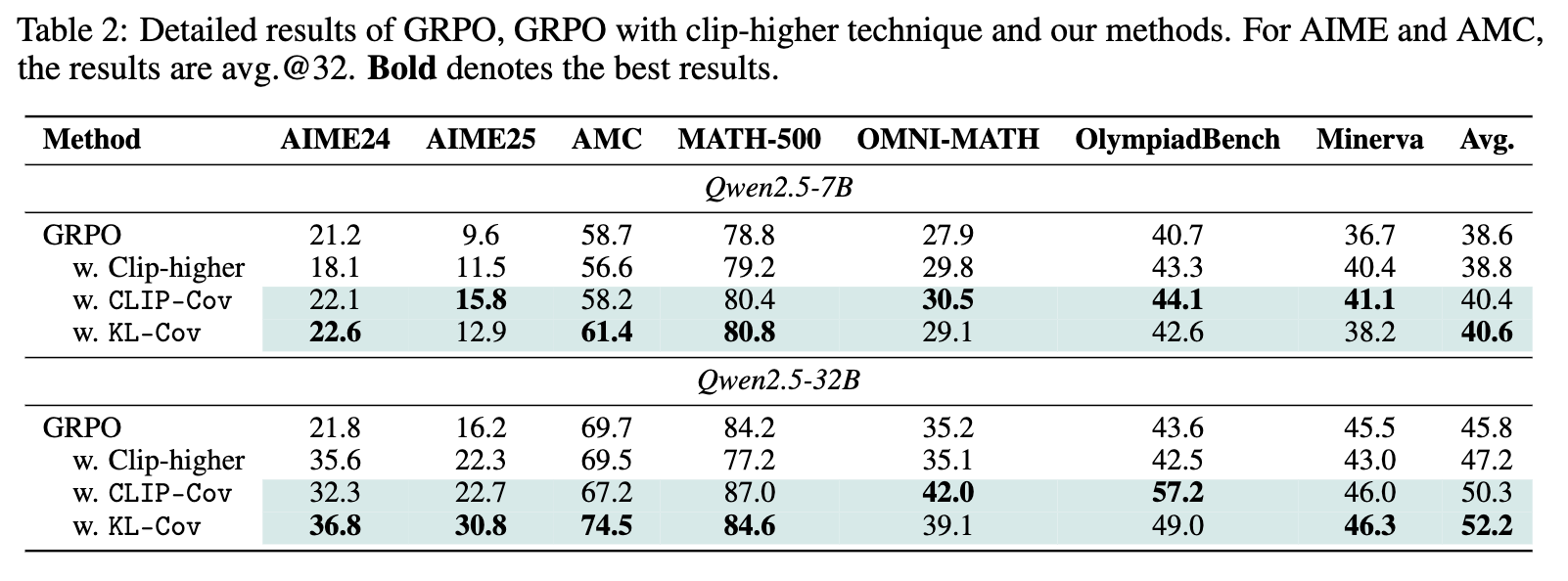
上表展示了在多个数学评测基准上的结果。可以看到:
-
无论是7B还是32B模型,Clip-Cov 和 KL-Cov 在几乎所有基准上都取得了超越基线 GRPO 和 Clip-higher 的性能。 -
这种提升在更大的 32B 模型上尤为显著。相比 GRPO,KL-Cov 在 AIME24 和 AIME25 这两个最具挑战性的基准上分别取得了 15.0% 和 14.6% 的巨幅性能提升。这说明,大模型本身蕴含着更大的潜力,一旦通过有效的熵管理解除了“探索诅咒”,它就能够学习到更多样、更高质量的策略。
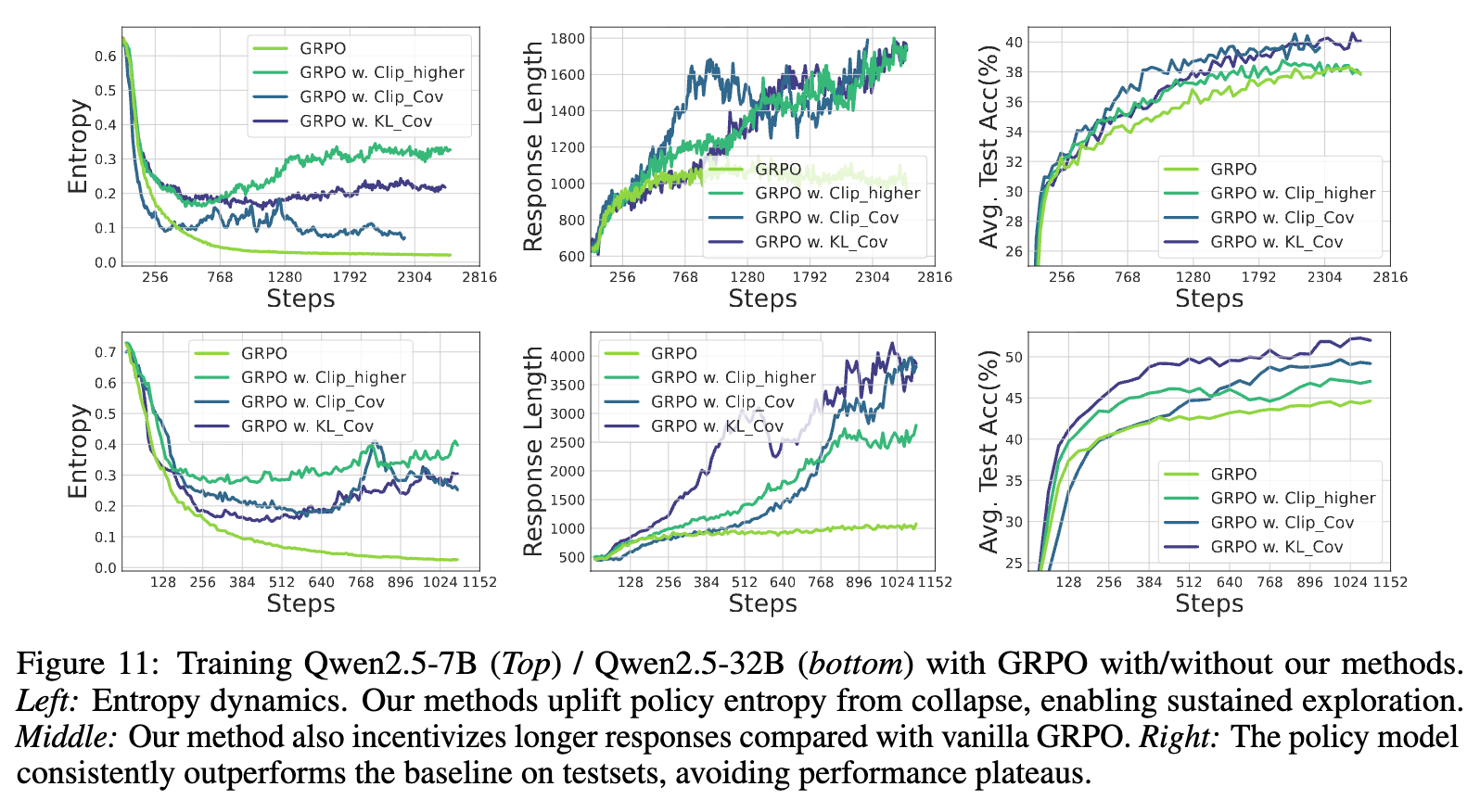
上图更直观地展示了训练过程中的动态差异。以 KL-Cov(绿色曲线)和基线 GRPO(蓝色曲线)为例:
-
左图(熵动态):GRPO 的熵迅速崩溃并维持在极低水平,而 KL-Cov 成功地将熵维持在了一个高出几个数量级的水平,实现了持续的探索。 -
中图(生成长度):KL-Cov 也激励模型生成更长的回答,这在复杂推理中通常意味着更详细的解题步骤和更高的成功率。 -
右图(测试准确率):GRPO 的性能很快饱和,而 KL-Cov 的性能则能持续、稳定地提升,最终达到了一个更高的平台。
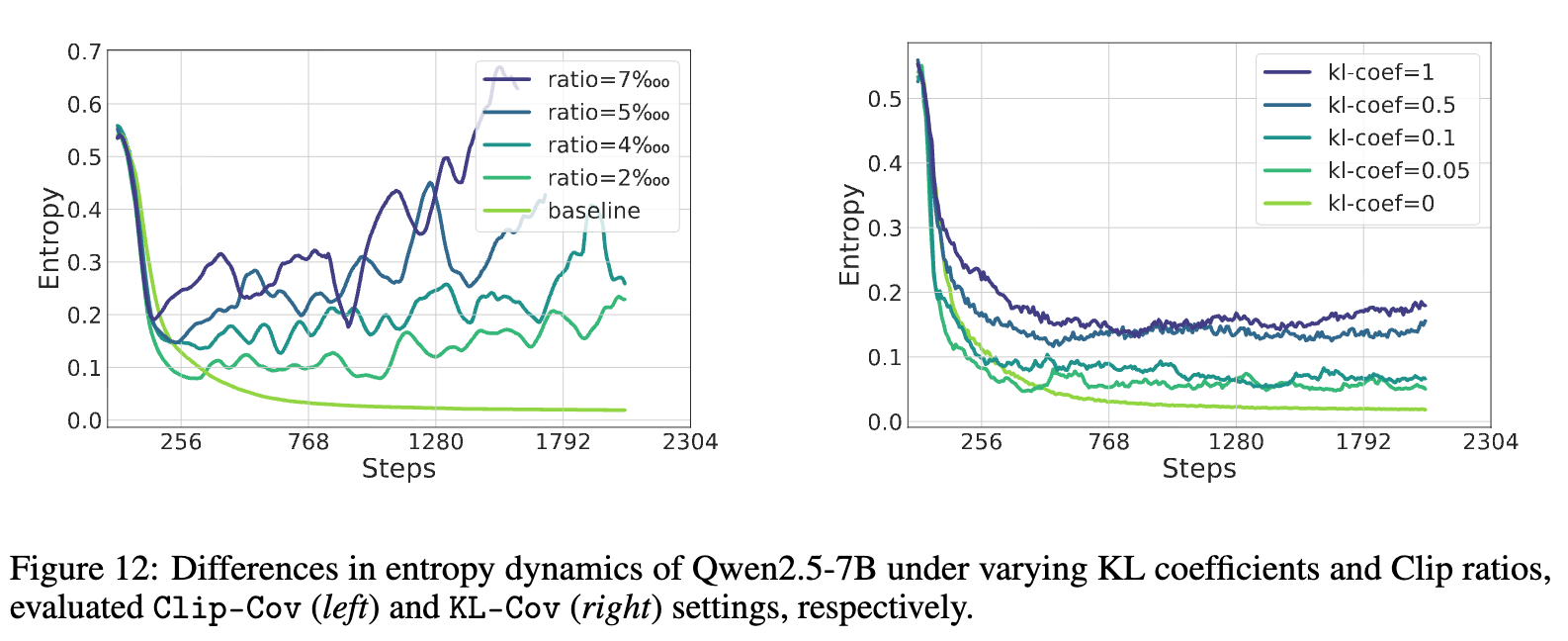
最后,研究者们还验证了他们的方法是否能方便地控制熵的水平。结果显示,对于 Clip-Cov,可以通过调整裁剪比例 来控制熵;对于 KL-Cov,则可以通过调整 KL 惩罚的系数 来控制。熵的水平随着超参数的增大而系统性地升高。这表明,研究者们不仅提供了一个能提升性能的方法,更提供了一个可控的“旋钮”,让使用者可以根据任务需求来精细地调节模型的探索程度。
第三部分的分析表明,通过精准识别并抑制高协方差词元的更新,Clip-Cov 和 KL-Cov 能够有效克服传统熵正则化方法的弊端,成功打破熵瓶颈,实现持续探索和性能的显著提升。
点评
这篇论文是一项非常扎实且具有影响力的研究工作,提出了“熵-性能”指数定律。在理解了熵崩溃的根源是“高协方差词元”后,论文提出的 Clip-Cov 和 KL-Cov 方法就显得水到渠成。
论文批评传统熵正则化方法对超参数敏感,但新提出的 Clip-Cov 和 KL-Cov 也引入了新的超参数(如裁剪比例 r,top-k 比例 k,KL系数 β等)。虽然论文展示了通过调节这些参数可以控制熵,但对于“如何选择最优参数”以及“性能对这些参数的敏感度如何”的讨论还不够深入。在实际应用中,如何高效地设定这些参数可能依然是一个挑战。
往期文章: