目前主流的 RLVR 方法普遍采用一种被称为 Pass@1 的目标进行优化。简单来说,只要模型生成的众多答案中有一个是正确的,就认为这次尝试是“成功”的,并给予正向奖励。这种机制虽然直观,却带来了一个深刻的难题——探索(Exploration)与利用(Exploitation)之间的失衡。
在 Pass@1 训练的驱动下,模型会倾向于变得“保守”。它会不断强化那些曾经带来过奖励的、最“自信”的推理路径,而不敢去尝试那些新颖但充满不确定性的路径。这导致模型极易陷入局部最优的困境:一旦它找到一个“还算不错”的解法,就很难再发现全局范围内可能存在的更优解,其性能提升很快就会停滞。
那么,我们能否找到一种更好的奖励机制,来鼓励模型进行更广泛的探索,从而跳出局部最优的陷阱呢?
本文介绍的这篇文章《Pass@k Training for Adaptively Balancing Exploration and Exploitation of Large Reasoning Models》,由来自中国人民大学和字节跳动 Seed 团队的研究者们共同完成,为我们提供了一个优雅且有效的解决方案。他们将目光投向了在代码生成等领域广泛使用的评估指标——Pass@k。Pass@k 评估的是模型在 k 次尝试内能否成功解决问题,这天然就蕴含了对多样性的鼓励。论文作者们创造性地提出,为何不直接将 Pass@k 用作 RLVR 训练过程中的奖励信号呢?

-
论文标题:Pass@k Training for Adaptively Balancing Exploration and Exploitation of Large Reasoning Models -
论文链接:https://arxiv.org/pdf/2508.10751
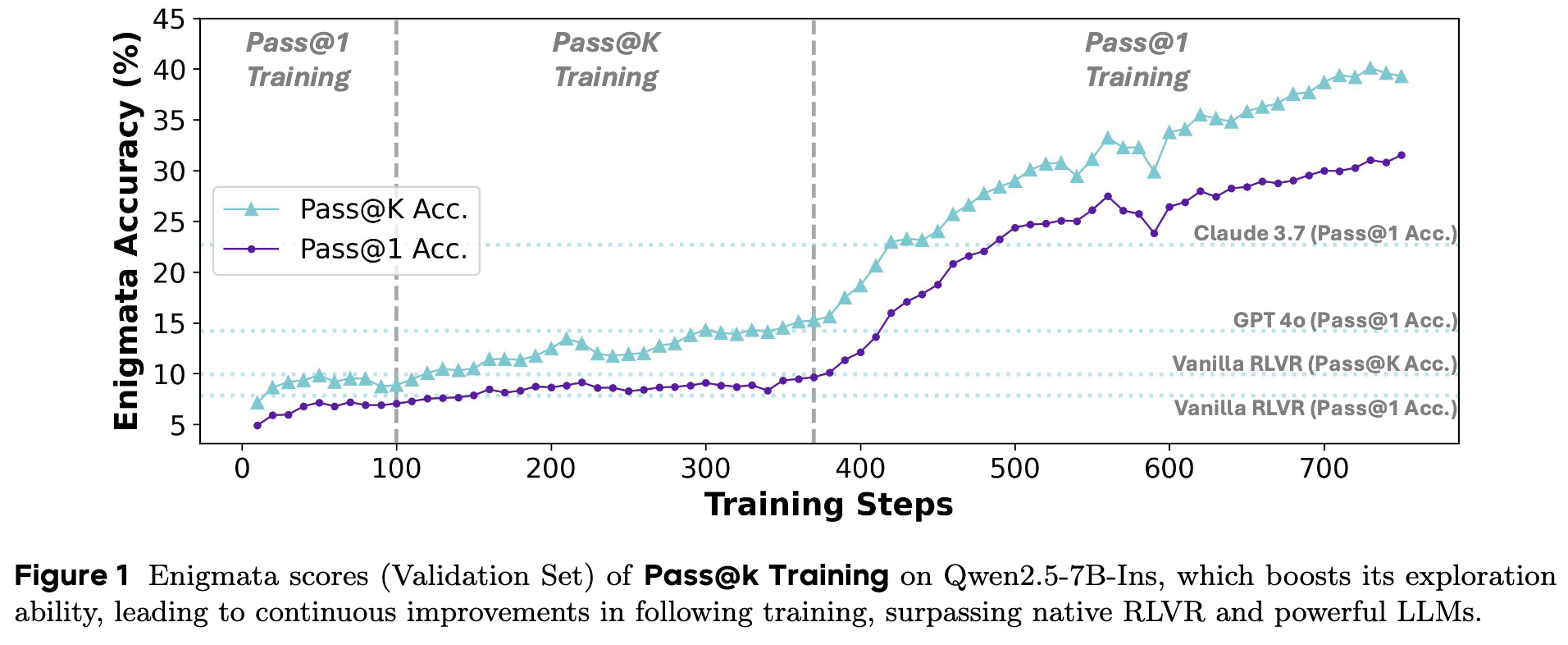
上图直观展示了该方法的核心成果。传统的 RLVR 训练(紫色虚线,Pass@1 Acc.)在训练初期有所提升后便迅速停滞,而 Pass@k 训练(紫色实线,Pass@K Acc.)则展现出持续、稳定的性能增长,并最终带动了 Pass@1 性能的显著超越,甚至超过了 Claude 3.7 和 GPT-4o 等强大的大模型。
本文将深入解读这篇论文,详细介绍:
-
Pass@k 训练 的核心思想及其从朴素实现到高效解析解的演进过程。 -
通过一系列精心设计的实验,剖析 Pass@k 训练为何能够有效平衡探索与利用。 -
揭示其成功的深层原因:独特的优势函数形态,并引出一种更广义的训练范式——隐式奖励设计。
RLVR 与 Pass@1 训练的内在局限
在深入了解 Pass@k 训练之前,我们有必要先回顾一下标准的 RLVR 流程以及 Pass@1 目标的具体工作方式。
RLVR 工作流程
一个典型的 RLVR 训练流程如下:
-
采样(Rollout): 给定一个问题(prompt),使用当前的模型策略 生成 个独立的候选答案 。 -
验证(Verification): 使用一个外部的、确定性的验证器 对每个答案 进行评估,并返回一个奖励信号 。通常,答对为正奖励(如 ),答错为负奖励(如 )。 -
优势估计(Advantage Estimation): 根据所有 个答案的奖励 ,计算每个答案的优势(Advantage) 。优势值衡量了某个具体答案比当前策略的“平均表现”好多少。正优势意味着这个答案值得鼓励,负优势则意味着需要抑制。 -
参数更新(Policy Update): 使用策略梯度算法(如 PPO)根据优势值 来更新模型参数 。具体来说,对优势值为正的答案 中的 token,增加其生成概率;对优势值为负的,则降低其生成概率。
Pass@1 训练的困境
当前最主流的 RLVR 设置,如 DeepSeek-R1,其优化目标是最大化 Pass@1。在训练中,这通常表现为:只要 个答案中至少有一个是正确的(即 ),就认为这是一次成功的 rollout,并以此为基础进行学习。
这种设置存在以下几个关键问题:
-
趋于保守,抑制探索:模型为了最大化获得正奖励的概率,会倾向于生成它最有把握的那个答案的变体。假设模型已经找到一个有 80% 把握的解法 A,同时它也知道一个可能通往更优解、但目前只有 30% 把握的解法 B。在 Pass@1 的驱动下,模型会不断地微调和重复解法 A,因为它能稳定地带来奖励。而尝试解法 B 风险太高,一旦失败,就会得到负奖励,从而抑制了这条探索路径。 -
陷入局部最优:上述的保守策略直接导致模型陷入局部最优。整个训练过程变成了对已知“最优解”的不断“利用”,而通往全局最优解的桥梁——“探索”——却被斩断了。从图 1 中可以看到,Vanilla RLVR 的 Pass@1 准确率在几百步训练后就进入了平台期,正是这一现象的体现。 -
对“有价值的失败”惩罚过重:在复杂的推理任务中,很多时候一个错误的答案可能包含了大量正确的推理步骤,只是在最后一步出错。例如,一道复杂的数学题,可能公式都列对了,只是最后计算错误。在 Pass@g1 训练中,这个答案和另一个完全胡乱猜测的答案一样,都会被赋予负奖励。这使得模型无法从这些“差一点就成功”的宝贵经验中学习,阻碍了其能力的提升。
正是意识到了 Pass@1 训练的这些内在局限,论文作者们开始思考,能否有一种奖励机制,能够从根本上鼓励模型生成更多样化、更具探索性的答案?答案就是 Pass@k。
Pass@k 训练
Pass@k 的核心理念是:在 次尝试内,只要有一次成功,就算成功。将这个理念转化为 RLVR 的奖励函数,就意味着我们不再评估单个答案,而是评估一组答案。
核心思想
与 Pass@1 训练不同,Pass@k 训练的奖励对象是一个包含 个答案的组(group)。
对于一个组 ,其奖励被定义为:
也就是说,只要这个组里至少有一个答案是正确的,整个组就会被赋予正奖励 。然后,这个组的奖励(或更准确地说,是优势值)会平等地分配给组内的所有 个成员。
这种机制带来了深刻的改变:
-
容忍错误:即使一个答案本身是错误的,但只要它和一个正确的答案被分在同一组,它也能分享到正向的激励。这极大地降低了模型进行探索的“试错成本”。 -
鼓励多样性:为了最大化组奖励,一个“聪明”的模型会意识到,生成 个高度相似的答案是不划算的。更好的策略是生成 个覆盖不同解题思路的、多样化的答案,这样“瞎猫碰上死耗子”的概率才会最大。这就从机制上激励了模型的探索行为。
接下来,我们来看看作者是如何将这个简单的思想,一步步优化成一个高效、稳定的训练算法的。
朴素实现 - 完全采样(Full Sampling)
最直接的实现方式被称为完全采样。
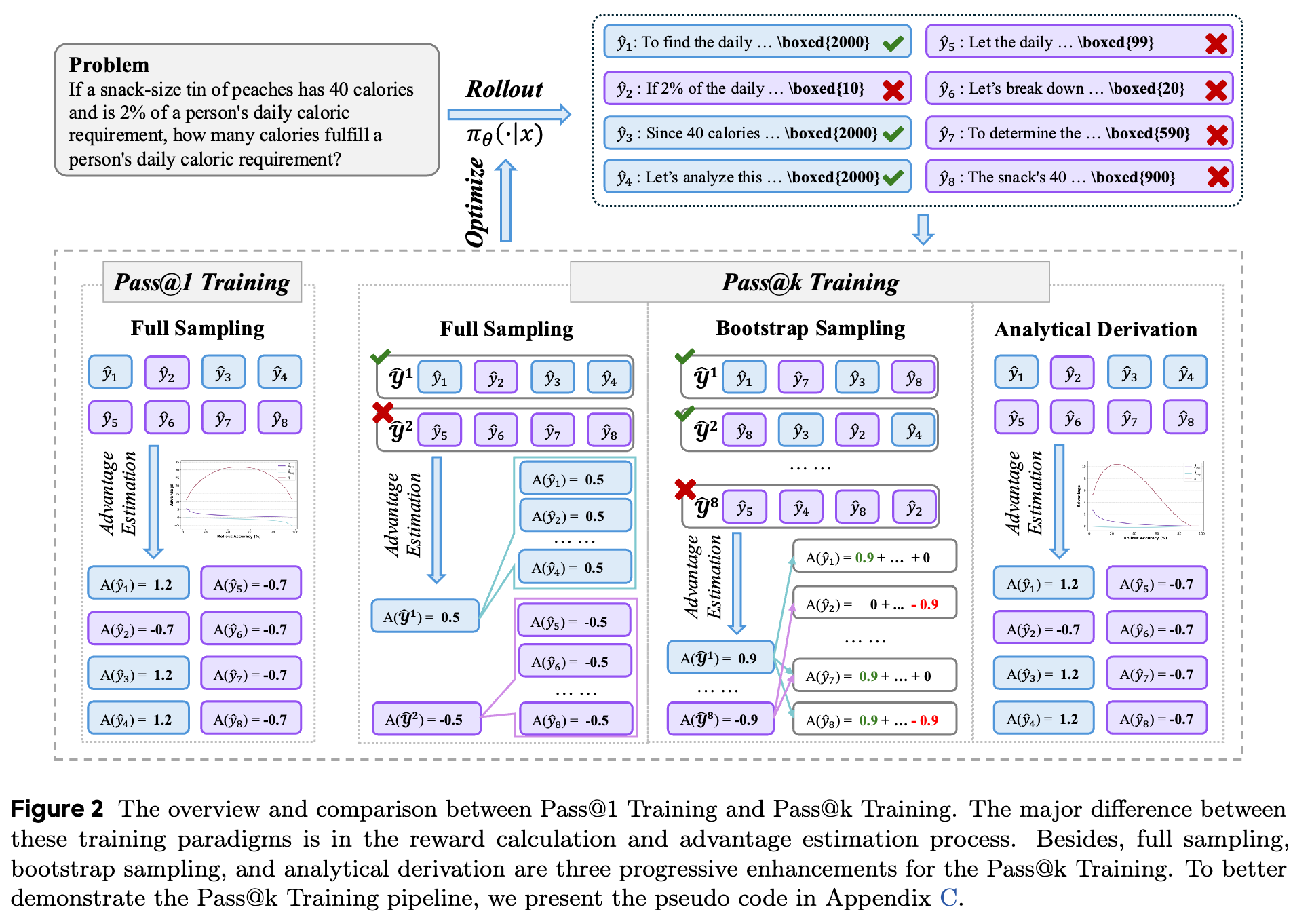
如上图所示,假设我们总共 rollout 了 个答案。
-
我们将这 个答案不重叠地分成 个组。 -
对每个组,我们计算其 Pass@k 奖励 。 -
然后,我们基于所有组的奖励,计算出每个组的组优势 。 -
最后,将每个组的优势 直接赋给其组内的所有 个成员。
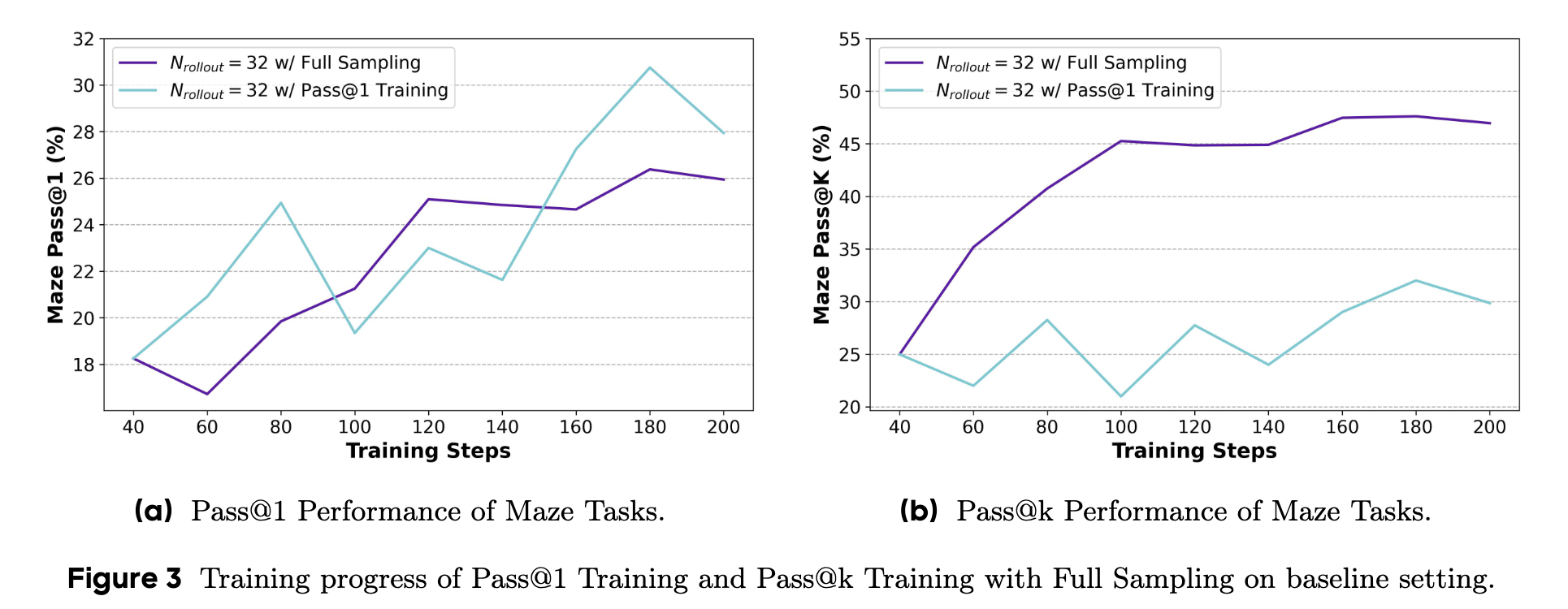
实验结果(图 3)初步验证了这一想法的有效性。与 Pass@1 训练相比,采用完全采样的 Pass@k 训练在 Pass@k 性能上取得了持续的进步,并且没有损害模型的 Pass@1 性能。这表明,Pass@k 训练确实能提升模型的探索能力,并且这种探索能力可以和“利用”能力协同发展。
然而,完全采样存在一个明显的问题:为了获得足够数量的组来进行稳定的优势估计,需要非常大的 ,这带来了巨大的计算开销。
效率优化 - 自助采样(Bootstrap Sampling)
为了解决完全采样的效率问题,作者们引入了统计学中经典的自助采样(Bootstrap Sampling)方法。
其核心思想是,我们不需要生成海量的答案,而是可以通过对少量答案进行重复采样来构造出大量的组。
具体流程如下:
-
我们只 rollout 一个相对较小的 (例如 32)。 -
为了构造一个组,我们从这 个答案中,有放回地随机采样 个。 -
我们重复这个过程 次(通常可以设置 ),从而得到 个组。 -
由于是带放回的采样,同一个答案可能会出现在多个不同的组中。因此,一个答案的最终优势,是它所在的所有组的优势的总和。
其中 是指示函数。
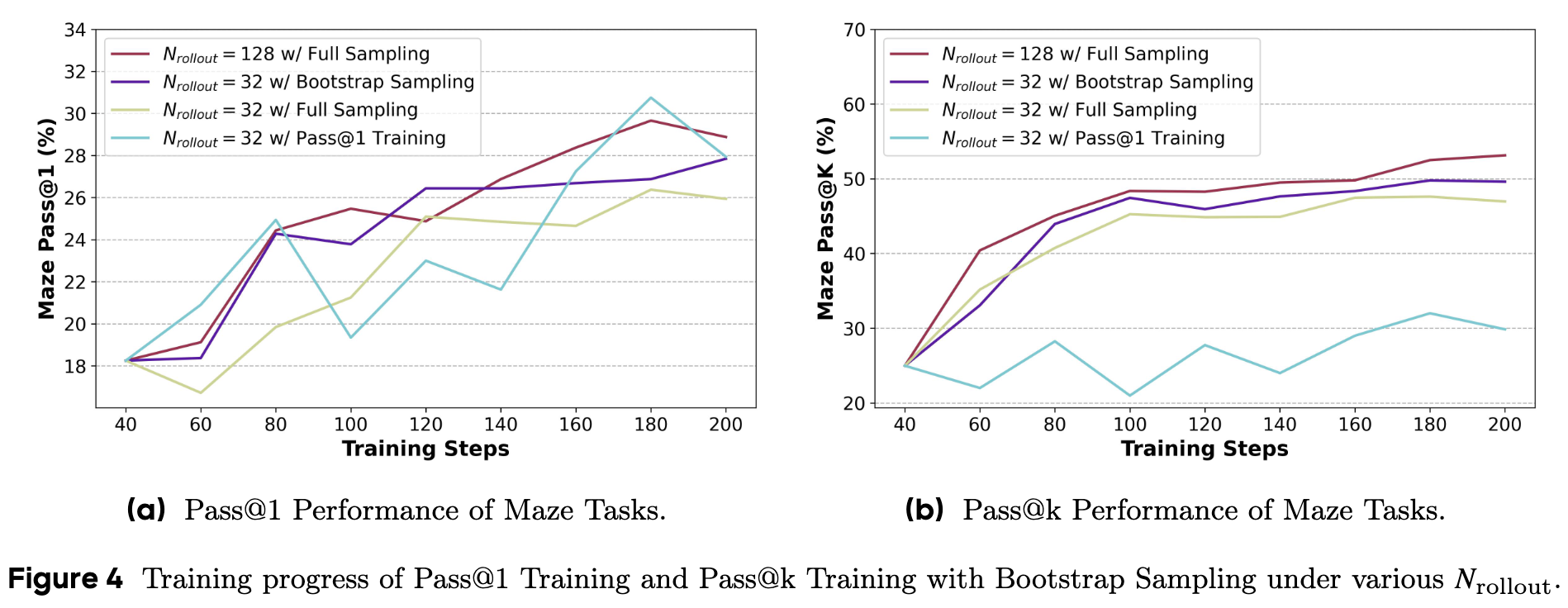
Bootstrap 采样的优势是巨大的。从图 4 可以看出,仅使用 32 个 rollout 的 Bootstrap 采样(紫色线),其性能甚至超过了使用 128 个 rollout 的完全采样(绿色线)。这意味着,我们用 1/4 的计算成本,取得了更好、更稳定的训练效果。其原因在于,Bootstrap 采样通过组合生成了更多样化的组,有效降低了因分组随机性带来的方差,使得优势估计更加准确。
解析推导(Analytical Derivation)
Bootstrap 采样虽然高效,但仍然引入了采样过程的随机性。每一次训练,构造出的组都不同,这会导致训练过程存在一定的波动。作者们追求极致,提出了一个问题:我们能否完全绕过“采样分组”这个过程,直接计算出每个答案的期望优势?
答案是可以的。通过一系列精妙的概率和组合数学推导,作者们得出了优势值的解析形式。
推导的思路大致如下:
-
分析组的统计特性:首先,我们需要知道所有可能构成的组的平均奖励 和标准差 。这取决于两个关键数字:rollout 的总数 和其中错误答案的数量 。 -
计算负面组概率:一个组是“负面组”(即组内所有答案都错误,奖励为 0),当且仅当它包含的 个答案全部从 个错误答案中选出。所有可能的组的总数是 ,而所有可能的负面组的数量是 。因此,一个随机组是负面组的概率是 。 -
计算组的平均奖励和标准差:由于奖励只有 0 和 1,所以平均奖励 。标准差也可以相应地计算出来:。 -
计算组的优势:有了平均值和标准差,我们就可以计算出“正面组”(奖励为 1)和“负面组”(奖励为 0)的优势值 和 。 -
将组优势分配到单个答案:这是最关键的一步。 -
对于一个正确答案(我们称之为 positive response),任何包含它的组都必然是“正面组”。因此,它的期望优势只与 有关。 -
对于一个错误答案(我们称之为 negative response),它既可能与 个其他错误答案组成“负面组”,也可能与至少一个正确答案组成“正面组”。我们需要计算这两种情况的概率,并据此加权平均 和 来得到它的期望优势。
-
最终,作者们推导出了正面响应优势 和负面响应优势 的精确解析公式:
(注意:此处公式为论文思想的简化表达,具体形式请参考原论文公式 14 和 15)
这个解析解的意义在于,只要我们完成了一次 rollout,获得了 和 ,我们就可以瞬间计算出每个正确答案和错误答案应该被赋予的优势值,完全不需要进行任何随机采样和分组!
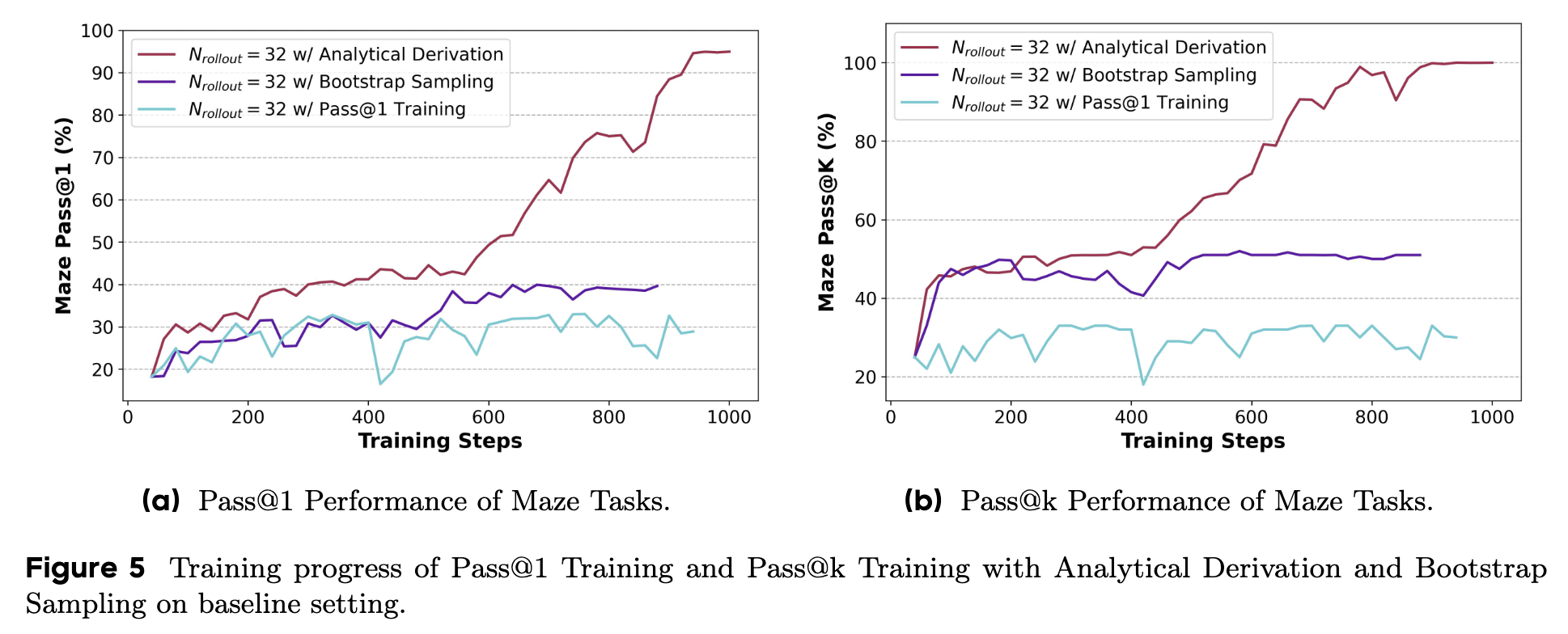
如图 5 所示,解析法(紫色线)相比 Bootstrap 采样(红色线),训练曲线更加平滑稳定,最终性能也达到了最高点。它代表了 Pass@k 训练在理论和实践上的完美结合,做到了既高效又有效。
Pass@k 训练为何如此有效?
我们已经了解了 Pass@k 训练是什么以及如何实现它。现在,让我们跟随作者的脚步,通过一系列对比实验,深入探究它成功的内在机制。
4.1 与其他探索增强方法的比较
为了证明 Pass@k 训练的优越性,作者将其与两种常见的探索增强方法进行了对比。
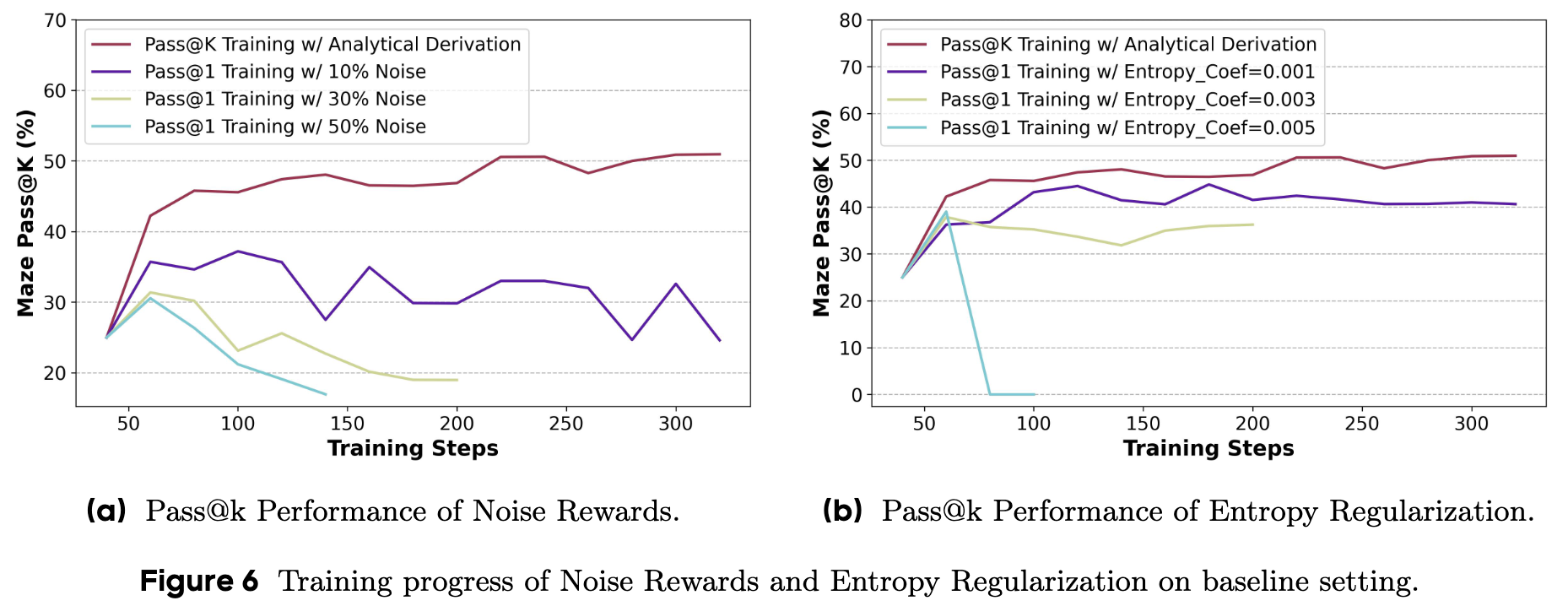
-
噪声奖励 (Noise Rewards) :一个直观的想法是,Pass@k 训练之所以有效,是不是因为它“偶尔”会给一些错误的答案正向激励?为了验证这一点,作者在标准的 Pass@1 训练中,随机地将一部分负面奖励(例如 10%、30%、50%)翻转为正面奖励。
结果如图 6a 所示,这种简单粗暴地注入噪声的方式,不仅没有提升模型性能,反而随着噪声比例的增加,性能显著下降。这说明,Pass@k 训练的成功并非源于随机的噪声,而是其结构化的奖励设计,它以一种有意义的方式将信用分配给了那些“可能”有价值的探索。
-
熵正则化 (Entropy Regularization) :这是另一种常用的鼓励探索的方法。它在损失函数中增加一项熵的正则项,惩罚那些策略分布过于“尖锐”(即过于自信、熵低)的模型,迫使模型保持一定的多样性。
如图 6b 所示,熵正则化确实能在一定程度上防止模型性能崩溃,但它引入了一个需要小心调节的超参数(熵系数)。系数太高会导致模型无法收敛,太低则效果不彰。更重要的是,它常常与最大化 Pass@1 的目标存在冲突,导致训练不稳定。相比之下,Pass@k 训练更自然地将探索和利用融为一体,没有这种内在的矛盾。
结论:Pass@k 训练在增强探索方面,优于简单的噪声注入和强制的熵正则化。
4.2 Pass@k 训练真的提升了探索能力吗?
为了更直观地衡量“探索能力”,作者从两个维度进行了分析。
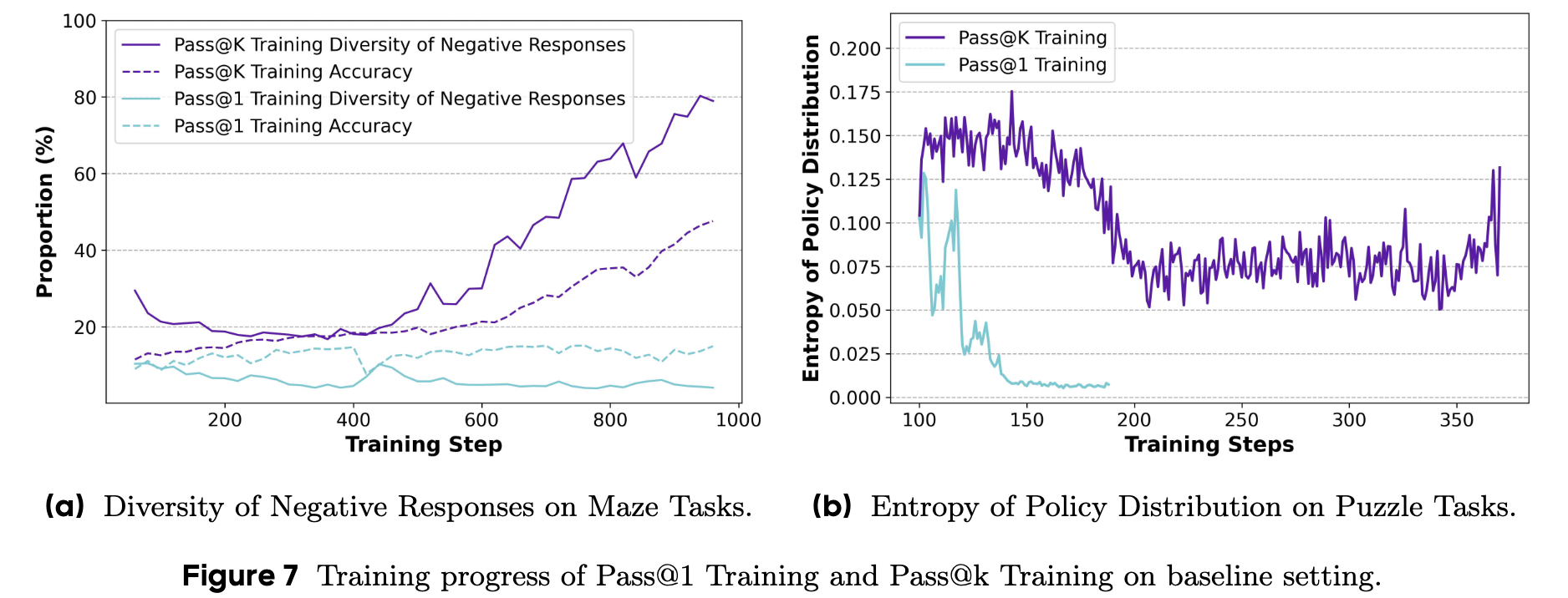
-
负样本多样性 (Answer Diversity of Negative Responses) :作者追踪了在训练过程中,模型生成的错误答案之间的多样性。
如图 7a 所示,在 Pass@1 训练(蓝色线)中,负样本的多样性一直维持在较低水平,说明模型倾向于犯一些“安全”的、类似的错误。而在 Pass@k 训练(紫色线)中,负样本的多样性持续增长,这表明模型正在积极地尝试各种不同的、前所未有的解题路径,即使这些路径最终是错误的。
-
策略分布熵 (Entropy of Policy Distribution) :作者还分析了模型在生成答案时,其内部策略分布的熵值。高熵意味着模型对下一步的选择更加不确定,可能性更多;低熵则意味着模型非常“固执”,倾向于只选择一两条路。
如图 7b 所示,Pass@1 训练(紫色线)导致策略熵迅速下降并收敛到一个低值。而 Pass@k 训练(绿色线)则能将策略熵维持在一个相对较高的水平,甚至在训练后期有所提升。这有力地证明了 Pass@k 训练确实保留了模型的探索天性。
结论:无论是从宏观的答案多样性,还是微观的策略熵来看,Pass@k 训练都显著地提升了模型的探索能力。
4.3 泛化能力如何?
探索能力的增强,不仅仅是为了在训练数据上取得好成绩,更重要的是能否泛化到未见过的新问题上。
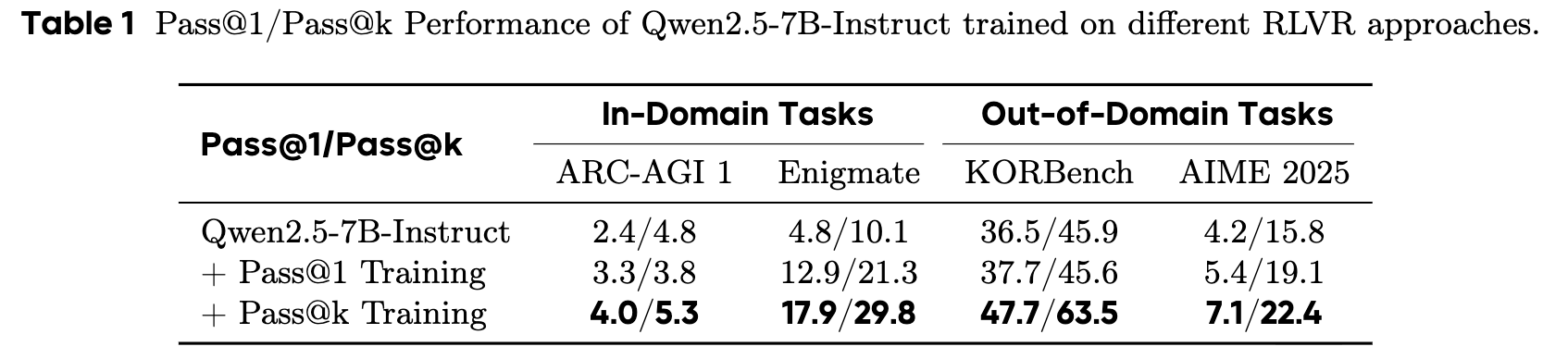
作者在多个领域内(In-Domain)和领域外(Out-of-Domain)的数据集上对模型进行了评估。如表 1 所示,与基线模型和经过 Pass@1 训练的模型相比,经过 Pass@k 训练的模型在所有任务上都取得了显著的性能提升。
这背后的原因是,Pass@k 训练鼓励模型学习的是更加普适和鲁棒的解题策略,而不是针对特定问题的“记忆性”解法。当模型面对一个新问题时,这种策略性的知识更容易被迁移和应用。相反,Pass@1 训练出的模型行为更保守,更倾向于套用已知的模板,因此在面对新情境时泛化能力较差。
结论:Pass@k 训练能显著提升模型的泛化能力。
4.4 对超参数 k 的鲁棒性如何?
一个好的训练方法不应该对超参数过于敏感。作者研究了 的取值(如 4, 8, 16)对训练过程的影响。
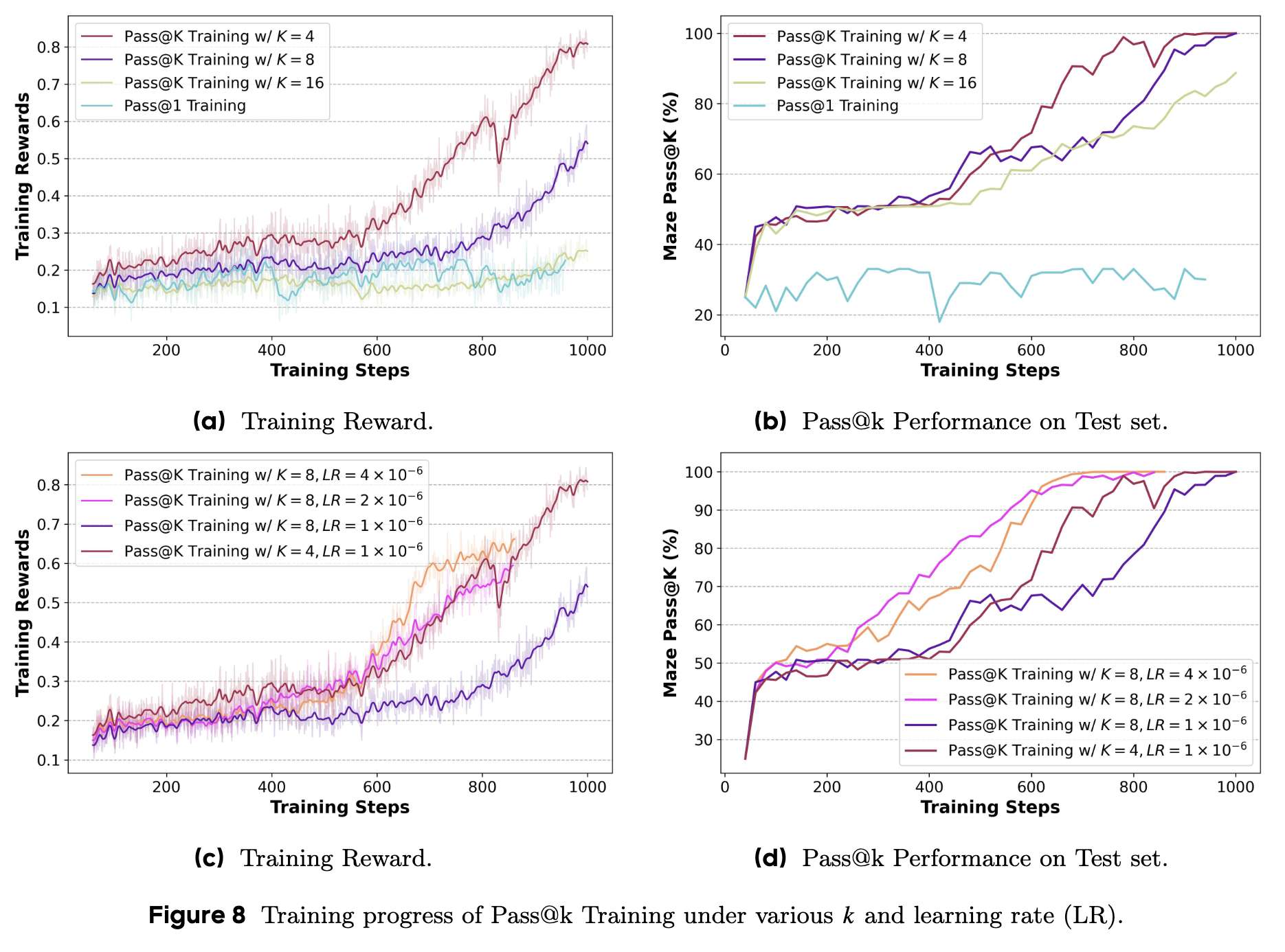
如图 8a, 8b 所示,不同的 值最终都能让模型达到很高的性能水平。一个有趣的现象是,随着 值的增大,训练效率似乎有所下降(达到同样性能所需的步数更多)。作者通过分析优势值的解析公式发现,更大的 会导致计算出的优势值绝对值更小,从而使得每一步的梯度更新幅度变小。
幸运的是,这个问题可以通过一个简单的技巧来解决:增大学习率(Learning Rate)。如图 8c, 8d 所示,当把 的学习率适当调高后,其训练效率甚至超过了 的情况。
结论:Pass@k 训练对 的选择具有很强的鲁棒性,其训练效率问题可以通过调整学习率轻松解决。
4.5 如何将 Pass@k 的收益迁移到 Pass@1?
这是本文最具实际应用价值的部分。在实际部署中,我们最关心的往往是模型单次推理的成功率,即 Pass@1 性能。我们如何将 Pass@k 训练阶段获得的强大探索能力,转化为实实在在的 Pass@1 性能提升呢?
作者提出了一个极其简单而有效的策略:两阶段训练法。
-
第一阶段:Pass@k 训练。在这一阶段,我们使用 Pass@k 作为奖励,鼓励模型进行广泛的探索,跳出局部最优。这好比是让模型从一个贫瘠的“旧大陆”出发,去探索一片物产丰饶的“新大陆”。 -
第二阶段:Pass@1 训练。在模型完成了充分的探索后,我们将其切换到 Pass@1 训练模式。此时,模型已经身处“新大陆”,拥有了更好的解题视野。Pass@1 训练则像是在这片新大陆上进行精耕细作,快速地“利用”已有的探索成果,收敛到那个之前未能发现的全局最优解。
这个“先探索,后利用”的策略取得了惊人的效果。
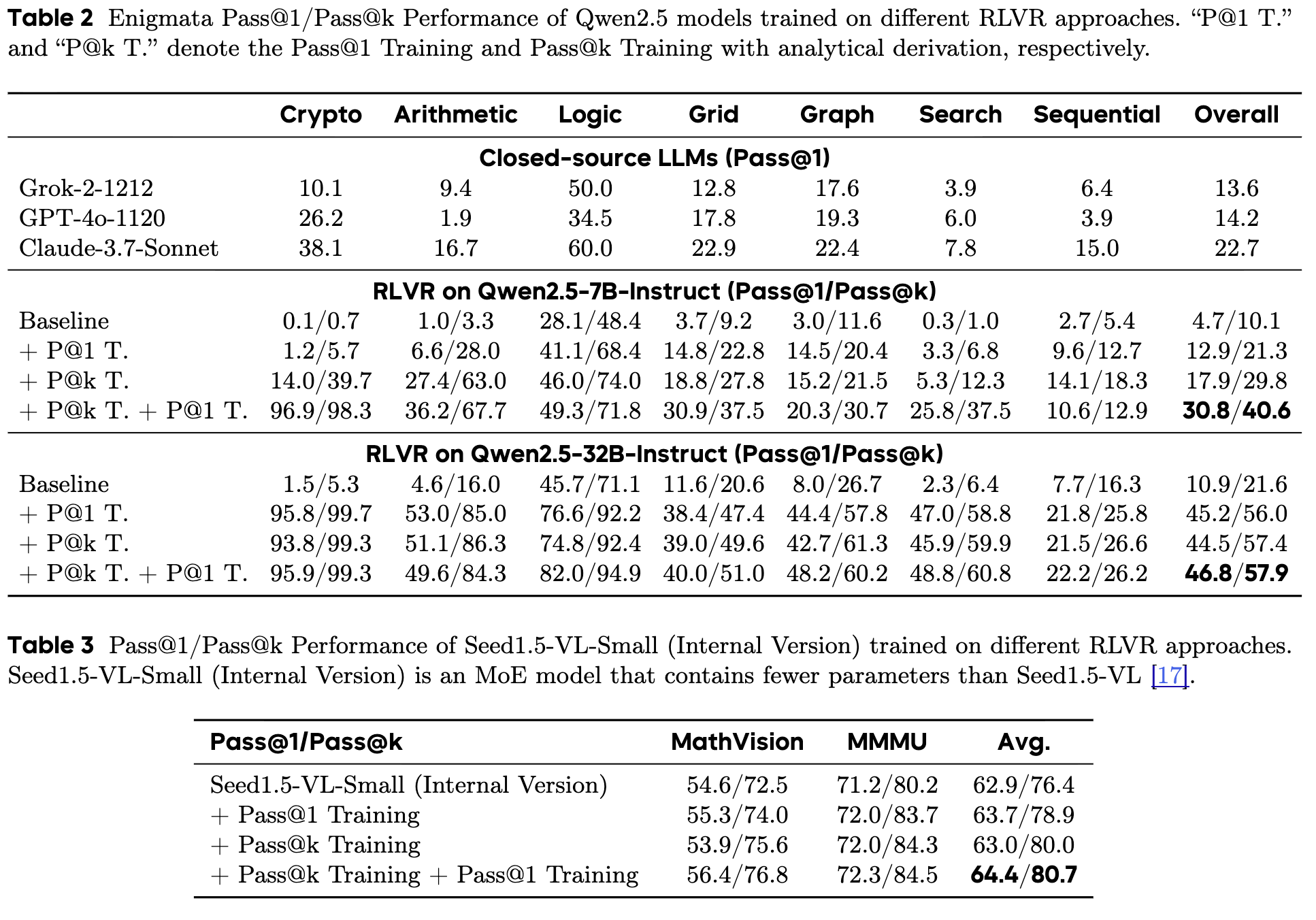
如表 2 和表 3 所示,在 Enigmata 逻辑谜题和 MathVision、MMMU 等多模态推理任务上,一个 7B 参数量的 Qwen2.5 模型,在经过“P@k T. + P@1 T.”两阶段训练后,其 Pass@1 性能 不仅远超单纯的 Pass@1 训练,甚至在多个任务上超过了 Grok-2, GPT-4o, Claude-3.7-Sonnet 等业界顶尖的闭源大模型。
这一结果充分证明了 Pass@k 训练的巨大价值。它不仅仅是提升了 Pass@k 指标本身,更是为后续的 Pass@1 精调提供了一个前所未有的高起点,从而根本性地释放了 LLM 的推理潜力。这个结论在不同大小的模型(7B, 32B)、不同架构(Dense, MoE)和不同任务类型(自然语言,多模态)上都得到了验证,具有极强的普适性。
从优势函数视角审视 Pass@k
作者们并未止步于实验的成功,他们进一步追问:从更深层的数学原理来看,Pass@k 训练与 Pass@1 训练的根本区别到底在哪里?
他们发现,答案隐藏在优势函数的形态中。
可视化优势函数
优势值是驱动整个强化学习过程的核心力量,它的大小决定了梯度更新的方向和幅度。作者将 Pass@1 和 Pass@k 训练中,优势函数的各项指标(正面优势 ,负面优势 ,以及总优化力度 )随“rollout 准确率”(即 ,可以理解为问题的难度)的变化绘制成了曲线。
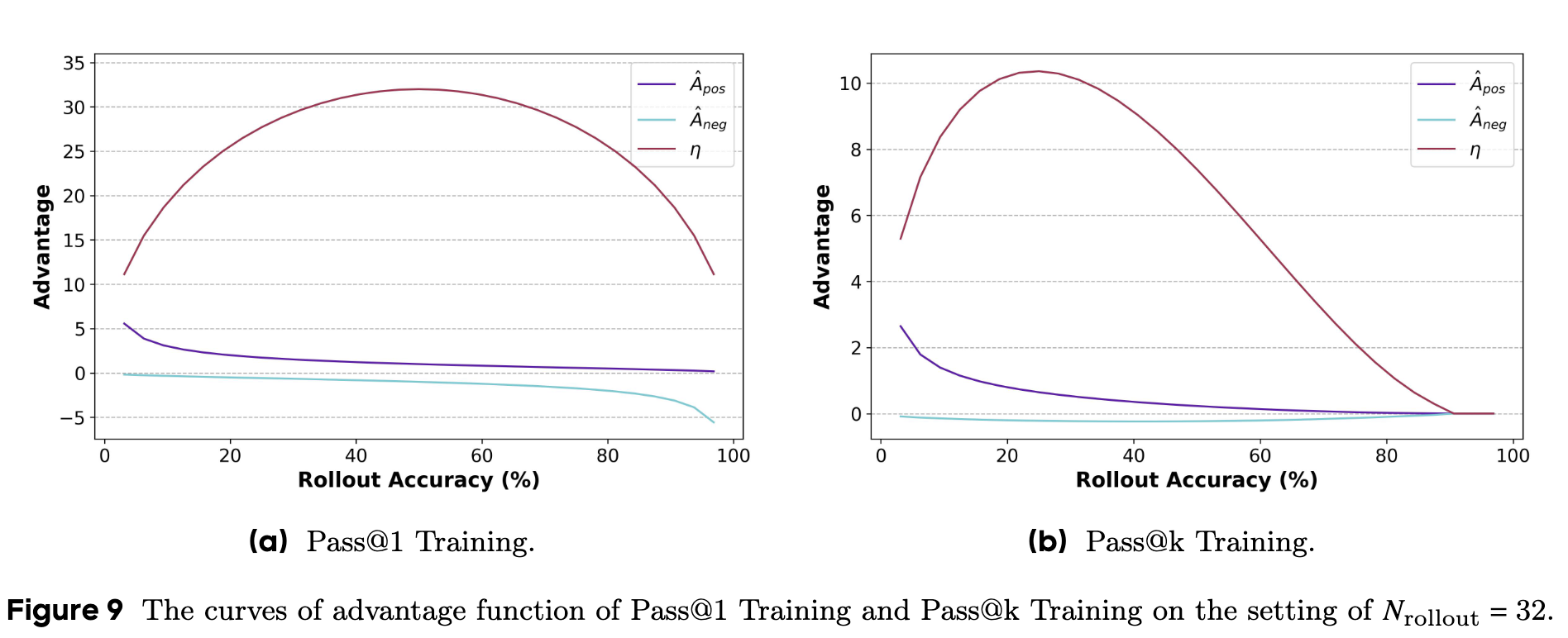
通过对比图 9(a) 和 9(b),我们能发现三个关键差异:
-
峰值大小:Pass@1 的总优化力度 的峰值远高于 Pass@k。但这并不关键,因为我们可以通过一个系数来缩放损失函数,调整整体的优化强度。 -
峰值位置 (Argmax of ):这是最核心的区别。 -
在 Pass@1 训练中,优化力度的峰值出现在准确率为 50% 的地方。这意味着,Pass@1 训练把最多的精力花在了那些中等难度的问题上。 -
在 Pass@k 训练(图中是 k=8 的情况)中,峰值则出现在准确率约为 25% 的地方。这意味着,Pass@k 训练更关注那些模型觉得“困难”的问题。它倾向于引导模型去攻克那些之前未能解决的难题。
-
-
曲线趋势 (Trend of ) : -
Pass@1 的曲线在 50% 处基本对称,意味着它对“简单问题”(准确率 > 50%)和“困难问题”(准确率 < 50%)的关注度是类似的。 -
Pass@k 的曲线则呈现出明显的偏态。当问题变得“简单”(例如准确率 > 60%)时,其优化力度 会迅速下降到接近于零。这意味着,Pass@k 训练会自动忽略那些模型已经基本掌握的问题,从而防止在简单问题上过度拟合,把宝贵的计算资源留给更具挑战性的任务。
-
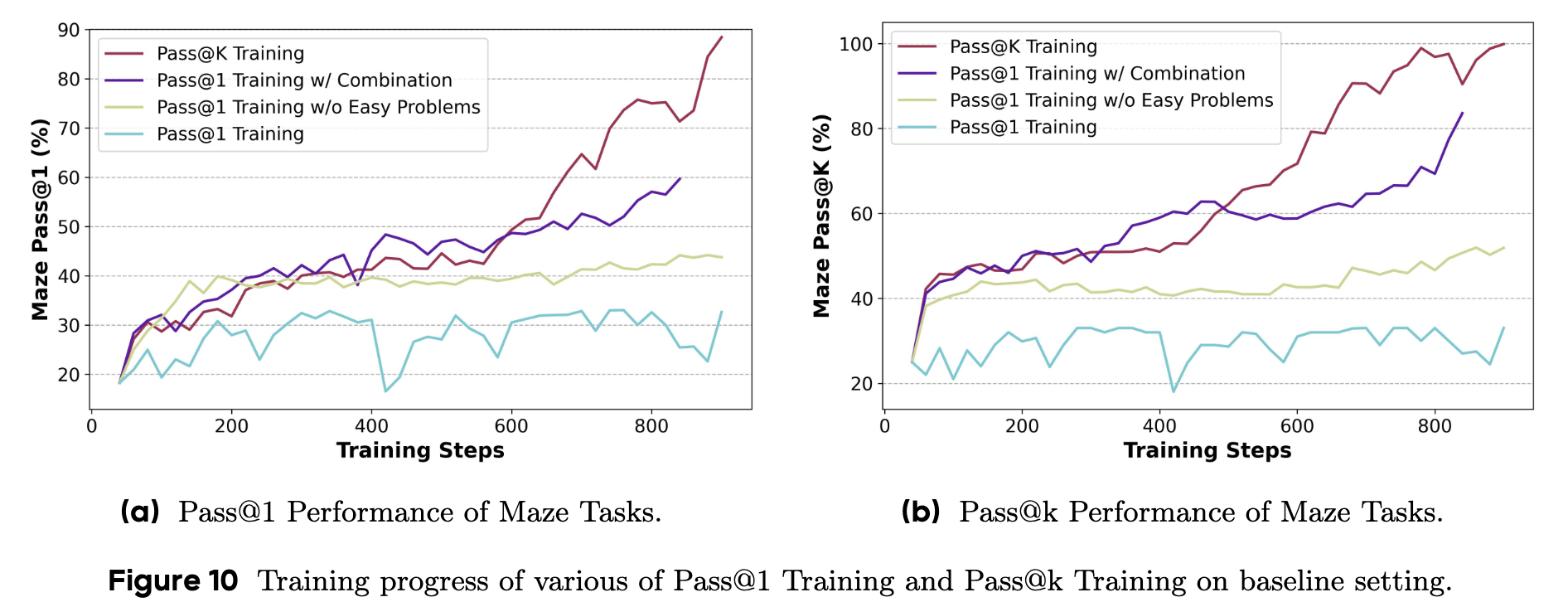
为了验证这些洞察,作者还设计了精巧的控制变量实验(如图 10)。例如,在 Pass@1 训练中,人为地移除了对简单问题(高准确率)的优化(w/o Easy Problems),发现模型性能确实得到了提升。这证明了“关注难题”和“忽略易题”确实是提升性能的关键所在。
隐式奖励设计:RLVR 的未来?
以上分析引出了一个极具启发性的想法:既然优势函数的形态如此关键,我们是否可以跳过“定义奖励函数 -> 推导优势函数”这一传统路径,直接去“设计”我们想要的优势函数形态呢?
这,就是作者提出的隐式奖励设计(Implicit Reward Design)。
我们不再纠结于奖励是 0 还是 1,是 Pass@1 还是 Pass@k。我们直接根据我们的优化目标,来“画”出我们想要的优势函数曲线。例如,如果我们希望模型更关注难题,就把优势函数的峰值向左移动;如果我们希望模型不要在简单题上浪费时间,就在曲线的右侧设置一个快速衰减。
作者对此进行了初步的探索:
-
Exceeding Pass@k Training:通过一个变换函数 ,将 Pass@k 优势函数的峰值进一步左移,使其更关注那些“极难”的问题。实验发现,这能让模型在训练早期更快地提升 Pass@k 性能。 -
Combination Training:根据当前 rollout 的准确率,动态地混合 Pass@1 和 Pass@k 的优势函数。在准确率低(问题难)时,更多地使用 Pass@1 的优势(其绝对值大,能提供更强的初始学习信号);在准确率高(问题简单)时,则切换到 Pass@k 的优势(避免过拟合)。这种自适应的组合策略在实验中取得了比单一方法更好的效果。 -
Adaptive Training based on Policy Entropy:更进一步,根据每个问题的策略熵来判断其探索阶段。对熵低的(探索已较充分)问题,使用 Pass@k 优势来鼓励更多探索;对熵高的(探索仍较混乱)问题,则使用 Pass@1 优势来帮助模型收敛和利用。
这些探索性实验都取得了积极的成果,有力地证明了“隐式奖励设计”是一个充满潜力的新方向。
点评
论文精准地指出了当前 RLVR 训练中 Pass@1 奖励机制导致模型“探索不足”的问题。论文不仅展示了结果,还深入探究了“为什么有效”。通过分析答案多样性和策略熵的变化,证明了 Pass@k 训练确实提升了模型的探索能力。
论文没有止步于 Pass@k 训练本身,而是将其抽象为一种“隐式奖励设计”(Implicit Reward Design)的范式。通过分析不同训练方法下的“优势函数”(Advantage Function)曲线,作者发现 Pass@k 训练更关注于解决模型尚未掌握的难题,而 Pass@1 训练则对中等难度的题目用力过猛,对难题和简单题的优化不足。
成本较高:尽管解析解方法避免了对 rollout 结果进行分组采样,但 Pass@k 训练的基础仍然是在每个训练步骤中为每个问题生成大量的候选答案(N_rollout)。相比于可能只需要少量候选者的 Pass@1 训练,这在训练时间和计算资源上的开销依然更大。
往期文章:




