优化大语言模型过程中,我们都会面临一个问题:通过强化学习(如 RLHF 或 RLVR)增强模型能力的同时,往往会以牺牲模型的校准度为代价,从而催生出更“自信的幻觉”。
来自麻省理工学院(MIT)的一组研究人员 Mehul Damani、Isha Puri、Stewart Slocum、Idan Shenfeld、Leshem Choshen、Yoon Kim 和 Jacob Andreas 在他们于 2025 年 7 月 22 日发布的论文《超越二元奖励:训练语言模型审视自身的不确定性》(Beyond Binary Rewards: Training LMs to Reason About Their Uncertainty)中,直面了这一挑战。他们提出了一种名为 RLCR(Reinforcement Learning with Calibration Rewards,即带校准奖励的强化学习) 的新方法,通过将恰当评分规则(Proper Scoring Rule),特别是布莱尔分数(Brier Score),直接整合进奖励函数,从而构建了一个能够同时优化准确率与校准度的复合目标。其最引人注目的贡献在于,论文不仅从理论上证明了该方法不会损害任务准确率,更通过详尽的实验展示了 RLCR 在大幅提升模型校准度和域外泛化能力上的卓越表现。

-
论文标题:Beyond Binary Rewards: Training LMs to Reason About Their Uncertainty -
论文链接:https://www.arxiv.org/pdf/2507.16806
一、问题的根源:“非黑即白”的二元奖励机制
为了理解 RLCR 的创新之处,我们首先需要了解当前训练推理模型的主流方法及其弊端。
目前,绝大多数成功的语言模型推理能力训练都依赖于一种称为 RLVR(Reinforcement Learning with Verifiable Rewards,即可验证奖励的强化学习) 的范式。 其核心思想非常直接:模型在回答问题前,会先生成一个自然语言形式的“推理链”,展现其“思考过程”。然后,系统会根据模型最终输出的答案是否正确,给予一个简单的二元奖励:答对则奖励为 1,答错则为 0(或-1)。
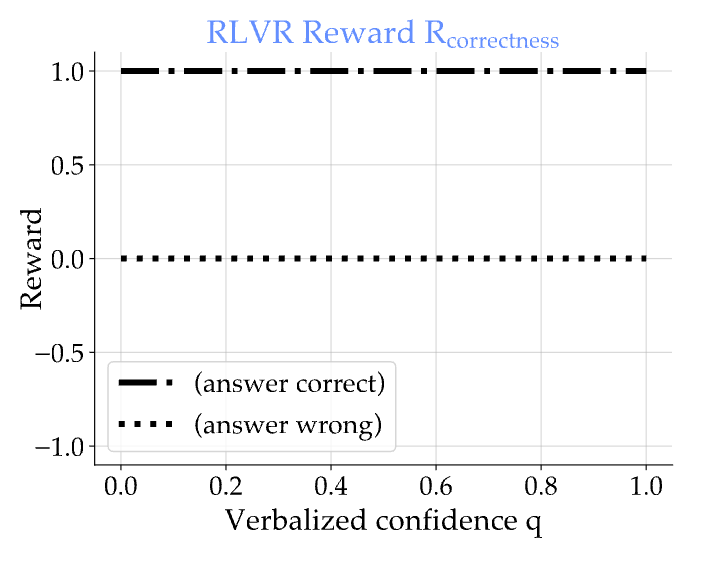
这种“成王败寇”式的奖励机制虽然在提升特定任务的准确率上简单有效,但其背后隐藏着一个巨大的缺陷。它无法区分两种截然不同的正确答案:一种是模型通过严谨推理得出的“确信的正确”,另一种则是模型在不确定情况下“蒙对的正确”。同理,它也无法区分“几乎答对的错误”和“离谱的幻觉”。
这种机制的直接后果是,模型没有动力去表达不确定性。为了最大化奖励,模型的最佳策略就是“假装自信”,即使是在猜测,也要给出最可能的答案。这导致了严重的 校准度(Calibration) 问题。一个模型的校准度,指的是其预测的置信度与其真实准确率之间的一致性程度。举个例子,如果一个模型对它给出“80%置信度”的那些答案,真实准确率确实是80%左右,那么它就是良好校准的。
然而,经过标准 RLVR 训练的 LLM,往往会变得 过度自信(Overconfident)。它们会对错误的答案给出极高的置信度,这在实际应用中极具误导性,甚至可能是危险的。论文指出,尤其是在处理高风险领域(如医疗诊断、法律咨询)或面对模型知识边界之外(out-of-domain)的问题时,我们需要的不仅仅是一个能给出答案的机器,更是一个能坦诚自己“知识局限性”的可靠伙伴。
这篇论文正是要解决这两个核心问题:
-
我们能否同时优化模型的正确性和校准度? -
模型的“推理链”本身,能否帮助提升其校准度?
二、RLCR 的诞生:引入“校准奖励”
为了解决上述问题,研究者们从统计决策理论中的“恰当评分规则(Proper Scoring Rules)”中汲取灵感,设计了全新的 RLCR 方法。
1. 恰当评分规则与布莱尔分数(Brier Score)
首先,我们需要一个工具来衡量“置信度”的好坏。这就是“评分规则”的作用。一个“恰当”的评分规则能够激励预测者给出最诚实的概率预测。其中,最经典、最常用的一个就是 布莱尔分数(Brier Score)。
对于一个二元事件(比如,答案正确或错误),假设模型的置信度为 (一个 0 到 1 之间的数值),而实际结果为 (正确为 1,错误为 0)。布莱尔分数的计算公式为:
这个分数越低越好。我们可以看到,当模型的置信度 越接近实际结果 时,分数就越低。例如,如果答案是正确的 (),模型给出的置信度是 0.9,那么布莱尔分数就是 ;如果给出 0.2,分数就是 。反之亦然。这个特性使得布莱尔分数成为评估和优化校准度的理想工具。
2. RLCR 的复合奖励函数
RLCR 的核心,就是设计了一个新的奖励函数,将传统的二元正确性奖励与布莱尔分数结合起来。
在 RLCR 的训练流程中,模型需要生成四个部分:
-
<think>标签:包含模型的思维链(Chain-of-Thought)。 -
<answer>标签:包含最终答案 。 -
<analysis>标签:模型对自身推理过程和不确定性的分析。 -
<confidence>标签:包含一个数值化的置信度评分 。

然后,研究者定义了 RLCR 的奖励函数:
其中, 是标准答案, 是一个指示函数,当模型答案 与标准答案 一致时为 1,否则为 0。
这个公式非常精妙。它由两部分组成:
-
正确性奖励 (): 和 RLVR 一样,答对就+1。 -
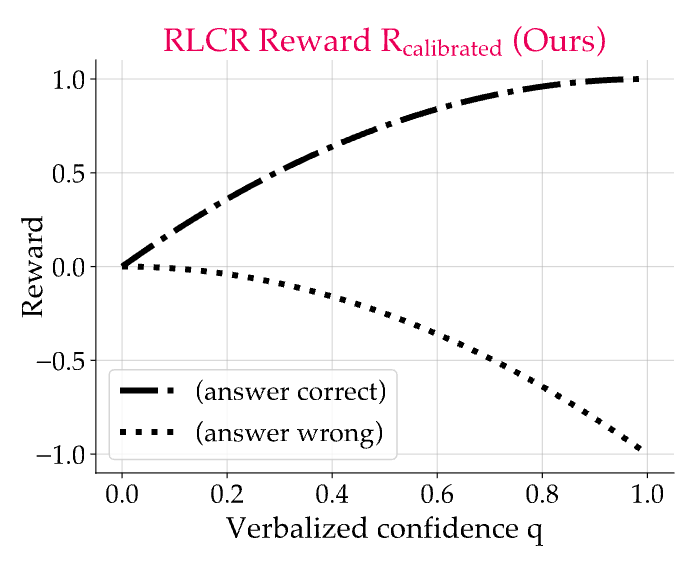
校准惩罚:后面一项是布莱尔分数的相反数(因为我们希望最大化奖励,而布莱尔分数是越小越好)。它惩罚的是“不准的自信”: -
当模型答对 (),但自信心不足 (例如 ),会受到惩罚:。 -
当模型答错 (),但盲目自信 (例如 ),会受到更严重的惩罚:。 -
当模型答错 (),且有自知之明 (例如 ),惩罚就小得多:。
-
3. 理论保证:准确性与校准度的双赢
你可能会担心,引入了校准惩罚,会不会让模型为了获得更好的校准分数而“躺平”,故意选择一些容易判断但错误的答案呢?比如,模型可以稳定输出一个错误答案,并稳定给出 0 的置信度,这样它的校准惩罚项一直很小。
论文通过定理 1 (Theorem 1) 从理论上证明了这种担心是多余的。该定理指出,RLCR 的奖励函数具有两个关键特性:
-
校准激励(Calibration incentive):对于任何给定的答案 ,当且仅当模型的置信度 等于该答案的真实成功概率 时,期望奖励最大化。这意味着模型被激励去做出最诚实的校准。 -
正确性激励(Correctness incentive):在所有已经良好校准的预测中,模型选择那个成功概率 最高的答案时,期望奖励最大化。这意味着模型仍然有最强的动力去寻找最可能正确的答案。
简而言之,校准惩罚项并没有以牺牲准确性为代价。模型的最优策略依然是:首先,尽最大努力找到最正确的答案;然后,对这个答案的成功可能性给出一个最诚实的评估。
论文还指出,这个理论不仅适用于布莱尔分数,对于任何有界的(bounded)恰当评分规则都成立。这一点非常重要,因为它排除了像对数损失(log loss)这样无界的评分规则,后者可能会为了追求无限的校准奖励而选择错误的答案。
三、实验验证:RLCR 的全面胜利
理论上的优雅需要通过实践来检验。研究者们进行了一系列详尽的实验,将 RLCR 与多种基线方法进行了比较。
1. 实验设置
-
基础模型:实验使用了当时性能强大的 Qwen2.5-7B 模型作为基础。 -
训练算法:使用 GRPO (一种强化学习算法) 进行训练。 -
数据集: -
HotpotQA:一个复杂的事实问答数据集,需要模型进行多跳推理。研究者还特意修改了该数据集,通过移除部分关键信息来创造不同程度的不确定性,以专门测试模型的校准能力。 -
Big-Math:一个大规模、高质量的数学问题数据集,用于评估模型在复杂逐步推理中的不确定性处理能力。
-
-
基线方法: -
Base:未经任何 RL 微调的预训练模型。 -
RLVR:使用标准二元奖励进行训练。 -
RLVR + Classifier(BCE/Brier):在 RLVR 模型之上,再训练一个独立的分类器来预测置信度(分别使用二元交叉熵损失和布莱尔分数损失)。 -
RLVR + Probe:一个更简单的版本,只在 RLVR 模型最后一层的表示上训练一个线性探针来预测置信度。 -
Answer Probability:使用 RLVR 模型生成答案时,计算 <answer>标签内 token 的平均概率作为置信度。
-
-
评估指标: -
Accuracy (↑):准确率。 -
AUROC (↑):衡量区分正负样本的能力。 -
Brier Score (↓):布莱尔分数,越低越好。 -
ECE (Expected Calibration Error) (↓):期望校准误差,越低越好。
-
2. 主要实验结果
实验结果有力地证明了 RLCR 的优越性,尤其是在校准度和泛化能力上。
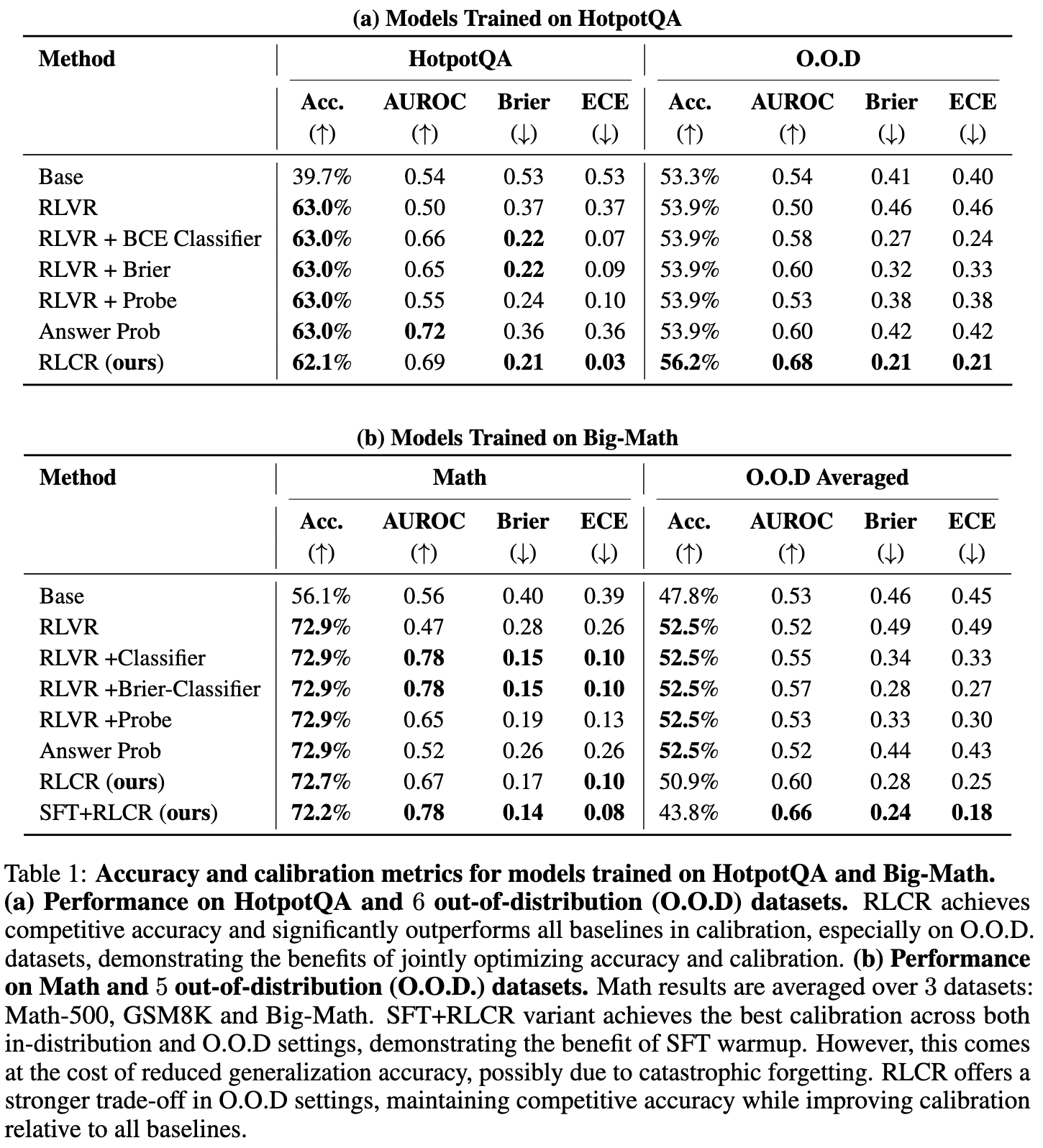
(1) 域内(In-domain)表现:准确不降,校准飞跃
在用于训练的 HotpotQA 和 Math 数据集上:
-
准确率:RLCR 的准确率与强大的 RLVR 基本持平。这印证了理论分析,即增加校准项不会损害模型的任务性能。 -
校准度:RLCR 的表现远超所有基线方法。以 HotpotQA 为例,RLCR 将 ECE 从 RLVR 的 0.37 惊人地降低到了 0.03。而在 Math 数据集上,ECE 也从 0.26 降至 0.10。这表明 RLCR 训练出的模型对自己“几斤几两”有了清晰得多的认识。相比之下,Base 模型和 RLVR 模型都表现出严重的过度自信。
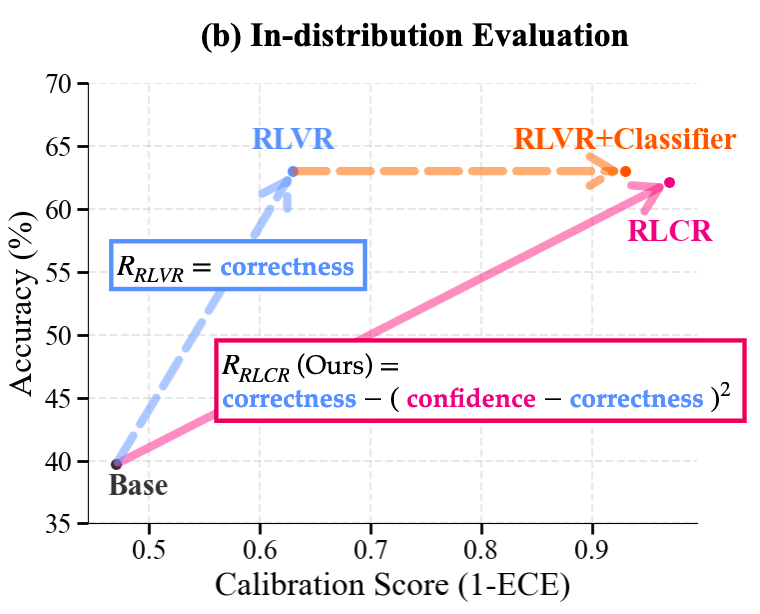
(2) 域外(Out-of-domain)泛化:真正的考验
模型能否将学到的能力泛化到未见过的数据上,是衡量其鲁棒性的关键。研究者在 TriviaQA、SimpleQA、GSM8K 等六个不同的 O.O.D. 数据集上进行了测试。
-
RLVR 的退化:一个惊人的发现是,标准的 RLVR 训练在 O.O.D. 任务上损害了模型的校准度,其表现甚至不如未经微调的 Base 模型。这说明,只关注正确性的强化学习会让模型变得“偏执”,在面对新问题时更加容易过度自信。 -
RLCR 的卓越泛化:与此形成鲜明对比的是,RLCR 在 O.O.D. 任务上依然表现出色。它不仅在校准度上全面碾压所有基线,甚至在准确率上略有提升。这表明,通过明确地对校准进行优化,可以产生更具通用性和可靠性的推理模型。
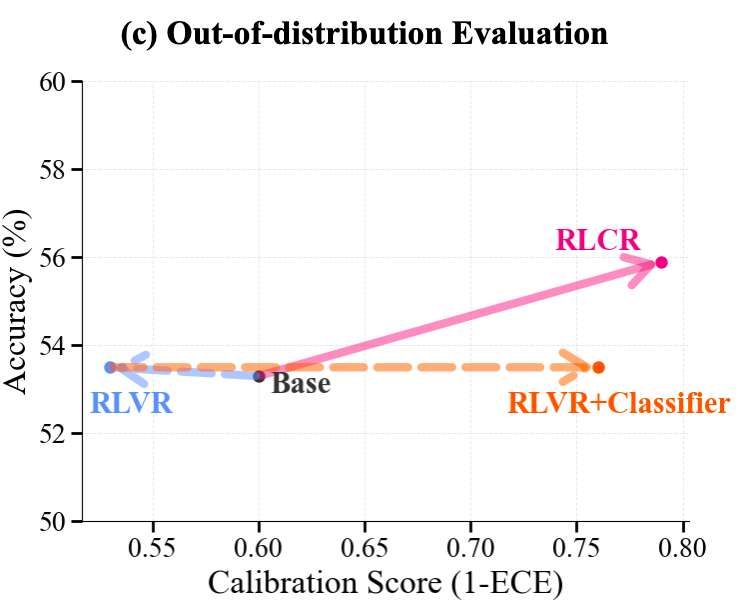
研究者推测,RLCR 优异的泛化能力可能源于三点:
-
关于不确定性的推理:模型在思维链中明确地对不确定性进行分析,这种“反思”过程本身就提升了校准能力。 -
RL 的训练动态:在 RL 训练中,模型的性能是不断变化的,这迫使置信度分析模块必须持续适应,这种“动态”学习过程可能促进了更鲁棒的知识学习。 -
共享表征:生成答案和校准置信度使用同一个模型,这使得校准任务可以利用答案生成过程中形成的内部表征,从而提高泛化能力。
3. “口头自信”的妙用:提升测试时性能
RLCR 模型学会了用数值 来表达自信。这种“口头自信”在测试时也能派上用场。通过对多次生成的答案进行置信度加权投票(confidence-weighted majority vote),可以进一步提升准确率,效果优于简单的多数投票(majority vote)和选择置信度最高的答案(max-confidence)。
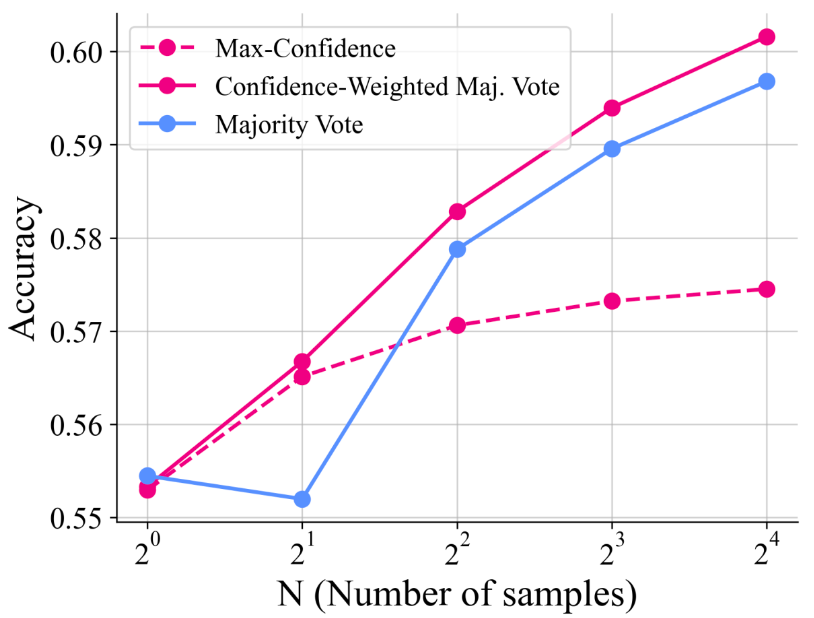
此外,通过对同一个答案多次生成不同的不确定性分析(<analysis>部分),然后将得到的多个置信度分数进行平均,可以进一步提升校准度(降低布莱尔分数)。
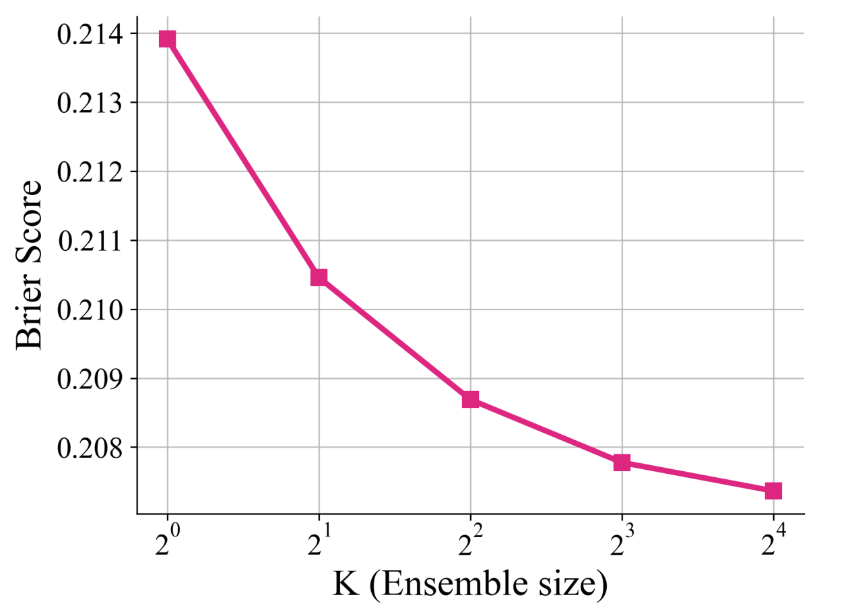
4. 推理过程真的有助于校准吗?
一个有趣的问题是,模型在 <analysis> 标签中生成的关于不确定性的推理,是真的为其最终的置信度分数提供了信息,还是仅仅是“事后诸葛亮”?
为了验证这一点,研究者训练了两个分类器:
-
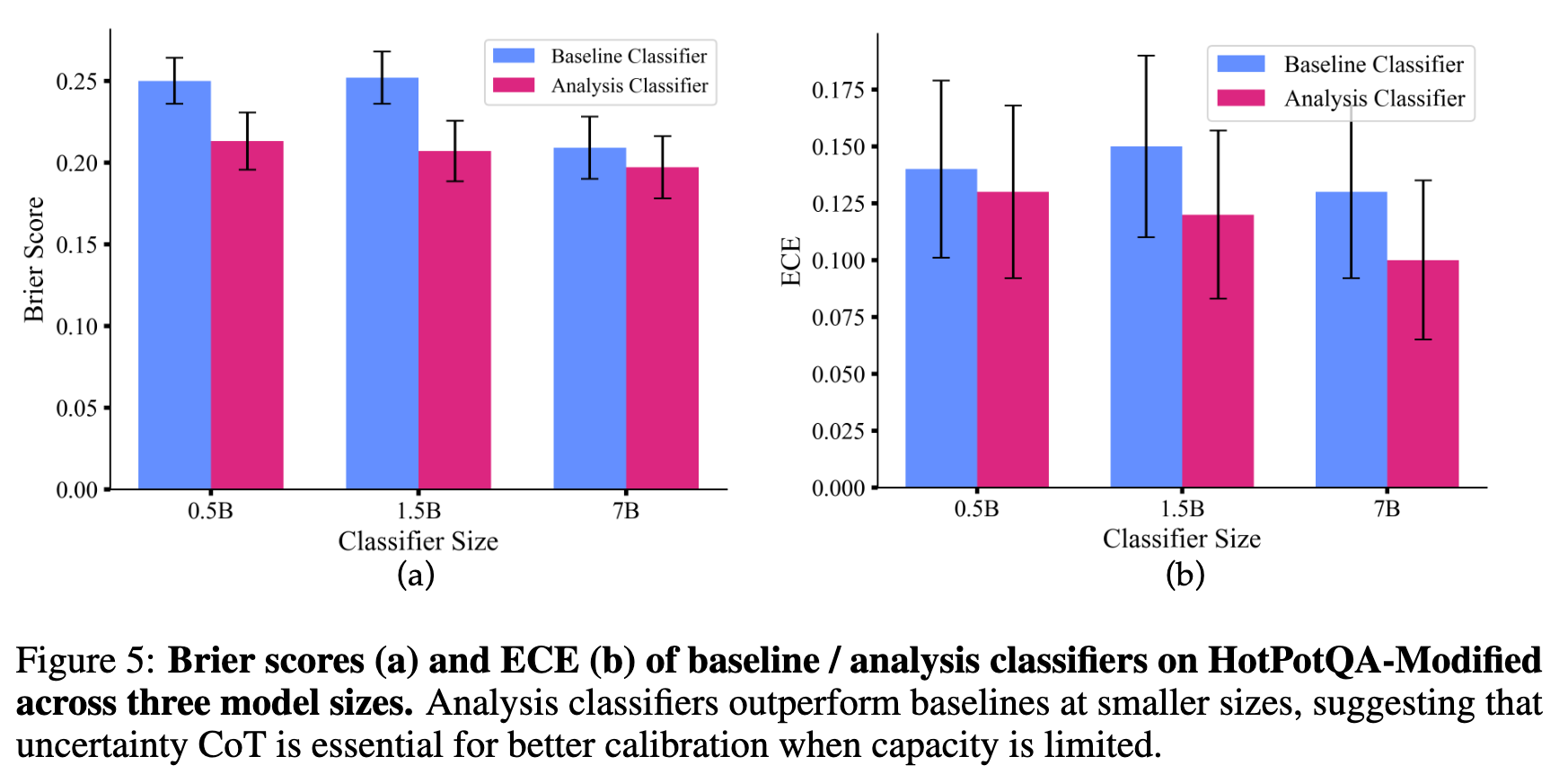
基线分类器:在不包含不确定性分析的 RLVR 模型输出上训练。 -
分析分类器:在包含不确定性分析的 RLCR 模型输出上训练(移除了最后的 <confidence>标签以防作弊)。
结果显示,在模型规模较小(如 0.5B, 1.5B)时,分析分类器的表现明显优于基线分类器。这说明,在模型能力有限时,明确的 uncertainty CoT (不确定性思维链) 对于更好的校准至关重要。而对于更大的 7B 模型,两者表现相似,这可能是因为大模型有足够的能力直接从答案和推理中推断出置信度相关特征。
5. 置信度的自洽性
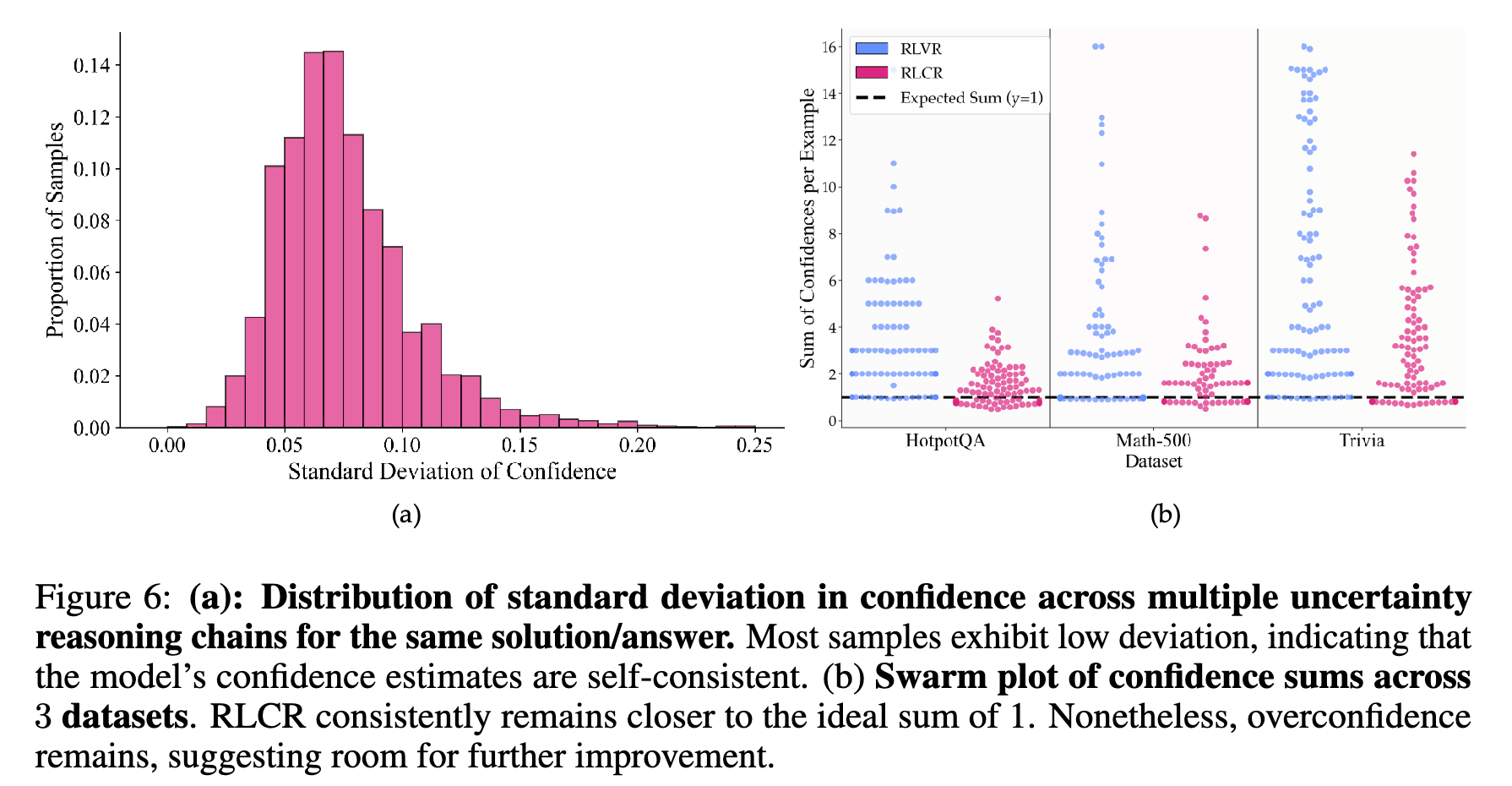
最后,研究者还检验了模型置信度的自洽性(self-consistency)。
-
内部一致性:对于同一个答案,多次生成的不确定性分析所给出的置信度分数是否稳定?结果显示,大多数情况下,这些置信度分数的标准差很低,表明模型对于同一个答案的信心是相当稳定的。 -
相互一致性:对于一个问题,模型对所有不同可能答案给出的置信度之和是否应该接近于 1(因为只有一个答案是正确的)?结果显示,RLCR 模型的置信度总和比 RLVR 更接近理想的 1,尤其是在域内数据集上。这表明 RLCR 模型的信念分布更加合理和校准。
点评
RLCR 框架引导模型生成一个单一的标量数值 q(0到1之间)来代表其置信度。尽管这在数学上易于处理并能与布莱尔分数完美结合,但它可能过度简化了“不确定性”这一复杂概念。
在现实世界中,不确定性有不同的来源:
-
认知不确定性 (Epistemic Uncertainty):源于模型自身知识的缺乏。比如问一个模型“2028年诺贝尔物理学奖得主是谁?”,模型因为不知道未来,所以应该感到不确定。这是可以通过获取更多信息来消除的。 -
偶然不确定性 (Aleatoric Uncertainty):源于问题本身的内在随机性或模糊性。比如问“明天是否会下雨?”,即使是全知的气象模型也只能给出一个概率,因为天气系统本身就是混沌的。
RLCR 的单一置信度 q 并没有区分这两种不确定性。模型学会的可能只是一个“模式匹配”的游戏:在看到某些特征(如问题中的模糊词汇、知识库中信息冲突)时,输出一个较低的 q 值以最小化奖励函数的惩罚。模型是真的在“理解”和“推理”自己的知识边界,还是仅仅在学习一种更复杂的输出格式? 这是一个更深层次的问题。一个更理想的系统或许应该能输出结构化的不确定性表达,例如:“我对[事实A]有90%的把握,但对[事实B]只有50%的把握,因此整体结论的置信度为70%。”
往期文章: