Google 在 LLM 持续学习方向有了新突破。
当前的大型语言模型(LLM)在预训练阶段结束后,其参数化知识(parametric knowledge)在很大程度上是静态的。尽管模型可以通过上下文学习(in-context learning)在推理时快速适应新信息,但这部分信息是暂时的,并不会整合到模型的核心参数中。这种现象类似于一种“顺行性遗忘症”(anterograde amnesia),即模型能够处理眼前的“短期记忆”,但无法形成新的“长期记忆”。为了解决这一根本性挑战,研究人员探索了多种路径,如持续微调(continual fine-tuning)、检索增强生成(Retrieval-Augmented Generation, RAG)等。然而,这些方法或面临灾难性遗忘的风险,或依赖于外部知识库,并未从根本上改变模型架构的静态本质。
我们能否设计一种学习范式,让模型的内部结构本身就具备持续学习和多层次、多速率适应的能力?
Google Research 的论文《Nested Learning: The Illusion of Deep Learning Architectures》为此提供了一个新的分析框架。他们提出的嵌套学习(Nested Learning, NL)范式,尝试将一个机器学习模型及其训练过程,统一表示为一组相互嵌套、多层次的优化问题。该框架不再将模型架构和优化器视为分离的组件,而是将它们共同视为一个整合的、动态的计算系统。它从一个独特的视角出发:从一个已知的高质量结果出发,“反向”推导出可能产生这个结果的、合乎逻辑的、类似人类的思考过程。这种新视角不仅为理解现有深度学习方法(如包含动量的优化器、注意力机制)提供了新的解释,也为设计具备更强表达能力和适应性的新模型架构(如论文中提出的 HOPE)指明了方向。

-
论文标题:Nested Learning: The Illusion of Deep Learning Architectures -
论文链接:https://openreview.net/pdf/9082b3fb3c37bdc2a3b5d69681382ebe783d49e3.pdf
1. 模型的“顺行性遗忘症”与来自大脑的启示
为了更清晰地阐述当前 LLM 的局限性,论文作者引入了一个生动的类比:顺行性遗忘症。患有此症状的病人无法在疾病发生后形成新的长期记忆,尽管他们之前的记忆完好无损。这导致他们不断地体验“当下”,仿佛每一刻都是全新的。
当前 LLM 的记忆处理系统表现出类似的模式。模型的知识被限制在两个区域:
-
即时上下文(Immediate Context):模型可以处理和利用其上下文窗口内的信息,这对应于“短期记忆”。 -
预训练知识(Pre-trained Knowledge):存储在模型参数(如 MLP 层的权重)中的知识,这对应于“长期记忆”,但这些记忆是在“预训练结束”这个事件之前形成的。
一旦预训练完成,模型就失去了将新信息整合进参数的能力。上下文中的新知识无法对模型的长期记忆参数产生影响。这种设计虽然在处理已有知识方面表现出色,但在需要持续学习和累积新知识的动态环境中则显得力不从心。
为了突破这一瓶颈,研究者们将目光投向了自然界中最高效的学习系统——人类大脑。
1.1 人脑的记忆巩固机制
人脑在持续学习方面表现出高度的效率和鲁棒性,这很大程度上归功于其神经可塑性(neuroplasticity)。近期研究表明,长期记忆的形成至少涉及两个互补的巩固过程:
-
在线巩固(Online Consolidation):也称为突触巩固(synaptic consolidation),在学习发生时或之后立即进行。新获得的、脆弱的记忆痕迹在这一阶段被稳定下来,并开始从短期存储向长期存储转化。 -
离线巩固(Offline Consolidation):也称为系统巩固(systems consolidation),通常发生在睡眠期间。海马体中的夏普波纹(sharp-wave ripples)会重放最近编码的模式,并与皮层的睡眠纺锤波和慢波振荡相协调,从而加强、重组记忆,并将其转移到皮层进行长期存储。
论文指出,当前 LLM 的设计在预训练后,类似于缺乏有效的“在线巩固”阶段。信息虽然进入了“短期记忆”(如注意力机制的处理),但无法有效启动通往“长期记忆”(参数更新)的通路。尽管“离线巩固”同样至关重要,但本研究的重点是模拟“在线”的记忆巩固过程。
1.2 大脑的多时间尺度更新
除了记忆巩固,大脑的另一个特征是其多时间尺度的信息处理方式。大脑的活动通过不同频率的脑电波(brain waves)来协调,例如:
-
Delta Waves (0.5 - 4 Hz): 慢波睡眠。 -
Theta Waves (4 - 8 Hz): 记忆形成与导航。 -
Alpha Waves (8 - 12 Hz): 放松、静息状态。 -
Beta Waves (12 - 30 Hz): 专注、主动思考。 -
Gamma Waves (30 - 100 Hz): 高级认知功能。

重要的是,大脑并不依赖一个单一的、中心化的时钟来同步所有神经元。不同的神经回路以不同的频率更新其活动。例如,早期感觉皮层的神经元可能以高频率快速更新,而更高级的联合皮层则以较慢的频率整合更长时间跨度的信息。
这种“多时间尺度更新”机制为设计新的人工神经网络提供了直接的灵感。嵌套学习范式正是试图将这种按频率分层的思想,形式化地引入到模型设计中。
2. 嵌套学习(NL)范式
嵌套学习(Nested Learning, NL)提出,一个机器学习模型可以被看作是一系列相互嵌套、多层次或并行的优化问题。每个问题(或称为“层级”)都有其自身的“上下文流”(context flow)和更新频率。为了建立这个框架,论文首先引入了一个统一的视角来描述学习过程的各个组件:缔合记忆(Associative Memory)。
2.1 缔合记忆
在神经科学中,缔合记忆是指形成和提取事件之间联系的能力。论文将其形式化为一个数学算子。
定义 1 (缔合记忆)
给定一个键集合 和一个值集合 ,缔合记忆是一个算子 。为了从数据中学习这个映射,一个目标函数 用来衡量映射的质量,算子 可以通过以下优化问题来确定:
这个定义非常宽泛,但它提供了一个统一的语言。在这里,“键”和“值”可以是任意的事件或数据,例如词元(tokens)、梯度(gradients)、子序列等。寻找最优算子 的过程就是“学习”,而算子 本身及其映射行为则是“记忆”或“记忆化”。这个过程也可以被看作是一种数据压缩,即将高维的键值对映射关系压缩到算子 的参数中。
接下来,我们将通过几个例子来展示这个框架如何应用于解构现有的深度学习方法。
2.2 案例分析 1:MLP 训练过程的分解
我们从一个最简单的例子开始:训练一个单层 MLP。
情况 A:标准梯度下降
假设我们用梯度下降法来优化一个单层 MLP 的权重 ,目标函数为 ,数据集为 。更新规则为:
其中 是模型输出。链式法则告诉我们 。
论文指出,这个更新过程可以被重新表述为寻找一个最优缔合记忆的过程。令 ,这个 可以被解释为一个“局部意外信号”(Local Surprise Signal, LSS),它量化了当前模型输出与目标函数所期望的结构之间的不匹配程度。
于是,梯度下降的单步更新等价于求解以下优化问题:
在这个视角下,训练过程就是一个学习缔合记忆 的过程,这个记忆系统学习将输入数据点 映射到它们对应的 LSS 。这是一个单层级(1-level)的学习系统。
情况 B:带动量的梯度下降
现在,我们将优化器换成带动量的梯度下降。更新规则变为:
(为简化,这里使用加法形式的动量,与论文中的减法形式略有不同,但思想一致)。
我们可以将动量项 的更新看作一个独立的优化问题。令 ,则 的更新可以写成:
(这里假设学习率为 )。
这个表述揭示了一个重要的结构:带动量的梯度下降是一个双层级(2-level)的缔合记忆系统:
-
内层(Inner Level):动量项 本身是一个无键(key-less)的缔合记忆。它通过优化上述目标函数,将历史梯度 压缩到其参数 中。这是一个快速更新的记忆。 -
外层(Outer Level):权重 是慢速更新的记忆。它利用内层记忆 的输出来进行更新。
这个简单的例子展示了嵌套学习的核心思想:将优化器本身也看作是一个学习模块,它有自己的目标函数和记忆状态。这种分解与快速权重编程(Fast Weight Programmers, FWPs)的思想有关,其中慢速网络()的权重更新由一个快速网络()生成。
2.3 案例分析 2:模型架构的分解
嵌套学习不仅可以分解优化器,还可以分解模型架构本身。以线性注意力(Linear Attention)为例,其状态更新可以写成:
这里的 是一个矩阵,可以看作是模型的记忆状态。正如早期的研究所指出的,状态更新规则 可以被看作是求解一个缔合记忆优化问题的单步梯度下降。具体来说,如果定义目标函数 ,并使用学习率为 1 的梯度下降来优化 ,我们得到:
这与线性注意力的状态更新规则完全相同。
因此,一个使用梯度下降训练的线性注意力模型,同样可以被看作一个双层级的优化过程:
-
内层(Inner Level):注意力记忆 的更新。这是一个快速过程,在每个时间步都发生,旨在将当前的键值对 压缩进记忆状态 。 -
外层(Outer Level):投影矩阵 的训练。这是一个慢速过程,旨在学习如何从输入 中提取有效的键、值和查询。
在这个分解中,内层优化 时,外层的 参数是固定的;反之,外层更新 时,不会有梯度反向传播到内层的 的更新过程中。它们是两个拥有独立梯度流的嵌套优化问题。
2.4 定义层级:更新频率
上述例子展示了如何将模型分解为多个优化问题,但如何为这些问题定义一个清晰的层次结构呢?论文引入了“更新频率”作为排序的标准。
定义 2 (更新频率)
对于模型的任意组件 (可以是一个参数,如权重;或一个非参数模块,如注意力),我们将其更新频率 定义为单位时间内的更新次数(单位时间可以定义为处理一个数据点)。
基于更新频率,我们可以对组件进行排序。我们称组件 比 快(记为 ),如果:
-
,或者 -
,但在计算 时刻的 的状态时,需要先计算 时刻的 的状态(即存在计算依赖)。
通过这个定义,一个机器学习模型可以被唯一地表示为一个有序的层级集合。层级越高,其组件的更新频率越低。每个组件都有其自身的优化问题和上下文流。
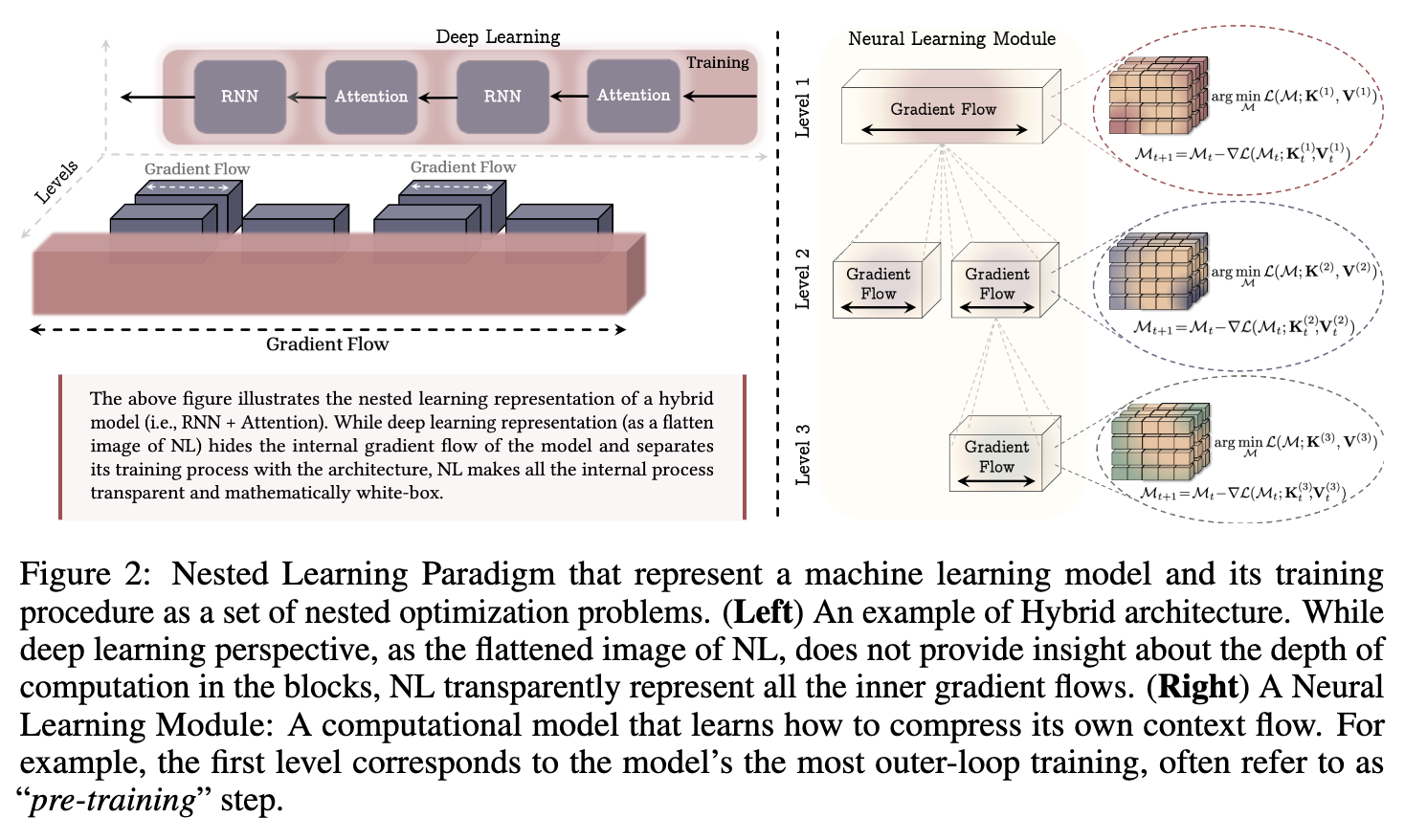
上图直观地展示了嵌套学习视角与传统深度学习视角的区别。传统视角是“扁平化”的,它隐藏了模型内部不同组件的梯度流和更新动态,并将训练过程与架构分离开。而嵌套学习则将所有内部过程透明化,将模型和训练统一为一个由嵌套优化问题组成的、数学上“白盒”的系统。
3. 将优化器重塑为学习模块
嵌套学习范式最有启发性的应用之一,是它为优化器提供了全新的视角。优化器不再是外部的、用于调整参数的工具,而是模型内部的一个可学习的、动态的记忆模块。
我们已经看到,带动量的梯度下降是一个双层级的嵌套学习系统。这个系统中的动量项是一个线性的、无键的缔合记忆,用于压缩历史梯度。这个视角揭示了其局限性,并为设计更具表达能力的优化器提供了思路。
3.1 扩展 1:更具表达力的缔合
标准动量项将所有梯度信息压缩到一个单一的值中。为了提升表达力,我们可以引入一个“值”参数 ,让动量项学习从梯度到某个目标值的映射。这对应于对梯度进行预处理(preconditioning)。更新规则变为:
这等价于动量项在学习一个缔合记忆,该记忆旨在压缩梯度项 和值 之间的映射关系。这为我们理解为什么像 Adam 这样的自适应优化器有效提供了新的解释:其二阶动量项(v)可以被看作是学习梯度的某种函数(例如,与Hessian矩阵相关的信息),为记忆提供了更有意义的映射目标。
3.2 扩展 2:更具表达力的目标函数
标准动量更新源于一个基于点积相似度的内部目标函数。这会导致类似 Hebbian 的学习规则,可能会使记忆效率不高。一个自然的扩展是使用 回归损失作为内部目标:
最小化这个损失函数会得到基于 Delta 法则的更新规则:
这种更新规则允许记忆模块更好地管理其有限的容量,从而更有效地记忆过去的梯度序列。
3.3 扩展 3:更具表达力的记忆模块
动量项本质上是一个线性的记忆模块(一个矩阵)。为了增强其学习能力,我们可以用一个更强大的模型来替换它,例如一个多层感知机(MLP)。这样,动量项本身就变成了一个小型神经网络,拥有更强的能力来捕捉梯度序列的复杂动态。这催生了论文中提出的深度动量梯度下降(Deep Momentum Gradient Descent, DMGD)。
3.4 扩展 4:非线性输出
另一个增强表达力的方法是在动量模块的输出上应用非线性函数 。
例如,如果 是 Newton-Schulz 迭代(一种计算矩阵逆的方法),并且记忆模块 是线性的,那么得到的优化器就等价于 Muon 优化器。
通过这一系列扩展,嵌套学习将优化器的设计从启发式规则的调整,转变为对一个内部学习模块(缔合记忆)的结构、目标和能力的设计。
4. HOPE
基于嵌套学习的理论框架,论文提出了一个名为 HOPE (Self-referential learning module with COntinuum MEmory) 的新学习架构。HOPE 的设计旨在将多时间尺度更新的思想直接付诸实践。
4.1 连续谱记忆系统(Continuum Memory System, CMS)
传统观点通常将记忆二分为“长期记忆”和“短期记忆”。HOPE 对此进行了扩展,提出了一个“连续谱”的记忆系统。该系统不再是二元的,而是一个由多个不同更新频率的记忆组件构成的层次结构。
形式上,CMS 是一系列 MLP 模块的链条:。每个模块 都与一个块大小(chunk size) 相关联,其参数 每隔 个时间步才更新一次。
其中 是某个优化器(如梯度下降)的误差项。
这个设计意味着:
-
高频模块( 较小)负责处理和压缩短期的、局部的上下文信息。 -
低频模块( 较大)负责整合和存储长期的、抽象的知识。
论文指出,传统的 Transformer 模块可以看作是 CMS 的一个特例()。其中的前馈网络(FFN)层扮演了低频记忆的角色,它在预训练阶段被更新,而在推理阶段保持不变(更新频率接近于 0)。而注意力层则可以看作是高频组件,但它是无状态的。
4.2 HOPE 架构
HOPE 架构将一个自引用序列模型(基于 Titans 模型)与 CMS 相结合。其核心思想是为模型的不同抽象层次配备不同频率的知识存储(FFN 层)。
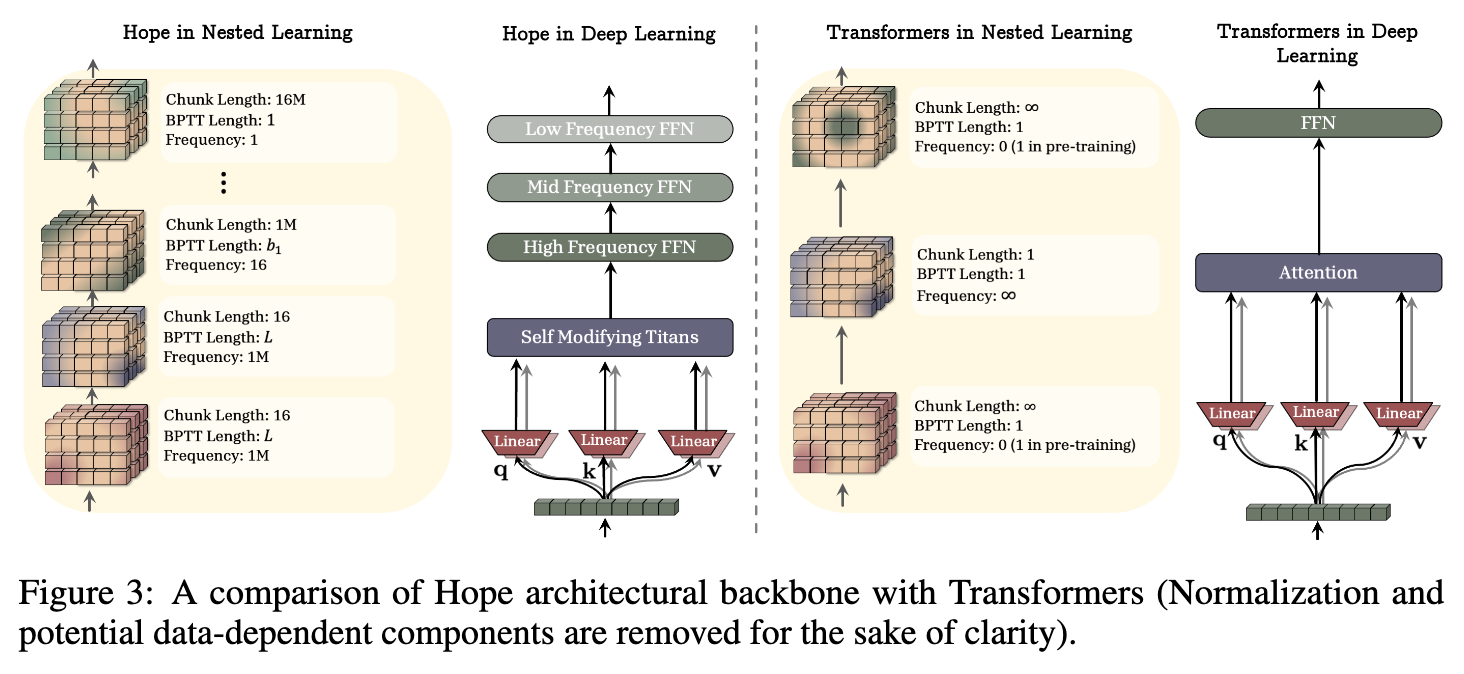
上图清晰地对比了 HOPE 和 Transformer 在嵌套学习视角下的结构差异:
-
Transformer (嵌套视角) :
-
高频层 (Attention) :更新频率理论上是无限的(每个 token 都在计算),但它是无状态的,不存储长期信息。 -
低频层 (FFN) :更新频率在推理时为 0,在预训练时为 1(相对于整个数据集)。它存储了模型的全部参数化知识。 -
这是一个典型的双层级系统,但两个层级的功能和更新速率差异巨大,中间存在巨大的空白。
-
-
HOPE (嵌套视角) :
-
多个频率的 FFN 层:架构中明确设计了低频、中频和高频的 FFN 层,分别对应不同的块大小和更新速率。 -
自修改的 Titans 模块:作为最高频的组件,负责处理 token 级别的动态。 -
HOPE 通过这种方式,构建了一个具有平滑过渡的、多层次的记忆系统,理论上更适合处理需要跨越不同时间尺度的依赖关系的任务,并为持续学习提供了可能。
-
5. 实验分析与讨论
为了验证 HOPE 架构的有效性,论文在一系列语言建模和常识推理任务上进行了评估,并与多种基线模型(包括 Transformer++、RetNet、DeltaNet 等)进行了比较。
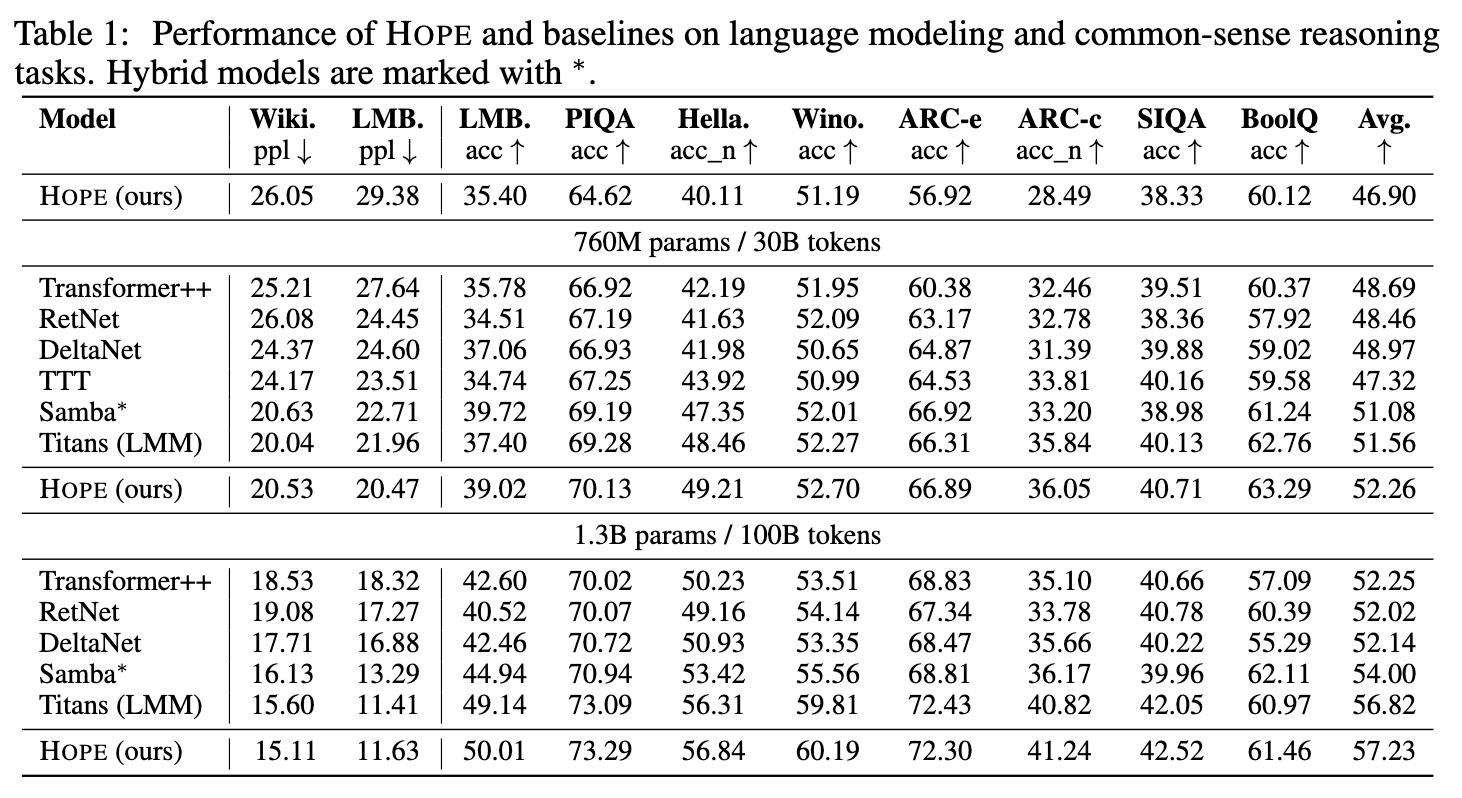
实验结果(如上表所示)显示,在 760M 和 1.3B 两种参数规模下,HOPE 在多个基准测试中均表现出有竞争力的性能。例如,在 1.3B 参数规模下,HOPE 在 WikiText-103 和 LAMBADA 数据集上的困惑度(ppl)低于多数基线模型,并在 PIQA、HellaSwag、WinoGrande 等常识推理任务的准确率上取得了较好的结果。
在各种常用且公开的语言建模和常识推理任务中,与现代循环模型和标准Transformer相比,Hope架构表现出更低的困惑度和更高的准确率。
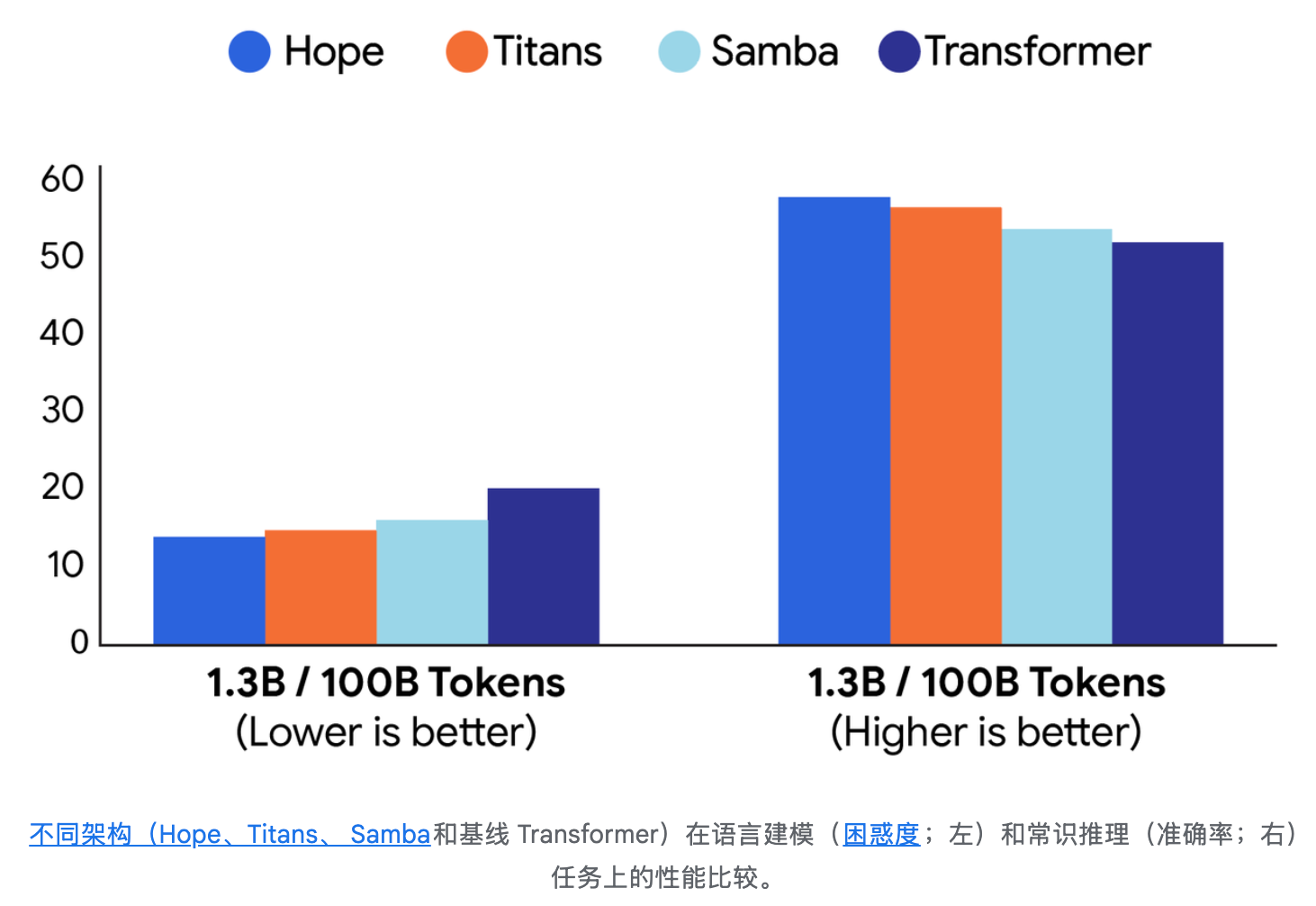
Hope 在长上下文大海捞针 (NIAH) 下游任务中展现出卓越的内存管理能力,证明 CMS 提供了一种更高效、更有效的方法来处理扩展的信息序列。
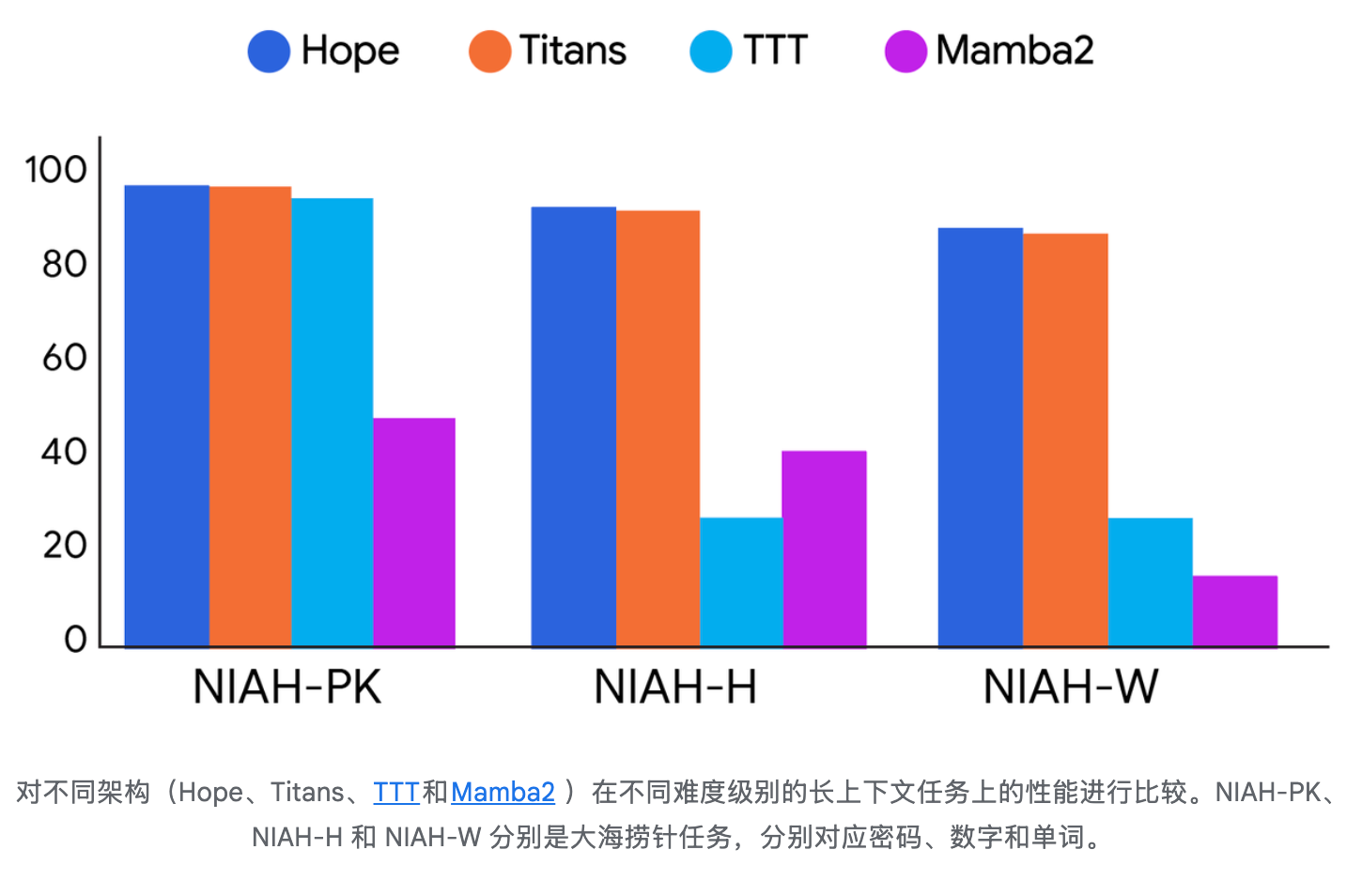
论文认为,这些结果表明,通过基于上下文动态地改变键、值、查询投影,并结合一个深度记忆模块,模型可以实现更低的困惑度和更高的下游任务准确率。
除了这些主要结果,论文的附录还报告了关于优化器、上下文学习的涌现、持续学习能力、消融研究和长上下文任务的更多实验。这些实验进一步支持了嵌套学习范式的设计原则。例如,多层次的记忆系统被认为有助于模型在持续学习场景中更好地保留旧知识、学习新知识。
讨论与启示
嵌套学习范式为我们理解和设计深度学习模型提供了几个重要的启示:
-
统一的视角:它打破了模型架构和优化器之间的壁垒,提供了一个统一的框架来分析整个学习系统。这使得我们可以将优化器的设计问题转化为一个模型设计问题。 -
超越“深度”:传统上,我们通过增加模型的层数(深度)来提升其表达能力。嵌套学习引入了一个新的维度——“层级”(levels)。通过增加嵌套的层级,即使模型的计算深度不变,我们也可以设计出表达能力更强的架构。 -
原则性的架构设计:更新频率为设计多时间尺度模型提供了一个清晰的、可操作的原则。HOPE 架构就是这一原则的直接产物。 -
对持续学习的潜在价值:通过为不同频率的组件分配独立的、可更新的记忆,模型可能更容易在不遗忘旧知识的情况下学习新知识。低频记忆负责稳定地存储核心知识,而高频记忆则负责适应新的、动态的信息。
6. 结论与展望
论文《Nested Learning: The Illusion of Deep Learning Architectures》并非提出了一种可以立即取代现有模型的具体技术,而是提供了一个审视深度学习的全新理论透镜。通过将模型重新解释为嵌套的优化问题,并以“更新频率”为核心来构建层次,嵌套学习范式为我们重新理解从优化器到 Transformer 架构的众多现有技术提供了深刻的洞见。
其核心贡献在于:
-
重新诠释优化器:将梯度下降与动量等优化器形式化为缔合记忆模块,并开辟了设计“深度优化器”的新方向。 -
连续谱记忆系统:超越了传统的长短期记忆二分法,为在模型中实现多时间尺度的信息处理和存储提供了新思路。 -
HOPE 架构:作为嵌套学习思想的实践,展示了基于该范式设计的模型在标准任务上的潜力。
当然,嵌套学习也留下了一些开放性问题。如何自动地确定最优的层级数量和各自的更新频率?“深度优化器”的理论性质和收敛性如何保证?以及,如何将大脑记忆巩固的“离线”阶段(如睡眠中的重放)也整合到这个框架中?这些问题都为未来的研究指明了方向。总而言之,嵌套学习为我们跳出“堆叠层数”的思维定式,从更根本的计算结构和动态过程出发,探索下一代学习机器,提供了一个有价值的参考框架。
往期文章:




