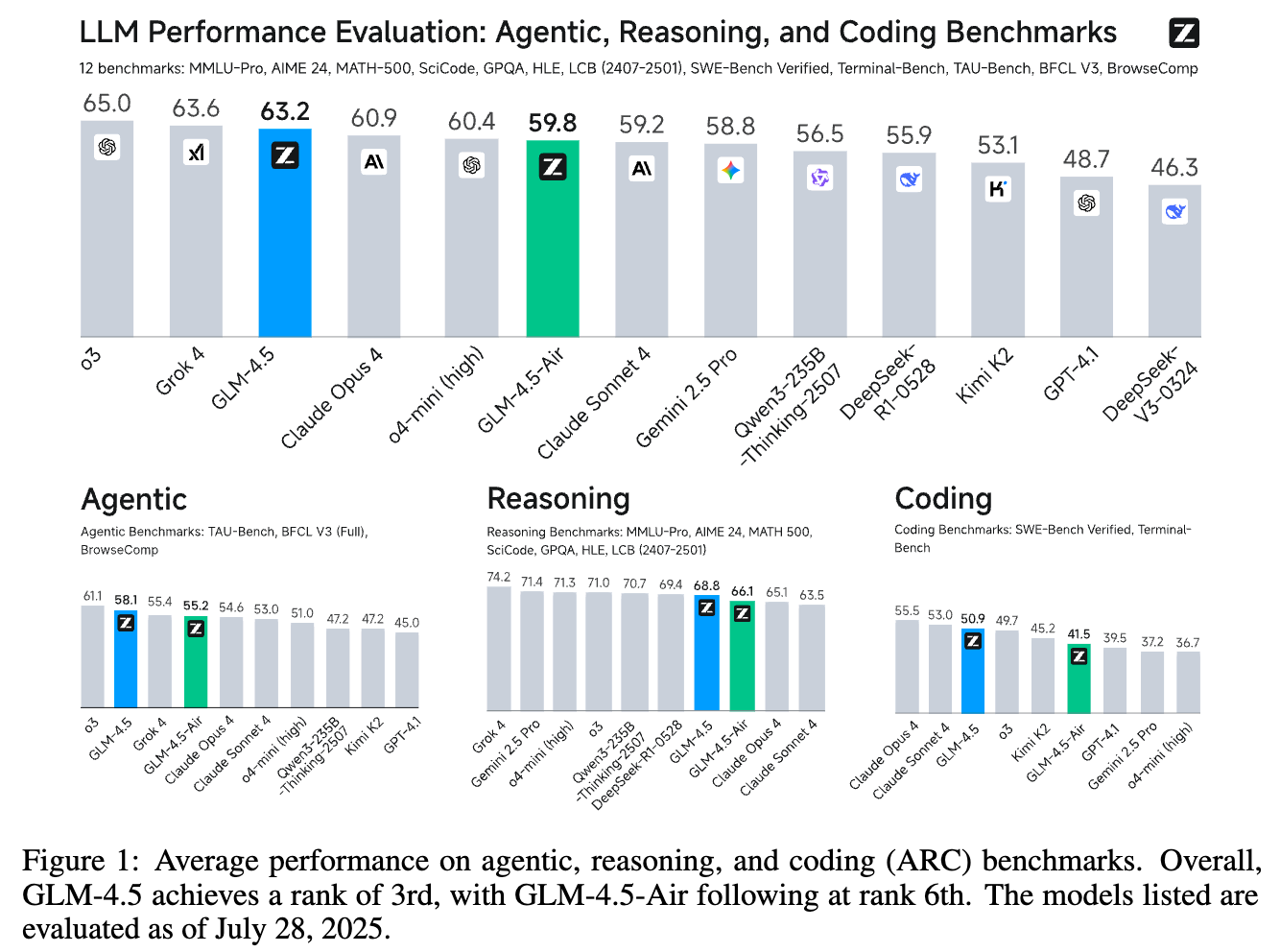
稀疏激活的混合专家模型(Mixture-of-Experts, MoE)已成为推动大型语言模型(LLM)能力边界的关键架构。然而,其庞大的参数量给实际部署带来了巨大挑战。近期,一篇来自清华大学和美团的研究论文《Unveiling Super Experts in Mixture-of-Experts Large Language Models》首次揭示了 MoE 模型中存在一类被称为“超级专家”(Super Experts, SEs)的特殊专家子集。这些数量极少但作用至关重要的专家,为我们理解 MoE 的工作机制、优化模型压缩策略提供了全新的视角。

-
论文标题:Unveiling Super Experts in Mixture-of-Experts Large Language Models -
论文链接:https://arxiv.org/pdf/2507.23279
1. 引言:MoE 模型的崛起与困境
1.1 什么是 MoE 模型?
近年来,大型语言模型(LLMs)的发展日新月异,其强大的能力正在深刻地改变着世界。然而,随着模型能力的提升,其参数量也呈指数级增长,这给模型的训练和推理带来了巨大的计算压力。为了在提升模型性能的同时有效控制计算成本,研究者们提出了一种名为混合专家模型(Mixture-of-Experts, MoE)的创新架构。
你可以将一个传统的(或称为“密集”的)LLM 想象成一个知识渊博但什么都懂一点的“通才”。无论你问他什么问题,他都需要调动他全部的知识储备来思考和回答。而 MoE 模型则不同,它像一个由多位“专家”组成的团队。 团队里有一位“调度员”(Router,路由网络)和多位各有所长的“专家”(Experts,通常是前馈神经网络 FFN)。 当一个问题(输入数据)到来时,“调度员”会迅速判断这个问题属于哪个领域,然后只激活(调用)一两位最相关的专家来协同解决问题。
这种稀疏激活(Sparse Activation) 的机制是 MoE 的核心优势。 它意味着,尽管 MoE 模型的总参数量(所有专家的参数总和)可能非常庞大,但在处理任何单个输入时,实际参与计算的参数量(被激活的专家的参数)却相对较小。这就好像一个拥有一万亿参数的 MoE 模型,其计算成本可能只相当于一个一千亿参数的密集模型。这种“用更少的计算撬动更大的模型容量”的特性,使得 MoE 架构在近年来大放异彩,催生了像 Google 的 Switch Transformer、Mistral AI 的 Mixtral 系列以及国内的 DeepSeek、Qwen 等一系列顶尖的开源和闭源模型。
1.2 参数爆炸:MoE 模型的“甜蜜的烦恼”
MoE 架构虽然巧妙地通过稀疏激活降低了计算成本,但它并没有减少模型的存储成本。模型的全部参数,包括所有专家(无论是否被激活)的参数,都需要被完整地加载到内存(通常是 GPU 显存)中才能运行。以拥有 8 个专家的 Mixtral-8x7B 模型为例,虽然每次推理只激活 2 个专家(约 13B 参数),但其总参数量高达 47B,需要消耗大量的显存。
这种巨大的参数量为 MoE 模型的实际部署带来了严峻挑战。 高昂的硬件成本、巨大的能源消耗,都限制了这些强大模型在更广泛场景下的应用,尤其是在手机、笔记本电脑等资源受限的边缘设备上。
1.3 模型压缩:为 MoE 模型“瘦身”的迫切需求
为了解决 MoE 模型部署的难题,模型压缩技术应运而生。就像为文件打包以节省硬盘空间一样,模型压缩旨在通过各种技术手段,在尽可能不损失模型性能的前提下,减小模型的尺寸和计算量。常见的压缩技术包括:
-
量化(Quantization):降低用于表示模型参数的数值精度(例如,从 32 位浮点数降到 8 位整数)。 -
知识蒸馏(Knowledge Distillation):用一个大的“教师模型”来训练一个小的“学生模型”,让学生模型学习教师模型的“知识精华”。 -
剪枝(Pruning):移除模型中被认为是“不重要”的参数或结构(如神经元、注意力头、甚至整个网络层)。
针对 MoE 模型的独特结构,研究者们也开发了专家级别的压缩方法。这些方法的核心思想是:并非所有专家都同等重要,我们可以通过识别并压缩那些“次要”的专家来为模型“瘦身”。例如,可以合并(merge)一些功能相似的专家,或者直接剪枝(prune)/跳过(skip)那些访问频率较低的专家。
然而,现有的专家压缩方法大多依赖于一些经验性的标准,比如专家的访问频率、激活值的统计特性等,来判断其重要性。这些方法虽然在一定程度上有效,但它们缺乏对专家异质性(即不同专家扮演着不同角色)的深入理解。一个根本性的问题一直悬而未决:
在 MoE LLM 中,是否存在一个独特的、对模型功能起着决定性作用的专家子集?它们的工作机制是什么?
这正是本文要深度解读的这篇研究的核心问题。来自清华大学和美团的研究团队通过深入的实证分析,给出了一个响亮的回答:是的,存在这样一群专家,他们称之为——超级专家(Super Experts, SEs)。
2. 风暴之眼:探寻“巨量激活”的根源
要理解“超级专家”的发现过程,我们必须先从一个在 LLM 中普遍存在的奇特现象说起——巨量激活(Massive Activations)。
2.1 神秘的“巨量激活”现象
在 2024 年初,一篇名为《Massive Activations in Large Language Models》的论文揭示,在各种 LLM 的内部,存在着一种非常特殊的激活值。 在模型进行前向推理的过程中,流经各层神经网络的数值被称为“激活值”。而“巨量激活”指的是,在模型的隐藏状态(可以理解为各层之间的信息流)中,有极少数(通常不到 0.1%)的激活值,其数值大小会比其他绝大多数激活值大上成千上万倍,甚至十万倍。
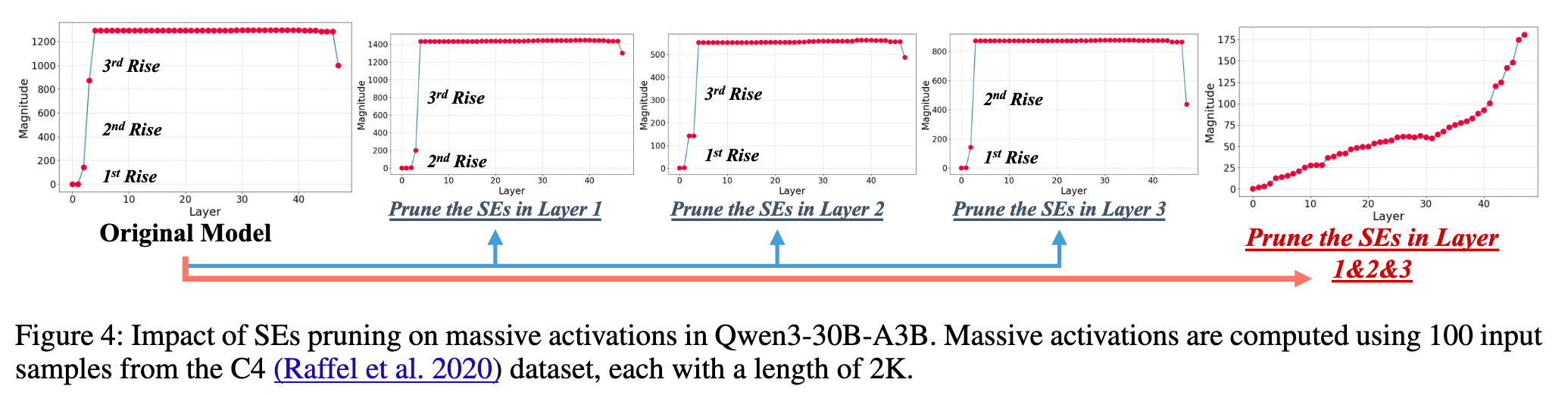
上图直观地展示了这一现象。可以看到,在模型的不同层(横轴)中,隐藏状态的最大激活值(纵轴)中存在一些远超正常范围的“尖峰”,这些就是“巨量激活”。
进一步的研究发现,这些“巨量激活”并非随机出现,而是具有以下几个有趣的特性:
-
普遍存在:在各种主流 LLM 中都能观察到。 -
位置固定:它们通常出现在特定的神经元维度上。 -
输入不敏感:它们的值基本不随输入文本的变化而改变,表现得像一个固定的偏置项(bias)。 -
至关重要:如果人为地移除这些“巨量激活”,模型的性能会急剧下降。
这些发现表明,“巨量激活”并非无意义的噪声或异常值,而是模型内部一种深刻且重要的机制。
2.2 MoE 模型中的“巨量激活”:是集体智慧还是个体英雄?
既然“巨量激活”在普通 LLM 中普遍存在,那么在结构更复杂的 MoE LLM 中,情况又会如何呢?这篇论文的研究者们首先验证了,是的,“巨量激活”现象同样存在于所有他们研究的 MoE LLM 中。
这立刻引出了一个更深层次的问题:在 MoE 模型中,“巨量激活”是如何形成的?
-
是所有被激活的专家共同作用的结果? -
还是仅仅由少数几个特定的专家所主导? -
或者,它可能与专家无关,而是由模型的其他部分(如注意力模块)产生的?
为了回答这个问题,研究者们对多个主流的开源 MoE 模型(如 Qwen 系列、DeepSeek 系列、Mixtral)进行了深入的“解剖”。他们追踪了模型内部的激活信号流动路径,试图找到“巨量激活”的源头。
3. “超级专家”横空出世:发现与定义
3.1 惊人发现:少数专家主导“巨量激活”
通过对模型内部的细致观察,研究者们有了一个惊人的发现:“巨量激活”的形成,并非所有专家的“集体智慧”,而是由一个极小的专家子集所主导。
这些特殊的专家,在它们的输出(具体来说是 FFN 结构中 down_proj 层的输出)中,会产生一些罕见但数值极其巨大的激活异常值。这些异常值虽然数量稀少,但其“能量”巨大。当它们通过残差连接(residual summation)被加到模型的隐藏状态中时,就形成了我们之前观察到的“巨量激活”现象。
这个过程就像在一个平静的湖水中投入一颗深水炸弹,虽然炸弹本身很小,但它能激起滔天巨浪。
3.2 什么是“超级专家”(Super Experts, SEs)?
基于这一发现,研究者们正式定义了这类特殊的专家,并将其命名为“超级专家”(Super Experts, SEs)。
超级专家(Super Experts, SEs):在 MoE LLM 中,一个独特的、数量极少的专家子集。它们的特征是在其
down_proj层的输出中产生罕见但极端的激活异常值,这些异常值通过残差连接注入到解码器层之间的隐藏状态中,从而诱导并形成了“巨量激活”现象。
简而言之,超级专家是“巨量激活”的直接缔造者。
3.3 “超级专家”的工作机制:逐层放大的激活信号
研究者们以 Qwen3-30B-A3B 模型为例,清晰地展示了“超级专家”的工作机制。
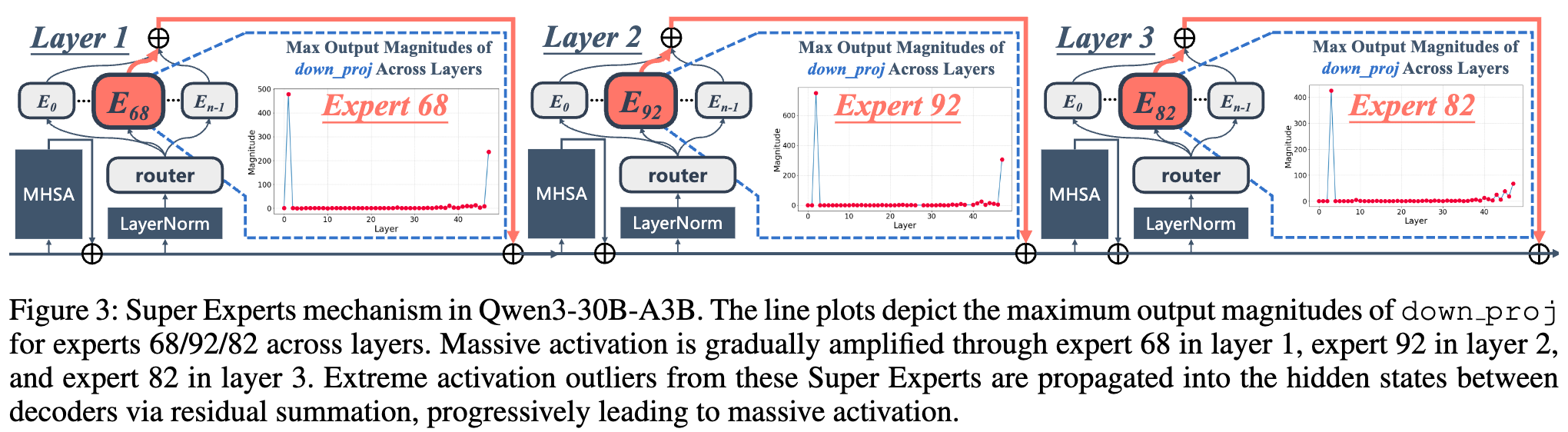
如上图所示,这个模型中有三个“超级专家”,分别位于第 1、2、3 层(Expert 68 in Layer 1, Expert 92 in Layer 2, Expert 82 in Layer 3)。
-
在第 1 层,超级专家 68 产生了第一个显著的激活异常值。 -
这个异常值被注入到隐藏状态中,并传递给下一层。 -
在第 2 层,超级专家 92 在接收到这个已经“被污染”的隐藏状态后,进一步将其放大,产生了更强的激活异常值。 -
这个过程在第 3 层的超级专家 82 这里再次被放大。
通过这种逐层接力放大的机制,一个微弱的初始异常信号被逐步放大,最终形成了稳定且贯穿整个模型的“巨量激活”现象。这种放大效应通常发生在模型较浅的几个层级,一旦形成,后续的层级便会维持这种状态。
4. 按图索骥:如何定位“超级专家”?
发现了“超级专家”的存在和机制后,下一个关键问题就是:如何在一个新的 MoE 模型中,快速、准确地找到它们?
4.1 提出“超级专家”的量化定义与自动化分析工具
为了实现对“超级专家”的系统性识别,研究者们提出了一个简洁而有效的量化定义。其核心思想是,“超级专家”产生的激活值,不仅在所有专家的所有激活值中是顶尖的(全局异常),而且在它自己所属的专家内部,也是顶尖的(局部异常)。
具体来说,他们计算了模型中每个专家在所有层级中 down_proj 输出的最大值。然后,一个位于 l 层、编号为 e 的专家被定义为“超级专家”,需要满足以下两个条件:
-
全局显著性:其最大激活值 必须大于整个模型所有专家激活值集合 A的 99.5 百分位数,即 。 -
局部主导性:其最大激活值 必须是整个模型最大激活值 的一个显著部分(例如,大于十分之一),即 。
这个定义可以用一个公式来表示:
基于这个清晰的定义,研究团队开发了一个自动化的分析工具,可以快速、精准地在任何新的 MoE 模型中识别出“超级专家”。这个工具也已经开源,为社区的研究提供了极大的便利。

上表展示了使用该工具在不同模型中识别出的“超级专家”的激活值。可以看到,被标记为粗体的“超级专家”激活值,远大于其他普通专家的激活值。
4.2 “超级专家”在不同模型中的分布
利用这个自动化工具,研究者们分析了多个主流 MoE 模型的“超级专家”分布情况,包括 Qwen3-30B-A3B、DeepSeek-V2-Lite-Chat 和 Mixtral-8x7B-Instruct-v0.1。
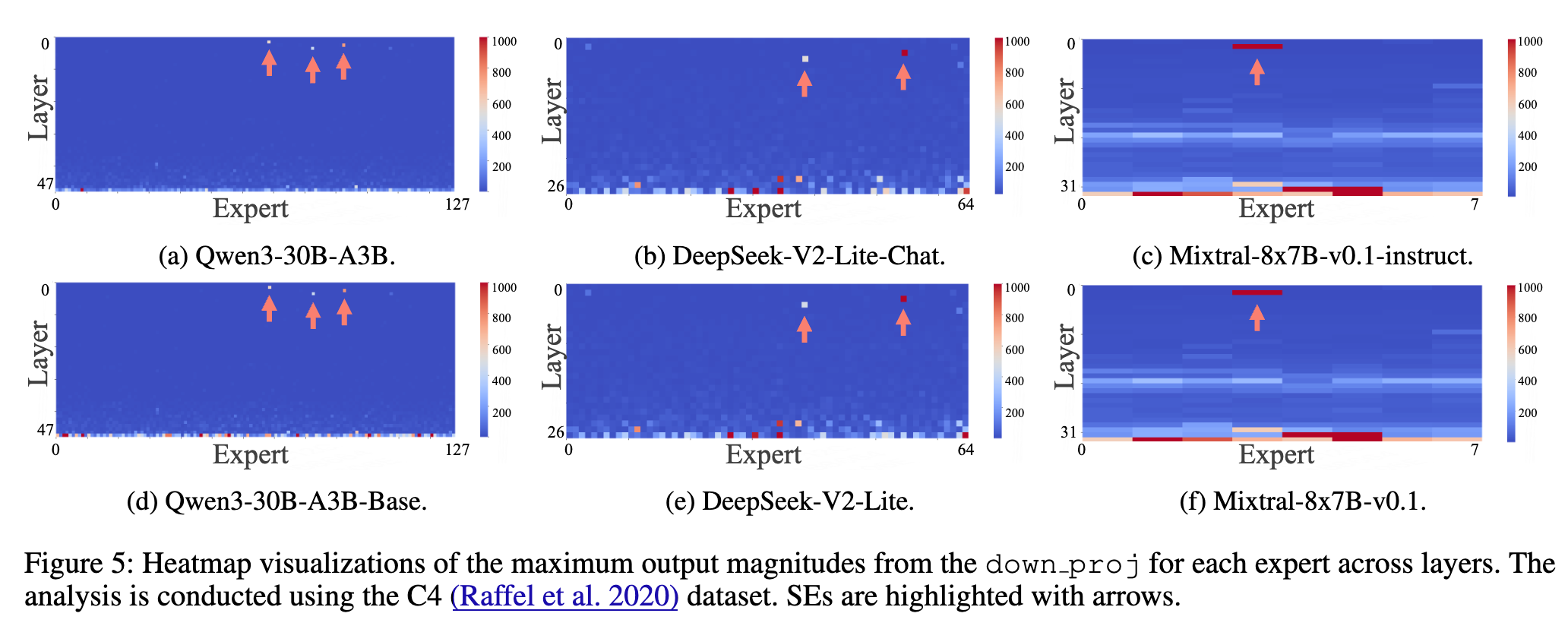
上图(Figure 5)和上表(Table 2)清晰地展示了这些模型中“超级专家”的位置。研究得出了几个关键结论:
-
普遍存在且数量稀少:在所有被研究的模型中都发现了“超级专家”,并且它们的数量占比极低,通常远小于 0.5%。例如,在 Qwen3-30B-A3B 模型中,总共 6144 个专家里只有 3 个是“超级专家”。 在 Mixtral-8x7B-Instruct-v0.1 中,256 个专家里只有 1 个。 -
分布模式各异:不同模型的设计架构不同,“超级专家”的分布模式也不同。在 Qwen 和 DeepSeek 模型中,“超级专家”分布在较浅的几个层。而在 Mixtral 模型中,它们则集中在单一层。
4.3 惊人的稳定性:“超级专家”不受后训练和数据领域变化的影响
为了进一步探究“超级专家”的特性,研究者们还进行了两项重要的稳定性分析:
-
后训练过程的影响:他们比较了模型的基础版本(Base Model)和经过指令微调等后训练过程的版本(如 Chat Model)。结果发现,“超级专家”的分布在后训练前后完全一致。这意味着,“超级专家”的形成和其功能角色是在模型的预训练阶段就已经确立的,并且在后续的微调中保持稳定。
-
输入数据领域的影响:他们使用了来自不同领域的多个数据集(如通用文本 C4、WikiText-2,代码 HumanEval,数学 GSM8K 等)来测试“超级专家”的分布。结果同样惊人:无论输入数据的领域如何变化,“超级专家”的分布都保持高度稳定。
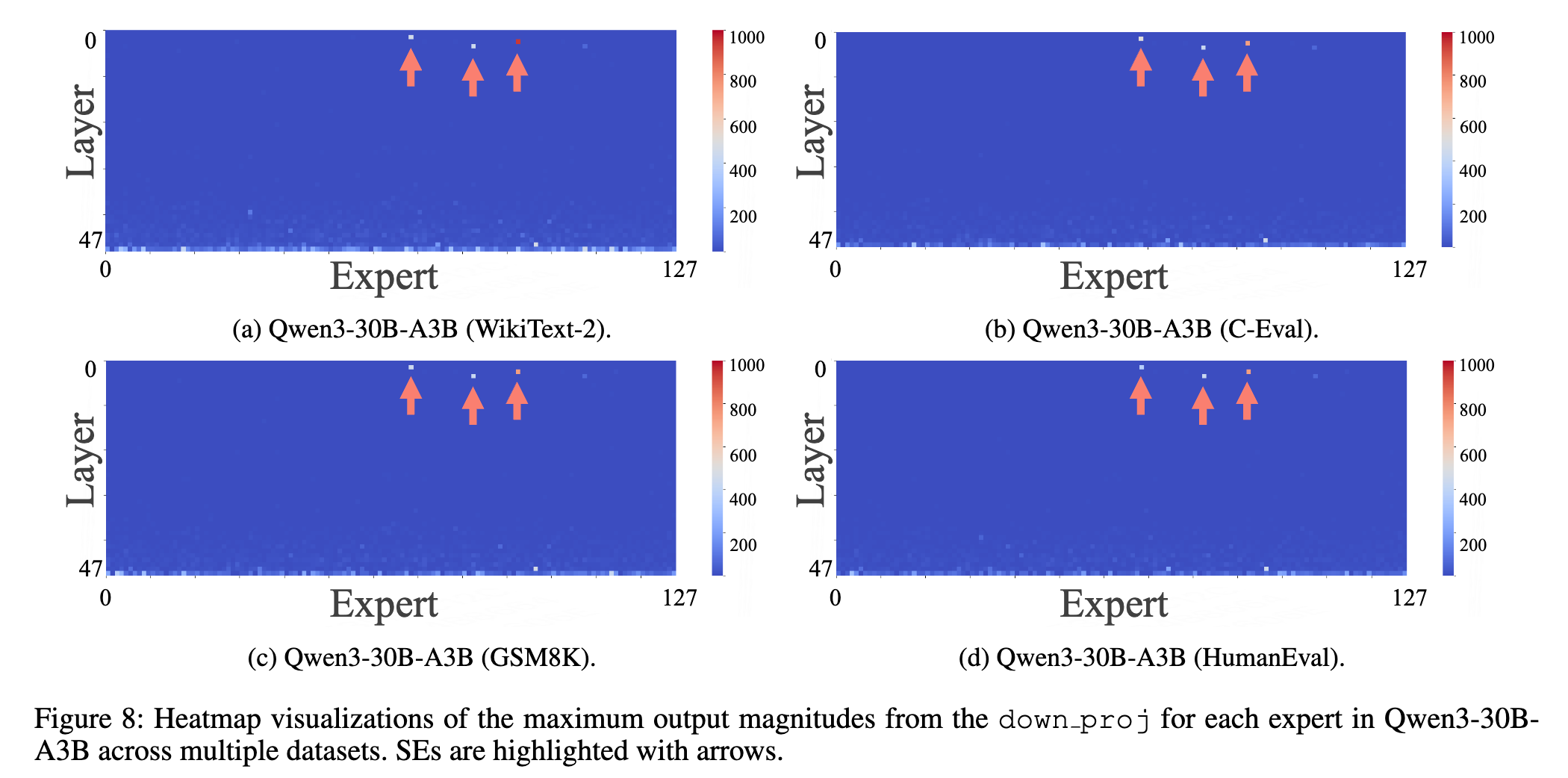
这两项发现有力地证明了,“超级专家”是模型固有的一种结构性特征,而非偶然或依赖于特定条件。它们是模型预训练过程中学到的、一种深刻且稳固的内在机制。
5. “超级专家”的重要性:不可或缺的基石
既然我们已经能够精准地定位“超级专家”,那么接下来的问题自然就是:它们到底有多重要? 如果我们把它们从模型中移除,会发生什么?
5.1 剪枝实验:验证“超级专家”的关键作用
为了回答这个问题,研究者们进行了一系列简单而直接的剪枝实验。他们设计了三组对比实验:
-
原始模型(Baseline):未经任何修改的模型。 -
剪枝超级专家(Prune SEs):只剪掉被识别出的那几个“超级专家”。 -
随机剪枝(Random Pruning):随机剪掉同等数量的其他普通专家,作为对照组。
他们通过一系列基准测试来评估模型在剪枝前后的性能变化。
5.2 对通用(非推理)能力的毁灭性打击
首先,在衡量通用能力的非推理任务上(如 MMLU、HellaSwag、OpenBookQA 等),结果非常震撼。
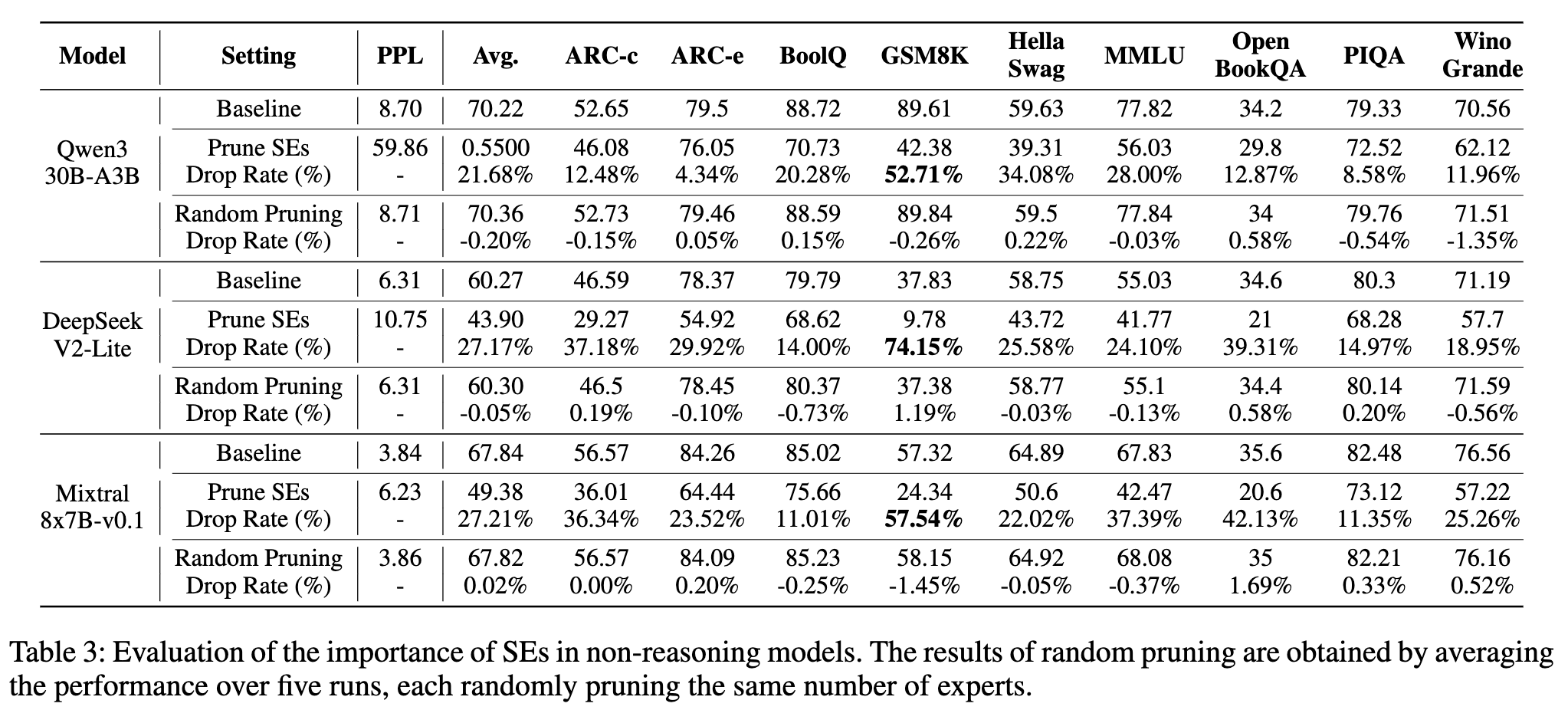
从上表可以看出:
-
剪枝“超级专家”导致性能雪崩:在 Qwen3、DeepSeek V2 Lite 和 Mixtral 三个模型上,仅仅剪掉数量极少的“超级专家”(Qwen3 只剪了 3 个),就导致了模型在所有任务上的性能大幅度下降。平均准确率下降幅度在 21.68% 到 27.21% 之间。尤其是在 GSM8K(小学数学应用题)这类需要一定推理能力的任务上,性能下降尤为惨烈,最高达到了 74.15% 的降幅! -
随机剪枝几乎无影响:与之形成鲜明对比的是,随机剪掉同等数量的普通专家,对模型的性能影响微乎其微,几乎可以忽略不计。
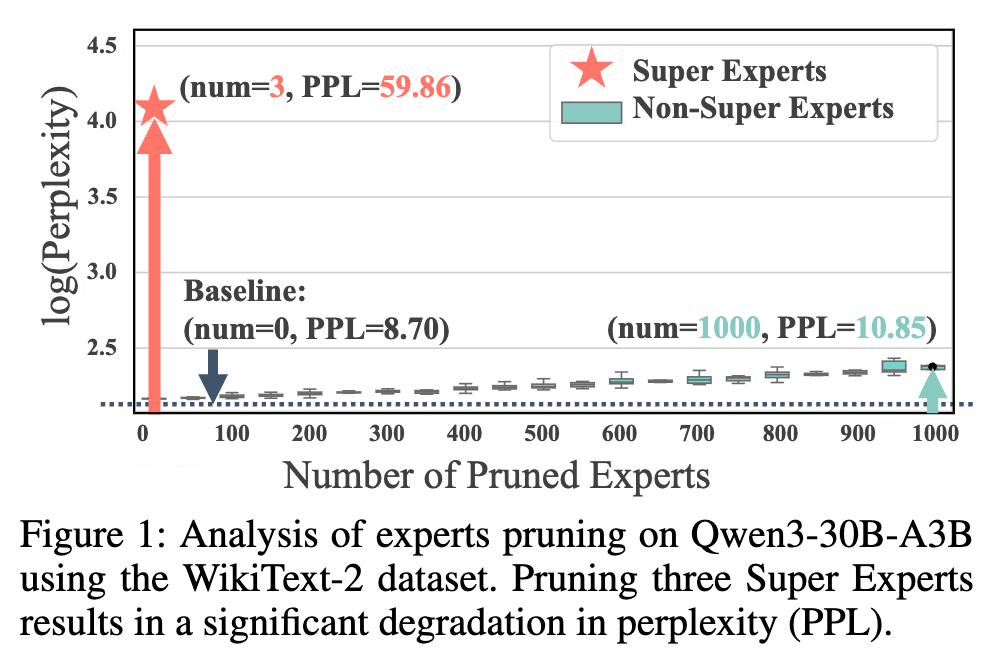
原论文开篇的这张图(Figure 1)极具说服力。它展示了在 WikiText-2 数据集上,模型的困惑度(Perplexity, PPL,一个衡量语言模型性能的指标,越低越好)随剪枝专家数量的变化。蓝线(Baseline)是原始模型的 PPL(8.70)。红线(Super Experts)显示,仅仅剪掉 3 个“超级专家”,PPL 就飙升到 59.86,模型几乎完全失效。而绿线(Non-Super Experts)显示,即使随机剪掉 1000 个普通专家,PPL 也只是轻微上升到 10.85。
这一结果无可辩驳地证明了“超级专家”的极端重要性。它们并非可有可无,而是模型能力的关键支柱。
5.3 对推理能力的“致命一击”:模型“失智”现象
如果说在通用任务上的表现已经足够惊人,那么在对逻辑、数学和代码等高级推理能力要求更高的任务上,“超级专家”的重要性则被体现得淋漓尽致。
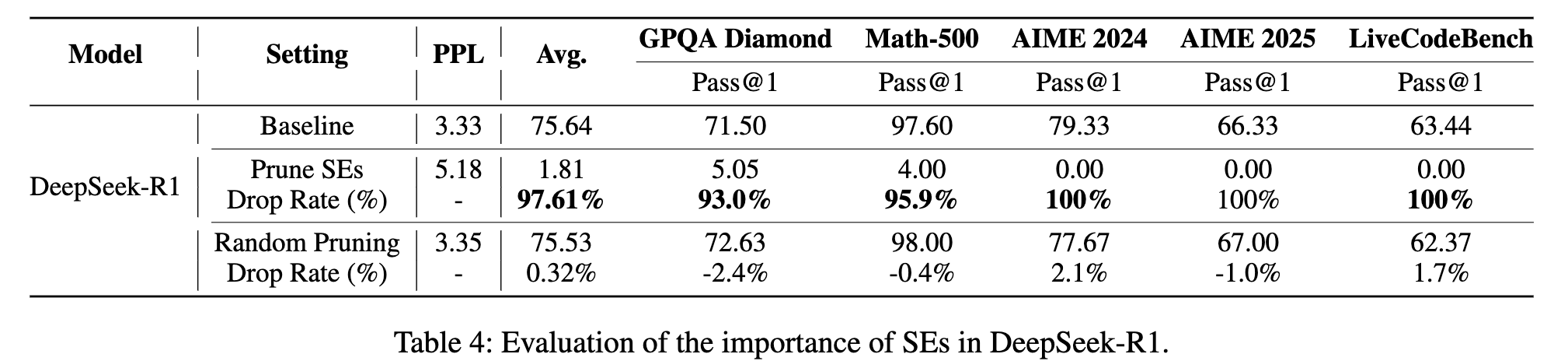
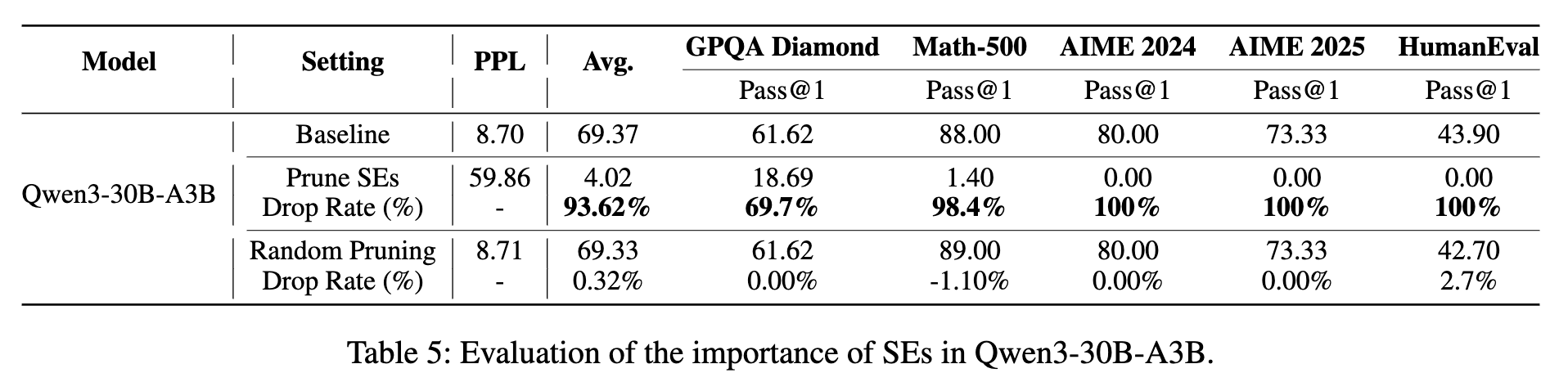
研究者们在 DeepSeek-R1 和 Qwen3-30B-A3B 的推理版本上进行了测试,结果如上两表所示。
-
推理能力完全丧失:剪掉“超级专家”后,模型在多个高难度数学推理和代码生成任务(如 AIME、LiveCodeBench)上的 Pass@1 分数直接降为零!这意味着模型完全丧失了解决这些问题的能力。整体性能的下降率达到了惊人的 93% 至 97%。 -
模型输出变得“胡言乱语”:更令人震惊的是,在审查模型在 MATH-500(数学问题)基准上的具体输出时,研究者发现了一个“模型失智”现象。

如上表所示,原始模型能够正常理解问题并开始推理。而剪掉了“超级专家”的模型,在面对同一个问题时,开始生成大量无意义的、不断重复的词语("the way, it's, the way, it's..."),直到达到输出长度上限。这种行为表明,模型的基础推理能力已经完全崩溃。
这些实验结果强有力地表明,“超级专家”不仅对通用能力至关重要,更是模型进行复杂推理的命脉。失去了它们,MoE 模型就如同失去了大脑,变成了一个只会胡言乱语的“空壳”。
6. 深层机制:“超级专家”与“注意力池”的隐秘关联
至此,我们已经知道了“超级专家”是什么,在哪里,以及有多重要。但还有一个更深层次的问题:它们究竟是通过什么机制来发挥如此关键作用的? 仅仅是产生“巨量激活”吗?“巨量激活”本身又有什么用?
这篇论文的另一大贡献,就是将“超级专家”与 LLM 中另一个重要但一直有些神秘的概念——“注意力池”(Attention Sink)——联系了起来。
6.1 什么是“注意力池”(Attention Sink)?
“注意力池”是近来在 LLM 研究中发现的一个有趣现象。它指的是,在自注意力(Self-Attention)机制中,模型会倾向于将不成比例的、大量的注意力分数分配给输入序列中最初的几个 token(词元),无论这些 token 的实际语义重要性如何。
这些初始 token 就像一个“水池”,吸收了大量本应分散开的“注意力”。虽然这些 token 本身可能只是些普通的起始符或者无意义的词,但“注意力池”这个机制本身,对于维持模型的稳定性和性能至关重要。特别是在处理长文本序列时,保留“注意力池”可以防止模型性能随着文本变长而衰减。
研究发现,“巨量激活”和“注意力池”之间存在着密切的联系。“巨量激活”所在的 token,往往就是吸引了大量注意力的“注意力池” token。
6.2 “超级专家”是“注意力池”的缔造者
基于已有的发现,这篇论文的研究者们提出了一个大胆的假设:既然“超级专家”是“巨量激活”的缔造者,而“巨量激活”与“注意力池”紧密相关,那么——
剪枝“超级专家”,是否不仅会消除“巨量激活”,还会同时破坏模型的“注意力池”机制?
为了验证这个假设,他们可视化了 Qwen3-30B-A3B 模型在剪枝“超级专家”前后的注意力图谱。
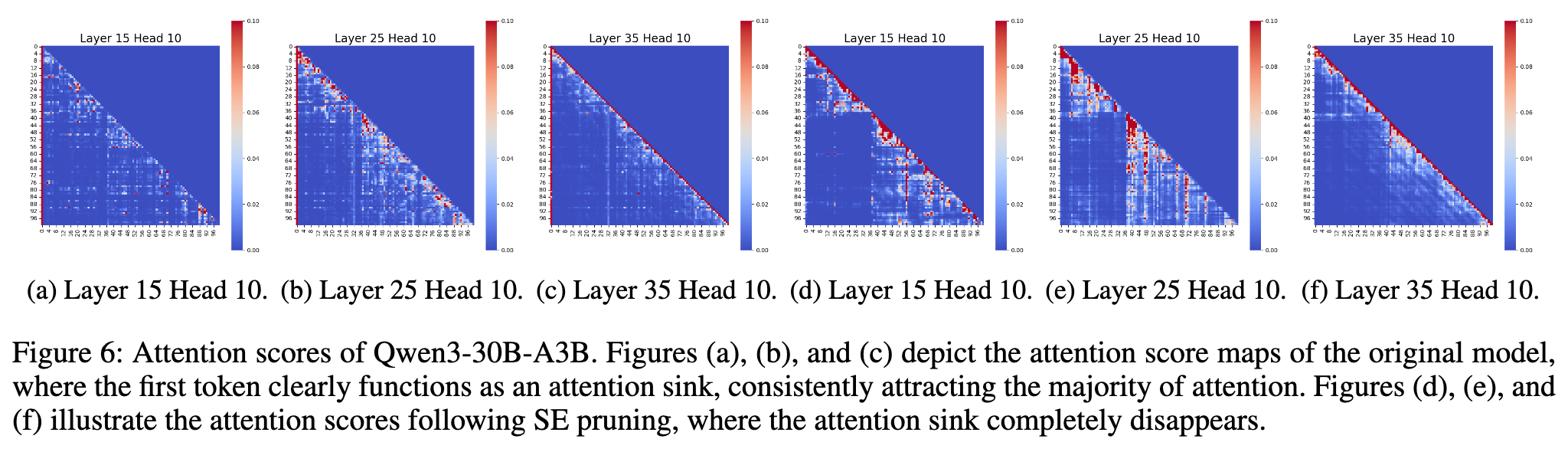
结果一目了然。如上图所示:
-
剪枝前(a, b, c):在原始模型中,注意力图谱上存在清晰的“注意力池”。第一列(代表第一个 token)的颜色非常深,表明它吸引了绝大多数的注意力。 -
剪枝后(d, e, f):在剪掉了“超级专家”之后,“注意力池”现象完全消失了!注意力分数变得弥散,不再集中于初始 token。
这个实验结果有力地证实了他们的假设:“超级专家”通过产生“巨量激活”,进而诱导了“注意力池”的形成。它们是“注意力池”机制的根本源头。
6.3 量化影响:引入“注意力池衰减率”
为了更定量地评估剪枝“超级专家”对“注意力池”的破坏程度,研究者们还提出了一个新的度量指标:注意力池衰减率(Attention Sink Decay Rate, )。
这个指标衡量的是,在剪枝后,原先流向“注意力池” token 的注意力分数,有多少比例“衰减”或“流失”了。其定义如下:
其中, 是注意力头的总数, 是“注意力池” token 的集合, 和 分别是剪枝前后的注意力分数。 的值越接近 1(或 100%),说明破坏得越严重。
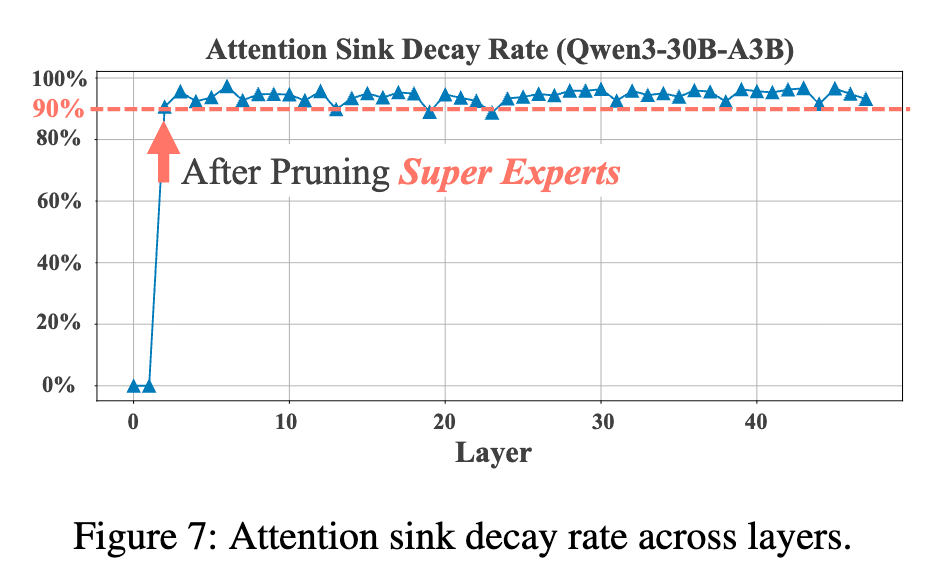
上图展示了在剪枝“超级专家”后,模型所有层的“注意力池衰减率”。可以看到,衰减率始终保持在 90% 以上,甚至接近 100%。
这再次从量化的角度证明,剪掉“超级专家”对“注意力池”机制造成了持续且毁灭性的破坏。现在,我们终于可以完整地串联起整个因果链条了:
剪枝超级专家 (Pruning SEs) → 消除巨量激活 (Eliminating Massive Activations) → 破坏注意力池 (Disrupting Attention Sinks) → 模型性能崩溃 (Model Performance Collapse)
这一清晰的机制解释,是该研究最核心的贡献之一,它为我们深入理解 MoE 模型的内部工作原理打开了一扇全新的大门。
点评
论文清晰地揭示了“SEs → 巨量激活 → 注意力池 → 模型性能”这一关键因果链,极大地加深了我们对 MoE 模型内部工作机制的理解。论文的实验设计严谨、论证充分、结论具有很强的说服力,为后续的 MoE 模型压缩和优化研究提供了至关重要的指导原则。
论文提出的 SEs 量化定义(P99.5 和 amax/10)是简洁且有效的,但它本质上是一个经验性(empirical)或启发式(heuristic)的阈值。这些阈值是否具有普适性?是否可能存在一些“准超级专家”或重要性介于“超级”和“普通”之间的专家,被这种二元划分(binary classification)所忽略?现实情况可能非简单的二元对立。
另外,本研究最重要的实践启示是“在压缩时必须保护好超级专家”,这是一个极其宝贵的“避坑指南”。
往期文章: