• 论文标题：A Unified View of Attention and Residual Sinks: Outlier-Driven Rescaling is Essential for Transformer Training
• 论文链接：https://arxiv.org/pdf/2601.22966

TL;DR

这篇由 Qwen 团队、爱丁堡大学、斯坦福大学和清华大学联合发表的论文，针对大型语言模型（LLM）中普遍存在的异常值（Outliers）现象提出了一个新的统一视角：异常值驱动的重缩放（Outlier-Driven Rescaling）。

传统的观点往往视异常值为量化的阻碍，试图通过剪裁（Clipping）或平滑（Smoothing）来消除它们。然而，本文研究发现，无论是 Attention Sinks（注意力汇聚点）还是本文新定义的 Residual Sinks（残差汇聚点），它们在模型训练中扮演着关键的功能性角色。这些异常值通过与 Softmax 或 RMSNorm 等归一化层相互作用，有效地重缩放（Rescale）了其他非异常特征的幅度，从而维持训练的稳定性。

基于这一发现，作者证明了简单地移除这些异常值会损害模型性能。相反，通过引入显式的门控机制（GatedNorm）或可学习的缩放参数（PreAffine），可以将这种重缩放功能“卸载”到参数或门控网络中，从而在消除激活值异常的同时，保持甚至提升模型性能。特别是 GatedNorm 方法，在 W4A4 低比特量化下显著提升了模型的鲁棒性。

1. 引言

Transformer 架构的大语言模型在训练过程中表现出显著的异常值现象。这些异常值的数值往往比常规激活值或 Logits 高出几个数量级。

1.1 已知的异常值类型

在本文之前，社区主要关注两种类型的异常值：

1. Attention Sinks (注意力汇聚点) ：
   最早由 StreamingLLM (Xiao et al., 2023b) 等工作指出。表现为少数几个特定的 Token（通常是序列的起始 Token）在所有层和所有 Head 中持续获得极高的注意力分数。
2. Massive Activations (MA, 巨型激活) ：
   表现为与 Attention Sink Token 相关的特征向量在特定维度上具有极大的激活值。这些 MA 在经过归一化层后，促进了 Attention Sinks 的形成。

1.2 本文定义的 Residual Sinks (残差汇聚点)

本文在残差流（Residual Stream）中识别出了一种独立于输入的异常值类型，命名为 Residual Sinks。

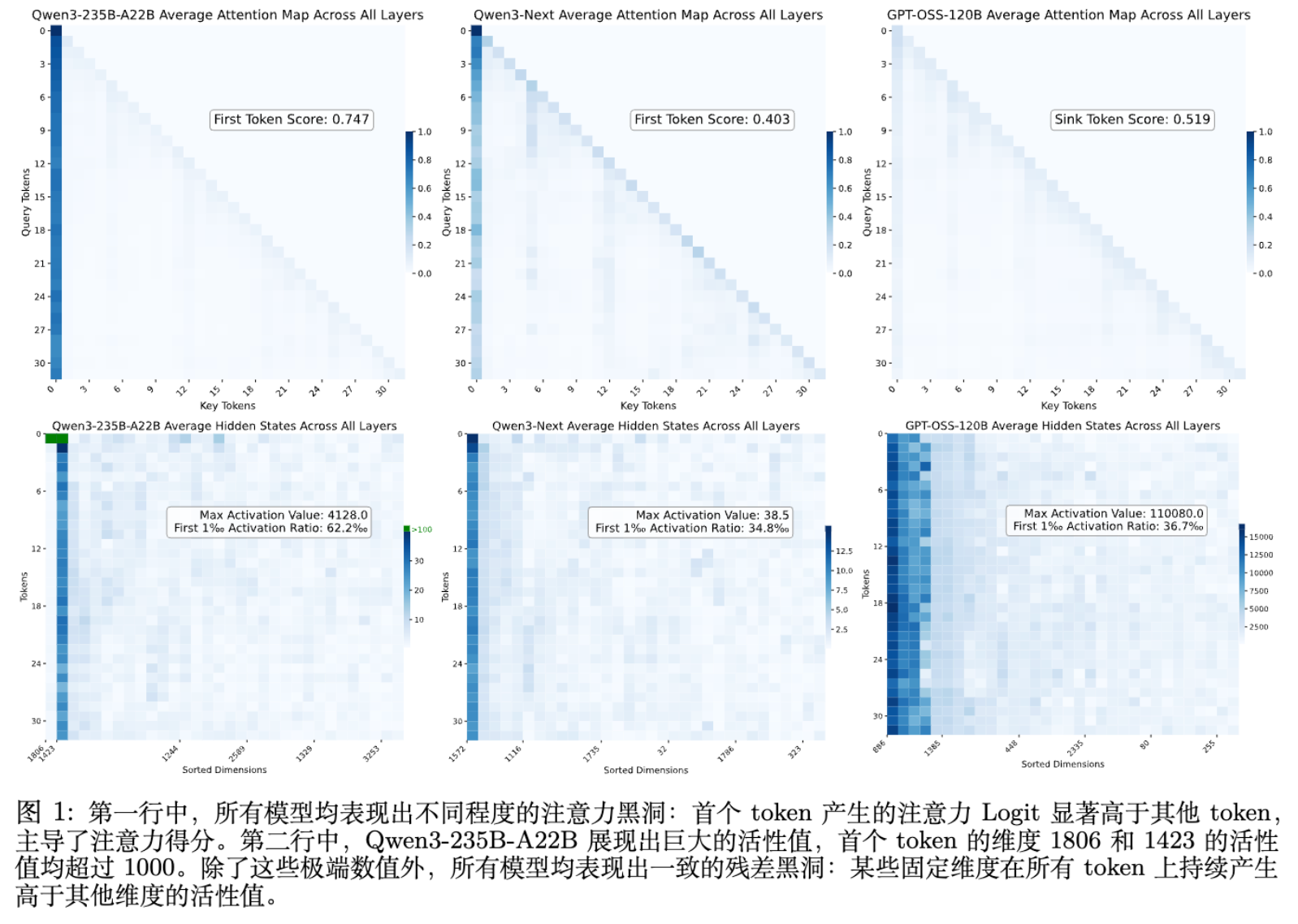
如上图所示，Residual Sinks 具有以下特征：

• 固定维度：异常值出现在绝大多数 Token 的固定特征维度上。
• 幅度巨大：其激活值比典型值高出几个数量级。
• 普遍存在：在 Qwen3-235B、DeepSeek-V3、GPT-OSS 等不同架构的模型中均被观察到。

传统的处理方法往往认为这些异常值是由于浮点误差累积或架构设计缺陷导致的“病理特征”，是量化（Quantization）的主要障碍。因此，大量工作致力于通过剪枝、旋转（Rotation）或平滑量化（SmoothQuant）来缓解这一问题。

然而，本文提出的核心假设是：这些异常值并非副作用，而是模型为了实现数值重缩放而自发演化出的功能性机制。

2. 统一视角：异常值驱动的重缩放机制

作者提出，Attention Sinks 和 Residual Sinks 虽然出现在不同的位置（前者在注意力机制中，后者在残差连接中），但它们共享相同的运作机理：利用归一化层的数学特性来压缩其他特征的幅度。

2.1 归一化中的重缩放原理

Softmax 中的重缩放 (Attention Sinks)

在 Self-Attention 中，Softmax 函数如下：

如果存在一个异常大的 logit ，分母 将主要由 决定。这将导致所有非 Sink Token 的注意力权重被压缩至接近零。Attention Sink Token 实际上充当了一个“调节旋钮”，控制着其他 Token 对当前输出的贡献程度。

RMSNorm 中的重缩放 (Residual Sinks)

RMSNorm（Root Mean Square Layer Normalization）的计算公式为：

其中 是输入向量， 是维度， 是可学习的缩放参数。

如果输入向量 在某个特定维度 上存在异常值 （即 ），那么 RMS 值将主要由 决定：

此时，对于任何普通维度 ()，其归一化后的输出变为：

由此可见，异常值 的幅度直接反比于其他维度的缩放比例。模型通过增大 ，可以有效地减小整个特征向量在归一化后的范数。

2.2 理论上界证明

作者在附录 A.1 中给出了严格的数学推导，证明了 RMSNorm 输出特征的范数上界随着异常值幅度的增加而减小。

假设存在一个异常维度 ，其幅度占比为 。经过 RMSNorm 后，特征向量的范数 满足：

其中 是 RMSNorm 的仿射参数。这个不等式表明，通过改变异常值的相对大小 ，模型可以灵活地控制归一化后的特征范数。

2.3 实验验证：异常值主要充当缩放因子而非内容贡献者

为了验证 Residual Sinks 的主要作用是“缩放”而非“传递信息”，作者检查了 RMSNorm 层中对应异常维度的可学习参数 （即文中的 ）。

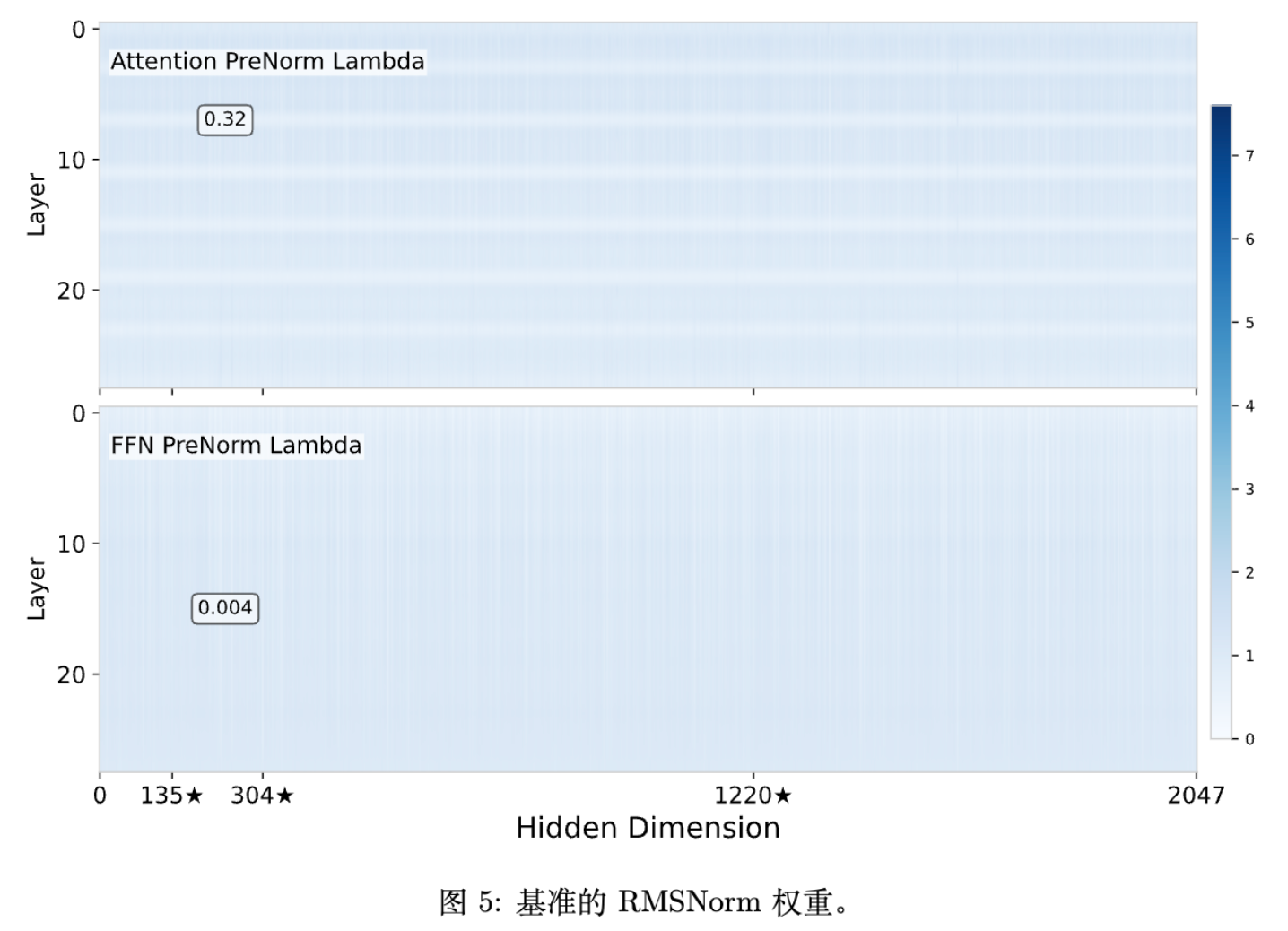
实验观察到：

• 极小的权重：在 outlier-prone 的维度上，RMSNorm 的权重 始终远小于平均值（例如 0.006 vs 1.0）。
• 信息抑制：这意味着异常值在通过归一化层计算出 RMS 并完成缩放任务后，其自身的信息在输出中被权重 极大地抑制了。这与 Attention Sink Token 的 Value Vector 范数较小的现象一致。

这一发现强有力地支持了假设：异常值的存在是为了服务于归一化过程中的分母，而非为了在分子中传递特征信息。

3. 验证假设：打破重缩放机制的后果

为了进一步确认异常值驱动重缩放的必要性，作者设计了一系列消融实验。实验基于 2B 参数模型，训练 Token 数为 120B，遵循 Llama3 和 Qwen3 的架构设计。

3.1 移除归一化层 (Removing Normalizations)

如果异常值是为了配合归一化层而产生的，那么移除归一化层应能消除异常值。

作者尝试使用逐点非线性函数 Dynamic Tanh (DyT) (Zhu et al., 2025) 替代 RMSNorm。DyT 的定义为：

DyT 仅进行逐点变换，不存在维度间的耦合，因此无法通过一个维度控制整体的缩放。

实验结果：

• 异常值消失：DyT 模型的激活值峰值从 6000 降至 73。
• 性能下降：尽管使用了搜索后的最优学习率，DyT 模型的 Final Loss 仍显著高于 Baseline (+0.259)。
• 训练不稳定：DyT 模型在训练初期极易发散，必须使用极小的学习率。

这说明，依赖归一化层进行的隐式重缩放对于 Transformer 的训练稳定性和最终性能至关重要。移除它虽然消除了异常值，但也破坏了模型的自我调节机制。

3.2 直接剪裁或约束异常值 (Clipping/Constraining)

如果保留归一化层，但强制禁止异常值的产生，会发生什么？

激活值剪裁 (Activation Clipping)

作者尝试对残差流进行剪裁（Clipping）。

• 当阈值设为 100 时，训练直接发散。
• 当阈值设为 1000 时，训练虽然收敛，但 Loss 显著增加 (+0.006)。

激活函数架构选择 (SwiGLU vs GLU)

现代 LLM 多采用 SwiGLU：

Swish 也是无界的，允许产生较大的激活值。如果将其替换为 Sigmoid（有界区间 ），即标准的 GLU：

• 异常值减少：GLU 模型的异常值幅度较小（1300 vs 6000）。
• 性能受损：GLU 模型的性能弱于 SwiGLU (+0.011)。

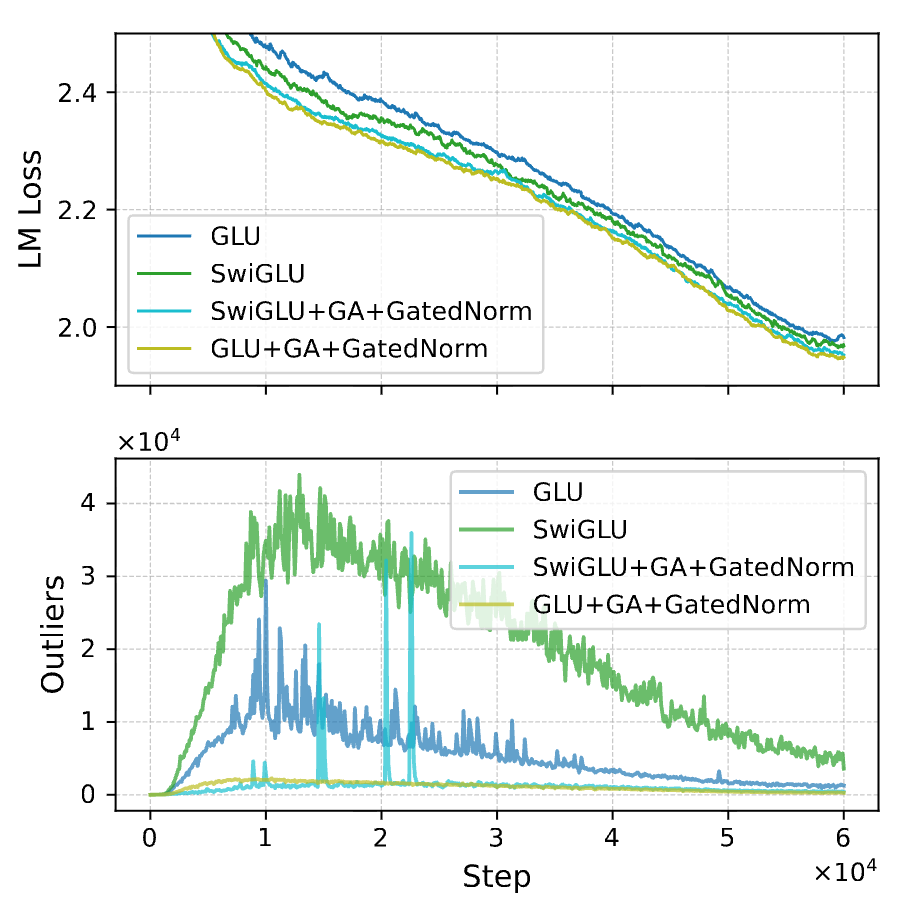
这一系列实验表明，在缺乏显式重缩放机制的情况下，模型“需要”异常值。人为压制异常值会阻碍模型进行必要的特征幅度调整，从而损害性能。

4. 解决方案：显式重缩放机制

既然重缩放是必须的，而通过异常值实现的隐式重缩放对量化不友好，作者提出了两种替代方案，旨在保留重缩放功能的同时消除激活异常值。

4.1 方法一：PreAffine (将异常值吸收到参数中)

Attention Sinks 可以通过引入可学习的 Bias 或 Sink Token 被吸收。类似地，作者提出 PreAffine，将 Residual Sinks 吸收到归一化层之前的参数中。

公式如下：

其中 是一个可学习向量。

原理：

• 如果模型需要通过某个维度 进行重缩放，它可以学习到一个巨大的 。
• 即使输入激活 保持平滑， 仍能产生巨大的值，从而触发 RMSNorm 的重缩放机制。
• 这样，异常值主要存在于静态权重 中，而非动态激活 中。

结果：

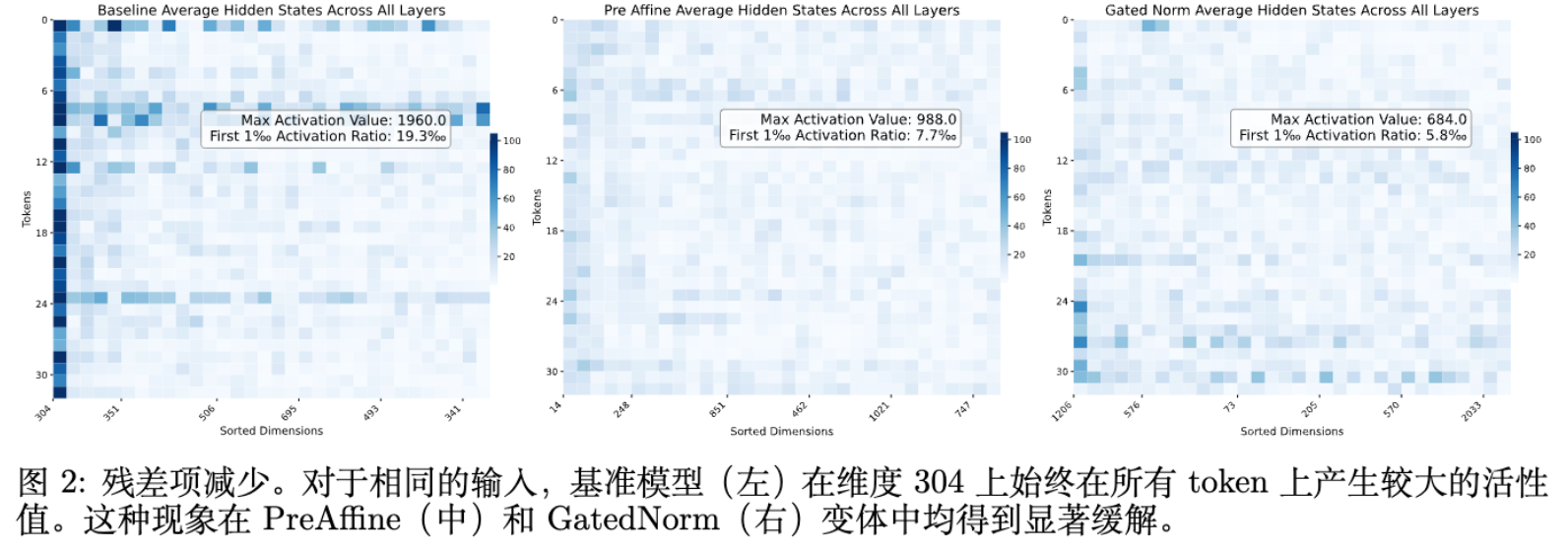
• 残差流的最大激活值显著降低（从 2800 降至 640）。
• 模型性能略有提升（Loss -0.003）。
• 可视化显示， 在特定维度上确实学到了极大的值（如 7.19），验证了模型将异常值的生成责任转移到了参数上。

4.2 方法二：GatedNorm (显式门控重缩放)

虽然 PreAffine 转移了异常值，但在计算 时，归一化层内部仍存在大数值。为了彻底解耦，作者提出了 GatedNorm。

GatedNorm 在每个归一化层后引入一个轻量级的、基于门控的重缩放机制，显式地赋予模型调整特征幅度的能力。

公式如下：
给定 ，计算：

其中，, ，且 （例如 ）。 为 Sigmoid 函数。

设计细节：

• 低秩投影：仅增加极少的参数量（2B 模型中增加约 3.7M，占 2%），且为了保持参数量公平，实验中相应减少了 FFN 的宽度。
• Sigmoid 激活：Sigmoid 的有界性和在零附近的细粒度控制对于稳定训练至关重要。实验表明 Tanh 或 SiLU 会导致训练不稳定。
• Element-wise Gating：相比于 Tensor-wise（标量）门控，Element-wise（向量）门控提供了更精细的维度级控制，性能提升更明显。

优势：

1. 消除异常值：模型不再需要生成 Residual Sinks 来控制 RMS，激活值变得更加平滑。
2. 提升性能：在各项基准测试中，GatedNorm 相比 Baseline 平均提升了约 2 个百分点。
3. 架构鲁棒性：引入 GatedNorm 后，原本表现较差的 GLU（Sigmoid-based）性能追平甚至超越了 SwiGLU。这表明一旦提供了显式的重缩放手段，模型对产生异常值的架构组件（如 Swish）的依赖降低了。

5. 实验结果与分析

作者在 7B 和 24B 参数规模的 MoE 模型上进行了扩展实验，训练数据量分别为 1.2T 和 500B Token。

5.1 知识与推理能力评估

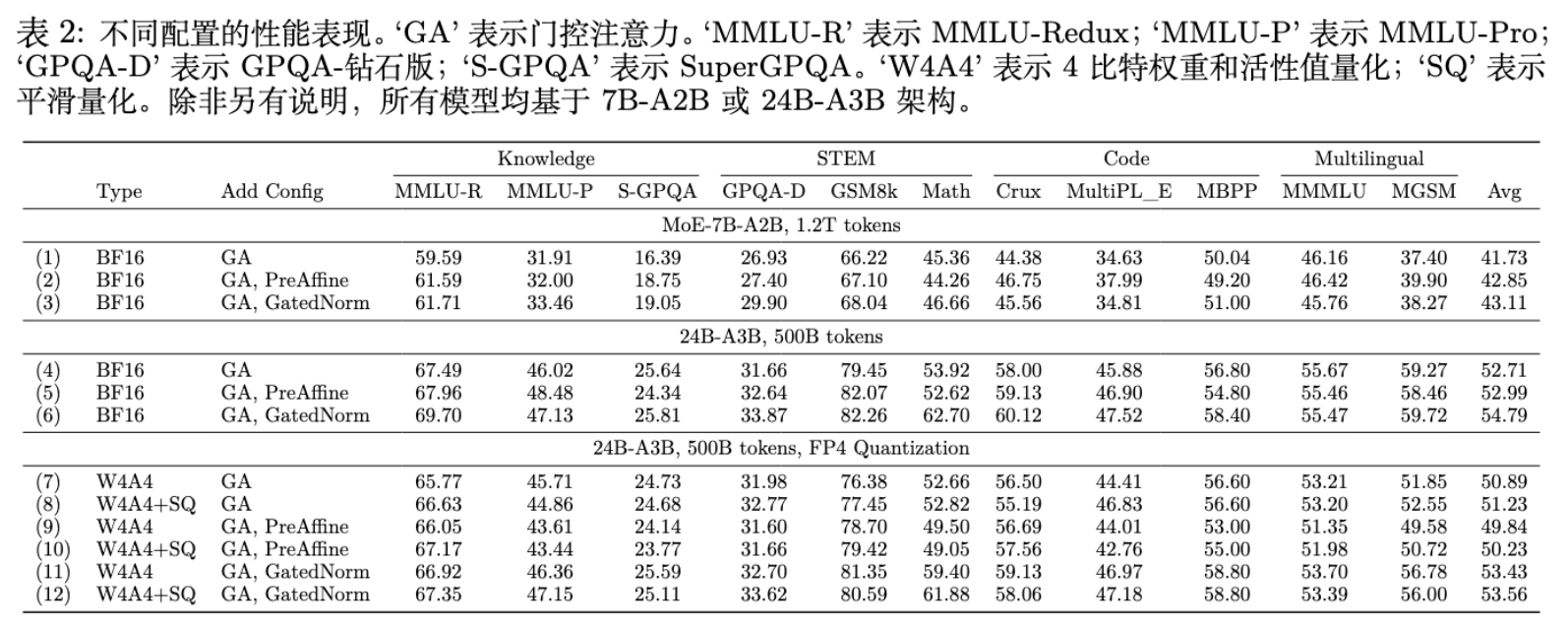
实验涵盖了 MMLU-Redux, MMLU-Pro, GSM8K, Math, MBPP 等多个数据集。

• GatedNorm 全面领先：在所有尺寸模型上，GatedNorm 均取得了最低的 Validation Loss 和最高的下游任务分数。
• PreAffine 表现稳健：优于 Baseline，但略逊于 GatedNorm。

5.2 量化鲁棒性 (Quantization Robustness)

这是本文最显著的应用成果。由于消除了异常值，激活分布变得更加平滑，极大地方便了低比特量化。

作者测试了激进的 W4A4 (4-bit Weight, 4-bit Activation) 量化设置。

• Baseline (Vanilla) ：由于存在巨大的异常值，直接量化会导致严重的精度损失。
• SmoothQuant：作为通用的量化增强技术，能带来约 0.5 分的提升。
• GatedNorm：

  • 在 W4A4 设置下，GatedNorm 模型的性能降幅最小。
  • 在 MGSM（多语言数学）任务上，其他方法下降近 10 分，而 GatedNorm 仅下降不到 5 分。
  • 即便不使用 SmoothQuant，GatedNorm 的原始量化性能也优于使用了 SmoothQuant 的 Baseline。

这表明，通过架构改进（GatedNorm）从源头解决异常值问题，比事后修补（SmoothQuant）更为有效。

5.3 效率分析

• 训练开销：由于 GatedNorm 引入了额外的投影层，训练时的计算开销略有增加。

  • 对于 hidden size = 2048 的小模型，开销约为 8.1%。
  • 对于 hidden size = 8192 的大模型，开销降至 3.6%。
  • 在 MoE 架构中，由于通信和路由占比较大，GatedNorm 的相对开销进一步降低至 3% 以下。
• 参数量：增加的参数量极少（< 2%），且可以通过调整 FFN 宽度完全抵消。

6. 讨论与相关工作

6.1 与量化工作的关系

先前的量化工作（如 LLM.int8(), SmoothQuant, QuIP

等）主要侧重于如何适应现有的异常值，例如采用混合精度分解或数学变换将异常值平摊到权重上。

6.2 与 Attention Sinks 的关系

Attention Sinks 是 Token 级别的异常值，利用 Softmax 进行重缩放。Residual Sinks 是维度级别的异常值，利用 RMSNorm 进行重缩放。两者本质相同。Gated Attention (GA) 解决了前者，而本文提出的 GatedNorm 解决了后者。实验表明，同时使用 GA 和 GatedNorm 能达到最佳效果。

6.3 深度思考：特征范数与学习

作者在文末的 Limitations 中提到，虽然证明了重缩放对于训练稳定性至关重要，但为什么模型需要如此频繁地调整特征范数仍是一个开放性问题。这可能与深层网络中的信号传播动力学或优化器的特性有关。

7. 总结

1. 功能性视角：异常值不是 Bug，而是 Feature。它们是模型在现有归一化（Softmax/RMSNorm）约束下，自发演化出的数值重缩放机制。
2. 统一理论：Attention Sinks 和 Residual Sinks 遵循相同的运作原理——通过极大的值主导归一化分母，从而压缩其他特征的表达。
3. 架构改进：通过 GatedNorm 显式地提供重缩放能力，模型不再需要生成极端的异常值。
4. 实际收益：这种架构改进不仅提升了 FP16/BF16 下的训练稳定性和模型性能，更关键的是，它产出了对量化（尤其是 W4A4）极度友好的“平滑”模型。

更多细节请阅读原文。

往期文章：

• Less is Enough——在大模型特征空间中合成多样化数据

• 腾讯混元提出 G-OPD：超越教师模型的广义在线蒸馏与奖励外推

• 腾讯混元提出 Composition-RL：通过合成可验证Prompt提升大模型强化学习效率

• 上交 & 千问提出 OPUS：论大模型预训练中数据选择与优化器几何的对齐

• 大语言模型强化微调中的熵动力学分析

• Sea AI Lab 提出 DPPO：重新审视 PPO 算法中的信任域

• MaxRL：重新审视强化学习与最大似然估计的统一

• Agentic RL 的新范式：在强化学习循环中融合规则、模型奖励与自然语言批评

• 自蒸馏优化 SDPO：如何利用富文本反馈打破 RLVR 的信用分配瓶颈？

• MIT 提出 SDFT：作为逆强化学习（Inverse RL）的在线自蒸馏

• GPT 之父 Alec Radford 新作：通过 Token 级数据过滤实现比 RLHF 更稳健的拒绝边界

• 美团 LongCat 技术报告解读：在高稀疏度下，Embedding 扩展优于专家扩展

• 阿里云提出 DASD 分布对齐的序列蒸馏：实现更优的长链思维推理

• DeepSeek-OCR 2: Visual Causal Flow 技术报告解读

• 美团 LongCat-Flash-Thinking-2601 技术报告解读

• Agentic Reasoning for Large Language Models 综述：基础、进化与协作

• 小米推出 JudgeRLVR：先判断后生成——打破推理模型“长思维链”的效率悖论

• 你的 GRPO 的优势估计是有偏差的：GRPO 中的统计陷阱与 HA-DW 修正方案

• Meta 提出 Dr.Zero：零数据训练的自进化 Search Agent

• 深度解析 Ministral 3：基于级联蒸馏的参数高效密集模型训练方法论

• Sparse-RL：通过稳定稀疏 Rollout 突破 LLM 强化学习的显存墙

• Qwen 发布 ArenaRL：解决开放域 Agent 的奖励建模难题

• NTU & 通义提出 AgentOCR：基于光学自压缩的智能体历史重构

• DeepSeek 新论文 Engram 深度解读

• Anthropic 提出 EDL 来量化大模型的泛化能力

• 小米 MiMo-V2-Flash 技术报告：MoE 架构、混合注意力机制与多教师在线蒸馏

• DeepSeek-R1 v2 发布：新增技术细节与训练流程全解读

• WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南