• 论文标题：Composition-RL: Compose Your Verifiable Prompts for Reinforcement Learning of Large Language Models
• 论文链接：https://arxiv.org/pdf/2602.12036

TL;DR

在基于可验证奖励的强化学习（RLVR）中，随着模型能力的提升，训练集中越来越多的 Prompt 变为“简单样本”（即模型能以 100% 概率解出），导致梯度估计的方差为零，无法提供有效的训练信号。本文介绍的 Composition-RL 提出了一种基于现有数据自动合成新 Prompt 的方法。该方法通过将多个简单的数学或逻辑问题串联组合，构建出更复杂的组合式问题（Compositional Prompts），从而将“简单样本”转化为具有挑战性的训练数据。实验表明，Composition-RL 在 Qwen3 系列模型（4B 至 30B）上显著提升了数学推理及跨域泛化能力，且这种组合带来的性能提升优于单纯的数据混合训练。

1. 背景

1.1 RLVR 的数据困境

随着 OpenAI o1 和 DeepSeek-R1 等模型的出现，基于可验证奖励的强化学习（Reinforcement Learning with Verifiable Rewards, RLVR）已成为提升大语言模型（LLM）推理能力的标准范式。RLVR 的核心依赖于大量带有确切答案（Ground Truth）的 Prompt，通过模型生成的答案与标准答案的一致性来计算奖励信号。

在 RLVR 训练过程中（通常采用 PPO 或 GRPO 算法），梯度更新依赖于优势函数（Advantage）的估计。对于一个 Prompt ，如果模型生成的多个回复 的正确率全是 0（Too Hard）或全是 1（Too Easy），则该 Prompt 提供的梯度方差接近于零，无法为策略更新提供有效信息。

现有的研究多集中于如何利用全错（Success Rate = 0）的“困难样本”，例如通过 Advantage Shaping 或 Hint-based Augmentation 来降低难度。然而，随着训练的进行，模型能力不断增强，训练集中会有越来越多的 Prompt 变为“简单样本”（Success Rate = 1）。

1.2 有效数据量的衰减

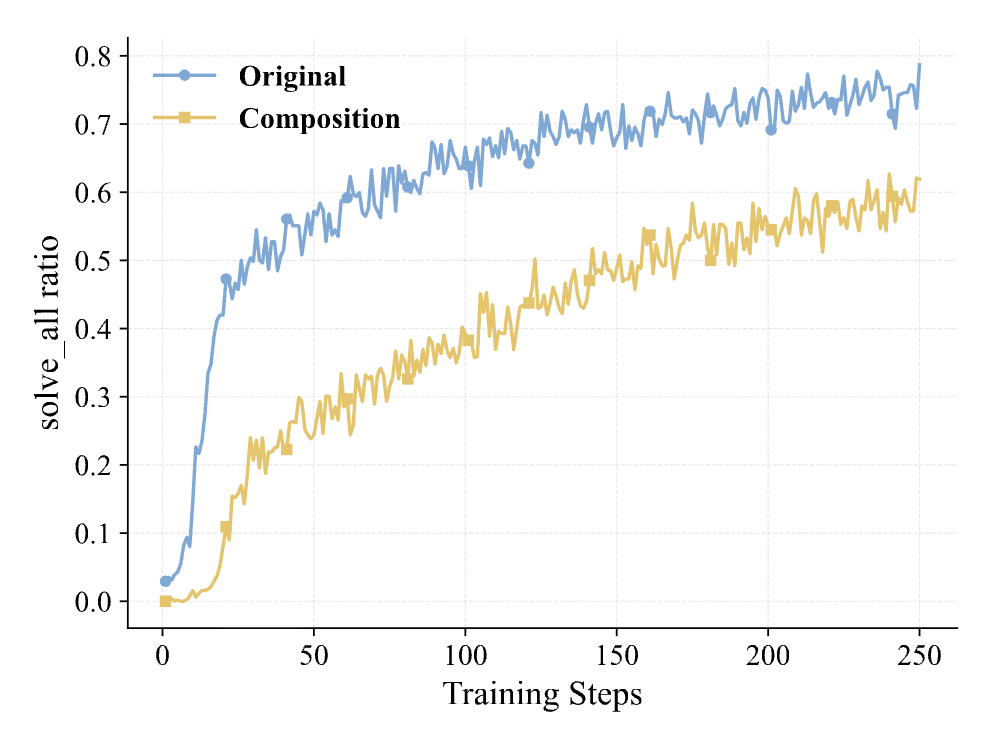
如上图所示，在 Qwen3-4B-Base 的训练过程中，初始阶段“全对样本”（solve_all）的比例接近 0，但仅经过 50 步训练后，该比例迅速攀升并稳定在 75% 左右。虽然通过动态采样（Dynamic Sampling）可以剔除这些零方差样本，但这实际上导致有效训练数据量大幅缩减（例如 12,000 条数据中仅剩约 3,000 条有效）。

针对这一问题，Composition-RL 的核心动机是：能否利用这些已经变得“简单”的 Prompt，通过某种变换，重新构建出对当前模型具有挑战性的“困难”样本，从而延续 RL 的训练收益？

2. Composition-RL

本文提出了一种名为 Composition-RL 的框架，其核心组件是顺序 Prompt 合成（Sequential Prompt Composition, SPC）算法。该方法利用 LLM 自身的能力，将现有的 个简单问题组合成一个深度为 的复杂问题。

2.1 顺序 Prompt 合成 (SPC)

假设我们有两个具有标准答案的 Prompt： 和 。SPC 的目标是构建一个新的组合 Prompt ，其标准答案为 （通常设为 ）。该过程分为三个步骤：

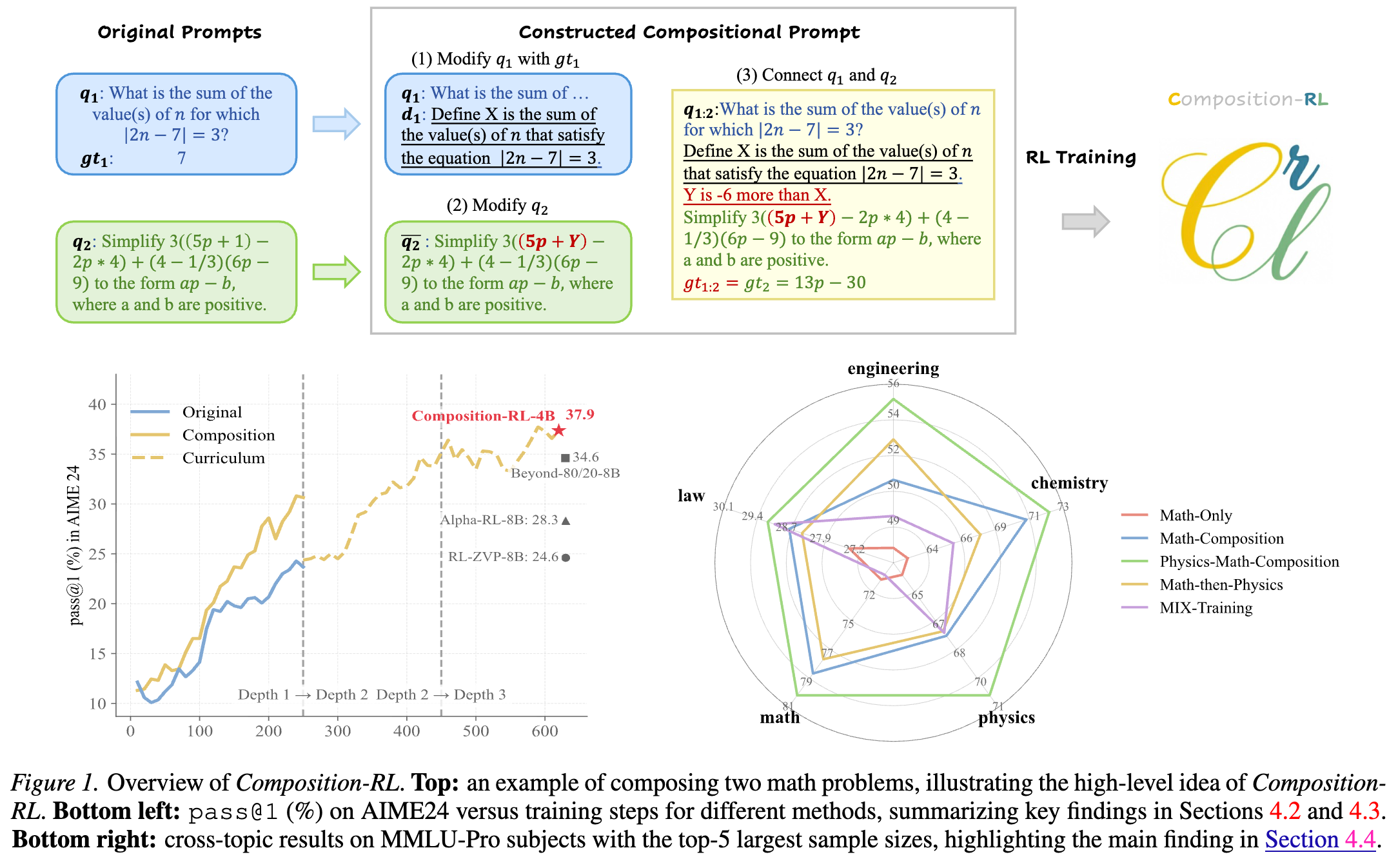
第一步：基于 修改

首先，从 中提取一个数值，记为 。接着，引入一个自然语言定义 ，用以描述这个数值。此时，原始问题 被转化为一个陈述性或定义性的语句 。

• 示例：

  • 原始 ："使得 的 的值之和是多少？"
  • 原始 ：7。
  • 提取 。
  • 添加定义 ："设 为使得 成立的 的值之和。"

第二步：修改

从 中提取一个常数值，并将其替换为新的变量名 ，得到修改后的问题 。

• 示例：

  • 原始 ："将 化简为 的形式，其中 为正数。"
  • 选取常数 1 作为被替换值，令 （但在 Prompt 中用变量 表示）。
  • 修改后 ："将 化简为 的形式..."

第三步：连接 和

计算 和 之间的数值关系，并用自然语言 表述出来。

• 示例：

  • 。
  • 关系：。
  • 约束描述 ："Y 比 X 小 6。"
  • 最终组合 Prompt ：。
  • 最终答案 即为原 （在此例中是 ）。

通过这种构造，求解 必须先正确求解 得到中间变量，再结合约束条件推导 的参数，最后解决 。这种非对称的依赖关系使得组合问题的难度显著高于单个子问题。

2.2 扩展至 个 Prompt

上述过程可以递归地推广到 个 Prompt。定义 为组合深度（Compositional Depth）。

其中 是由后 个问题递归合成得到的。这意味着解决深度为 的问题需要模型具备更长的推理链条（Chain-of-Thought）和更强的上下文维持能力。

2.3 训练目标与动态采样

Composition-RL 使用 GRPO（Group Relative Policy Optimization）作为基础优化算法。目标函数为最大化组合数据的期望可验证奖励：

其中 是通过 SPC 构建的组合数据集。

为了提高训练效率，方法中依然保留了动态采样（Dynamic Sampling）机制。对于每个 Batch：

1. 从候选集中采样一批 Prompt。
2. 模型进行 次 Rollout。
3. 计算每个 Prompt 的平均奖励 。
4. 过滤掉 （全错）和 （全对）的样本，只保留 的样本进行梯度更新。

Meta-Experiment 结果显示，经过 SPC 处理后，原本高达 75% 的 solve_all 比例在 OpenMath-Reasoning-1.5B 模型上降至 41.4%，在 JustRL-1.5B 上降至 60.0%。这证明 SPC 有效地“重启”了简单样本的训练价值。

3. 实验设置

为了全面评估 Composition-RL 的有效性，论文在不同参数规模的模型和不同领域的数据集上进行了广泛实验。

3.1 基础设置

• 模型：Qwen3 系列（4B-Base, 8B-Base, 14B-Base, 30B-A3B-Base）。
• 训练框架：VeRL (Sheng et al., 2024)。
• 超参数：Learning Rate ，Batch Size 256，无需 Warm-up。
• Rollout：Temperature 1.0, 8 samples per prompt, Max Tokens 16K。
• 验证器：Math-Verify（基于规则的验证器）。
• 训练集：

  • MATH12K：原始 MATH 训练集（约 12k 条）。
  • MATH-Composition-199K：基于 MATH12K 构建的深度为 2 的组合数据集（约 199k 条有效数据）。

3.2 评测基准

• 域内数学任务（In-Domain）：

  • AIME 24 / AIME 25（高难度竞赛题）。
  • Beyond AIME。
  • IMOBench。
• 域外多任务（Out-Of-Domain）：

  • GPQA-Diamond。
  • MMLU-Pro。

所有评测均报告 Pass@1 准确率，部分通过多次采样取平均（如 Avg@32）。

4. 实验

4.1 组合数据的普遍增益

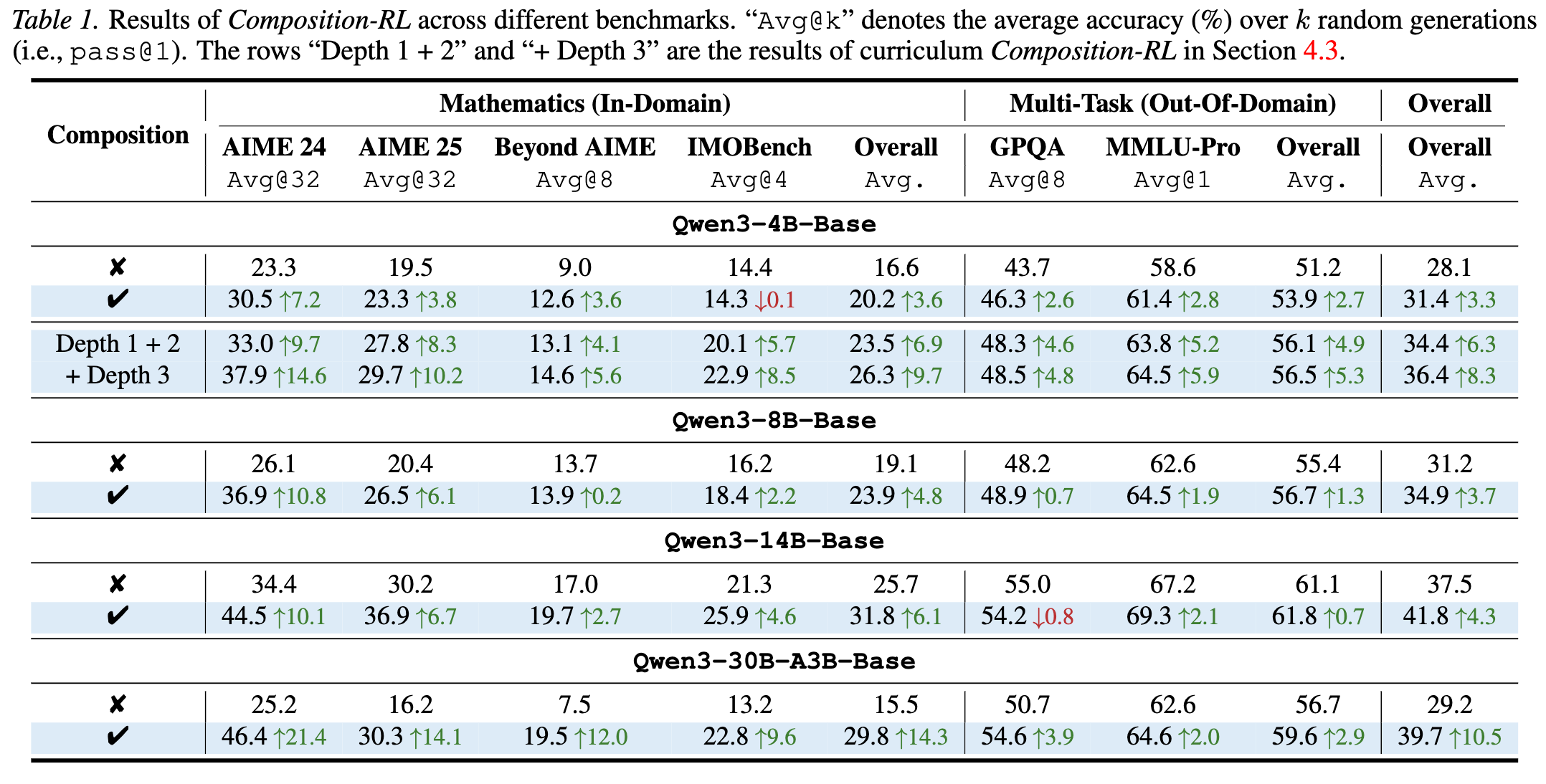
实验结果表明，Composition-RL 在所有模型尺寸和所有基准测试中均优于在原始数据上进行 RL 训练的基线。

1. 整体性能提升：

   • Qwen3-4B: 整体平均分提升 +3.3%。
   • Qwen3-14B: 整体平均分提升 +4.3%。
   • Qwen3-30B-A3B: 整体平均分提升 +10.5%。
     这显示出明显的Scaling Law特性：模型参数量越大，从组合数据中获得的收益越高。这可能是因为大模型具备更强的长窗口处理能力和基础推理能力，能够更好地消化长推理链的训练数据。

2. 高难度任务表现：
   在 AIME 24 这一高难度数学竞赛基准上，Composition-RL 带来的提升尤为显著：

   • 4B 模型提升 +7.2%。
   • 8B 模型提升 +10.8%。
   • 30B 模型提升 +21.4%。
     这表明通过组合简单问题，确实能够激发模型解决复杂问题的潜力。

3. 域外泛化（OOD）：
   尽管训练数据仅包含数学题目，但模型在 GPQA（研究生水平问答）和 MMLU-Pro 上的表现也有所提升。例如 30B 模型在 MMLU-Pro 上提升了 +2.0%。这暗示了 RLVR 训练获得的推理能力具有一定的通用性。

4.2 课程学习（Curriculum Learning）的效果

论文进一步探索了从深度 1（原始数据）逐步过渡到深度 2、深度 3 的课程学习策略。

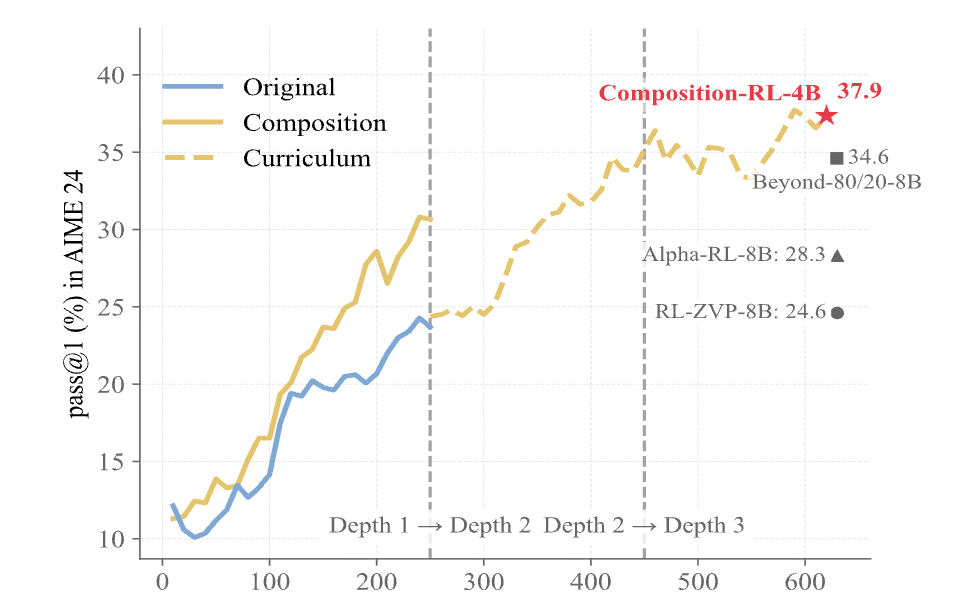
• 现象：直接在 MATH12K（Depth 1）上训练，性能在一定步数后趋于饱和，这是因为 solve_all 比例过高导致梯度消失。
• 策略：当 Depth 1 训练饱和后，切换到 Depth 2 数据集继续训练，solve_all 比例骤降，模型性能重新开始增长。随后切换至 Depth 3，性能进一步提升。
• 数据：

  • Depth 1 -> Depth 2：在 AIME 24 上额外获得 +9.7% 的提升。
  • Depth 3：进一步获得 +2.0% 的整体提升。

这一结果验证了通过不断增加组合深度，可以持续挖掘现有数据的潜力，突破模型性能的“天花板”。

4.3 跨领域组合（Cross-Domain Composition）

除了数学内部的组合，论文还尝试了将物理（Physics）题目作为 ，将数学（Math）题目作为 进行跨域组合。

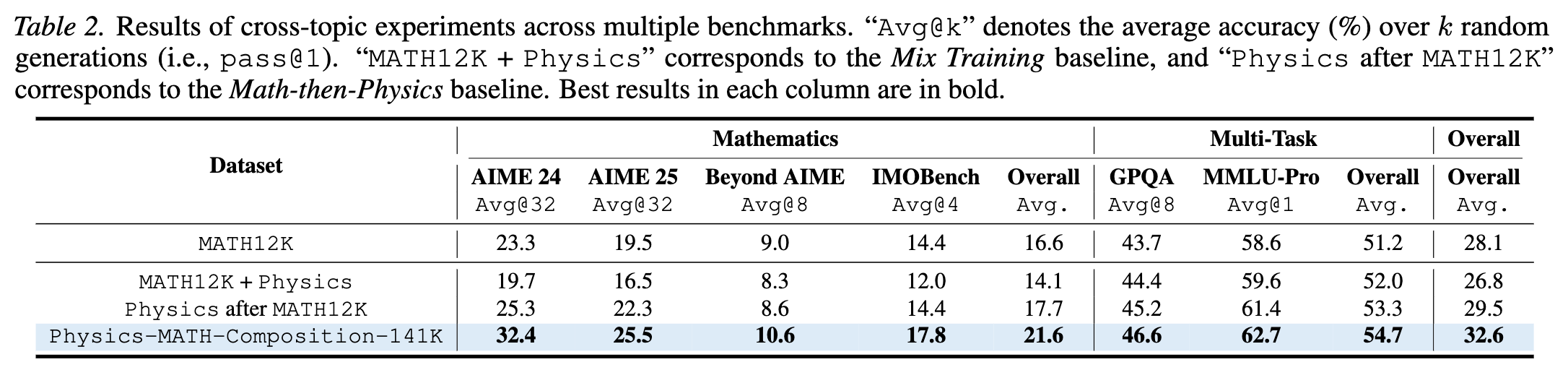
实验设置了三个对比组：

1. Mix Training：简单混合数学和物理题目进行训练。
2. Math-then-Physics：先训数学，再训物理。
3. Composition-RL：物理与数学的组合题目。

主要发现：

• 组合优于混合：Composition-RL 在所有指标上均显著优于 Mix Training 和 Sequential Training。
• 双向促进：

  • 在数学基准（AIME 24）上，Composition-RL 达到了 32.4%，高于 Mix Training 的 19.7% 和 Math-then-Physics 的 25.3%。
  • 在域外任务（OOD）上，Composition-RL 同样表现最佳。
• 解释：物理问题通常需要数学工具来解决。将物理场景（提供变量和约束）与数学计算（求解）强制结合，模拟了实际应用中“建模 -> 求解”的完整过程，比单纯学习孤立的知识点更有效。

5. 为什么 Composition-RL 有效？

论文通过定性和定量分析，将 Composition-RL 的成功归因于两个主要因素：组合泛化（Compositional Generalization）和隐式过程监督（Implicit Process Supervision）。

5.1 组合泛化能力

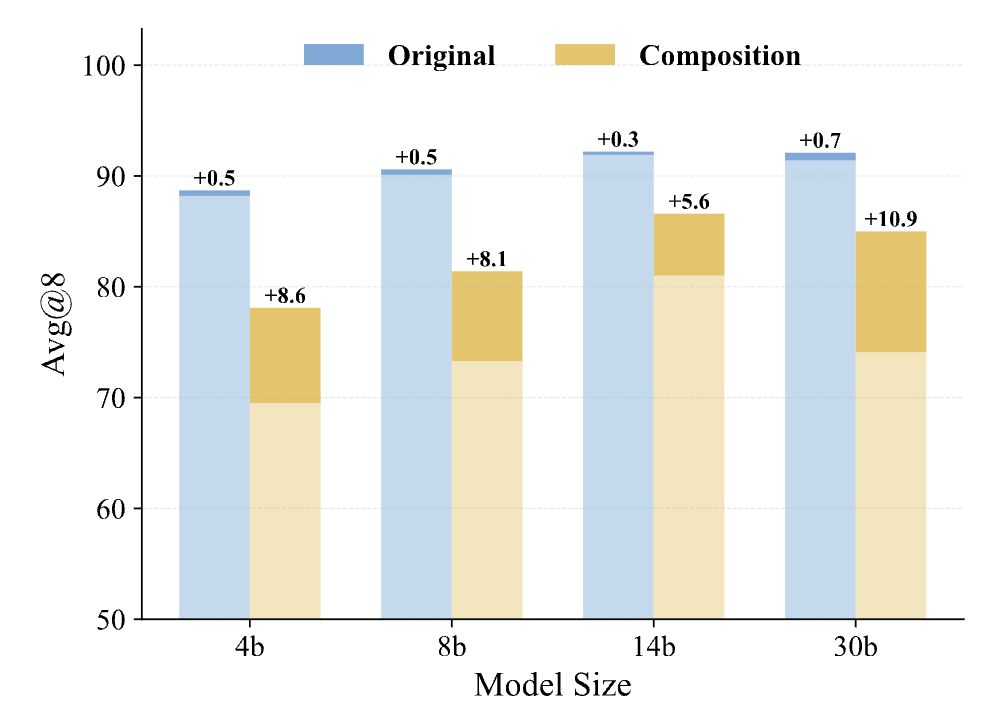
作者构建了一组测试数据，对比了模型在 Depth-1（原始）和 Depth-2（组合）测试题上的表现。结果显示，经过 Composition-RL 训练的模型，不仅在标准测试集上表现更好，在 Depth-2 的测试题上优势更大。这说明模型并非单纯记忆了题目，而是学会了如何处理更复杂的逻辑结构，即习得了“将已知技能组合起来解决新问题”的能力。

5.2 隐式过程监督

这是一个非常深刻的观点。在标准的 RLVR 中，通常只有最终答案正确才给奖励（Outcome Reward Matrix, ORM）。对于长链条推理，这通常被称为“稀疏奖励”问题。

但在 Composition-RL 中，题目 的结构决定了：如果第一步 的答案 算错了，那么带入 的参数就是错的，最终答案 几乎不可能正确。

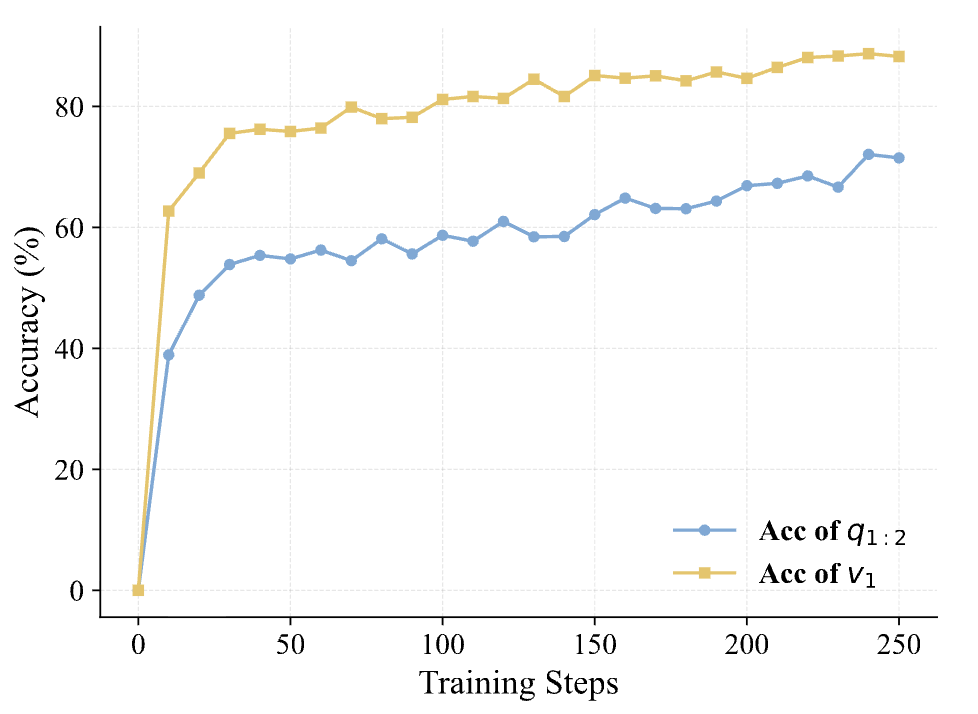
实验数据表明，随着模型对组合问题 解决率的提升，模型对中间变量 的计算正确率也在同步提升。
这意味着：

1. 组合 Prompts 本身充当了一种结构化的验证机制。
2. 为了得到最终奖励，模型被迫在中间步骤（求解 ）保持精确。
3. 这种机制在没有人工标注过程标签（Process Reward Model, PRM）的情况下，实现了类似过程监督的效果。

6. 实现细节与消融实验

6.1 数据的可靠性过滤

自动合成 Prompt 最大的风险在于生成错误的问题或产生逻辑矛盾。论文在附录 D 中详细描述了基于 LLM 的自验证流程：

1. 验证提取（Verify Extraction）：在提取 后，让 LLM 重新根据 和 计算 ，如果计算结果与提取结果不一致，则丢弃。
2. 验证修改（Verify Modification）：同理，验证 中的变量替换是否保持了原题逻辑。
3. 验证连接（Verify Connection）：检查 和 连接后是否存在变量名冲突或语意不通顺。

通过这一系列严格的过滤，错误率被控制在 2% 以下，保证了大规模训练数据的质量。

6.2 候选集 的选择

在构建组合数据时，如何选择 和 的来源？论文比较了不同的采样策略（附录表 3）：

• Variant A： 均来自小样本随机子集。
• Variant B： 全集， 小样本子集。
• Composition-RL (Default) ： 小样本子集（20个种子题）， 全集。

结果显示，默认配置效果最好。分析认为，由于组合问题 的最终答案由 决定，因此 的多样性（覆盖全集）对于保证最终答案分布的广泛性至关重要。而 仅作为条件引入，少量的种子题即可提供足够的上下文扰动。

6.3 验证器（Verifier）的选择

实验主要使用 Math-Verify 这一基于规则的验证器。对于物理题目（MegaScience Physics），由于 LLM 生成的答案可能包含单位、不同格式的科学计数法，规则验证器容易误判。因此，作者采用了“保守过滤”策略：如果 DeepSeek-R1 或其他强模型生成的 8 个回复都被 Math-Verify 判错，说明该题目的格式可能验证器无法识别，直接剔除。最终保留了约 8.2K 条物理题目。

7. 相关工作对比

7.1 与 Hint-based Augmentation 的区别

最近有工作（如 Li et al., 2025a）提出通过给困难问题（Solve_none）增加 Hint 来降低难度，使其变为可学习的样本。
Composition-RL 的思路恰恰相反：它是针对简单问题（Solve_all），通过组合增加难度。
两者在 RL 生命周期中是互补的：

• 初期：使用 Hint-based 方法启动训练，解决“太难”的问题。
• 中后期：使用 Composition-RL，解决“太简单”的问题，持续提升上限。

7.2 与 Synthetic Data 的区别

许多工作致力于从零生成合成数据。Composition-RL 的优势在于它重用（Reuse）了经过验证的高质量现有数据。这避免了从零生成时可能引入的幻觉（Hallucination）或事实错误，同时也保证了 Ground Truth 的可靠性。

更多细节请阅读原文。

往期文章：

• 上交 & 千问提出 OPUS：论大模型预训练中数据选择与优化器几何的对齐

• 大语言模型强化微调中的熵动力学分析

• Sea AI Lab 提出 DPPO：重新审视 PPO 算法中的信任域

• MaxRL：重新审视强化学习与最大似然估计的统一

• Agentic RL 的新范式：在强化学习循环中融合规则、模型奖励与自然语言批评

• 自蒸馏优化 SDPO：如何利用富文本反馈打破 RLVR 的信用分配瓶颈？

• MIT 提出 SDFT：作为逆强化学习（Inverse RL）的在线自蒸馏

• GPT 之父 Alec Radford 新作：通过 Token 级数据过滤实现比 RLHF 更稳健的拒绝边界

• 美团 LongCat 技术报告解读：在高稀疏度下，Embedding 扩展优于专家扩展

• 阿里云提出 DASD 分布对齐的序列蒸馏：实现更优的长链思维推理

• DeepSeek-OCR 2: Visual Causal Flow 技术报告解读

• 美团 LongCat-Flash-Thinking-2601 技术报告解读

• Agentic Reasoning for Large Language Models 综述：基础、进化与协作

• 小米推出 JudgeRLVR：先判断后生成——打破推理模型“长思维链”的效率悖论

• 你的 GRPO 的优势估计是有偏差的：GRPO 中的统计陷阱与 HA-DW 修正方案

• Meta 提出 Dr.Zero：零数据训练的自进化 Search Agent

• 深度解析 Ministral 3：基于级联蒸馏的参数高效密集模型训练方法论

• Sparse-RL：通过稳定稀疏 Rollout 突破 LLM 强化学习的显存墙

• Qwen 发布 ArenaRL：解决开放域 Agent 的奖励建模难题

• NTU & 通义提出 AgentOCR：基于光学自压缩的智能体历史重构

• DeepSeek 新论文 Engram 深度解读

• Anthropic 提出 EDL 来量化大模型的泛化能力

• 小米 MiMo-V2-Flash 技术报告：MoE 架构、混合注意力机制与多教师在线蒸馏

• DeepSeek-R1 v2 发布：新增技术细节与训练流程全解读

• WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南