
-
论文标题:Learning beyond Teacher: Generalized On-Policy Distillation with Reward Extrapolation -
论文链接:https://arxiv.org/pdf/2602.12125
TL;DR
今天解读一篇来自腾讯混元的论文《Learning beyond Teacher: Generalized On-Policy Distillation with Reward Extrapolation》。该研究揭示了在线蒸馏(On-Policy Distillation, OPD)本质上是密集 KL 约束强化学习(RL)的一个特例,其中奖励函数与 KL 正则项的权重被固定为 1:1。基于此理论洞察,作者提出了广义在线蒸馏(Generalized On-Policy Distillation, G-OPD)框架,通过引入奖励缩放因子 和灵活的参考模型 来扩展标准 OPD。
核心发现包括:
-
ExOPD(奖励外推):当设置 时,学生模型能够超越教师模型的能力边界。特别是在多教师(Multi-Teacher)知识融合场景下,ExOPD 能够整合多个领域专家(RL-finetuned)的能力,得到的单一学生模型在所有领域均优于对应的领域教师。 -
奖励修正(Reward Correction):在“强师弱生”的蒸馏场景中,利用教师的预训练基座(Pre-RL base model)而非学生的初始策略作为参考模型 ,能够提供更准确的隐式奖励信号,从而进一步提升蒸馏效果。
1. 引言
在大型语言模型(LLM)的生命周期中,后训练(Post-training)阶段对于对齐人类偏好、提升特定领域能力至关重要。传统的知识蒸馏(Knowledge Distillation, KD)通常采用离线策略(Off-Policy),即学生模型在教师模型生成的轨迹上进行监督微调(SFT)。这种方法虽然简单有效,但存在显著的局限性:学生模型学习的是模仿教师的行为,而非理解行为背后的奖励机制,且存在由于分布偏移(Distribution Shift)导致的协变量偏移问题。
近年来,在线蒸馏(On-Policy Distillation, OPD)逐渐成为研究热点。与离线方法不同,OPD 要求学生模型在自身生成的轨迹上,通过最小化与教师模型输出分布的逆 KL 散度(Reverse KL Divergence)来进行学习。实证研究表明,OPD 在提升学生性能方面通常优于离线蒸馏和传统的强化学习范式。
然而,尽管 OPD 在工程上取得了成功,社区对其内在机理的理解尚显不足:
-
OPD 与强化学习(RL)的数学联系究竟是什么? -
为何 OPD 能实现比单纯 SFT 更高效的能力迁移? -
是否存在一种通用的框架,能够涵盖 OPD 并推导出更具威力的变体?
2. 从强化学习到在线蒸馏
为了理解 G-OPD,我们首先需要重新审视 OPD 的目标函数,并将其映射到强化学习的理论框架中。
2.1 离线蒸馏与在线强化学习
离线蒸馏(Off-Policy Distillation)
给定输入分布 、学生策略 和教师策略 ,离线蒸馏的一般形式(如 SFT)可以表示为:
这等价于在教师生成的数据上最小化交叉熵损失。其核心缺陷在于“离线”性质:学生在测试时面对的可能是自身产生的错误累积,而训练时从未见过这些状态。
在线强化学习(On-Policy RL)
RL 的目标通常是在最大化奖励的同时,约束策略不偏离参考模型 太远。目标函数如下:
其中 是奖励函数, 是 KL 惩罚系数。RL 的挑战在于奖励信号通常是稀疏的(Sparse Reward),例如仅在序列生成的末尾获得一个标量分数,这导致了信用分配(Credit Assignment)的困难。
2.2 在线蒸馏(OPD)的数学本质
OPD 的核心思想是让学生模型生成轨迹,并在这些轨迹的每一个 Token 上对齐教师的 logits。其目标函数为:
注意,这里的期望是基于学生策略 的,这使得它成为一种在线算法。
为了揭示其与 RL 的联系,作者进行了一系列推导。我们将 OPD 的目标函数展开:
此时,我们引入一个任意的参考模型 ,对上式进行恒等变换:
观察上式,我们可以得出本文的第一个重要理论结论:
理论结论 1:OPD 是密集 KL 约束 RL 的特例
OPD 等价于一个特定的 RL 目标,其中:
-
奖励函数 。 -
KL 正则化系数 。 -
参考模型 可以是任意模型。
这一结论非常关键。它不仅建立了监督学习(蒸馏)与强化学习之间的桥梁,还揭示了 OPD 的两个独特优势:
-
密集奖励(Dense Rewards):与标准 RL 仅在句末获得奖励不同,OPD 中的奖励可以分解到 Token 级别。对于序列中的第 个 Token,其即时奖励为:
这种密集的信用分配极大提升了学习效率。 -
隐式奖励建模:这种形式的奖励实际上度量了教师模型相对于参考模型的“对数概率偏移”。这与 DPO(Direct Preference Optimization)等研究中的隐式奖励公式不谋而合。
3. 广义在线蒸馏(G-OPD)框架
基于上述理论推导,作者发现标准 OPD 实际上对 RL 目标施加了强约束:它强制奖励项与 KL 项的权重相等(即 的逆形式),并且在原始公式中隐含了参考模型的选择。
为了释放 OPD 的潜力,作者提出了 Generalized On-Policy Distillation (G-OPD)。G-OPD通过引入两个自由度来扩展标准形式:
-
奖励缩放因子 :控制奖励项相对于 KL 正则项的权重。 -
灵活的参考模型 :不再局限于特定的隐含模型。
G-OPD 的目标函数定义为:
3.1 梯度分析
为了实现 G-OPD,我们需要计算其梯度。根据策略梯度定理及 OPD 的相关推导,G-OPD 的近似梯度为:
其中,Token 级别的优势函数 为:
注:论文中的公式 (14) 写法略有不同,但本质是上述各项的组合。根据论文公式 (14),优势项展开为:
这里需要仔细校对论文原文的符号。原文公式 (14) 为:
(实际上,当 时,第二项消失,退化为标准 OPD 的梯度,即最小化 KL 散度。)
3.2 奖励插值与外推
G-OPD 的最优解满足以下对数概率关系:
这揭示了 的物理含义:
-
(奖励插值):学生模型学习的目标分布是教师与参考模型的加权插值。这会导致学生表现介于两者之间,是一种保守的策略。 -
(标准 OPD):学生完全模仿教师。 -
(奖励外推,ExOPD):这是本文的核心创新点。学生模型将沿着“参考模型 教师模型”的方向进行外推。换言之,它不仅学习教师相对于参考模型的优势,而且会放大这种优势。这与 Classifier-Free Guidance (CFG) 在扩散模型中的作用有异曲同工之妙。
4. 实验场景一:多教师知识融合与 ExOPD
第一个主要实验场景关注同等规模下的模型蒸馏,特别是如何将多个领域专家(Domain Experts)的能力融合回基座模型。
4.1 实验设置
-
基座模型:Qwen3-4B-Non-Thinking。 -
教师模型:通过 GRPO(Group Relative Policy Optimization)在数学(Math)和代码(Code)数据上分别训练得到的 Qwen3-4B-RL-Math 和 Qwen3-4B-RL-Code。 -
参考模型 :固定为学生的初始状态(即 Qwen3-4B-Non-Thinking)。 -
数据集:DeepMath(数学)和 Eurus-RL-Code(代码)。 -
评估基准:AIME24/25, HMMT25 (Math); HumanEval+, MBPP+, LiveCodeBench (Code)。
4.2 单教师蒸馏结果分析
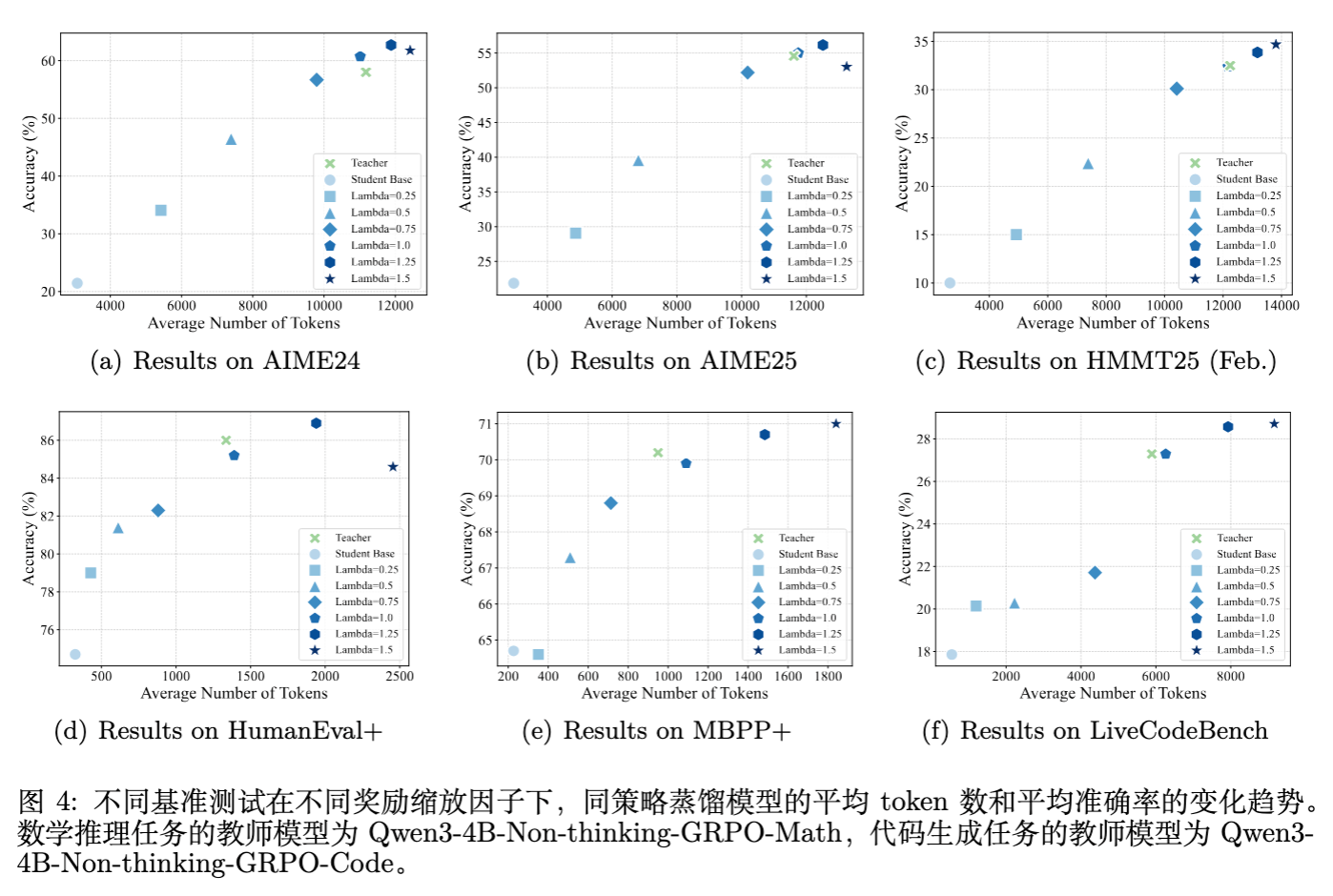
在单教师设置下(例如,用数学 RL 模型蒸馏回基座),研究者探索了 从 0.0 到 1.5 的变化对性能的影响。
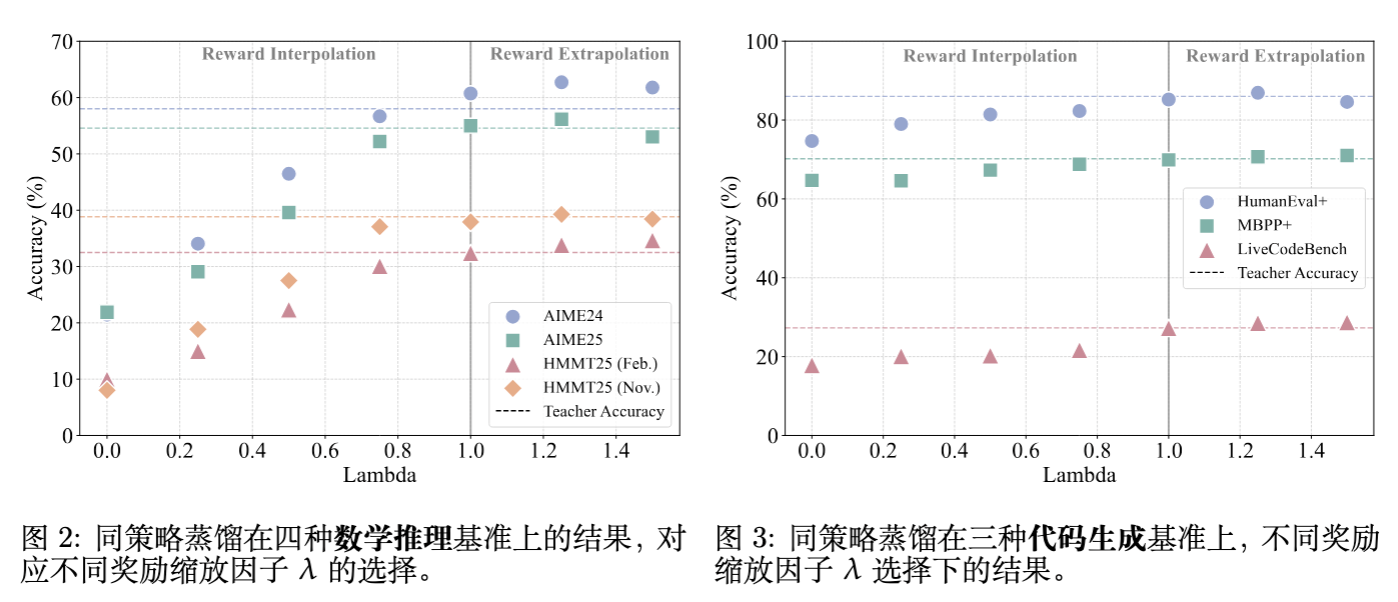
主要发现:
-
标准 OPD () 的局限:OPD 能够完全恢复教师模型的性能,但很难超越教师。这验证了模仿学习的上限通常受限于教师。 -
插值 () 的行为:性能随着 的增加而单调上升,介于基座和教师之间。 -
外推 () 的威力:当 时,ExOPD 在所有基准上均超越了教师模型。例如,在 AIME24 上,ExOPD 达到了 62.7% 的准确率,而教师模型仅为 58.0%。
为什么外推有效?
通过放大 ,ExOPD 实际上是在强化那些“教师模型认为比基座模型更好”的 Token。由于 RL 训练后的教师模型在关键推理步骤上会赋予比基座更高的概率,外推操作进一步增强了对这些关键步骤的选择倾向。
然而,外推并非没有风险。当 时,性能开始下降。这可能是因为过度的外推导致模型“Hack”了隐式奖励,过分拟合了某些高对数比率的 Token,破坏了生成的连贯性。
4.3 多教师蒸馏
最具挑战性的设置是将数学专家和代码专家的能力同时蒸馏到一个学生模型中。
对比基线:
-
SFT:在教师生成的轨迹上进行监督微调。 -
ExPO (Model Weight Extrapolation) :一种无需训练的方法,直接对模型权重进行加权外推。
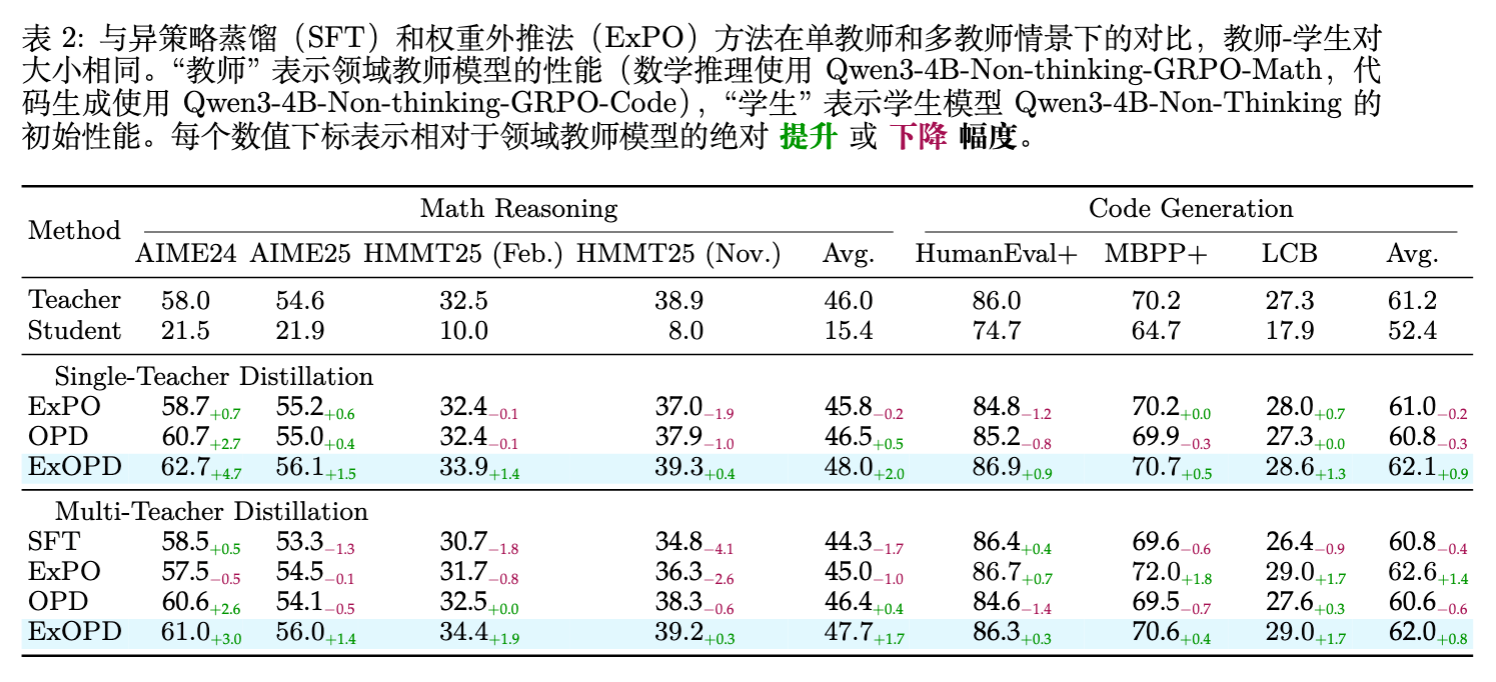
实验结果:
-
SFT:效果最差,且存在负迁移现象。 -
OPD:能够较好地平衡两个领域,但性能上限被各个领域的教师锁死。 -
ExOPD ():结果令人印象深刻。得到的统一学生模型不仅兼顾了数学和代码能力,而且在两个领域都分别超越了对应的领域专家教师。 -
数学平均分:47.7 (ExOPD) vs 46.0 (Teacher) -
代码平均分:62.0 (ExOPD) vs 61.2 (Teacher)
-
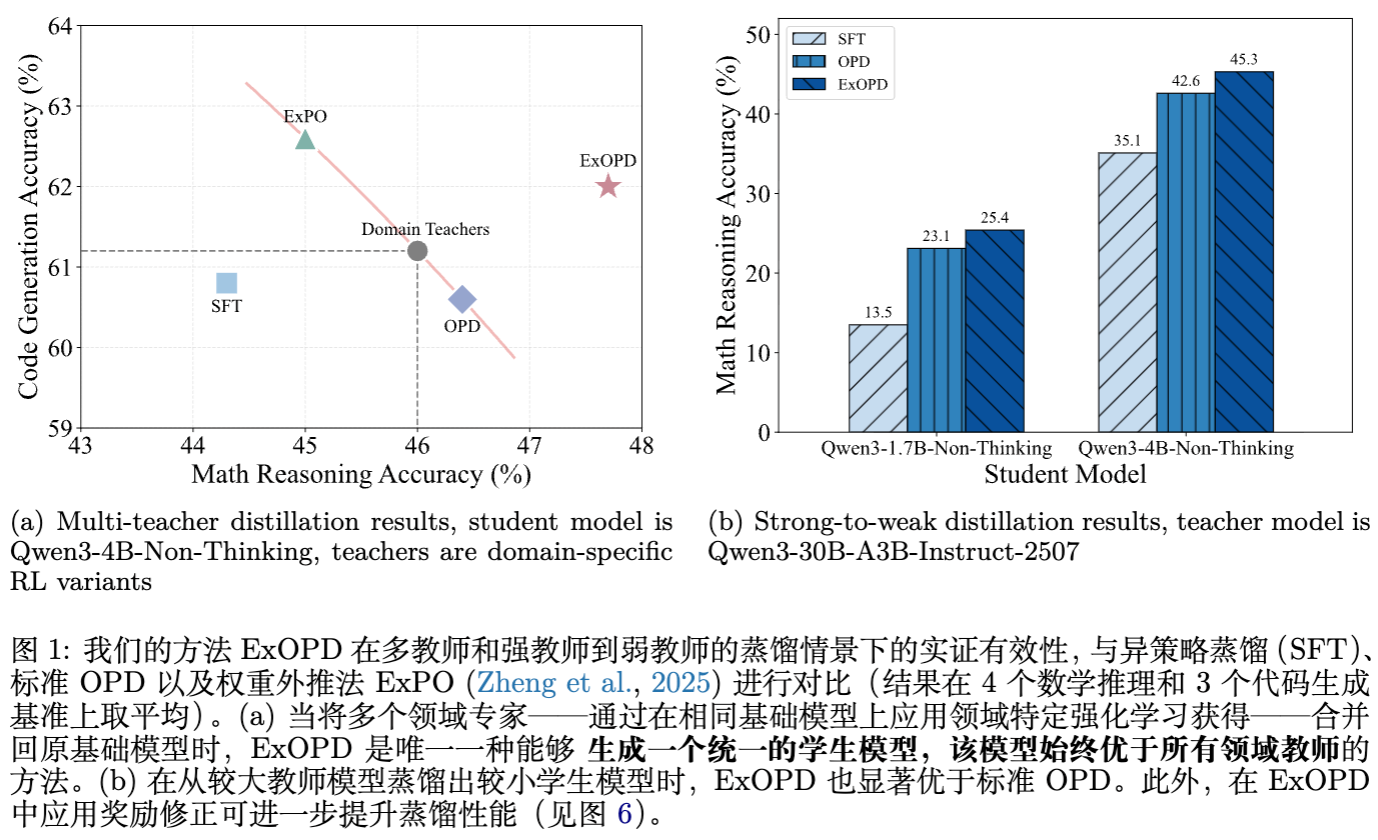
这表明 ExOPD 是实现“超对齐”(Super-alignment)和模型能力融合的有效手段,它通过动态地从自身生成的数据中学习,实现了比单纯权重合并更深层次的知识整合。
5. 实验场景二:强师弱生与奖励修正
第二个实验场景是经典的知识蒸馏设置:用一个强大的大模型指导一个小模型。
5.1 实验设置
-
教师模型:Qwen3-30B-Instruct。 -
学生模型:Qwen3-1.7B-Non-Thinking 和 Qwen3-4B-Non-Thinking。 -
领域:主要集中在数学推理。
5.2 默认 ExOPD 的表现
在默认设置下,参考模型 依然设为学生的基座模型 ()。即便如此,ExOPD 依然表现出对标准 OPD 的显著优势。
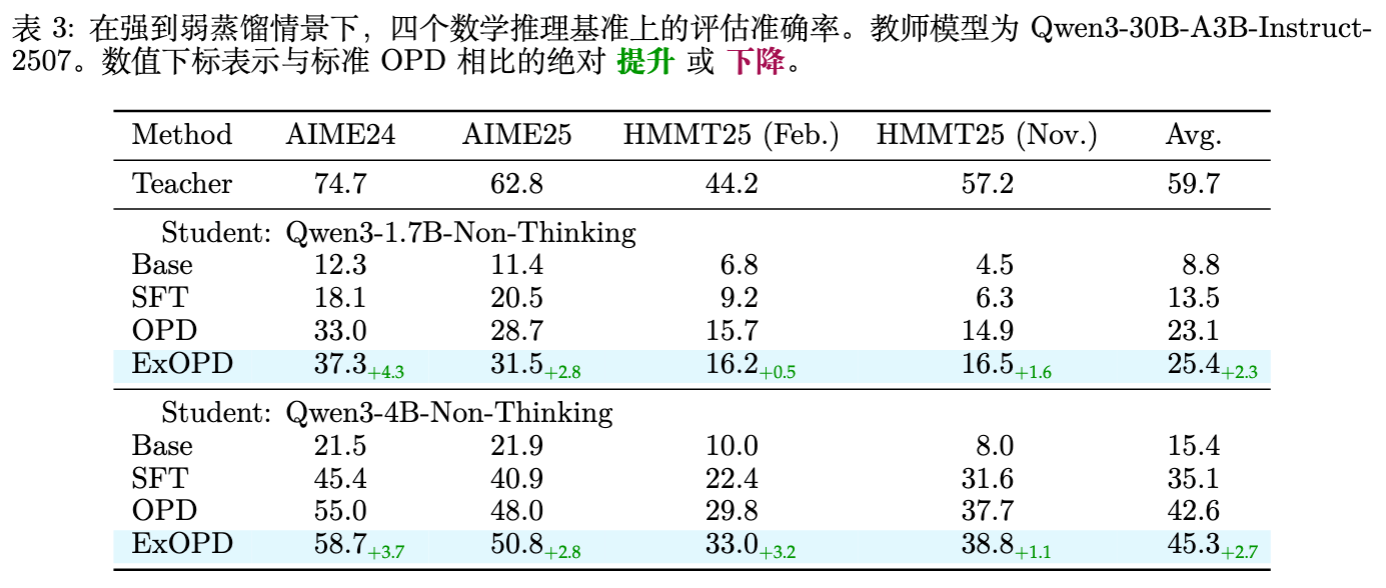
以 Qwen3-1.7B 为学生为例:
-
Base: 8.8% -
SFT: 13.5% -
OPD: 23.1% -
ExOPD: 25.4%
ExOPD 通过放大来自 30B 教师的信号,帮助 1.7B 小模型突破了常规蒸馏的限制。
5.3 奖励修正(Reward Correction)
这是论文提出的另一个重要洞察。在 G-OPD 公式中,隐式奖励项为:
在默认设置中,。然而,理论上更准确的奖励信号应该来源于教师模型相对于其自身基座能力的提升。换句话说,如果我们能获得教师的预训练基座 (即 Teacher Pre-RL),用它作为参考模型,就能构建出更纯净的奖励信号:
这被称作“奖励修正”。
为什么需要修正?
因为 和 之间存在巨大的能力鸿沟(Capacity Gap)。直接对比 30B 的教师和 1.7B 的基座,其中的对数概率差异可能不仅仅包含推理能力的提升,还包含词汇偏好、表达风格等与推理无关的差异(Noise)。使用 可以对消掉这些模型架构带来的固有偏差,只保留 RL 训练带来的增量价值。
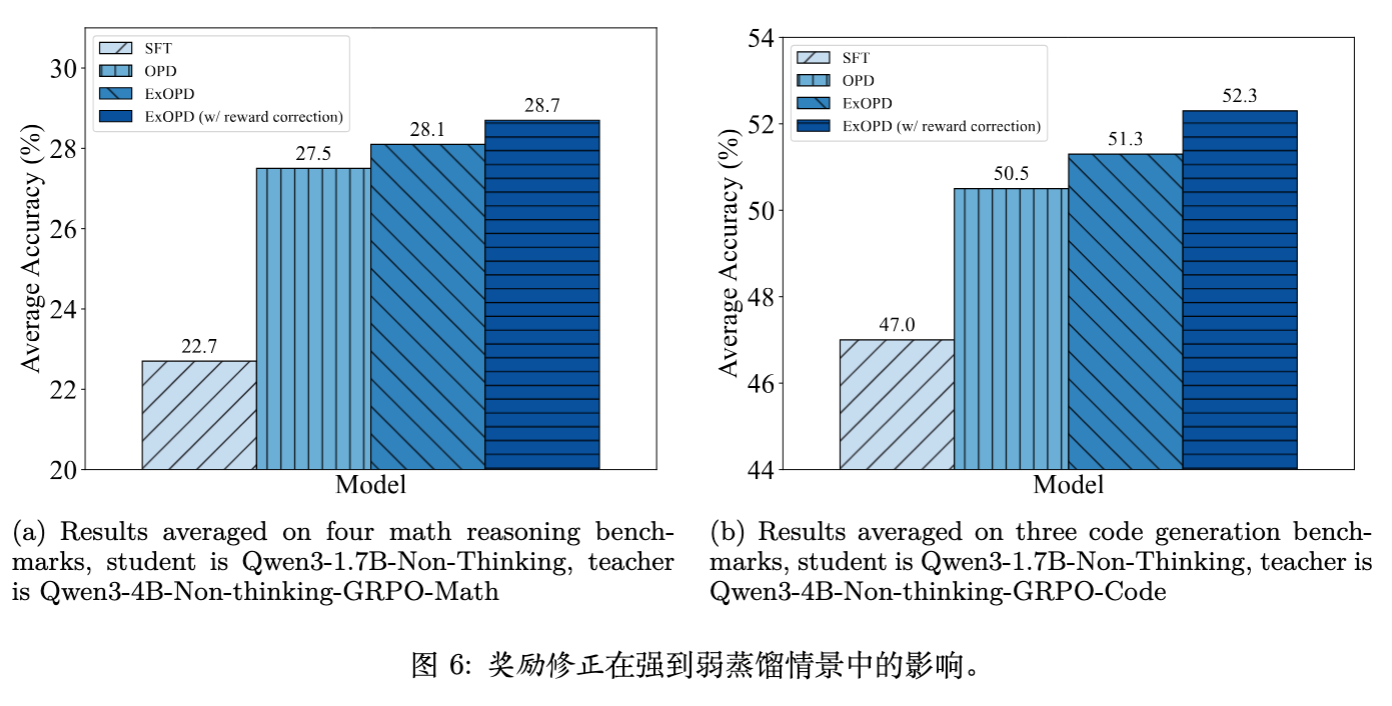
实验验证:
作者由于无法获得 Qwen3-30B 的原始基座,因此在 Qwen3-4B(教师) -> Qwen3-1.7B(学生)的设置下验证了此假设。
结果显示,使用 ExOPD (w/ reward correction) 进一步提升了性能。例如在代码生成任务中,标准 OPD 得分 50.5,普通 ExOPD 得分 51.3,而带有奖励修正的 ExOPD 得分达到了 52.3。
尽管这种方法需要额外的计算开销(需要运行教师的基座模型来计算 log-prob),但它为追求极致蒸馏性能提供了明确的方向。
6. 深入分析与讨论
6.1 训练动态分析
为了探究 ExOPD 到底改变了什么,作者可视化了训练过程中的几个关键指标。
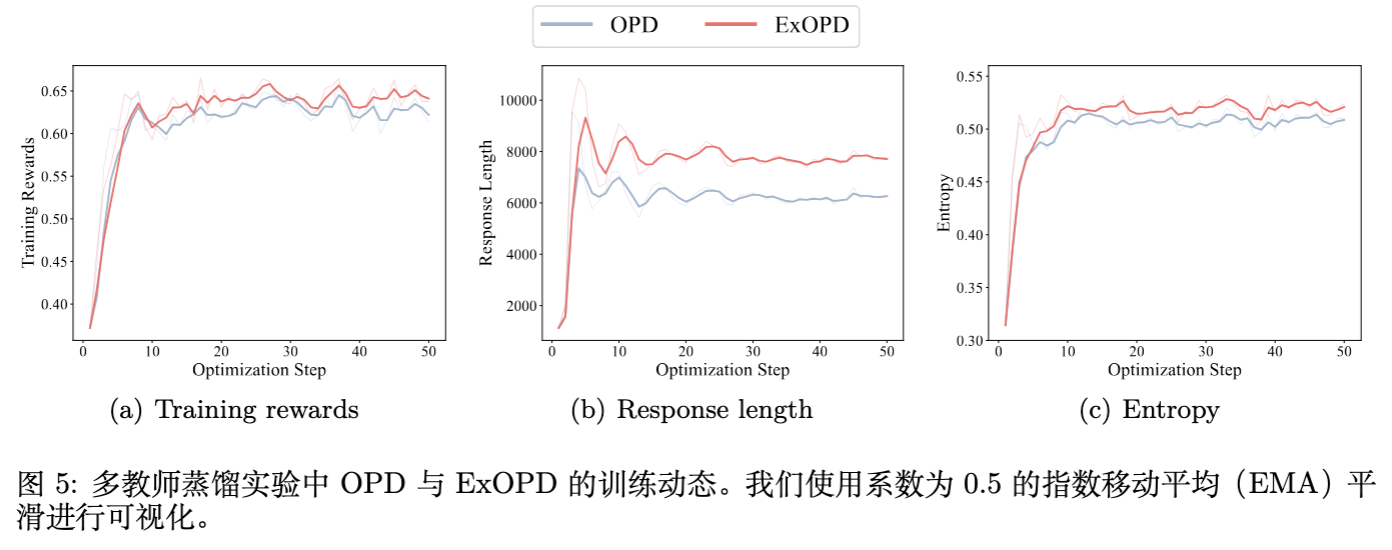
-
响应长度(Response Length):ExOPD 训练出的学生模型倾向于生成更长的回复。随着 的增加,回复长度显著增长。这与 Reasoning 模型(如 o1, R1)的趋势一致,暗示 ExOPD 鼓励学生进行更充分的思维链(CoT)推理。 -
熵(Entropy):ExOPD 保持了较高的输出熵,这意味着生成的回复具有更高的多样性,避免了模型坍缩到单一的模式中。 -
训练奖励:ExOPD 实现了更高的训练奖励,这验证了优化目标的有效性。
6.2 计算成本与权衡
G-OPD 的引入并非没有代价。
-
标准 OPD:需要一次学生前向传播(生成),一次学生前向传播(训练),一次教师前向传播(计算 Logits)。 -
ExOPD:如果 是学生初始状态(固定的),则计算量与 OPD 基本持平(如果参考模型可以被冻结并高效推理)。 -
ExOPD (Reward Correction) :需要额外加载并运行 ,这使得显存占用和计算量增加,尤其是在教师模型很大的情况下。
然而,考虑到 ExOPD 带来的显著性能提升(在某些情况下甚至超过了继续训练教师模型本身带来的收益),这种额外的推理开销在后训练阶段通常是可以接受的。
6.3 与相关工作的联系
-
DPO/IPO:G-OPD 的隐式奖励形式与 DPO 类似,但应用场景不同。DPO 用于偏好对齐,需要成对数据;G-OPD 用于蒸馏,只需要教师模型。 -
ExPO:ExPO 是权重的线性外推,操作简单但缺乏对生成分布的细粒度控制。ExOPD 是概率空间的外推,通过梯度下降优化,具有更好的泛化性和可控性。 -
Self-Correction / Self-Distillation:G-OPD 可以看作是一种广义的自我进化框架。如果将教师模型设为学生模型自身的一个更优版本(例如通过 Rejection Sampling 得到的),G-OPD 就可以演变为一种 Self-Improvement 算法。
更多细节请阅读原文。
往期文章:



