
TL;DR
在基于采样的推理任务(如数学解题、代码生成)中,强化学习(RL)通常被视为一种针对不可微优化的解决方案。然而,来自 CMU、清华大学、UC Berkeley 等机构的研究者在论文《Maximum Likelihood Reinforcement Learning》中提出一个核心观点:现有的强化学习目标(最大化预期奖励/通过率)仅仅是最大似然估计(MLE)的一阶近似。
论文提出了 MaxRL,这是一种基于采样的框架,旨在通过强化学习技术来近似最大似然目标。MaxRL 定义了一个以计算量(采样次数)为索引的目标函数族,随着采样计算量的增加,该目标从标准的 RL 平滑过渡到精确的 MLE。
核心贡献:
-
理论统一:证明了标准 RL 仅优化了 MLE Maclaurin 展开式的第一项。 -
新算法:提出了一种极其简单的 On-Policy 梯度估计器。与 REINFORCE/GRPO 相比,其主要区别在于归一化方式:MaxRL 使用成功样本的数量 进行归一化,而不是总样本数 。 -
实验结果:在 Math 500、AIME 等基准测试中,MaxRL 在 Qwen2.5/3 等模型上 Pareto 优于 GRPO 和 RLOO,特别是在保持生成多样性(Pass@k)和防止过拟合方面表现出显著优势。
1. 引言
在现代大语言模型(LLM)的后训练阶段,强化学习(RL)已成为提升模型推理能力的标准范式(如 RLHF, RLVR)。特别是对于数学问题求解、程序合成等任务,环境反馈通常是二元的(Binary):答案正确或错误。
在这种设置下,业界普遍采用的目标是最大化预期回报(Expected Return),在二元奖励下等价于最大化通过率(Pass Rate, )。常用的算法包括 PPO、RLOO 以及最近流行的 GRPO(Group Relative Policy Optimization)。
然而,这篇论文提出了一个根本性的反思:为什么我们要最大化通过率,而不是最大化正确路径的对数似然(Log-Likelihood)?
在完全可微的监督学习(Pre-training/SFT)中,最大似然(MLE)是绝对的主导原则。它具有良好的统计特性,并且随着模型容量和计算量的增加能稳定提升性能。在推理任务中,我们实际上也希望模型生成正确答案的概率最大化。RL 之所以被使用,往往是因为中间的推理步骤(Chain-of-Thought)包含不可微的采样过程,阻碍了直接的梯度传播。
论文指出,RL 实际上是 MLE 的一种低阶近似。当通过率较低时,RL 的行为与 MLE 差异巨大。MaxRL 的动机便是弥合这一差距,利用额外的采样计算量(Test-time compute / Training-time rollouts)来更逼近 MLE 目标。
2. 问题形式化与核心理论
2.1 潜在生成模型 (Latent Generation Models)
考虑输入 (Prompt)和输出 (Answer)。在推理模型中,模型并不直接生成 ,而是生成一个潜在变量 (CoT 推理过程),然后通过确定性函数 得到最终答案。
正确性由二元奖励函数定义:如果 ,则奖励为 1,否则为 0。
模型生成正确答案的边际概率(Marginal Probability),即通过率(Pass Rate),定义为:
2.2 两种优化范式的对比
最大似然估计 (MLE) 的目标是最大化正确答案的对数概率:
其梯度为:
注意这里的 项,它意味着 MLE 会对困难样本(低通过率)给予极大的权重。
强化学习 (RL) 的目标是最大化预期奖励(即通过率):
其梯度为:
可以看出,两者的核心区别在于是否包含 这一加权项。
2.3 核心洞察:Maclaurin 展开
为了建立 RL 和 ML 的联系,论文利用了 的 Maclaurin 级数展开。令 ,则:
其中 表示连续 次采样均失败的概率。
对上式求导,得到 ML 的梯度展开式:
其中 是至少一次成功的概率。
结论:
-
标准 RL 仅优化了该级数的第一项(),即 。 -
MLE 优化的是所有 梯度的加权和。
这解释了为什么 RL 是 MLE 的一阶近似。当 很小时,高阶项()包含关于“罕见成功”的关键梯度信息,而标准 RL 忽略了这些信息。
3. MaxRL:基于计算量的目标函数族
受上述展开式的启发,论文定义了 Truncated Maximum Likelihood (MaxRL) 目标函数,截断至第 项:
其梯度为:
这个公式定义了一个以 为索引的目标族:
-
当 时,恢复了 RL。 -
当 时,恢复了 MLE。 -
中间的 值在两者之间插值。
这意味着,我们可以通过增加采样计算量(增大 ),来获得对 MLE 更高保真度的近似。
4. 梯度估计器:从理论到实践
如何估计 ?直接估计每一项 的梯度是复杂的。论文推导出了一个令人惊讶的简单估计器。
4.1 理论基础:条件期望表示
定理 1 指出,MLE 的梯度可以表示为条件期望:
即:MLE 梯度等于仅在成功轨迹上计算的 Score Function 的期望。
4.2 MaxRL 估计器
基于定理 1,论文构建了以下估计器:
对于输入 ,采样 条轨迹 。令 为成功的轨迹数量, 为指示变量(成功为 1,失败为 0)。
定义估计器 :
定理 2 (Estimator-Objective Equivalence):
估计器 是 MaxRL 目标 的无偏估计:
4.3 与 REINFORCE 的对比
这是本文最精彩的部分之一。让我们对比一下标准 RL (REINFORCE) 和 MaxRL 的估计器形式:

注: 是 Score Function。
关键差异:
-
RL 除以总采样数 。随着 增加,RL 只是减少了方差,但优化的目标仍然是 (Pass Rate)。 -
MaxRL 除以成功采样数 。随着 增加,MaxRL 优化的目标本身在发生变化,包含了更高阶的 项,从而逼近 MLE。
这意味着,在 MaxRL 中,增加训练时的 Rollout 数量不仅能减少方差,还能提升优化目标的质量(bias reduction regarding MLE)。
4.4 方差缩减 (Control Variates)
为了在 较小时减少方差,论文引入了一个均值为 0 的基线(Control Variate),即无条件分数的平均值:。
最终的 MaxRL 优势函数(Advantage)形式非常简单。在 On-Policy 实现中,假设 是当前 Batch 的平均奖励,MaxRL 的更新规则实际上是对 Advantage 进行了重加权。
Algorithm 1 的核心差异:
在计算 Advantage 时,MaxRL 使用:
而 GRPO 使用:
RLOO 使用:
MaxRL 的分母是均值 ,这实际上在模拟 的加权效果。
5. 统一视角:权重函数分析
为了深入理解不同目标函数的行为,论文将所有方法的梯度统一写成如下形式:
通过推导,可以得到各方法的权重函数 :
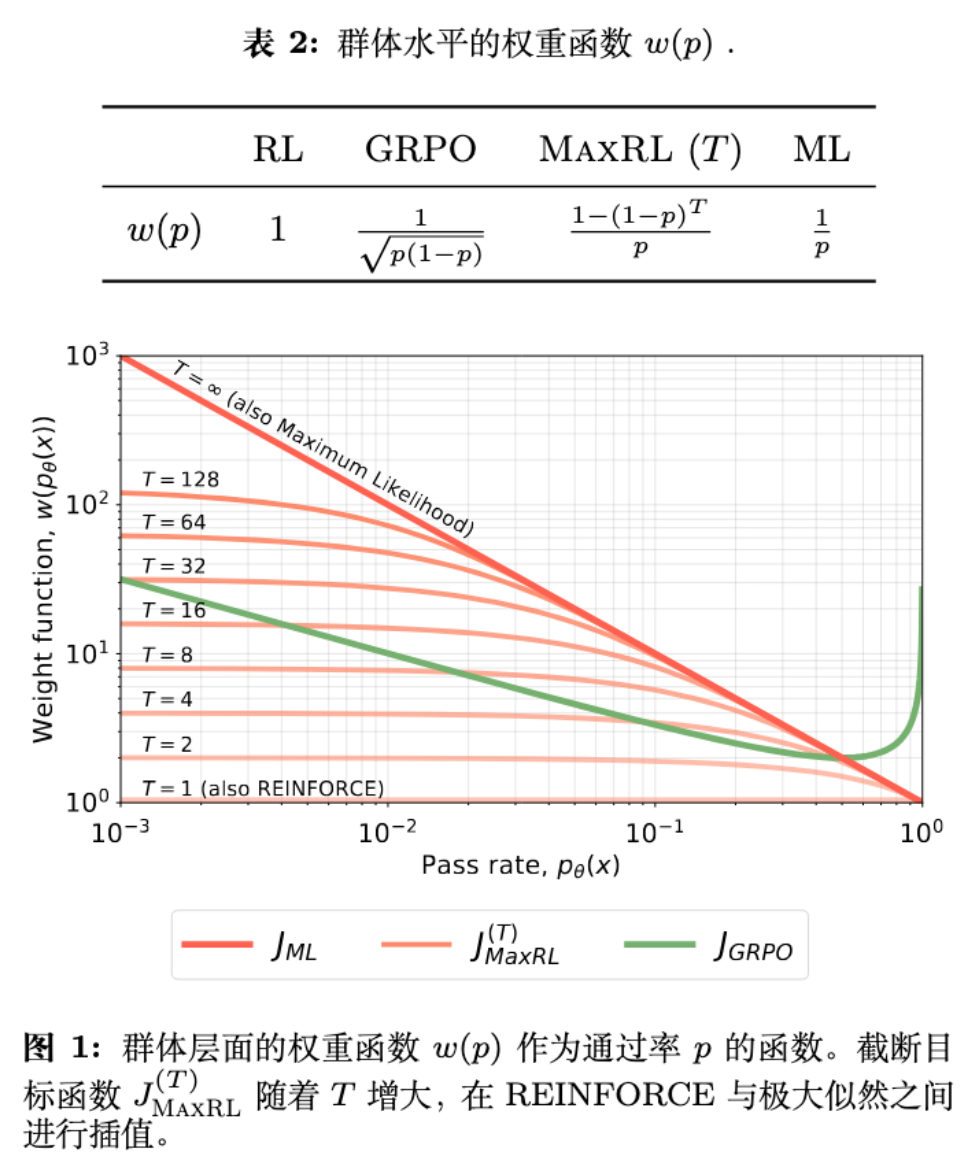
深入分析 GRPO 的缺陷:
论文指出,GRPO 的权重函数在 时会反转上升。这意味着 GRPO 会给那些通过率很高(非常简单)的样本分配较大的梯度权重。这可能导致 Distribution Sharpening(分布锐化)问题,即模型在简单任务上过拟合,导致输出多样性下降(Pass@k 覆盖率降低)。
相比之下,MaxRL 和 MLE 在 时权重单调递减,使得模型能持续专注于未解决的困难样本。
6. 实验验证
论文在多个维度进行了详尽的实验,从完全可控的合成环境到大规模 LLM 训练。
6.1 ImageNet:逼近 MLE 的能力验证
这是一个教学性质的实验(Didactic Experiment)。研究者在 ImageNet 上训练 ResNet-50,将分类问题视为二元奖励的 RL 问题。
-
设置:对比 Exact MLE (Cross Entropy)、RL (REINFORCE) 和 MaxRL。
-
结果:
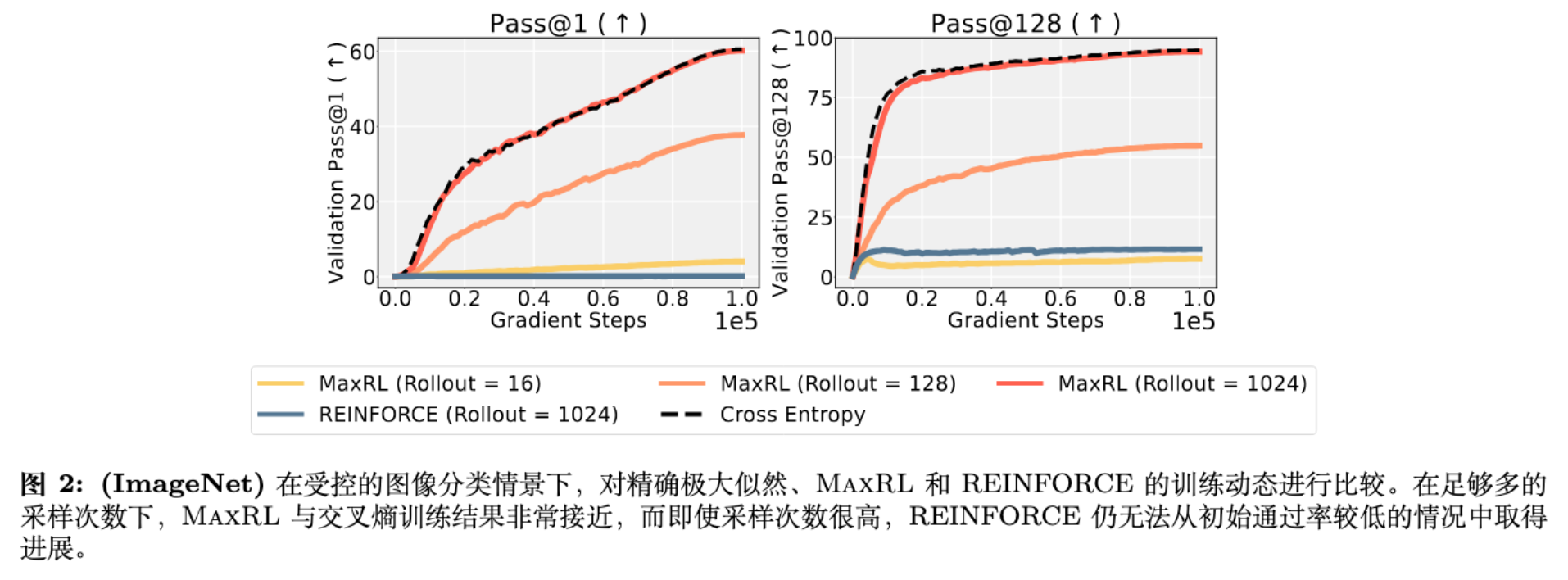
-
随着 Rollout 数量增加(),MaxRL 的训练曲线逐渐逼近 Exact MLE。 -
标准 RL 即使在 时也无法有效学习,因为初始 Pass Rate 极低(),梯度信号微弱。
-
结论:在无限算力(无限采样)极限下,MaxRL 确实收敛于 MLE。
6.2 Maze:无限数据下的 Scaling
-
设置:程序生成的迷宫导航任务,训练集包含 100 万个不同迷宫(模拟无限数据)。模型为 3M 参数的 Transformer。
-
结果:
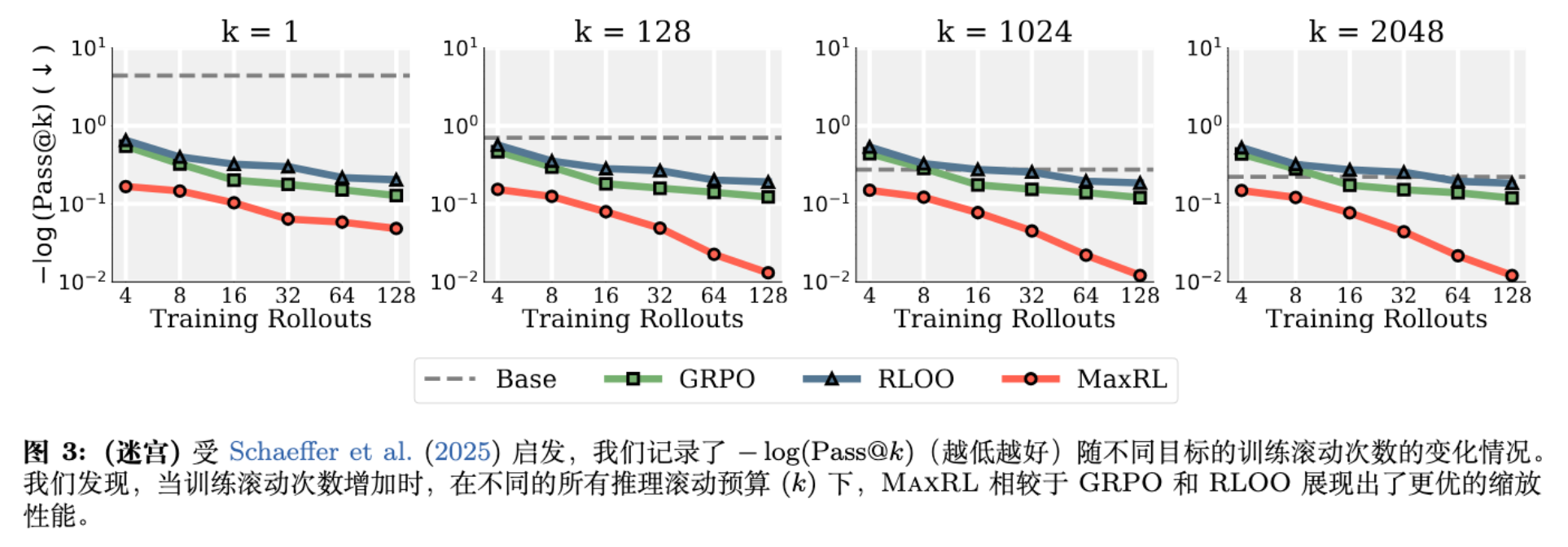
-
在相同的训练步数下,MaxRL 随着 Rollout 数量()的增加,性能持续提升。 -
相比之下,RLOO 和 GRPO 在高 Rollout 设置下收益递减,甚至不如低 Rollout 的 MaxRL。
-
结论:在数据丰富的情况下,MaxRL 能够更有效地利用额外的采样计算量。
6.3 GSM8K:数据稀缺下的过拟合研究
-
设置:使用 SmolLM2-360M-Instruct 模型在 GSM8K 固定训练集上训练 50 个 Epoch。这是为了模拟真实世界中高质量推理数据有限的场景。
-
结果:
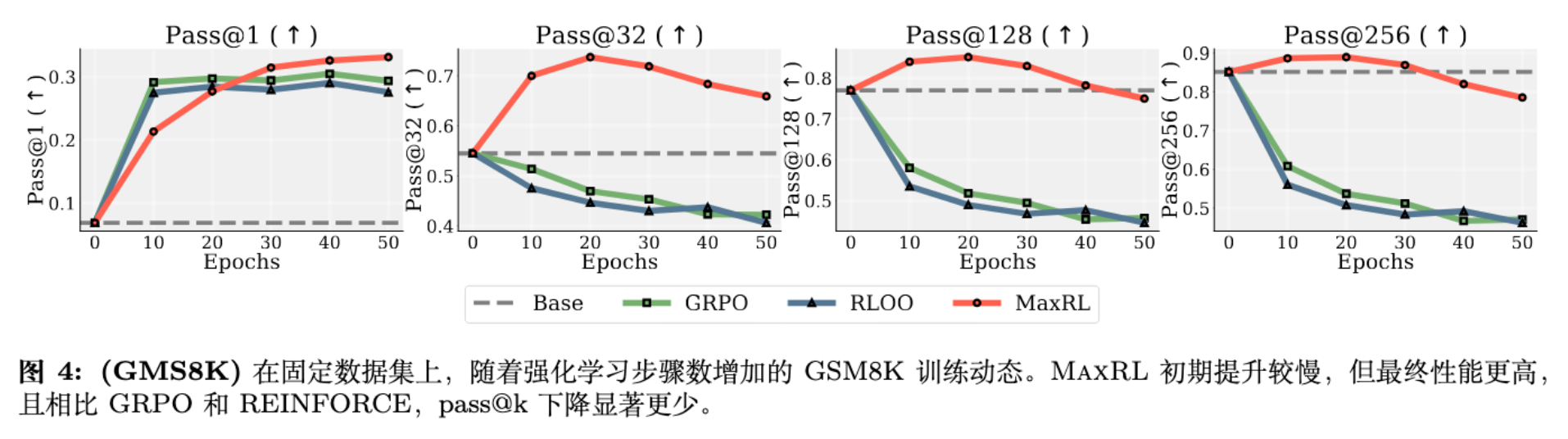
-
Pass@k 坍塌 (Collapse) :GRPO 和 RLOO 在训练后期,虽然 Pass@1 略有提升,但 Pass@128 等高阶指标大幅下降。这表明模型失去了多样性,变成了只会背答案的机器。 -
MaxRL 的鲁棒性:MaxRL 在长时间训练中保持了健康的 Pass@k,并未出现严重的模式坍塌。它在 Epoch 30 左右反超 GRPO,并达到更高的峰值。
-
结论:MaxRL 对过拟合具有更强的抵抗力,能更好地保持生成多样性。
6.4 大规模 LLM 训练:Qwen 系列
-
设置:
-
模型:Qwen3-1.7B-Base 和 Qwen3-4B-Base。 -
数据:POLARIS-53K 数学推理数据集。 -
超参:Batch 256,每条 Prompt 采样 16 条回复()。 -
基准:AIME 2025, MATH-500, Minerva 等。
-
-
结果:
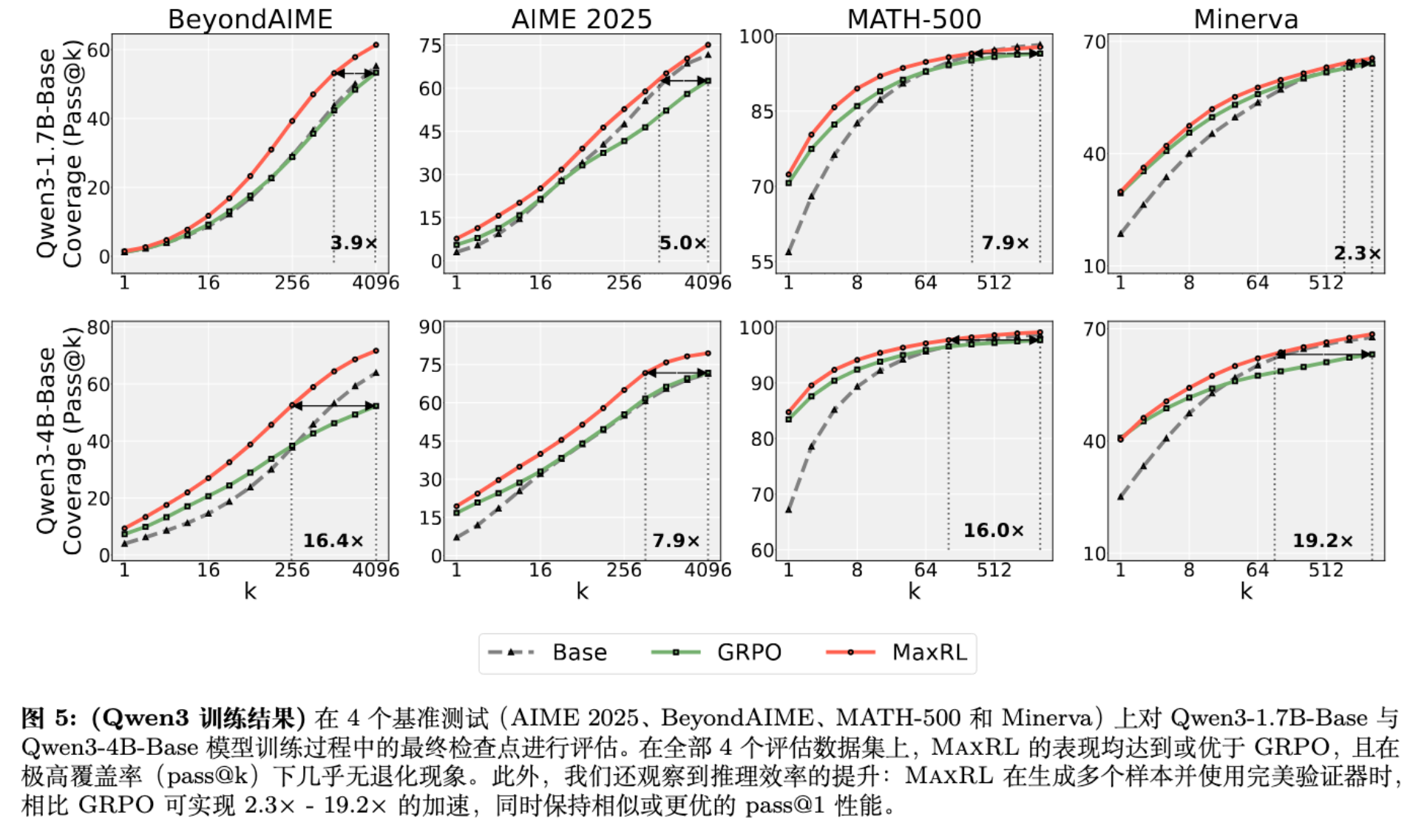
-
Pareto 优势:在 Pass@1 和 Pass@k 的权衡曲线上,MaxRL 始终位于 GRPO 的右上方。 -
推理效率:由于 Pass@k 更高,MaxRL 在使用 Best-of-N 采样(配合验证器)时,能获得高达 20倍 的推理效率提升(即达到相同准确率所需的采样次数更少)。
-
结论:MaxRL 的优势可以扩展到十亿参数级别的现代 LLM 训练中。
7. 深入分析:MaxRL 为什么有效?
7.1 梯度范数与样本难度
论文分析了不同难度样本上的梯度范数(Gradient Norm)。
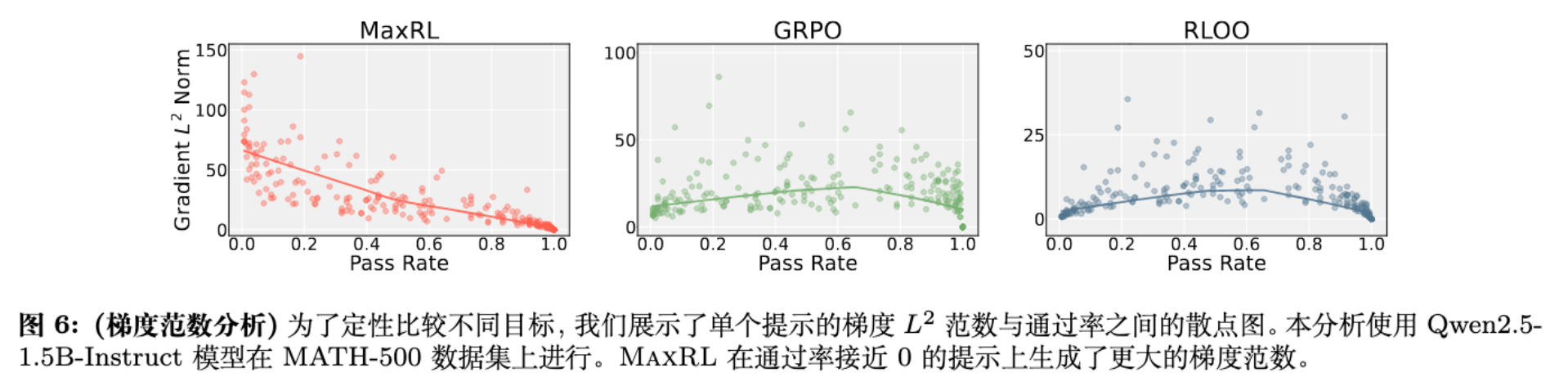
-
MaxRL 与 Cross-Entropy 相似:在 Pass Rate 接近 0 的困难样本上,梯度范数最大;在简单样本上,梯度几乎为 0。 -
GRPO 的反常行为:在 Pass Rate 接近 0.5(中等难度)时梯度最大,但在极难样本上梯度消失。更糟糕的是,在 Pass Rate 接近 1 时,GRPO 仍保留了不必要的梯度权重。
7.2 训练动态:从数据中挖掘更多信号
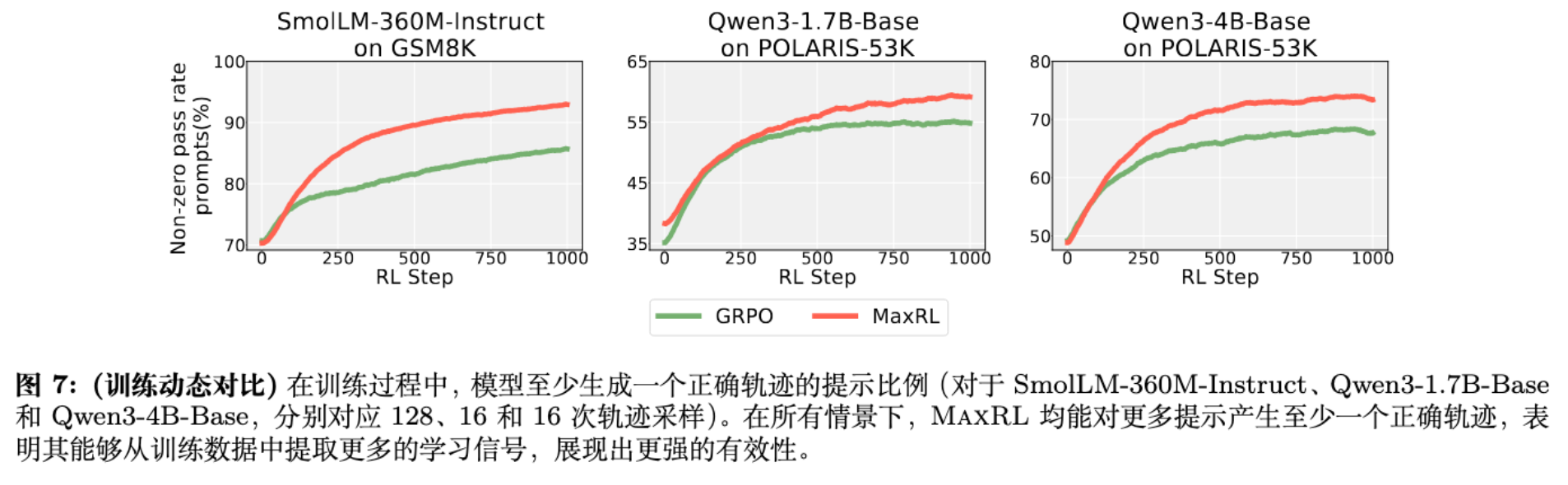
7.3 关于探索 (Exploration)
虽然 MaxRL 本身没有引入显式的探索项(如熵正则化),但其目标函数天然鼓励优化 。由于 关注的是“ 次尝试中至少一次成功”,这隐式地鼓励模型去覆盖那些当前概率较低但在多次尝试下可能正确的路径,从而保留了多样性。
8. 讨论与相关工作对比
8.1 与 GRPO 的对比
GRPO 是目前 DeepSeek-R1 等模型背后的核心算法。它的优势在于不需要 Value Network,节省显存。MaxRL 同样不需要 Value Network,具有相同的系统优势。
但从优化目标来看,GRPO 的 归一化导致了对简单样本的过度关注(Inverse Weighting)。MaxRL 的 归一化则实现了类似 Inverse Probability Weighting (IPW) 的效果,更符合 MLE 的统计原理。
8.2 与 RLOO 的对比
RLOO (REINFORCE Leave-One-Out) 是标准 RL 的方差缩减版本。它虽然无偏,但优化的是 Pass@1。实验证明,在有限数据和算力下,Pass@1 目标容易导致过拟合和多样性丧失。
8.3 局限性
-
二元奖励假设:目前的推导依赖于奖励是 0/1 二元的。对于连续奖励(如由 Reward Model 给出的分数),MaxRL 的理论推导需要扩展。 -
On-Policy 效率:MaxRL 目前是完全 On-Policy 的。虽然这保证了无偏性,但在样本效率上可能不如 PPO 等 Off-Policy 方法(虽然 PPO 在大模型推理中也常被简化为 On-Policy)。
9. 结论
MaxRL 这篇论文为我们提供了一个优雅的理论框架,重新审视了强化学习在推理任务中的角色。它指出:我们之所以用 RL,是因为中间过程不可微,但我们的终极目标应该是 MLE。
通过简单的算法改动(归一化因子的变化),MaxRL 实现了:
-
理论上的正当性:随算力增加收敛至 MLE。 -
实践上的优越性:在 Math Reasoning 任务上全面超越 GRPO。 -
鲁棒性:有效缓解了 RL 训练中的多样性坍塌问题。
这篇论文暗示了一个重要的方向:在 Post-training 阶段,盲目追求 Reward Maximization 可能会导致模型走偏(过拟合简单模式)。回归 MLE 的统计本源,利用训练时的多样本(Rollout)来逼近更优的目标函数,可能是通往 Strong Reasoning 的一条更稳健的道路。
更多细节请阅读原文。
往期文章:



