• 论文标题：Your Group-Relative Advantage Is Biased
• 论文链接：https://arxiv.org/pdf/2601.08521

TL;DR

在 DeepSeek-R1 等推理模型取得成功后，基于组相对策略优化（Group-Relative Policy Optimization, GRPO）及其变体（如 GSPO, DAPO）已成为大模型后训练（Post-training）的主流范式。这些方法通过组内均值作为基线（Baseline）来计算优势（Advantage），从而省去了独立的 Critic 模型。然而，Beihang、UC Berkeley 等机构的最新研究《Your Group-Relative Advantage Is Biased》揭示了一个被长期忽视的统计学问题：在非退化采样条件下，组相对优势估计器相对于真实优势存在系统性偏差。 具体而言，该估计器倾向于低估困难 Prompt 的优势，并高估简单 Prompt 的优势。这种偏差导致模型在困难任务上学习不足，而在简单任务上过度拟合。为此，论文提出了历史感知自适应难度加权（History-Aware Adaptive Difficulty Weighting, HA-DW），通过引入演变难度锚点和自适应重加权机制，在理论和实验上有效修正了这一偏差，显著提升了数学推理任务的性能。

1. 引言

随着大语言模型（LLM）在推理任务上的能力不断提升，强化学习从验证器奖励（Reinforcement Learning from Verifier Rewards, RLVR）已成为一种简单而强大的训练范式。在这一领域，PPO（Proximal Policy Optimization）曾是主导算法，但其需要维护一个与 Policy 模型大小相当的 Value (Critic) 模型，带来了巨大的显存和计算开销。

为了解决这一问题，GRPO（Shao et al., 2024）被提出。GRPO 的核心思想是放弃 Critic 模型，转而对于每个 Prompt 采样一组输出（Group of outputs），利用这组输出的平均奖励作为基线（Baseline）来计算优势函数。这一设计极大地降低了资源消耗，并衍生出了 GSPO、DAPO、Dr.GRPO 等多种变体。

尽管 GRPO 类方法在工程上取得了成功，但其理论性质，特别是组内优势估计（Intra-group advantage estimation）的统计特性，尚未得到充分研究。现有的直觉认为，只要采样次数 足够大，组均值就能很好地近似真实期望。然而，实际训练中受限于计算成本，采样次数通常很小（如 ）。

本文将深入解读《Your Group-Relative Advantage Is Biased》一文，剖析组相对优势估计中存在的固有偏差（Inherent Bias），并通过详尽的数学推导和实验分析，展示这种偏差如何影响模型训练，以及如何通过 HA-DW 算法进行修正。

2. 组相对优势估计是无偏的吗？

在深入数学推导之前，我们需要先定义问题。

2.1 定义与符号

假设在训练步数 ，我们从数据集 中采样一个 Prompt 。基于当前策略 ，我们独立采样 个回复 。
每个回复获得一个标量奖励 。在数学推理任务中，通常假设奖励是二值的（Binary），即 。

• 真实期望奖励（Expected Reward）：
  对于 Prompt ，策略 的真实期望奖励定义为：

  这也代表了 Prompt 的真实难度。 越小，题目越难。

• 真实期望优势（Expected Advantage）：
  对于某个特定回复 ，其真实优势定义为实际奖励减去真实期望：

  
  

• 组相对优势估计（Group-Relative Advantage Estimator）：
  在 GRPO 中，我们不知道 ，只能用组内样本均值 来近似：

  其中 是组内总奖励。于是，估计的优势为：

  
  

2.2 偏差的来源：非退化条件

如果我们在所有可能的情况下计算 ，根据大数定律，它是 的无偏估计。但是，在实际的策略梯度更新中，并非所有样本都参与更新。

当组内所有回复的奖励完全相同（全 0 或 全 1）时：

此时梯度为 0，参数不会更新。这意味着，模型的学习仅发生在“组内奖励有差异”的那些 Batch 中。我们将这种有效更新的事件称为非退化事件 ：

关键洞察： 我们关心的不是全局期望，而是在发生有效更新的条件下（即条件 下），优势估计是否无偏。

2.3 理论分析：偏差的方向

论文提出了核心定理，揭示了条件期望下的偏差方向。

定理 1 (Theorem 1)：
给定 Prompt 和采样次数 ，在条件 下：

1. 对于困难 Prompt ()： 优势估计的期望小于真实优势。

   
   这意味着模型会低估正确答案的价值，导致探索不足。

2. 对于简单 Prompt ()： 优势估计的期望大于真实优势。

   
   这意味着模型会高估正确答案的价值，导致过度利用（Over-exploitation）。

3. 仅当 时，估计才是无偏的。

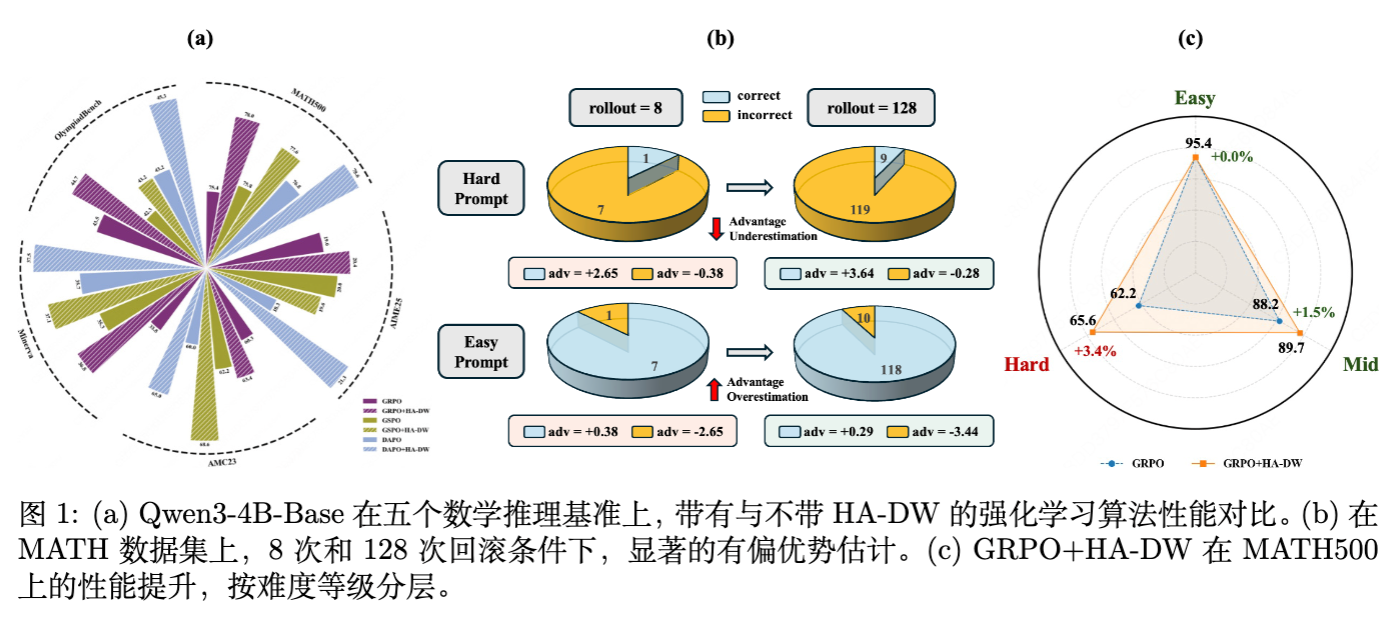
直观解释：
考虑一个极难的 Prompt ()。

• 大多数情况下，采样 个样本全都是错的 ()，这部分被过滤掉了（不发生更新）。
• 偶尔，我们会采样到包含少量正确答案的组（例如 1 个对，7 个错）。
• 在这种情况下，组内均值 ，远大于真实期望 。
• 基线 被高估了，导致计算出的优势 被低估（例如正确答案的优势从 变成了 ）。

反之，对于简单 Prompt，我们丢弃了全对的情况，保留下来的样本往往包含“运气不好”做错的情况，拉低了组均值 ，从而使得算出来的优势偏大。

2.4 偏差的量化与概率界

仅仅知道期望是不够的，论文进一步利用 Hoeffding 不等式和条件概率公式，推导了偏差的概率分布。

推论 1 (Corollary 1)：
在 的典型设置下，且 均匀分布时：

• 对于困难 Prompt ()，估计值 小于真实值 的概率超过 63% 。
• 对于极难 Prompt ()，这一概率超过 78% 。

这意味着，这种偏差不是偶尔出现的噪声，而是系统性的、高概率的现象。随着 Prompt 难度趋向极端（极难或极易），偏差会进一步加剧。

3. 数学证明的细节

为了满足深度解读的需求，我们在此展开定理 1 的证明逻辑，这有助于理解问题的本质。

证明目标： 比较 与 的大小。

根据条件期望的定义：

展开右边：

其中 服从二项分布 。
是非全对且非全错的概率：

分子部分 去掉了 （本身就是0）和 的项：

代入上式，得到条件期望的闭式解：

我们需要判断函数 的正负。

化简分子：

这个式子的符号决定了偏差的方向。
通过分析函数 在 上的性质，可以证明：

• 当 时，，意味着 。
  注意： 基线 被高估了。
• 因为优势 ，基线被高估导致优势被低估。

这严谨地证明了 GRPO 在处理困难样本时，系统性地压低了其优势值。

扩展到非二值奖励 (Appendix D.5)

论文不仅限于二值奖励，还在 Appendix D.5 中将结论扩展到了连续有界奖励（如 Beta 分布或截断高斯分布）。证明使用了顺序统计量（Order Statistics）和条件概率密度函数。结论表明：只要奖励是有界的，且依赖于非退化采样进行更新，这种偏差模式（难样本低估，易样本高估）就会存在。

4. 历史感知自适应难度加权 (HA-DW)

既然偏差来源于仅使用当前 Batch 的小样本均值作为基线，那么自然的思路是引入更多的历史信息来校准对 Prompt 难度的估计。论文提出了 HA-DW (History-Aware Adaptive Difficulty Weighting) 。

HA-DW 包含两个核心模块：

1. 演变难度锚点 (Evolving Difficulty Anchor) ：利用历史信息估计当前的全局能力。
2. 自适应难度加权 (Adaptive Difficulty Weighting) ：基于难度动态调整优势的权重。

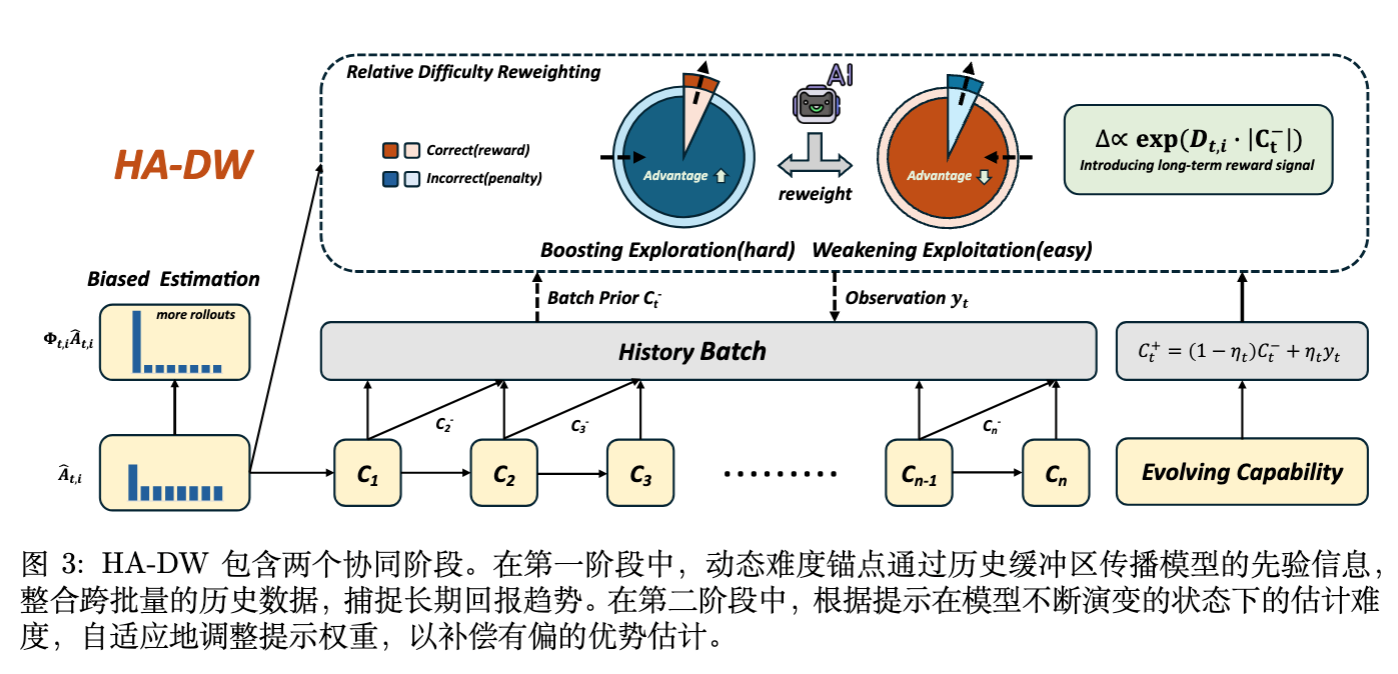
4.1 演变难度锚点 ()

模型在训练过程中能力是不断变化的，因此不能简单地累积历史平均值。论文将模型的解题能力 建模为一个潜在的信念状态（Latent Belief State），并使用类似卡尔曼滤波（Kalman-style）的方式进行更新。

在训练步 ，观测到的当前 Batch 准确率为 （其中 是总奖励， 是总样本数）。
更新公式为：

其中 是先验， 是后验。

动态遗忘因子 ：
为了平衡历史信息的稳定性与对模型能力快速变化的适应性，遗忘因子 是动态计算的：

其中 是过去 个 Batch 信念的标准差。

• 训练初期，模型变化快， 大， 变大，更多地采纳当前观测。
• 训练后期，模型趋于稳定， 小， 变小，更多地依赖历史平滑，减少噪声。

这个 作为一个历史感知的基线，比当前 Batch 的 更准确地反映了模型对当前难度分布的掌握程度。

4.2 自适应难度加权

HA-DW 并不直接用 替换 来计算优势（这样可能引入 off-policy 问题），而是用它来计算一个重加权因子 ，以此修正 。

步骤 1：定义历史相对难度 (History-based Prompt Difficulty)

这个值衡量了当前 Prompt 相对于模型当前能力的难易程度。

步骤 2：确定调整方向与幅度
定义调整方向 ：

定义调整幅度 ：

步骤 3：计算重加权因子

机制解析：

• 对于困难 Prompt ( 很低，)：

  • 根据理论分析，GRPO 倾向于低估其优势。
  • HA-DW 会使得 （对于正奖励），从而放大其优势，鼓励模型探索。
• 对于简单 Prompt ( 很高，)：

  • GRPO 倾向于高估其优势。
  • HA-DW 会使得 ，抑制其优势，防止过拟合。

理论保证 (Theorem 3)：
论文证明了存在一个缩放因子 ，使得加权后的优势估计在期望上比原始 GRPO 估计更接近真实优势：

4.3 算法集成

HA-DW 是一个即插即用的模块，可以无缝集成到现有的算法中：

• GRPO + HA-DW
• GSPO + HA-DW
• DAPO + HA-DW

以 GRPO 为例，修正后的目标函数变为：

仅仅是在优势项上乘了一个 。

5. 实验验证

为了验证 HA-DW 的有效性，研究团队在数学推理任务上进行了广泛的实验。

5.1 实验设置

• 模型： Qwen3-4B-Base, Qwen3-8B-Base, LLaMA-3.2-3B-Instruct。
• 基准算法： GRPO, GSPO, DAPO。
• 数据集： MATH (7.5k 训练), MATH500, AIME25, AMC23, Minerva, OlympiadBench (测试)。
• 硬件： 8 NVIDIA A100 GPU。

5.2 主实验结果

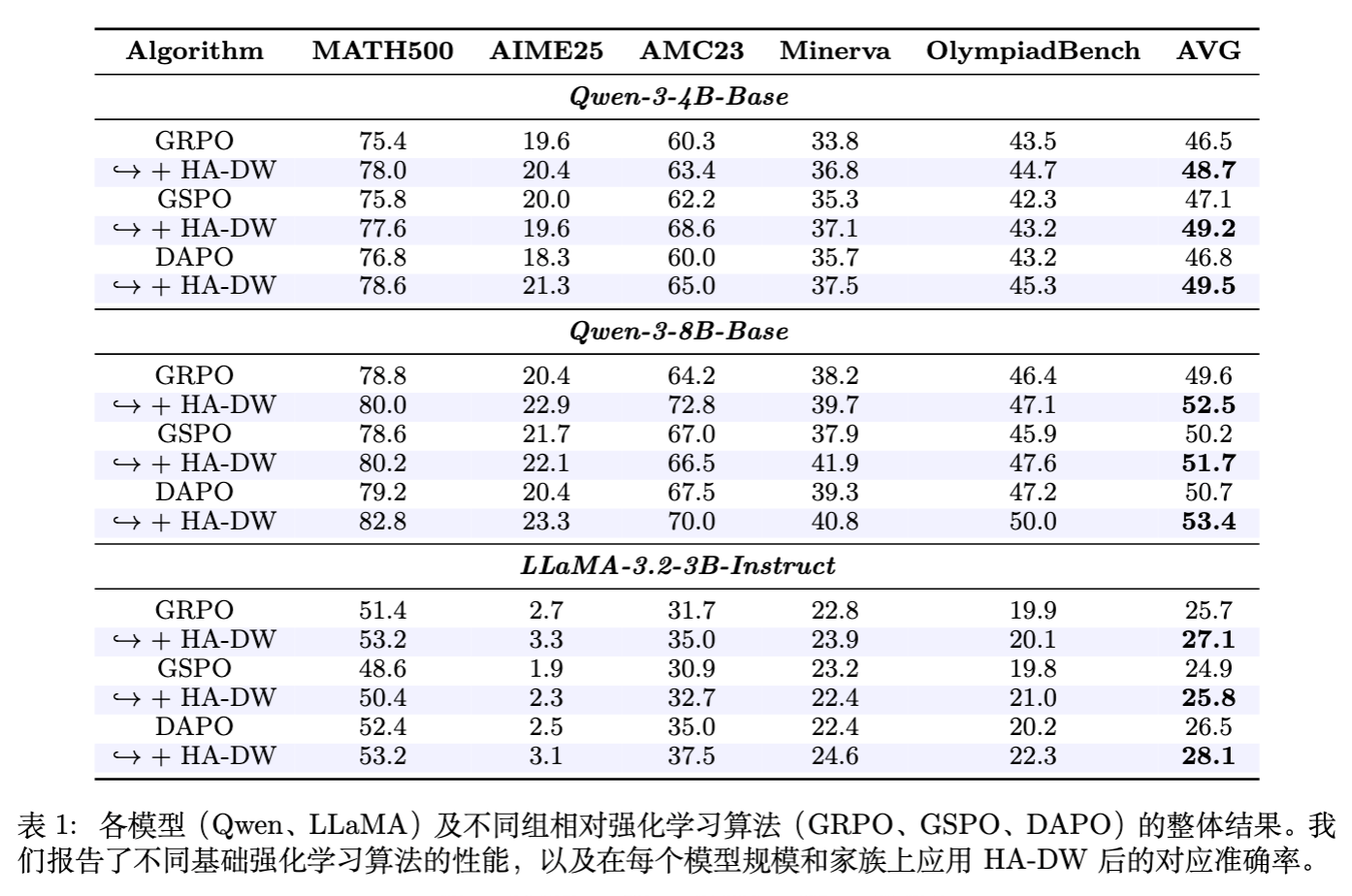
实验结果表明，在所有模型和所有基准算法上，HA-DW 都取得了一致的性能提升。

• Qwen3-4B-Base:

  • GRPO: 46.5% 48.7% (+2.2%)
  • GSPO: 47.1% 49.2% (+2.1%)
  • DAPO: 46.8% 49.5% (+2.7%)
• Qwen3-8B-Base:

  • 平均提升约 3% 。
• LLaMA-3.2-3B:

  • 平均提升约 2.4% 。

特别是在高难度的竞赛题（如 AIME25, OlympiadBench）上，HA-DW 的提升尤为明显。这印证了理论分析：HA-DW 能够有效修正对困难样本优势的低估，从而激励模型攻克难题。

5.3 难度分层分析

为了更直观地看到 HA-DW 对不同难度题目的影响，研究者将 MATH500 数据集按难度分为 Easy, Medium, Hard 三组。

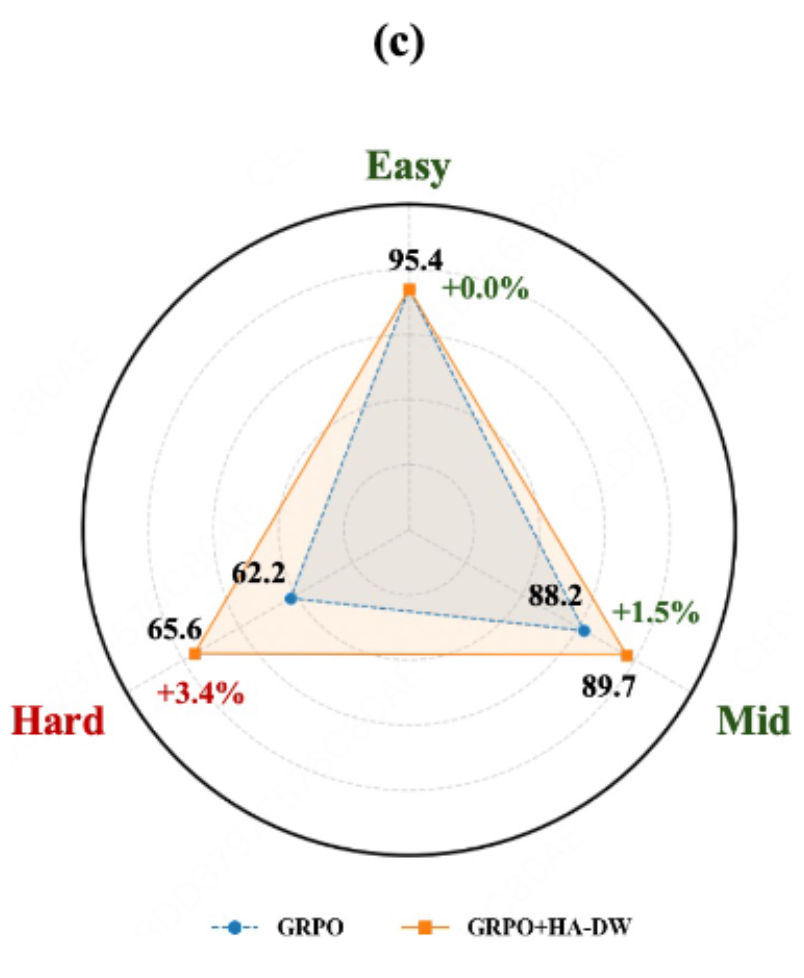
结果显示：

• Easy/Medium 提升幅度较小。
• Hard 组提升幅度最大（+3.4%）。
  这直接证明了 HA-DW 确实通过纠正偏差，增强了模型在长尾困难样本上的探索和学习能力。

5.4 训练动力学 (Training Dynamics)

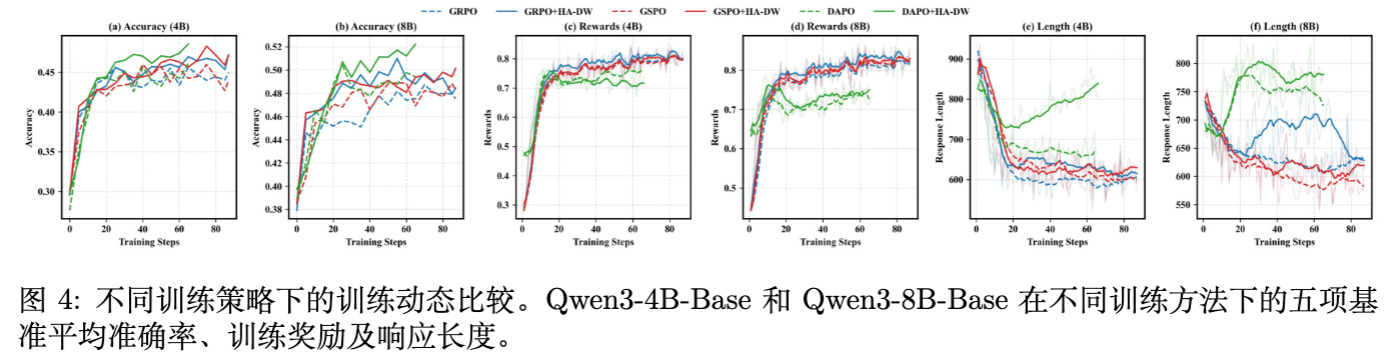
• 准确率与奖励： HA-DW 收敛到了更高的平台。
• 响应长度： 值得注意的是，应用 HA-DW 后，模型的响应长度（CoT 长度）普遍比原始算法更长。这意味着模型学会了通过更复杂的推理链来解决困难问题，而不是尝试走捷径或放弃。

5.5 消融实验

• 关于 的消融： 如果移除动态锚点 ，仅使用固定阈值，性能会有所下降，但仍优于 Baseline。这说明动态跟踪模型能力至关重要。
• 关于 Rollout 数量 ： 增加 （从 8 到 16）确实能缓解偏差，提升 GRPO 性能。但实验表明， 的 GRPO+HA-DW 性能甚至优于 的原始 GRPO。考虑到增加 会成倍增加显存和计算开销，HA-DW 显然是一种更高效的方案。
• 关于 ： 存在一个最优区间（1.3 ~ 1.5），过大或过小都会影响效果。

6. 讨论与展望

6.1 为什么这一发现很重要？

1. 揭示了 GRPO 的理论盲点： 社区长期以来默认 Group Normalization 是完美的替代 Critic 的方案。这项工作指出了其在小样本采样下的统计缺陷。
2. 解释了“偏科”现象： 很多从业者发现 RLVR 训练后的模型容易在简单题上过拟合，而在难题上停滞不前。偏差理论为此提供了完美的解释。
3. 低成本高性能： HA-DW 不需要额外的 Critic 模型，不需要增加采样次数 ，仅需极小的计算代价（维护一个标量 和简单的加权计算），就能获得显著提升。

6.2 局限性

• 依赖历史 Buffer： 虽然开销很小，但算法逻辑上需要维护跨 Batch 的状态。
• 主要针对组相对方法： 该分析主要适用于 GRPO 类方法，对于 PPO 或其他基于 Value Model 的方法不直接适用（虽然它们也有自己的偏差问题）。

更多细节请阅读原文。

往期文章：

• Meta 提出 Dr.Zero：零数据训练的自进化 Search Agent

• 深度解析 Ministral 3：基于级联蒸馏的参数高效密集模型训练方法论

• Sparse-RL：通过稳定稀疏 Rollout 突破 LLM 强化学习的显存墙

• Qwen 发布 ArenaRL：解决开放域 Agent 的奖励建模难题

• NTU & 通义提出 AgentOCR：基于光学自压缩的智能体历史重构

• DeepSeek 新论文 Engram 深度解读

• Anthropic 提出 EDL 来量化大模型的泛化能力

• 小米 MiMo-V2-Flash 技术报告：MoE 架构、混合注意力机制与多教师在线蒸馏

• DeepSeek-R1 v2 发布：新增技术细节与训练流程全解读

• WAIT, WAIT, WAIT... WHY DO REASONING MODELS LOOP?

• 陈丹琦团队新作：负样本强化在 LLM 推理中的有效性机制

• 深度解读 Recursive Language Models：利用递归与环境交互突破 LLM 上下文限制

• 论大语言模型强化学习训练中的 KL 正则化

• 阿里新作 Let It Flow: Agentic Crafting on Rock and Roll 深度解读

• DeepSeek 新作 mHC：为何要把超连接约束在流形上？

• 字节 Seed 新作：通过辅助损失实现 MoE 专家与路由器的紧密耦合 (ERC Loss)

• Bottom-up Policy Optimization: 自下而上的策略优化——语言模型内部潜藏的子策略

• Google DeepMind 新作：自回归模型中的涌现时间抽象实现了分层强化学习

• 被牺牲的元认知：效率导向优化如何改变了模型的推理结构

• Who is Adam? 重新审视大模型 RLVR 阶段的优化器选择

• 代码大模型的 Scaling Laws：编程语言差异性与多语言混合策略研究

• 从 0.5B 到 72B：揭秘 RL Post-Training 中的计算、数据与模型规模权衡

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题