
-
论文标题:Sparse-RL: Breaking the Memory Wall in LLM Reinforcement Learning via Stable Sparse Rollouts -
论文链接:https://arxiv.org/pdf/2601.10079v1
TL;DR
在大语言模型(LLM)的强化学习(RL)训练(如 PPO、GRPO)中,Rollout 阶段的长序列生成导致 Key-Value (KV) Cache 占用大量显存,成为限制训练吞吐量和 Batch Size 的主要瓶颈。虽然 KV Cache 压缩技术在推理阶段已证明有效,但直接将其应用于 RL 训练会导致严重的策略失配(Policy Mismatch)和训练坍塌。
本文解读的论文 "Sparse-RL: Breaking the Memory Wall in LLM Reinforcement Learning via Stable Sparse Rollouts" 提出了一种名为 Sparse-RL 的框架。该框架通过理论推导,将稀疏 Rollout 带来的偏差分解为策略过时(Policy Staleness)和稀疏性诱导的失配(Sparsity-induced Mismatch)。为了修正这些偏差,作者提出了 稀疏感知拒绝采样(Sparsity-Aware Rejection Sampling) 和 基于重要性的重加权(Importance-based Reweighting)。实验表明,Sparse-RL 在数学推理任务上,能够在节省约 40%-50% KV 显存的情况下,达到与全量 KV Cache 训练相当的效果,并且训练出的模型在稀疏推理场景下具有更强的鲁棒性。
1. 引言
随着 OpenAI o1 和 DeepSeek-R1 等推理模型的出现,通过强化学习(RL)激发 LLM 的复杂推理能力已成为社区共识。与传统的指令微调不同,RL 鼓励模型探索更长的思维链(Chain-of-Thought, CoT),从而优化其行为以符合人类偏好或完成复杂的逻辑任务。
然而,RL 训练的计算成本极高。现代 RL 训练主要分为两个阶段:
-
Rollout(采样/生成)阶段:模型根据当前策略生成样本。 -
Training(训练/更新)阶段:基于生成的样本计算梯度并更新参数。
研究表明,Rollout 阶段占据了 RL 执行时间的约 70%。更关键的是,随着推理思维链长度的增加,KV Cache 的显存占用呈线性增长。在长尾样本(Long-tail samples)生成过程中,不断膨胀的 KV Cache 极易导致显存溢出(OOM)。为了防止 OOM,研究人员往往不得不限制 Rollout 的 Batch Size,这直接导致了 GPU 利用率下降和训练吞吐量的受限。这就是所谓的“显存墙(Memory Wall)”问题。
为了解决这一问题,一个自然的思路是将推理阶段成熟的 KV Cache 压缩技术(如 H2O, StreamingLLM, SnapKV, R-KV 等)应用到 RL 的 Rollout 阶段。如果可行,这将把显存复杂度从线性降低到固定预算(Fixed Token Budget),从而支持更大的 Batch Size。
然而,本文的研究发现,直接将这些免训练(Training-free)的压缩方法应用于 RL 训练并非易事,会导致训练过程的不稳定甚至坍塌。本文将详细探讨这一现象背后的原因,并介绍 Sparse-RL 的解决方案。
2. 为何直接稀疏化会导致训练坍塌?
2.1 现象观测
论文作者首先尝试了一个朴素的基线(Naive Sparse Rollout):在 GRPO(Group Relative Policy Optimization)算法的 Rollout 阶段,直接使用 R-KV 或 SnapKV 算法压缩 KV Cache,保留固定数量的 Token(例如 512 个)。
结果显示,这种做法会导致灾难性的后果。如下图所示,在大约 200 步训练后,奖励(Reward)开始大幅下降,同时梯度范数(Gradient Norm)出现剧烈尖峰。
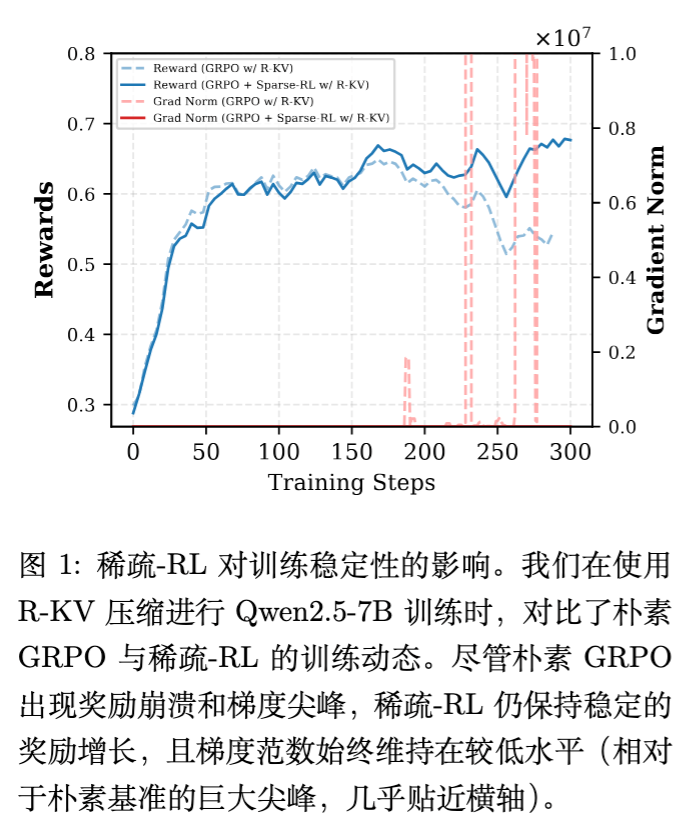
2.2 原因探究
作者将导致训练坍塌的原因归结为两个核心因素的共同作用:
(1) 策略失配(Policy Mismatch)
在标准的 On-policy RL(如 PPO)或 GRPO 中,采样策略和训练策略通常被假设为同一分布(或者通过重要性采样进行修正)。但在稀疏 Rollout 设置下,这三者出现了明显的分歧:
-
稠密旧策略(Dense Old Policy, ):理想的、未压缩的策略,基于完整的上下文历史。 -
稀疏采样策略(Sparse Sampler Policy, ):实际用于生成响应的策略。由于使用了 KV 压缩算子 ,其条件概率依赖于压缩后的历史信息。 -
学习者策略(Learner Policy, ):当前正在优化的策略,使用全量注意力计算梯度。
这种不匹配引入了根本性的 Off-policy 偏差。梯度更新是基于稠密策略计算的,但数据是由稀疏策略生成的。
(2) 异常样本(Anomalous Samples)
现有的 KV 压缩算法主要针对静态推理设计,未考虑到 RL 探索阶段的随机性。在采样过程中,压缩导致的信息丢失可能会诱发模型生成异常样本。
论文在附录 F 中展示了一个典型的例子:在解决数学题时,由于关键信息的丢失,模型陷入了无限重复(Infinite Repetition)的循环中。
这些异常样本(如无限循环、逻辑断裂)会产生巨大的负梯度或极大的噪声。
结论:策略失配放大了被破坏轨迹的影响,而异常样本引入了极端梯度和高方差更新,两者结合导致了训练的数值不稳定和性能崩溃。
3. Sparse-RL 框架
为了解决上述问题,Sparse-RL 提出了一套基于重要性采样理论的修正框架。其核心思想是:识别并拒绝严重偏离稠密策略的异常样本,并对保留的有效样本进行分布修正。
3.1 策略失配的分解
为了获得 的无偏梯度估计,理论上需要使用总的重要性采样(IS)权重:
作者观察到,学习者策略与稀疏采样策略之间的差异源于两个部分:
-
策略过时(Policy Staleness): 与 的差异。 -
稀疏性引起的失配(Sparsity-induced Mismatch): 与 的差异。
因此,重要性权重可以分解为:
基于此分解,Sparse-RL 设计了两个组件来分别处理这两部分偏差。
3.2 稀疏感知拒绝采样
目的:过滤掉因压缩导致严重偏离稠密策略分布的异常轨迹(如幻觉、循环)。
定义稀疏一致性比率(Sparsity Consistency Ratio):
在时间步 ,定义该比率为稠密概率与稀疏概率之比:
-
当 时,意味着稀疏策略与稠密策略在局部是一致的。 -
当 时,意味着稀疏策略进入了稠密模型不支持的状态空间区域(即发生了严重的分布偏移)。
机制:
对于推理任务,单步的幻觉可能导致整个思维链无效。因此,采用序列级的严格约束。定义序列拒绝权重 :
其中 是阈值(例如 1e-4)。这意味着如果稀疏策略生成的任何一个 Token 在稠密策略看来概率极低,整个序列的权重将被置为 0,即不参与梯度计算。
3.3 基于重要性的重加权
目的:对于通过了拒绝采样的“有效”样本,虽然其逻辑大致正确,但分布仍存在偏差。需要通过重加权恢复稠密策略下的期望估计。
目标函数:
Sparse-RL 基于 GRPO 构建。对于给定的提示词 ,稀疏策略生成一组输出 。目标函数形式化为:
其中:
-
将异常轨迹的贡献清零。 -
作为外部系数(在 clip 算子之外),用于无偏地修正采样分布。 -
仅处理策略过时问题,并被 clip 限制在信任域内。
梯度分析:
对上述目标函数求导,得到的梯度形式(简化版)如下:
其中 是通过拒绝采样过滤后的有效轨迹集合。
3.4 机制解释
这个梯度公式揭示了 Sparse-RL 的双层修正机制:
-
序列级过滤(Sequence-level Filtering, ):直接剔除包含幻觉或异常推理步骤的轨迹,确保优势估计 不受分布外(OOD)样本的污染。 -
Token 级重加权(Token-level Reweighting, ):对于接受的轨迹,利用 对 Token 级梯度进行加权,消除稀疏策略与稠密策略之间的分布差异。
4. 实验设置
4.1 实验配置
-
模型:Qwen2.5 (1.5B, 3B, 7B) 和 Llama-3.2-1B-Instruct。 -
数据集:SimpleRL-Zoo,包含 GSM8K 和 MATH 的训练集。 -
基准测试:7 个数学推理榜单,包括 GSM8K, MATH500, Gaokao, Minerva, Olympiad, AIME24, AMC23。 -
KV 压缩方法:主要对比 R-KV(基于冗余去重)和 SnapKV(基于注意力分数)。 -
参数:KV Budget 设为 512(即 Rollout 时仅保留 512 个 Token)。Rollout Batch Size 为 1024。
4.2 对比基线
-
Base:无 RL 训练的基础模型。 -
GRPO (Dense Rollout) :标准 GRPO,使用全量 KV Cache。这是性能上限。 -
GRPO (Naive Sparse Rollout) :直接应用 KV 压缩,无修正机制。这是为了展示坍塌现象。 -
GRPO + Sparse-RL (Ours) :本文提出的方法。
5. 实验结果与分析
5.1 主要结果
实验结果显示,Sparse-RL 在固定 Token 预算下,能够达到与 Dense Rollout 相当的性能,并在部分指标上甚至略有超越。
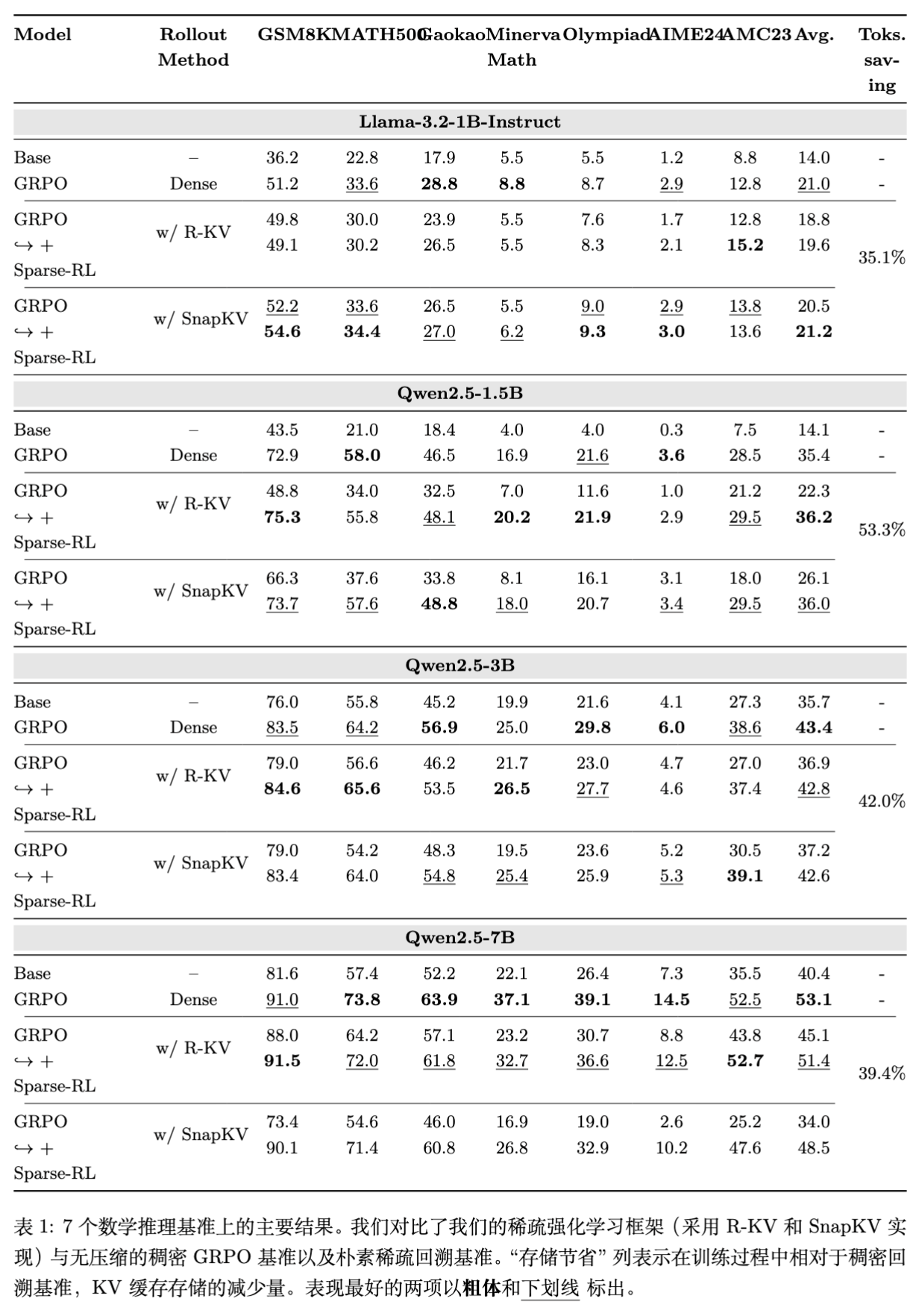
关键发现:
-
性能恢复:Naive Sparse 方法导致性能严重下降(例如 Qwen2.5-1.5B 上 Dense 为 35.4,Naive R-KV 降至 22.3)。而 Sparse-RL 将其恢复至 36.2,甚至超过了 Dense 基线。 -
显存节省:在 Llama-3.2-1B, Qwen2.5-1.5B/3B/7B 上,分别节省了 35.1%, 53.3%, 42.0%, 39.4% 的 KV Cache 存储。 -
尺度扩展性:在 Qwen2.5-7B 上,Sparse-RL 保持了 Dense 模型 96.8% 的性能,证明该方法可扩展至更大模型。 -
压缩算法通用性:无论是使用 R-KV 还是 SnapKV,Sparse-RL 均表现出稳健的性能提升,说明该框架对具体的压缩算子不敏感。
5.2 训练动态分析
为了验证训练的稳定性,作者可视化了训练过程中的各项指标:
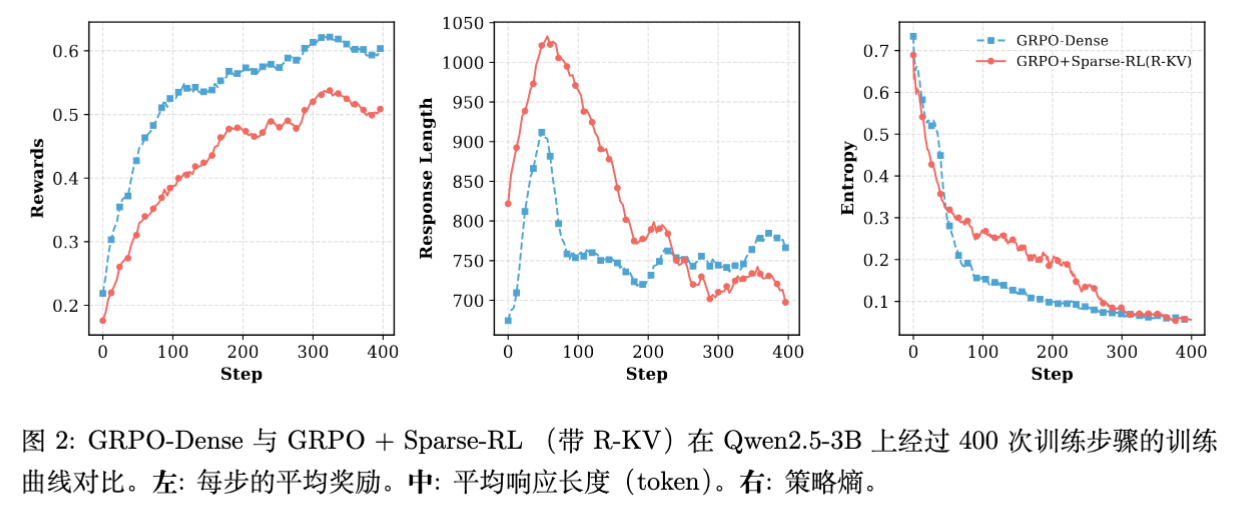
-
奖励曲线:Sparse-RL 的奖励增长虽然略低于 Dense 基线,但紧密跟随,完全避免了 Naive 方法中的骤降。 -
响应长度:Sparse-RL 训练初期生成的序列较长(可能是由于信息丢失导致的重复),但随着训练进行,长度迅速回归并与 Dense 基线对齐。这表明模型学会了在严格的 KV 预算下进行高效推理。 -
策略熵(Entropy):Sparse-RL 在训练中期保持了比 Dense 基线更高的熵,这意味着压缩引入的噪声在一定程度上起到了正则化作用,防止策略过早收敛到局部最优,促进了探索。
5.3 拒绝率与 Clip 比率
论文统计了拒绝采样和梯度截断的动态:
-
平均拒绝率:约为 0.07。这意味着绝大多数由稀疏策略生成的轨迹满足一致性约束,计算浪费可控。 -
Clip 比率:保持在 量级。这证实了 Importance-based Reweighting 成功修正了 Off-policy 偏差,使得策略更新始终保持在信任域内。
6. 深入讨论:稀疏感知训练
除了解决训练显存问题,Sparse-RL 还带来了一个意外的收获(Bonus):增强了模型在稀疏推理场景下的鲁棒性。
6.1 推理时的分布偏移问题
通常情况下,我们用全量 KV Cache 训练模型,但在推理时为了加速,可能会使用 KV 压缩算法。这种“训练-推理”的不一致(Train-Test Discrepancy)通常会导致性能下降。
6.2 Sparse-RL 的优势
由于 Sparse-RL 在训练阶段就在 Rollout 中使用了压缩,并强迫 Learner 策略去适应这种稀疏的上下文,这实际上构成了一种 Sparsity-Aware Training。
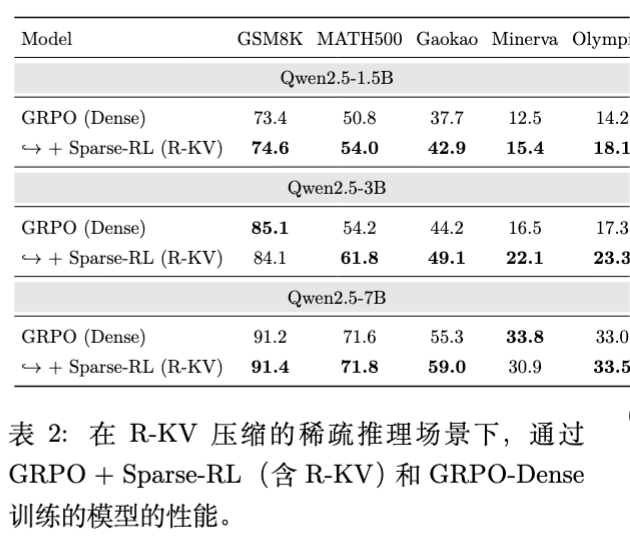
实验表明,当推理时强制使用 R-KV (Budget=512) 进行压缩:
-
使用 Dense GRPO 训练的模型性能显著下降。 -
使用 Sparse-RL 训练的模型在多数基准上表现更优。例如在 Qwen2.5-3B 上,Sparse-RL 在 MATH500 上的得分为 61.8,远高于 Dense 基线的 54.2。
这一结果表明,Sparse-RL 不仅是一种高效的训练方法,也是一种有效的对齐手段,使模型能够内化压缩逻辑,在信息受限的情况下进行更准确的推理。
7. 局限性与未来工作
尽管 Sparse-RL 表现优异,但论文也诚恳地指出了其局限性:
-
任务泛化性:目前的实验主要集中在具有可验证二元奖励的逻辑推理任务(数学)。对于开放式生成任务(如创意写作),“异常 Token”的定义较为模糊,注意力模式也可能不同,Sparse-RL 的分布修正机制是否有效尚待验证。 -
采样效率权衡:拒绝采样机制虽然保证了稳定性,但本质上是一种计算资源的浪费。如果压缩预算过于激进导致拒绝率飙升,训练效率将大打折扣。未来的方向可能是探索 Token 级别的在线修正,而非序列级的拒绝。
更多细节请阅读原文。
往期文章:




