• 论文标题：Scaling Behaviors of LLM Reinforcement Learning Post-Training: An Empirical Study in Mathematical Reasoning
• 论文链接：https://arxiv.org/pdf/2509.25300

TL;DR

今天解读一篇来自中国科学技术大学联合上海人工智能实验室的一篇论文，研究验证了 Sutton 的 "The Bitter Lesson" 在 RL post-training 阶段依然部分成立，但也看到了天花板。

基于 Qwen2.5 全系列模型（0.5B 至 72B）的系统性实验，研究团队得出了以下核心结论：

1. 学习效率与模型规模正相关：大模型在计算（Compute）和数据（Data）指标上均表现出更高的学习效率。
2. 幂律关系显著：测试损失（Test Loss）、计算量与数据量之间遵循可预测的幂律关系，该规律在 Base 模型和 Instruct 模型中均成立。
3. 效率饱和效应：虽然大模型效率更高，但学习效率系数 随模型增大呈现饱和趋势，不会无限增长。
4. 数据复用的有效性：在数据受限场景下，对高质量数据的重复使用（Data Reuse）是有效的。最终性能主要取决于优化总步数，而非样本的唯一性。

1. 引言

在大语言模型（LLM）的研究历程中，预训练阶段的扩展定律（Scaling Laws）已被广泛研究。Kaplan 等人（2020）和 Hoffmann 等人（2022）的工作量化了模型架构、参数量、计算成本、数据量与下游性能之间的关系。这些定律不仅解释了学习动力学，更为计算资源的分配提供了指导（如 Chinchilla 最优计算配置）。

然而，随着强化学习（RL）成为提升 LLM 推理能力（尤其是数学推理）的主流后训练策略，RL 后训练阶段是否存在类似的扩展定律，目前尚缺乏充分的实证研究。

本研究聚焦于数学推理任务，通过三个关键资源维度展开分析：

1. 计算受限（Compute-constrained）：固定 FLOPs 预算下，如何权衡模型大小与训练步数。
2. 数据受限（Data-constrained）：固定唯一样本数量下，模型大小对性能的影响。
3. 数据复用（Data Reuse）：固定计算预算下，唯一数据量与重复优化步数之间的权衡。

2. 实验设置与方法论

为了推导可靠的扩展定律，实验设计必须控制变量并确保可复现性。

2.1 模型与框架

实验统一采用 Qwen2.5 稠密模型系列，覆盖了从 0.5B 到 72B 的参数范围（0.5B, 1.5B, 3B, 7B, 14B, 32B, 72B）。由于该系列模型共享相同的架构设计，参数量（Parameter Count, ）成为分析中唯一的变量。

训练框架使用 VeRL（HybridFlow），这是一个支持大规模 LLM RL 训练的平台。

2.2 数据集设置

• 训练数据：Reasoning360 项目 guru-RL-92k 数据集的数学子集。数据经过严格去重和难度筛选，并按难度递增（基于 Qwen2.5-7B-Instruct 的通过率）排序，以实现课程学习（Curriculum Learning）。
• 评估数据：

  • 拟合扩展定律：从训练分布中留出的 500 道同分布（In-domain）数学题。
  • 泛化性评估：涵盖数学（AIME2024, AMC2023, GSM8K, MATH500）、代码（HumanEval）、逻辑（Zebra Puzzle）和科学（SuperGPQA）的广泛基准测试。

2.3 RL 算法：GRPO

实验采用 Group Relative Policy Optimization (GRPO) 算法。与 PPO 不同，GRPO 省去了 Critic 模型，通过对同一提示（Prompt）采样一组输出并归一化奖励来估计优势（Advantage），从而降低显存成本并保持训练稳定。

GRPO 的目标函数如下：

其中：

• 为一组采样的输出数量。
• 是重要性采样权重。
• 优势 通过组内归一化计算：

2.4 评估指标

主要度量指标为 测试损失（Test Loss, ）。在 RL 设置中，这作为基于奖励的性能代理。

其中 是正确解的数量， 是总数。采用“测试损失”这一术语是为了与基础神经扩展定律文献保持一致。在 RL 语境下，最小化 等价于最大化奖励。奖励信号是二元的（Pass@1）：通过规则匹配提取答案，正确得 1，否则得 0。

3. 核心扩展定律与实证结果

研究团队基于实验数据，提出了统一的预测公式来描述测试损失 、模型大小 和资源预算 （计算量 或数据量 ）之间的关系。

3.1 核心扩展公式

数据表明，测试损失与资源预算之间呈现对数线性（Log-linear）关系：

其中， 代表 学习效率（Learning Efficiency）。

3.2 学习效率的饱和特性

一个关键发现是，学习效率 并不会随着模型规模增加而无限增长，而是表现出饱和趋势。研究提出以下公式对 进行建模：

• ：理论上的最大学习效率。
• ：特征模型规模参数。

该公式表明，尽管大模型始终表现出更高的学习效率，但随着模型尺寸增大，边际增益逐渐递减，渐近趋于 。

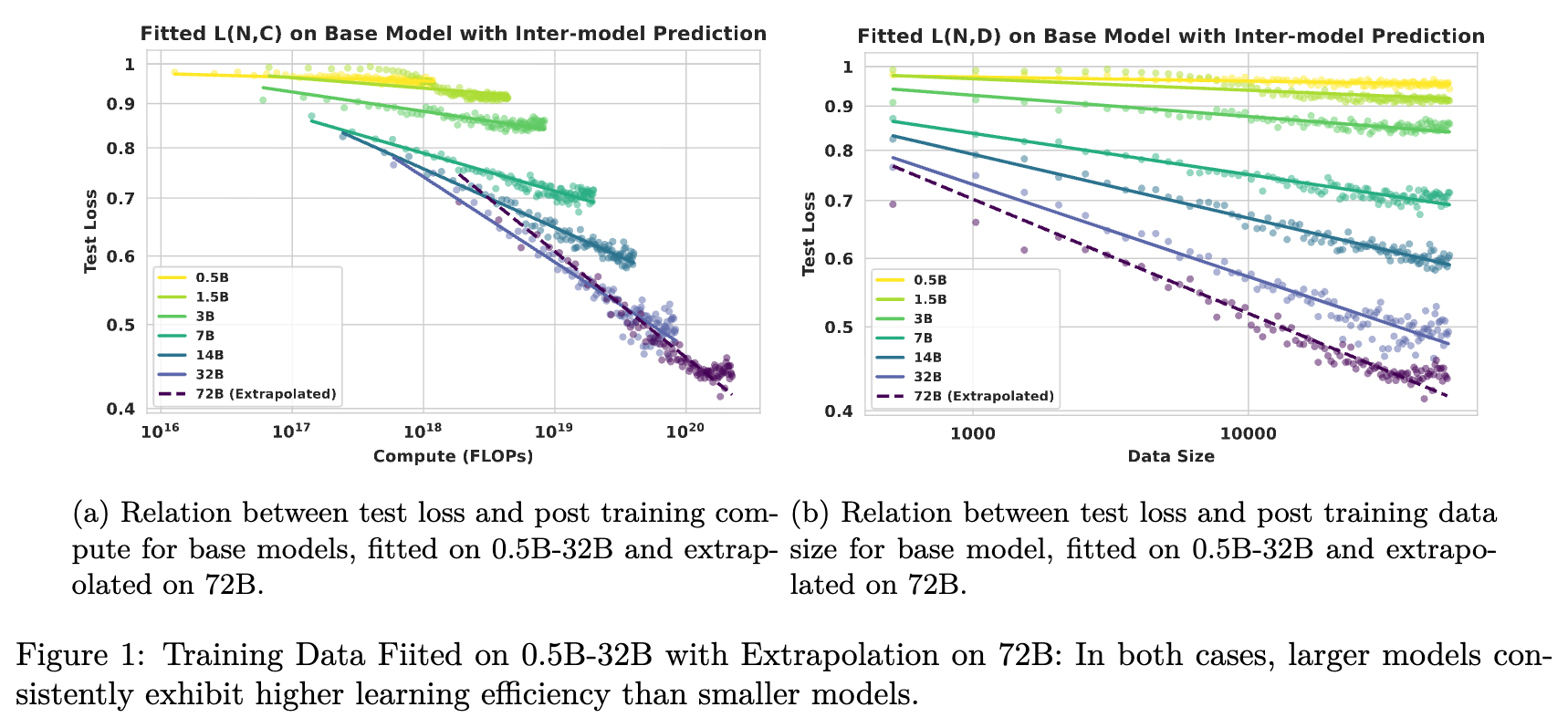
如图 1 所示，无论是计算扩展还是数据扩展，基于小模型（0.5B-32B）拟合的曲线都能较好地预测 72B 模型的表现。

3.3 计算最优扩展 (Compute-Optimal Scaling)

在计算受限场景下，目标是在给定 FLOPs 预算 的情况下，寻找最优模型大小 以最小化测试损失。

实验结果（图 2）显示，损失-计算关系遵循公式 (6)：

其中 服从上述饱和公式。

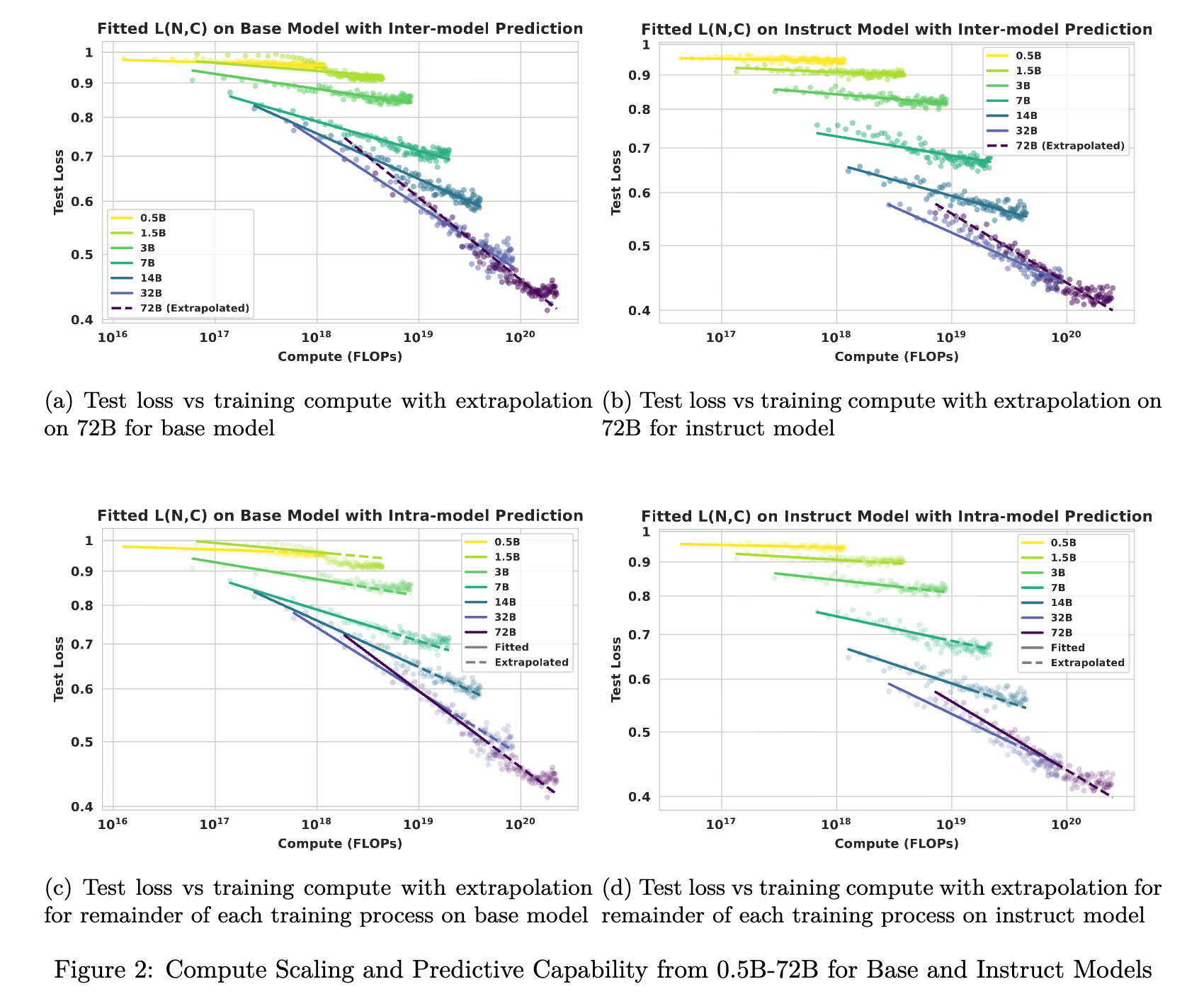
观察 1：在 0.5B 到 32B 的范围内，给定固定预算 ，优先选择较大的模型通常能获得更低的测试损失。然而，在 32B 和 72B 之间，由于学习效率的饱和，扩展带来的边际收益减少，导致模型规模与训练步数之间出现了更明显的权衡（Trade-off）。即在某些计算预算下，较小的模型（如 32B）因能训练更多步数，可能暂时优于较大的模型（72B）。

图 3 进一步量化了这一点，展示了拟合出的 曲线。在 32B 之后，效率增长明显放缓。

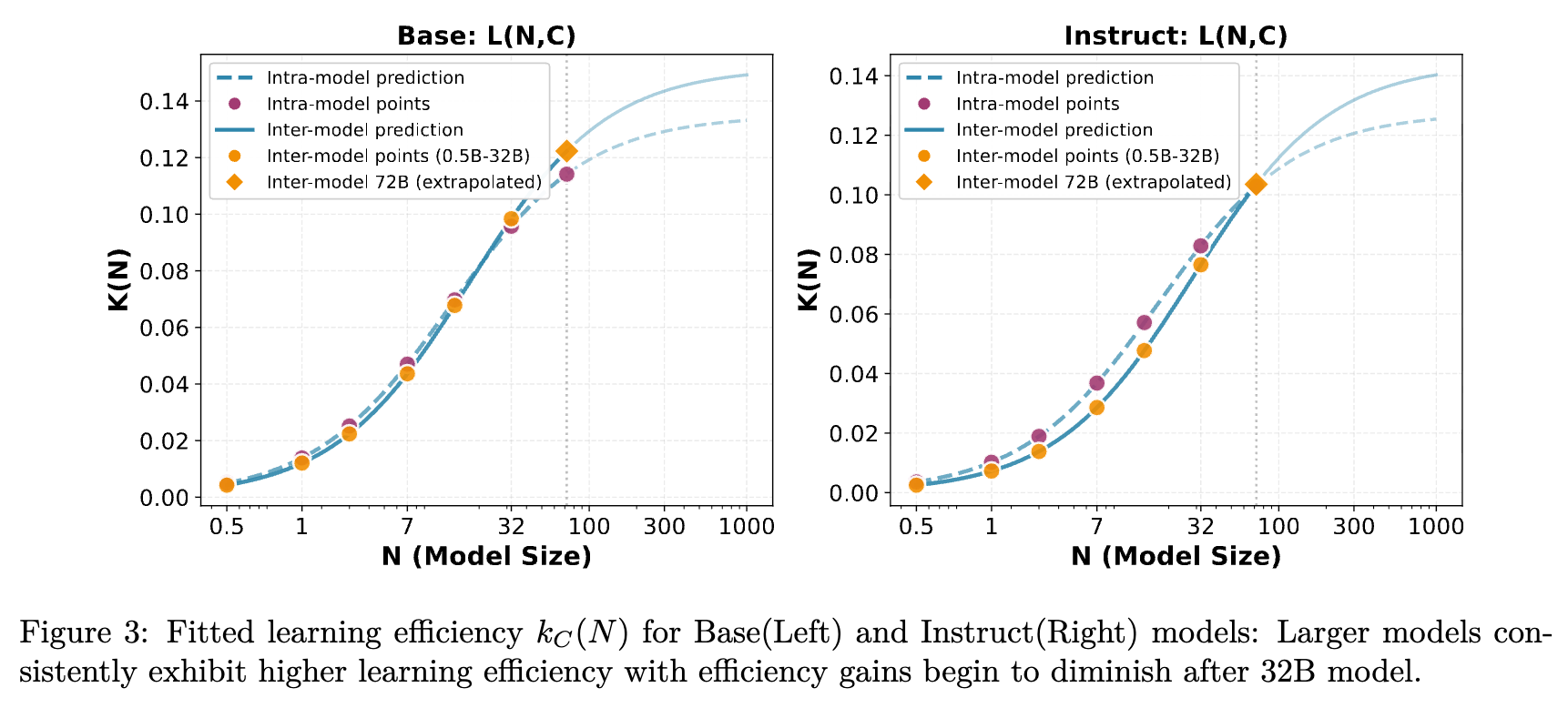
3.4 数据最优扩展 (Data-Optimal Scaling)

在许多实际应用中，瓶颈往往是高质量推理数据的稀缺性。数据受限场景定义为：在给定有限唯一训练数据量 的情况下，确定产生最低测试损失的模型大小 。

实验结果遵循类似的规律：

观察 2：在 0.5B 到 72B 的范围内，对于固定的唯一训练数据量 ，较大的模型始终表现出优越的样本效率（Sample Efficiency），实现更低的测试损失。

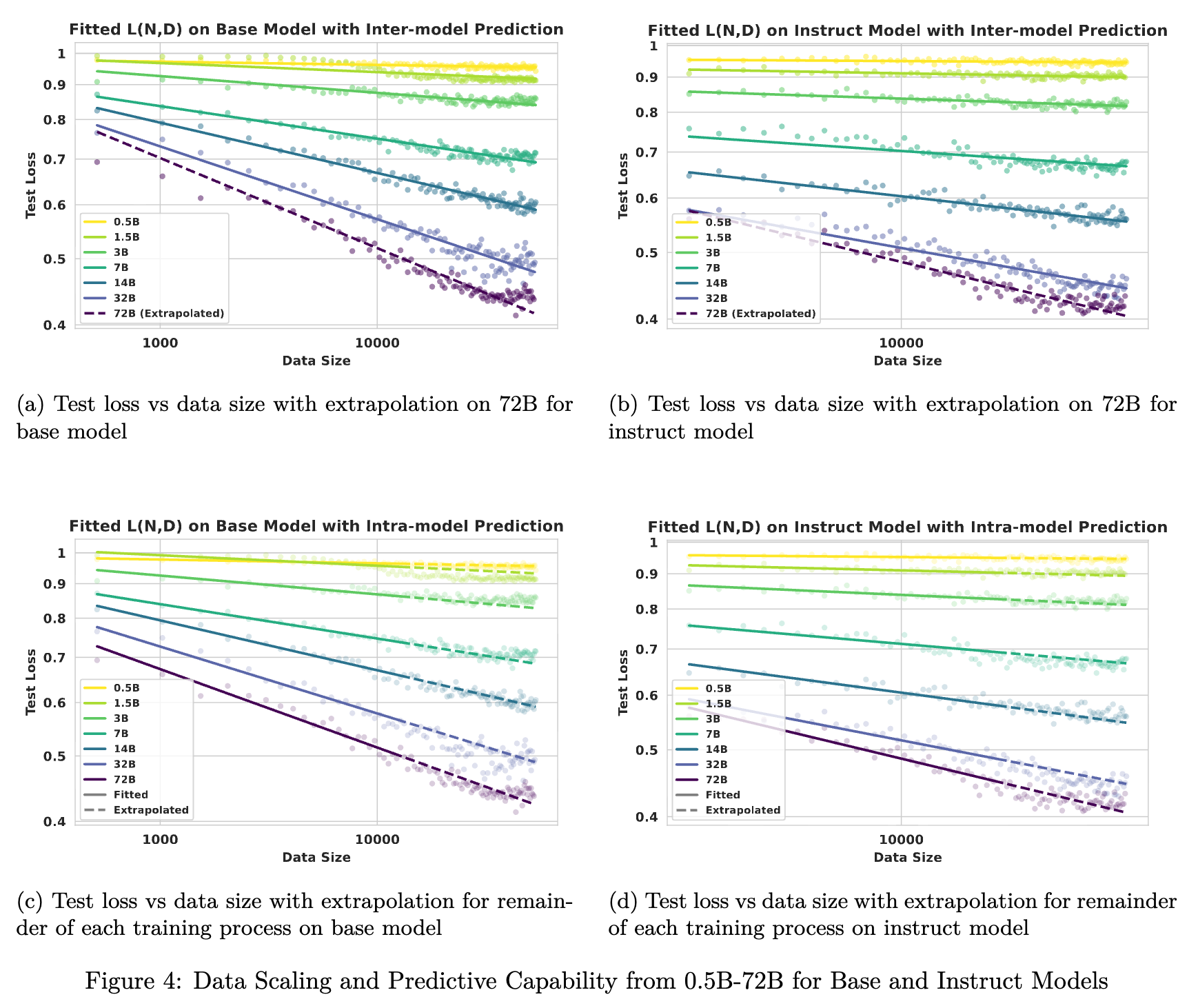
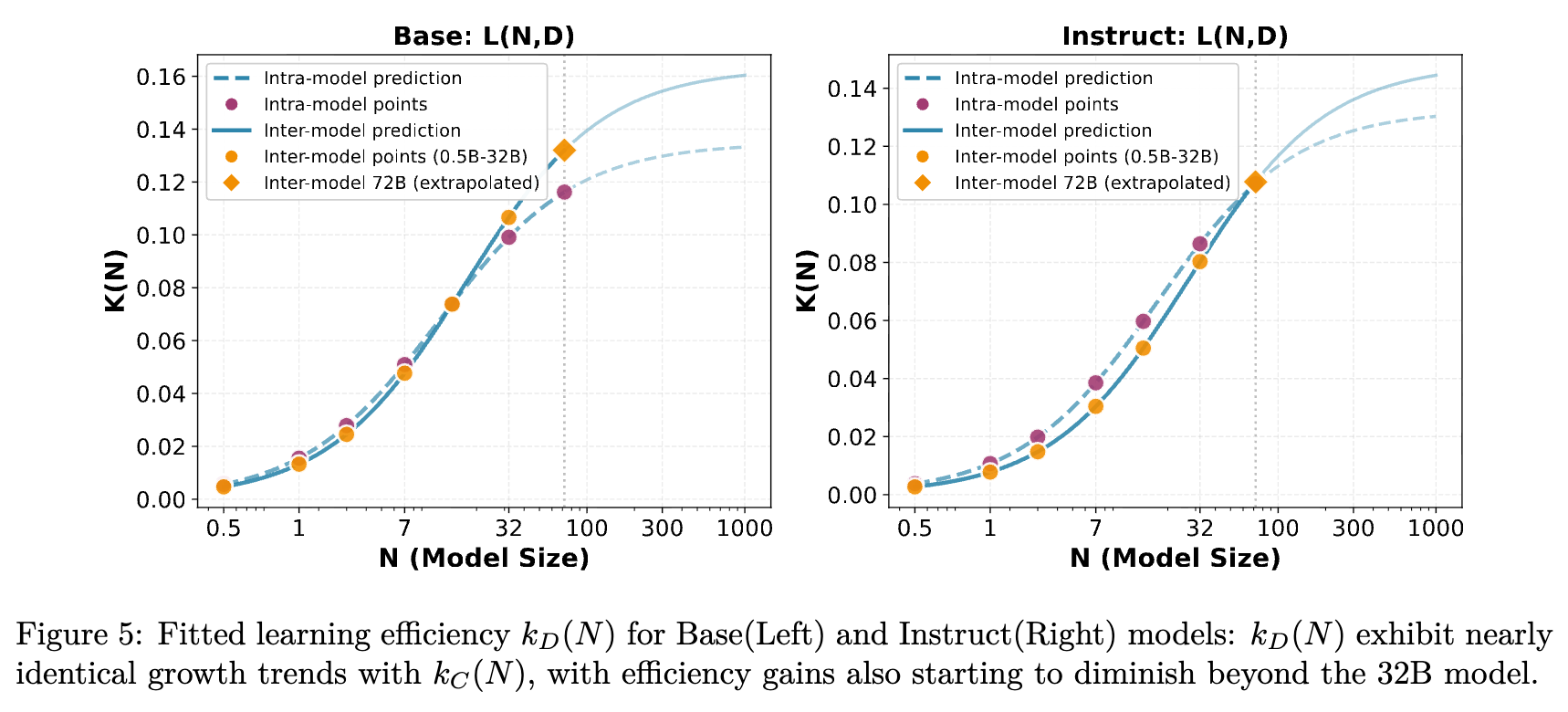
与计算扩展类似，数据效率系数 也遵循相同的饱和曲线（图 5）。这表明大模型从每个数据点提取知识的能力虽然更强，但也存在物理极限。

3.5 模型规模的扩展 (Scaling up Model Size)

当模型在足够大的数据集上训练至收敛时，测试损失随模型大小单调递减。

观察 3：测试损失随模型大小单调下降，但趋势偏离了严格的幂律。

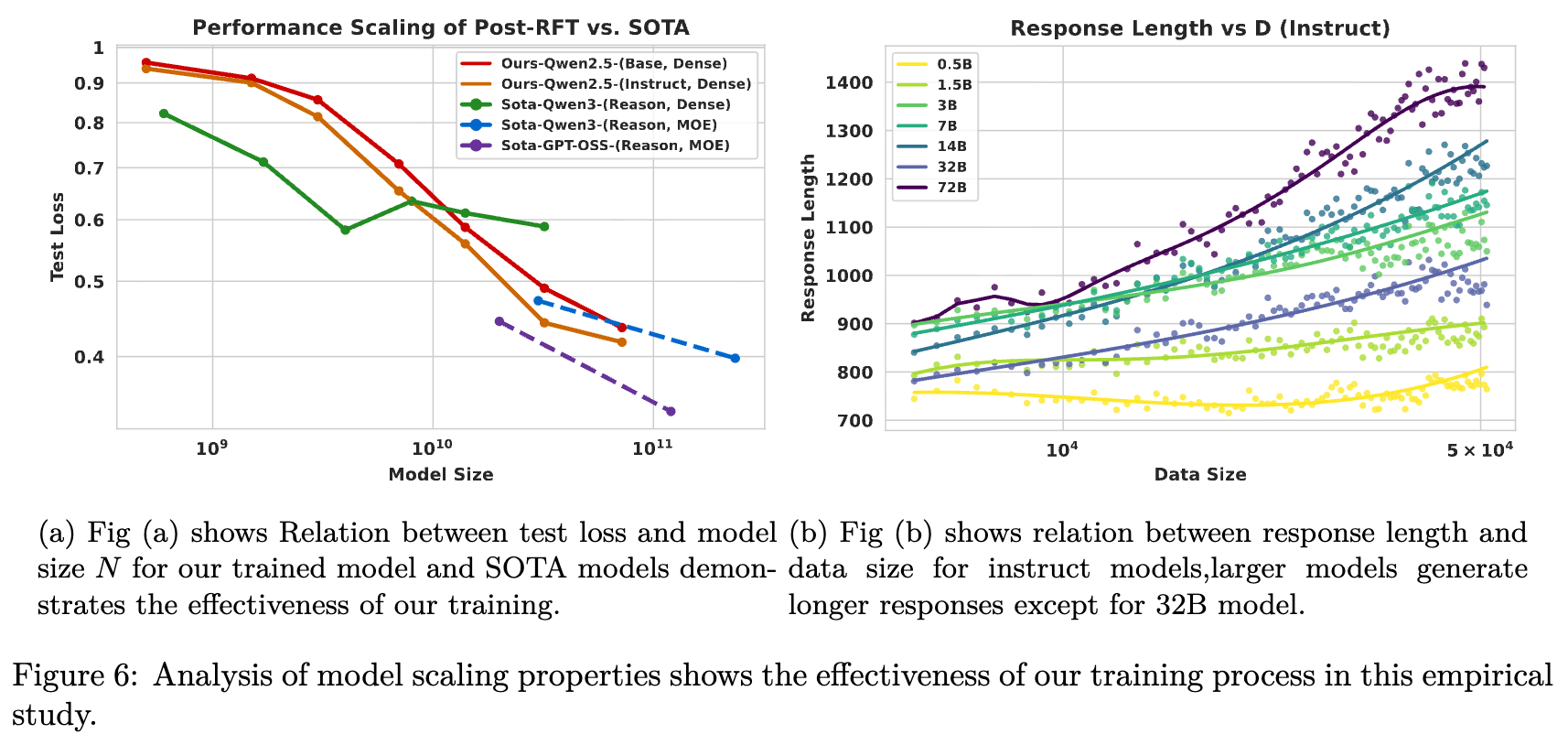
如图 6(a) 所示，较小的模型收益较弱，这表明在低参数量下存在收益递减。一个可能的解释是，大模型继承了更丰富的预训练表征，RL 微调能够比单纯的参数增长预测更好地利用这些表征。

此外，图 6(b) 展示了一个有趣的现象：推理时间扩展效率（Test-time Scaling Efficiency）。随着 RL 训练的进行，除了 32B 模型外，更大的模型倾向于生成更长的响应（Response Length）。这与更高的准确率相关，表明大模型能通过生成更多的推理 Token 来获得更大的性能增益。

3.6 数据复用与受限数据扩展

当唯一数据稀缺时，一个关键问题是：重复使用数据是否有效？研究定义了 数据复用场景：固定总数据预算（Total Data Budget），改变复用因子 （Reuse Factor）。即 。

观察 4：在数据受限的设置中，性能主要由 使用的数据总数（） 决定。在固定的 下，最终测试损失对数据复用因子 不敏感，直到 都没有显著的性能退化。

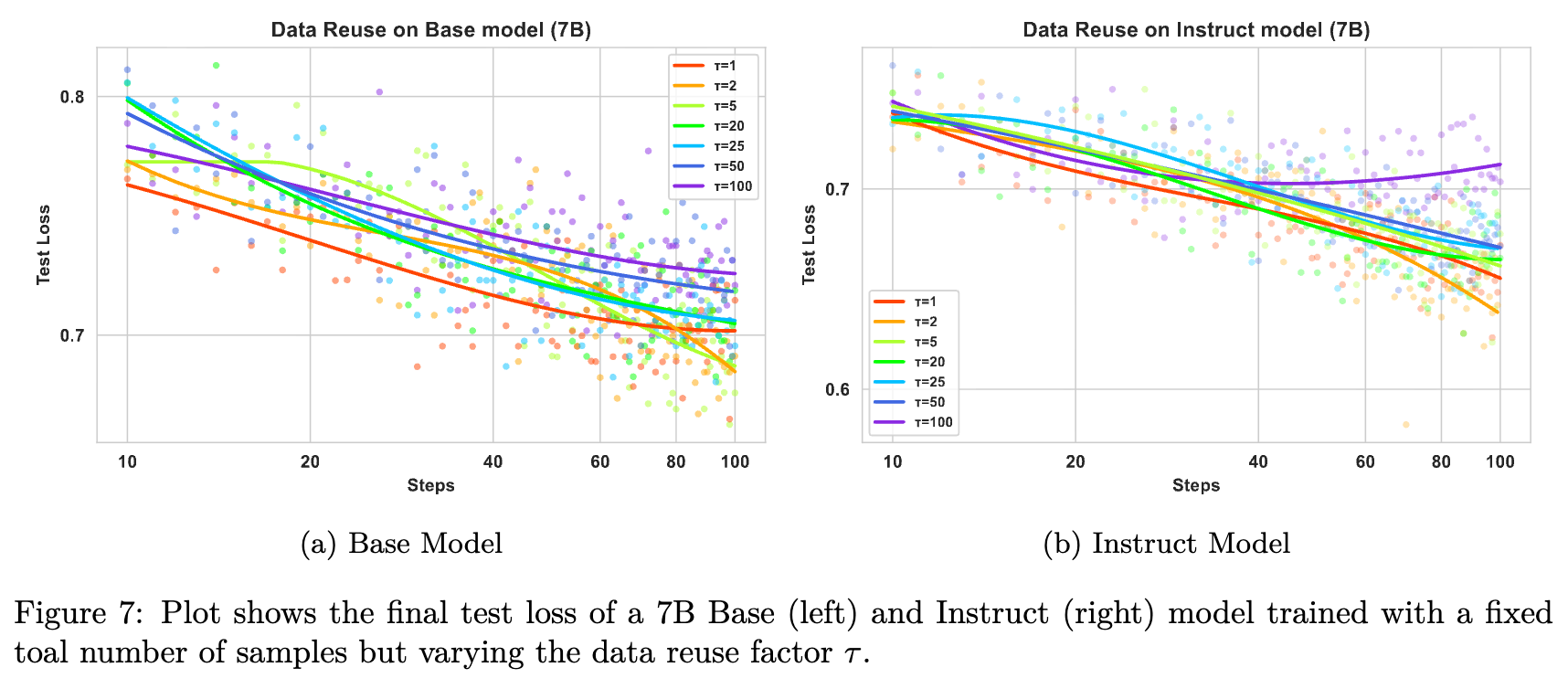
如图 7 所示，当 时，性能几乎保持不变。但当 时，观察到了明显的过拟合迹象。这表明：

1. 最终性能主要受优化步数总量的控制，而非样本的唯一性。
2. 适度的数据复用是 RL 微调在有限数据集下的有效策略。

为了验证这一点，实验通过将训练集划分为较小的子集并多次循环来实现不同的 ，同时保持课程学习的难度顺序不变（详见附录 A.4）。

4. 泛化性与领域迁移

RL 后训练获得的数学推理能力是否能迁移？

观察 5：数学推理的 RL 后训练在不同难度的同领域（In-domain）任务上产生了泛化提升，但在跨领域（Out-of-domain, OOD）任务上的迁移效果微乎其微。

4.1 域内泛化（In-Domain）

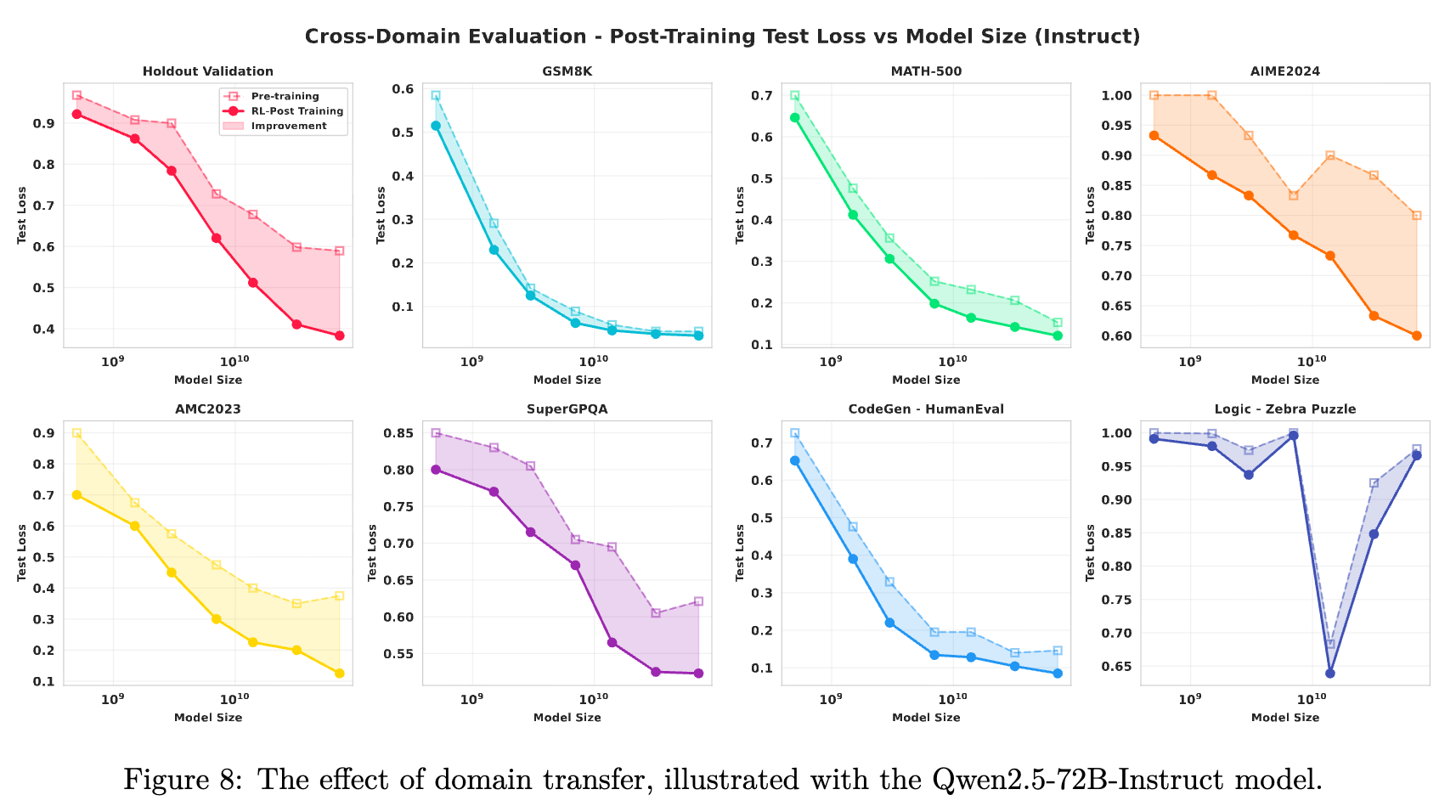
如图 8 和图 10 所示，在未见过的数学任务上（从简单的 GSM8K 到困难的 AIME2024），测试损失随着训练计算量的增加而稳步下降。这表明 RL 后训练增强了数学领域内可迁移的推理技能。

4.2 域外泛化（Out-of-Domain）

• 代码（HumanEval）与科学（SuperGPQA）：性能几乎保持平稳，表明数学 RL 微调具有高度的专业化特征，技能并未发生迁移。
• 逻辑推理（Zebra Puzzle）：观察到负迁移现象。随着训练进行，大模型（特别是 14B 以上）的性能出现退化（测试损失上升）。这表明对数学推理的高强度优化可能会干扰或“损害”其他不同类型的推理能力。

5. 讨论与局限性

5.1 评估环境与指标的依赖性

与 AlphaZero 下围棋不同，文本生成的 RL 缺乏定义明确的客观环境奖励，必须依赖人类构建的数据集作为代理。因此，测试损失是一个实用但不完美的指标。它虽然收敛，但高度依赖于数据集的构建和任务难度。这使得拟合出的扩展定律系数（）难以在不同环境间通用。

5.2 学习效率的饱和

实验明确指出， 存在上限 。这意味着将模型扩展到某一点后，虽然绝对性能仍有提升，但效率的边际收益会急剧下降。

5.3 算法依赖性

本研究基于 GRPO。虽然此前有研究（Cui et al., 2025）表明不同 RL 算法（如 PPO）在训练曲线上差异不大，但更先进的算法是否能改变扩展前沿（Scaling Frontier）仍是开放问题。

6. 附录深度解析

6.1 损失分解模型（Loss Decomposition Model）

在附录 D 中，作者提出了一个更通用的损失分解模型，作为对主文中幂律公式的补充。

该公式将损失分解为三个部分：

1. （不可约损失）：即使有无限模型容量和无限数据也无法消除的固有损失（如环境的随机性）。
2. （模型受限损失）：在无限数据极限下，由有限模型容量 决定的渐近损失底线。建模为 。
3. （可学习容量与进度）：

   • 是模型通过后训练能实现的最大损失降低量。
   • 是归一化的学习进度函数，取值 ，建模为 Logistic 函数：

     
     

这个分解模型在仅使用前 30% 的训练步数进行预测时（Intra-model prediction），表现出了极强的拟合能力。它揭示了学习曲线在对数-对数坐标下呈现 S 形（S-shaped）转换的内在结构。

6.2 扩展系数的数学一致性

附录 C.2 证明了计算扩展定律和数据扩展定律在数学形式上的一致性。
假设 （其中 为常数，代表每 Token 的 FLOPs），通过代入推导可得：

这从理论上解释了为什么图 3 和图 5 中计算效率和数据效率呈现出几乎相同的饱和曲线。

6.3 GRPO 超参数消融

附录 B.2 对 GRPO 的关键超参数 Rollout Group Size () 进行了消融研究。

• 数据视角：较大的 （如 32）始终能带来更好的样本效率。因为每个 Prompt 采样更多回复能提供方差更小的优势估计。
• 计算视角：最优的 随计算预算变化。在低预算下，较小的 更优（因为 大意味着单次更新消耗更多 FLOPs）；在高预算下，较大的 更优。这意味着 应该根据可用计算资源进行动态调整。

6.4 FLOPs 计算方法

训练步的总计算成本估算如下：
前向传播 ，反向传播 。
单步训练成本：

其中 是处理的 Token 总数（包含输入和输出）。实验中记录了每步处理的确切 Token 数来计算累积 FLOPs。

7. 结论

这项研究通过对 Qwen2.5 全系列模型的详尽实证分析，确立了 RL 后训练在数学推理任务上的扩展定律。

关键启示：

1. 大模型不仅起步高，学得也快：在相同数据/计算下，大模型效率更高。
2. 效率有天花板：不能指望通过无限扩大模型来线性获得效率收益，必须考虑饱和效应。
3. 数据复用是实用的：在数据匮乏时，多跑几个 Epoch 没问题，总步数到位就行。
4. 专业化的代价：数学能力的增强可能以逻辑推理能力的退化为代价，且难以直接迁移到代码或科学领域。

更多细节请阅读原论文。

往期文章：

• 【深度专访】Gemini 3 预训练负责人：我们不再只是构建模型，而是构建 AI 系统

• 为什么 RM 总是学不好推理？揭秘 BT Loss 中被忽视的“距离偏差”

• QwenLong-L1.5：长上下文推理与记忆管理的后训练方案

• Motif-2-12.7B-Reasoning：RL 训练配方与全栈优化实践指南

• NVIDIA 提出端到端 RL 编排，8B 模型在 HLE 榜单超越 GPT-5

• LayerNorm 真的不可或缺吗？一文读懂超越归一化层的 Derf

• UBC & DeepMind 揭示“短上下文主导”现象：80%的生成任务只需最后96个Token

• 谷歌 DeepMind & MIT 发布智能体 Scaling Law

• Native Parallel Reasoner: 基于自蒸馏强化学习的原生并行推理框架

• 预训练、中期训练与强化学习在推理模型中的相互作用

• Differential Smoothing——缓解 RL 微调中的分布坍缩并提升 LLM 推理能力

• Natural Language Actor-Critic: 语言空间中的可扩展异策略学习 (NLAC)

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• 复现 Search-R1 总是失败？GRPO 训练不稳定的幕后真凶与对策

• AAAI 2026：DeltaEdit 实现 LLM 连续知识编辑

• PretrainZero：将强化学习前置到预训练阶段的主动学习框架

• LLM-as-a-Judge 评估中的偏差修正与置信区间构建

• 字节阿里腾讯联手发布300页硬核报告：从 Code LLM 到 Agent 应用

• Qwen 推出 MiniRL：关于大规模 RL 训练稳定性的研究和实践

• DeepSeek-V3.2 技术报告深度解析：架构演进、RL 扩展与 Agent 合成数据

• Qwen3-VL 技术报告深度解析

• Qwen 团队推出 SAPO，相较于 GRPO、GSPO 稳定且更优

• 主打自验证数学推理：DeepSeekMath-V2 技术报告解读

• Anthropic 新作：利用“接种提示”可以阻止 Reward Hacking 引发的非对齐泛化

• 弱师出高徒：COLM 2025 Delta Learning 揭示弱模型偏好数据如何驱动 SOTA 级后训练

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题