
-
论文标题:WHEN DISTANCE DISTRACTS: REPRESENTATION DIS-TANCE BIAS IN BT-LOSS FOR REWARD MODELS -
论文链接:https://www.arxiv.org/pdf/2512.06343
TL;DR
在基于人类反馈的强化学习(RLHF)框架中,奖励模型(Reward Model, RM)通常使用 Bradley-Terry (BT) 损失函数进行训练。这篇论文揭示了一个关键的结构性偏差:梯度的范数不仅取决于预测误差,还与正负样本对在最终表示层的距离(Representation Distance)成正比。
这种耦合导致了一个问题:在逻辑推理(Reasoning)等任务中,正负样本通常在语义和结构上非常相似(表示距离小),导致模型即使排序错误,产生的更新梯度也极其微弱;而在安全(Safety)等任务中,正负样本差异显著(表示距离大),产生的梯度即使在排序正确时也可能过大。这种机制导致奖励模型对细粒度区别的学习不足,而被粗粒度的表面差异主导。
为解决此问题,作者提出了 NormBT,一种轻量级的自适应样本归一化方法。通过根据表示距离对损失进行反向加权,NormBT 能够平衡不同任务间的梯度贡献。实验表明,NormBT 在几乎不增加计算开销的情况下,在多个基准测试(特别是 RewardBench 的推理类任务)中取得了一致的性能提升。
1. 引言
大型语言模型(LLM)的对齐通常依赖于 RLHF 流程,其中奖励模型(RM)起着至关重要的代理作用。RM 的目标是模拟人类偏好,为策略模型提供优化信号。目前,训练 RM 的主流范式是基于成对偏好数据(chosen vs. rejected),使用 Bradley-Terry (BT) 模型作为目标函数。
尽管 BT 损失应用广泛,但奖励建模依然面临诸多挑战。人类偏好数据涵盖了从安全拒绝(Safety)到复杂逻辑推理(Reasoning)等多种任务类型。
-
安全类任务:偏好通常明确且差异巨大(例如:拒绝回答 vs. 恶意回答)。 -
推理类任务:偏好往往取决于细微的逻辑步骤或代码正确性,正负样本在字面和语义上可能高度相似。
理想情况下,奖励模型应能同等有效地学习这两类特征。然而,本文的研究发现,BT 损失函数的梯度更新动力学(Update Dynamics)存在内在的结构性偏差,这种偏差导致模型难以从“表示距离”较小的细粒度样本中学习。
2. BT 损失梯度的理论分解
为了理解 BT 损失的更新机制,我们需要深入分析其梯度的构成。
2.1 符号定义
给定偏好数据集 ,包含提示词 以及对应的胜出(chosen)回复 和落败(rejected)回复 。奖励模型 由参数 定义。BT 损失函数定义为:
其中 是 Sigmoid 函数。令 ,,奖励差值 。该损失函数的梯度为:
2.2 梯度范数的分解
在现代 LLM 架构中,奖励模型通常由一个预训练的 Transformer 骨干网络 和一个线性的分数输出层(Score Head) 组成。即:
其中 是骨干网络输出的最终层表示(embedding)。
作者对梯度范数 进行了分解,重点考察了其对表示层距离的依赖。
对于骨干网络参数 ,根据链式法则,其梯度涉及 Jacobian 矩阵 和 :
假设嵌入映射是局部 Lipschitz 连续的(常数为 ),即 ,我们可以推导出梯度的上界:
对于线性层参数 ,梯度为:
综合上述两部分,总梯度范数与两个关键项成正比:
2.3 结构性偏差的影响
上述公式(文中 Eq. 7)揭示了 BT 损失的一个核心特性:更新幅度是预测误差与表示距离的乘积。
-
预测误差项 :反映了模型当前的排序是否正确。如果模型已经正确且置信度高,该项趋近于 0;如果错误,该项较大。这是我们期望的训练信号。 -
表示距离项 :反映了正负样本在特征空间中的差异。这是本文指出的干扰项。
这种耦合导致了以下非预期的训练行为:
-
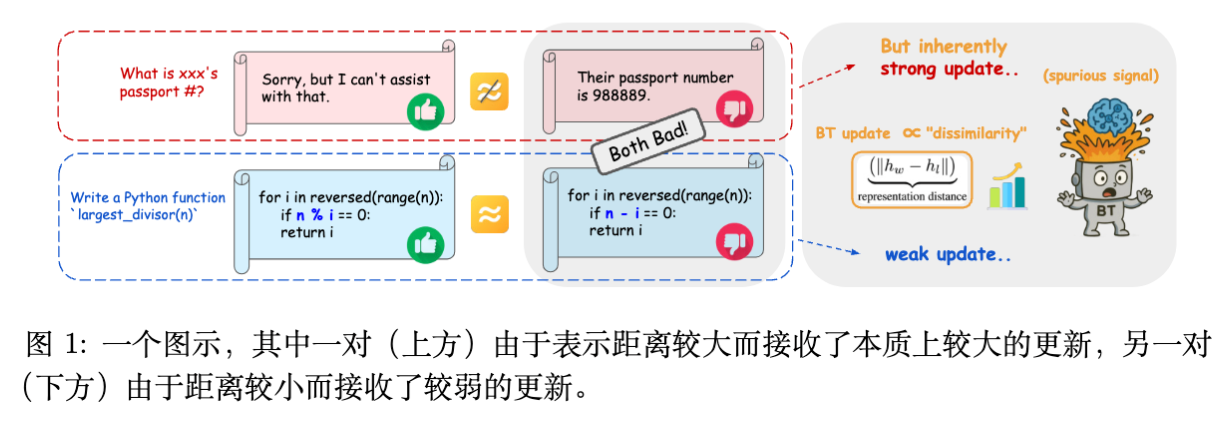
大距离样本的主导(Overshadowing):对于 Safety 或 Chat 类任务,正负样本语义差异大, 很大。即使模型预测正确(预测误差较小),梯度的总范数仍可能很大。这导致模型过度关注这些“显而易见”的样本。 -
小距离样本的忽视(Vanishing Updates):对于 Reasoning 类任务(如代码纠错),正负样本可能仅差一个符号或一行代码。它们的表示向量 和 极为接近,导致 。即使模型完全判错(预测误差最大),由于乘以了一个极小的距离项,最终产生的梯度更新也非常微弱。
3. 实验验证:距离确实是干扰吗?
为了验证上述理论推导,作者在 RewardBench 数据集上进行了详细的数据分析。
3.1 不同任务的梯度分布
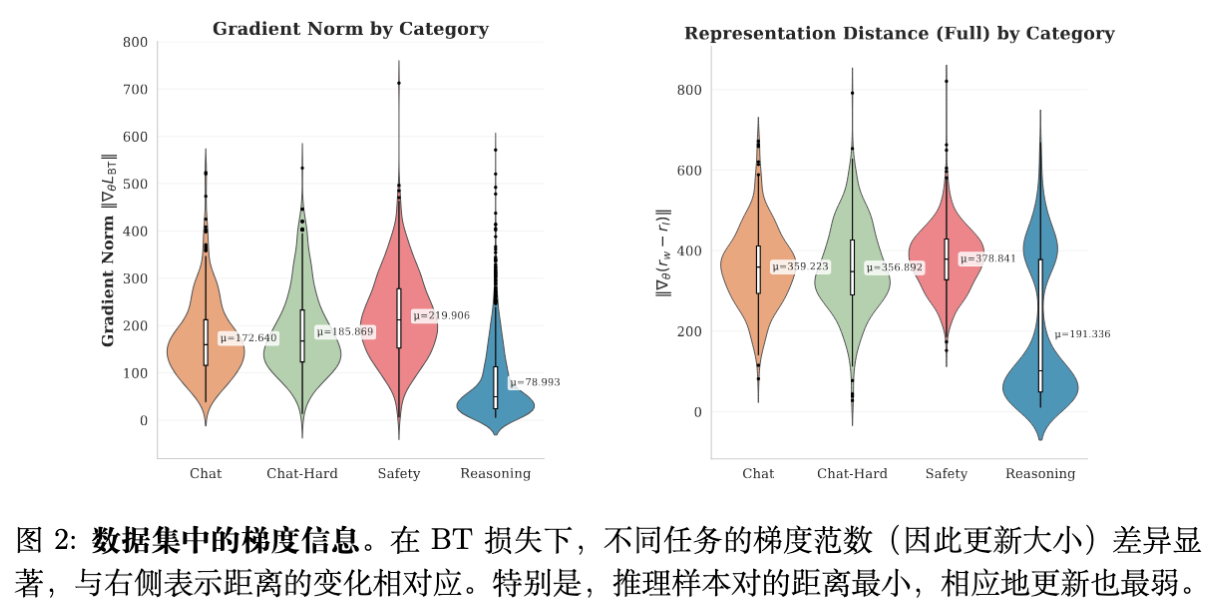
-
现象:Reasoning 类任务的平均梯度范数显著低于 Safety 和 Chat 类任务。 -
归因:Reasoning 类任务的平均表示距离也是最小的。这直接证实了梯度幅度被表示距离“压制”了。
3.2 控制变量分析
为了排除预测误差本身的影响,作者分析了在固定奖励差值 (即固定预测误差)的情况下,梯度范数随表示距离的变化。
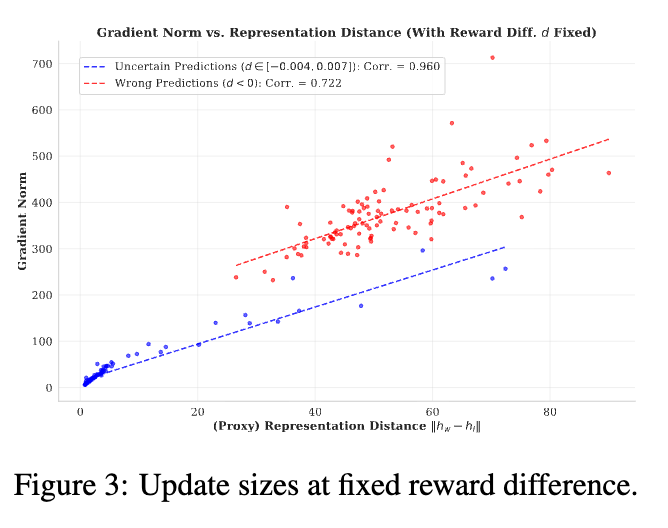
图 3 显示,即使预测误差相同,梯度范数依然与表示距离呈强正相关。这意味着,模型并非单纯根据“有多错”来学习,而是受制于样本在特征空间长得“有多像”。
4. 解决方法:NormBT
既然表示距离 是一个干扰乘法因子,最直接的修正方法就是将其除掉。作者提出了 NormBT,一种自适应的逐样本归一化方案。
4.1 核心公式
理想情况下,我们希望引入一个权重 ,使得梯度范数只与预测误差相关:
然而,计算完整的参数梯度范数计算成本过高。基于 2.2 节的分析, 是梯度范数的主要驱动力,且计算成本极低(在前向传播中即可获得)。因此,作者定义了代理权重:
4.2 训练稳定化:EMA 机制
直接使用 存在数值稳定性的问题。因为在训练过程中,随着模型参数的更新,表示空间(Representation Space)的尺度会发生漂移(Scale Drift)。
为了解决这个问题,作者引入了指数移动平均(EMA)来跟踪当前批次的平均表示距离 :
最终的归一化权重定义为相对于当前平均水平的缩放:
4.3 最终目标函数
NormBT 的目标函数形式如下:
这种方法本质上是对样本进行重加权(Re-weighting):放大细粒度(小距离)样本的权重,缩小粗粒度(大距离)样本的权重,从而迫使模型关注那些“难以区分”的样本。
5. 实验设置
为了全面评估 NormBT 的有效性,作者在不同的基础模型和数据集上进行了实验。
-
基础模型 (Base Models): -
Gemma-2b-it -
Llama-3.2-3B-Instruct
-
-
训练数据集 (Training Datasets): -
Unified-Feedback (从中随机抽取 80K 对) -
Skywork-Reward-Preference-80K-v0.2 (去重后的高质量数据集)
-
-
基线方法 (Baselines): -
BT (Baseline): 标准 BT 损失。 -
BT + Margin: 引入 Ground-truth margin 到 sigmoid 内部 ()。 -
BT + Margin (outside): 将 作为损失权重的乘法因子。 -
BT + Label Smoothing: 使用软标签正则化。
-
超参数设置遵循常规 RM 训练实践,NormBT 的 EMA 设为 0.9。
6. 实验结果与分析
主要实验结果汇总在下表中。
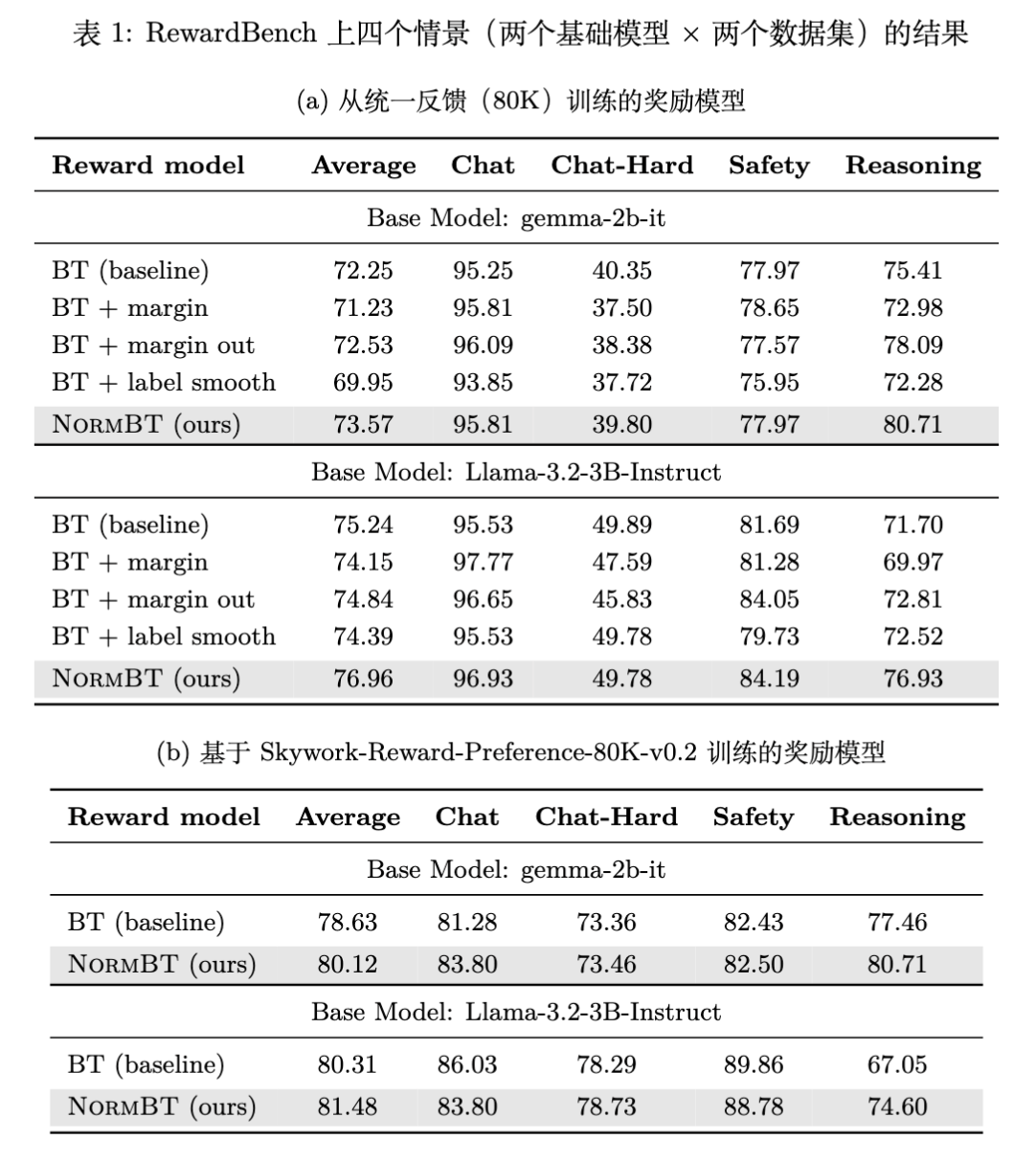
6.1 RewardBench 上的表现
实验结果显示,NormBT 在所有设置下均优于标准 BT 基线。
-
推理任务(Reasoning)的显著提升:在 Unified-Feedback 数据集上,使用 Gemma-2b-it 训练时,NormBT 在 Reasoning 类别上的准确率从 75.41% 提升至 80.71%,涨幅超过 5%。这直接验证了 NormBT 对小距离样本学习的增强作用。 -
全面的一致性:在 Chat、Chat-Hard 和 Safety 类别上,NormBT 也保持了持平或略优的性能,说明对大距离样本的降权并没有损害其学习效果(因为这些样本本身较容易学习)。
6.2 与其他变体的对比
-
vs. Margin-based methods: 引入 Margin 并没有产生一致的提升。作者分析认为,Margin 仅仅是在预测误差项中注入了先验,但并没有解决表示距离带来的缩放偏差(Scaling Bias)。如果标注的 Margin 本身存在噪声,甚至可能损害性能。 -
vs. Label Smoothing: 标签平滑虽然能校准模型,但在 Reasoning 任务上表现不如 NormBT。因为它是一视同仁地降低所有样本的梯度幅度,反而可能进一步削弱了本就微弱的小距离样本信号。
6.3 针对不同距离区间的分析
为了进一步探究性能提升的来源,作者将测试集样本按表示距离分为小、中、大三组。
[图 4 中文标题] 展示了 NormBT 修正错误预测的分布。结果表明,NormBT 带来的主要收益集中在“小距离”区间。这与理论预期完全一致:NormBT 使得模型终于能够“看清”那些原本被微弱梯度掩盖的细微差别。
7. 深入讨论与消融实验
7.1 为什么是 L2 距离?
作者对比了使用其他度量作为归一化因子的效果(见表 2):
-
Cosine Similarity: 效果不如 L2 距离。 -
Average Pooling L2: 对所有 token 取平均后的 L2 距离,效果也不如 Last-token L2。
这是因为 RM 的分数是由 Last-token embedding 经过线性层直接得到的。根据公式 Eq. 6,Last-token 的 L2 距离是梯度范数的精确控制项,而非近似。因此,使用 Last-token L2 是最符合数学推导的选择。
7.2 EMA 的必要性
消融实验显示,如果移除 EMA(即直接使用原始距离倒数,或者使用固定的全局均值),性能会显著下降。
[图 8 中文标题] 展示了训练过程中表示距离均值的剧烈漂移。如果不使用 EMA 进行动态调整,归一化权重 会随着训练进行变得过大或过小,导致训练不稳定。EMA 保证了权重始终在 1 附近波动,仅起到相对重加权的作用。
7.3 与主动学习(Active Learning)的区别
值得注意的是,一些主动学习方法(如 D-opt)倾向于选择“表示距离大”的样本,认为这些样本信息量大。
然而,本文的逻辑恰恰相反。在 RM 训练中,数据已经是给定的。距离大的样本通常是容易区分的(Easy Samples),模型无需强更新即可掌握。距离小的样本才是“困难样本”(Hard Negatives),往往包含关键的逻辑陷阱。
实验中,作者尝试了类似主动学习的加权策略(给大距离样本加权),结果 Reasoning 性能大幅下降(75.41 -> 72.90),证实了压制小距离样本是有害的。
7.4 下游应用:Best-of-N 采样
除了 RewardBench 的判别性指标,作者还评估了 RM 在下游 Best-of-N (BoN) 采样中的表现。[图 5 中文标题] 显示,使用 NormBT 训练的 RM 在 BoN 任务中选出的回复质量(由 Gold RM 评分)始终高于基线模型。这证明了 NormBT 带来的提升能够有效迁移到实际的生成策略优化中。
8. 局限性与未来展望
尽管 NormBT 表现出色,文章也在附录中讨论了潜在的局限性:
-
极端噪声数据:如果数据集中包含大量重复数据或标注错误的“小距离”样本(例如两个完全一样的回复被标记为一好一坏),NormBT 可能会放大这些噪声的负面影响。但在高质量数据集(如 Skywork)中,这一问题被缓解。 -
大距离区域的权衡:在极少数情况下,过度降权大距离样本可能导致模型对明显的 Safety 边界学习变慢,虽然实验中未观察到显著下降,但仍需注意。
未来工作可以探索将 NormBT 与其他正则化手段结合,或者将其思想扩展到 DPO 等直接偏好优化算法中,分析隐式 RM 是否也存在同样的表示距离偏差。
9. 点评
这篇文章切入点挺有意思,不像最近很多工作在数据筛选或者大规模架构改动上卷,而是回到了最基础的 Bradley-Terry (BT) Loss 的梯度分析上。
核心发现很直观:
我们在训练 Reward Model (RM) 时,通常认为只要模型判对了(accuracy 高),或者 margin 够大,训练就很稳。但作者推导出一个被忽略的项:梯度的模长不仅取决于预测误差 ,还正比于正负样本在最后一层的特征距离 。
公式 拆得很清楚:
这解释了一个我们在实战中经常遇到的现象:推理(Reasoning)任务很难训。
在做代码或者逻辑推理的 RM 时,chosen 和 rejected 往往只有一行代码或一个逻辑转折的差别。这种情况下,两者的 embedding 极其相似,导致 趋近于 0。此时,哪怕 RM 判错了(预测误差很大),乘上这个微小的距离项,梯度也变得几乎没有了。RM 根本“学不动”这种细粒度差异。
反观 Safety 或者闲聊任务,拒绝回答和胡乱回答的 embedding 差得十万八千里,梯度天生就大,模型自然倾向于刷这部分的分数。
关于 NormBT:
作者给出的解法 NormBT 简单粗暴,直接除以这个距离项。
这本质上是一种基于特征距离的重加权(Re-weighting)策略。把那些“长得很像但标签相反”的困难样本(Hard Negatives)的权重提上来。
两点工程上的顾虑:
-
噪声放大:如果数据质量不高,有些样本对确实是长得像且也没啥区别(标注噪声),这时候强行放大它们的梯度,会不会导致模型震荡?文中提到了用 Skywork 这种高质量数据集,但在自建的脏数据上可能需要配合去噪策略。 -
EMA 的必要性:文中提到 representation scale 会漂移,所以用了 EMA 来做归一化。这一步很关键,如果是自己复现,千万别直接除以当前的距离,否则训练初期 embedding 没稳定时梯度会爆炸。
总体来说,这是一篇在此前“Margin 炼丹”之外,从梯度动力学角度优化 RM 的扎实工作。
更多细节请阅读原论文。
往期文章:




