对于大型语言模型(LLMs)的后训练(Post-Training)实践常常依赖于一个基础假设:在 SFT 阶段取得更高性能分数的模型,在后续的 RL 阶段也理应会取得更好的最终成果。
这个假设带来了操作上的便利。它允许我们将 SFT 和 RL 两个阶段解耦,交由不同的团队各自负责优化。SFT 团队的目标变得清晰而直接:最大化模型在标准评估基准上的 SFT 分数(例如 Pass@1 准确率)。然而,这种看似合理的流程划分,却可能隐藏着深刻的矛盾。当最终模型的性能未达预期时,问题归因变得异常困难:是 SFT 阶段提供的模型起点不佳,还是 RL 阶段的训练方法存在问题?RL 训练的计算成本极为高昂,在这样一个可能存在问题的起点上投入大量资源,无疑带来了巨大的风险和效率损失。
这一实践中的关键分歧构成了一个重要的研究空白:SFT 阶段的性能提升,是否真的能有效地传导至最终的 RL 性能?如果不能,我们又该如何在前 RL 阶段,可靠地评估一个 SFT 模型的真实潜力,以避免在错误的道路上投入宝贵的计算资源?
来自 Meta 和弗吉尼亚理工大学的作者发表的论文《Quagmires in SFT-RL Post-Training: When High SFT Scores Mislead and What to Use Instead》,对这一基础假设发起了系统性的挑战。这项研究通过在高达 12B 参数规模的模型上进行的大量实验,揭示了 SFT 分数与最终 RL 性能之间的显著脱节。研究结果表明,单纯追求高 SFT 分数不仅具有误导性,在某些情况下甚至会损害模型在 RL 阶段的潜力。

-
论文标题:Quagmires in SFT-RL Post-Training: When High SFT Scores Mislead and What to Use Instead -
论文链接:https://www.arxiv.org/pdf/2510.01624
1. SFT 指标陷阱
SFT 团队以最大化 SFT 评估指标为目标,而这一局部最优解,并不等同于 RL 阶段的全局最优解。为了系统性地验证这一“SFT 指标陷阱”,作者设计了两类具有代表性的实验场景,以模拟和分析在实际操作中常见的做法。
1.1 数据集层面
在数据集层面,作者使用固定的数据分布(即来自同一个数据集的样本),但改变训练的配置,例如训练的轮数(epochs)或学习率。这种设置与工业界实践高度相关:当高质量数据有限时,从业者可能会倾向于在现有数据上进行多轮重复训练以提升 SFT 性能;反之,如果数据充足,则可能选择在更多唯一数据上只训练一个 epoch。
研究发现,这两种基于直觉的实践都可能是次优的。一个显著的现象是,在相同的数据上进行更多轮次的训练,通常能稳定地提升模型的 post-SFT 性能。然而,这种性能提升的背后,是模型潜力的不断损耗。过度训练的 SFT 模型,在进入 RL 阶段后,其性能提升的潜力反而会下降。
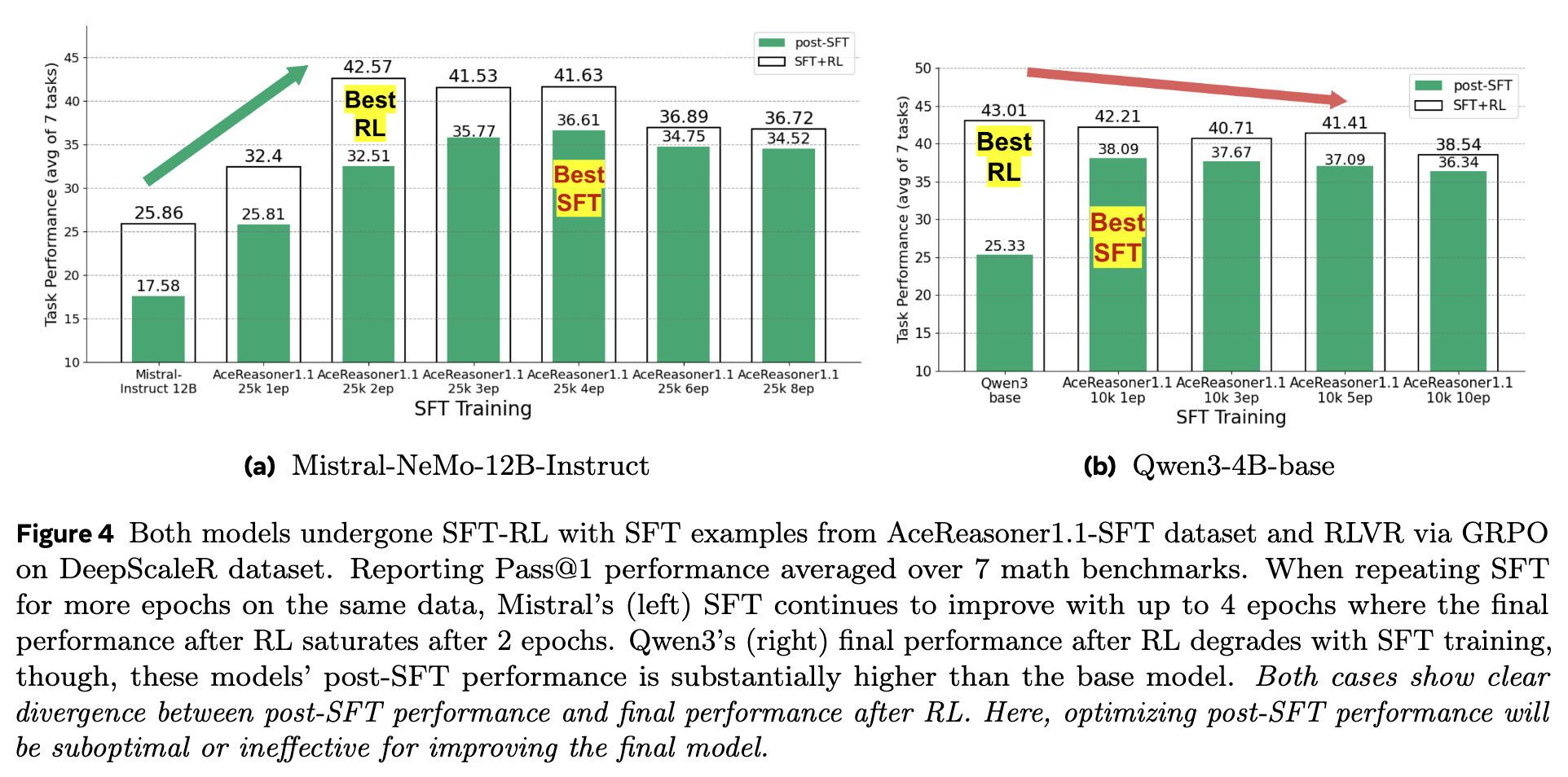
如图 4 所示,对于 Mistral 模型(左图),在 AceReasoner1.1 数据集上重复训练从 1 个 epoch 增加到 4 个 epochs 时,其 post-SFT 性能(蓝色柱)持续提升。然而,其最终的 post-RL 性能(绿色柱)在 2 个 epochs 后就已饱和,继续增加 SFT 训练轮数并不能带来进一步的收益。对于 Qwen3 模型(右图),情况更为极端,随着 SFT 训练的加强,其 post-RL 性能甚至出现了下降的趋势。
这揭示了一个深刻的问题:SFT 阶段的过度训练,即使在评估指标上显示为“更好”,实际上却可能限制了模型的策略空间(policy space)。模型过度拟合了 SFT 数据集中的特定模式和解题路径,导致其在 RL 阶段进行探索(exploration)的能力被削弱。强化学习的成功在很大程度上依赖于模型能够探索并发现新的、更优的策略,而一个被 SFT “固化”了思维模式的模型,自然难以在 RL 阶段取得突破。
1.2 样本层面
在样本层面,作者固定了模型和训练流程,但改变了用于 SFT 的数据集。这主要关注 SFT 数据的筛选和构建策略,即一个在特定类型数据集上表现优异的 SFT 模型,是否也能在 RL 后表现出色。
当前许多数据筛选方法倾向于选择更“简单”或更“同质化”的样本,因为模型在这些样本上能更快地提升性能指标。作者通过实验对比了在不同特征的数据子集上训练的效果,例如“最长样本”、“最短样本”和“随机样本”。
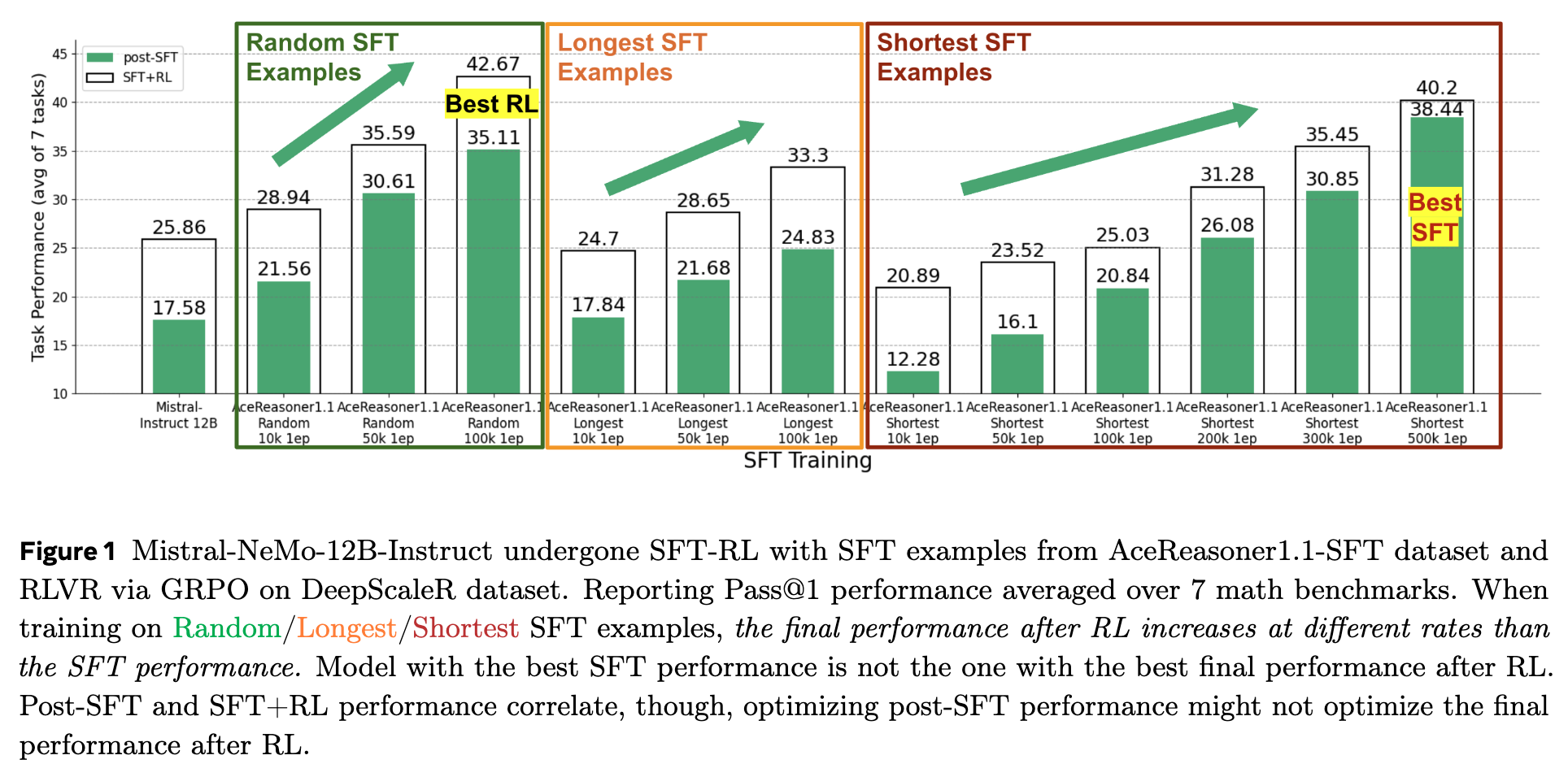
图 1 的结果提供了有力的反证。右侧图表显示,使用“最短 SFT 样本”(Shortest SFT Examples)进行训练时,模型的 post-SFT 性能(蓝色柱)提升速度最快,并且在训练了 500k 样本后达到了所有 SFT 实验中的最高点(Best SFT)。然而,这个拥有最佳 SFT 性能的模型,在经过 RL 训练后,其最终性能却远低于使用“随机 SFT 样本”(Random SFT Examples)或“最长 SFT 样本”(Longest SFT Examples)训练的模型。实际上,最终 RL 性能最好的模型(Best RL),其对应的 SFT 性能并非最高。
这一现象表明,高 SFT 分数可能偏向于那些模型更容易学习的、模式化的、或者更简单的样本。虽然模型在 SFT 阶段迅速掌握了这些“捷径”,但它并未能真正建立起解决复杂问题所需的、更具泛化性的推理能力。当进入要求更高探索性和鲁棒性的 RL 阶段时,这种能力的缺失便暴露无遗。
1.3 微弱的性能相关性
为了更直观地展示 SFT 性能与 RL 性能之间的脱节,作者对 post-SFT 性能和 post-RL 性能进行了线性拟合。
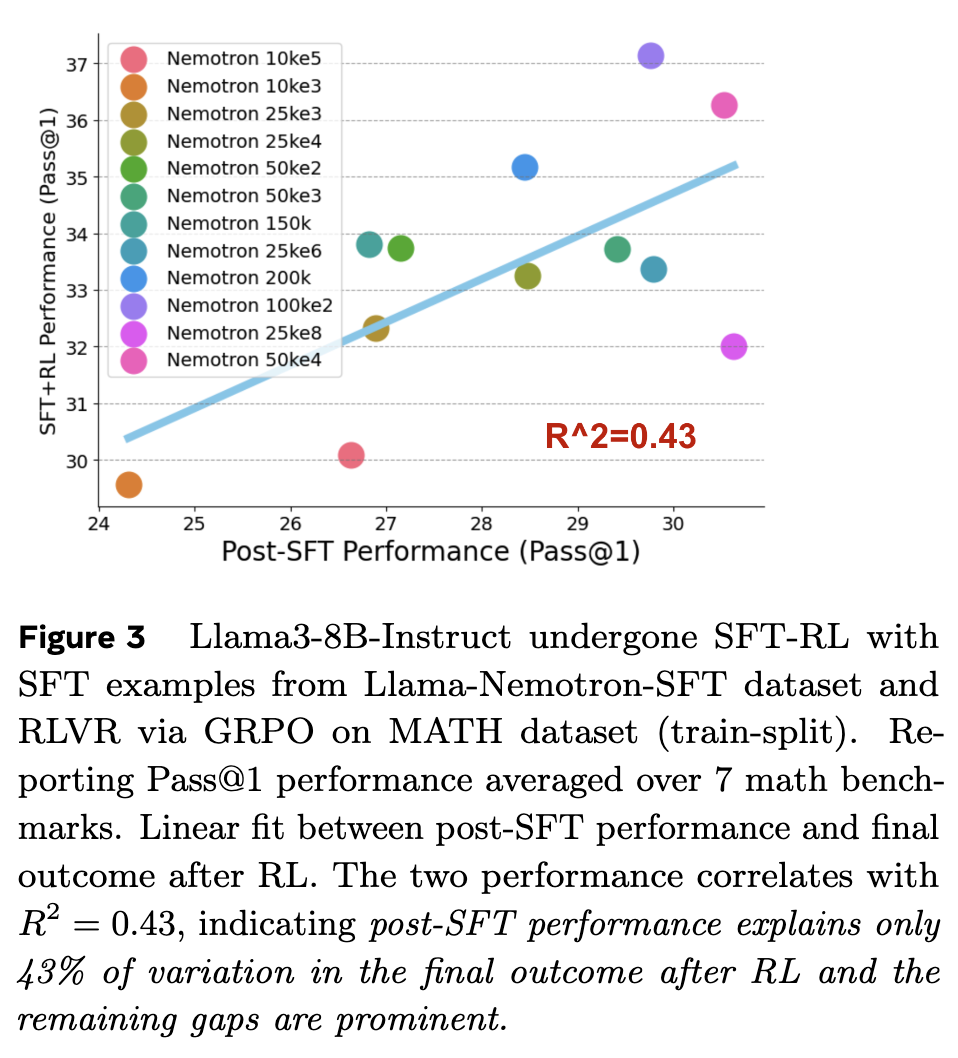
如图 3 所示,在使用 Llama-Nemotron 数据集对 Llama3-8B 模型进行训练后,post-SFT 性能(横轴)和 post-RL 性能(纵轴)之间的相关性决定系数()仅为 0.43。这意味着,post-SFT 的性能分数只能解释 post-RL 最终性能变化的 43%。剩余的 57% 的变数,则是由 SFT 阶段的其它潜在因素(如过拟合程度、学习到的能力多样性等)决定的。这个数值清晰地表明,依赖 post-SFT 性能来预测最终结果是不可靠的。
2. 可靠的代理指标
既然传统的 post-SFT 性能指标 Pass@1 不可靠,那么是否存在更有效的代理指标(proxy metrics),能够帮助我们在投入昂贵的 RL 训练之前,就准确地评估 SFT 模型的潜力呢?论文的第二部分,也是其核心贡献所在,便是提出并验证了两个这样的新指标。
2.1 指标一:在验证集上的泛化损失 (Generalization Loss)
第一个指标是 SFT 训练后,模型在留存的(held-out)验证集上的泛化损失。这个想法的直觉来自于机器学习的基本原理:一个真正学到泛化能力的模型,其在训练集和验证集上的表现应该是一致的。当模型的训练准确率持续上升,但在验证集上的损失(loss)也开始上升时,这便是典型的过拟合信号。
作者发现,这个过拟合的信号与模型在后续 RL 阶段的潜力密切相关。
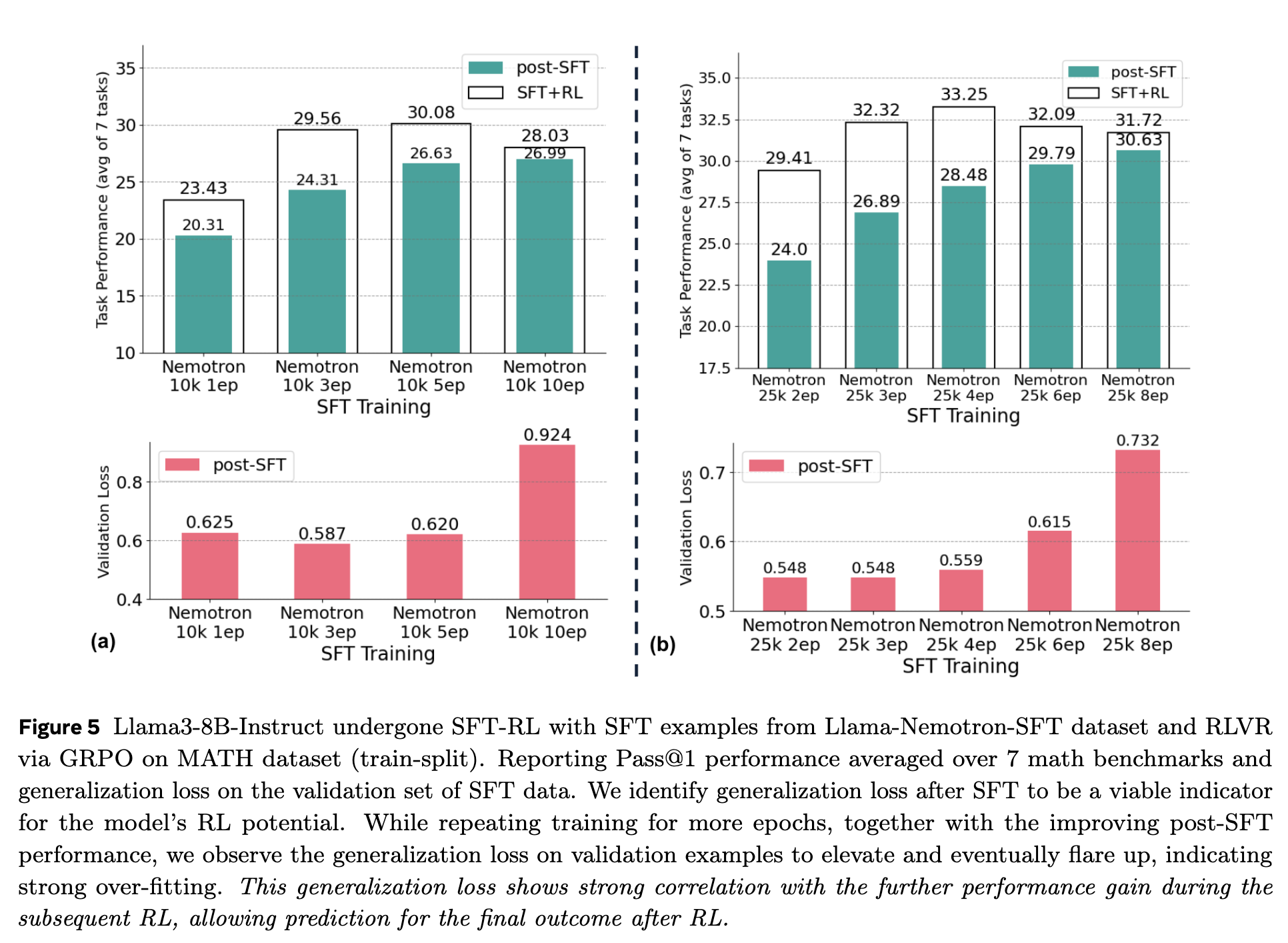
图 5 将任务性能与 SFT 验证集上的泛化损失(Validation Loss)并置进行了对比。可以清晰地看到一个反向相关的模式:随着 SFT 训练的进行(例如,在相同数量的数据上增加训练轮数),post-SFT 任务性能在提升,但泛化损失(下图)在经过初期的下降后开始显著上升。而这种损失的“抬头”或“飙升”,恰恰预示着后续 RL 性能增益的减弱。
这个指标的有效性在于,它捕捉了模型的“健康状况”。一个泛化能力强的模型,意味着它学习到的是更本质、更通用的推理模式,而不是仅仅记住了 SFT 训练数据中的特定样本。这样的模型为 RL 阶段提供了一个更广阔、更鲁棒的探索起点。反之,一个严重过拟合的模型,其策略已经高度特化,难以通过 RL 进行有效的调整和优化。
因此,泛化损失 成为了一个在 数据集层面 优化 SFT 训练范式(例如决定最佳训练轮数)的有力工具。
2.2 指标二:在大 k 值下的 Pass@k 准确率
第二个指标是 Pass@k 准确率,特别是在一个较大的 值(例如 )下的表现。要理解这个指标,首先需要理解 RLVR(特别是论文中使用的 GRPO 算法)的工作机制。
RLVR 的目标,本质上是将模型在多次尝试中(次)能够答对题目的能力(Pass@k),压缩到单次尝试就能答对的能力(Pass@1)。换言之,强化学习的优化过程,只有在模型至少有一定概率生成正确答案时(即 Pass@k > 0 for some k > 1)才能有效进行。如果一个模型无论尝试多少次都无法得到正确答案,那么 RL 算法就缺乏正向的奖励信号来进行优化。
传统的 Pass@1 指标是一个非常稀疏的奖励信号。一个模型在 Pass@1 上得分为 0,并不能说明它完全没有解决问题的能力。它可能在 Pass@100 上有 30% 的准确率,这意味着它生成的 100 个答案中有 30 个是正确的。相比之下,另一个模型可能在 Pass@1 上有 1% 的准确率,但在 Pass@100 上也只有 5% 的准确率。从 RL 的角度看,第一个模型虽然 Pass@1 更低,但其“内在潜力”远大于第二个模型,因为它为 RL 提供了更丰富的、可供放大的正确解题路径。
因此,Pass@large k 提供了一个比 Pass@1 更细粒度的、更能衡量模型真实推理能力广度的指标。它反映了模型生成正确解空间的多样性和可能性,这正是 RL 成功所需要的。
为了高效地计算 Pass@k,作者利用了以下无偏估计公式:
其中, 是为每个问题生成的总响应数, 是其中正确的响应数。这个公式允许在生成 个样本后,一次性估计出所有 的 Pass@k 值,避免了重复采样的巨大开销。
这个指标的优势在于,它衡量的是模型固有的生成正确答案的能力,因此对于不同 SFT 数据集之间的分布差异不那么敏感。这使得 Pass@large k 成为一个在 样本层面 进行预测(例如,从多个候选数据集中挑选出最优的一个)的理想工具。
3. 大规模实证研究
为了证明上述两个新指标的有效性,作者进行了一系列严谨的大规模实验。
3.1 实验设置
-
模型: Llama3-8B-Instruct, Mistral-NeMo-12B-Instruct, Qwen3-4B-base。 -
SFT 数据集: Llama-Nemotron, AceReasoner1.1-SFT。 -
RL 数据集: MATH, DeepScaleR。 -
RL 算法: 基于 GRPO (Group Relative Policy Optimization) 的 RLVR。 -
评估基准: 最终性能在 7 个数学基准(MATH-500, GSM8k, AIME 等)上进行评估,报告 Pass@1 准确率。 -
计算规模: 整个研究耗费了超过 100 万个 GPU 小时,这保证了实验结果的充分性和可靠性。
3.2 数据集层面的预测
这个用例旨在解决一个常见的实践问题:在一个固定的数据集上,如何确定最优的 SFT 训练配置(例如,训练多少轮)?作者对比了基线指标(post-SFT Pass@1)和新提出的指标(泛化损失、Pass@64)在预测最终 RL 性能上的准确性。
他们使用了两个核心评估维度:
-
斯皮尔曼等级相关系数 (Spearman's Rank Correlation): 衡量预测指标对模型最终性能进行排序的准确性。系数越接近 1,说明排序越准。 -
决定系数 (): 衡量预测指标能在多大程度上解释最终性能的变化。 越高,说明基于该指标的预测值越接近真实值。
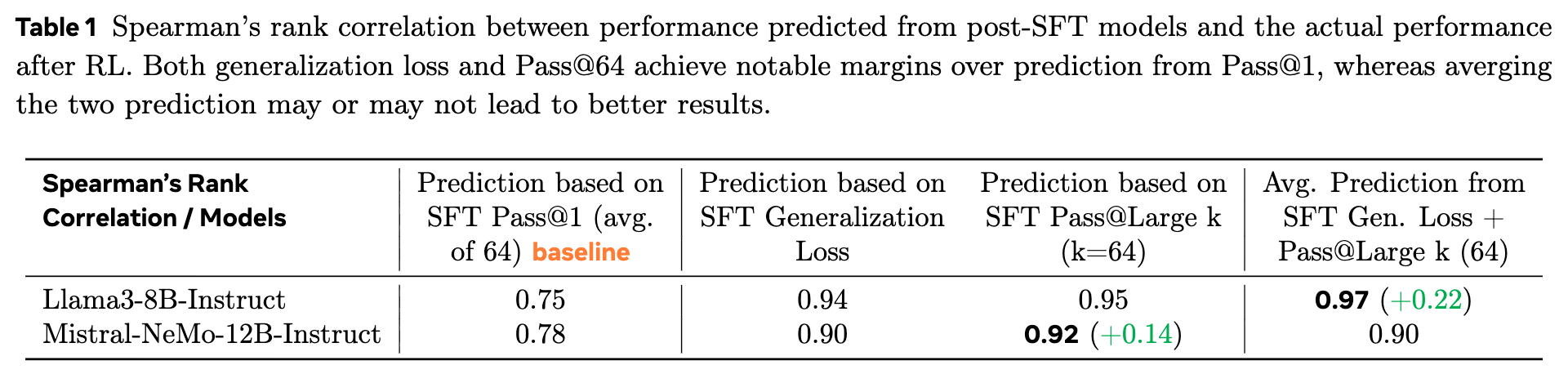

如表 1 和表 2 所示,新指标取得了显著的优胜。以 Mistral-NeMo-12B 模型为例:
-
在排序能力上(表 1),基线 Pass@1 的斯皮尔曼系数为 0.78,而泛化损失和 Pass@64 分别达到了 0.90 和 0.92,能够更准确地识别出最优的 SFT 模型。 -
在预测准确性上(表 2),基线 Pass@1 的 仅为 0.29,表现出很差的预测能力。而泛化损失将 提升至 0.79(提升了 0.50,即近 2 倍的改进),这意味着它能解释 79% 的最终性能变化,提供了有力的预测依据。
这些结果表明,泛化损失 和 Pass@large k 都是优化 SFT 训练配置的有效工具,其中泛化损失在预测数值准确性上表现尤为突出。
3.3 样本层面的预测
这个用例旨在解决 SFT 数据选择的问题:给定多个经过不同策略筛选出的候选 SFT 数据集,如何选择能带来最佳最终 RL 性能的那个?
在这个场景下,由于不同 SFT 数据集可能来自不同的分布,使用验证集损失作为指标会引入“分布漂移”的干扰,因此不再适用。而 Pass@large k 作为衡量模型内在能力的指标,则表现出了强大的鲁棒性。


如表 3 和 表 4 所示,Pass@64 的表现远超基线。以 Llama3-8B 模型为例:
-
在排序能力上(表 3),Pass@64 的斯皮尔曼系数从基线的 0.69 提升至 0.94。 -
在预测准确性上(表 4),Pass@64 的 从基线的 0.58 提升至 0.92(提升了 0.34)。
这证明了 Pass@large k 是一个在不同 SFT 数据集间进行选择的、高度准确和鲁棒的指标。它能够有效地识别出那些最能赋予模型强大而泛化的推理能力的 SFT 数据集。
4. 总结
这项研究系统地揭示了当前 SFT-RL 后训练流程中的一个核心困境,并提供了走出困境的实用工具。其结论对于大模型研发具有重要的指导意义。
核心结论:
-
SFT 分数陷阱是真实存在的:盲目地、孤立地优化 post-SFT 性能指标,不仅无法保证、甚至可能损害最终的 RL 性能。高 SFT 分数可能源于对简单、同质化或重复数据的过拟合。 -
存在更可靠的预测指标: -
泛化损失 是优化 SFT 训练配置(如 epoch 数)的强大指标。 -
Pass@large k 是选择最优 SFT 数据集 的鲁棒指标。
-
实践建议:
基于论文的发现,研究人员和工程师可以采用如下的优化工作流来降低 RL 阶段的风险和成本:
-
初步筛选:当面对多个 SFT 候选模型或配置时,可以首先使用 泛化损失 进行快速过滤。那些表现出低 SFT 性能和高泛化损失的模型可以被认为是次优选择,并被提前排除。 -
精确排序:对于通过初步筛选的候选者,使用 Pass@large k 进行评估和排序,以识别出最具潜力的 SFT 模型。 -
性能预测:如果目标是预测最终性能的具体数值(例如,用于评估 SFT 成本与预期收益的权衡),可以采用一种混合策略:在少数(例如,2-3个)SFT 模型上运行完整的 RL 流程以获取校准数据。然后,利用这些数据,基于泛化损失或 Pass@large k 拟合一个线性预测器,从而以低成本估算出所有其他 SFT 候选模型的最终性能。
局限性与未来方向:
论文也指出了当前研究的局限性,例如研究主要集中在数学推理任务上,RL 算法仅限于在线的 GRPO。未来,将这些发现扩展到更广泛的推理任务(如代码生成、科学推理)和 agentic use cases,以及探索其在离线 RL 或 DPO 等其他后训练范式中的适用性,将是重要的研究方向。此外,评估 Pass@large k 的计算成本依然存在,研究更高效的估计方法也值得探索。
往期文章:




