• 论文标题：Souper-Model: How Simple Arithmetic Unlocks State-of-the-Art LLM Performance
  • 论文链接：https://arxiv.org/pdf/2511.13254

TL;DR

今天分享一篇 Meta SuperIntelligence Labs、FAIR at Meta 和 UCL 联合发布的论文《Souper-Model: How Simple Arithmetic Unlocks State-of-the-Art LLM Performance》。该研究提出了一种名为“类别专家融合”（Soup Of Category Experts, SoCE）的模型融合（Model Souping）方法。不同于以往的均匀平均策略，SoCE 基于基准测试的组成结构，利用类别间的性能相关性分析，识别出在弱相关类别上的“专家”模型，并通过非均匀加权平均的方式进行融合。实验结果表明，该方法在 Berkeley Function Calling Leaderboard (BFCL) 上取得了 SOTA 结果（70B 模型提升 2.7%，8B 模型提升 5.7%），并在数学推理（MGSM）和长上下文（-Bench）任务中表现出优于单一模型和均匀融合的性能。该方法揭示了通过简单的算术操作，可以在不进行额外昂贵训练的情况下，显著提升模型的性能和鲁棒性。

1. 引言

随着大型语言模型（LLMs）的快速发展，其训练成本日益高昂。如何在不进行大规模再训练的前提下提升模型性能，成为了研究的热点。模型融合（Model Souping），即对同一架构的多个模型的权重进行平均，作为一种高效的后训练（post-training）技术，被证明可以提升模型的泛化能力并缓解灾难性遗忘。

然而，现有的模型融合技术（如 Uniform Souping, Greedy Souping）通常存在两个局限性：

  1. 模型选择的任意性：往往缺乏原则性的筛选机制来决定哪些模型应该参与融合。
  2. 均匀权重的假设：通常假设所有模型对最终结果的贡献是相等的，这忽略了不同模型在不同任务上的能力差异。

本文介绍的 SoCE 方法旨在解决上述问题。通过深入分析基准测试中不同类别的性能相关性，SoCE 提出了一种系统化的方法来选择模型并优化融合权重。研究发现，基准测试中的不同类别往往表现出较低的性能互相关性（inter-correlations），这意味着不同的模型可能在不同的子领域具备“专家”能力。SoCE 利用这一观察，合成了一个集各家之长的“超级模型”。

2. 相关工作回顾

2.1 模型融合

模型融合并非新概念，但在 LLM 时代焕发了新生。Wortsman 等人 (2022) 展示了对微调后的模型进行权重平均可以优于单个最佳模型。他们提出了三种策略：

  • Uniform Souping：所有候选模型权重均等。
  • Greedy Souping：按性能降序逐个添加模型，若性能提升则保留。
  • Learned Souping：通过梯度下降学习融合权重。

Jang 等人 (2025) 提出了基于几何洞察的方法，利用模型与预训练起点的距离来减少所需模型数量。本文提出的 SoCE 方法与 Jang 等人的工作最为接近，但进一步引入了基准测试内部的指标相关性和合作博弈论（Cooperative Game Theory）来形式化候选者选择和权重分配。

2.2 自动模型合并

除了简单的平均，研究界还探索了基于进化算法或熵最小化的自动合并技术。例如，Akiba 等人 (2025) 应用进化算法自动发现开源模型的有效组合。然而，这些方法通常计算复杂度较高，且往往针对特定领域。SoCE 提供了一种更具解释性和计算效率的替代方案。

3. 类别专家融合 (SoCE)

SoCE 的核心洞察在于：基准测试中不同类别的模型性能表现呈现出异质的相关性模式。某些模型在特定类别上表现强相关，而在其他类别上则可能弱相关甚至负相关。

为了量化这一点，研究者分析了 BFCL 基准测试。如图 1 所示，相关性热图揭示了相关类别（如各类多轮对话任务）之间存在强正相关，而不相关类别（如多轮基础任务与实时准确率）之间存在弱相关。

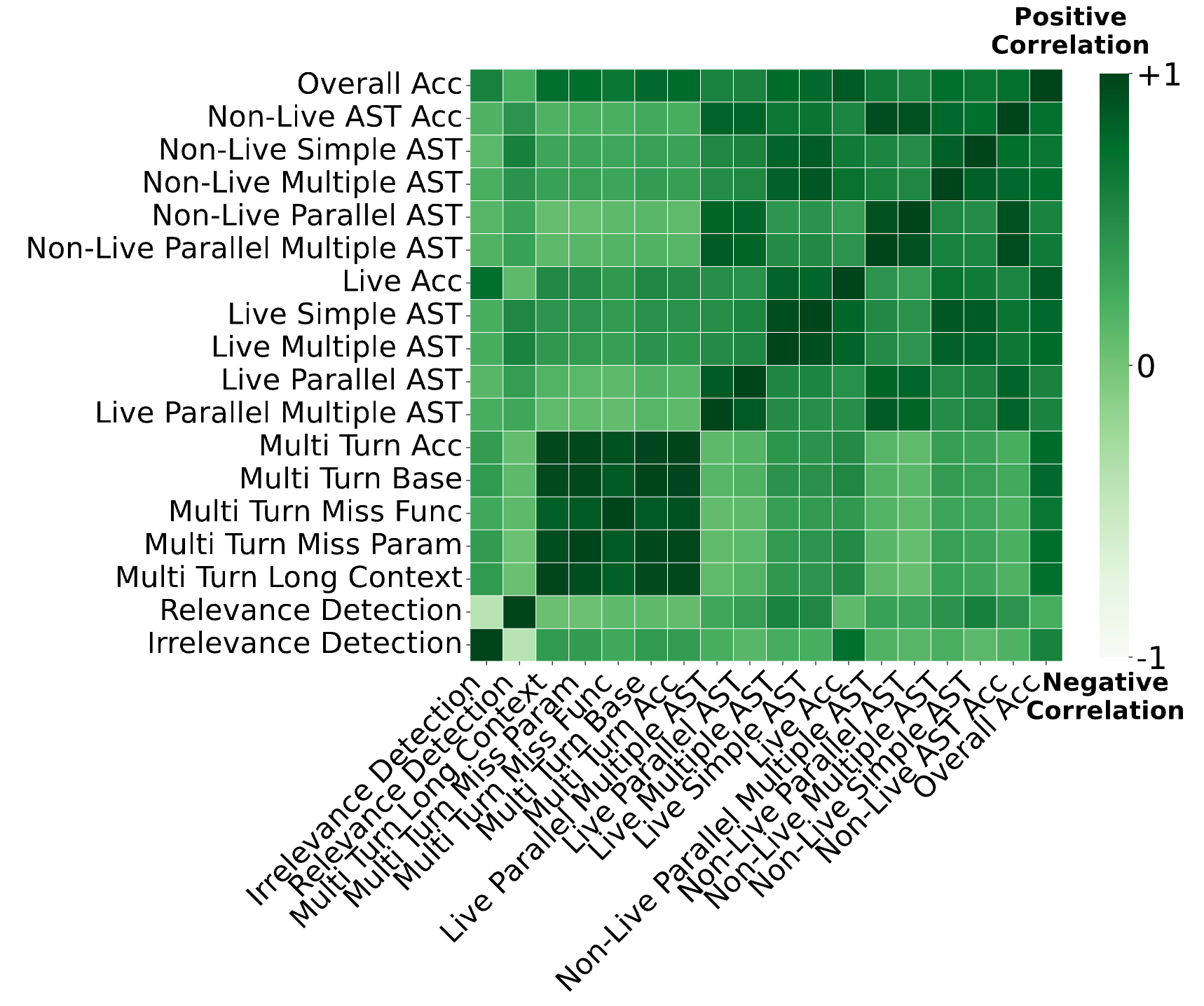
图 1 BFCL 排行榜模型性能的皮尔逊相关性热图
图 1 BFCL 排行榜模型性能的皮尔逊相关性热图

SoCE 利用这些相关性模式来策略性地选择和加权模型。具体流程如下所示。

3.1 算法流程

SoCE 包含四个关键步骤：

  1. 分析（Analysis）：识别弱相关的类别对。
  2. 专家模型选择（Expert Model Selection）：基于性能排名为每个类别选择专家。
  3. 权重优化（Weight Optimization）：搜索最优权重组合以最大化聚合性能。
  4. 模型融合（Model Souping）：生成最终模型。
步骤 1：分析

给定基准数据集 及其类别 ，以及候选模型集合 。
首先计算每对类别 之间的皮尔逊相关系数 。相关系数是基于所有模型在对应类别上的性能向量 和 计算得出的。
设定阈值 ，筛选出相关性低于该阈值的类别集合

步骤 2：专家模型选择

对于集合 中的每一个弱相关类别 ，从候选模型集合 中选择在该类别上表现最好的模型 ：

这一步确保了融合的模型池中包含了各个差异化领域的“专家”。

步骤 3：权重优化

生成权重向量 ，满足 且 。
为了找到最优权重，SoCE 在一个离散的权重空间内进行网格搜索。具体来说，权重的搜索步长设为 0.1，每个模型的权重范围限制在 [0.1, 0.9] 之间（同时包含均匀权重的特例）。
目标函数是最大化融合模型在所有类别上的总性能：

步骤 4：模型融合

利用优化后的权重 和选定的专家模型 ，通过加权平均计算最终的融合模型参数 ：

4. 实验设置

4.1 基准测试

为了全面评估 SoCE 的有效性，实验涵盖了以下三个主要基准：

  1. Berkeley Function Calling Leaderboard (BFCL) ：评估 LLM 的工具调用和函数执行能力，包含多轮交互、无关性检测、跨语言函数调用等多个类别。
  2. Multilingual Grade School Math (MGSM) ：评估跨语言的数学推理能力。
  3. -Bench：评估长上下文处理能力，测试模型在长序列中保持连贯性和提取信息的能力。
  4. FLORES-101：用于消融研究，评估多语言翻译质量。

4.2 基线对比

实验将 SoCE 与以下基线进行了对比：

  • 单一模型候选者：排行榜上现有的最佳单体模型。
  • Uniform Souping (All Candidates) ：对所有候选模型进行简单平均。
  • Uniform Souping with SoCE Model Selection：仅使用 SoCE 的策略选择模型，但使用均匀权重。这用于分离“模型选择”带来的收益。

5. 实验结果与分析

5.1 BFCL 基准测试结果：SOTA 性能

在 BFCL 上，研究者分别对 70B 和 8B 参数量的模型进行了实验。

70B 模型组：
候选模型包括 xLAM-2-70b, CoALM-70B, watt-tool-70B 等。

  • 最佳单一模型 (xLAM-2-70b) 准确率：78.56%
  • Uniform Souping 准确率：68.33%（性能下降）
  • SoCE (Proposed) 准确率：80.68%

SoCE 相比最佳单一模型提升了 2.7%，且显著优于均匀融合。最优权重配置为：xLAM (0.5), CoALM (0.2), watt-tool (0.3)。

8B 模型组：
候选模型包括 xLAM-2-8b, ToolACE-2-8B, watt-tool-8B 等。

  • 最佳单一模型 (xLAM-2-8b) 准确率：72.37%
  • Uniform Souping 准确率：69.80%
  • SoCE (Proposed) 准确率：76.50%

SoCE 相比最佳单一模型提升了 5.7%。最优权重配置为：xLAM (0.7), ToolACE (0.2), watt-tool (0.1)。

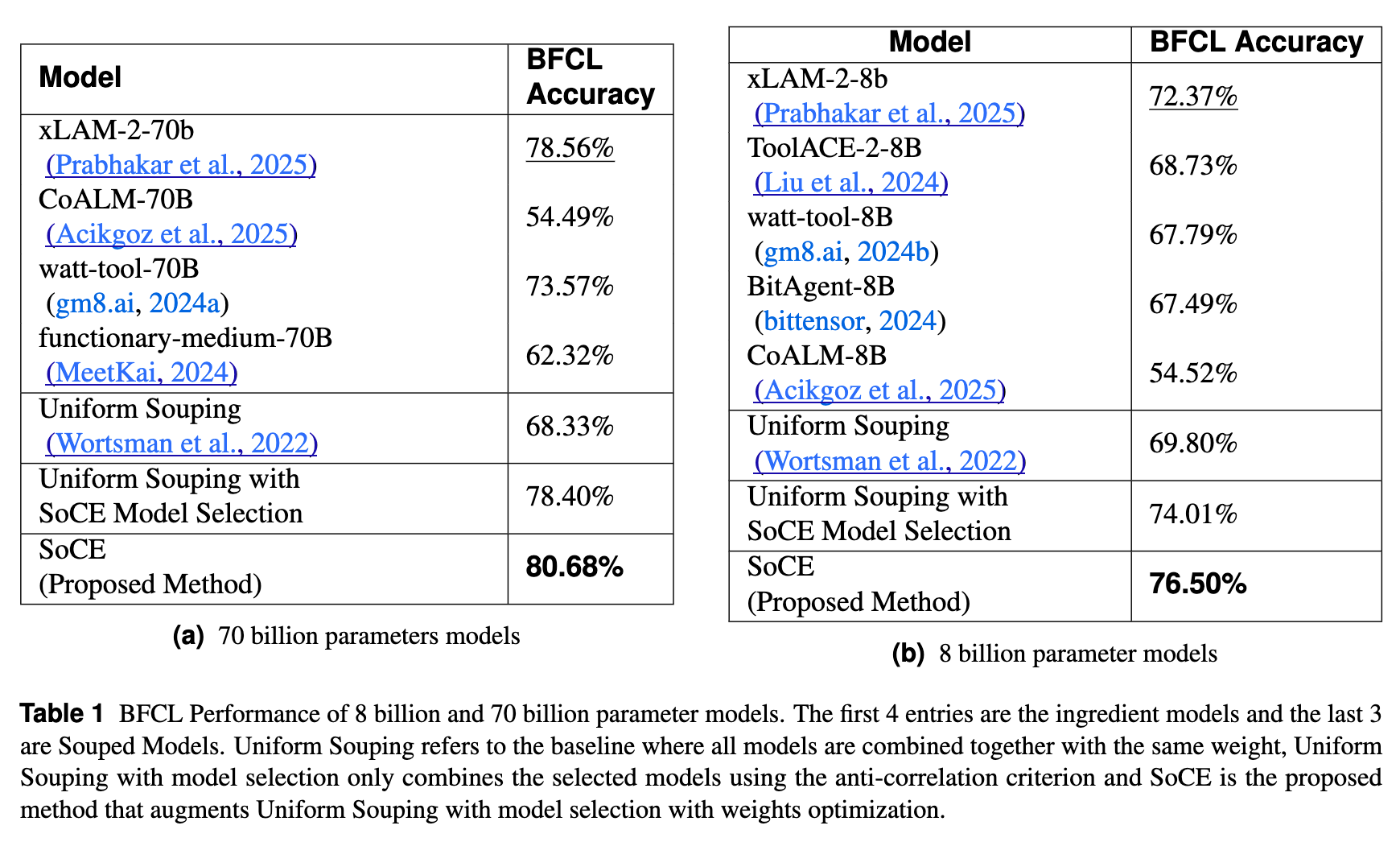
8B 和 70B 参数模型在 BFCL 上的性能对比
8B 和 70B 参数模型在 BFCL 上的性能对比

消融分析：
对比“Uniform Souping with SoCE Model Selection”和完整 SoCE 的结果显示，单纯的模型选择带来了显著提升，而进一步的权重优化则在 70B 和 8B 模型上分别带来了 2.28% 和 3.44% 的额外相对提升。这验证了策略性选择和权重优化两者缺一不可。

5.2 MGSM 和 -Bench 结果

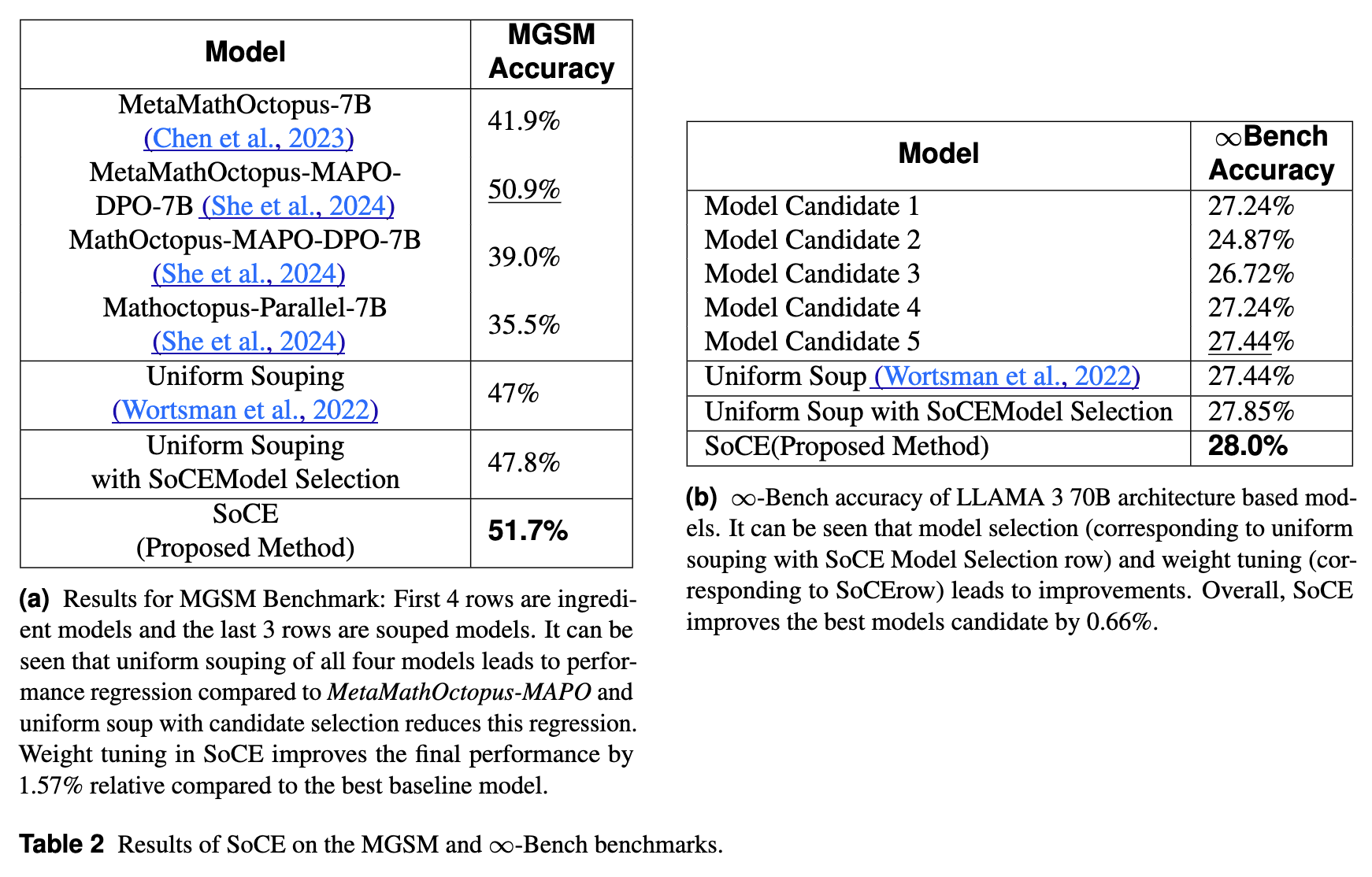
在 MGSM（多语言数学）基准上，SoCE 同样展现了优势。

  • 最佳单一模型 (MetaMathOctopus-MAPO-DPO-7B) 准确率：50.9%
  • Uniform Souping (All) 准确率：47%
  • SoCE 准确率：51.7%

在 -Bench（长文本）上：

  • 最佳单一模型准确率：27.44%
  • SoCE 准确率：28.0%

尽管在长文本任务上的提升幅度较小（0.66%），但 SoCE 依然保持了相对于单一模型和均匀融合的优势，且没有出现性能倒退。

SoCE 在 MGSM 和 -Bench 上的结果
SoCE 在 MGSM 和 -Bench 上的结果

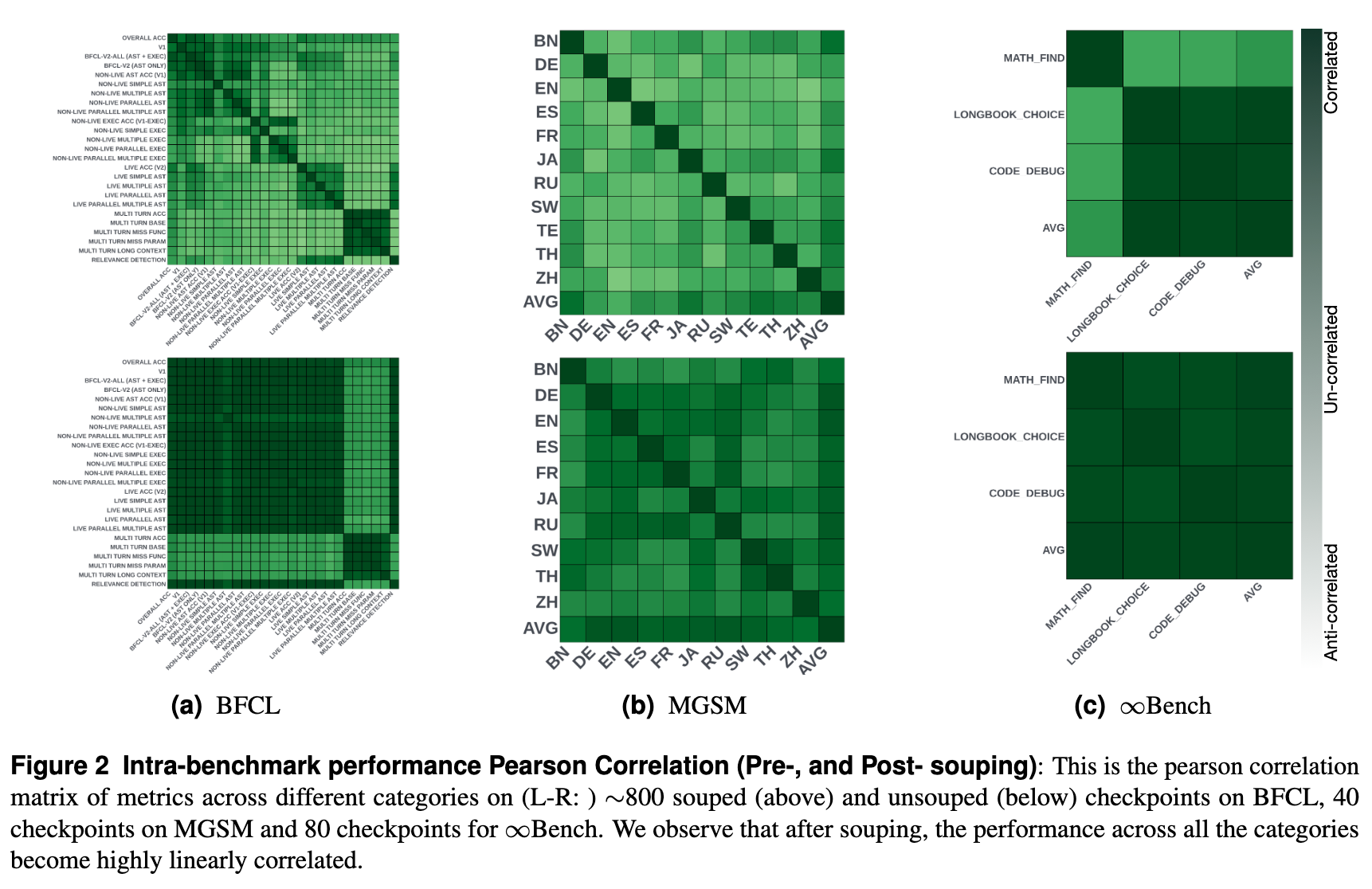
5.3 模型一致性分析

研究者通过大规模实证分析发现，模型融合增强了基准类别间性能的一致性。
如图 2 所示，对比融合前（Top row）和融合后（Bottom row）的皮尔逊相关系数矩阵：

  • 融合前：类别间的相关性模式复杂，存在弱相关或负相关区域。
  • 融合后：类别间的线性相关性显著增加（颜色变深）。

这意味着融合后的模型在各个类别上的表现更加协调和稳健，减少了“偏科”现象。

融合前后基准测试内部性能的皮尔逊相关性对比
融合前后基准测试内部性能的皮尔逊相关性对比

6. 为什么 SoCE 有效？

6.1 合作博弈论与 Shapley 值

为了解释模型选择的合理性，论文引入了合作博弈论中的 Shapley 值（Shapley Value）概念。
将模型融合看作一个合作博弈：

  • 玩家 (Players) ：候选模型 。
  • 联盟 (Coalition) ：参与融合的模型子集 。
  • 特征函数 (Characteristic Function) ：子集 融合后的性能。

Shapley 值 衡量了模型 对联盟总体性能的平均边际贡献。公式如下：

其中 是所有玩家排列的集合， 是排列 中位于 之前的玩家集合。

分析结果：
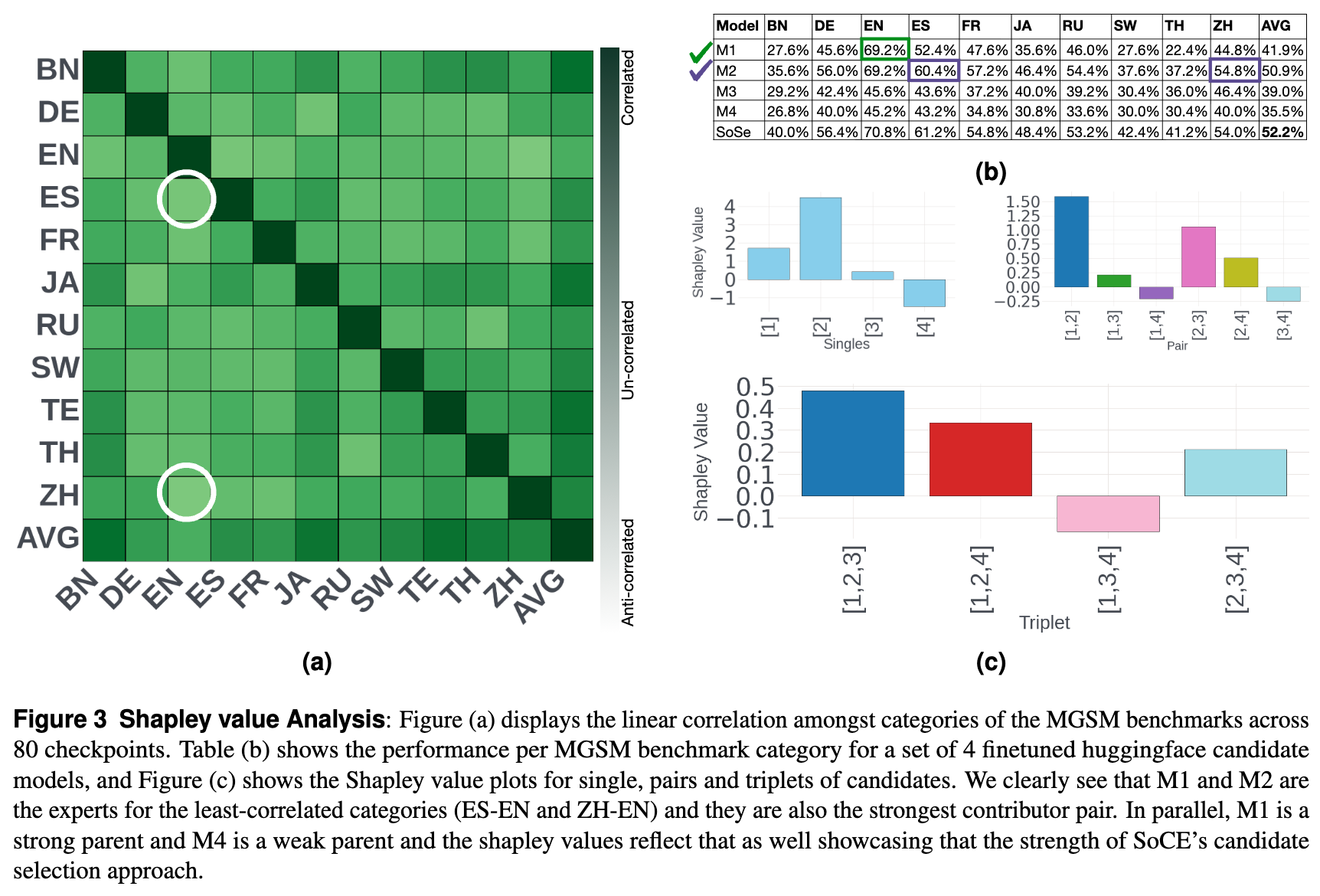
研究计算了 MGSM 任务中候选模型的 Shapley 值（图 3）。

  • 结果显示，SoCE 选出的模型组合（即“专家”模型）具有显著更高的 Shapley 值。
  • 例如，模型 M1 和 M2 分别是弱相关类别（ES-EN 和 ZH-EN）的专家，它们构成了贡献最大的配对。
  • 这从理论上证实了 SoCE 能够识别出对整体性能贡献最大的模型组合，排除了那些冗余或贡献微弱的模型（如 M4）。
MGSM 基准上模型 Shapley 值分析
MGSM 基准上模型 Shapley 值分析

6.2 胜率分析

在 BFCL 70B 模型组的详细分析中：

  • 保留能力：SoCE 成功解决了单一模型能解决的绝大多数任务（覆盖率 > 97%）。
  • 互补能力：当所有单一候选模型在某个任务上都失败时，SoCE 仍有 8.4% 的概率成功解决该任务。这表明融合模型产生了新的能力（emergent capability）。
  • 鲁棒性：当单一模型中只有部分模型失败时，SoCE 能够以 93.0% 的概率完成任务，显示了极强的鲁棒性。

7. 实践

在实践 SoCE (Soup Of Category Experts) 方法时，核心在于数据驱动的模型选择和加权策略。整个流程可以分为四个阶段：准备与评估、相关性分析与选择、权重优化、模型实际合并。以下是详细实践：

阶段一：准备工作与数据收集

前提条件：

  1. 同源模型：参与融合的候选模型必须基于相同的预训练底座（例如都是 Llama-3-8B 的微调版），否则权重无法直接相加。
  2. 基准测试集：需要一个包含多个子类别（Categories）的测试集（如 BFCL, MGSM, MMLU 等）。

任务：
你需要获得所有候选模型在各个子类别上的分数矩阵。

实践步骤：

  1. 收集 个候选模型（Checkpoint）。
  2. 在验证集或测试集上运行评估。推荐使用 LM Evaluation Harness 或针对特定任务的脚本。
  3. 构建性能矩阵 ，其中 表示模型 在类别 上的得分。

代码示例（构建数据）：

import pandas as pd
import numpy as np

# 假设你有5个候选模型，在BFCL的4个子类别上的得分
data = {
    'Model': ['Model_A', 'Model_B', 'Model_C', 'Model_D', 'Model_E'],
    'Multi-turn': [80.5, 60.2, 75.0, 55.0, 78.0],
    'Irrelevance': [20.0, 88.5, 40.0, 90.0, 30.0], # 假设 Model_B/D 擅长拒识
    'Java': [70.0, 65.0, 85.0, 60.0, 72.0],        # 假设 Model_C 擅长 Java
    'Simple': [90.0, 88.0, 89.0, 87.0, 91.0]
}

df = pd.DataFrame(data).set_index('Model')
print("性能矩阵：")
print(df)

阶段二：相关性分析与专家选择

核心逻辑：
计算类别之间的皮尔逊相关系数。如果两个类别的得分高度相关（例如 ），说明模型在这两个能力上往往“同进退”；如果相关性低甚至负相关，说明需要不同的专家。

实践步骤：

  1. 计算类别的相关性矩阵。
  2. 设定阈值 （论文中使用动态观察，一般可选 0.5-0.7）。
  3. 对弱相关或负相关的类别，分别选出该类别下的 Top-1 模型。

代码实现：

import seaborn as sns
import matplotlib.pyplot as plt

# 1. 计算类别间的皮尔逊相关系数
# 注意：我们要看的是“类别”间的相关性，基于不同模型的表现
# 因此需要对转置后的矩阵计算相关性
correlation_matrix = df.T.corr(method='pearson') # 这里的逻辑需注意，论文是 calculate correlation between category performances across all models
# 正确逻辑：每一列是一个Category，每一行是一个样本(Model)。我们要看列与列的相关性。
cat_corr = df.corr(method='pearson')

print("\n类别相关性矩阵：")
print(cat_corr)

# 2. 专家选择算法 (简化版)
selected_experts = set()
categories = df.columns
threshold = 0.5 # 设定阈值

# 简单策略：遍历所有类别，为每个“独特”的类别组找最佳模型
# 论文中使用了聚类或成对判断，这里简化为：
# 为每个类别找到得分最高的模型，加入候选池
for cat in categories:
    best_model = df[cat].idxmax()
    selected_experts.add(best_model)
    print(f"Category: {cat}, Best Expert: {best_model}, Score: {df.loc[best_model, cat]}")

expert_list = list(selected_experts)
print(f"\n最终入选的专家模型: {expert_list}")

阶段三：权重优化

核心逻辑：
在确定了专家模型集合后（假设选出了 3 个模型），需要在单纯形空间（Simplex space，即 ）中搜索最优权重。

搜索策略：

  • 步长：论文建议 0.1。
  • 范围：每个模型权重 。
  • 目标：最大化验证集上的总分。由于在大模型上针对每组权重都进行一次完整的推理（Inference）成本极高，通常有以下两种近似方法：

    1. Logits 代理（高精度）：保存每个专家在验证集上的 Logits，在内存中进行加权融合后计算 Loss/Metric。
    2. 线性代理（低成本，本文隐含）：假设性能与权重呈线性关系（虽然不完全准确，但在局部有效），或者在小规模验证集上进行快速验证。

这里演示基于 Logits 的 Grid Search（这是最科学的方法）：

import itertools

def generate_weights(n_models, step=0.1):
    """生成总和为1的权重组合"""
    # 这里是一个简化的生成器逻辑，实际可用递归实现
    # 假设步长0.1，生成如 (0.7, 0.2, 0.1) 的组合
    ticks = int(1/step)
    for combination in itertools.product(range(1, ticks), repeat=n_models):
        if sum(combination) == ticks:
            yield tuple(c * step for c in combination)

def evaluate_soup(weights, expert_logits, targets):
    """
    在内存中计算Soup的性能
    expert_logits: list of tensors [Batch, Seq, Vocab]
    weights: list of floats
    """
    # 融合 Logits (Softmax前) 或 Probabilities (Softmax后)
    # Wortsman等人建议在 Prob space 做 ensemble，但 Souping 通常指 weights merging
    # 注意：权重空间的融合对应到输出空间并非直接线性
    pass

# 模拟搜索过程
best_score = -1
best_weights = None
experts = ['Model_A', 'Model_B', 'Model_D'] # 假设选出的专家

for w in generate_weights(len(experts)):
    # 伪代码：实际需要执行模型合并后的推理
    # current_score = run_inference(merge(experts, w)) 
    # print(f"Weights: {w}, Score: {current_score}")
    pass

工程上的妥协方案：
如果计算资源有限，无法对每组权重做推理，可以采用贪心策略：

  1. 以该类别的专家模型为锚点（权重 0.5-0.7）。
  2. 混合其他互补类别的专家（权重 0.1-0.3）。
  3. 只验证 3-5 组最有希望的组合（例如 [0.7, 0.2, 0.1], [0.5, 0.3, 0.2]）。

阶段四：模型合并

确定权重 后，执行实际的参数平均。推荐使用 mergekit，这是目前社区最标准的模型合并工具，支持 GPU/CPU 内存优化。

使用 Mergekit

  1. 安装：
pip install mergekit
  1. 编写配置 (config.yml) ：
    假设你找到了最优权重：Model A (0.5), Model B (0.3), Model C (0.2)。
models:
  - model: /path/to/Model_A
    parameters:
      weight: 0.5
  - model: /path/to/Model_B
    parameters:
      weight: 0.3
  - model: /path/to/Model_C
    parameters:
      weight: 0.2
merge_method: linear
dtype: float16
  1. 运行合并：
mergekit-yaml config.yml ./output_souped_model --cuda

往期文章：