标准的 CoT 过程是建立在离散的语言词元(discrete tokens)之上的。在推理的每一步,模型都必须从词汇表中采样一个确定的词元,这相当于在一个庞大的决策树中选择一条特定的路径。这种“硬决策”机制带来了几个问题:
-
表达能力的限制:每一步的采样都是一个不可逆的承诺,一旦选定,就无法回头或同时考虑其他可能性。这限制了模型探索多样化推理路径的能力,容易陷入局部最优解。 -
与人类认知的差异:人类的思维过程往往不是严格线性的、符号化的,而是在一个更抽象、更流动的概念空间中进行的。我们可以在脑海中同时权衡多种假设和可能性,这更像一种“叠加态”。离散的 CoT 难以模拟这种并行和模糊的思考方式。 -
训练的挑战:为了引导模型学习更优的推理路径,研究者们通常依赖强化学习(RL)或指令蒸馏。然而,RL 在离散空间中的探索效率不高,而指令蒸馏则需要高质量的、由更强大模型生成的“教师”推理路径,成本高昂且学生模型的能力受限于教师。
这些瓶颈共同构成了一个关键的研究空白:我们能否让 LLM 的“思考”过程摆脱离散词元的束缚,在一个连续的概念空间中进行,从而获得更强的表达能力和更高的推理效率?
来自 Meta FAIR、阿姆斯特丹大学和纽约大学的研究者在论文《Soft Tokens, Hard Truths》中提供了一个新的视角。他们提出了一种可扩展的、基于强化学习的方法,用于训练模型生成连续的思维链,而无需依赖任何预先存在的、由离散词元构成的“真值”推理路径。该方法不仅在理论上具有吸引力,更在实践中展示了其有效性和鲁棒性。

-
论文标题:Soft Tokens, Hard Truths -
论文链接:https://www.arxiv.org/pdf/2509.19170
1. 背景
1.1 离散 CoT 的局限性
正如前文所述,离散 CoT 迫使模型进行序贯决策(sequential exploration)。这在解决需要广度优先搜索或并行探索多个假设的问题时效率低下。例如,在复杂的数学证明或逻辑推理中,一条看似有前景的路径可能最终走向死胡同。如果模型能够同时“心算”多条路径,其成功的概率和效率都将得到提升。
1.2 连续 CoT 的理论潜力
为了克服离散 CoT 的局限,研究界提出了“连续 CoT”(Continuous CoTs)或“软思考”(Soft Thinking)的概念。其核心思想是,在 CoT 的中间步骤,不再生成一个具体的、“硬”的词元,而是使用一个“软”的表示——通常是词汇表中所有词元嵌入(embeddings)的概率加权平均。
这个软表示可以被看作是一个“概念向量”或“思维叠加态”,它同时编码了多种下一步的可能性。从理论上讲,这种方法具备显著优势:
-
更强的表达能力:连续的向量空间比离散的词元空间要丰富得多,能够表达更细微和复杂的语义概念。 -
并行的推理模拟:一个连续的“思维向量”可以被理解为多个推理前沿的叠加,使得模型能够隐式地并行探索多条推理路径。论文《A theoretical perspective on chain of continuous thought》在图可达性问题上从理论上证明了,使用连续 CoT 的浅层 Transformer 能够比使用离散 CoT 的模型更高效地解决问题。
1.3 连续 CoT 的实践困境
尽管理论上前景广阔,但将连续 CoT付诸实践却面临着巨大的挑战,主要集中在训练上:
-
缺乏监督信号:我们如何知道一个“好的”连续思维向量应该是什么样子?由于不存在人类标注的“连续思维”数据,训练变得十分困难。 -
计算成本高昂:一些早期工作,尝试通过将已有的离散 CoT 蒸馏(distill)到连续表示中来解决监督问题。但这不仅需要高质量的离散 CoT 真值,而且依赖于通过整个连续 CoT 过程进行时间反向传播(Backpropagation Through Time, BPTT),计算和内存开销巨大,导致其 CoT 长度被限制在极少数(例如 6 个)词元内。 -
推理时应用受限:另一类方法,则完全跳过训练,直接在预训练好的、使用离散词元训练的模型上进行推理时应用软词元。这种方法虽然巧妙,但效果并不稳定,后续研究表明其性能提升有限,甚至有时会下降。
因此,一个核心问题摆在面前:如何开发一种可扩展的、计算高效的、并且不依赖于真值 CoT 路径的训练方法,来真正释放连续 CoT 的潜力? 这正是《Soft Tokens, Hard Truths》这篇论文所要解决的核心问题。
2. 基于强化学习的连续思维链训练
该论文提出了一种新颖的框架,通过在软词元生成过程中引入噪声,巧妙地将其转化为一个可以通过强化学习(Reinforcement Learning, RL)进行优化的随机过程。
2.1 符号与标准 LLM 流程回顾
为了理解其方法,我们首先回顾一下标准 LLM 的生成过程。
-
设词汇表大小为 。一个词元 可以表示为一个 one-hot 向量 。 -
嵌入层 (Embedding Layer) :将 one-hot 向量序列 映射为嵌入向量序列 。
其中 是词元嵌入矩阵。 -
Transformer 栈 (Transformer Stack) :处理嵌入序列,输出上下文相关的隐藏状态序列 。
-
解码层 (Decoding Layer) :将隐藏状态映射为对数(logits)。
其中 是解码矩阵。 -
Softmax 层:将 logits 转换为下一个词元的概率分布 。
其中 是温度参数。
在标准(硬)CoT中,模型根据概率分布 采样一个 one-hot 向量 ,然后将其嵌入后作为下一个时间步的输入,循环往复。
2.2 “软思考”及其对 RL 的挑战
在“软思考”中,模型跳过了采样步骤。它直接使用概率向量 来计算下一个输入嵌入 ,即所有词元嵌入的加权平均:
这个过程是完全确定性的。给定一个提示(prompt),整个连续 CoT 的生成过程是固定的,没有随机性。这导致标准的、基于采样的强化学习算法(如 REINFORCE)无法直接应用,因为 RL 的核心依赖于通过探索(exploration)来发现高奖励的策略。
2.3 带噪声的软思考(Noisy Soft Thinking)
本文的核心创新在于,通过一个简单的操作——注入噪声——来打破这种确定性,从而为 RL 训练打开大门。在计算下一个输入嵌入时,他们在软嵌入的基础上增加一个高斯噪声:
其中 是噪声的标准差。
这个噪声的引入至关重要:
-
提供了探索机制:噪声使得 CoT 的生成过程变成了一个随机过程。即使对于同一个前缀,每次生成的连续 CoT 也会因为噪声的存在而有所不同。这种随机性正是 RL 算法进行策略探索所需要的。 -
使能 RL 优化:现在,整个过程可以被建模为一个策略 。该策略在每个时间步输出一个概率分布(由前一步的 决定),然后通过添加噪声来“采样”一个连续的动作(即带噪声的嵌入 )。
论文进一步定义了两种连续词元类型:
-
软词元 (Soft Tokens) :在生成 CoT 时使用一个适中的温度(如 ),使得概率分布 比较平滑,生成的软嵌入是多种可能性的混合。 -
模糊词元 (Fuzzy Tokens) :使用一个趋近于 0 的温度(如 )。此时,softmax 的输出会高度集中在概率最大的那个词元上,使得 几乎变成一个 one-hot 向量。因此, 会非常接近于最可能词元的嵌入。这种“模糊词元”可以看作是在离散决策的嵌入上增加噪声。
2.4 强化学习框架
引入噪声后,就可以应用标准的 RL 算法(如 REINFORCE 及其变体)进行训练。其目标是最大化一个任务的期望奖励 ,其中 是模型在生成 CoT 后给出的最终答案。
目标函数为:
其中 是当前的模型策略。
根据 REINFORCE 算法,损失函数(需要最小化)为:
这里的 是给定连续 CoT 后,生成最终答案的对数概率,这部分可以通过标准的最大似然进行优化。
关键在于如何计算 ,即生成特定连续 CoT 序列的对数概率。由于噪声是高斯分布,在每个时间步 ,生成 的对数概率可以很容易地计算出来:
其中 是无噪声的软嵌入,它是之前步骤 的可微函数。整个 CoT 的对数概率是所有时间步对数概率的总和。
这种方法的计算开销非常小,仅需要在每一步存储概率向量 (大小为 )并注入噪声。与需要完整 BPTT 的蒸馏方法相比,其效率大大提高,使得训练数百个词元长度的连续 CoT 成为可能。
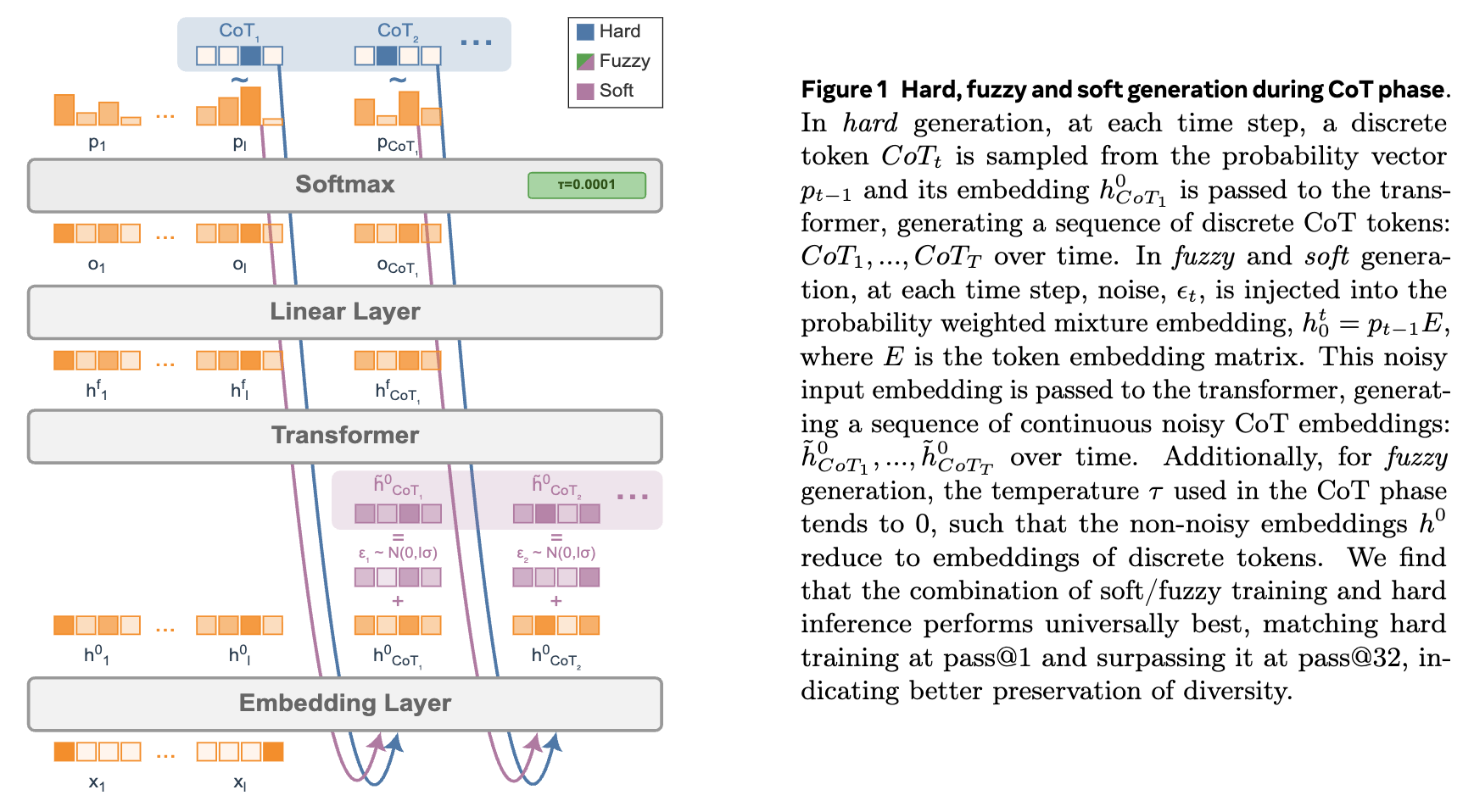
上图直观地展示了硬生成、模糊生成和软生成在 CoT 阶段的区别。硬生成从 Softmax 输出的概率分布中采样一个离散词元。而模糊和软生成则将概率加权的嵌入混合体(可能带有噪声)直接送入下一层。
3. 实验
为了验证方法的有效性,研究者们进行了一系列详尽的实验。
-
基础模型:Llama 3.2 3B Instruct, Llama 3.1 8B Instruct, 和 Qwen 2.5 3B Instruct。 -
训练数据集:涵盖不同难度的数学推理数据集,包括 GSM8K(小学数学应用题)、MATH(高中竞赛数学)和 DeepScaleR(一个更具挑战性的数学推理数据集)。 -
训练方法对比: -
硬词元 (Hard) :标准的离散 CoT,使用 RL 进行微调。 -
软词元 (Soft) :本文提出的方法,使用 的温度。 -
模糊词元 (Fuzzy) :本文提出的方法,使用 的温度。
-
-
强化学习算法:使用了 RLOO(Reinforce with Leave-One-Out),这是一种通过组内样本均值作为基线(baseline)来减小方差的 REINFORCE 变体。 -
评估方式:为了全面评估,作者们解耦了训练方法和推理方法。对于每一种训练好的模型(Hard, Soft, Fuzzy),他们都评估了六种不同的推理设置(例如,硬贪婪解码、硬采样解码、软贪婪解码等)。 -
评估指标: -
pass@k:生成 个答案,只要其中有一个是正确的,就算通过。pass@1 衡量的是模型的单次最佳性能,而 pass@32 则能更好地衡量模型生成答案的多样性。 -
域外(Out-of-domain)鲁棒性:在通用基准(如 HellaSwag, ARC, MMLU)上评估模型性能,以检验微调是否损害了模型的通用能力。评估指标包括准确率和正确答案的负对数似然(Negative Log-Likelihood, NLL)。NLL 越低,表示模型对正确答案的预测越自信。
-
4. 核心发现与结果分析
实验结果揭示了一些深刻的、有时甚至是反直觉的结论,呼应了论文标题中的 Hard Truths 。
4.1 发现一:pass@1 性能持平,pass@32 优势显著
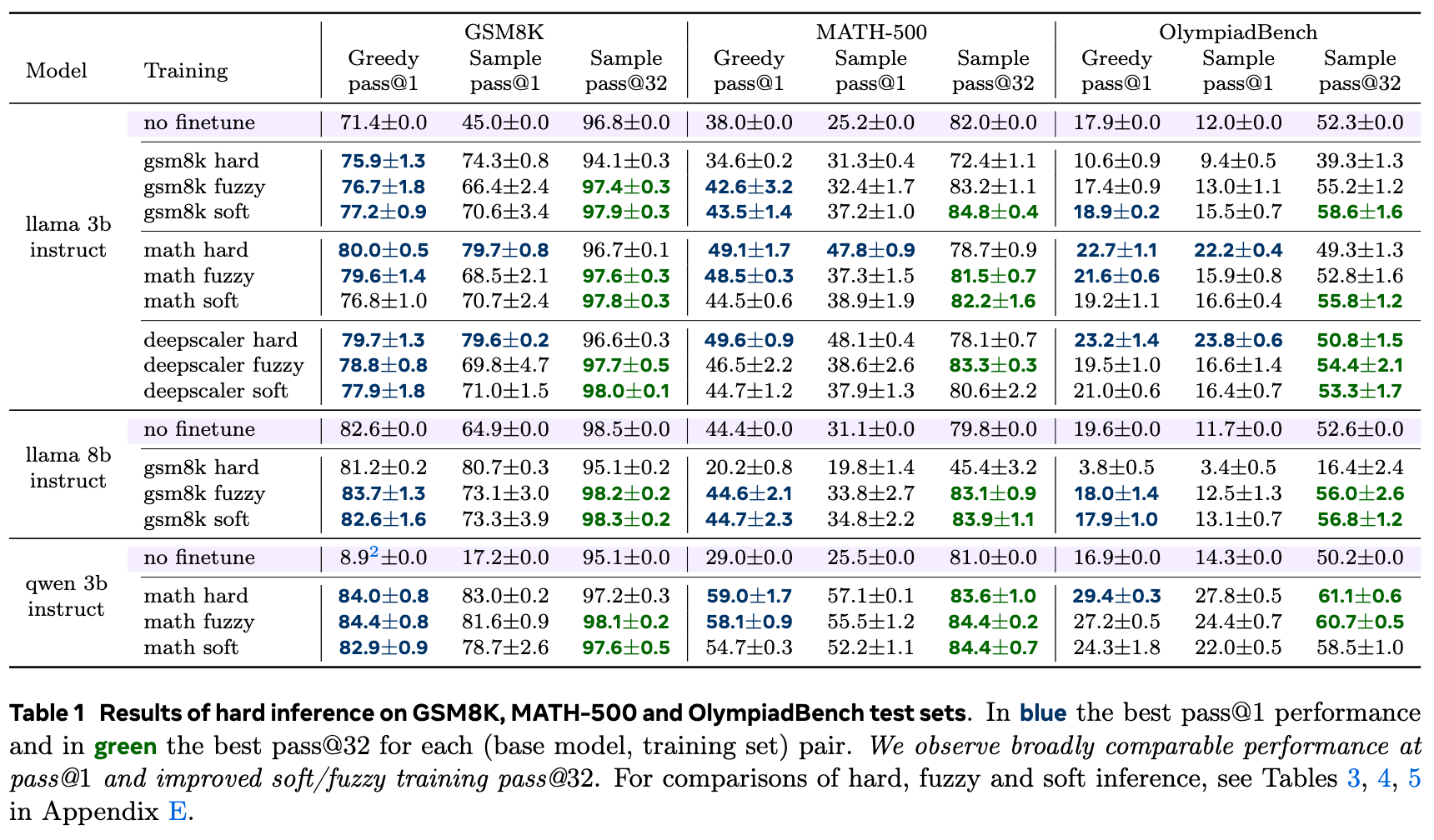
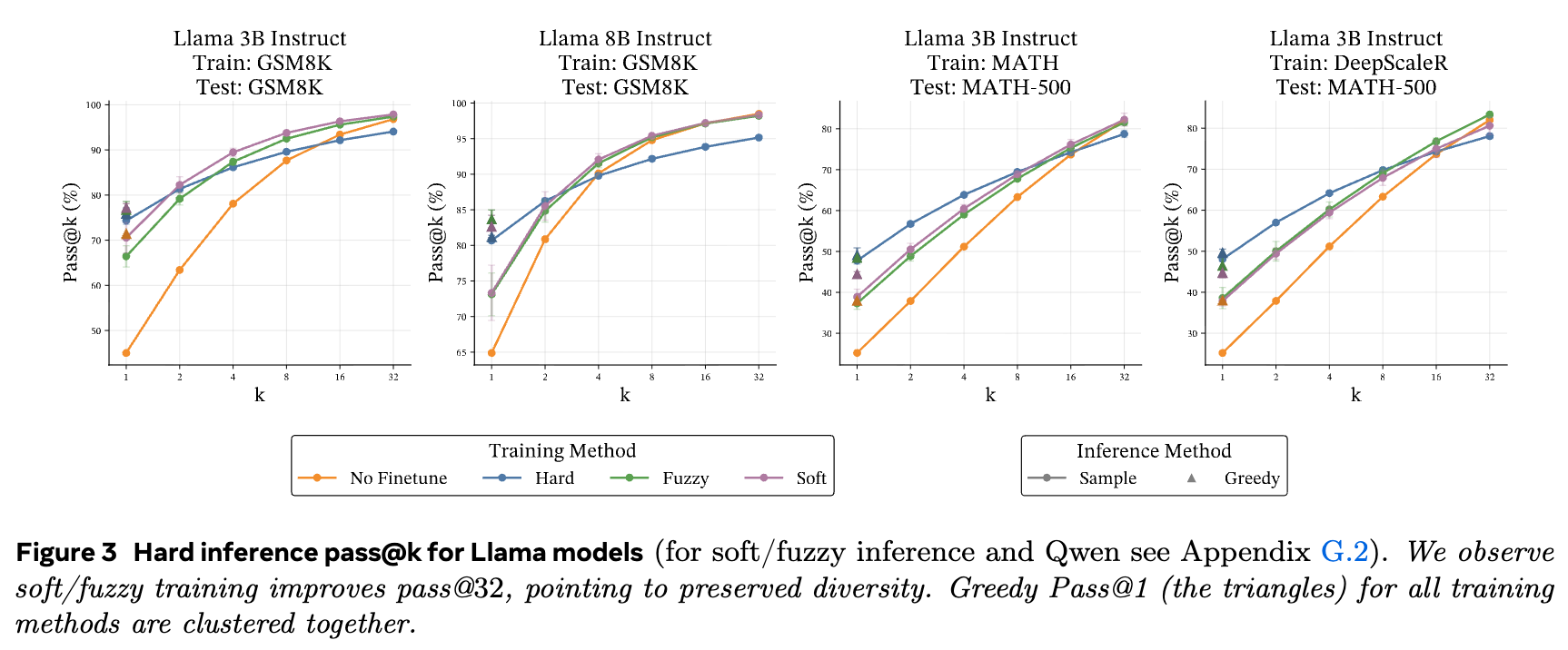
从实验结果(如表1和图3)中可以清晰地看到一个趋势:
-
在 pass@1 指标上,软词元和模糊词元训练的模型与传统的硬词元训练的模型性能大致相当。这表明,在追求单次最佳答案的场景下,连续 CoT 训练并未带来显著的性能损失。 -
然而,在 pass@32 指标上,软词元和模糊词元训练的模型明显优于硬词元训练的模型。这说明通过连续 CoT 训练的模型,其生成的推理路径和最终答案具有更高的多样性。由于模型在训练中探索了一个更平滑、更连续的空间,它学会了产生更多样化的有效解决方案,而不是仅仅收敛到单一的最优路径。
这一发现具有重要的实践意义:对于需要创意或多种解决方案的任务,连续 CoT 训练提供了一种有效提升多样性的方法。
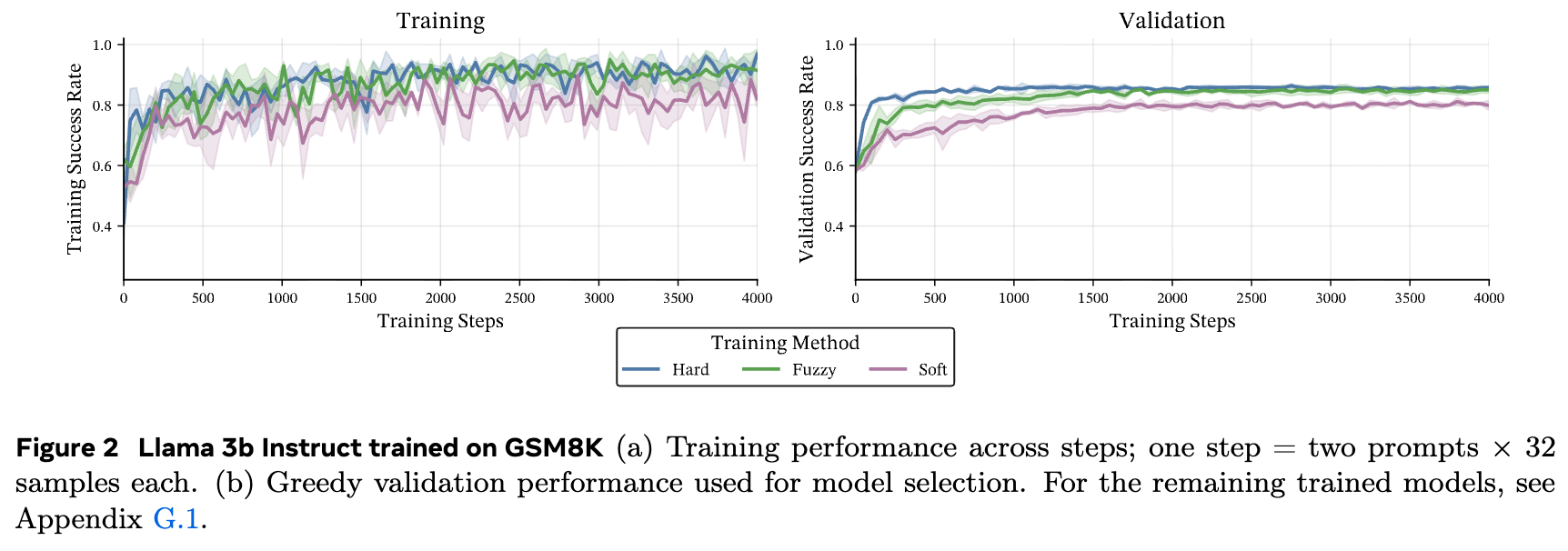
上图展示了在 GSM8K 数据集上的训练过程。可以看到,三种训练方法(Hard, Fuzzy, Soft)的训练和验证成功率曲线非常接近,表明软/模糊训练方法的稳定性和有效性。
4.2 发现二:软模型上的硬推理效果最佳
一个有些出人意料的发现是,无论模型是使用哪种方式训练的(硬、软或模糊),在推理时使用标准的离散(硬)解码通常能获得最佳性能。
这意味着,即使模型在训练时学会了在连续空间中“思考”,将这种“软”能力转化为最终结果的最佳方式仍然是通过传统的“硬”词元采样。论文明确指出,他们未能复现之前一些工作中所声称的“在硬训练模型上进行软推理能提升性能”的结论。
这揭示了一个核心观点:连续 CoT 的优势主要体现在训练阶段。它是一种更有效的学习和探索机制,能够让模型学到更鲁棒、更多样化的内部表示。但到了应用(推理)阶段,确定性的、离散的决策过程依然是最高效的。这便是标题中“Soft Tokens, Hard Truths”的精髓所在——用软的方法去训练,用硬的方法去应用。
4.3 发现三:更好的域外鲁棒性
微调 LLM 的一个常见风险是“灾难性遗忘”或在特定任务上过拟合,从而损害其在其他任务上的通用能力。实验通过在 HellaSwag、ARC 和 MMLU 等基准上进行测试,评估了不同训练方法对模型通用性的影响。
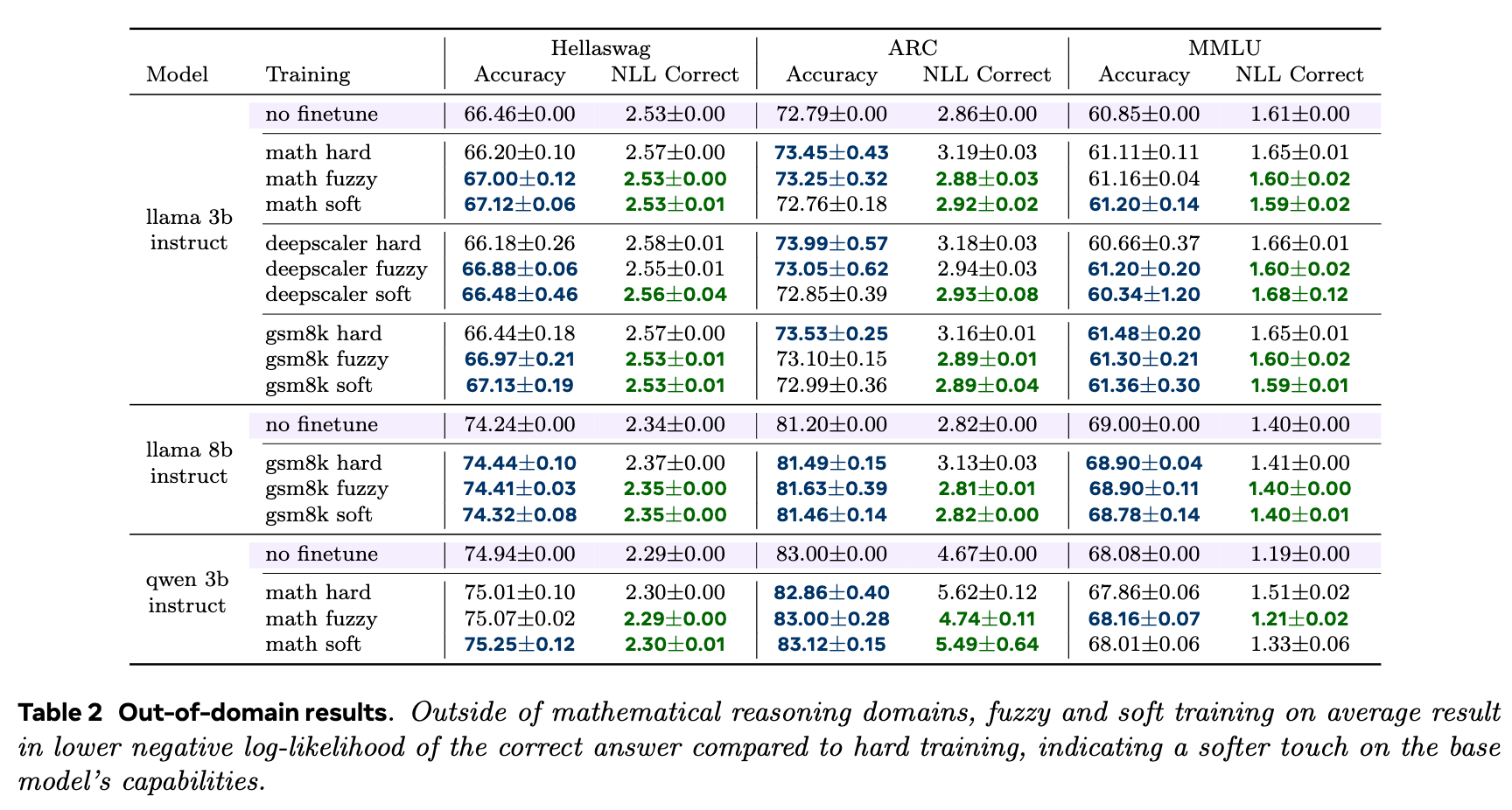
结果(如表2所示)显示:
-
在准确率上,三种方法表现相近。 -
但在负对数似然(NLL)上,差异变得明显。硬词元训练普遍导致模型在域外任务上的 NLL 上升,意味着模型对这些任务的正确答案变得不那么自信了。相比之下,软词元和模糊词元训练更好地保持了基础模型的 NLL 水平。
这表明,连续 CoT 训练对基础模型的“扰动”更小,是一种“更温柔的微调”(a softer touch)。它在提升特定任务推理能力的同时,更好地保留了模型预训练时学到的通用知识。
一个特别有说服力的例子是,在 Llama-8B-Instruct 模型上,使用 GSM8K(小学数学)进行硬词元微调后,其在更难的 MATH(高中数学)测试集上的性能出现了严重崩溃。而使用软/模糊词元进行微调,不仅在 GSM8K 上保持了高性能,还显著提升了在 MATH 上的性能,表现出更强的泛化能力。
4.4 发现四:熵分析揭示行为差异
为了从更深层次理解不同训练方法带来的行为差异,研究者们分析了模型在生成 CoT 过程中的熵(entropy)。熵衡量了模型在预测下一个词元时的不确定性。熵越高,表示模型认为多种选择都有可能;熵越低,表示模型非常确定下一步该生成什么。
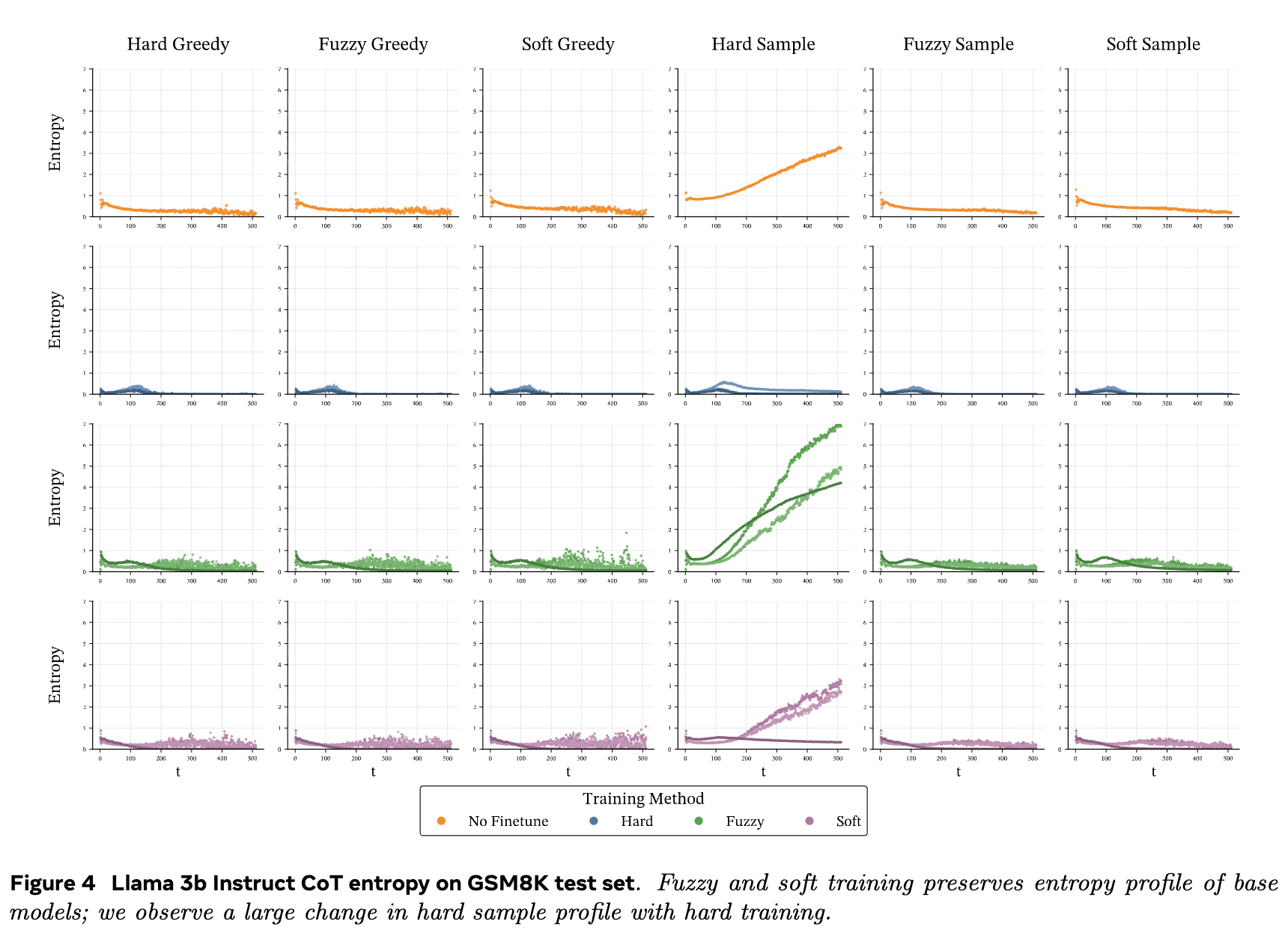
分析(如图4所示)揭示了深刻的差异:
-
基础模型(未微调):在使用采样(高温度)生成 CoT 时,随着 CoT 长度增加,熵会显著上升。这很直观,因为推理链越长,不确定性累积得越多。 -
硬词元训练模型:经过硬词元 RL 微调后,即使在采样模式下,其熵分布也变得非常低,与贪婪解码(零温度)时的熵分布类似。这表明硬词元训练使得模型变得过于自信(overconfident)。模型被强化去追求单一的、高奖励的路径,从而抑制了对其他可能性的探索。这与 pass@32 性能下降和域外 NLL 变差的宏观表现完全吻合。 -
软/模糊词元训练模型:这两种方法训练的模型,其熵分布与基础模型基本保持一致。这再次证明了软/模糊训练是一种更“温和”的优化过程,它在引导模型向高奖励区域学习的同时,保留了其内在的不确定性估计和探索能力。
往期文章:




