我们知道可验证奖励的强化学习(Reinforcement Learning with Verifiable Reward, RLVR)会提高模型的Pass@1但会降低Pass@k,这种现象通常与“灾难性遗忘”(Catastrophic Forgetting)和“多样性坍塌”(Diversity Collapse)紧密相关。
为了解决这一问题,研究社区提出了一些方法。部分工作尝试完全移除在策略优化中用于约束的 KL 散度项,希望给予模型更大的探索自由。另一些工作则诉诸于熵正则化,试图直接维持模型输出的多样性。然而,这些方法往往效果有限,甚至会引入新的问题,例如 Pass@1 性能的下降,或者引入了难以调节的超参数。
在此背景下,一篇题为《THE CHOICE OF DIVERGENCE: A NEGLECTED KEY TO MITIGATING DIVERSITY COLLAPSE IN REINFORCEMENT LEARNING WITH VERIFIABLE REWARD》的研究论文,将目光投向了一个被长期忽视却至关重要的环节:散度项的选择。论文的核心论点是,我们不应将散度项仅仅视为一个防止策略过度偏离的“约束”,而应主动地将其作为一种“机制”,用以积极地维护和保留模型的知识多样性。

-
论文标题:THE CHOICE OF DIVERGENCE: A NEGLECTED KEY TO MITIGATING DIVERSITY COLLAPSE IN REIN-FORCEMENT LEARNING WITH VERIFIABLE REWARD -
论文链接:https://arxiv.org/pdf/2509.07430
论文提出了一种名为多样性保留混合强化学习(Diversity-Preserving Hybrid RL, DPH-RL) 的新框架。该框架的核心是利用具有“质量覆盖(mass-covering)”特性的 f-散度(如前向 KL 散度和 JS 散度),来充当一种“排练机制”(rehearsal mechanism)。通过持续参考模型的初始策略,DPH-RL 迫使模型在探索新解法的同时,不断回顾和巩固其原有的知识库,从而保持广泛的解决方案覆盖。
1. 背景
在深入探讨论文的方法之前,我们首先需要对几个关键概念和当前 RLVR 面临的挑战有一个清晰的认识。
1.1 RLVR 与 Pass@k 性能退化
RLVR 的基本流程是:给定一个问题(如一道数学题),模型生成一个或多个解决方案。这些解决方案通过一个外部验证器(verifier)来判断其正确性,并据此生成奖励信号。强化学习算法(如 PPO 或其变种 GRPO)利用这些奖励信号来更新模型的参数,以期增加生成正确答案的概率。
Pass@k 指标衡量的是,在 次独立采样中,模型至少有一次生成正确答案的概率。Pass@1 是其特殊情况。理论上,一个 Pass@1 提升的模型,其 Pass@k 也应该相应提升或至少保持不变。但现实是,许多经过 RLVR 微调的模型,尽管在 Pass@1 上表现更优,其 Pass@k 却低于微调前的基础模型。
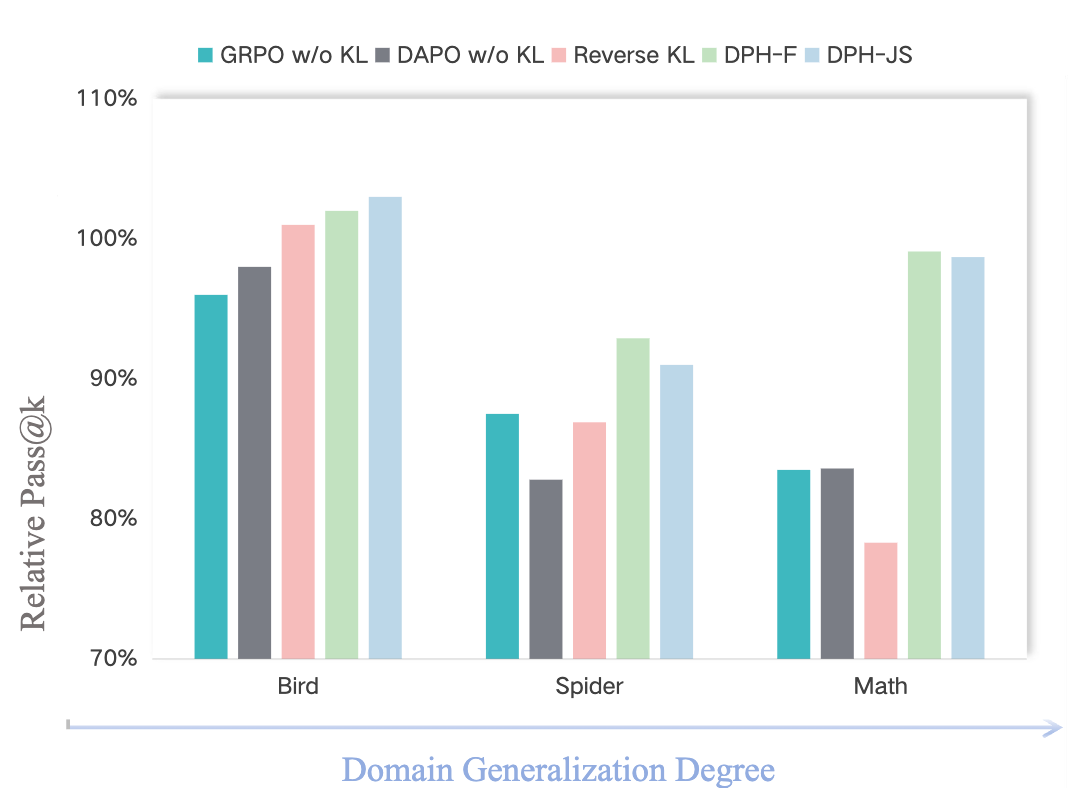
如上图所示,在从 Bird(SQL 数据集)迁移到 Spider 和 Math 等不同领域的任务上,一些主流的 RLVR 算法(如 GRPO 和 DAPO,在移除 KL 约束项后)的相对 Pass@k 分数显著低于 100%,这表明其性能相较于基础模型出现了退化。这直接印证了“多样性坍塌”的存在:模型可能学会了以更高的概率生成一两种“标准答案”,但失去了生成其他同样正确但形式不同的答案的能力。当这几种“标准答案”恰好不适用于某个问题时,模型便束手无策,导致多次尝试也无法成功。
1.2 KL 散度
在 PPO 等策略梯度算法中,通常会加入一个 KL 散度项,用于惩罚当前策略 与某个参考策略 (通常是微调前的初始策略或上一轮迭代的策略)之间的偏差。其目标是确保训练过程的稳定,防止策略更新步子迈得太大导致性能坍塌。
标准的 RL 微调流程普遍采用反向 KL 散度(Reverse KL Divergence):
其中 是给定的问题(context), 是模型生成的答案(action)。这个公式的期望是基于当前策略 的样本计算的。
反向 KL 散度有一个广为人知的特性,即“模式寻求”(mode-seeking)。为了最小化 , 会倾向于将概率质量集中在 分布中概率密度最高的区域(即“模式”)。如果 而 ,那么 KL 散度会变得非常大,对策略更新产生巨大的惩罚。这迫使 “不敢”探索 认为不太可能的区域。
在 RLVR 的场景下,当模型通过奖励信号发现某一种解题路径 A 的回报很高时,策略 会迅速向该路径靠拢。反向 KL 散度的模式寻求特性会加剧这一过程,因为它会惩罚模型去探索其他可能同样正确但初始概率较低的路径 B 或 C。最终,模型的所有概率质量都集中在路径 A 上,从而丢失了生成 B 或 C 的能力,导致了多样性的坍塌。
1.3 前向 KL 散度
与反向 KL 散度相对的是前向 KL 散度(Forward KL Divergence):
注意,这里的期望是基于参考策略 的样本计算的。
前向 KL 散度具有“质量覆盖”(mass-covering) 的特性。观察其公式,如果 而 , 内的分数会趋向于无穷大,导致 KL 散度爆炸。为了最小化前向 KL 散度, 必须确保在 具有显著概率质量的所有地方,自己也分配足够的概率质量。换句话说, 必须“覆盖”住 的整个分布形态。
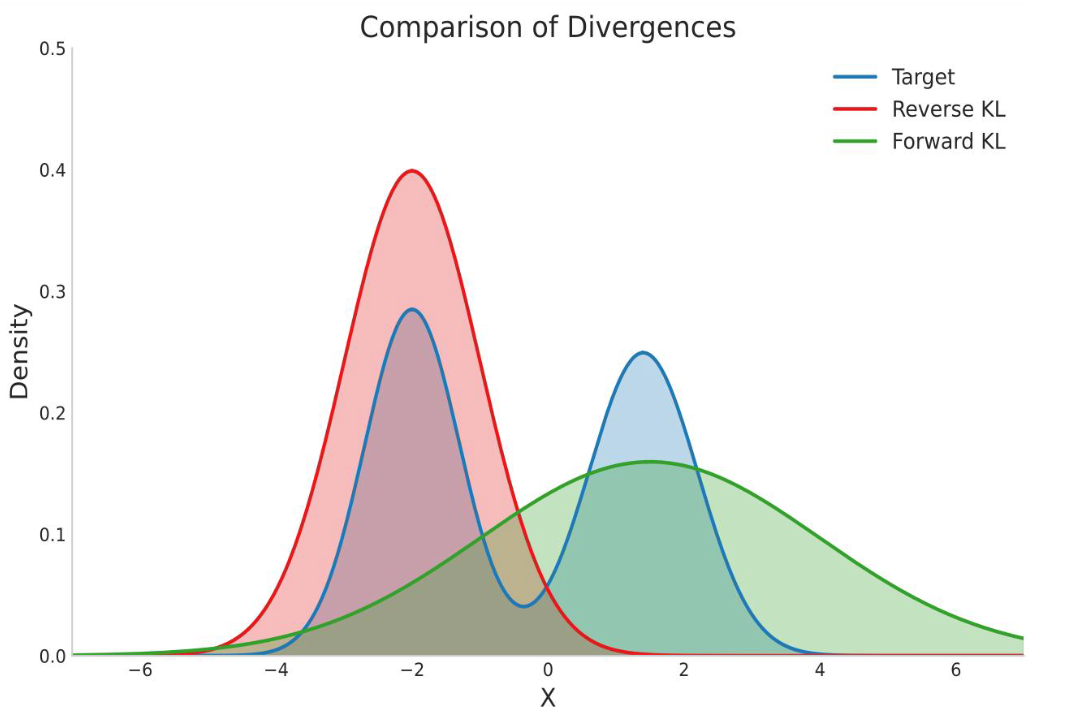
上图直观地展示了两种 KL 散度的区别。假设目标分布(Target)是双峰的,反向 KL(Reverse KL)会试图匹配其中一个峰(模式寻求),而前向 KL(Forward KL)则会用一个更宽的分布去覆盖两个峰(质量覆盖)。
将这个特性应用于 RLVR,使用前向 KL 散度意味着,只要某个解法在初始模型 中是可能被生成的(即 ),那么微调后的模型 就必须持续保持生成该解法的能力(即确保 不会趋近于 0)。这相当于一种“排练机制”,强迫模型不能忘记它本来会的东西,从而天然地保留了多样性。
1.4 f-散度
KL 散度只是衡量两个概率分布差异的众多方法之一。它们都可以被归入一个更广泛的家族,称为 f-散度(f-Divergence)。其通用定义如下:
其中 是一个凸函数,且满足 。通过选择不同的生成函数 ,我们可以得到不同类型的散度度量。

如上表所示:
-
当 时,得到的是反向 KL 散度。 -
当 时,得到的是前向 KL 散度。 -
Jensen-Shannon (JS) 散度也是 f-散度的一种,它具有对称性,可以看作是前向和反向 KL 的一种结合。
这篇论文的高明之处在于,它没有将问题局限于“反向 KL vs. 前向 KL”,而是将其提升到了 f-散度的高度。论文的核心论点是:具有模式寻求(mode-seeking)特性的散度(如反向 KL)会加剧多样性坍塌,而具有质量覆盖(mass-covering)特性的散度(如前向 KL 和 JS 散度)则能有效缓解这一问题。
2. DPH-RL 框架详解
基于上述洞察,论文提出了 Diversity-Preserving Hybrid RL (DPH-RL) 框架。其核心思想是将整个训练过程分为两个阶段,并对不同类型的数据施加不同的学习目标,从而在“探索”新知识和“保留”旧知识之间取得平衡。
2.1 预采样阶段(Pre-sampling Stage)
在正式开始 RL 训练之前,DPH-RL 首先会进行一个预采样阶段。具体步骤如下:
-
数据生成:对于初始数据集 中的每一个问题 ,使用基础模型 进行 次独立采样,生成 个候选答案。 -
数据评估:使用验证器评估这 个答案的正确性。 -
数据划分:根据评估结果,将初始数据集 划分为两个子集: -
(perfect dataset) :这个子集包含那些基础模型 已经能够“近乎完美”解决的问题。例如,如果 次采样中有接近 次都是正确的,那么这个问题就属于 。对于这些问题,我们会保存一个由 生成的正确答案及其对应的对数概率 。 -
(exploration dataset) :这个子集包含那些基础模型表现不佳、需要通过强化学习来提升的问题。
-
这个数据划分的设计是整个框架的关键。它清晰地分离了两种学习目标:
-
对于 中的问题,我们希望模型能积极探索,找到新的、正确的解题路径。 -
对于 中的问题,我们希望模型能有效保留,确保其已经掌握的知识和多样的解题风格不被遗忘。这部分数据将作为“排练”材料。
2.2 在线训练阶段(Online Training Stage)
在训练过程中,模型会同时从 和 中采样数据,并根据数据来源应用不同的损失函数。
针对 的损失:纯策略优化
对于来自探索集 的样本,目标是最大化奖励。因此,DPH-RL 在这部分数据上完全移除了 KL 散度惩罚项。其损失函数就是标准的 PPO-clip 目标:
其中 是重要性采样比率, 是优势函数。这种设计允许模型在这些具有挑战性的问题上进行更激进的探索,而不受制于初始策略的束缚。
针对 的损失:基于 f-散度的排练
对于来自完美集 的样本,目标是保留多样性。这里的损失函数直接定义为当前策略 和参考策略 之间的 f-散度:
论文重点探讨了两种具体的 f-散度实现:
-
DPH-F (基于前向 KL) :
当 f-散度选择为前向 KL 时,损失项为:由于我们在预采样阶段已经保存了来自 的样本(正确的答案)和它的概率,这个期望可以很方便地通过 Monte Carlo 采样来估计。这种基于生成器的实现方式(Generator-based Implementation)是计算高效的,因为它避免了在训练循环中需要一个在线的参考模型来进行前向传播。
-
DPH-JS (基于 JS 散度) :
JS 散度更稳定且具有对称性。其损失项为:其中 。同样,这个损失也可以通过预采样的 数据集高效计算。
总体损失函数
最终,对于一个混合批次(mini-batch)的数据,总损失是上述两种损失的加权和:
其中 是一个超参数,用于平衡探索和保留的强度。损失函数会根据每个样本的来源( 或 )来应用对应的计算方式。
2.3 理论保证
除了经验性的设计,论文还提供了一定的理论支持。作者推导出了一个增强的单调策略改进保证(Enhanced Monotonic Improvement Guarantee)。该理论表明,与原始的 TRPO 等算法相比,DPH-RL 的策略更新在每一步都获得了一个更强的性能下界。这个下界不仅与当前策略和旧策略的差异有关,还额外包含了一个与参考策略 相关的正向项 。这从理论上说明了,通过参考一个高质量的“完美”策略,DPH-RL 能够更稳健地提升策略性能。
3. 实验
论文通过在 SQL 生成和数学推理两大任务上的大量实验,系统地验证了 DPH-RL 框架的有效性。
3.1 实验设置
-
模型:Llama-3.1-8B-Instruct, Qwen2.5-Math-7B, OmniSQL-32B 等。 -
任务: -
SQL:在 BIRD 数据集上进行训练,同时在 BIRD (in-domain) 和 Spider (out-of-domain) 数据集上进行测试,以评估模型的泛化能力。 -
数学推理:在 DAPO-17k 数据集上训练,并在 AIME, AMC23, Math500 等多个数学竞赛数据集上测试。
-
-
基线模型: -
Base Model:未经 RL 微调的基础模型。 -
GRPO:一种主流的 RLVR 算法。 -
DAPO:另一种先进的 RLVR 算法,特点是移除了 KL 约束。 -
RKL:标准的、使用反向 KL 散度的 RL 算法。
-
3.2 SQL 任务上的核心结果
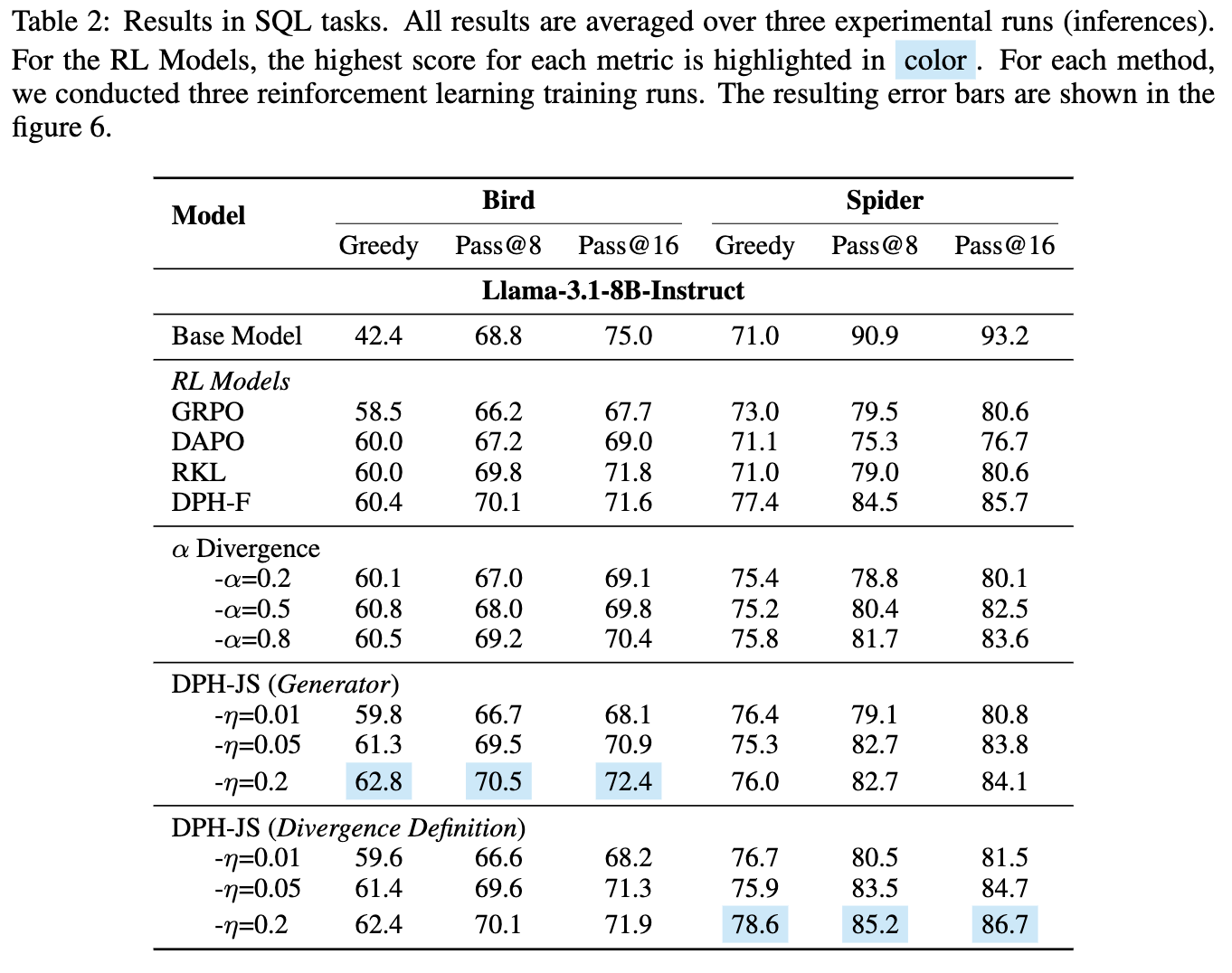
域内(In-Domain)性能:Pass@k 的恢复
在 BIRD 数据集上,结果清晰地显示:
-
GRPO 和 DAPO 虽然可能提升了 Greedy(相当于Pass@1)表现,但它们的Pass@8和Pass@16分数均低于 Base Model,证实了多样性坍塌的存在。 -
RKL(反向 KL)的表现同样不佳, Pass@k下降。 -
DPH-F 和 DPH-JS 不仅 Greedy分数最高,其Pass@8和Pass@16分数也超过了 Base Model。这直接证明,DPH-RL 成功地解决了Pass@k性能退化的问题。DPH-JS 的Pass@8分数比 GRPO 高出 4.3%。
域外(Out-of-Domain)性能:泛化能力的保持
在 Spider 数据集上,所有 RL 模型都表现出一定程度的性能下降,这是 OOD 任务的普遍挑战。但关键在于相对表现:
-
DPH-F 和 DPH-JS 的 Pass@k分数显著高于其他所有 RL 方法,最接近 Base Model 的原始水平。 -
DAPO 在 OOD 任务上表现得不稳定,性能保留能力不如 DPH-F。DPH-F 的 Pass@16分数比 DAPO 高出 9.0%。 -
这表明,通过保留解决方案的多样性,DPH-RL 能够更好地防止灾难性遗忘,从而在面对新领域问题时保持更强的泛化能力。
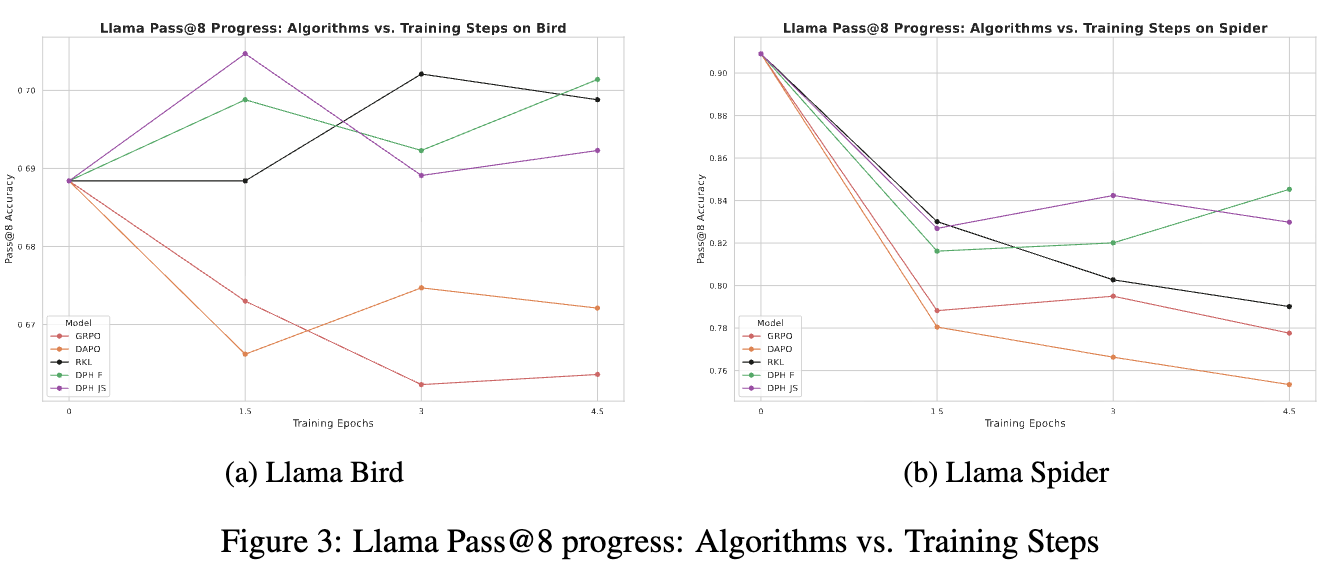
上图展示了训练过程中 Pass@8 分数的变化。可以观察到:
-
GRPO 的性能随着训练的进行逐渐坍塌。 -
DAPO 的性能持续震荡,非常不稳定。 -
RKL 在域内(Bird)表现尚可,但在域外(Spider)上同样出现了性能的逐渐坍塌。 -
DPH-F 和 DPH-JS 则在整个训练过程中都保持了比初始水平更高的 Pass@8分数,表现出良好的稳定性和性能。
3.3 深入分析:保留(Keep)与探索(Exploration)
为了更深入地理解 DPH-RL 的工作机制,论文进行了一项精巧的分析。他们将基础模型在测试集上的 Pass@8 结果分为两部分:基础模型能做对的样本()和做错的样本()。然后,他们考察 RL 微调后的模型在这两部分样本上的表现:
-
保留率(Keep Rate):在 上依然能做对的比例。这衡量了模型对已有知识的遗忘程度。 -
额外探索率(Additional Exploration Rate):在 上转而做对的比例。这衡量了模型学习新知识的能力。
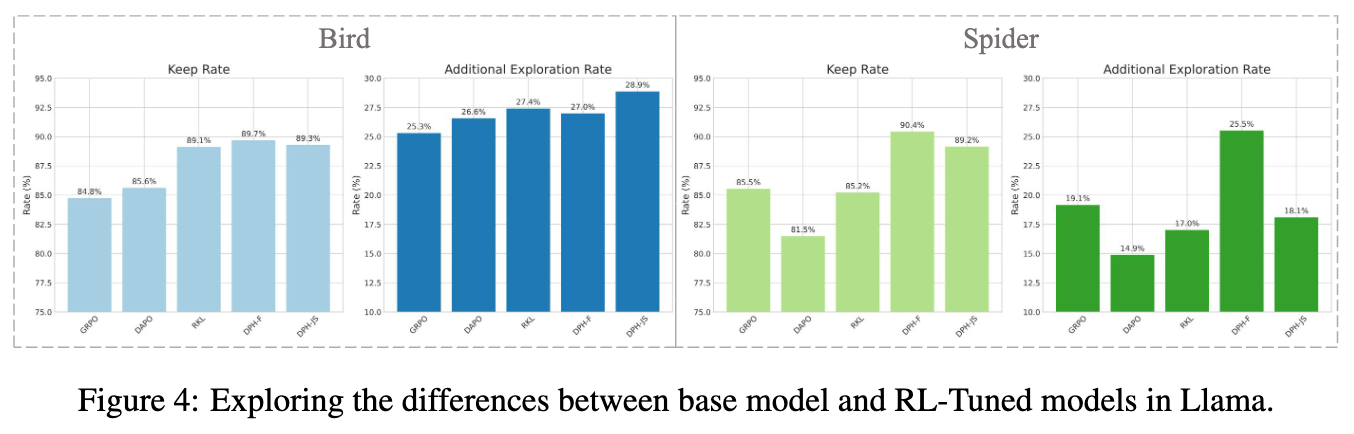
分析上图可以得出结论:
-
GRPO 和 DAPO 在两个数据集上的保留率都下降了。这说明它们在学习新知识的过程中,把原来会的也忘了。 -
RKL 仅在与其训练集同分布的 Bird 数据上保持了高保留率,但在 OOD 的 Spider 数据上,其保留率大幅下降,与 GRPO 相当。这再次印证了反向 KL 导致模型过拟合于训练分布,牺牲了泛化性。 -
DPH-F 和 DPH-JS 在保持高探索率的同时,维持了最高的保留率。这完美地解释了它们为何能取得优越的 Pass@k表现:既学会了新的解法,又没有忘记旧的。
3.4 数学推理任务上的表现
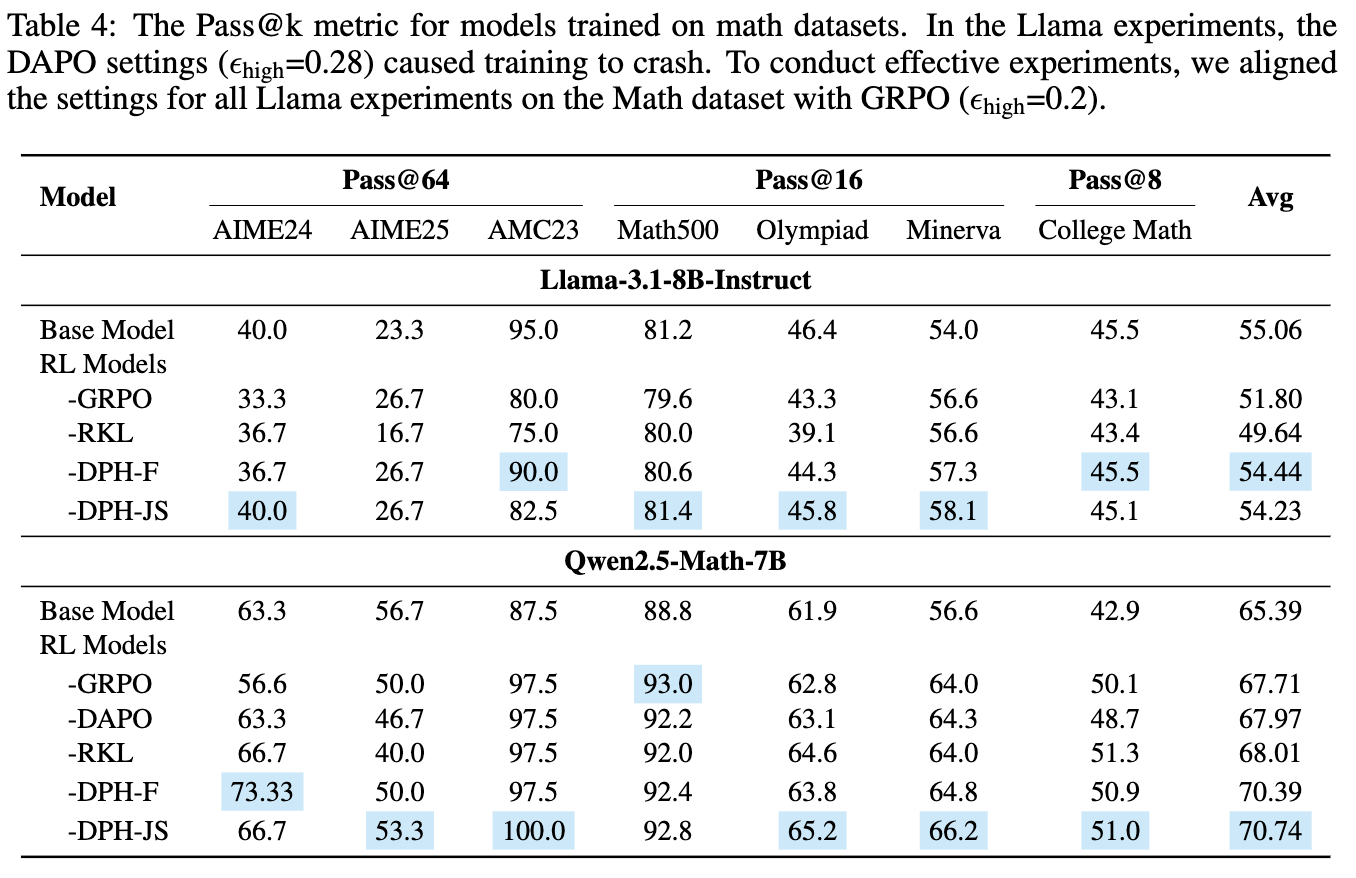

在数学任务上,不同模型架构表现出不同的特性:
-
对于 Llama 模型:RL 对其性能的提升空间有限,甚至 GRPO 会导致 Pass@k和Mean@k平均分的下降。在这种困难的情况下,DPH-JS 依然能够在维持Pass@k均值(54.23 vs Base 55.06)的同时,显著提升Mean@k均值(22.06 vs Base 20.01)。这展示了 DPH 方法在探索和保留之间的平衡能力。 -
对于 Qwen 模型:这个模型对 RL 微调更为敏感,性能提升显著。在所有方法中,DPH-F 和 DPH-JS 取得了最高的 Pass@k和Mean@k平均分。这表明 DPH-JS 能够巧妙地应对不同数据集上的性能权衡,在需要保留多样性的 AIME 数据集上更接近基础模型,而在其他数据集上则最大化了成功率。
3.5 不同 f-散度的比较
实验结果系统地比较了不同 f-散度的影响:
-
无散度(GRPO/DAPO):在域内和域外都遭遇了严重的 Pass@k坍塌。 -
反向 KL(RKL):在域内能维持 Pass@k,但在域外泛化能力上表现最差,性能下降严重。 -
α-散度:作为前向和反向 KL 的一种插值,其表现也介于两者之间。随着 α 值从 0.2 增加到 0.8(越来越接近前向 KL),模型的 OOD 性能和 Pass@k表现也呈现出稳步提升的趋势。 -
前向 KL 和 JS 散度(DPH-F/DPH-JS):在所有任务上都表现出最强的泛化能力和多样性保留能力。
这些结果为论文的核心论点——“质量覆盖”优于“模式寻求”——提供了坚实的经验证据。
往期文章:




