对于具有客观、可验证答案的推理任务(verifiable reasoning tasks),例如完成数学证明、生成一段功能代码或解决科学问题,其核心目标是找到那个唯一的、正确的“最终答案”。在这一领域,一种强大且主流的增强模型能力的方法是基于结果的强化学习(Outcome-based Reinforcement Learning)。该方法通过一个简单的奖励机制——只奖励最终答案的正确性——来直接优化模型的准确率,并已在多个基准测试中取得了显著的成功。
然而,这种方法的成功背后隐藏着一个重要的代价,它引出了一系列新的困境和瓶颈:
-
多样性坍塌的困境(Dilemma of Diversity Collapse):基于结果的强化学习在强化正确答案的推理路径时,会系统性地抑制其他可能性,导致模型生成内容的多样性急剧下降。这并非一个无足轻重的问题,因为它直接削弱了模型在现实世界中的可扩展性。诸如多数表决(majority voting)或树搜索(tree search)这类依赖于多个不同候选解的测试时增强技术,在多样性坍塌的模型面前会变得收效甚微甚至完全失效。 -
探索不足的瓶颈(Bottleneck of Under-Exploration):模型会迅速学会在它已经掌握的问题上“过度利用”已知的正确路径,从而获得稳定的奖励。这种行为虽然在短期内提升了在简单问题上的表现,但却牺牲了对更广阔解空间的探索。其结果是,模型可能会失去发现更复杂问题新颖解法的能力,甚至在经过充分训练后,其解决难题的总量反而不如未经过强化学习的基础模型。
这两个瓶颈共同构成了一个关键的研究空白:我们如何在享受强化学习带来的准确率提升的同时,有效避免其导致的探索停滞和多样性坍塌?换言之,如何设计一个能够精确平衡“利用”与“探索”的 LLM 推理训练框架?
来自 Meta、CMU 和 NYU 的研究者在 arXiv 上提交的论文 《Outcome-based Exploration for LLM Reasoning》 为此问题提供了一个深刻而实用的答案。他们提出的基于结果的探索(Outcome-based Exploration)范式,从一个新颖的视角重新审视了 LLM 推理中的探索问题。它不再将探索的目标设定在难以处理的、指数级的“推理路径”空间中,而是另辟蹊径:将探索的重心转移到维度低、可处理的“最终答案”空间上,并以此为基础设计了一系列精巧的探索算法。

-
论文标题:Outcome-based Exploration for LLM Reasoning -
论文链接:https://arxiv.org/pdf/2509.06941
为了直观展示其方法的有效性,论文在开篇第一页就给出了核心的实验结果对比图。它清晰地回答了最关键的问题:与标准的强化学习方法相比,新的探索策略究竟带来了多大的提升?
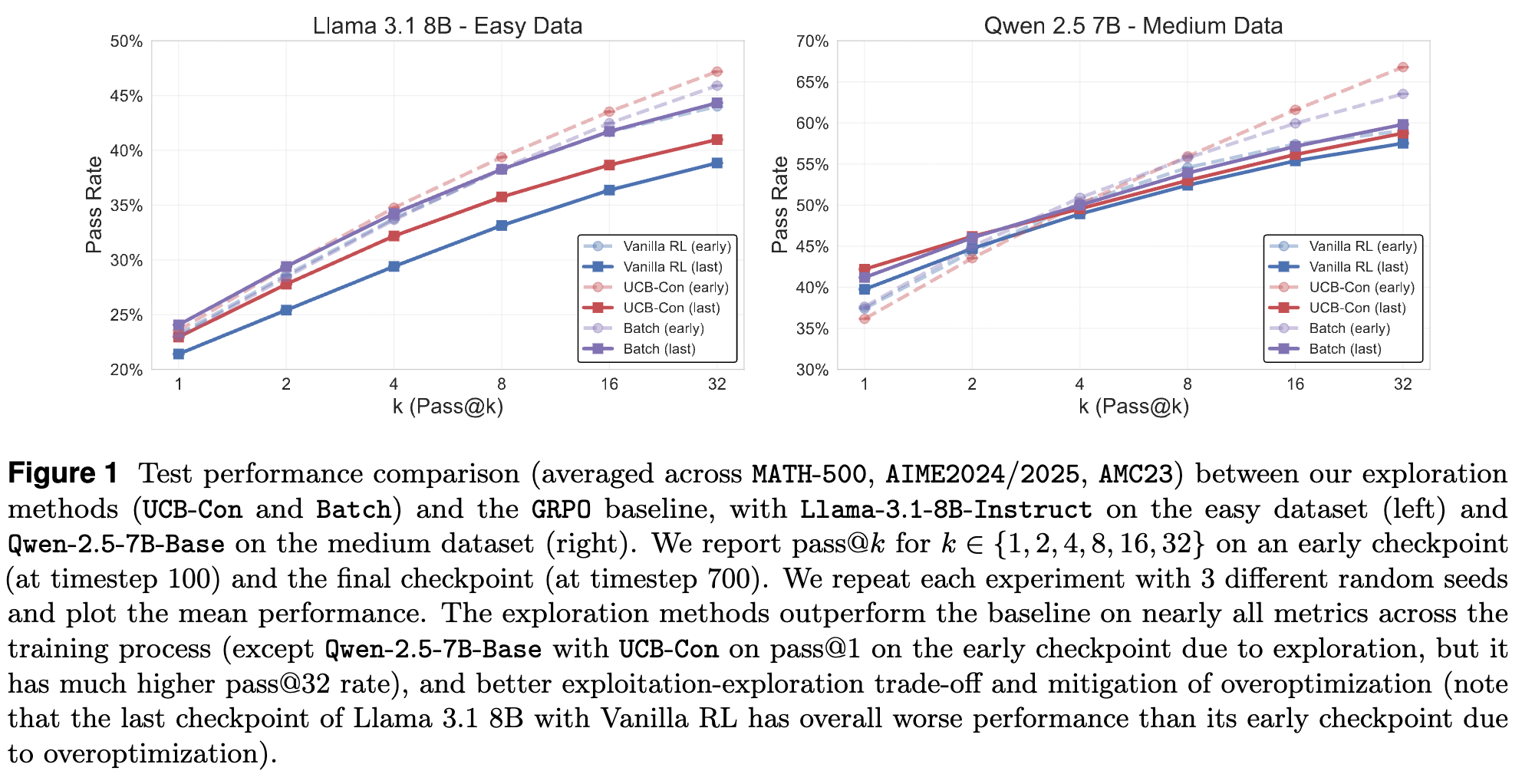
这张图展示了在两个不同模型(Llama-3.1-8B 和 Qwen-2.5-7B)和两个不同难度数据集(简单和中等)上的测试性能。我们需要关注以下几个关键点:
-
横坐标 k (Pass@k):代表在测试时,我们允许模型对同一个问题生成k个不同的答案。 -
纵坐标 Pass Rate:代表在这k个答案中,至少有一个是正确的概率。 -
Pass@k指标的意义 :pass@1衡量的是模型的单次生成准确率,而pass@k(当k > 1时) 则同时衡量了模型的准确率和生成多样性。一条好的性能曲线应该在k=1时有较高的起点,并随着k的增大而快速上升。
通过观察图 1,我们可以得到三个核心结论:
-
探索方法全面优于基线:在几乎所有的
k值上,论文提出的两种探索方法——UCB-Con 和 Batch ——的pass@k性能都稳定地高于基线方法 Vanilla RL 。这证明新方法不仅提升了单次生成的准确率(更高的pass@1),也通过生成更多样化的答案,显著提升了多次采样下的成功率(更高的pass@kfork>1)。 -
有效缓解“过优化”现象:图 1 左侧的 Llama 模型实验结果尤其引人注目。请注意比较“Vanilla RL (early)”和“Vanilla RL (last)”。我们发现,经过更多训练后,基线模型的最终性能反而比其早期检查点要差。这是一种典型的过优化(overoptimization)现象:模型过度拟合了训练中的某些模式,牺牲了泛化能力,导致性能退化。
与之形成鲜明对比的是,UCB-Con 和 Batch 方法的最终检查点性能普遍优于或持平于其早期检查点。这强有力地证明了,基于结果的探索策略能够引导模型进行更健康的学习,有效抑制过优化,从而获得更鲁棒的性能。 -
提供了更优的“利用-探索”权衡:无论是旨在优化历史探索的 UCB-Con,还是旨在优化即时多样性的 Batch,它们都找到了比 Vanilla RL 更好的“利用-探索”平衡点。
1. 背景
为了充分理解论文所提方法的动机,我们首先需要深入探讨其试图解决的问题:在利用强化学习对大模型进行后训练以增强其推理能力时,为何会出现多样性的系统性损失。
1.1 LLM 推理中的强化学习范式
在可验证的推理任务(如数学题解答)中,我们可以将 LLM 建模为一个策略(policy) 。给定一个问题 ,模型会生成一个包含中间推理过程(chain of thought) 和最终答案 的样本 。我们拥有一个奖励函数 ,它只判断最终答案 是否正确。
RL 训练的目标是最大化期望奖励。在实践中,通常采用 KL-散度正则化的目标函数,以防止训练后的策略 过度偏离初始的基座模型 :
其中, 是控制 KL 惩罚强度的超参数。论文中采用了完全在线(fully on-policy)的 GRPO 算法(Generalized Reward Policy Optimization)作为基线(Vanilla RL)。
评估模型性能时,除了看单次采样的准确率(pass@1),我们更关心 pass@k 指标。pass@k 指的是从模型中采样 次,只要有一次答案正确,就算通过。这个指标能够同时评估模型的准确性和多样性。一个好的模型不仅要有高的 pass@1,在 增大时,pass@k 也应该持续稳定地提升,这意味着模型能够生成多个不同的、可能正确的解题路径。
然而,大量研究和实践发现,经过 RL 训练后,模型的 pass@1 提高了,但当 较大时(如 ),pass@k 的表现反而不如训练前的基座模型。这就是所谓的多样性坍塌(Diversity Collapse)。
1.2 多样性退化的动态分析
以往的研究多是比较训练前后的模型快照,而本文提供了一个更动态的视角:将整个 RL 训练过程看作是在训练集上的一个大规模采样过程。
在每个训练轮次 ,对于训练集中的每个问题 ,我们都会采样 个轨迹。整个训练过程总共会为每个问题采样 个轨迹。我们可以将这个过程与直接从基座模型 中采样等量()的轨迹进行对比。
通过这种方式,我们可以观察两个核心指标在训练过程中的动态变化:
-
已解决问题总数: 对应于 pass@k。 -
已发现的不同答案总数: 对应于 diff@k,即采样 次后发现的唯一答案的数量。
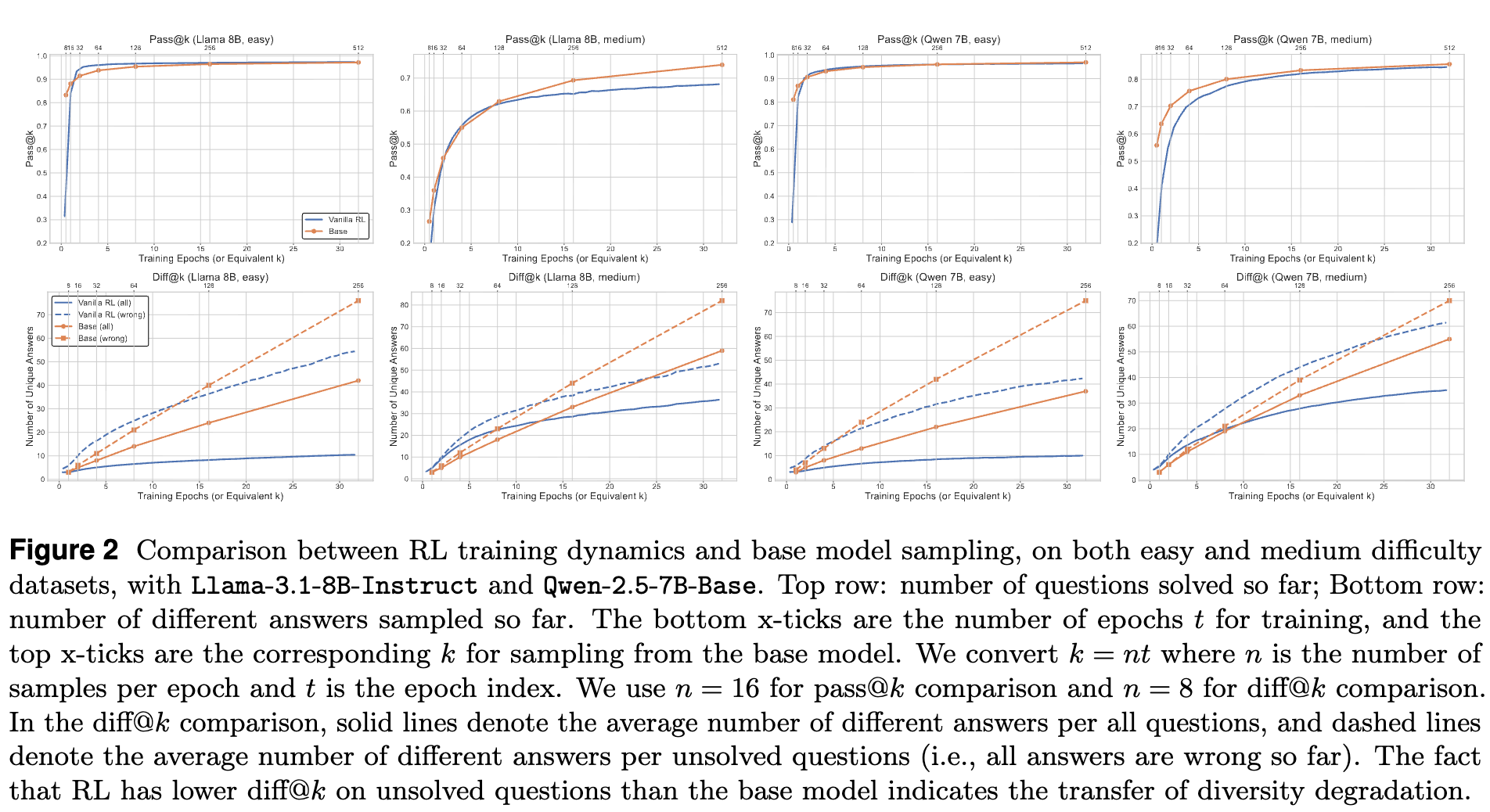
上图展示了 RL 训练和基座模型采样的动态对比。通过这张图,论文得出了三个关键的观察:
观察一:RL 最终解决的问题数少于基座模型
-
在图的上半部分,我们可以看到,在训练初期,RL解决问题的速率高于基座模型。这是符合预期的,因为 RL 会快速强化那些模型能够轻易答对的问题的正确路径。 -
然而,随着训练的进行,RL 解决新问题的能力逐渐下降,其曲线变得平缓,最终被持续采样的基座模型超越。这意味着,如果给予足够多的采样机会,基座模型反而能“暴力破解”更多问题,而 RL 模型则陷入了某种“局部最优”,反复利用已知的解法,探索新解法的能力受损。
观察二:多样性退化的跨问题转移
-
理想情况下,如果模型对不同问题的更新是独立的,那么对于那些尚未解决的问题(即从未采样到正确答案的问题),RL 模型的行为应该等同于基座模型。 -
然而,图的下半部分揭示了一个令人不安的现象。实线表示所有问题上的平均不同答案数,虚线表示在未解决问题上的平均不同答案数。我们可以看到,RL 训练不仅在所有问题上的多样性低于基座模型,甚至在那些它从未成功解决过的问题上,其生成答案的多样性也显著低于基座模型。 -
这说明,当模型在已解决问题上集中其概率分布(为了最大化奖励)时,这种多样性的损失会通过模型参数的泛化效应,“传播”或“转移”到未解决的问题上。模型变得更加“固执”,倾向于在所有问题上都生成更少的几种答案,从而严重削弱了其探索未知解空间的能力。
观察三:可验证领域中答案空间的可处理性
-
在自然语言生成的开放域中,衡量两个生成文本是否“语义不同”是一个棘手的问题,其可能空间是指数级的。 -
但在可验证领域(如数学),我们可以用最终答案作为生成多样性的一个代理(proxy)。如果两个推理过程产生了两个数学上不等价的答案,我们就认为它们是不同的。 -
从图 2 的 diff@k曲线中可以看到,即使有大量的采样预算,每个问题平均也只能采样出不到 50 个不同的答案。这表明,最终答案的outcome space是相对小且可处理的(tractable)。这个特性是本文所提方法的基石:既然答案空间不大,我们就可以直接在这个空间里进行显式的探索。
这三个观察共同描绘了 RL 训练中多样性退化的困境,并指明了解决问题的潜在方向:利用答案空间的可处理性,设计一种机制来对抗多样性的转移性退化。
2. 基于结果的探索
基于以上分析,论文的核心思路是:既然 token 级别的探索空间过大且难以处理,而 outcome (最终答案) 空间相对较小,那么我们可以直接在 outcome 空间中引入探索奖励。
2.1 通过 UCB 鼓励访问稀有答案
这个思路的灵感来源于经典的赌博机问题(multi-armed bandit)和强化学习中的 UCB(Upper Confidence Bound)算法。UCB 的核心思想是“乐观面对不确定性”(optimism in the face of uncertainty):对于那些我们知之甚少(即访问次数少)的“臂”(action),我们给予其一个探索奖励(exploration bonus),这个奖励的大小与其访问次数成反比。
论文将此思想应用于 LLM 推理。在这里,每个 (问题 ,答案 ) 对可以被看作一个“臂”。我们根据一个答案在历史上被采样到的次数来给予它探索奖励。具体来说,训练目标函数被修改为:
其中, 是优势函数(advantage), 是超参数,而 UCB 探索奖励 定义为:
是在历史上,针对问题 ,答案 被采样到的总次数。这个奖励项会鼓励模型去探索那些历史上很少出现的答案。
2.1.1 朴素 UCB (Naive UCB) 的局限性
直接应用上述 UCB 奖励(论文中称为 Naive UCB),实验结果(如下图所示)表明,它虽然能够在训练过程中提升性能(解决更多问题,发现更多独特答案),但在测试集上的表现却不尽如人意,有时甚至没有提升。
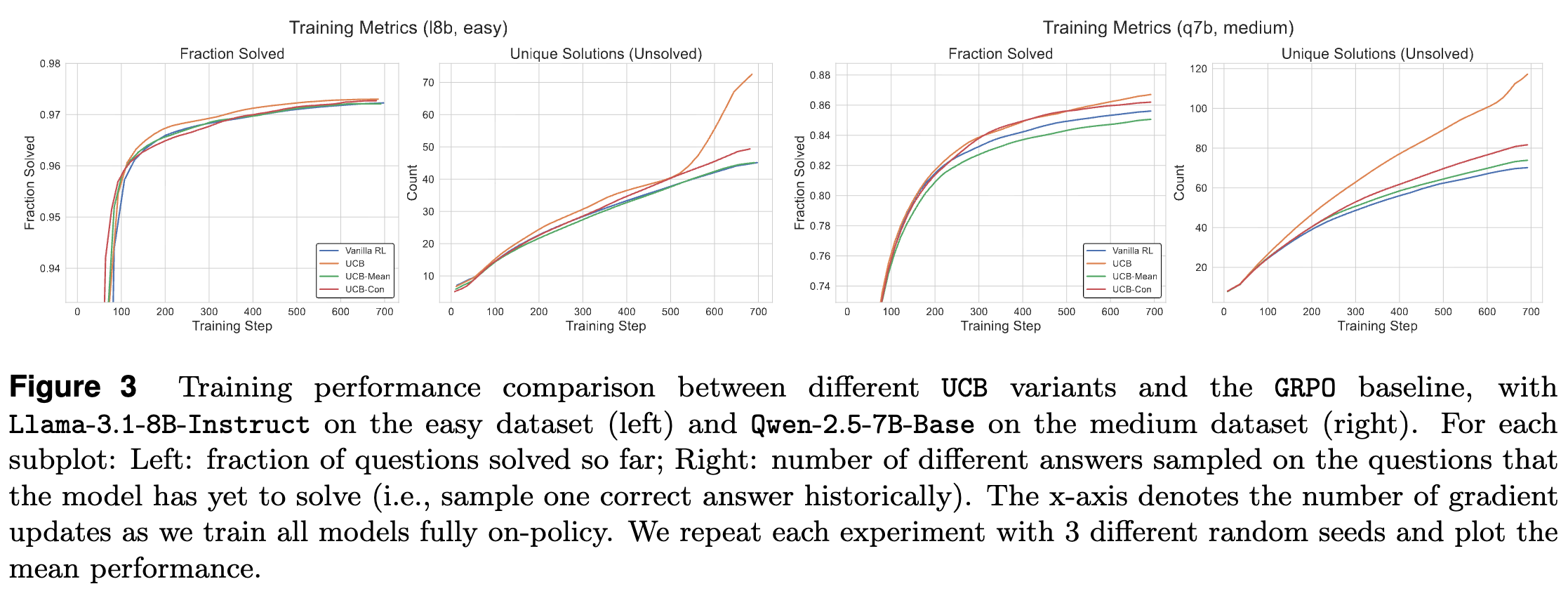
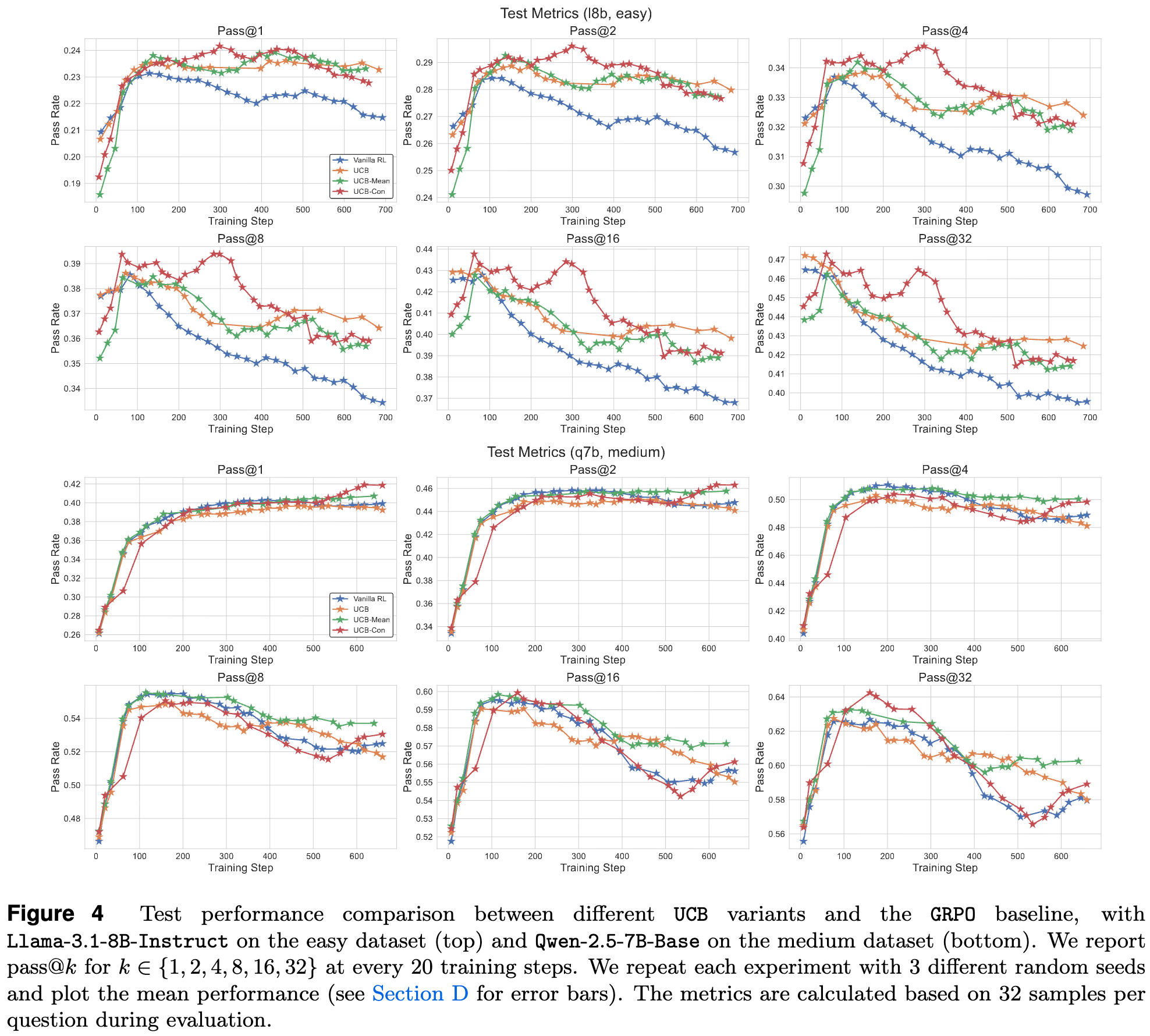
论文推测,其原因是 LLM 推理与传统 RL 环境的一个关键区别:环境是确定性的。在一个错误的推理路径上,无论你重复多少次,得到的奖励永远是 0。朴素的 UCB 持续地给予未充分探索的错误答案正向的探索奖励,这可能导致模型在这些无效路径上浪费了过多的“精力”,从而损害了其泛化到测试集的能力。仅仅提供正向的探索信号可能不是最优策略。
2.1.2 引入基线的 UCB (UCB with a Baseline)
为了解决上述问题,论文提出在探索奖励中引入一个基线(baseline),使得探索信号可以是正的,也可以是负的。这类似于在奖励函数中使用基线来减小方差。
-
UCB-Mean: 采用批次内(in-batch)其他样本的 UCB 奖励均值作为基线。
这个方法直观地鼓励模型生成那些在当前批次中相对稀有(即 值高于批次均值)的答案。
-
UCB-Con: 采用一个可调的常数 作为基线。
例如,如果我们设置 ,那么只有当一个答案的历史访问次数少于 4 次时(),它才会获得正的探索奖励,否则将受到惩罚。这提供了一种更直接的方式来平衡探索与利用(exploration vs. exploitation),并对那些已经被探索过多次的错误答案施加负向信号。
从图 3 和图 4 的实验结果中可以看出,引入基线后,特别是 UCB-Con,在训练性能略有下降的情况下,测试性能得到了持续且显著的改善。它在几乎所有的 pass@k 指标上都优于 Vanilla RL 和 Naive UCB,成为了历史探索方法中的最佳变体。这证明了在探索机制中引入负向信号的重要性。
2.2 直接优化测试时多样性
历史探索(无论是 Naive UCB 还是 UCB-Con)的根本目标是找到最优的确定性策略(maximizing pass@1)。它通过探索来更好地估计各个答案的价值,最终目的是为了收敛。
然而,在 LLM 推理的场景下,我们有时更关心模型在测试时生成多样化答案的能力(maximizing pass@k for large k)。这与传统 RL 的目标有微妙但根本的区别。
为此,论文提出了一种完全不同的探索策略,称为批次探索(Batch Exploration)。它不关心一个答案在历史中出现了多少次,只关心它在当前批次内是否重复。其奖励函数直接惩罚重复:
这个奖励函数会给批次内重复的答案一个负的奖励,从而直接激励模型在单次生成(一个批次 个样本)中产生更多不同的答案。
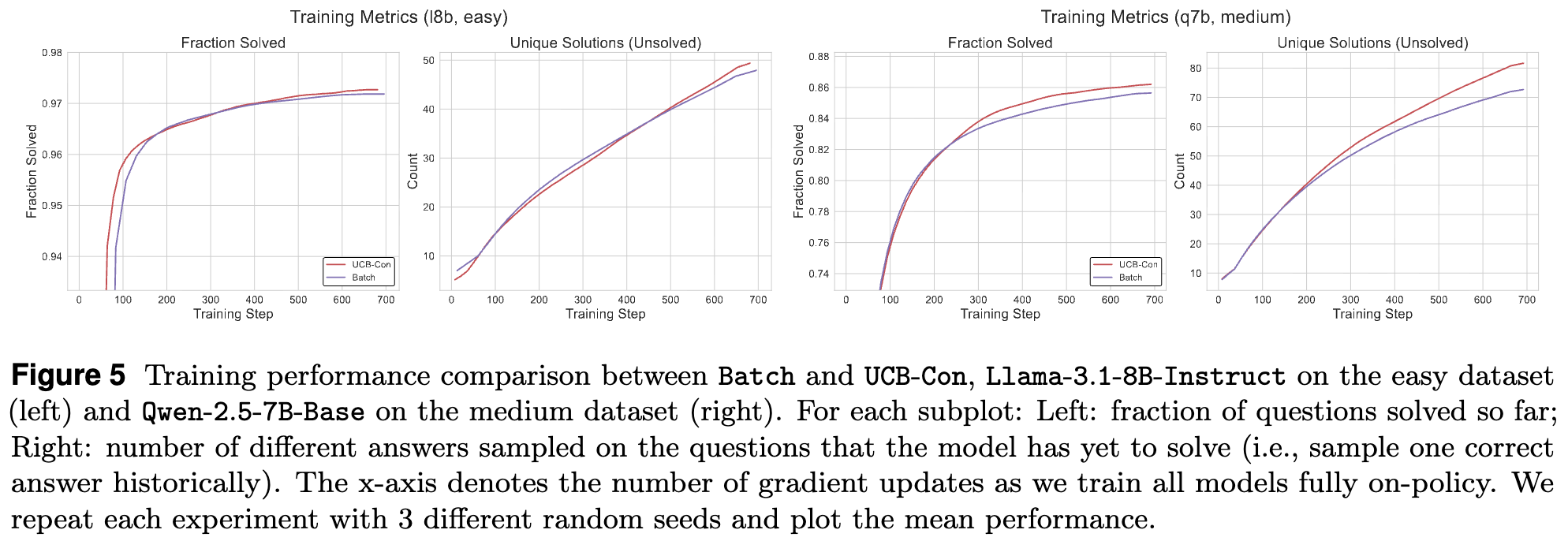
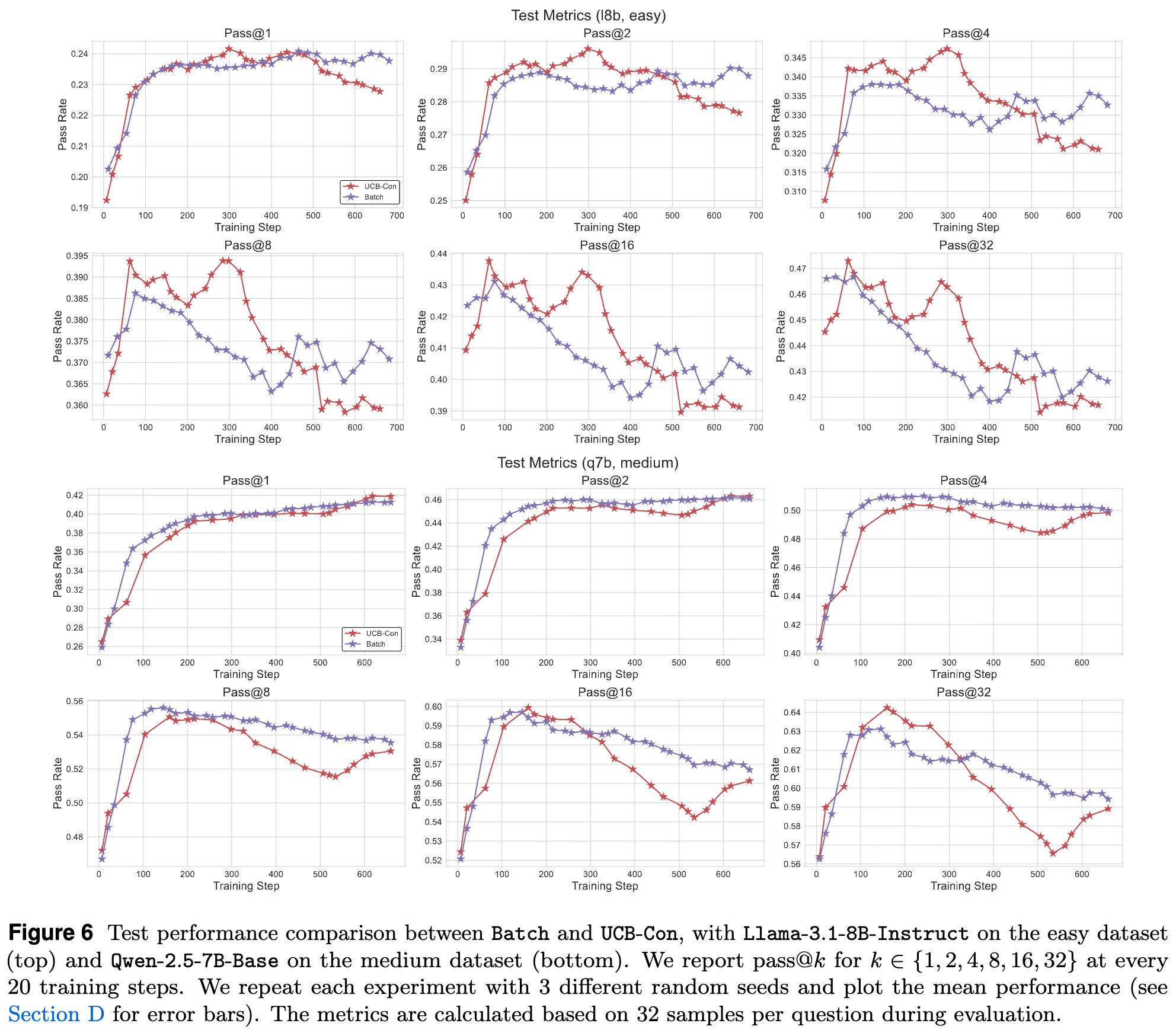
实验结果(图 5 和图 6)显示:
-
训练性能:Batch 方法在训练过程中的表现(无论是解题数还是发现的独特答案数)通常不如 UCB-Con。这不难理解,因为它没有利用历史信息来指导探索,可能在一个小的答案集合里循环。 -
测试性能:尽管峰值性能(best checkpoint)可能与 UCB-Con 相当或略低,但在训练的后期,Batch 方法在 pass@k(特别是大 值)上表现出更优的性能和稳定性。它能更好地保持生成多样性。
这表明,Batch 探索和 UCB-Con 代表了两种不同的设计哲学,分别侧重于测试时多样性和训练时效率。
3. 深入分析与讨论
在提出了两种探索方法后,论文进一步对它们进行了深入的比较和理论分析。
3.1 历史探索 vs. 批次探索
为了更细致地比较这两种策略,论文从两个维度进行了分析:生成熵和批次内多样性。
生成熵 (Generation Entropy)
熵可以用来衡量模型输出的随机性或多样性。论文在训练到第 400 步时,计算了模型生成轨迹(包括推理过程和答案)的 token 级别熵。
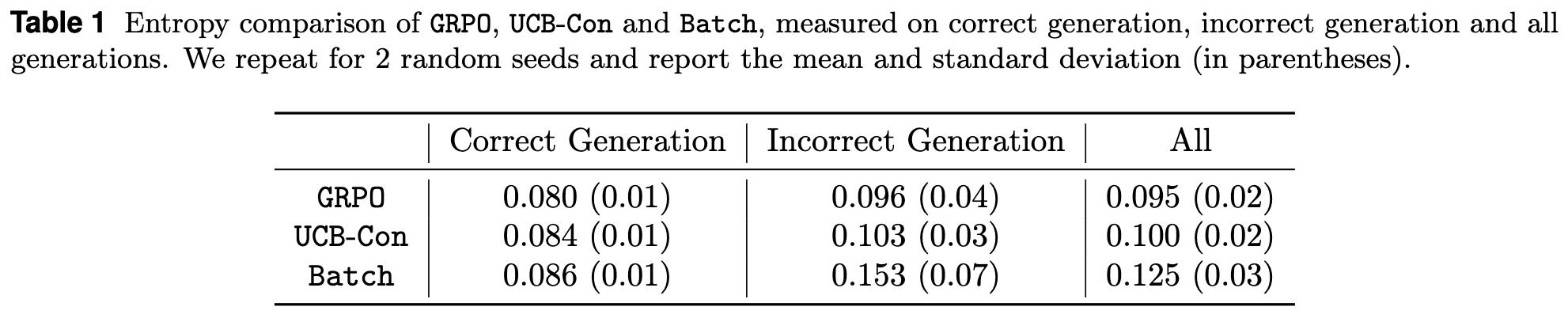
如上表所示,无论是哪种方法,正确生成的轨迹(Correct Generation)熵都低于错误生成的轨迹(Incorrect Generation),这说明正确的解法通常更加“确定”。关键在于,在错误生成的轨迹中,Batch 方法的熵值显著高于 GRPO 和 UCB-Con。这表明 Batch 探索确实能让模型在探索未知解时产生更多样化、更不确定的输出。
批次内生成多样性 (Batch Generation Diversity)
论文直接统计了在一个大小为 8 的批次中,生成的不同答案的数量。
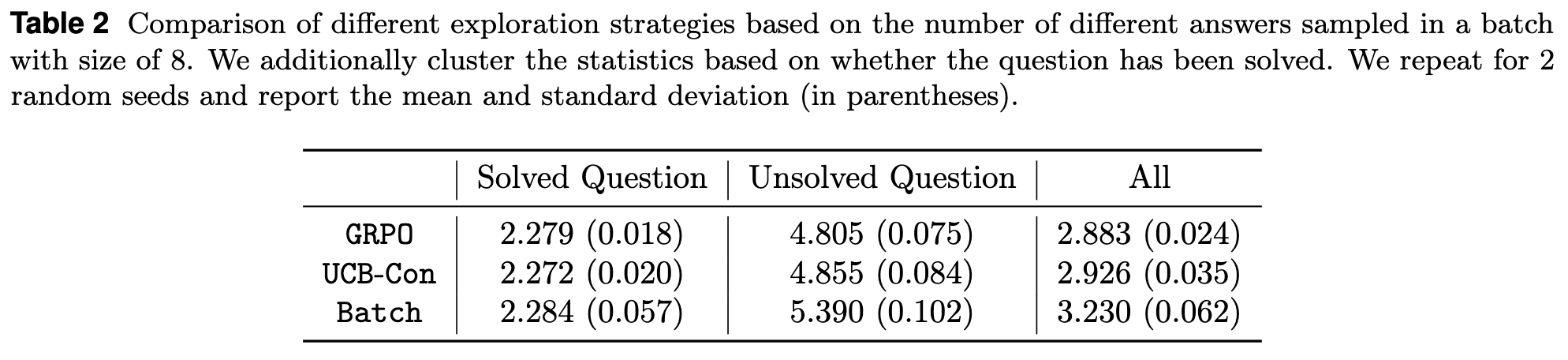
结果符合预期:Batch 方法在批次内能产生最多的不同答案,因为它正是为此而设计的。有趣的是,无论是在已解决还是未解决的问题上,Batch 都表现出最高的多样性。
总结与关系
-
历史探索 (UCB-Con) :更“聪明”,利用历史信息来指导对新答案的探索。它在训练过程中效率更高,能更快地找到正确答案,从而在测试性能的峰值上表现优异。 -
批次探索 (Batch) :更“直接”,强制模型在每次输出时都保持多样性。这可能导致训练效率稍低,但它为模型保留了更强的测试时多样性,在需要多样本投票或搜索的场景下可能更有优势。
论文指出,这两种方法并非互斥,而是互补的。历史探索通过扩大在训练空间中的覆盖范围,为批次探索提供了更多可供选择的多样化“原材料”;而批次探索通过维持批次内的变化,反过来防止了历史探索过程中的过早收敛。
3.2 理论分析:基于结果的赌博机模型
为了给“在结果空间探索”的有效性提供理论依据,论文构建了一个名为“基于结果的赌博机”(Outcome-Based Bandits)的理论模型。
这个模型抽象了 LLM 推理的核心设定:
-
有一个非常大的“臂”集合 ,代表所有可能的推理路径(traces),其数量为 。 -
有一个小得多的“结果”集合 ,代表所有可能的最终答案,其数量为 ,。 -
每个“臂”(推理路径) 都唯一地映射到一个“结果”(答案)。 -
奖励只依赖于结果,即 。
研究者们自然希望算法的懊悔界(regret bound)能够依赖于较小的 ,而不是巨大的 。
理论结果一 (Theorem 4.1):
在没有任何额外假设的情况下,即使存在这种“结果-分区”结构,问题的难度下界依然与 相关,即懊悔至少是 。这意味着,如果模型从一条推理路径上的学习不能泛化到产生相同答案的其他路径上,那么探索仍然需要在巨大的路径空间中进行,问题依然是 intractable 的。
理论结果二 (Theorem 4.2):
论文引入了一个关键的泛化假设:当智能体(learner)通过拉动一个“臂” 观察到结果 后,它就能识别出所有能产生结果 的其他“臂”。在这个假设下,存在一个算法,其懊悔上界为 。
这个结果的意义在于,它从理论上证明了:只要模型具备一定的泛化能力(即对一条解法的学习能够触及到其他相似的解法),那么将探索的重心放在数量更少的“结果”空间上,是合理且高效的。这为本文提出的所有 outcome-based exploration 方法提供了坚实的理论基础。
4. 实验
-
模型: Llama-3.1-8B-Instruct 和 Qwen-2.5-7B-Base。 -
数据集: -
训练: 使用了 MATH 数据集的训练集(简单)和 DAPO 数据集的子集(中等)。 -
测试: 在 MATH-500, AIME2024/2025, AMC23 等多个标准数学推理测试集上进行评估。
-
-
基线: Vanilla RL (GRPO)。 -
方法: UCB (Naive UCB), UCB-Mean, UCB-Con, Batch。
论文提供了在最佳检查点(peak performance)和最终检查点(final performance)的详细量化数据。
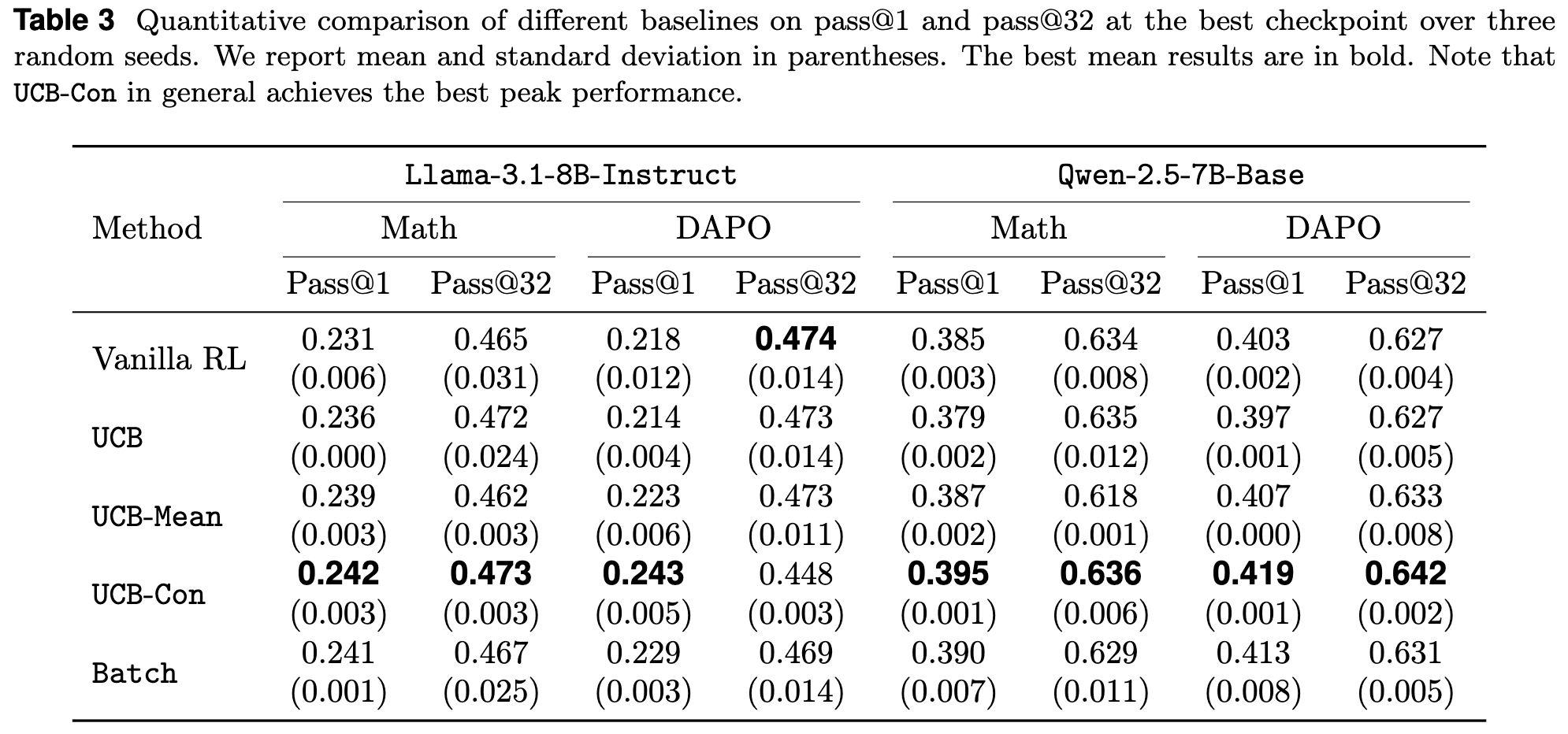
最佳检查点分析 (Table 3):
-
在 pass@1指标上,UCB-Con 表现最为突出,在多个模型和数据集的组合上都取得了最高分。这说明,通过有效的历史探索,模型可以达到更高的单次采样准确率。 -
在 pass@32指标上,UCB-Con 同样表现强劲,这说明在达到峰值准确率的同时,它也保持了不错的的多样性。
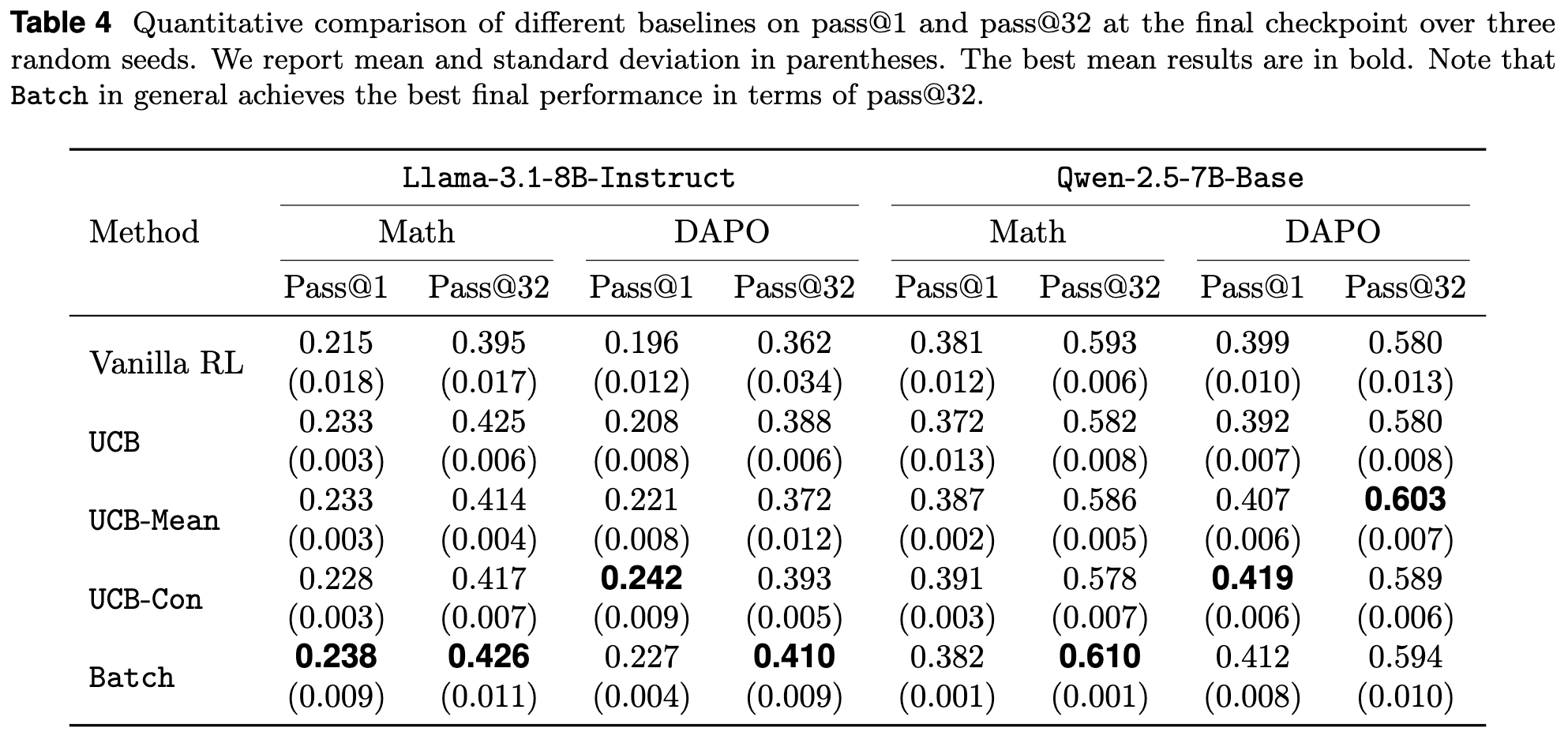
最终检查点分析 (Table 4):
-
一个重要的现象是,Vanilla RL 存在过优化(overoptimization)问题。它的最终性能(尤其是在 Llama 3.1 8B 上)相比其最佳性能有明显下降。 -
相比之下,所有引入了探索机制的方法都表现出更好的稳定性,有效缓解了过优化。 -
在最终检查点,Batch 方法在 pass@32指标上表现出了优势。例如,在 Llama 3.1 8B 的 Math 数据集上,它的pass@32(0.426) 高于 UCB-Con (0.417)。这证实了批次探索在长期保持多样性方面的价值。
综合来看,如果研究者追求的是模型能达到的最高准确率,UCB-Con 是一个优选策略。如果目标是获得一个在训练末期依然保持高度生成多样性的模型,那么 Batch 探索是更合适的选择。
往期文章:




