思维链（Chain-of-Thought, CoT）是主要依赖于一种顺序性的、单线程的推理模式。这种模式模拟了人类解决问题时一步接一步的思考过程，虽然在一定程度上提升了模型的逻辑连贯性，但可能限制了模型探索问题解决空间的能力，容易陷入局部最优解。

认知科学的研究表明，人类在进行复杂思考时，并非总是采用纯粹的线性模式。我们常常会同时考虑多种可能性、从不同角度切入问题，这种并发探索多个推理路径的能力被称为“并行思维”（Parallel Thinking）。Google Gemini团队在国际数学奥林匹亚竞赛（IMO）上取得的成功，部分归功于其引入的并行思维能力，这凸显了该方法在提升LLM推理上限方面的潜力。

然而，如何在模型中有效地激活并训练这种并行思维能力，是一个开放性的技术问题。现有的方法主要分为两大类：

  1. 测试时（Test-time）策略：例如，思维树（Tree of Thoughts, ToT）或多路径自洽性（Multi-path Self-consistency）。这类方法在推理阶段生成多个独立的推理路径，然后通过投票或其他启发式规则进行筛选和整合。它们的缺点是会带来巨大的推理开销（inference overhead），且依赖于固定的、预先定义的调度策略，缺乏适应性。
  2. 训练时（Training-based）策略：主要是通过在包含并行推理路径的合成数据上进行监督微调（Supervised Fine-tuning, SFT）。这类方法类似于行为克隆（behavioral cloning），模型学习模仿预先生成的推理轨迹。然而，这种方式存在几个固有局限：

    • 数据依赖性：高质量的并行思维训练数据难以获取，尤其是在复杂问题上。合成数据的过程本身就非常复杂和昂贵。
    • 泛化能力有限：模型倾向于学习数据的表面模式匹配，而非内在的、可泛化的并行推理技能。它能很好地复现已知的模式，但难以将学到的策略应用到新的、更困难的问题上。
    • 抑制探索：SFT的本质是“教师强制”（teacher-forced），模型被动地学习给定的路径，缺乏主动探索和发现更优推理策略的机会。

为了克服上述方法的局限性，来自腾讯AI Lab、马里兰大学等机构的研究人员共同发表了技术报告《Parallel-R1: Towards Parallel Thinking via Reinforcement Learning》。该工作首次提出了一个强化学习（Reinforcement Learning, RL）框架，旨在让LLM从零开始，在通用的数学推理任务上学习并掌握并行思维能力。

  • 论文标题：Parallel-R1: Towards Parallel Thinking via Reinforcement Learning
  • 论文链接：https://arxiv.org/pdf/2509.07980

1. Parallel-R1

Parallel-R1 的设计哲学是，真正的并行思维能力不应仅仅通过模仿来获得，而应通过探索和经验来学习。强化学习天然地为这种学习范式提供了数学框架：模型（Agent）通过在环境中进行试错（生成推理路径）来学习一种策略（Policy），这种策略能够最大化累积奖励（Reward，例如，解题的最终正确性）。

相较于SFT，RL在学习并行思维方面具备以下优势：

  • 可扩展性（Scalability）：RL允许模型在没有高质量标注数据的情况下，通过与环境（例如，一个数学问题求解器）的交互来自主探索。这绕过了为复杂问题构建并行思维数据集的瓶颈。
  • 鼓励探索（Encouraging Exploration）：RL的机制天然地鼓励模型尝试不同的推理路径，有可能发现超越SFT数据集中存在的、更有效或新颖的解题策略。
  • 泛化性（Generalization）：通过在多样的任务和奖励信号下进行训练，模型有望学习到更底层的、可泛化的并行推理原则，而不仅仅是特定问题的模式。

然而，将RL直接应用于训练LLM的并行思维面临着严峻的挑战，其中最为关键的是冷启动（Cold-start）问题。预训练和标准SFT阶段的LLM从未见过并行思维的特定格式（例如，用于标记不同推理路径的特殊token或结构）。因此，在RL的探索初期，模型根本无法自发地生成这种结构化的并行轨迹，也就无法获得相应的奖励信号，导致学习过程无法启动。

为了解决这一核心矛盾，Parallel-R1 提出了一种渐进式课程学习（Progressive Curriculum Learning）的策略，将复杂的并行思维学习任务分解为多个循序渐进的阶段。其核心思想可以概括为：先学“形”，再学“神”。

  1. 阶段一：格式学习（Format Learning）。利用SFT，在相对简单的任务上，使用易于生成的高质量数据，让模型首先学会并行思维的基本语法和结构。这个阶段的目标不是让模型学会解决难题，而是让它知道“什么是并行思维的表达方式”。
  2. 阶段二：能力泛化（Ability Generalization）。在模型掌握了基本格式后，切换到RL框架。在更困难、更通用的任务上，模型利用其已知的格式进行探索，并通过最大化任务奖励（如解题正确率）来学习何时以及如何有效地运用并行思维，从而将这项技能泛化到更广泛的问题领域。

这种由简到繁、由SFT过渡到RL的课程设计，巧妙地解决了冷启动问题，为RL框架的顺利运行铺平了道路。

2. 方法

2.1 并行思维行为的定义与实现

在 Parallel-R1 中，一次完整的并行思维过程被形式化为两个阶段的循环：

  1. 探索（Exploration）：当模型在顺序推理过程中遇到一个“关键步骤”（critical step），即存在不确定性或有多种可能解决方案的节点时，它会暂停主推理链。随后，模型会启动多线程搜索，同时生成 条独立的推理轨迹（trajectories）。
  2. 总结（Summary）：在所有并行轨迹生成完毕后，模型会对这些轨迹的输出进行聚合、提炼关键信息、解决潜在的冲突，并形成一个统一的、更高质量的结论。这个结论随后被整合回主推理链，继续进行后续的顺序推理。

为了在模型的生成文本中实现这一过程，研究者引入了三个特殊的控制标签（control tags）：

  • <Parallel>...</Parallel>：标记并行探索阶段的开始和结束。
  • <Path>...</Path>：包裹每一条独立的并行推理路径。
  • <Summary>...</Summary>：包裹对所有并行路径进行聚合后的总结陈述。

在推理阶段，模型的工作流程如下：

模型以标准的自回归方式生成文本。当它预测出 <Parallel> 标签时，主生成过程暂停。随后，模型会并发地在多个独立的上下文中生成被 <Path>...</Path> 包裹的内容。所有路径生成完毕后，模型再将所有路径的内容作为上下文，生成 <Summary>...</Summary> 块。最后，整个 <Parallel>...</Parallel> 块连同其内容被整合回主上下文，模型继续自回归生成，直到得出最终答案。这个过程可以根据需要在一次完整的推理中重复多次。

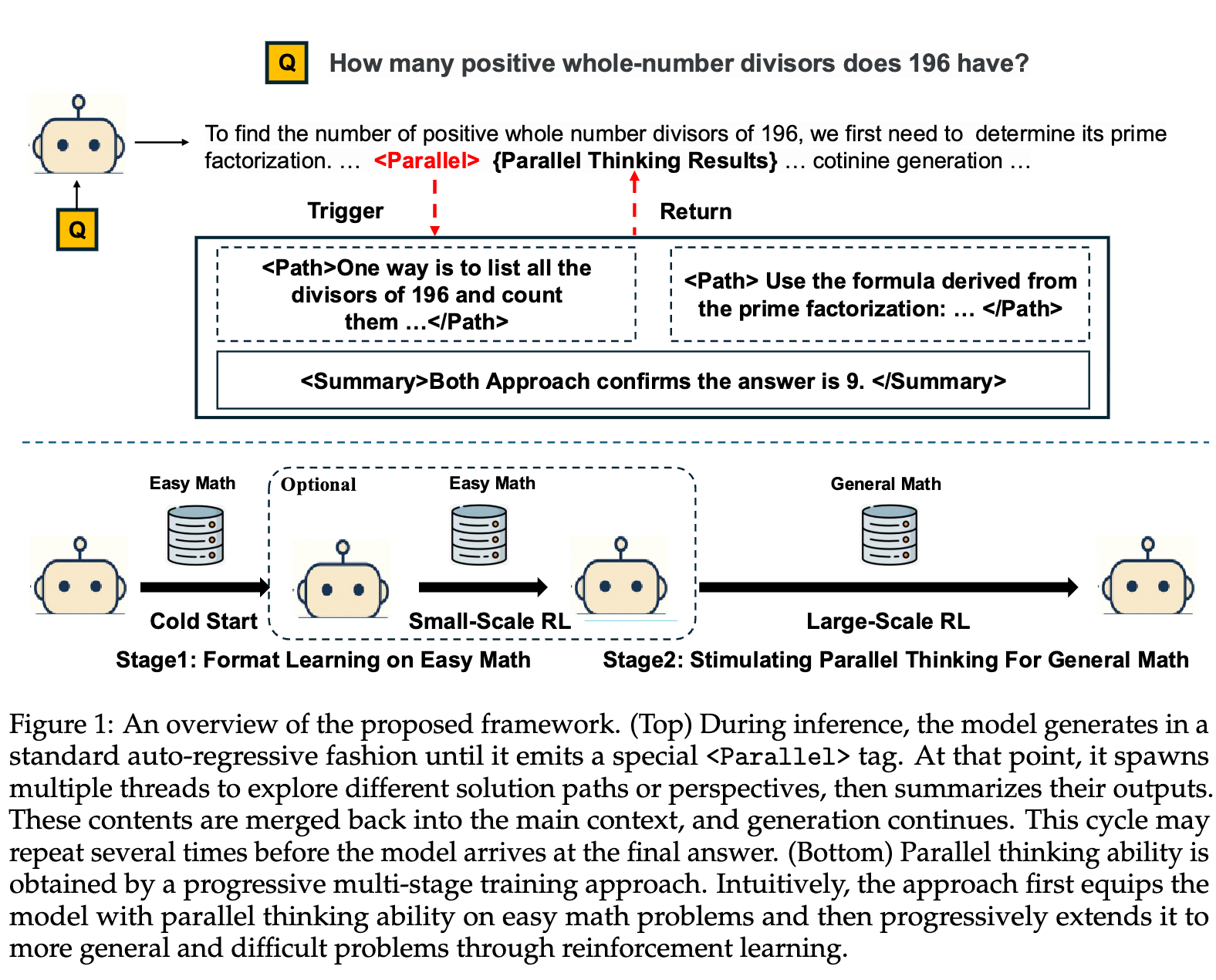
并行思维框架概览
并行思维框架概览

上图清晰地展示了这一动态、自适应的推理流程。模型并非在固定的位置进行分支，而是根据自身的判断，在需要时自主触发并行思考。

2.2 数据生成流程

如前所述，高质量的并行思维数据是启动整个学习过程的关键。现有方法（如 Yang et al., 2025b）依赖于复杂的多阶段数据流水线，例如将一个长的CoT分解为多个并行的子问题，计算量大且可扩展性有限。

Parallel-R1 的研究者通过一个简单的实验发现了一个关键现象（Key Finding 1）：强大的LLM（如DeepSeek-R1-0528-Qwen-3-8B）在使用简单的提示（prompting）时，能够为简单的数学问题（如GSM8K数据集）生成有效的并行思维轨迹，成功率达到83.6%；但对于更复杂的数学问题（如DAPO数据集），同样的提示方法却完全失败，成功率为0.0%。

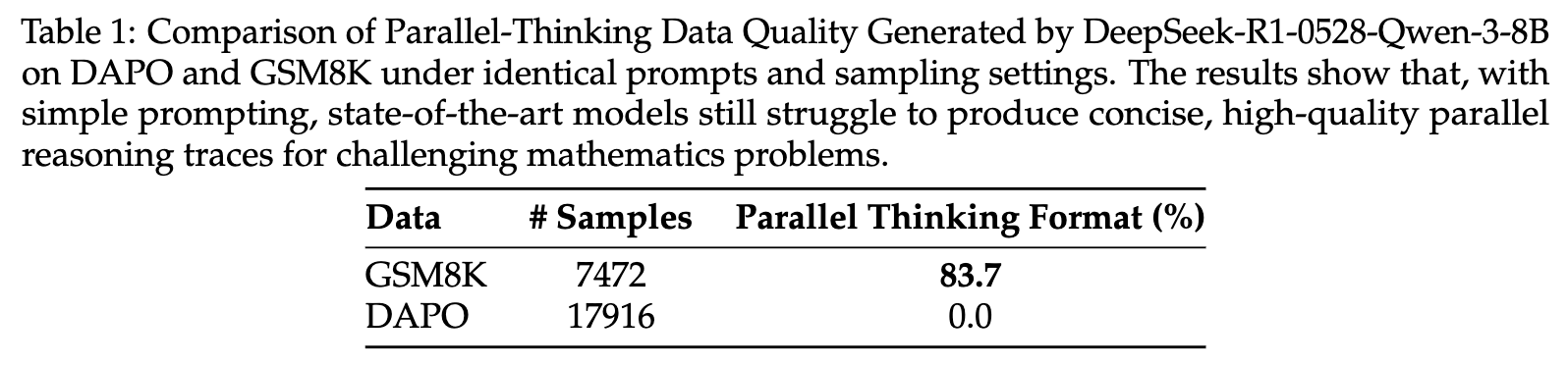
不同数据集上并行思维数据的生成质量对比
不同数据集上并行思维数据的生成质量对比

这一发现揭示了一个重要的事实：对于简单问题，我们无需复杂的数据工程，仅通过精心设计的零样本提示（zero-shot prompt）就能构建一个大规模、高质量的“冷启动”数据集。基于此，研究者们构建了一个名为 Parallel-GSM8K 的数据集，专门用于初始的SFT阶段，教模型学会并行思维的格式。

这个数据生成流程的优点在于其简单性和可扩展性，它绕过了为难题合成数据的复杂性，并巧妙地利用了LLM自身在简单问题上的能力。

2.3 训练流程与奖励模型设计

Parallel-R1 的整体训练流程分为三个阶段，并针对两种不同的模型架构（Causal Model 和 Structure Model）设计了不同的训练策略。

2.3.1 针对因果模型（Causal Models）的训练流程

这里的因果模型指的是标准的、没有对注意力机制等结构进行修改的Transformer模型。其训练流程如下：

  1. 冷启动阶段（Cold-Start Stage）：在 Parallel-GSM8K 数据集上对初始的LLM进行SFT。这一步的目标是让模型学会并行思维相关的特殊标签（<Parallel>, <Path>, <Summary>）的基本用法和语法结构。

  2. 简单数学任务上的RL（RL on Easy Math）：在冷启动之后，模型虽然具备了生成并行格式的基本能力，但这种行为尚不稳定。此阶段继续在GSM8K的训练集上进行小规模的RL训练，以强化和稳定模型的格式学习。此阶段的奖励函数 R_final 设计得非常严格，它结合了并行结构奖励 R_parallel 和准确率奖励 R_acc：

    其中， 评估最终答案的正确性， 检查生成中是否包含至少一个并行思维单元。奖励被设计为二元的：只有当同时满足“包含并行结构”和“答案正确”两个条件时，奖励为+1，否则为-1。这种设计强制模型将并行思考与解决问题的正确性联系起来。

  3. 通用数学任务上的RL（RL on General Math）：在模型能够稳定生成正确的并行格式后，将其应用到更具挑战性的通用数学数据集上（例如DAPO）。在此阶段，训练的主要目标是提升任务的性能。因此，奖励函数简化为只使用准确率奖励 R_acc。模型需要自主探索何时使用并行思维才能最大化最终的解题正确率。

该三阶段流程体现了从“格式”到“行为”再到“泛化”的渐进式学习思想。

2.3.2 针对结构模型（Structure Models）的训练流程与奖励设计

因果模型的RL框架虽然有效，但存在一个潜在问题：在标准的自注意力机制下，一条 <Path> 中的信息理论上可以“泄露”到另一条并行的 <Path> 中，因为每个token都可以关注到它之前的所有token。这违背了并行路径在“探索”阶段应相互独立的初衷。

为了解决这个问题，研究者们提出了一个结构化的变体，称为 Parallel-Unseen。该模型通过修改注意力机制来强制实现路径间的隔离：

  • 路径窗口掩码（Path-window masking）：在注意力计算中加入一个掩码，使得一个 <Path> 块内的token只能关注到该路径内部和共享的上下文（<Parallel>标签之前的内容），而不能关注到其他并行的 <Path> 块。
  • 多宇宙位置编码（Multiverse position encodings）：为每个并行的 <Path> 分配一个不相交的位置索引集合，确保它们在位置嵌入空间中也是独立的。
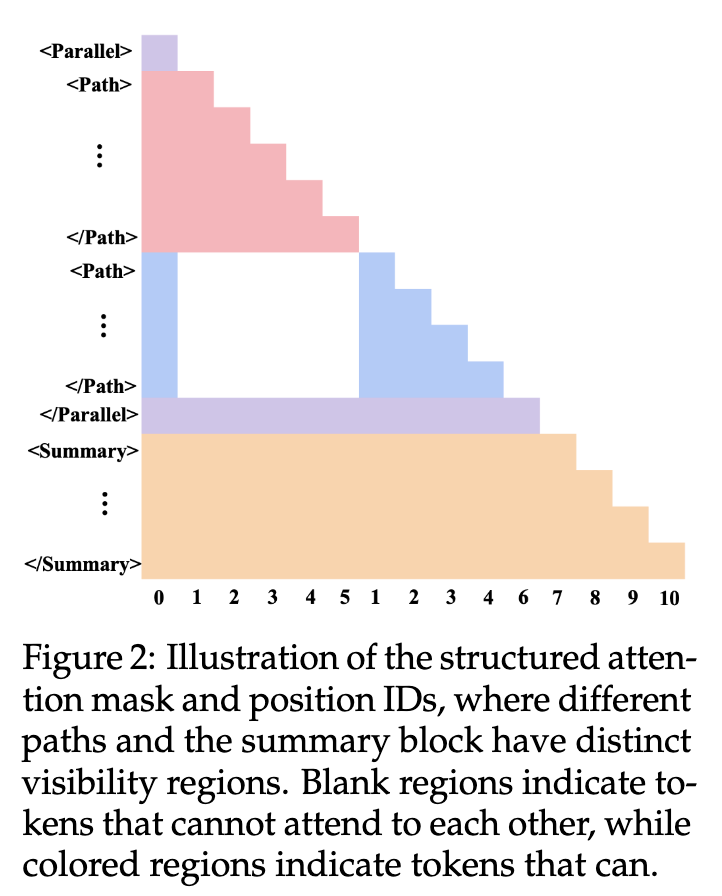
结构化注意力掩码和位置ID示意图
结构化注意力掩码和位置ID示意图

对于这种结构化模型，研究者发现直接套用因果模型的渐进式训练配方是无效的。在简单任务上学到的注意力掩码模式很难泛化到更难的任务，容易导致对表面模式的过拟合。

因此，他们为结构模型设计了不同的训练和奖励策略，移除了在简单数学上的RL阶段，并探索了两种奖励方案：

  • (S1) 只奖励准确率（Accuracy-only）：优化目标完全集中在任务的正确性上，不直接激励模型使用并行结构。
  • (S2) 交替奖励准确率与并行（Alternating accuracy and parallel）：这是一种更精巧的设计。在一个固定的训练窗口（例如10个step）内，80%的时间使用标准的准确率奖励 R_acc。剩下的20%的时间，使用一个分层的奖励系统来温和地鼓励并行思考：

    • +1.2：如果生成中包含并行单元 且 最终答案正确。
    • +1.0：如果生成中不含并行单元 但 最终答案正确。
    • -1.0：其他所有情况（即答案错误）。

这个交替和分层的奖励设计，旨在实现并行使用率和最终性能之间的平衡。它既为使用并行结构提供了额外的激励，又不会让模型为了追求并行而牺牲逻辑的正确性，避免了对并行模式的过度拟合。

3. 实验

3.1 实验设置

  • 基础模型（Backbone Model）：实验使用了 Qwen-3-4B-Base 模型，这是一个在性能和效率之间取得良好平衡的开源模型。
  • 评估基准（Benchmarks）：模型在四个具有挑战性的标准数学推理基准上进行评估，包括 AIME'24, AIME'25, AMC'23 和 MATH。
  • 基线模型（Baselines）：

    1. 直接在 DAPO 数据集上使用标准RL（GRPO算法）进行训练的模型。
    2. 在标准RL的基础上，增加了一个在 GSM8K 数据上进行RL训练的阶段，以进行公平比较。
  • 训练算法：所有RL训练均采用 Group Relative Policy Optimization (GRPO) 算法。

3.2 主要实验结果

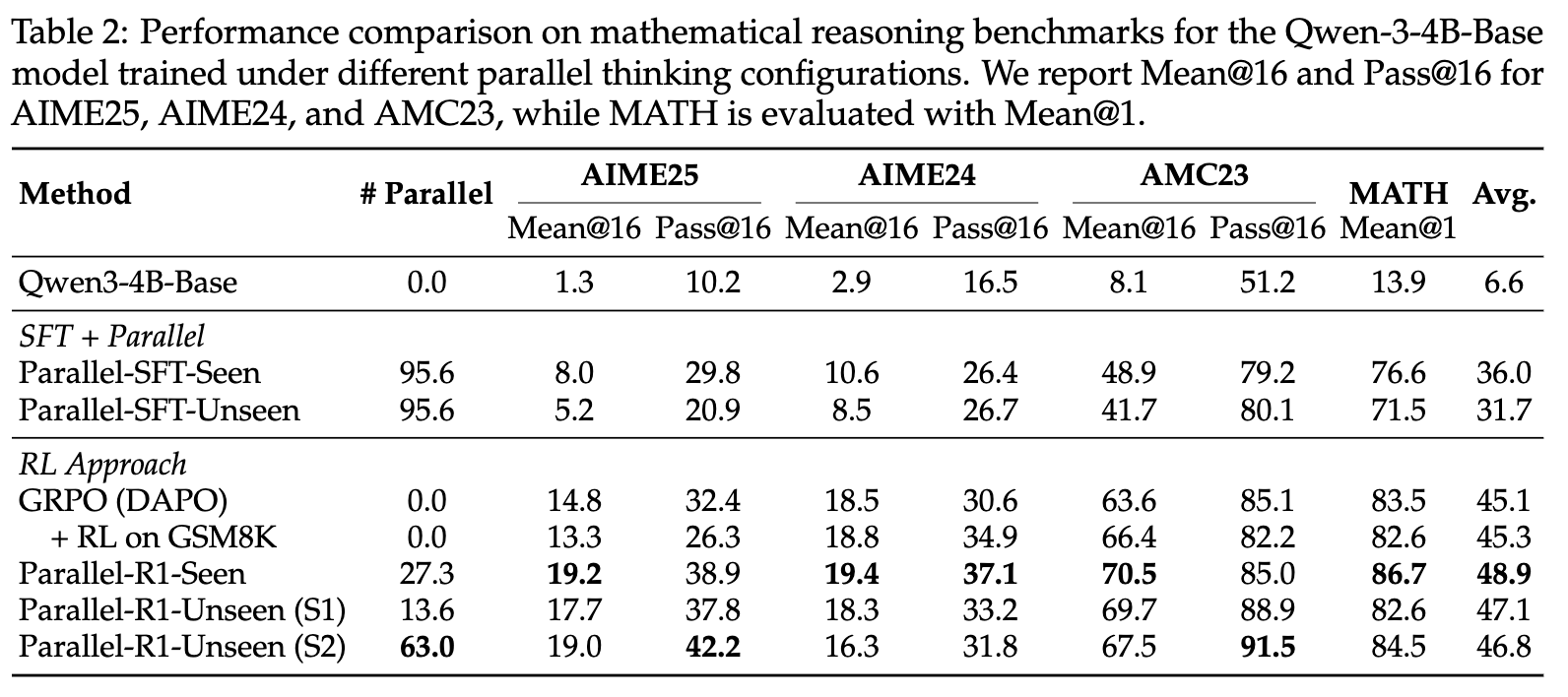
不同并行思维配置下的模型性能对比
不同并行思维配置下的模型性能对比

从上表的结果中，我们可以得出几个核心结论：

  1. Parallel-R1 框架的有效性：无论是因果变体（Parallel-R1-Seen）还是结构变体（Parallel-R1-Unseen），都显著优于所有基线模型。其中，表现最佳的 Parallel-R1-Seen 模型在所有四个基准上的平均分达到了 48.9，超过了标准RL基线（45.1）。这证明了通过渐进式课程学习和RL来教授并行思维的策略是成功的。
  2. SFT 的局限性：单独使用SFT（Parallel-SFT-Seen/Unseen）虽然能带来一定的性能提升（相较于Base模型），但其效果远不及经过RL训练的模型，也比不上标准的RL基线。这印证了仅靠模仿学习难以掌握高级推理技能的观点。
  3. 简单的RL预热效果有限：在标准RL流程中简单地加入一个在GSM8K上的RL阶段（+ RL on GSM8K），带来的平均性能提升微乎其微（45.3 vs 45.1）。这说明，如果没有一个明确的、针对并行思维格式和行为的“冷启动”SFT阶段，模型很难从简单的RL任务中自发学习到有用的结构化推理能力。这反过来验证了Parallel-R1中“先SFT后RL”这一课程设计的必要性和高明之处。
  4. 模型架构的权衡：因果模型（Seen）的性能普遍优于其结构化对应方（Unseen）。这表明，尽管在理论上强制的路径隔离（Unseen）更符合并行思维的直觉，但这种严格的架构修改可能对RL训练的灵活性和泛化能力产生负面影响，使其更难优化。标准的因果模型可能通过其更灵活的表示空间，更好地适应和利用RL信号。
  5. 奖励设计的重要性：对于结构模型Parallel-R1-Unseen，采用交替奖励策略（S2）的模型，其并行使用率（

    Parallel = 63.0）远高于只奖励准确率的策略（S1，# Parallel = 13.6），并且在平均性能上略有优势。这凸显了奖励工程在引导模型学习特定行为（如并行思考）和平衡多重目标（如并行率与准确率）中的关键作用。

3.3 消融研究：深入理解训练动态

为了更深入地探究Parallel-R1框架中不同组件的作用，研究者进行了一系列的消融实验。

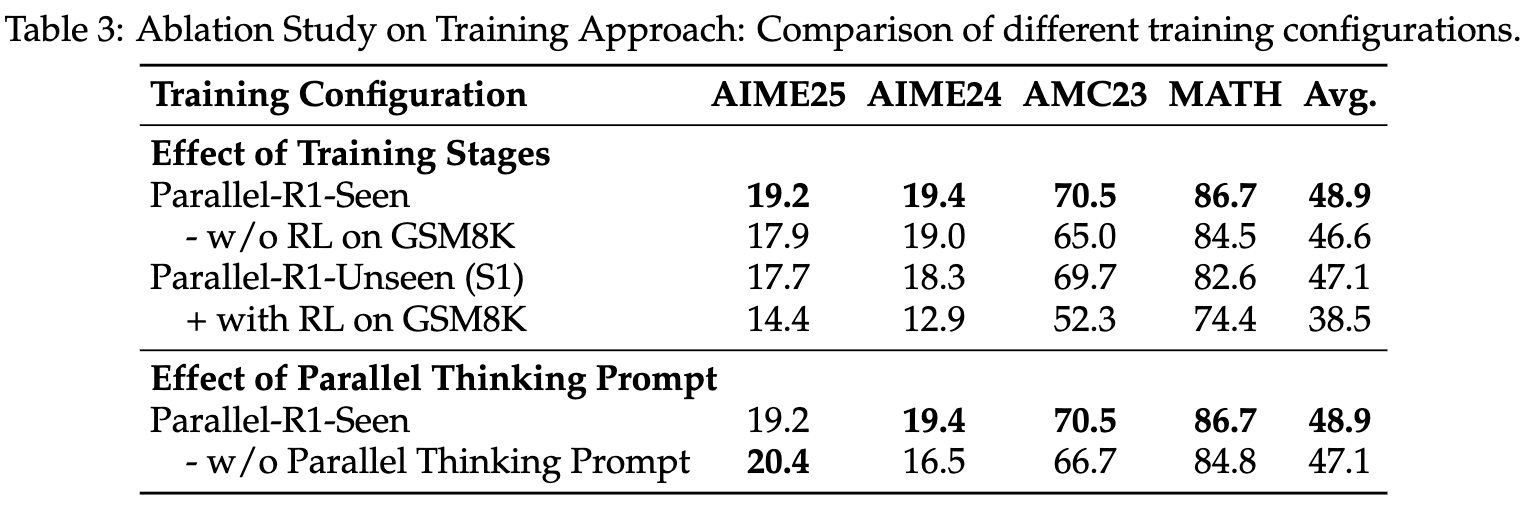
训练方法消融研究
训练方法消融研究

3.3.1 训练阶段的影响

  • 对于因果模型（Parallel-R1-Seen）：如果移除在GSM8K上的RL阶段（- w/o RL on GSM8K），模型的平均性能从48.9下降到46.6。这说明，对于因果模型，仅有SFT的格式学习是不够的，需要在简单任务上通过RL对这种行为进行稳定和强化，才能为后续在困难任务上的泛化打下坚实的基础。
  • 对于结构模型（Parallel-R1-Unseen）：有趣的是，结构模型表现出相反的趋势。为其增加在GSM8K上的RL阶段（+ with RL on GSM8K）反而导致性能大幅下降（从47.1降至38.5）。研究者推测，这是因为在简单任务（GSM8K）上学到的严格的结构化注意力模式（attention mask）过拟合了简单问题的特征，无法很好地迁移到问题分布有显著变化的困难任务上。

这一对比揭示了一个深刻的洞见：不同的模型架构对训练课程的敏感度是不同的。对于灵活的因果模型，一个渐进的、从易到难的RL课程是有效的。而对于带有强归纳偏置的结构模型，可能需要一个更直接、端到端的训练范式，以避免在中间阶段陷入“知识”的局部最优。

Parallel-R1-Unseen 模型奖励建模的消融研究
Parallel-R1-Unseen 模型奖励建模的消融研究

3.3.2 奖励模型的影响

上表详细展示了针对结构模型的三种奖励策略的效果：

  • 只奖励准确率（Accuracy）：这种策略在AMC 23等基准上表现最好，但模型的并行使用率极低（13.6%）。这表明，模型在没有明确激励的情况下，并不会自发地采用并行推理这种更复杂的策略，即使它可能是有益的。追求单一的准确率目标会让模型倾向于走最直接、风险最低的单路径推理。
  • 只奖励并行（Parallel）：这种策略极大地提升了并行使用率（80.3%），证明了模型对奖励信号的响应是直接且有效的。然而，这也导致了在多数基准上的性能显著下降。这揭示了一个关键的权衡：无约束地鼓励并行行为，可能会让模型本末倒置，优先考虑生成特定的结构形式，而不是追求逻辑的正确性，从而损害了其核心的问题解决能力。
  • 交替奖励（Alternating Acc./Parallel）：该策略在并行使用率（63.0%）和整体性能之间取得了最佳的平衡。特别是在最具挑战性的AIME 25基准上，它的表现甚至超过了只奖励准确率的策略。这证明了通过周期性地切换奖励目标，可以有效地引导模型在不牺牲核心性能的前提下，更多地探索和利用并行思维。

4. 核心发现

除了框架的有效性，Parallel-R1的研究还揭示了LLM在学习和使用并行思维时的一些深层次行为模式和规律。

4.1 发现一：并行思维行为的演化——从探索到验证

研究者分析了在RL训练过程中，<Parallel>模块在整个推理链中出现的位置变化。他们发现了一个清晰且一致的趋势：随着RL训练的进行，<Parallel>块的平均相对位置逐渐后移。

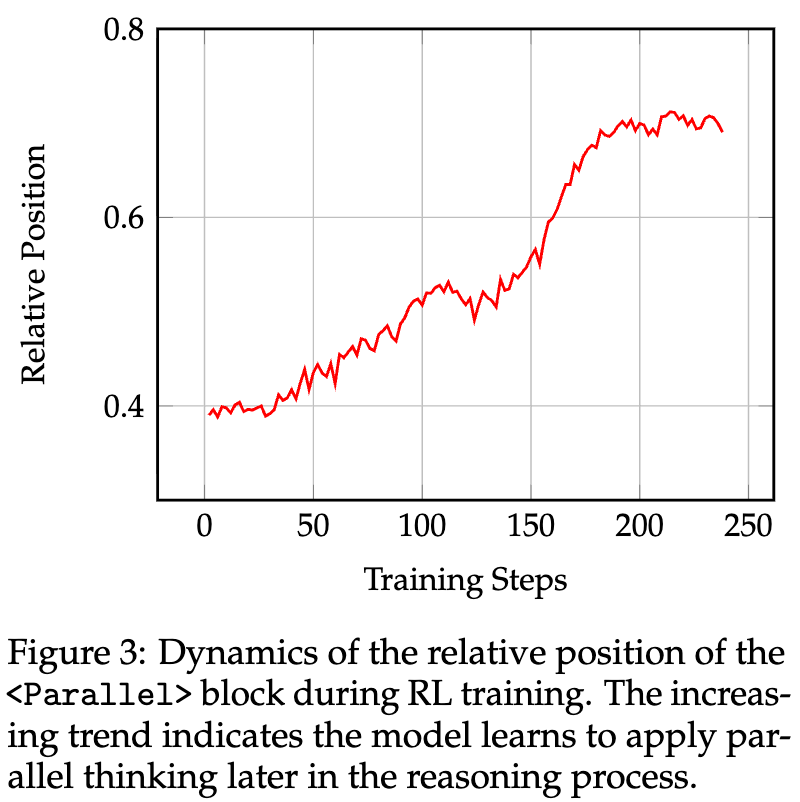
RL训练过程中块相对位置的动态变化
RL训练过程中<Parallel>块相对位置的动态变化

这一发现（Key Finding 2）揭示了模型策略的演化过程：

  • 训练早期：当模型的内在推理能力较弱时，它倾向于在推理过程的早期就使用并行路径。这时的并行思维主要扮演着计算探索（computational exploration）的角色。模型不确定哪条路是正确的，因此通过并发地探索多种可能性，来增加找到潜在解决方案的概率。这是一种高方差（high-variance）的策略。
  • 训练后期：随着模型核心推理能力的增强，它变得更加自信。此时，在早期进行探索的风险（可能引入错误路径）超过了其收益。因此，模型学会了一种更保守、更风险规避的策略。它会首先沿着一条高置信度的路径推导出一个初步的答案，然后在推理过程的末期才部署<Parallel>块。这时的并行思维，其角色从“探索”转变为多视角验证（multi-perspective verification）。模型利用并行的路径来检查、确认和巩固已经得出的结论，以最大化获得最终奖励的概率。

这种从“发散式探索”到“收敛式验证”的策略转变，是模型在“最大化最终答案正确率”这一奖励目标驱动下，自主学习到的智能行为。它深刻地揭示了LLM推理策略的动态性和适应性。

4.2 发现二：并行思维作为一种“中段训练探索脚手架”

研究者进一步提出了一个更大胆的假设（Key Finding 3）：并行思维本身可以作为一种有效的结构化探索机制，来提升RL的训练效果，即使最终的模型不再高频使用它。

强化学习的一个核心挑战是确保模型能充分探索策略空间，以避免陷入局部最优。研究者认为，通过在训练中强制模型生成多个并行的思考路径，可以引入一种强大的归纳偏置，迫使模型进行更结构化、更多样化的探索，从而引导模型发现更鲁棒的策略空间。

为了验证这一假设，他们设计了一个两阶段的训练课程：

  • 阶段一：探索阶段（0-200步）：采用前述的交替奖励策略（Parallel-R1-Unseen S2），明确激励模型使用并行思维，维持高的并行率，强制模型进行广泛的探索。
  • 阶段二：利用阶段（200步以后）：将奖励切换为只奖励准确率，让模型在第一阶段探索到的策略空间中，进行精细化的利用和提炼，以最大化任务性能。
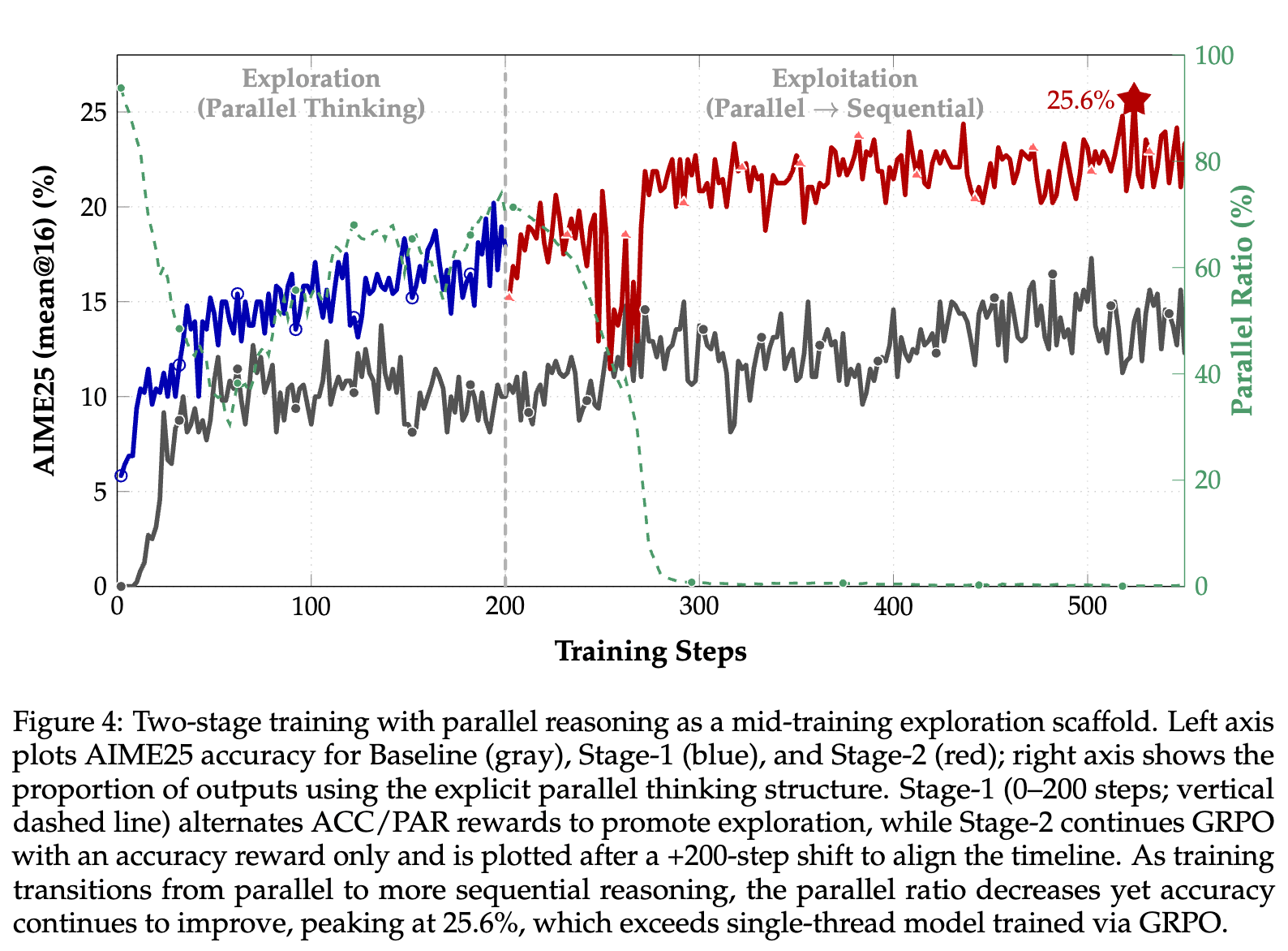
将并行推理作为中段训练探索脚手架的两阶段训练
将并行推理作为中段训练探索脚手架的两阶段训练

实验结果令人信服。如上图所示，在进入第二阶段后，尽管模型的并行使用率（图中的绿色虚线，对应右轴）因奖励的改变而急剧下降，但其在AIME25上的准确率（红色实线）却持续攀升，最终达到了 25.6% 的峰值。这一性能不仅显著高于基线GRPO模型，也高于在整个训练过程中都保持高并行率的模型。

这一结果证明了“并行思维作为训练脚手架”的价值。在训练初期强制进行的并行探索，像一个脚手架一样，帮助模型构建了一个更好的“认知结构”或策略基础。一旦这个基础建立起来，即使后续拆除“脚手架”（即不再强制使用并行），模型也能在此基础上达到比没有脚手架时更高的性能天花板。

这个发现对于更广泛的RL for LLM研究具有重要启示：在训练过程中引入临时的、结构化的探索机制，可能是一种解锁LLM更高性能潜力的有效手段。

往期文章：