现有的RLVR框架在实际应用中仍面临性能提升的瓶颈,今天分享的这篇论文《DEPTH-BREADTH SYNERGY IN RLVR: UNLOCKING LLM REASONING GAINS WITH ADAPTIVE EXPLORATION》剖析了这一问题,指出当前方法在两个关键维度上的探索不足,即“深度”(Depth)和“广度”(Breadth)。
-
深度(Depth):指模型能够解决的最困难的问题。 -
广度(Breadth):指在单次训练迭代中处理的样本数量。

-
论文标题:DEPTH-BREADTH SYNERGY IN RLVR: UNLOCKING LLM REASONING GAINS WITH ADAPTIVE EXPLORATION -
论文链接:https://arxiv.org/pdf/2508.13755
1. 现有RLVR框架的困境
论文首先将矛头指向了当前流行的RLVR算法——GRPO(Group Relative Policy Optimization) 及其变体。GRPO通过对一个问题生成多个候选答案(即rollouts),并根据答案的正确与否计算“优势(advantage)”,从而指导模型的优化方向。这个过程摒弃了传统PPO算法中需要额外训练一个价值模型(Value Model)的复杂环节,提升了训练效率。
1.1 GRPO算法的核心思想
GRPO的核心在于其优势计算方式。对于一个给定的问题,模型会生成 个不同的答案。由于是可验证的奖励环境,每个答案的奖励(reward)是二元的,即正确为1,错误为0。
该组答案的平均奖励 就是这组答案的准确率。GRPO计算每个答案 的优势 时,会使用组内的平均奖励和标准差 对其进行归一化。论文中提到了两种优势计算方式:
-
标准化优势 (std-based advantage):
其中 是第 个答案的奖励, 是该组答案的平均奖励, 是奖励的标准差。对于二元奖励,。 -
非标准化优势 (non-std advantage):
这种方式在Dr. GRPO等变体算法中使用,忽略了标准差项。
1.2 “累积优势”暴露出的系统性偏差
论文作者敏锐地发现,仅仅分析单个答案的优势是不够的,需要从“组”的层面考察算法对不同难度问题的重视程度。为此,他们定义了“累积优势”(Cumulative Advantage) ,即一个问题组内所有样本优势绝对值的总和:
累积优势直观地反映了算法在处理一个特定问题时,所产生的梯度信号的总强度。累积优势越大,意味着模型从这个问题中学到的信息越多,对模型参数的更新影响也越大。
通过数学推导,论文给出了两种优势计算方式下,累积优势与问题难度(即准确率 )之间的函数关系:
-
对于标准化优势:
-
对于非标准化优势:
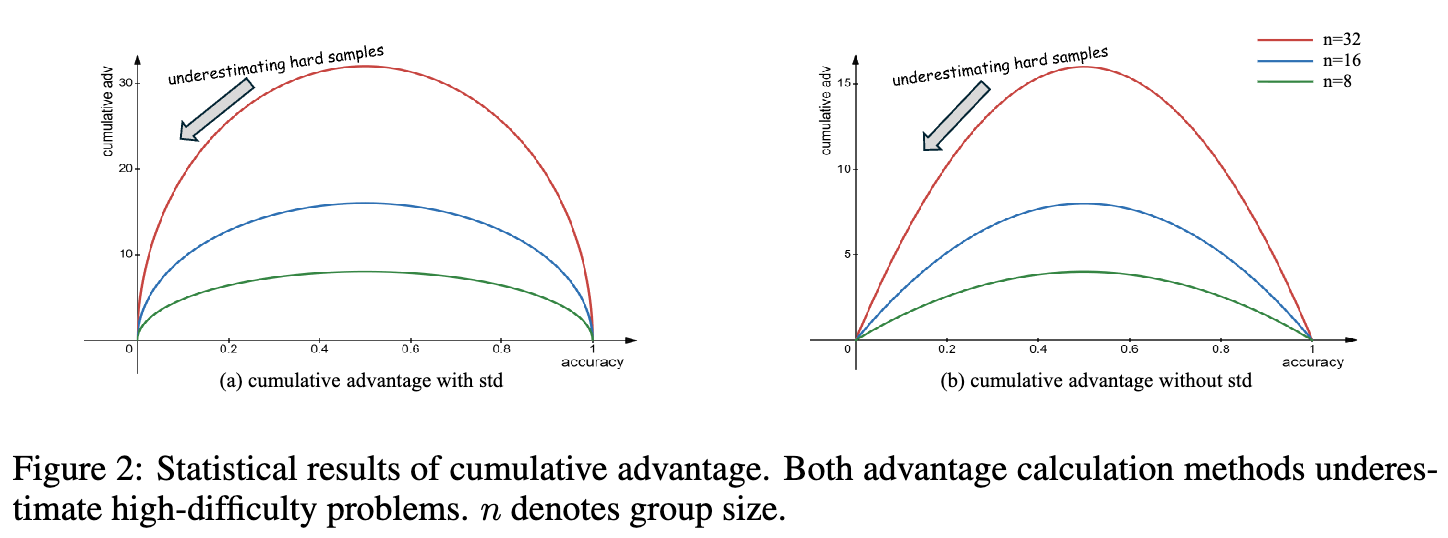
将这两个函数绘制成图表(如图2所示),可以清晰地看到一个系统性的偏差:
-
函数曲线呈倒U型:无论是哪种计算方式,累积优势都在准确率 时达到峰值。这意味着,对于中等难度的问题(模型有一半的概率答对),算法给予的关注度最高,产生的学习信号最强。 -
两端优势递减:对于非常简单的问题()和非常困难的问题(),累积优势都趋近于0。
这种偏差是致命的。对于简单问题,模型本已掌握,减少关注是合理的。但对于那些对提升模型推理能力上限至关重要的难题(低准确率问题),GRPO算法却“视而不见”,给予了极少的权重。当一个问题组内所有答案都错误时(),累积优势为0,模型将不会从这次失败中学到任何东西,产生所谓的“梯度消失”现象。
这种对高难度样本的“深度忽视”,从根本上限制了模型解决最难问题的能力,也即是论文所定义的“深度”(Depth),直接导致了 Pass@K 指标的停滞。
1.3 Pass@K 指标的含义
Pass@K 是一个常用于评估代码生成和数学推理等任务的指标。它衡量的是,对于一个问题,模型生成 个候选答案,只要其中至少有一个是正确的,就认为该问题得到了解决。Pass@K反映了模型在多次尝试下解决问题的“上限能力”或“潜力”。
GRPO对难题的忽视,使得模型很难在探索中找到通往正确答案的稀疏路径,从而难以提升其解决问题的上限能力,最终体现在Pass@K指标上增长乏力,甚至在训练后期出现下降。
1.4 “天真”地增加Rollout数量并不可行
一个自然的想法是:既然难题的信号稀疏,那么增加每个问题的采样数量(即rollout size, )是否能缓解这个问题?更多的采样意味着有更大的概率获得正确的答案,从而产生非零的梯度。
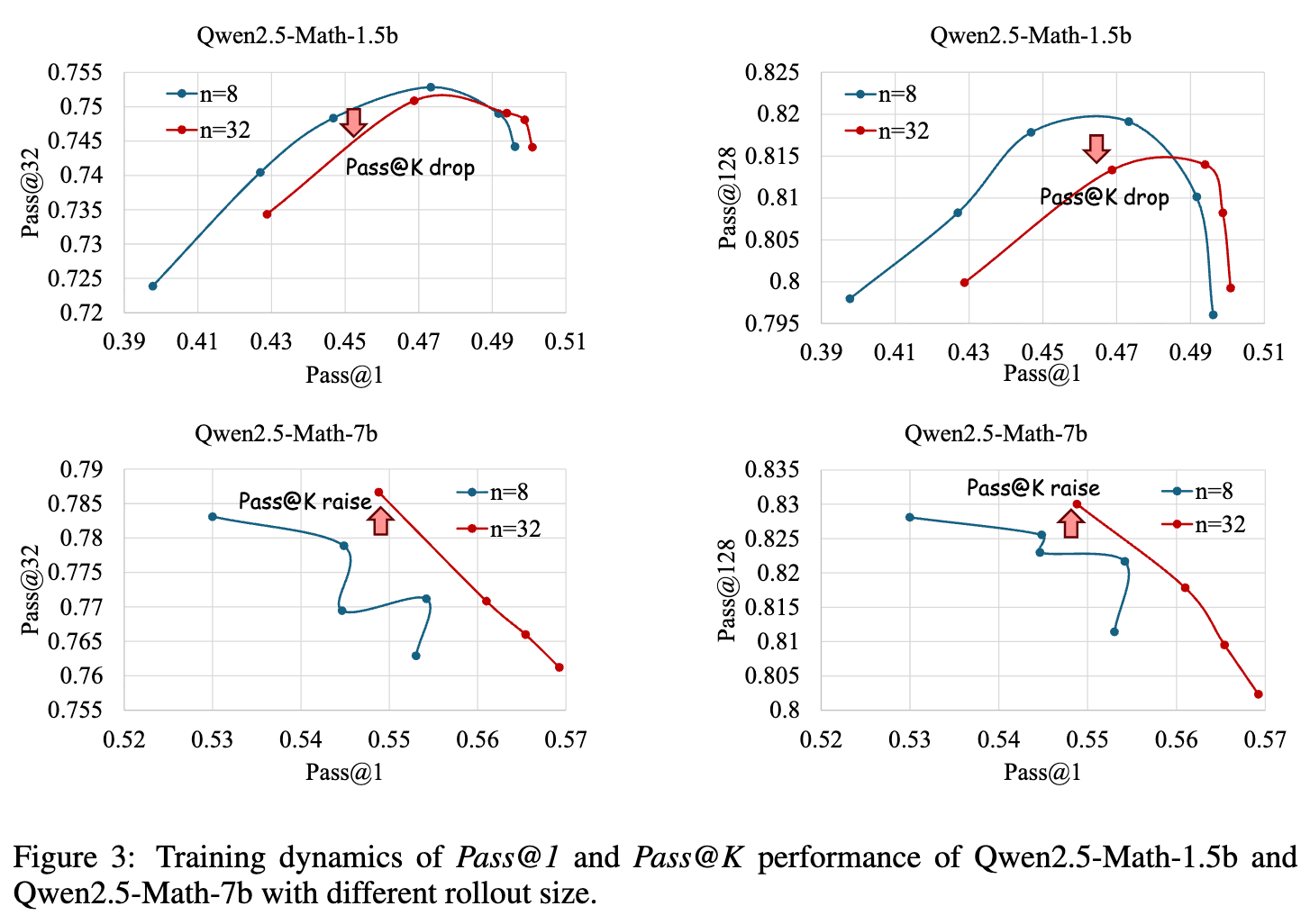
然而,论文通过实验(如图3所示)证明,简单地增加rollout数量(例如从8增加到32)并非万能药。对于某些模型(如Qwen2.5-Math-7b),这样做确实能带来Pass@K的提升;但对于另一些模型(如Qwen2.5-Math-1.5b),这种“天真”的缩放甚至会损害Pass@K的性能,导致其在训练过程中不升反降。这表明,盲目地增加计算开销并不能稳定地解决“深度”问题,需要更智能的策略。
2. 难度自适应 rollout 采样 (DARS)
为了解决上述“深度忽视”的问题,论文提出了一种名为“难度自适应Rollout采样”(Difficulty-Adaptive Rollout Sampling, DARS) 的新方法。DARS的核心思想是,不再对所有问题一视同仁地分配计算资源,而是将更多的计算(即rollouts)动态地、有针对性地分配给那些模型认为更困难的问题。
DARS的执行过程分为两个阶段:
阶段一:预Rollout难度估计
在正式的训练迭代开始前,DARS首先对批次中的每一个问题 进行一次轻量级的“试探性”采样。它会生成一个较小的、固定数量(比如 )的候选答案,并计算出该问题的初始经验准确率 。
然后,定义一个“难度分” 。这个分数直观地反映了问题的难度:准确率越低,难度分越高,越接近1。
阶段二:多阶段Rollout重平衡
在估算出每个问题的难度后,DARS进入核心的重平衡阶段。它的目标是重新分配额外的rollout资源 ,使得困难问题的累积优势得到提升,从而“放大”来自这些难题的学习信号。
为了实现这一目标,论文设计了两种不同的重平衡策略(re-balancing schedules):
策略一:平等待遇 (Equal-Treatment, ET)
ET策略的目标是“劫富济贫”,将所有困难问题()的累积优势提升到中等难度问题()的水平。我们知道,中等难度问题在原始GRPO下获得的累积优势是最大的,ET策略相当于为所有难题提供了“最高标准”的关注度。
根据累积优势的公式,可以反推出需要增加的rollout数量 :
其中, 是准确率为 时的累积优势, 是一个与优势计算方式相关的缩放函数,而 是一个为了控制总计算开销而设定的额外rollout数量上限。
策略二:硬度加权 (Hardness-Weighted, HW)
HW策略则更进一步,它不仅要提升难题的关注度,还要让这种关注度随着难度的增加而单调递增。也就是说,越难的问题,获得的累积优势应该越大。具体来说,它将目标累积优势设置为与难度分 成正比:
同样,可以计算出所需的额外rollout数量 :
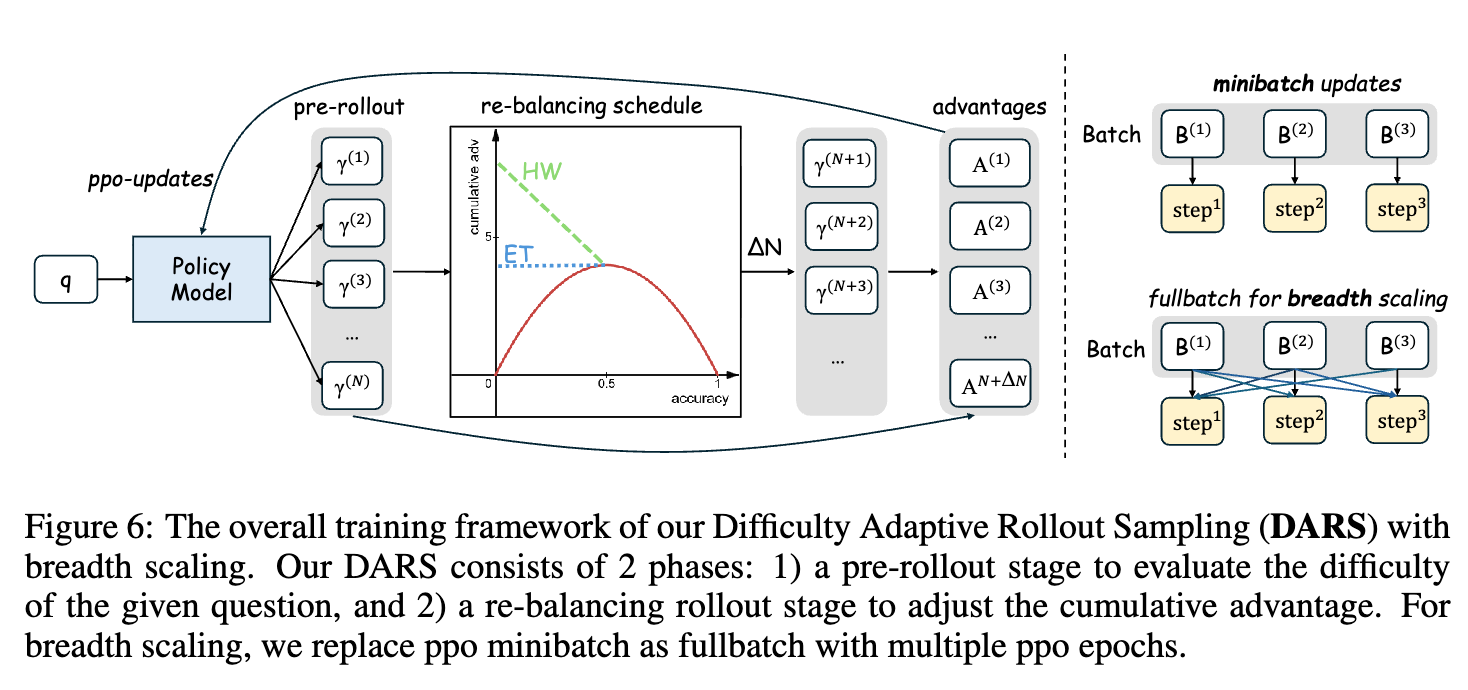
通过这两阶段的过程,DARS有效地将计算资源从模型已经掌握得比较好的中等难度问题,重新分配给了那些对提升模型推理上限至关重要的难题。这不仅解决了GRPO的累积优势偏差问题,而且由于其动态和自适应的特性,它只在必要时增加计算量,相比于“天真”地全局增加rollout数量,DARS在收敛时几乎没有额外的推理成本。
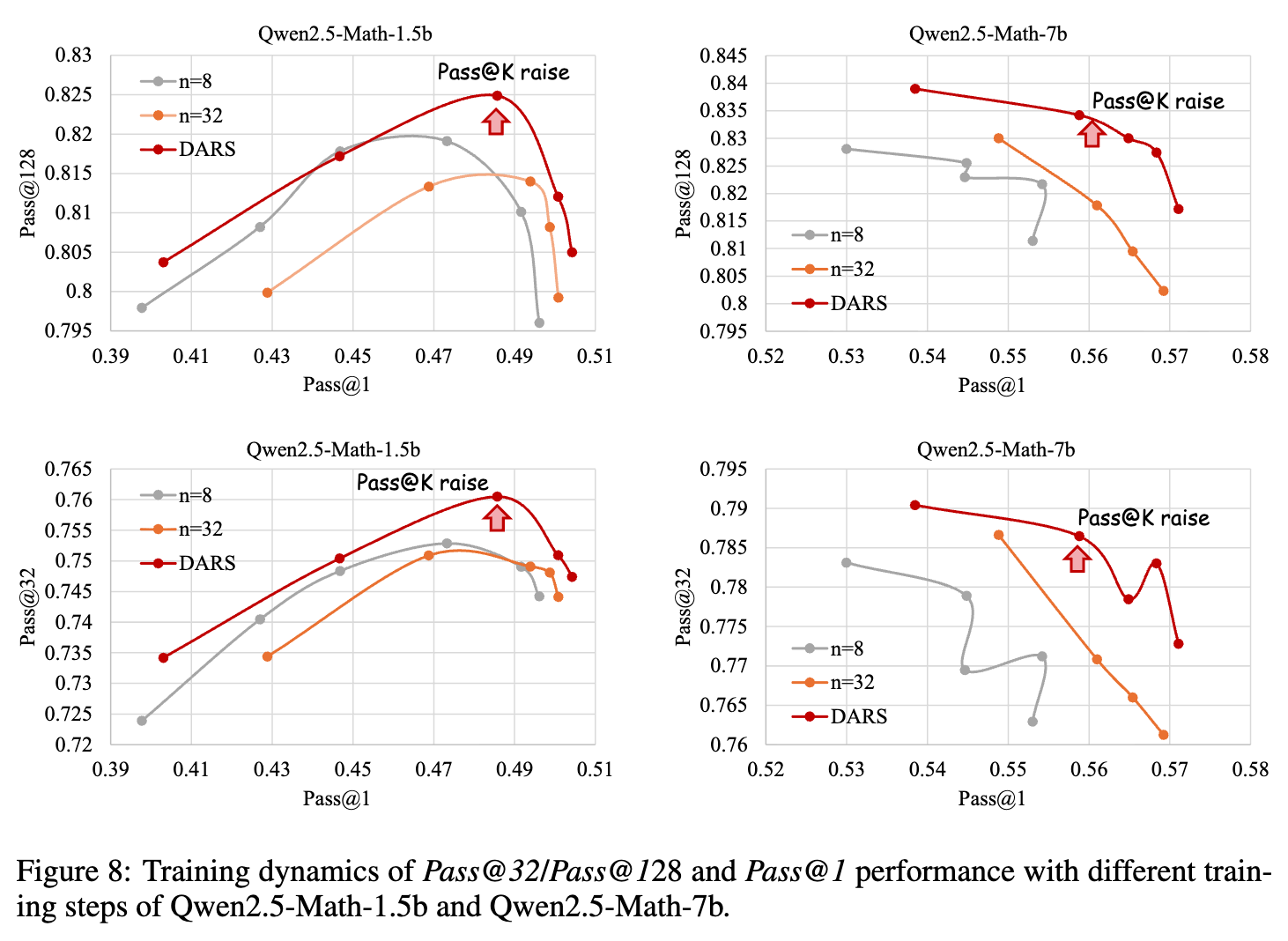
实验结果(如图8所示)证明了DARS的有效性。在相同的Pass@1水平下,DARS训练的模型始终能获得比基线方法(GRPO)和天真缩放方法更高的Pass@K分数。这表明DARS成功地提升了模型解决难题的“深度”和“上限能力”。
3. 现有RLVR框架的“广度”问题:探索不足
在解决了“深度”问题后,论文将目光转向了另一个被忽视的维度——“广度”(Breadth),即单次训练迭代中使用的样本实例数量。在传统的RLVR设置中,这个数量(即批次大小, batch size)通常被设置得比较小,例如128。
3.1 广度的重要性:提升Pass@1性能
Pass@1 指标与Pass@K不同,它衡量的是模型在第一次尝试时就成功解决问题的概率。这更贴近许多实际应用场景,反映了模型的“单次命中率”或“可靠性”。
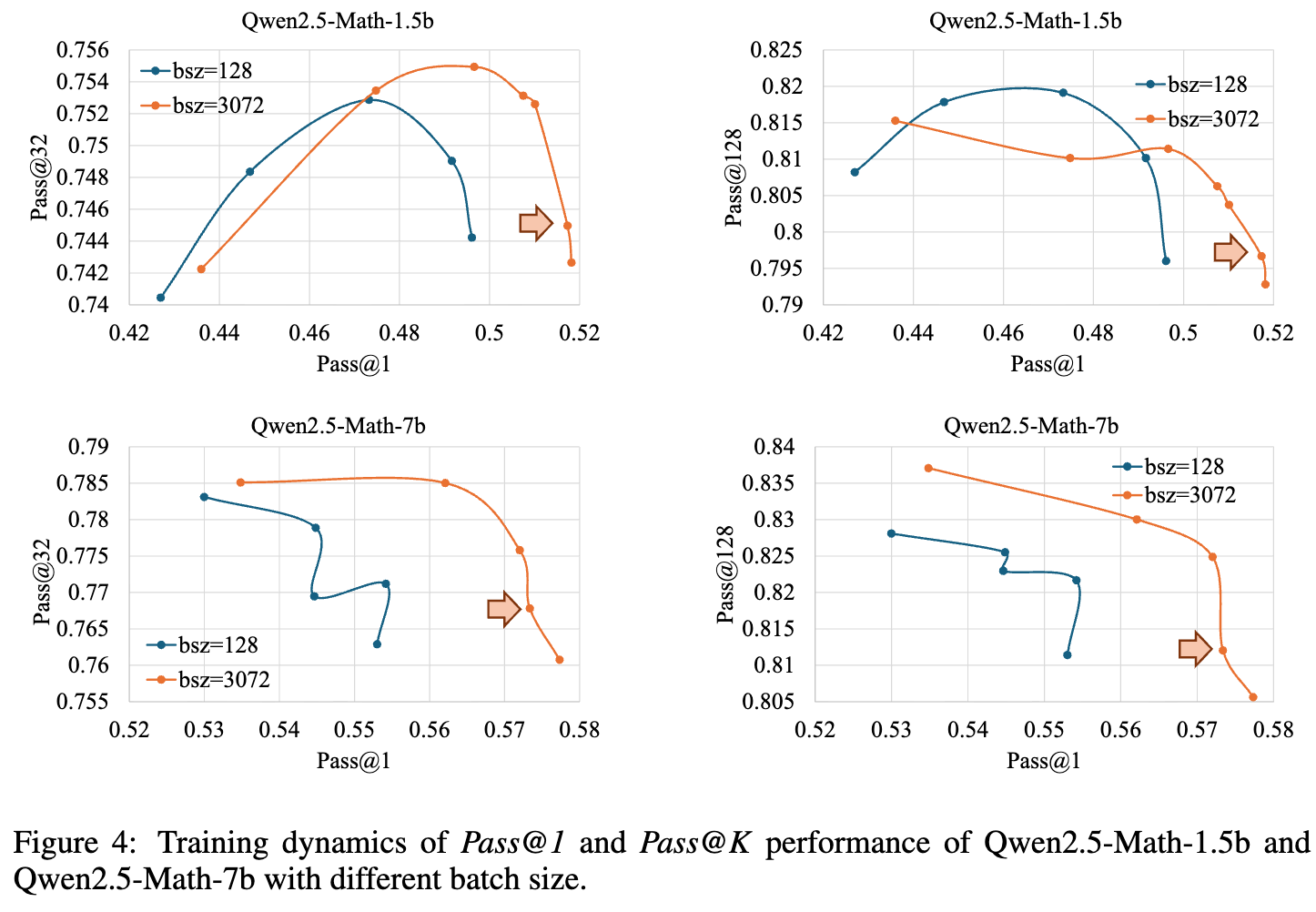
论文通过实验(如图4所示)发现,大幅增加训练的批次大小(例如从128增加到3072),可以显著提升模型的Pass@1性能。这一看似简单的改动,背后蕴含着深刻的机理。
3.2 广度如何发挥作用:隐式熵正则化
作者进一步分析了广度与模型探索行为之间的关系,引入了“词元熵”(token-level entropy) 这一指标。熵在信息论中用来度量不确定性,在LLM训练中,更高的输出词元熵意味着模型在生成答案时更具多样性和探索性,而不是过早地收敛到少数几个固定的模式。
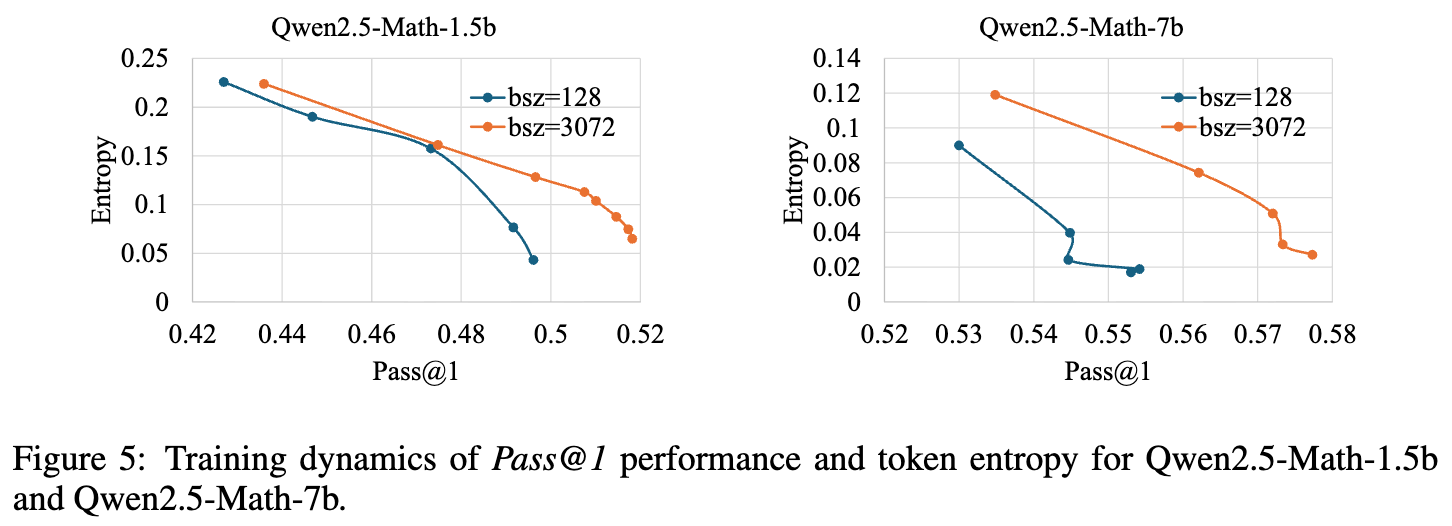
实验结果(如图5所示)显示,采用大批次(大广度)训练的模型,在达到相同的Pass@1准确率时,其词元熵始终高于小批次训练的模型。这揭示了大广度训练的一个关键作用:
-
减少梯度噪声:更大的批次意味着单次迭代的梯度估计更准确,减少了因小批次采样带来的随机性噪声,使模型的优化方向更稳定。 -
维持探索状态:更稳定的梯度和更多样的样本使得模型能够在更长的时间里保持较高的探索性(高熵),避免了“过早收敛”(premature convergence)的陷阱。模型不会轻易地满足于找到的局部最优解,而是会继续探索更广阔的解空间。
因此,大广度训练扮演了一种“隐式熵正则化”(implicit entropy regularization) 的角色,它通过维持模型的探索能力,最终转化为Pass@1性能的提升。
4. 论文的核心方案二:深度与广度协同 (DARS-B)
论文已经分别论证了“深度”(通过DARS解决)和“广度”(通过大批次训练解决)对于提升LLM推理能力的重要性,并且它们分别对应着Pass@K和Pass@1两个关键指标。一个自然而然的问题是:我们能否将两者结合起来,实现两个指标的同时提升?
这就是论文最终提出的集成方案——DARS-B (DARS with large Breadth) 。
4.1 架构上的挑战与解决方案
直接将DARS与大广度训练结合存在一个架构上的冲突。DARS的动态rollout分配机制,使得在一个批次内,不同问题的样本数量是动态变化的。而传统的大规模分布式训练中常用的PPO算法依赖于固定的、小的“微批次”(mini-batch)进行多次迭代更新。动态变化的样本数与固定的微批次划分方式难以兼容。
为了解决这个问题,DARS-B做出了一个关键的改动:用全批次梯度下降(full-batch gradient descent)替代PPO的微批次更新。具体来说,在每次优化步骤中,模型会使用整个(经过DARS动态调整后的)大批次数据计算一次梯度,并进行多次(multiple PPO epochs)参数更新。
4.2 全批次训练的优势
这种全批次更新的方式带来了两大好处:
-
消除了微批次梯度噪声:彻底避免了因微批次划分带来的梯度估计偏差,使得每次更新都基于当前迭代最准确的全局信息。 -
最大化训练广度:确保了DARS动态分配资源的优势与大批次训练维持探索能力的优势能够被同时利用。
4.3 DARS-B:实现1+1>2的效果
DARS-B框架将深度探索和广度探索这两个正交的维度完美地结合在了一起:
-
DARS负责深度:通过自适应采样,确保模型能够持续挑战高难度问题,从而提升Pass@K。 -
大批次全量更新负责广度:通过稳定梯度、维持高熵,确保模型在单次生成时有更高的准确率,从而提升Pass@1。
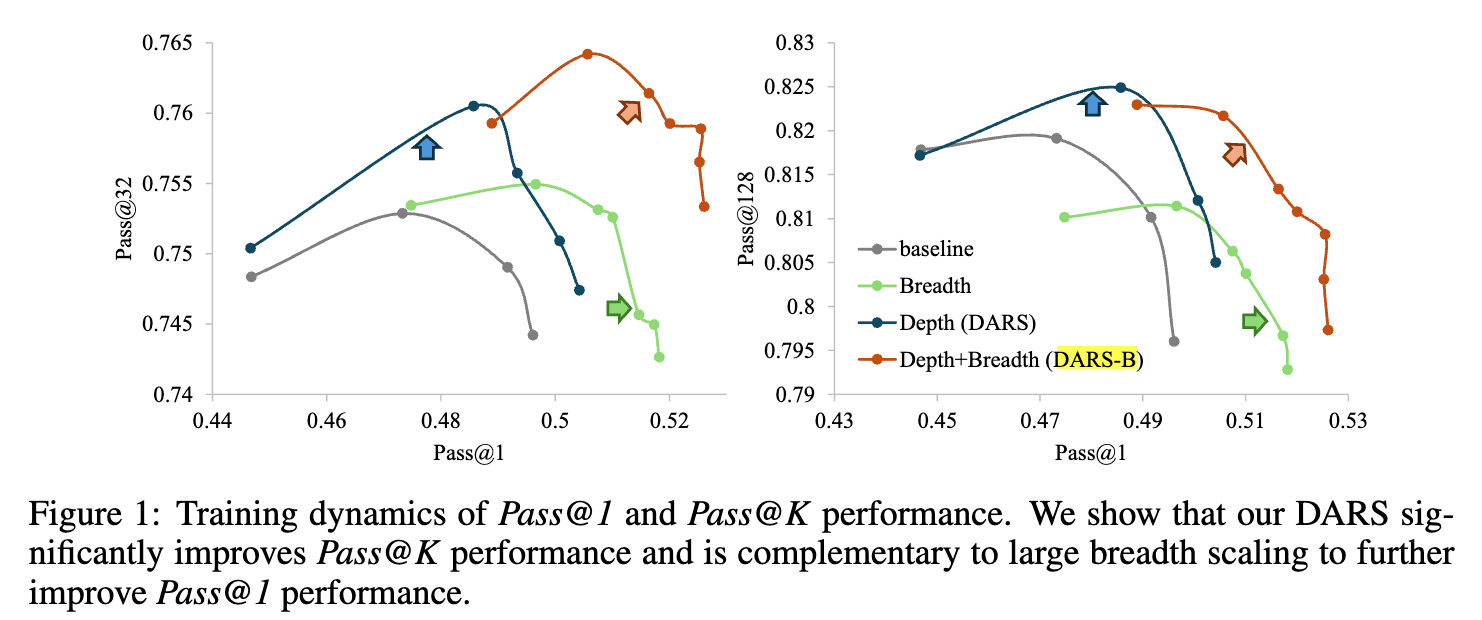
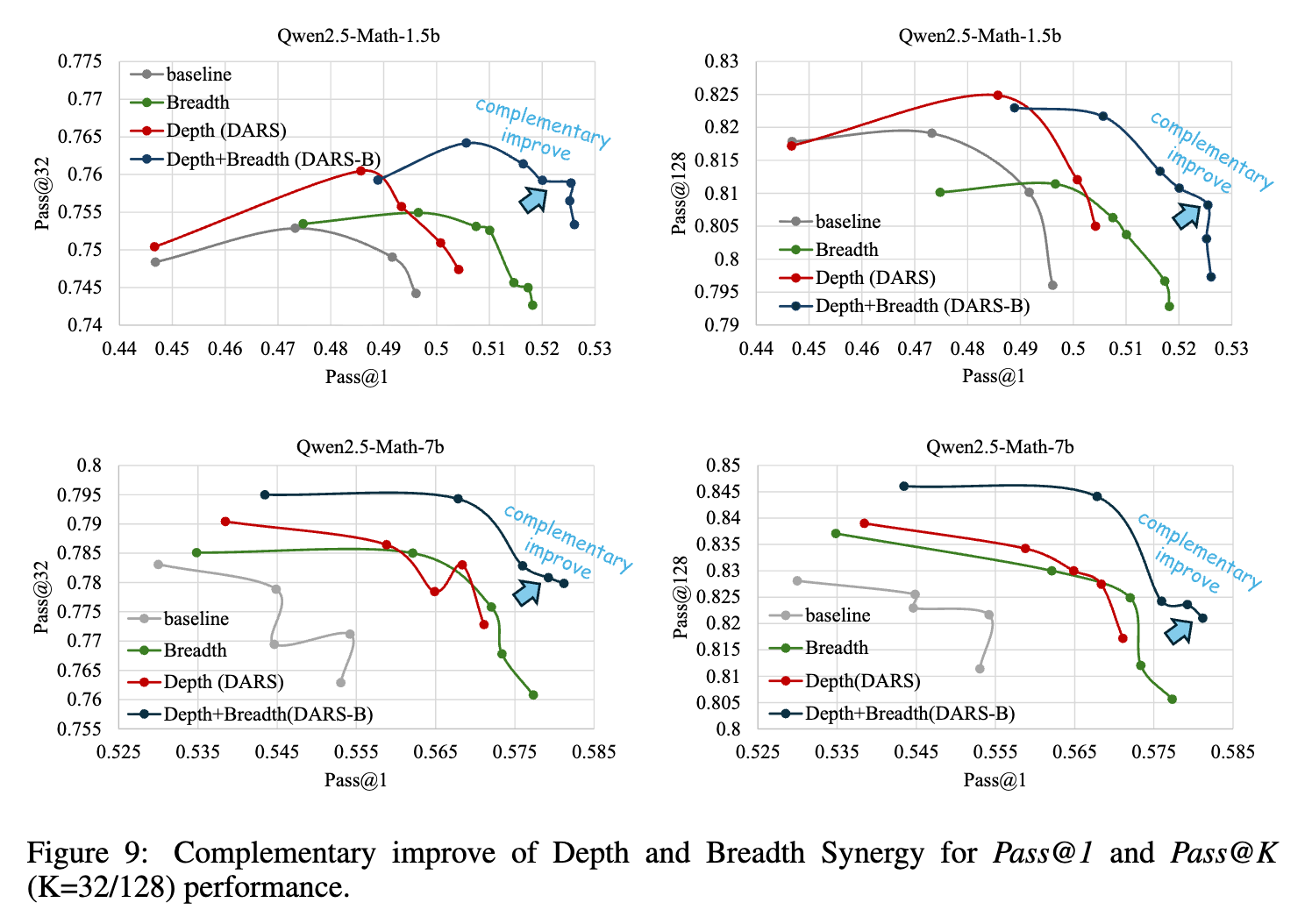
最终的实验结果(如图1和图9所示)证明了这种协同作用。在Pass@1 vs Pass@K的二维图上,DARS-B的性能曲线完全包络了所有其他方法(基线、仅有深度、仅有广度),位于图的最外层。这表明DARS-B不仅在Pass@1上达到了最佳性能,同时也显著提升了Pass@K,实现了两个维度的同步增益。
5. 实验设置与结果分析
为了验证上述理论和方法的有效性,论文进行了一系列详尽的实验。
-
模型:实验主要基于 Qwen2.5-Math 系列模型进行,涵盖了1.5B和7B两种尺寸。Qwen2.5-Math是为数学推理任务特别优化的模型系列。 -
数据集:训练数据使用了OpenR1-Math-220k的一个子集。评估则在包括MATH-500、OlympiadBench、MinervaMath等5个广泛使用的数学推理基准上进行。 -
对比方法: -
GRPO-baseline: 采用小批次(128)、小rollout数(8)的基准设置。 -
Depth-Naive: 简单增加rollout数到32。 -
Breadth-Naive: 简单增加批次大小到3072。 -
DARS (ours): 论文提出的深度优化方法。 -
DARS-B (ours): 论文提出的深度与广度协同方法。
-
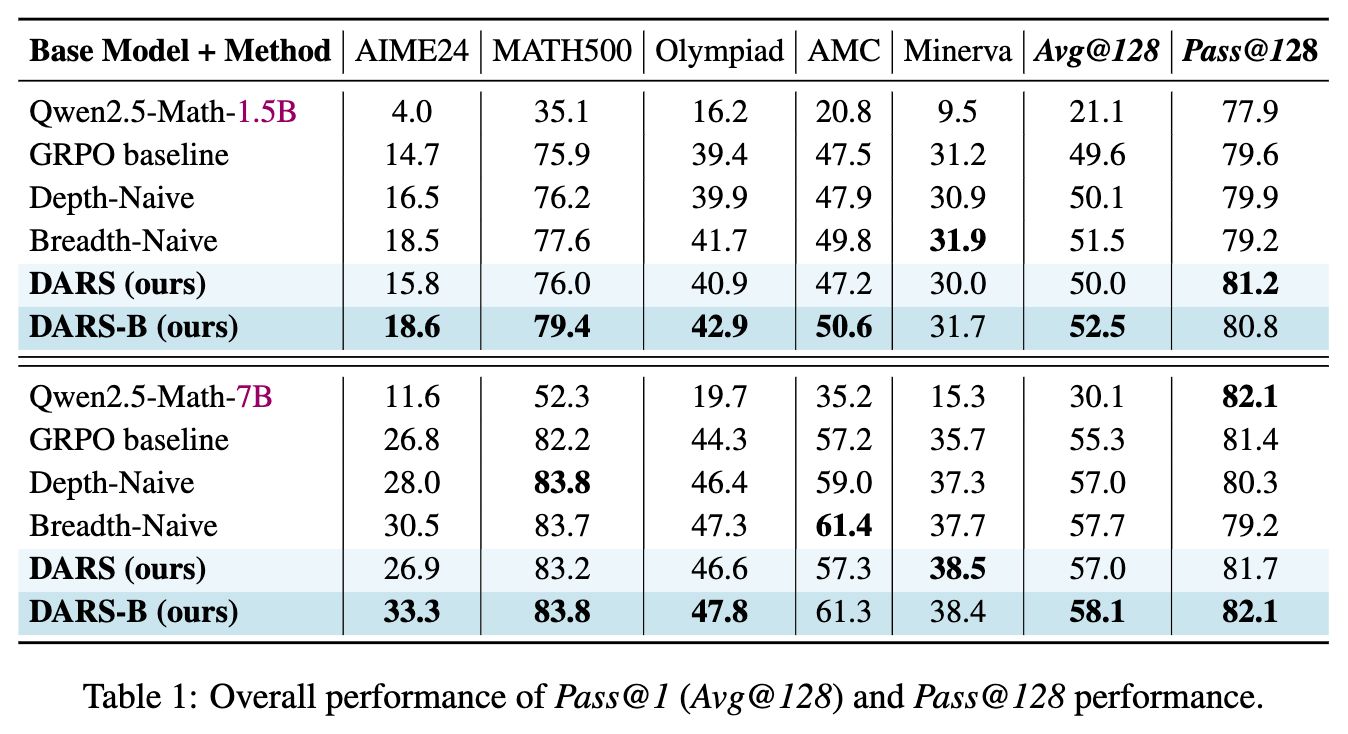
主要实验结论:
-
广度缩放效果显著:在所有模型规模和任务上,“Breadth-Naive”方法的Pass@1性能都超过了基线和“Depth-Naive”方法,证明了增加广度的直接有效性。 -
深度与广度的互补性得到验证:DARS-B的性能稳定地超过了所有单一维度优化的方法(DARS和Breadth-Naive)。这证实了论文的核心假设:深度和广度是两个互补而非竞争的资源,它们的协同对于充分释放LLM的推理潜力至关重要。 -
同时提升上限与可靠性:DARS-B不仅在Pass@1(反映单次推理的可靠性)上取得了最高分,同时在Pass@128(反映重度采样下的能力上限)上也达到了顶级水平。这表明,DARS-B的自适应策略不仅提高了快速找到正确解的概率,也提升了整个解空间中正确解的密度。
训练动态分析:
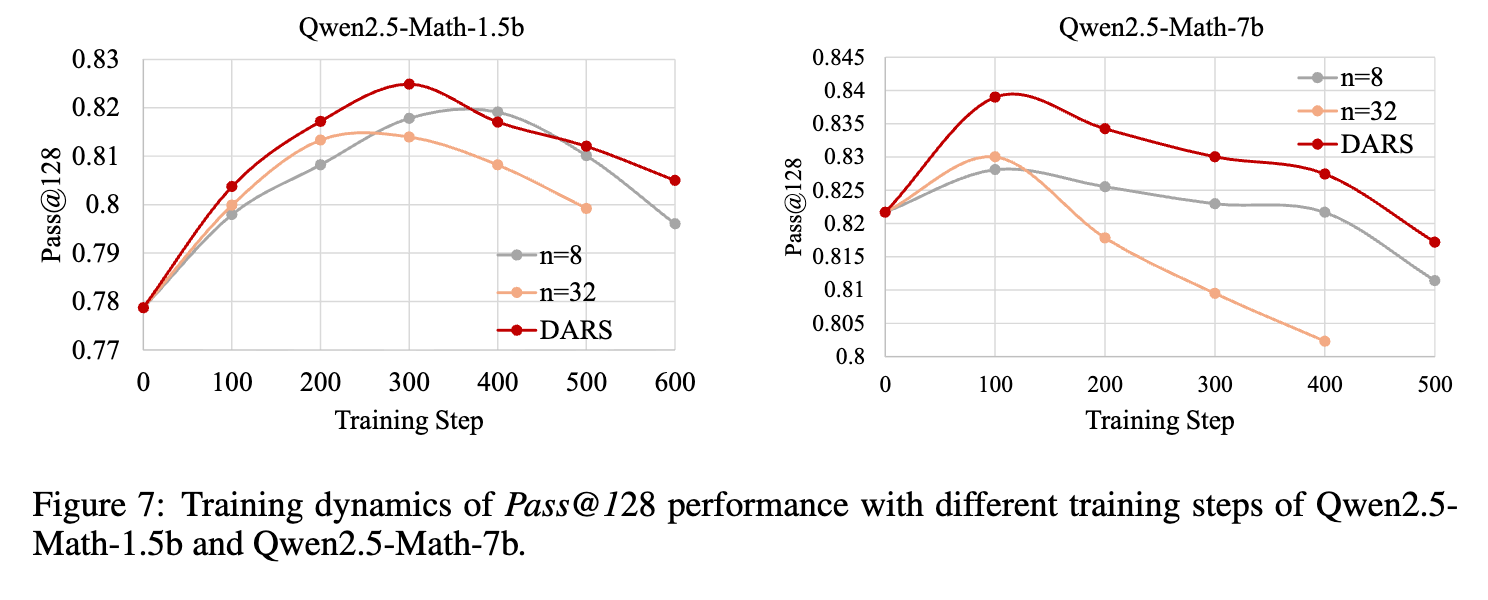
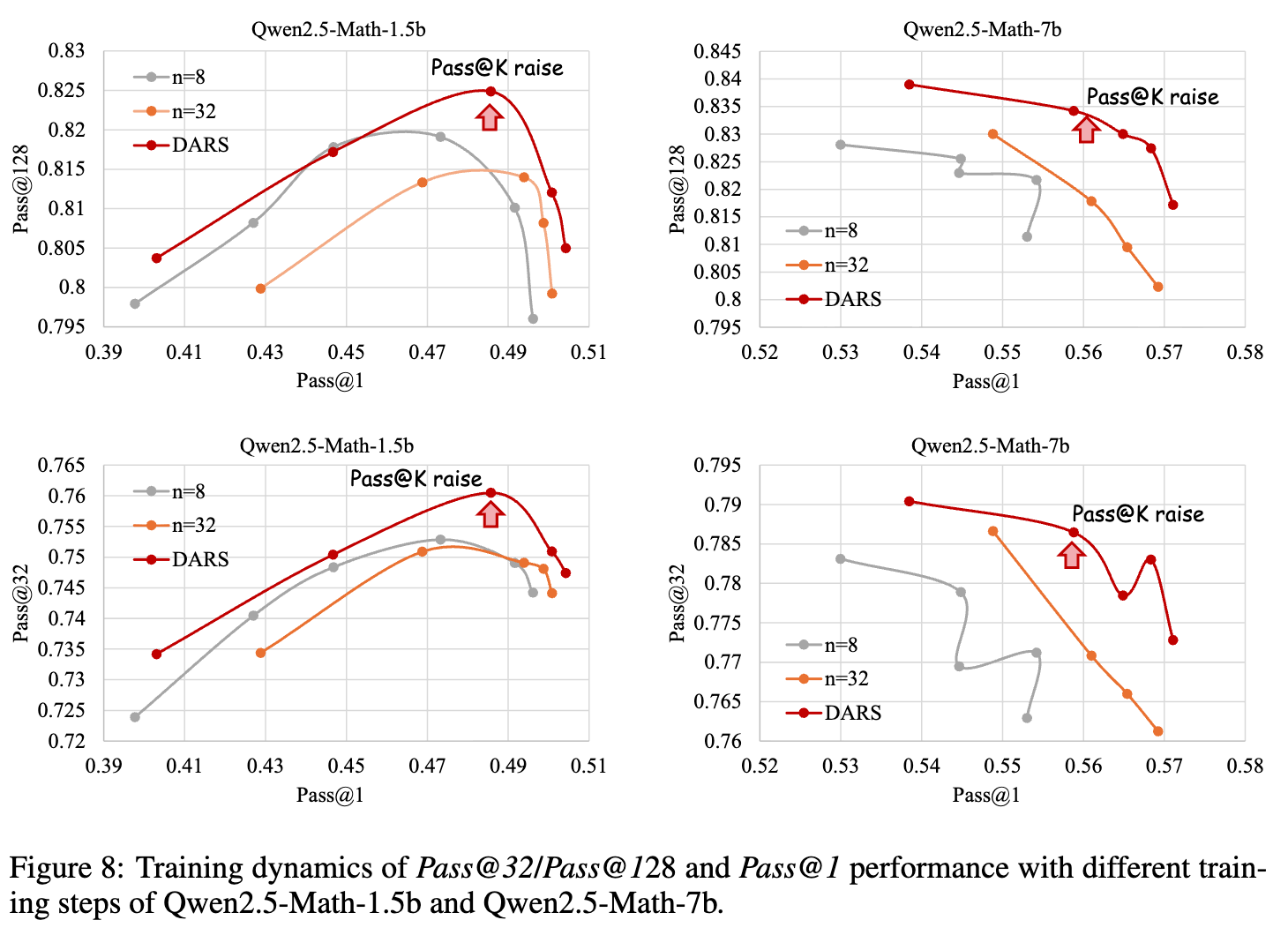
论文还通过绘制训练过程中的性能曲线(如图7和图8),展示了不同方法的动态行为。一个有趣的发现是,对于所有方法,Pass@128性能在训练初期会快速达到峰值,然后开始下降。这表明对于RLVR训练存在“过拟合”或“过度优化”的风险,持续的训练可能会损害模型在重度采样下的多样性和上限能力。而DARS在整个训练过程中,不仅能达到更高的Pass@128峰值,还能在一定程度上延缓其下降趋势。
往期文章:




