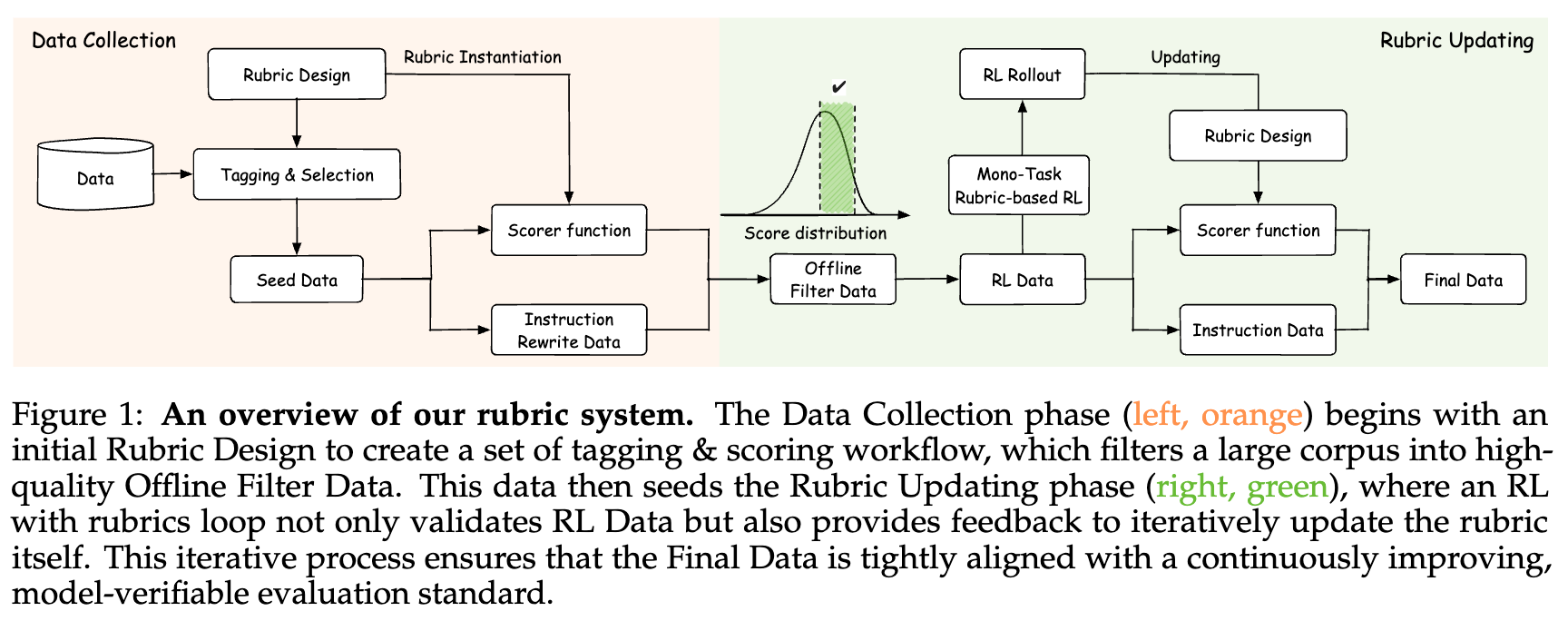
传统的优化范式,如依赖人类反馈的强化学习(RLHF)和依赖可验证奖励的强化学习(RLVR),尽管在特定任务上取得了显著成效,但它们普遍面临着标注成本高昂、适用范围受限等瓶颈。为了突破这些局限,来自字节跳动(ByteDance Seed)与南京大学的研究团队共同提出了一种名为 DuPO(Dual Preference Optimization)的创新框架。该框架基于对偶学习的思想,并创造性地引入了“广义对偶”(Generalized Duality)概念,旨在为大语言模型提供一种无需人工标注、可扩展、且通用的自监督优化路径。

-
论文标题:DuPO: Enabling Reliable LLM Self-Verification via Dual Preference Optimization -
论文链接:https://arxiv.org/pdf/2508.14460
DuPO 的核心思想在于,通过构建一个与主任务(Primal Task)互补的对偶任务(Dual Task),利用对偶任务的完成质量来生成自监督的奖励信号,进而指导主任务的学习。这一过程完全摆脱了对外部标注数据的依赖。更重要的是,DuPO 通过将任务输入分解为“已知”和“未知”两部分,并让对偶任务仅聚焦于重建“未知”部分,成功地将对偶学习的应用范围从严格可逆的任务(如机器翻译)扩展到了大量现实世界中的不可逆任务(如数学推理、代码生成等)。
论文通过在多语言翻译和数学推理这两大具有代表性的任务上进行的大量实验,充分验证了 DuPO 框架的有效性。实验结果表明,DuPO 不仅能够显著提升现有顶尖开源模型的性能,甚至在某些指标上使其表现超越了更大规模的闭源模型。此外,DuPO 还能作为一种无需训练的推理时重排(Inference-time Reranking)策略,在不改变模型参数的情况下,通过增加少量计算来换取性能的大幅提升。
1. 对偶学习
要理解 DuPO 的创新之处,我们首先需要回顾一下“对偶学习”这一经典框架。
1.1 对偶学习的核心思想
对偶学习最早由在 2016 年为机器翻译任务提出,其核心思想是利用任务之间的“对偶性”来构建一个闭环的学习过程,从而在无需平行语料的情况下实现模型性能的提升。
一个典型的例子是英汉互译。英语翻译到汉语(En → Zh)是一个任务,我们称之为主任务(Primal Task)。而汉语翻译回英语(Zh → En)则是其对偶任务(Dual Task)。这两个任务构成了一个天然的闭环。如果我们有一个英语句子 x,通过主任务模型 Tp 翻译成汉语得到 y = Tp(x),再将 y 通过对偶任务模型 Td 翻译回英语,得到 x' = Td(y)。一个直观的假设是:如果 y 是一个高质量的翻译,那么 x' 应该和原始的 x 非常接近。 这就是所谓的“循环一致性”(Cycle Consistency)。
基于这个原理,我们可以定义一个自监督的奖励信号。我们可以用一个度量函数 d(x, x') 来衡量原始句子 x 和重构句子 x' 之间的距离(例如,使用 BLEU 分数)。距离越小,说明翻译质量越高。于是,这个距离就可以作为奖励信号,用于指导和优化主任务模型 Tp 和对偶任务模型 Td。整个过程完全不需要任何已标注的英汉平行句对,仅仅利用了大量的单语语料库,展现了自监督学习的巨大潜力。
对偶学习的框架很快被扩展到其他领域,例如:
-
跨模态任务: 图像标注(Image Captioning)和文本生成图像(Text-to-Image Generation)可以构成对偶任务对。 -
知识图谱与自然语言: 知识库路径生成与自然语言问句解析也可以形成对偶关系。 -
语音处理: 文本到语音(TTS)与自动语音识别(ASR)也是一对经典的对偶任务。
1.2 传统对偶学习在 LLM 时代的挑战
尽管对偶学习的思想非常优雅,但在将其普适性地应用于现代大型语言模型的优化时,却面临着两大严峻的挑战。而这,也正是 DuPO 试图解决的核心问题。
挑战一:不可逆任务中的“对偶性缺失” (Limited Duality in Irreversible Tasks)
传统对偶学习的有效性,建立在一个很强的假设之上:主任务和对偶任务是相互可逆的。也就是说,主任务的输出 y 必须包含足够的信息,以便对偶任务能够几乎完美地重构出原始输入 x。
对于机器翻译这类任务,这个假设在很大程度上是成立的。因为一次好的翻译会保留源语言句子的绝大部分语义信息。然而,在现实世界中,LLM 需要处理的大量任务本质上是信息压缩或信息抽象的,因而是不可逆的。
让我们以一个简单的数学推理任务为例。
-
主任务 (Primal Task): 问题 x为:“一个盒子里有 3 个红球和 5 个蓝球,请问一共有多少个球?” -
输出 (Output): 模型 Tp给出答案y = 8。
现在,我们尝试构建对偶任务:从输出 y=8 重构出原始问题 x。这几乎是不可能的。答案“8”可以对应无数个可能的问题,例如:“10 - 2 等于多少?”,“氧元素的原子序数是多少?”,等等。这种从 y 到 x 的“一对多”关系,彻底打破了对偶学习所依赖的闭环,导致基于 d(x, x') 的自监督奖励信号变得不可靠。我们无法判断模型给出的答案“8”究竟是好是坏,因为它无法帮助我们还原那个唯一的问题。
这种不可逆性广泛存在于各种任务中,包括:
-
摘要生成: 从一篇长文生成摘要,摘要必然会损失原文的大量细节信息。 -
代码生成: 从自然语言需求生成代码,代码本身通常不足以反推出原始的、包含各种模糊描述和潜在假设的自然语言需求。 -
开放域问答: 很多问题的答案都是一个简洁的事实,而问题本身可能包含复杂的上下文。
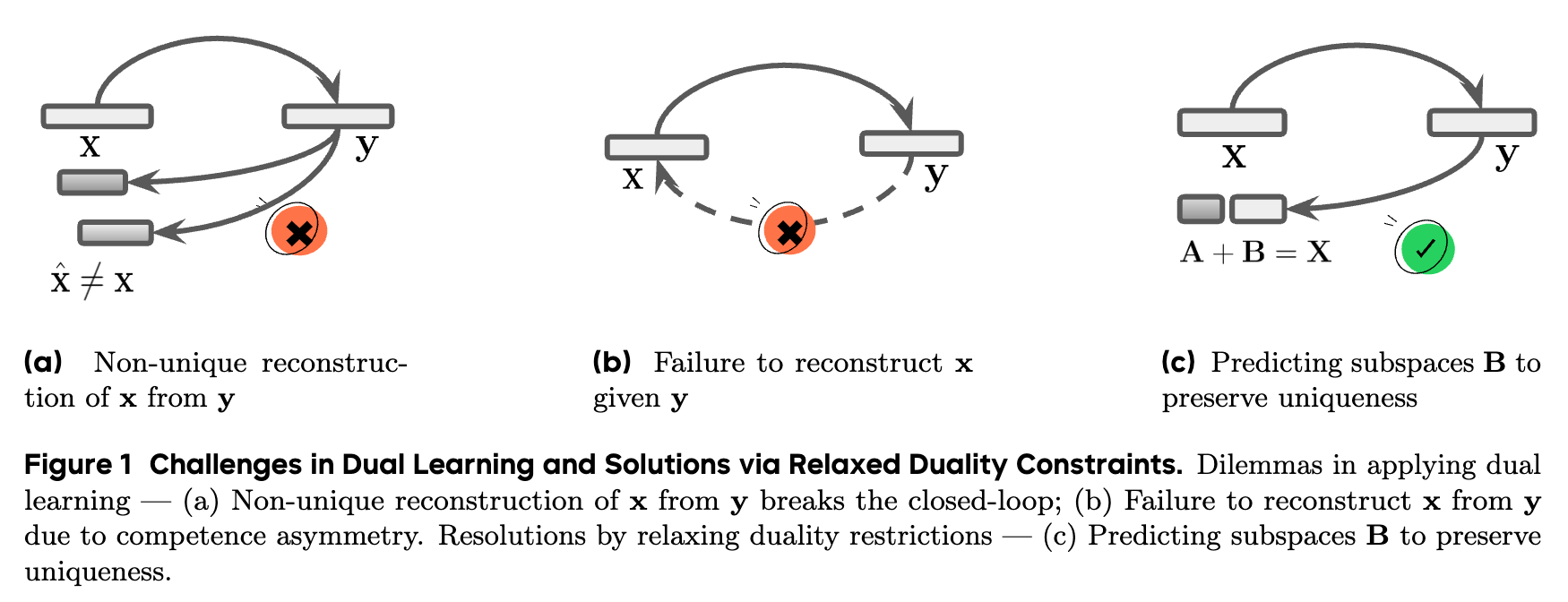
上图(a)和(b)形象地展示了这个问题。在(a)中,非唯一的重构使得闭环失效。在(b)中,由于信息损失,根本无法完成重构。这些问题使得传统对偶学习的应用范围被严重限制。
挑战二:模型的“双向能力不对称” (Bidirectional Competence Asymmetry)
即便对于那些理论上可逆的任务,LLM 在处理主任务和对偶任务时,其“能力”也往往是不对称的。
LLM 的强大能力来源于其在海量数据上的预训练。这种预训练过程赋予了模型广泛而多样的能力,但这些能力的发展是不均衡的。一个模型可能非常擅长解决数学问题(正向任务),但在给定答案和部分条件的情况下,生成一个合理的数学问题(逆向任务)的能力却可能很弱。
让我们再回到机器翻译的例子。一个在大量“英译汉”数据上微调过的模型,可能在 En → Zh 方向上表现优异。但是,它在 Zh → En 方向上的能力可能就相对平庸。在这种情况下,即使主任务模型 Tp 产生了一个非常高质量的中文翻译 y,能力较弱的对偶任务模型 Td 在进行回译时,也可能因为词汇选择不当、句法结构处理不好等原因,生成一个与原始输入 x 有偏差的回译结果 x'。
-
原始输入 (x): "The quick brown fox jumps over the lazy dog." -
高质量翻译 (y): "敏捷的棕色狐狸越过了懒惰的狗。" -
能力较弱的回译 (x'): "The agile brown fox jumps over the lazy dog."
在这个例子中,x' 将 "quick" 翻译成了 "agile",虽然语义相近,但与原文产生了偏差。如果我们严格地用 d(x, x') 作为奖励,那么这个高质量的翻译 y 就会被错误地惩罚。来自弱对偶任务的“噪声”信号,会严重干扰主任务的优化过程,降低整个框架的有效性。
这种能力的不对称性,使得即使对于可逆任务,传统对偶学习的应用也充满了不确定性。
综上所述,不可逆性和能力不对称这两大挑战,使得将传统对偶学习框架直接应用于通用 LLM 优化变得非常困难。这正是 DuPO 旨在攻克的难题。
2. DuPO 框架:广义对偶与自监督偏好优化
为了应对上述挑战,DuPO 提出了一套全新的、基于广义对偶框架(Generalized Duality Framework) 的偏好优化方法。其核心思想是对传统的对偶关系进行“松绑”,不再要求对整个输入进行严格的、可逆的重构,而是转向一种更灵活、更具普适性的互补关系。
2.1 广义对偶的核心:从重构输入到重构未知
DuPO 的第一个关键创新,是重新定义了对偶任务的目标。它不再试图从输出 y 中重构整个原始输入 x,而是将 x 分解为两个互不相交的部分:
-
已知组件 (Known Components), : 输入中我们选择在对偶任务中保持不变、作为已知信息的部分。 -
未知组件 (Unknown Components), : 输入中我们希望对偶任务去重构的部分。
于是,原始输入可以表示为 。
在 DuPO 框架下:
-
主任务 (Primal Task), : 和以前一样,是从完整的输入 生成输出 。即 。 -
互补对偶任务 (Complementary Dual Task), : 其目标不再是 ,而是利用主任务的输出 y和已知的组件 一起,来重构未知的组件 。即 。
这样一来,对偶学习的闭环就被重新构建了。我们不再比较 和 ,而是比较原始的未知组件 和重构出的未知组件 。
互补一致性原则 (Complementary Consistency Principle): 如果主任务的输出 y 是高质量的,那么利用 y 和 应该能够准确地重构出 。也就是说, 应该很小。
这个简单的转变,却带来了根本性的变化。让我们用一个“两数相加”的例子来说明这个广义对偶框架是如何工作的。
示例 1:A + B = C
-
主任务 : 计算两个数的和。
-
输入 : 两个数字 (A, B)。 -
我们进行分解:将 A视为已知组件 ,将B视为未知组件 。 -
输出 : 它们的和 C = A + B。
-
-
互补对偶任务 :
-
输入: 主任务的输出 y=C和已知组件 。 -
目标: 重构未知组件 。 -
操作: 。
-
现在,我们可以通过比较原始的未知组件 B 和重构出的 是否相等,来判断主任务的输出 C 是否正确。如果 B == \hat{B},说明 C 是一个正确的和,应该给予高奖励;反之,则给予低奖励。
这个自监督的奖励信号可以被形式化为:
其中 d(·) 是一个距离度量函数(在上述例子中,可以是一个判断是否相等的指示函数), 是一个控制奖励敏感度的超参数。
2.2 广义对偶如何解决传统挑战
DuPO 的广义对偶框架,精准地解决了传统对偶学习面临的两大难题。
1. 克服不可逆性约束 (Overcomes the Invertibility Constraint)
通过将对偶任务的目标从“重构整个输入”转变为“在已知部分信息的辅助下,重构未知部分”,DuPO 从根本上绕开了对任务严格可逆性的要求。
回到之前的数学推理例子:
-
主任务 : -
输入 : "一个盒子里有 3 个红球和 5 个蓝球,请问一共有多少个球?" -
输出 : "8"
-
现在,我们可以这样构建对偶任务:
-
分解输入: -
: "一个盒子里有 3 个红球和 [未知数量]个蓝球,一共有 8 个球。" (其中y=8也被用作已知信息) -
: 5 (蓝球的数量)
-
-
互补对偶任务 : -
输入: 和 的模板。 -
任务: 填空,即回答:“在上述条件下,蓝球的数量是多少?” -
输出 : 模型需要回答 "5"。
-
通过比较模型输出的 是否与原始的 相符,我们就能得到一个非常可靠的自监督奖励信号,来评判主任务的答案“8”是否正确。
这个设计是通用且灵活的。对于任何一个任务,我们都可以通过将输入中的某些关键实体(如数字、专有名词、关键参数等)替换为变量来构建对偶任务。这为在数学、代码、逻辑推理等大量不可逆任务上应用对偶学习打开了大门。
2. 缓解能力不对称问题 (Mitigates the Competence Asymmetry)
广义对偶框架通过两种方式显著降低了对偶任务的难度,从而缓解了模型双向能力不对称带来的问题。
-
提供强大的上下文锚点: 在对偶任务中,已知组件 充当了一个强大的上下文锚点。模型不再需要凭空从 y中重构x,而是在一个已经非常明确的、带有“脚手架”的语境下进行“填空”。这极大地约束了重构的解空间,降低了任务难度。在数学题的例子中,模型只需要做一个简单的减法,而不需要去生成一个完整的、合乎逻辑的数学问题。 -
灵活选择未知组件: 我们可以策略性地选择那些既容易重构,又对主任务答案质量有强指示作用的组件作为 。例如,在数学题中,我们通常选择数字作为 ;在翻译任务中,我们可以选择一些关键的专有名词或术语。这种灵活性确保了我们能够构建一个模型“擅长”的对偶任务,从而获得一个可靠、低噪声的奖励信号,避免了“弱对偶”问题。
通过这种方式,DuPO 巧妙地将复杂的“开放式生成”任务转化为了相对简单的“约束性填空”任务,从而保证了自监督信号的质量。
2.3 DuPO 的整体优化流程
DuPO 作为一个偏好优化框架,其核心目标是利用上述方法生成的自监督奖励 来优化 LLM。这个过程可以与多种强化学习算法相结合。
整体流程如下:
-
任务定义与分解: 对于一个给定的任务(例如,数学题),首先定义其主任务 。然后,设计一种策略来将每个输入 分解为已知组件 和未知组件 。 -
采样生成: 给定一个输入 ,让当前的 LLM(策略 )生成一个或多个候选输出 。 -
对偶任务与奖励计算: 对于每个候选输出 ,构建并执行其对应的互补对偶任务 ,得到重构结果 。通过计算 来得到该输出 的奖励分数 。 -
模型优化: 使用计算出的奖励分数,通过强化学习算法(论文中采用了 Group Relative Policy Optimization, GRPO,因为它在高维参数空间中表现稳定)来更新 LLM 的参数 ,使得模型更倾向于生成能够获得高奖励的输出。 -
迭代: 重复步骤 2-4,不断迭代优化模型。
值得注意的是,整个流程是完全自监督的,不需要任何形式的人工标注或外部验证器。模型通过“解决问题”和“反思验证”的闭环,实现了能力的自我提升。
3. 实验验证:DuPO 在两大任务上的表现
为了全面评估 DuPO 框架的有效性和通用性,论文作者在两个差异巨大且具有挑战性的任务上进行了详尽的实验:多语言机器翻译和数学推理。
3.1 实验设置
-
基础模型: 实验覆盖了多种规模和架构的强大开源模型,以验证 DuPO 的普适性。 -
翻译任务: 使用了当时最强的开源翻译模型之一 Seed-X-7B-Instruct。 -
数学推理任务: 覆盖了从 1.5B 到 7B 的多个模型,包括 DeepSeek-R1-Distill-Qwen-1.5B/7B, Qwen3-4B, 以及 OpenReasoning-Nemotron-7B 等,确保了在不同基础能力模型上的效果评估。
-
-
数据集与评测基准: -
翻译: 在包含 28 种语言、756 个翻译方向的大规模数据集上进行训练和评测,使用了 BLEU, COMET, BLEURT 等多种自动化评测指标,并额外在 Seed-X-Challenge 这个高难度基准上进行了人工评测。 -
数学推理: 在多个公开的数学竞赛数据集(如 AMC23, AIME24, AIME25)上进行评测,这些数据集代表了高中乃至奥林匹克竞赛水平的数学难题。
-
3.2 多语言翻译任务上的结果
在多语言翻译任务上,DuPO 展现出了强大的性能提升能力。
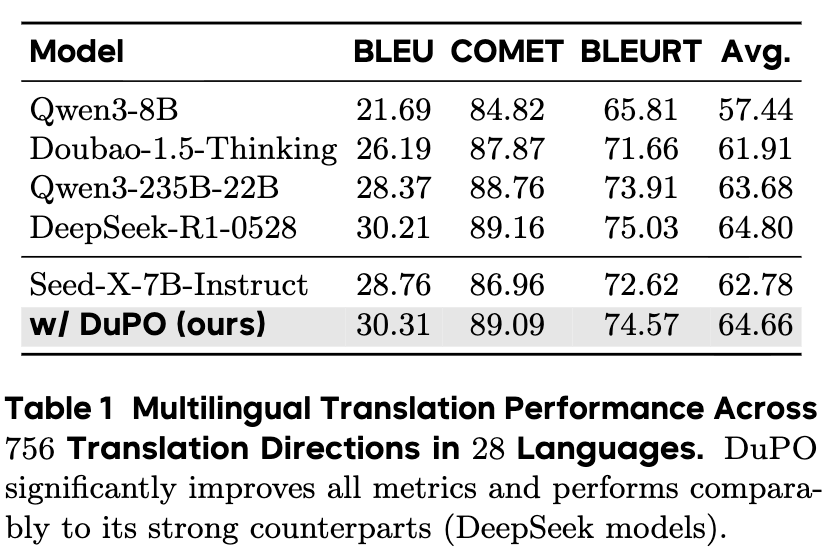
从上表可以看出,将 DuPO 应用于 Seed-X-7B-Instruct 模型后(w/ DuPO (ours)),所有自动化评测指标都得到了显著提升。平均分从 62.78 提升到了 64.66。这一性能不仅超越了像 Doubao-1.5-Thinking 和 Qwen3-235B-22B 这样更大规模的模型,甚至与当时顶尖的 DeepSeek-R1-0528 模型不相上下。
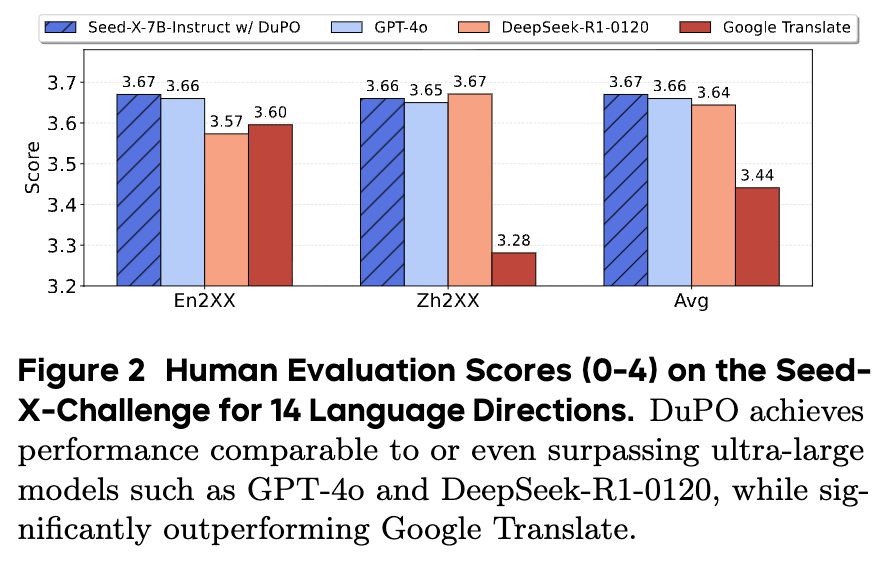
在更具挑战性的人工评测中,结果同样令人印象深刻。上图展示了在 Seed-X-Challenge 基准上的人工评分(0-4 分,越高越好)。可以看到,经过 DuPO 优化的 Seed-X-7B 模型(条纹蓝柱)在“英译其他”和“中译其他”两个方向上的表现,均能与 GPT-4o(浅蓝柱)和 DeepSeek-R1-0120(橙色柱)等顶级的超大规模闭源模型相媲美,并且显著优于强大的商业翻译系统谷歌翻译(红色柱)。
这些结果有力地证明,DuPO 提供的自监督信号是高质量的,能够有效引导模型学习更精准、更流畅的翻译能力,使其在 7B 这个参数级别上,达到了远超其规模的性能水平。
3.3 数学推理任务上的结果
数学推理是衡量 LLM 复杂推理能力的核心指标之一。DuPO 在这个不可逆任务上的表现,是其框架通用性的关键试金石。
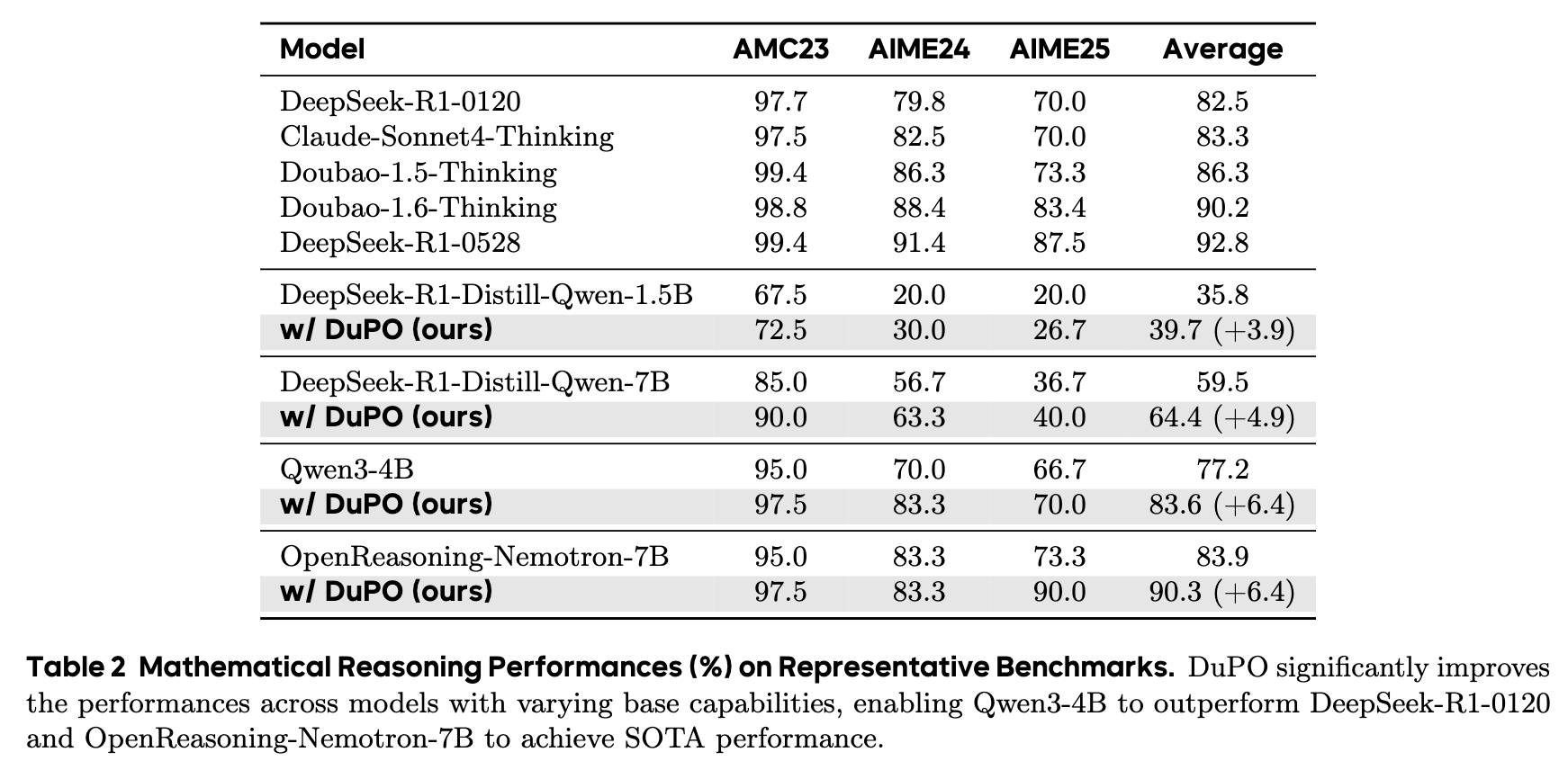
上表展示了在三个数学竞赛基准上的准确率。结果清晰地表明,DuPO 对所有不同规模、不同基础能力的模型都带来了一致且显著的性能提升。
-
对于能力最强的 OpenReasoning-Nemotron-7B 模型,DuPO 将其平均准确率从 83.9% 提升到了 90.3%,提升了 6.4 个百分点,达到了新的 SOTA 水平。 -
对于中等规模的 Qwen3-4B 模型,性能也从 77.2% 提升到 83.6%,同样是 6.4 个百分点的提升,使其超越了规模远大于它的 DeepSeek-R1-0120 模型。 -
即使是规模最小、基础能力最弱的 DeepSeek-R1-Distill-Qwen-1.5B 模型,也获得了 3.9 个百分点的稳定提升。
这种跨模型、跨规模的一致性提升,强有力地证明了 DuPO 框架的鲁棒性和有效性。它所提供的自监督信号,能够切实地增强模型的数学逻辑推理能力。
4.4 DuPO 的扩展能力与深入分析
除了上述主要结果,论文还进行了一系列深入的实验,以探索 DuPO 框架的更多潜力。
1. 跨架构的通用性 (Scales to Various Backbones Effectively)
为了验证 DuPO 不仅仅适用于特定模型家族,研究者们还在 LlaMA 架构的模型(LlaMA-3.1-8B)上进行了实验。结果显示,DuPO 同样能带来巨大的性能增益,将模型的平均分从 8.1% 提升到了 32.1%,充分证明了其作为一种通用增强技术的潜力。
2. 从零唤醒推理能力 (Incentivizes Reasoning Capability on Base Model)
一个更有趣的实验是,研究者们尝试将 DuPO 直接应用于一个未经任何指令微调的“基础模型”(Base Model)。通常认为,基础模型虽然蕴含了大量知识,但缺乏直接解决复杂任务的“能力”。
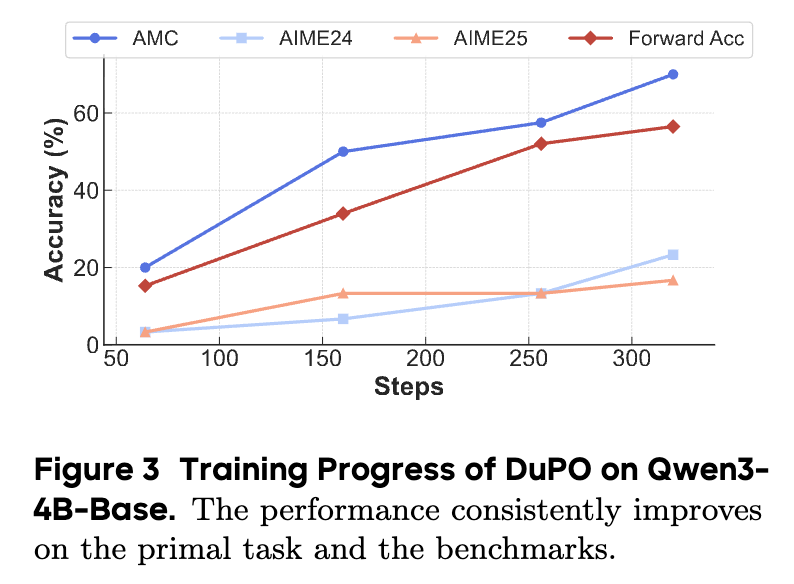
上图追踪了在 Qwen3-4B-Base 模型上使用 DuPO 进行训练时的性能变化。蓝线代表了在训练集上的准确率(“Forward Acc”),可以看到,随着训练的进行,模型的解题能力从最初的 15.2% 稳步提升到了 56.5%。更重要的是,这种能力能够很好地泛化到未见过的测试集上(其他几条线),在 AMC23, AIME24, AIME25 上的性能都得到了同步的大幅提升。这个实验表明,DuPO 的自监督信号不仅能“优化”一个已有的能力,甚至能“唤醒”和“塑造”模型潜在的复杂推理能力。
3. 作为推理时重排策略 (Scales Reasoning during Inference without Training)
DuPO 的核心机制——通过对偶任务来评估输出质量——天然地可以作为一种无需训练的推理时优化策略。这个过程被称为“重排”(Reranking)。
具体流程如下:
-
生成多个候选答案: 对于一个给定的问题,让模型采用集束搜索(Beam Search)或多次采样(Sampling)的方式,生成 K 个不同的解题路径和答案。 -
用对偶任务为候选答案打分: 对于这 K 个候选答案中的每一个,都构建并执行其对应的互补对偶任务。对偶任务的完成度(即重构 的准确率)被用作该候选答案的得分。 -
选择最优答案: 选择得分最高的那个候选答案作为最终输出。
这个过程没有对模型参数进行任何更新,只是在推理时增加了额外的计算量(K 次对偶任务的执行),来从多个可能性中“优中选优”。
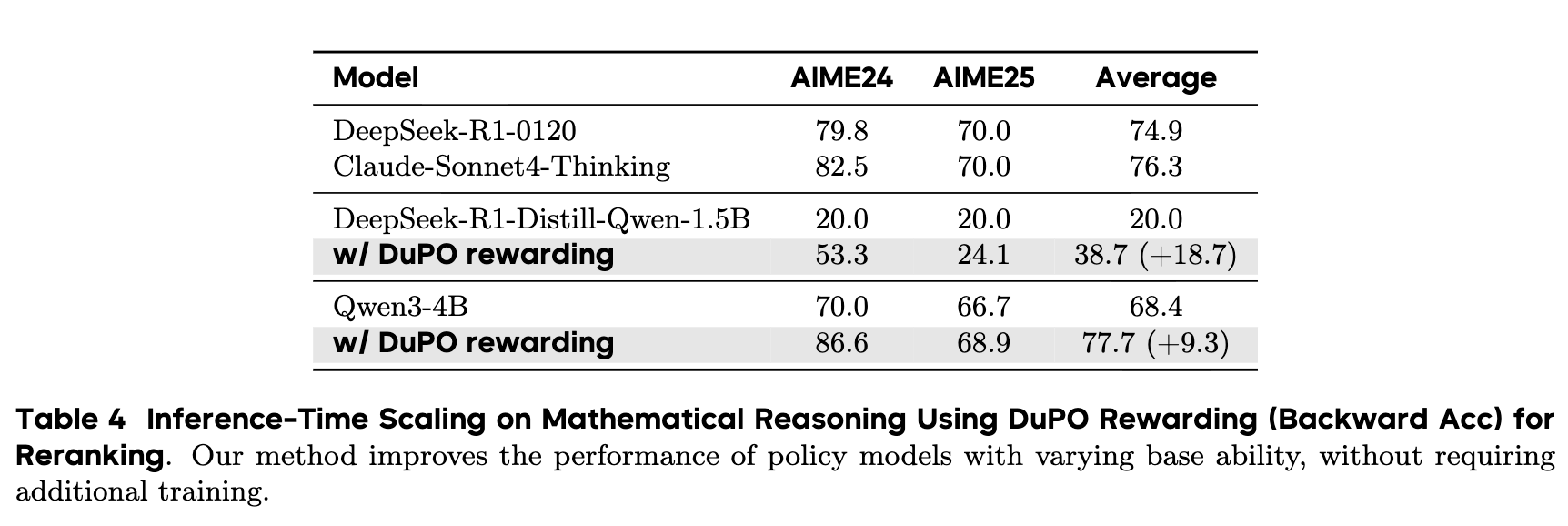
上表的结果非常引人注目。仅仅通过这种重排策略,Qwen3-4B 模型的平均准确率就从 68.4% 提升到了 77.7%,净增 9.3 个百分点。这一性能已经超越了 Claude-Sonnet4-Thinking 等顶尖闭源模型。对于能力较弱的 1.5B 模型,提升效果更为显著,增加了 18.7 个百分点。
这表明,DuPO 框架不仅是一个有效的训练方法,也是一个强大的推理时增强工具。它为如何在资源有限的情况下(例如,无法重新训练一个大模型),通过“用计算换精度”的方式来提升模型性能,提供了一条极具价值的路径。
4. 消融实验:广义对偶的必要性 (Effects of Task Duality)
为了证明 DuPO 提出的广义对偶框架(特别是对未知组件 的选择和过滤机制)是其成功的关键,研究者们进行了一项消融实验。他们移除了对偶任务生成过程中的数据过滤步骤,这意味着会引入一些质量较差的、不满足“互补一致性”的对偶任务对来进行训练。
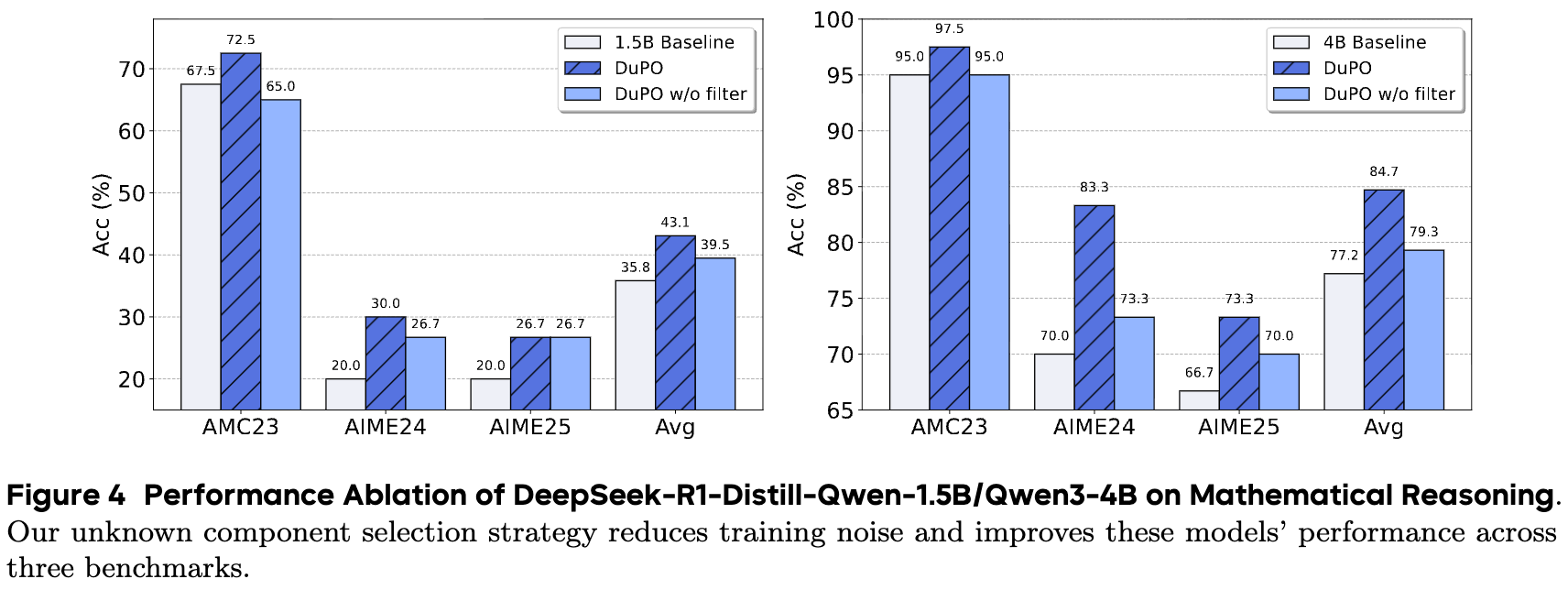
上图的结果非常清晰。无论是对于 1.5B 模型还是 4B 模型,完整版的 DuPO(蓝色柱)都显著优于没有数据过滤的“ poorer duality”版本(绿色柱)。这证明了 DuPO 框架中确保高质量对偶关系的设计是至关重要的,它直接关系到自监督奖励信号的质量,并最终决定了模型的性能提升幅度。
点评
对偶学习本身不是一个新概念,但它在LLM时代的应用一直受限于“任务可逆性”和“模型能力对称性”。本文最大的创新点在于提出了“广义对偶”(Generalized Duality)框架,通过将输入分解为“已知”和“未知”组件,巧妙地绕开了严格的可逆性要求。它将对偶任务从复杂的“完全重构”降维到了相对简单的“约束性填空”,拓宽了对偶学习的应用范围,使其能够赋能数学推理这类典型的不可逆任务,是一个重要的理论贡献。
论文的核心是构建互补对偶任务,但这需要为特定任务类型设计“已知/未知”组件的分解策略。对于数学题,策略是替换数字;对于翻译,是反向翻译。但对于更复杂的任务,如法律文书分析、创意写作、代码库级Bug修复等,如何巧妙地设计出既简单有效又能准确反映输出质量的对偶任务,本身就是一个不小的挑战。这种对偶任务的设计目前还依赖于人类的先验知识和启发式规则,其设计的优劣直接影响最终效果,这构成了一种“隐性”的设计成本和专业门槛。
DuPO在具有客观或半客观评价标准(如数学答案正确性、翻译语义保真度)的任务上表现出色。但对于那些强依赖于主观偏好的任务,例如提升对话的趣味性、共情能力,或生成特定风格的诗歌,DuPO框架可能难以应用。因为这类任务的“好坏”很难通过结构化的、一致性的重构任务来衡量。这限定了DuPO的应用范围,使其更偏向于“能力增强”,而非RLHF所擅长的“价值对齐”。
往期文章: