今天给大家解读的论文是《Do Not Let Low-Probability Tokens Over-Dominate in RL for LLMs》(arXiv:2505.12929v1),从一个新颖且此前鲜被关注的视角切入——梯度。论文的作者们发现,在标准的强化学习训练流程中,一个微妙但影响深远的现象普遍存在:低概率词元(low-probability tokens)在模型更新中产生了不成比例的巨大影响。这些罕见的词元(token)由于其巨大的梯度,往往会“过度主导”整个模型的参数更新过程,从而抑制了那些对于模型性能至关重要的高概率词元的有效学习。

-
论文标题:Do Not Let Low-Probability Tokens Over-Dominate in RL for LLMs -
论文链接:https://arxiv.org/pdf/2505.12929
这种“过度主导”现象就像合唱团里一个跑调但嗓门巨大的成员,他的声音盖过了所有唱对的人,导致整个合唱的质量下降。在 LLM 的 RL 训练中,这种主导作用阻碍了模型对概率分布的精细调整,从而影响了最终的性能。
为了解决这一关键问题,该论文提出了两种简洁而高效的创新方法:
-
优势重加权(Advantage Reweighting, AR):通过重新调整不同概率词元的优势(advantage)权重,直接削弱低概率词元的影响力。 -
低概率词元隔离(Low-Probability Token Isolation, Lopti):将更新过程分解为两个阶段,先更新低概率词元,再更新高概率词元,通过隔离来避免梯度干扰。
实验结果表明,这两种方法极大地提升了基于 GRPO 训练的 LLM 的性能,在 K&K 逻辑谜题推理任务上取得了高达 46.2% 的相对性能提升。这项工作为我们理解和优化 LLM 的强化学习过程提供了全新的见解和强大的工具。接下来,让我们一同深入这篇论文的细节,探索低概率词元主导问题的根源,并学习如何巧妙地解决它。
背景知识:强化学习与 GRPO 算法
在深入探讨论文的核心贡献之前,我们有必要先了解一些基础概念,特别是强化学习如何应用于 LLM,以及作为本文实验基础的 GRPO 算法。
强化学习优化 LLM 的基本框架
在强化学习的语境下,一个 LLM 可以被看作是一个策略(Policy),我们通常用 来表示,其中 是模型的参数。
-
状态(State):在文本生成任务中,状态通常是当前的输入提示(prompt)以及模型已经生成的部分文本序列。 -
动作(Action):模型在当前状态下,从其词汇表(vocabulary)中选择下一个词元(token)进行生成。 -
奖励(Reward):当模型生成一个完整的回答后,一个奖励函数 会对这个回答(output, )的质量进行打分,这个分数就是奖励。奖励可以来自人类的评分、一个训练好的奖励模型,或者基于规则的评价体系(例如,代码是否能成功运行,数学题答案是否正确)。
RL 的目标是调整模型参数 ,使得生成的回答能够获得最大化的期望奖励。这个过程可以表示为:
其中 是 prompt 的数据集。
从 PPO 到 GRPO:算法的演进
PPO (Proximal Policy Optimization) 是 RLHF 中最经典和常用的算法之一。它的核心思想是在更新策略时,限制新旧策略之间的变化幅度,防止模型更新步子迈得太大导致性能崩溃。PPO 的一个关键组成部分是价值模型(Value Model),它需要与 LLM 本身同步训练,用于估计在某个状态下可能获得的未来奖励的期望值。价值模型能够帮助计算优势函数(Advantage Function),从而更稳定地指导策略更新。然而,价值模型本身也拥有大量参数,这使得 PPO 的训练过程在计算资源和实现上都相当复杂。
GRPO (Group Relative Policy Optimization) 是一种旨在简化 RL 训练流程的算法,它巧妙地移除了对价值模型的需求。其核心思想是组内相对比较:
-
对于同一个 prompt ,不再只生成一个回答,而是采样生成一个包含 个不同回答的组 。 -
计算这个组内所有回答的平均奖励,以此作为对当前 prompt 的价值 的估计,即 。 -
对于组内的每一个回答 ,其优势值 就可以通过它自身的奖励与组内平均奖励的差值来估计,通常还会用奖励的标准差进行归一化:
通过这种方式,GRPO 将价值估计问题转化为了一个简单的组内统计问题,极大地降低了显存开销(约 50%)和单步训练时间(超过 60%)。
GRPO 的优化目标函数如下所示(这是论文中采用的一个变体):
其中:
-
是新旧策略在词元 上的概率比。 -
是词元 的优势值,在 GRPO 中,同一个回答中的所有词元共享相同的优势值,即 。 -
clip函数用于裁剪概率比,这是 PPO 算法的核心机制,用于限制更新幅度。 -
是 KL 散度,用于惩罚新策略 与某个参考策略 (通常是初始模型)之间的差异,以保持生成的多样性。 -
都是手动设置的超参数。
理解了 GRPO 的工作机制,我们就可以更好地理解论文所要解决的问题是在哪个环节产生的。
核心问题:低概率词元的“过度主导”现象
论文的核心洞察在于,上述的强化学习更新机制中,存在一个未被充分认识的系统性偏差。作者通过详尽的实验分析和严谨的理论推导,揭示了低概率词元是如何“绑架”模型更新过程的。
实验证据:眼见为实
作者首先通过一个在 K&K 逻辑谜题数据集上训练 Qwen2.5-7B 模型的实验,直观地展示了这一现象。
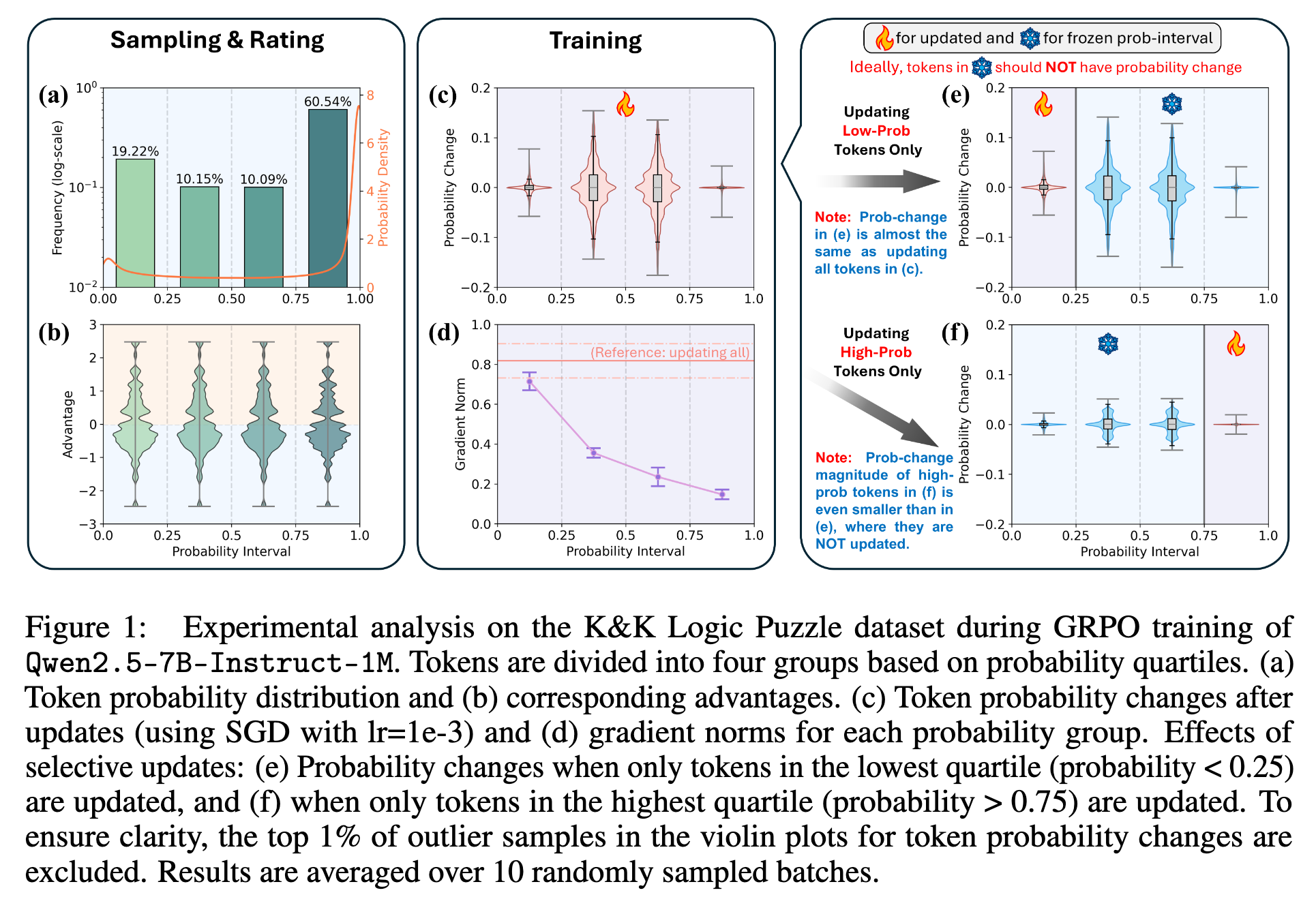
上图是这篇论文的灵魂图示,它清晰地揭示了问题的全貌。作者将生成过程中的所有词元根据其被模型预测的概率,分成了四个区间(0-0.25, 0.25-0.5, 0.5-0.75, 0.75-1.0)。
-
图1(a) 词元概率分布:可以看到,绝大多数(60.54%)被采样到的词元都属于高概率区间(>0.75),而低概率词元(<0.25)只占很小一部分(10.15%)。这符合我们的直觉:模型在生成文本时,大部分时候会选择它认为最有可能的词。 -
图1(b) 优势值分布:不同概率区间的词元所对应的优势值(Advantage)分布没有显著差异。这意味着,无论是高概率还是低概率的词元,它们对最终奖励的贡献在统计上是相似的,都可能是有益的(正优势)或有害的(负优势)。 -
图1(d) 梯度范数分布:这是最关键的发现。图1(d)展示了每个概率区间的词元所产生的梯度范数(Gradient Norm)的分布。我们能清楚地看到一个强烈的负相关趋势:词元的概率越低,其产生的梯度范数就越大。概率最低的区间(<0.25)的梯度范数中位数,要比概率最高的区间(>0.75)高出一个数量级。梯度范数的大小直接决定了该词元对模型参数更新的影响力。 -
图1(c), (e), (f) 更新效果对比: -
图1(c) 是标准情况,更新所有词元,可以看到各个概率区间的词元概率都发生了变化。 -
图1(e) 只用低概率词元(<0.25)的梯度来更新模型。惊人的是,其结果与图1(c)(更新所有词元)非常相似。甚至那些未被更新的高概率词元(>0.75),其概率也发生了显著变化。 -
图1(f) 只用高概率词元(>0.75)的梯度来更新模型。结果显示,模型参数几乎没有发生有意义的改变。高概率词元的概率变化幅度甚至比图1(e)中它们未被更新时还要小。
-
这组对比实验无可辩驳地证明了论文的观点:在 RL 更新的混合梯度中,低概率词元的梯度占据了绝对的主导地位,而数量众多且对性能至关重要的高概率词元的梯度信号则被严重压制,几乎被淹没了。
理论解释:为何会如此?
为什么词元的概率越低,梯度反而越大?作者通过对 LLM 的梯度反向传播过程进行数学推导,给出了一个简洁而深刻的解释。他们证明了对于一个 LLM 中的任意一层激活,由单个词元 产生的梯度范数 存在一个上下界。这个界可以简化地理解为:
其中 是该词元的概率。
这个结论非常直观:
-
当一个词元的概率 趋近于 1 时,意味着模型对这个选择非常确定。此时 趋近于 0,梯度也几乎为零。这很好理解,模型对于已经“学会”的东西,自然不需要太大的调整。 -
当一个词元的概率 趋近于 0 时,意味着模型认为这个选择非常“意外”。此时 趋近于 1,梯度也相应地变得非常大。模型会对这种“意外”做出强烈的反应。
在 RL 训练的每一步中,模型都会处理成千上万个词元。这些词元的梯度被平均(或求和)后,用于更新模型的数亿甚至数十亿参数。由于低概率词元的梯度在数量级上远大于高概率词元,即使它们的数量很少,它们的“声音”也会在平均过程中盖过其他所有词元,从而主导了参数更新的方向。
这种主导作用的负面影响是什么?作者通过图3进一步揭示。
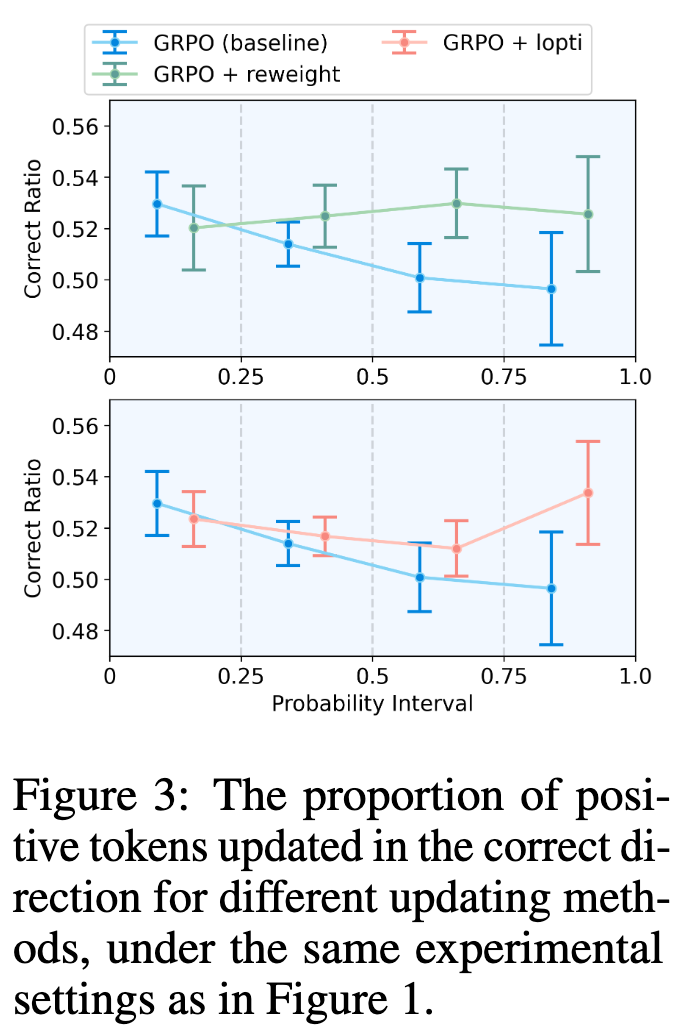
理论上,对于一个优势值为正的词元(即它对好的结果有贡献),一次成功的 RL 更新应该使其概率上升。图3(蓝线,基线GRPO)显示,随着词元概率的增加,其概率被正确提升的比例反而下降了。对于概率大于 0.75 的正优势词元,其更新方向正确的比例甚至略低于 50%,这意味着更新对它们来说弊大于利,就像在进行随机扰动。
这证明了低概率词元的梯度干扰,使得模型无法对高概率词元进行精细、正确的调整。而这些高概率词元往往构成了语言流畅性和逻辑连贯性的骨架,对它们的有效学习至关重要。
解决方案:优势重加权与低概率词元隔离
识别了问题的根源后,作者对症下药,提出了两种简单而巧妙的解决方案。
方法一:优势重加权 (Advantage Reweighting, AR)
既然问题出在低概率词元的影响力过大,一个最直接的想法就是“削弱”它们。优势重加权(AR)正是基于这一思想。它通过修改每个词元的优势值来实现对梯度的间接调整。
具体来说,原始的优势值 会被重新计算为一个新的优势值 :
其中 是一个介于 [0, 1] 之间的超参数。这个公式的核心在于引入了一个与词元概率 线性相关的权重项 。
-
当 时,权重项为 1,公式退化为原始的 GRPO,没有任何改变。 -
当 时: -
对于一个高概率词元( 接近 1),权重项接近 。 -
对于一个低概率词元( 接近 0),权重项接近 。
-
通过设置一个合适的 (例如 0.3),低概率词元的优势值会被按比例缩小,从而其在梯度计算中的影响力也被相应削弱。如上文图3的上半部分所示(橙色线),应用了优势重加权后,高概率词元的更新正确率得到了显著提升,证明了该方法的有效性。
AR 方法的最大优点是计算开销极小。它仅仅是在计算优势值时增加了一个简单的乘法操作,几乎不带来任何额外的计算负担,非常易于在现有 RL 框架中实现。
方法二:低概率词元隔离 (Low-Probability Token Isolation, Lopti)
Lopti 提供了另一种解决思路:与其在“大锅烩”里调整权重,不如直接将不同类型的词元分离开,进行“小灶”处理。这种方法的思想是隔离梯度,分步更新。
具体流程在算法1中有详细描述:

Lopti 的核心步骤如下:
-
划分词元:首先,预先设定一个概率阈值 (例如 0.5)。在一个 mini-batch 中,所有词元根据其旧概率 被分为两组: -
低概率组: -
高概率组:
-
-
第一阶段更新(低概率优先):模型仅使用低概率组的词元及其对应的优势值进行一次参数更新。 -
第二阶段更新:接着,模型仅使用高概率组的词元及其对应的优势值进行第二次参数更新。
这里的更新顺序至关重要,必须是先低后高。其背后的直觉非常精妙,蕴含着一种自适应调节机制:
-
在第一阶段,低概率词元的更新会间接影响整个模型的概率分布,包括那些尚未被更新的高概率词元。 -
假设一个正优势的高概率词元,在第一阶段更新中受到了“好的”影响(即它的概率被间接提升了),那么根据 的梯度关系,它在第二阶段更新时产生的梯度将会变得更小。这是一种良性循环,模型确认了正确的方向,就不再需要大的调整。 -
反之,如果一个正优势的高概率词元受到了“坏的”影响(概率被间接降低了),那么它在第二阶段产生的梯度将会变得更大,从而获得更多的“关注”,有机会“纠正”第一阶段带来的负面扰动。
这种机制使得 Lopti 能够更智能地平衡不同词元间的学习。如图3下半部分所示(绿色线),Lopti 同样显著提升了高概率词元的更新正确率。
Lopti 方法的代价是需要进行两次独立的模型更新,因此其训练时间约是标准 GRPO 的两倍。这是一个在效果和效率之间的权衡。
值得注意的是,这两种方法可以同时使用,有可能达到更好的效果,这在后续的实验中也得到了验证。
实验验证与结果分析
为了验证所提方法的有效性和泛化性,作者在两类具有挑战性的任务上进行了详尽的实验:逻辑推理和数学解题。
实验一:K&K 逻辑谜题 (Knights and Knaves Logic Puzzles)
K&K 逻辑谜题是一类经典的逻辑推理问题,要求根据一群“骑士”(只说真话)和“无赖”(只说假话)的陈述来判断每个人的身份。这类任务高度考验模型的逻辑推理能力,并且由于其未在预训练数据中出现,非常适合评估模型的“持续学习”能力。
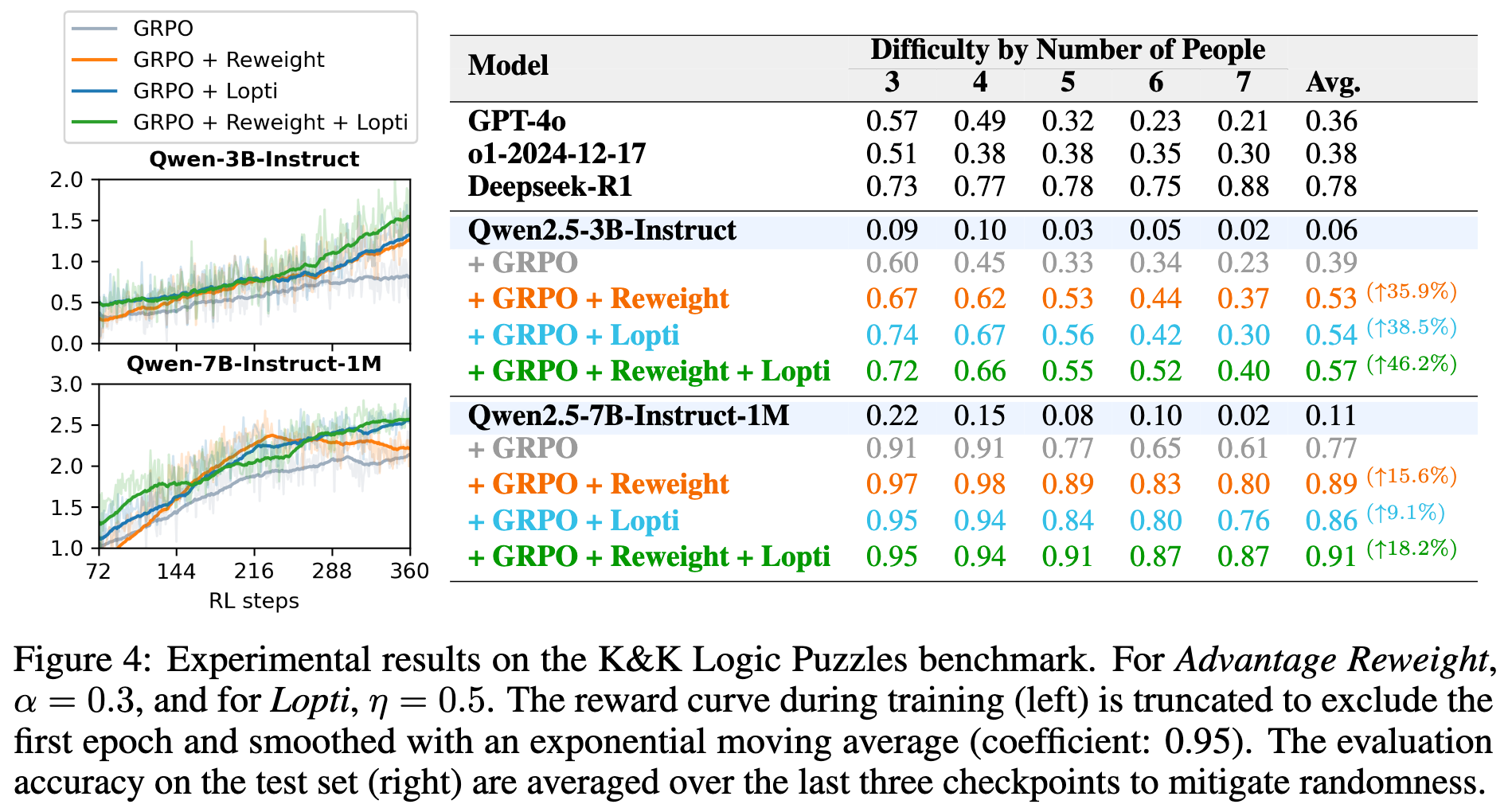
上图右侧的表格展示了在不同难度(由人数决定)的 K&K 谜题上的测试准确率。
-
基线模型:无论是 Qwen2.5-3B 还是 7B 模型,在经过标准 GRPO 训练后,性能都有了显著提升(例如 3B 模型从平均 0.06 提升到 0.39),证明了 RL 在激发推理能力上的有效性。 -
性能提升: -
单独使用 Advantage Reweight (AR) 或 Lopti 都能带来巨大的性能提升。以 3B 模型为例,AR 和 Lopti 分别将平均准确率提升到了 0.53 和 0.54,相对基线 GRPO 分别提升了 35.9% 和 38.5%。 -
当两者结合使用时,效果最好。3B 模型达到了 0.57 的平均准确率,相对基线提升了 46.2% 。7B 模型也观察到了类似的显著提升。
-
-
难度挑战:可以看到,随着谜题人数的增加,任务难度急剧上升,所有模型的性能都有所下降。但在更困难的任务上,新方法带来的性能优势更加明显,这说明它们在高难度、正样本稀疏的场景下尤为有效。
语言学分析
为了更深入地理解模型性能提升的内在原因,作者还进行了一项有趣的语言学分析。他们统计了模型在生成推理过程(Chain-of-Thought)时,不同类别词语的频率与最终回答得分的关系。
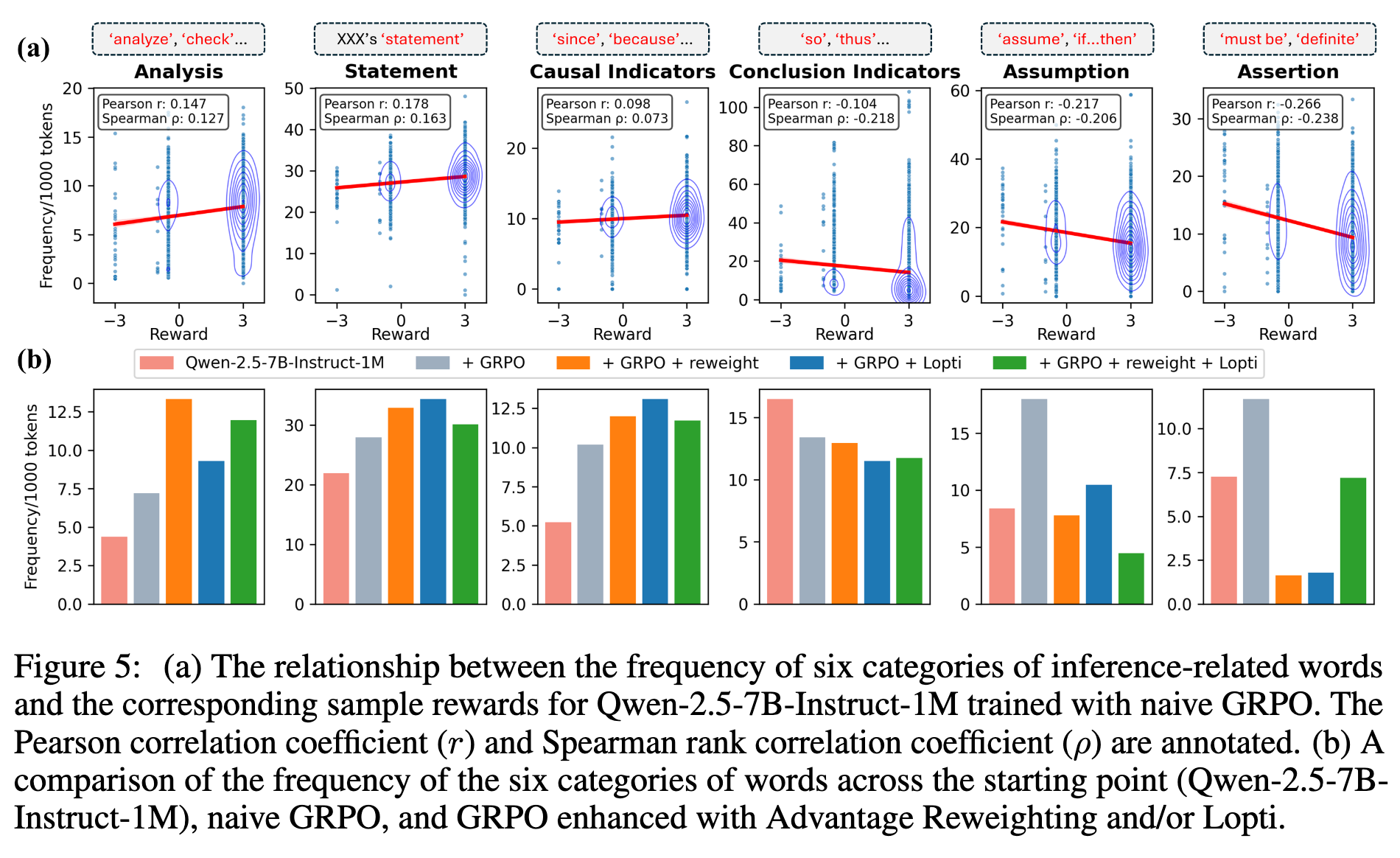
-
图5(a) 显示,在使用标准 GRPO 训练的模型中,“分析”类(如 'analyze', 'check')、“陈述”类(如 'statement')和“因果指示”类(如 'since', 'because')词语的频率与奖励呈正相关。这意味着模型进行越多的分析和因果推理,越有可能得到正确答案。 -
相反,“结论指示”类(如 'so', 'thus')、“假设”类(如 'assume')和“断言”类(如 'must be', 'definite')词语的频率与奖励呈负相关。这可能意味着过于草率的假设和武断的结论是导致错误推理的原因。 -
图5(b) 对比了不同方法训练后,这些词语的频率。结果非常清晰:经过 AR 和/或 Lopti 优化的模型,其生成文本中正相关词语的频率显著更高,而负相关词语的频率则显著更低。
这组分析提供了强有力的定性证据,表明所提出的方法不仅仅是提升了测试分数,更是实实在在地改善了模型的推理行为模式,使其更倾向于进行严谨、有条理的逻辑分析。
实验二:数学推理数据集
为了检验方法的泛化能力,作者还在两个数学相关的数据集(DSR-Uniform 和 ORZ)上进行了实验,并在多个数学基准测试(如 Olympiad Bench, MATH-500, AIME 2024 等)上进行评估。
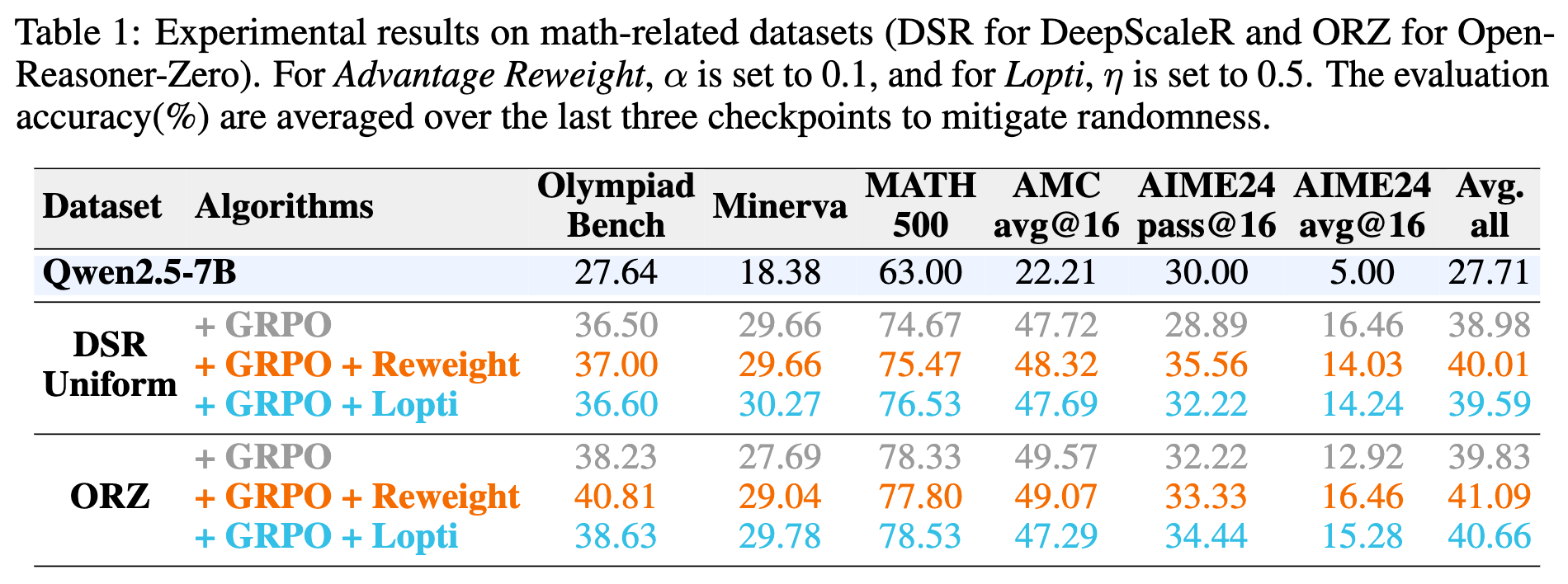
实验结果(如上表所示)表明:
-
在数学任务上,AR 和 Lopti 同样能带来稳定且一致的性能提升。例如,在 DSR-Uniform 数据集上,基线 GRPO 的平均准确率为 38.98%,而加入 AR 后提升至 40.01%。 -
一个有趣的发现是,在数学任务中,联合使用 AR 和 Lopti 并没有带来额外的收益。因此,对于这类任务,作者建议单独使用其中一种方法(尤其是计算开销更低的 AR)。
这部分实验证明了论文方法的普适性,说明解决低概率词元主导问题对于提升 LLM 在不同领域的推理能力都具有积极作用。
消融研究:探究成功的关键
为了确保实验结论的可靠性,并深入理解方法为何有效,作者进行了一系列消融研究。
-
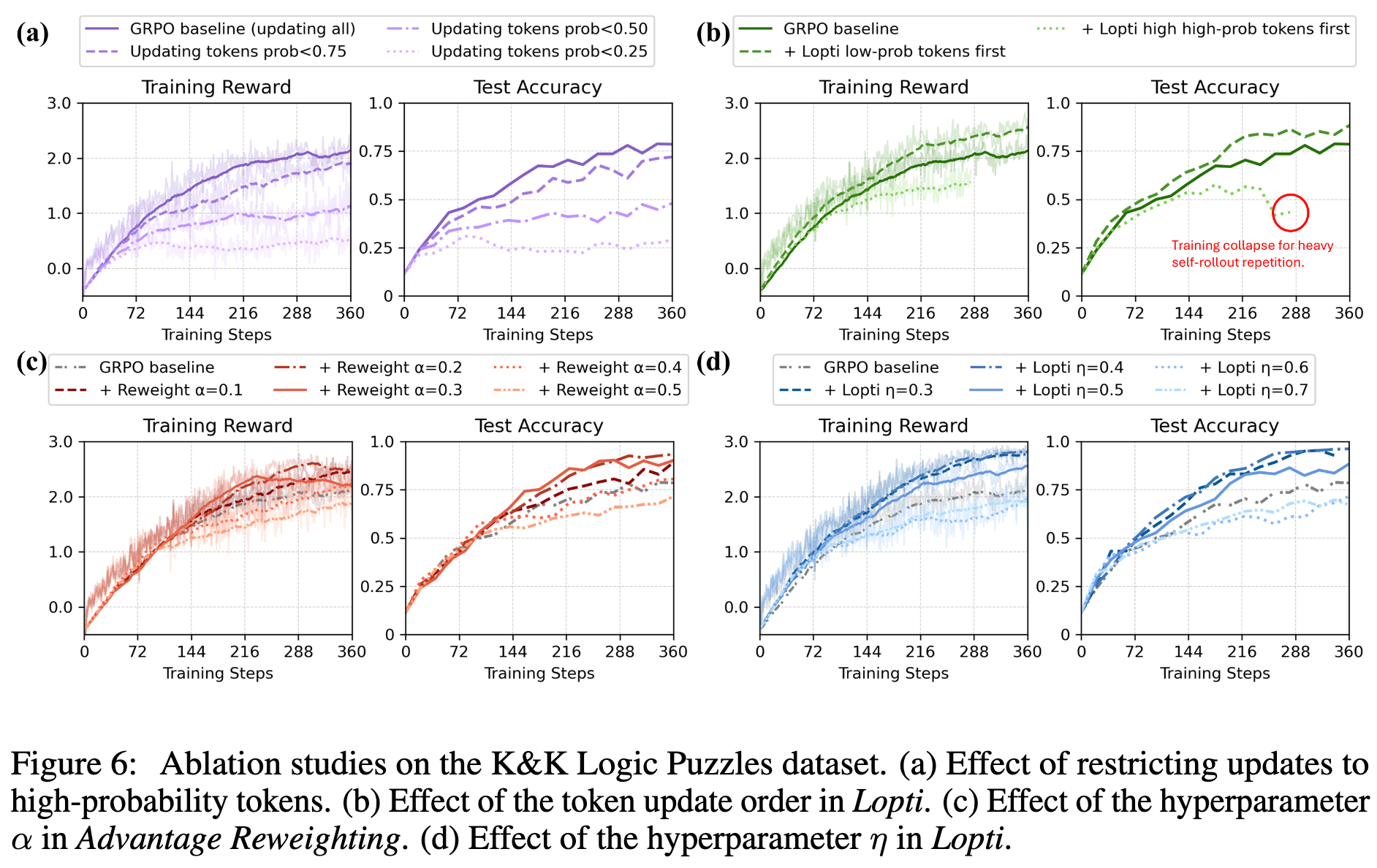
高概率词元至关重要:有人可能会想,既然高概率词元的梯度那么小,我们干脆在更新时忽略它们,只用中低概率的词元不就行了吗?图6(a)的实验否定了这一想法。结果显示,如果屏蔽掉高概率词元,模型的性能会比基线 GRPO 更差。这说明高概率词元虽然梯度信号微弱,但它们对模型的贡献是不可或缺的。我们的目标是平衡梯度影响,而非简单地抛弃一部分。
-
Lopti 的更新顺序是成功的关键:Lopti 的核心是“先低后高”的更新顺序。如果把顺序颠倒,变成“先高后低”,会发生什么?图6(b)给出了答案——训练过程在第四个 epoch 后彻底崩溃,性能远差于基线。这个实验强有力地验证了前文所述的 Lopti 自适应调节机制的直觉:只有先处理高梯度、影响大的低概率词元,才能为后续高概率词元的精细调整创造条件。 -
超参数的敏感性:图6(c)和6(d)展示了模型性能对 AR 的超参数 和 Lopti 的超参数 的敏感性。结果表明,这两个参数需要在一定的合理区间内取值才能达到最佳效果。例如,在K&K任务上, 的推荐范围是 [0.2, 0.3], 的推荐范围是 [0.3, 0.5]。这也提醒实践者,在使用这些方法时需要进行适当的超参数调整。
点评
本文通过梯度范数对比、以及选择性更新(只更新低/高概率词元)的对比实验,证明了传统RLVR“低概率词元的主导作用”和“高概率词元信号被淹没”的事实:低概率词元的梯度干扰,使得模型无法对高概率词元进行精细、正确的调整。而这些高概率词元往往构成了语言流畅性和逻辑连贯性的骨架,对它们的有效学习至关重要。
新方法引入了两个关键超参数:AR 的 和 Lopti 的 。从消融研究(Figure 6)中可以看出,模型的最终性能对这两个超参数的取值相当敏感,存在一个最佳的“甜点区间”。这意味着在将这些方法应用到新的模型、新的任务或新的数据集时,可能需要投入额外的精力进行超参数搜索和调整,这在一定程度上增加了方法的使用门槛。
往期文章:




