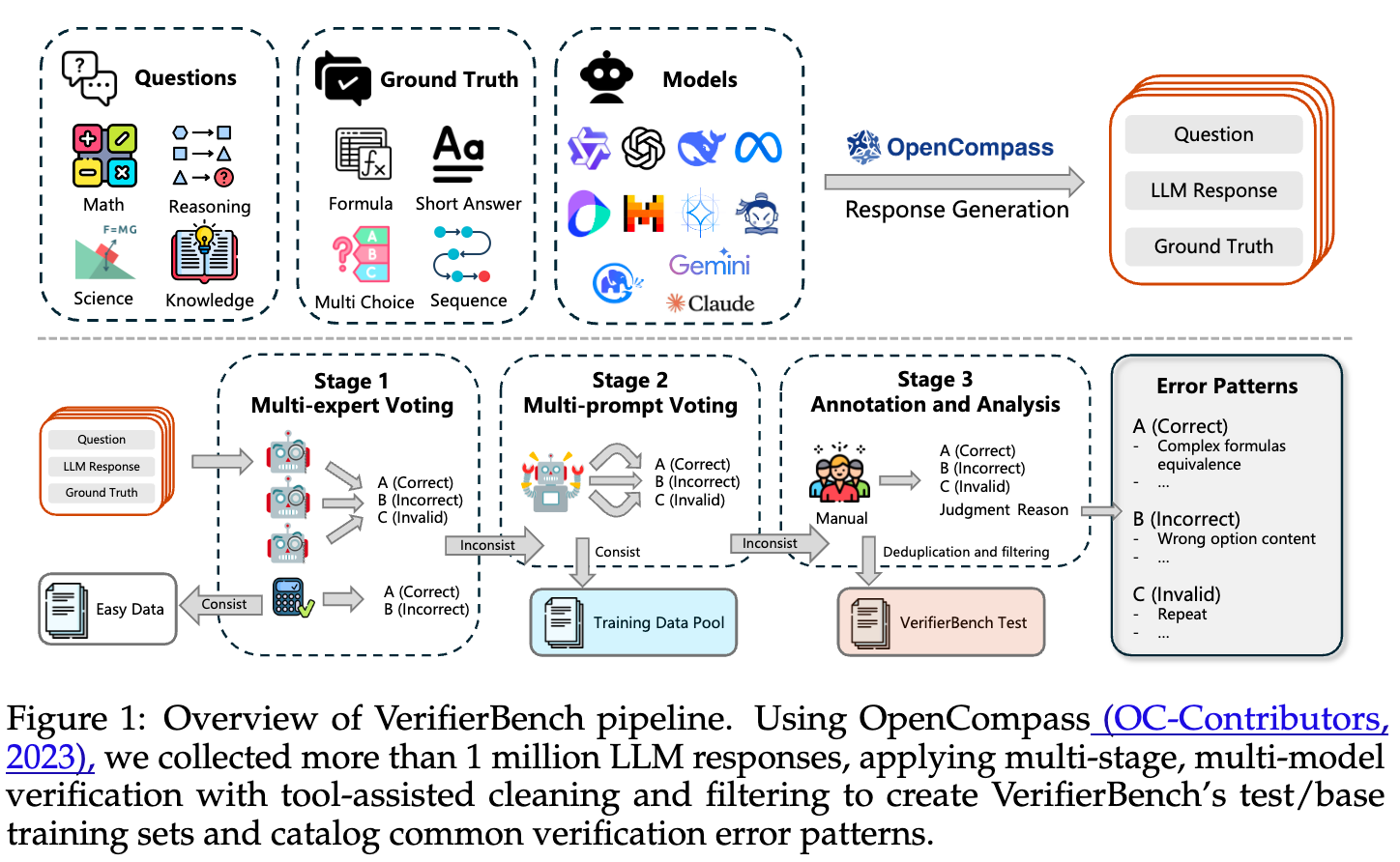
在大型语言模型 (LLM) 的世界里,如何让模型更好地理解并遵循人类的指令,即所谓的“对齐”,始终是核心议题。目前,主流的技术路线分为两条:监督微调(Supervised Fine-Tuning, SFT)和基于人类反馈的强化学习 (Reinforcement Learning from Human Feedback, RLHF)。
SFT 简单直接,就像教一个学生做题,直接给他看大量的“问题-标准答案”对,让他去模仿。 这种方法易于实现,能让模型快速学会特定任务的“套路”。然而,它的弊病也十分明显——模型容易“死记硬背”,学到的知识很“脆”,泛化能力差,遇到没见过的题型就可能“翻车”。
相比之下,RLHF 更像是请一位教练来指导学生。它不直接给出答案,而是对模型的不同回答给出评分(奖励),让模型在不断的尝试和反馈中,自己探索出更好的策略。但它的问题在于,训练过程极其复杂,需要耗费大量的计算资源,对超参数敏感,且依赖一个高质量的奖励模型,这在很多场景下难以实现。
那么,有没有一种方法,能够兼具 SFT 的简单高效和 RL 的强大泛化能力呢?
一篇来自东南大学、加州大学洛杉矶分校等机构的最新研究论文《On the Generalization of SFT: A Reinforcement Learning Perspective with Reward Rectification》给出了一个令人拍案叫绝的答案。研究者们不仅从理论上揭示了 SFT 泛化能力不足的根本原因,还提出了一种名为 动态微调 (Dynamic Fine-Tuning, DFT) 的方法。惊人的是,这个方法的核心改动仅仅是一行代码,却在多个极具挑战性的数学推理任务上,显著超越了标准 SFT,其性能提升甚至可以与更复杂的 RL 方法相媲美。

-
论文标题:On the Generalization of SFT: A Reinforcement Learning Perspective with Reward Rectification -
论文链接:https://arxiv.org/pdf/2508.05629
本文将带你深入解读这篇论文,看看 DFT 是如何用“一行代码”撬动 SFT 的性能,实现其“文艺复兴”的。
SFT的“隐痛”:为何它在泛化上输给强化学习?
要解决问题,首先要找到根源。论文的核心洞见,在于首次从强化学习的视角对 SFT 进行了重构和剖析。
我们知道,SFT 的目标是最小化模型在专家示范数据上的负对数似然,也就是交叉熵损失。其目标函数如下:
其中, 是输入(问题), 是专家给出的标准答案, 是模型生成标准答案的概率。SFT 的梯度更新就是让模型更倾向于输出概率更高的标准答案。
论文的作者们通过一个精妙的数学变换——重要性采样 (Importance Sampling),将 SFT 的梯度表达式改写成了与强化学习中的策略梯度 (Policy Gradient) 极其相似的形式。
策略梯度的通用形式是这样的:
它表示,模型根据当前策略 采样一个动作(回答),然后环境会给出一个奖励 ,梯度更新的方向是让获得高奖励的动作的概率变大。
经过推导,论文指出 SFT 的梯度可以等价地看作一种特殊的策略梯度:
这个公式揭示了 SFT 的“隐痛”所在:
-
隐式奖励 (Implicit Reward) 极其稀疏:SFT 的奖励函数 是一个示性函数 。这意味着,只有当模型生成的答案 与标准答案 一字不差完全相同时,才能获得奖励 1,否则奖励为 0。这种非黑即白的奖励机制过于严苛和稀疏,无法对那些“部分正确”或“有价值”的回答给予鼓励。
-
病态的重要性权重 (Pathological Importance Weight):SFT 的梯度中存在一项 ,即模型生成该答案概率的倒数。这个权重是导致 SFT 泛化能力差的罪魁祸首。当模型对于某个正确的专家答案 分配的概率 很低时(即模型认为这个答案很“冷门”或很难),它的倒数就会变得非常大。这会导致梯度更新的方差极大,优化过程变得非常不稳定。模型会过度地关注那些罕见的、难以拟合的样本,试图“死记硬背”下来,而忽略了对数据中普遍规律的学习,最终导致过拟合(Overfitting)。
简单来说,SFT 就像一个有强迫症的老师,他不仅要求学生必须写出标准答案,还对那些学生觉得最难、最不可能的题目给予了不成比例的超高关注度,逼着学生去钻牛角尖,而不是掌握通用的解题方法。
DFT的“神来之笔”:动态奖励修正
找到了病根,如何“对症下药”?论文提出的 DFT 方法,其思路简单而优雅。
既然问题出在那个病态的重要性权重 上,那我们想办法把它“修正”掉不就行了?DFT 的做法是,在计算损失时,直接给原始的 SFT 损失乘上一个修正项,这个修正项恰好就是模型自身的概率 。
这样,修正后的 DFT 梯度就变成了:
其中 是 stop-gradient 算子,意味着在反向传播计算梯度时,不对这个修正项求导,只把它当作一个动态调整的权重。
于是,DFT 的损失函数就变成了一个简单的重加权损失 (reweighted loss):
在实践中,为了计算稳定,这个操作在 token 级别进行:
这个改动意味着什么?
从强化学习的角度看,原来的奖励是 ,现在被修正成了 。这意味着,对于所有正确的专家示范,奖励不再是固定的 1,而是模型当前认为这个示范的“可信度”。对于模型已经很有把握的“简单”样本,奖励接近 1;对于模型觉得很困难的“冷门”样本,奖励接近 0。
这彻底改变了 SFT 的学习动态:它不再疯狂地去拟合那些低概率的困难样本,避免了梯度爆炸和过拟合。相反,它让模型更加稳定地从整个数据集学习,促进了泛化。
更有趣的是,论文指出 DFT 的损失函数 与著名的 Focal Loss 在形式上恰好相反。Focal Loss 旨在让模型关注难分类的样本( 较小),而 DFT 则有意地降权 (downweight) 了模型认为难的样本,这可能反映了在 LLM 时代,过拟合比欠拟合是更需要关注的问题。
惊人的实验效果:DFT 全面“碾压”SFT
理论说得再好,也要靠实验结果说话。论文在多个模型和极具挑战性的数学推理基准上,对 DFT 进行了严苛的验证。
实验设置:
-
模型:涵盖了多种主流架构和尺寸,包括 Qwen2.5-Math-1.5B/7B、LLaMA-3.2-3B/3.1-8B 和 DeepSeekMath-7B。 -
数据集:使用了包含约 86 万个数学问题和解题步骤的大规模数据集 NuminaMath CoT 进行训练。 -
评估基准:选用了五个公认的高难度数学推理基准,包括 Math500、Minerva Math、Olympiad Bench、AIME 2024和 AMC 2023。这些基准涵盖了从高中到奥林匹克竞赛级别的数学难题。
核心结果:
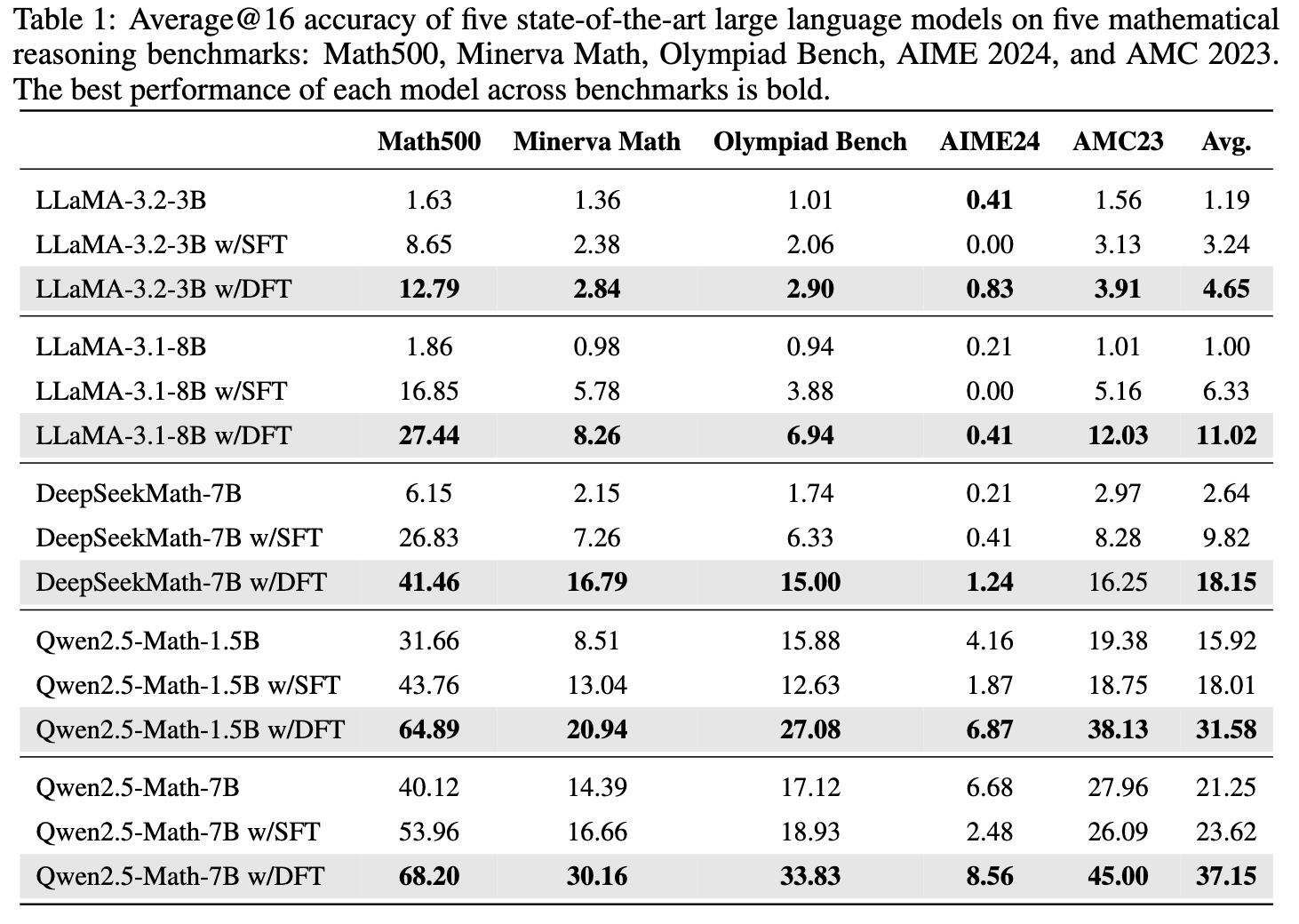
从表格数据可以清晰地看到:
-
DFT 性能增益巨大:与基础模型相比,DFT 带来的平均性能提升远超 SFT。例如,在 Qwen2.5-Math-1.5B 上,SFT 仅提升了 2.09 个百分点,而 DFT 带来了高达 15.66 个百分点的巨大提升,是 SFT 的 5.9 倍以上。 这个规律在所有测试模型上都成立。 -
SFT 在难题上可能“帮倒忙”,而 DFT 力挽狂澜:在 Olympiad Bench 和 AIME24 这样的高难度基准上,标准 SFT 甚至会导致性能下降。例如,在 Qwen2.5-Math-1.5B 上,SFT 让模型在 Olympiad Bench 上的准确率从 15.88% 降至 12.63%。而 DFT 则将其提升至 27.08%,实现了超过 11 个点的增益。 这充分证明了 DFT 优异的泛化能力和鲁棒性。 -
学习效率更高:
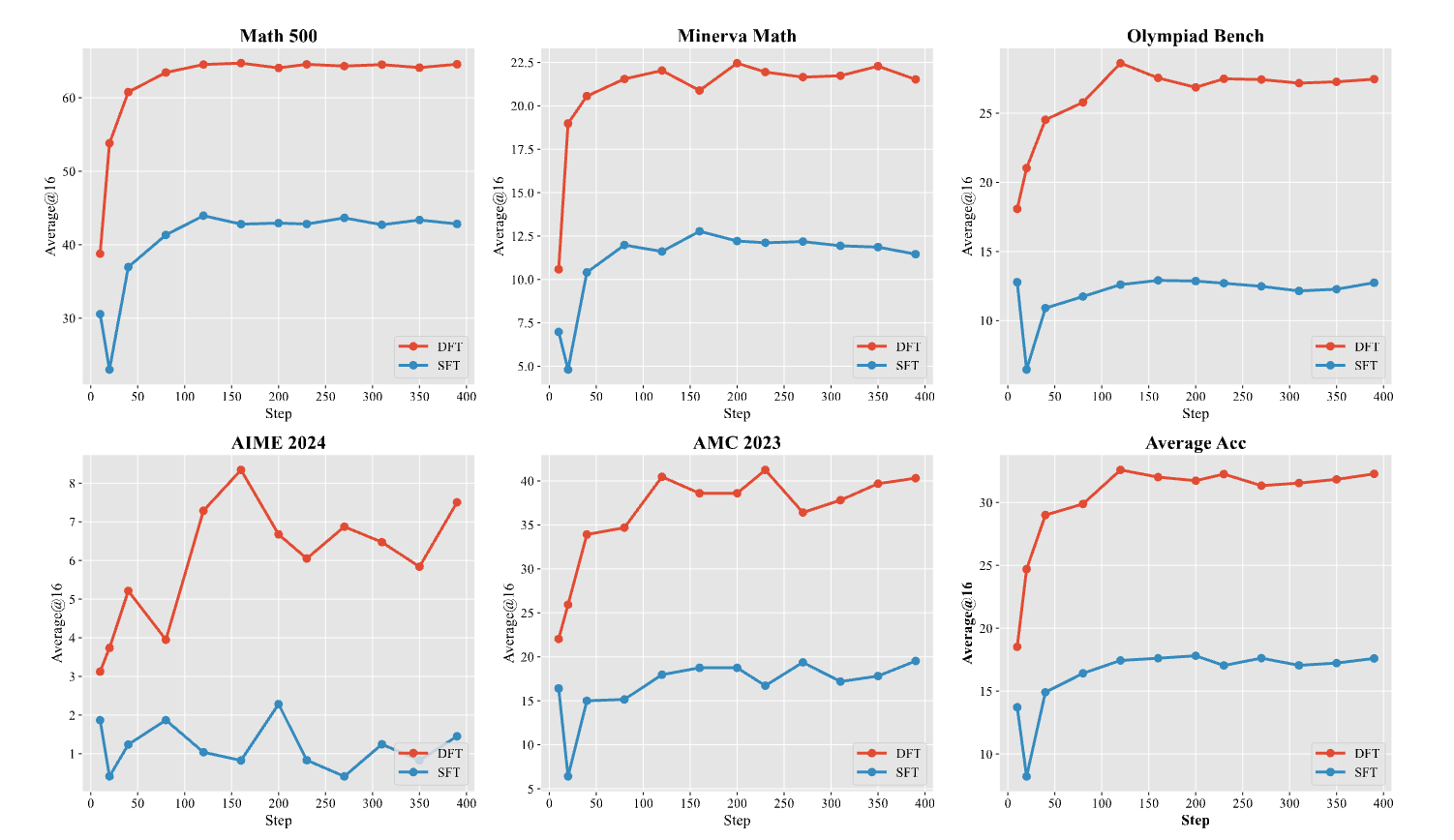
上图展示了 Qwen2.5-Math-1.5B 在训练过程中的准确率变化。可以发现,DFT 的学习曲线不仅收敛速度更快,而且在训练早期(10-20步)就已经超越了 SFT 训练完成后的最佳性能,体现了其更高的样本效率和更有效的梯度更新。
此外,论文还将 DFT 与同期的另一个改进方法 Importance-Weighted SFT (iw-SFT) 进行了比较。
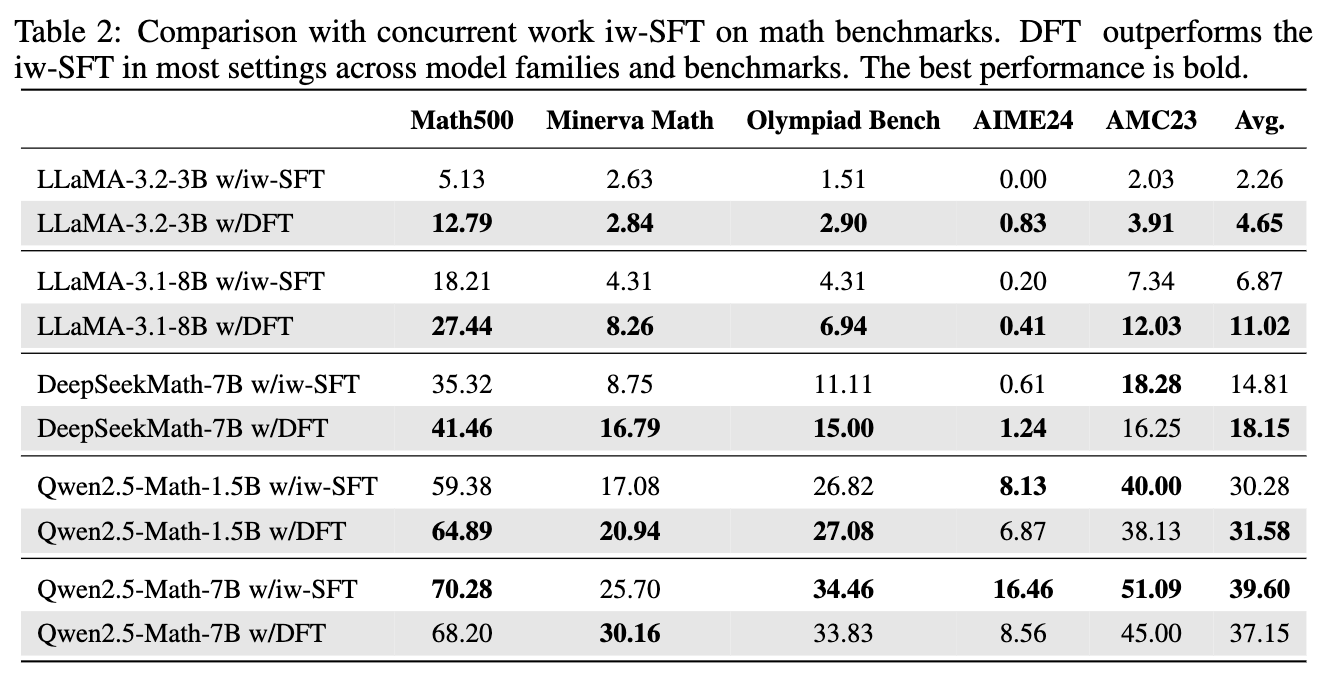
结果显示,在绝大多数模型和基准上,DFT 的性能都优于 iw-SFT,尤其是在 LLaMA 系列模型上,iw-SFT 甚至出现了性能不稳定的情况,而 DFT 则始终保持稳健的提升。
不止于SFT:DFT在离线强化学习中的亮眼表现
为了进一步探索 DFT 的潜力,研究者们将其应用到了离线强化学习 (Offline RL) 的场景中。他们使用拒绝采样的方法,先用基础模型生成多个答案,然后筛选出正确的答案作为更高质量的训练数据。
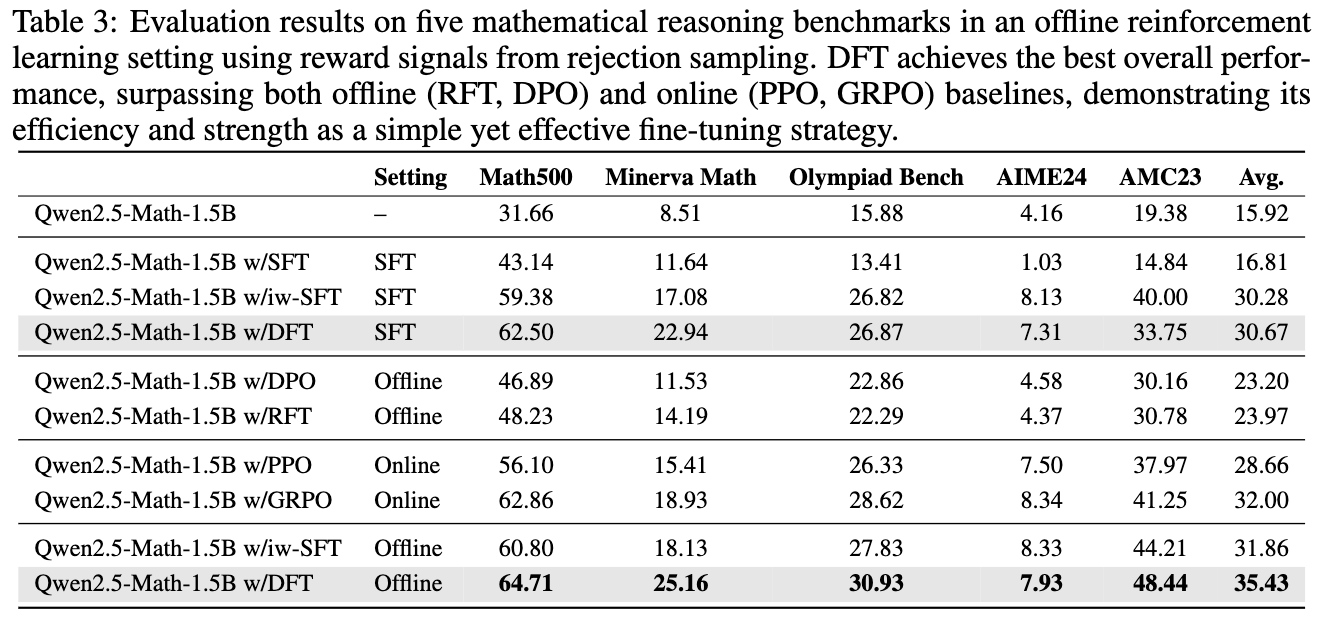
实验结果再次令人震惊。在离线 RL 的设定下,DFT 的表现不仅远超其他离线 RL 方法如 DPO 和 RFT,甚至还优于 PPO 和 GRPO 这两种强大的在线 RL 算法。在 Qwen2.5-Math-1.5B 模型上,DFT 的平均分达到了 35.43,超过了最强的在线 RL 基线 GRPO(32.00)。这表明,DFT 这种简单的重加权思想,能够非常有效地利用带有奖励信号(即使只是正确/错误)的数据,其效果甚至超过了许多复杂的 RL 优化算法。
深入“模型内心”:DFT是如何重塑学习过程的?
DFT 为什么能取得如此好的效果?论文通过分析训练后模型在训练集上的 token 概率分布,为我们提供了更深入的洞察。
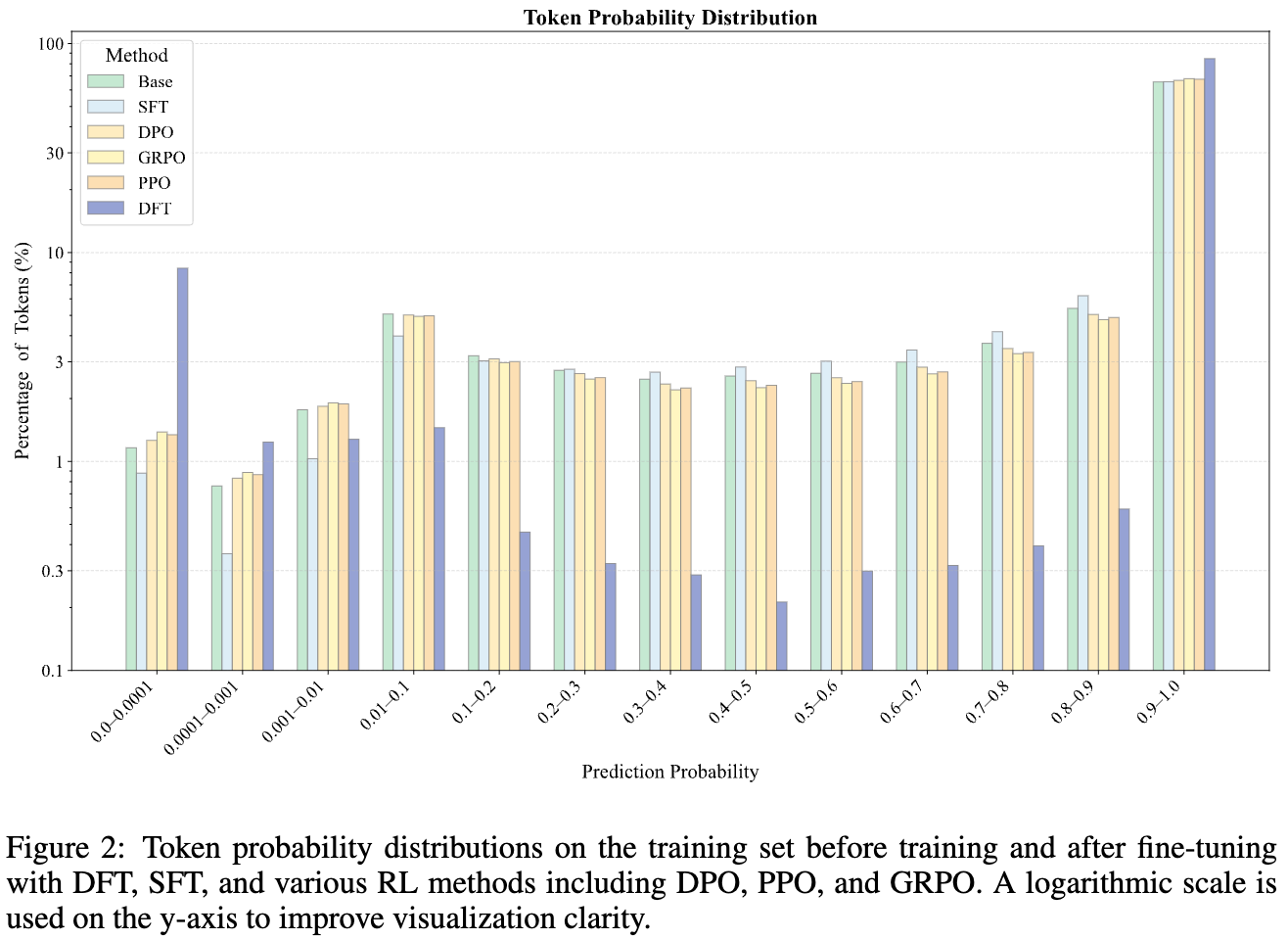
上图(y轴为对数尺度)揭示了不同训练方法如何改变模型的概率“景观”:
-
SFT:倾向于统一地提升所有 token 的概率,试图让每个 token 的置信度都变高。 -
DFT:则表现出一种极化效应 (polarizing effect)。它会显著提升一部分 token 的概率(让它们接近 1),同时主动地抑制另一部分 token 的概率(让它们接近 0)。这使得最终的概率分布呈现出两头高、中间低的两极化形态。其他 RL 方法(DPO, PPO, GRPO)也表现出类似趋势,但程度远不如 DFT 明显。
研究者们进一步探究了那些被 DFT 压低概率的 token,发现它们大多是诸如 'the', 'let', ',', '' 等语法功能词或标点符号。这说明,DFT 促使模型学会了区分 token 的重要性:将学习的重点放在携带核心语义内容的关键 token 上,而降低对那些语法结构性、但对解题本身意义不大的 token 的关注。这种学习策略显然更加智能和鲁棒,类似于人类学生会专注于理解核心概念,而不是在连接词的用法上吹毛求疵。
点评
这篇论文无疑是高质量且具有重要启发性的,它提出的理论视角新颖,方法简洁优雅。抛开优点,我们理性分析下其潜在的缺点和局限性。
该论文的理论框架隐含了一个前提,即 SFT 所用的“专家数据”是高质量且无误的。但在现实世界中,SFT 数据集往往包含噪声、次优答案,甚至是事实错误。DFT 的机制会降低模型对低概率(即模型觉得“意外”或“困难”)样本的关注度。如果一个样本之所以概率低,是因为它是一个非常新颖、巧妙但正确的解法,那么 DFT 可能会错误地忽视掉这个宝贵的学习机会,反而去迁就模型已有的“偏见”。它无法区分“困难的正确样本”和“真正的噪声样本”。
论文将 DFT 带来的 token 概率两极分化视为一种积极的学习策略,并以人类教学作类比。 但这种解释是后验的,并且可能存在未被探讨的副作用。全面压低常见功能词的概率,是否会在某些情况下导致模型生成语法不通顺、逻辑不连贯的句子? 论文中缺乏对生成样本的定性分析,我们无从得知 DFT 模型所犯的错误类型是否与 SFT 有何不同,也无法评估其生成文本的整体质量(例如,流畅度、连贯性)。
实验中,离线 RL 的数据是通过对基础模型进行拒绝采样后得到的,包含了约 14 万个被验证为正确的样本。 这批数据的质量和分布与主实验中用于 SFT 的 10 万样本数据集是不同的。因此,当论文比较“离线 DFT”和“标准 SFT”的性能时,其巨大的提升(从 30.67 提升至 35.43)是更优的算法和更高质量的数据共同作用的结果。 这使得我们很难清晰地剥离出 DFT 算法本身到底贡献了多少。
结语:我们可以将 DFT 视为一个极具潜力的候选方案和一个成功的领域特定解决方案,但要宣称它是在所有场景下对 SFT 的“根本性改进”,还需要在更广泛的任务、更多样的模型以及更深入的分析上进行大量后续验证。
往期文章: