近年来,大型语言模型(LLM)通过一种名为“思维链”(Chain-of-Thought, CoT)的提示技术,展现了令人惊叹的复杂推理能力。它们能够像人类一样,通过一步步的逻辑推导来解决问题,这让人们普遍认为,我们距离通用人工智能(AGI)又近了一步。然而,来自亚利桑那州立大学的研究团队发表了一篇颠覆性的论文——《Is Chain-of-Thought Reasoning of LLMs a Mirage? A Data Distribution Lens》,对这一乐观的看法提出了严峻的挑战。这篇论文的核心论点是:LLM的CoT推理能力,很大程度上可能只是一种“脆弱的海市蜃楼”,其本质是精巧的模式匹配,而非真正的、可泛化的逻辑推理。 本文将带您深入解读这篇论文,从一个全新的“数据分布”视角,揭开CoT推理背后的真相。

-
论文标题:Is Chain-of-Thought Reasoning of LLMs a Mirage? A Data Distribution Lens -
论文链接:https://www.arxiv.org/pdf/2508.01191
引言:思维链(CoT)——开启LLM推理时代的钥匙?
在大型语言模型的世界里,我们经常被其强大的能力所震撼。从写诗、编代码到进行多轮对话,LLM的表现越来越接近人类。其中,最引人注目的突破之一便是“思维链”(Chain-of-Thought, CoT)提示技术的出现。
什么是思维链(CoT)?
简单来说,CoT是一种prompt工程技术,它通过引导LLM在给出最终答案之前,先生成一系列中间的、连贯的推理步骤。 比如,当被问到一个数学应用题时,一个启用CoT的LLM不会直接给出答案,而是会先写出解题的思路和计算过程,最后才得出结论。这种“自言自语”式的推理过程,极大地提升了LLM在算术、常识推理和符号推理等需要多步骤思考的任务上的表现。
这一技术的成功,让许多研究者和从业者备受鼓舞,认为LLM已经开始具备类似人类的、深思熟虑的推理能力。似乎,我们只要不断扩大模型规模,就能解锁更强大的推理能力,最终实现通用人工智能。
然而,事实果真如此吗?一些初步的研究已经开始对这种乐观的看法提出质疑。
CoT推理的“裂痕”:一个简单的例子
论文开篇就用一个直观的例子,揭示了CoT推理中令人不安的矛盾。
问题:“美国成立的那一天(1776年7月4日)是在闰年还是平年?”
当研究者使用CoT提示词(如“让我们一步步思考”)向一个先进的LLM(Gemini)提问时,模型给出了如下回应:
“美国成立于1776年。1776能被4整除,但不是百年,所以它是一个闰年。因此,美国成立的那一天是在一个平年。”
这个回答令人困惑。模型正确地阐述了判断闰年的规则(能被4整除但不能被100整除),也正确地应用了规则得出了“1776年是闰年”的中间结论。然而,它最终却给出了一个与其中间步骤完全矛盾的、错误的最终答案。
这个例子生动地说明了一个核心问题:LLM生成的看似合乎逻辑的推理链,与最终的结论之间可能存在脱节。 它能够熟练地“背诵”和“模仿”推理的步骤,但这并不代表它真正理解了这些步骤背后的逻辑因果关系。这种现象促使论文作者们提出了一个更深层次的疑问:我们所看到的CoT推理,究竟是真正的智能涌现,还是一种更为肤浅的表象?这也与更广泛的讨论相呼应,即LLM究竟是在进行推理,还是仅仅在做高级的模式识别。
为了系统地回答这个问题,作者们提出了一个全新的分析框架——数据分布视角(Data Distribution Lens)。
核心视角:数据分布——决定LLM能力边界的“无形之手”
传统的观点认为,CoT是一种涌现能力,是模型内在推理能力的体现。而这篇论文反其道而行之,提出了一个根本性的假设:
CoT推理并非LLM内生的、通用的逻辑能力,而是一种从训练数据中学到的、结构化的归纳偏见(structured inductive bias)。
换句话说,LLM之所以能进行CoT推理,是因为它在海量的训练数据中见过了大量类似“问题 -> 推理步骤 -> 答案”的模式。它的“推理”过程,本质上是一个条件生成任务:在给定一个测试问题时,模型会生成一个与它在训练数据中见过的最相似的推理路径。
因此,CoT的有效性从根本上受限于训练数据和测试查询之间的“分布差异”(Distribution Discrepancy)。 当测试问题与训练数据在分布上高度相似时(即“分布内”或In-Distribution),LLM表现优异;而一旦测试问题超出了训练数据的分布范围(即“分布外”或Out-of-Distribution, OOD),其看似强大的推理能力就会迅速崩溃,如同海市蜃楼般消散。
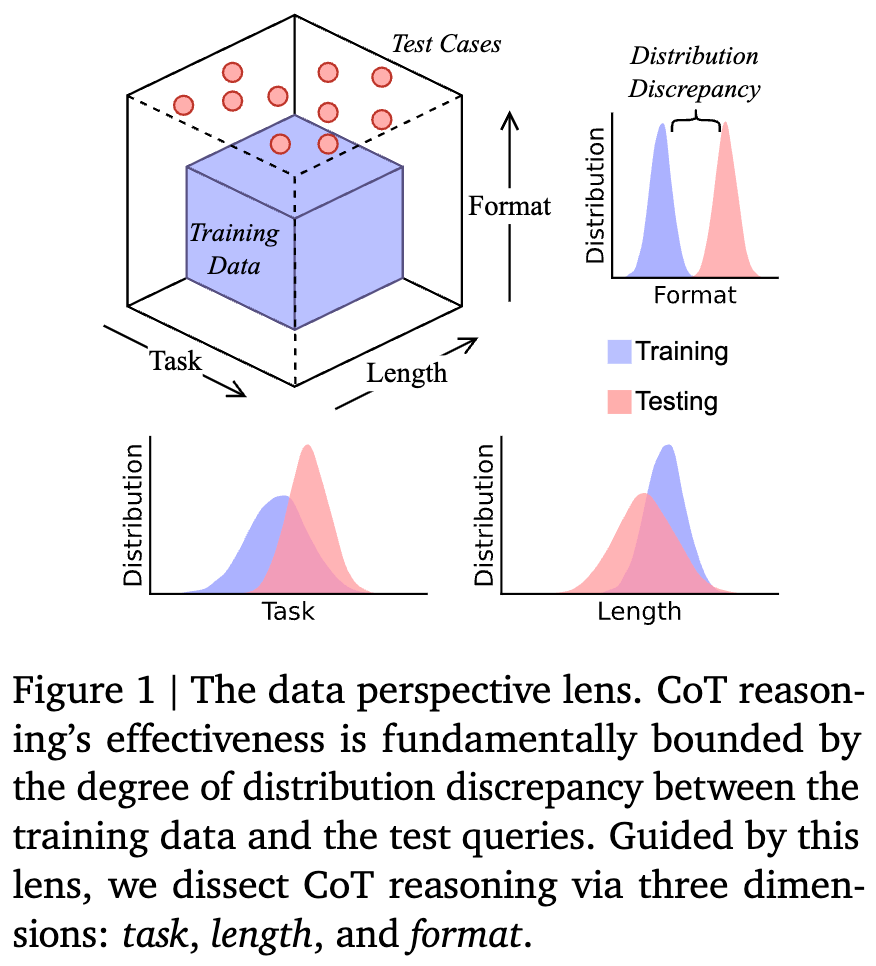
理论化“数据分布视角”
为了让这个视角更加严谨,作者们引入了数学语言来对其进行形式化。
首先,他们将CoT推理建模为一个条件生成过程。假设是训练数据的分布,其中包含了大量的输入-输出对,代表一个推理问题,代表包含中间推理步骤的完整解答。模型通过在上最小化经验风险来学习一个近似函数。
训练的期望风险可以定义为:
其中,是一个任务相关的损失函数(例如,交叉熵或词元级别的准确率)。
而在推理时,模型面对的是一个可能来自不同分布的测试输入。其测试风险为:
模型从泛化到的能力,就取决于这两个分布之间的差异,作者称之为分布差异(Distributional Discrepancy),并用一个散度度量来量化:
基于这个框架,作者提出了一个关键的理论界限——CoT泛化界限(CoT Generalization Bound):
定理 3.1 (CoT Generalization Bound):
对于一个在上训练好的模型,其在测试分布上的期望测试风险有一个上界:
这个公式虽然看起来复杂,但它的含义非常清晰:
-
:模型在测试集上的表现(误差)。我们希望它越小越好。 -
:模型在训练集上的表现。 -
:这是核心项。它表明,测试误差的上界与训练-测试分布差异成正比。分布差异越大,潜在的性能下降就越严重。是一个依赖于模型架构和任务复杂度的利普希茨常数。 -
:这一项与训练样本数量有关,表示随着训练数据增多,泛化误差会减小。
这个定理为“数据分布决定CoT能力”的假设提供了坚实的理论基础。它告诉我们,要理解CoT何时成功、何时失败,关键在于分析和度量训练与测试之间的分布差异。
实验设计:在受控环境中“炼金”,解剖CoT的脆弱性
理论需要实验来验证。为了能在一个纯净、可控的环境中精准地研究分布差异对CoT的影响,避免大型预训练模型中海量、未知数据带来的干扰,研究者们设计并构建了一个名为DataAlchemy的合成数据集框架。
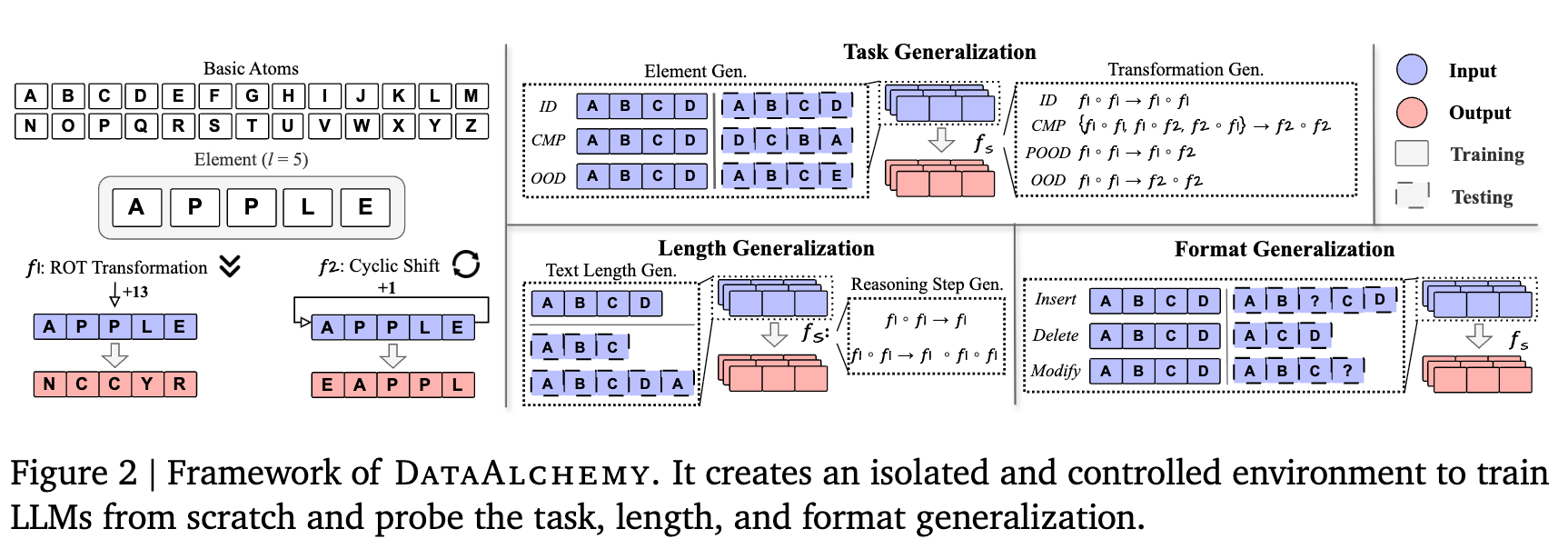
DataAlchemy可以被看作一个“LLM炼金术”的实验室。它允许研究者从零开始训练语言模型,并对数据分布的方方面面进行精细的控制和操纵。
-
基本原子(Basic Atoms):实验从最基础的元素——26个英文字母 {A, B, C, ..., Z}开始。 -
元素(Elements):一个“元素”是由这些原子组成的有序序列,例如 APPLE。元素的长度可以自由控制。 -
变换(Transformations):为了模拟推理任务,作者定义了两种基础的变换操作: -
ROT变换(f_rot):类似于凯撒密码,将元素中的每个字母在字母表上循环移动n位。例如, f_rot(APPLE, 13)会得到NCCYR。 -
循环位置移位 (f_pos):将元素中的字母位置循环移动n位。例如, f_pos(APPLE, 1)会得到EAPPL。
-
-
组合变换(Compositional Transformation):通过将这两种基础变换像积木一样组合起来,可以构建出任意复杂的多步推理链。例如, f1 o f2就代表先执行变换f2,再执行变换f1。
在这样的环境中,一个CoT任务的样本看起来是这样的:
Query: APPLE, Transformation: f_rot(13) o f_pos(1)
CoT Steps: APPLE -> [f_pos(1)] -> EAPPL -> [f_rot(13)] -> RNCYC
Answer: RNCYC
通过控制训练集和测试集中包含的“元素”、“变换组合”以及“序列长度”等,研究者们可以精确地创造出不同类型和程度的“分布差异”。
剖析CoT的三个维度
基于“数据分布”这个核心视角,论文将CoT的泛化能力沿着三个关键维度进行了系统性的“解剖”:
-
任务泛化(Task Generalization):模型能否处理在训练中未见过的新任务结构? -
长度泛化(Length Generalization):模型能否处理比训练样本更长或更短的推理链? -
格式泛化(Format Generalization):模型对提示词的表面形式变化有多敏感?
接下来,我们将逐一深入探讨在这三个维度上的惊人发现。
维度一:任务泛化 —— 当LLM遭遇“新考题”
任务泛化是衡量模型是否具备真正推理能力的核心标准。一个真正理解了规则的模型,应该能将知识应用到全新的问题上。在DataAlchemy的框架下,“新任务”可以指代新的元素(即模型没见过的字母组合)或新的变换(即模型没见过的推理规则或规则组合)。
1. 变换泛化(Transformation Generalization)
这是最严峻的考验。模型能否理解并执行一个它从未见过的变换组合?
实验设置:
研究者定义了四种递进的分布偏移场景:
-
In-Distribution:测试集和训练集的变换完全相同。例如,训练和测试都只包含 f1 o f1。 -
Composition (CMP):测试集包含训练中见过的变换的新组合。例如,训练集包含 f1 o f1和f2 o f2,测试集则考察f1 o f2或f2 o f1。 -
Partial Out-of-Distribution (POOD):测试集的变换组合中,包含至少一个训练时未见过的新变换。 -
Out-of-Distribution (OOD):测试集的变换组合是完全新颖的。例如,训练集只见过 f1 o f1,而测试集要处理f2 o f2。

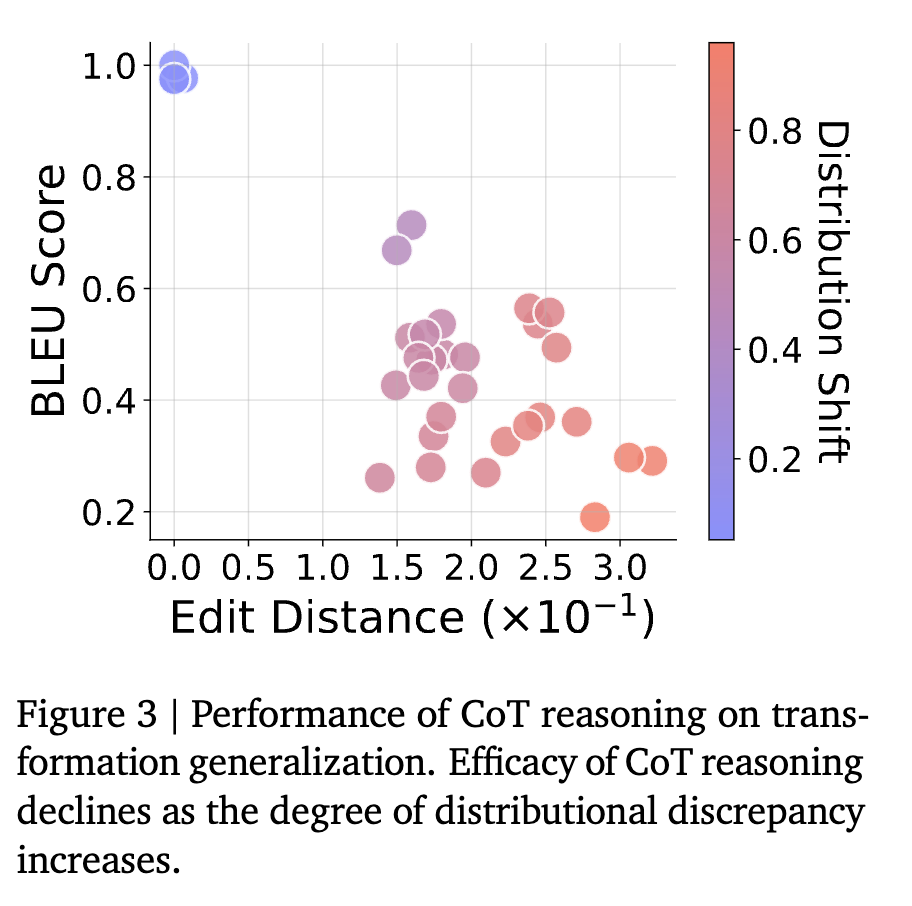
实验结果与发现:
结果令人震惊。如上表和上图所示,LLM的性能随着分布差异的增大而急剧下降。
-
在ID场景下,模型表现完美(Exact Match为100%)。 -
一旦进入CMP场景,即便是对见过的规则进行简单的新组合,模型的准确率就骤降至几乎为零(0.01%)。 -
在更困难的POOD和OOD场景下,模型的表现更是惨不忍睹,完全无法正确完成任务。
深入分析:
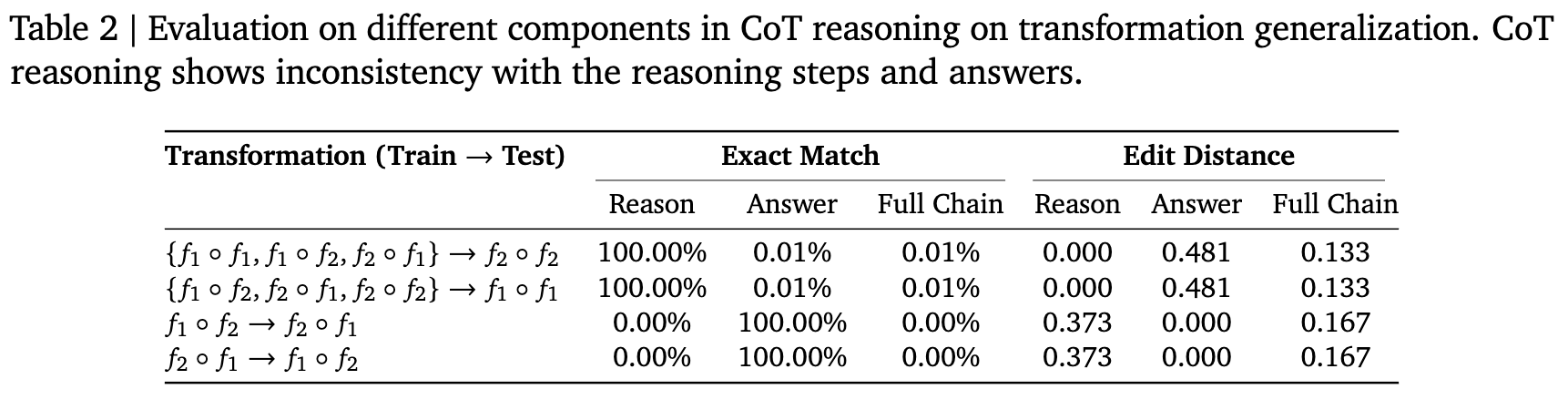
一个有趣的发现是,在CMP场景中,虽然模型的最终答案几乎都是错的,但它生成的推理步骤却是100%正确的! 表 2这再次印证了引言中的“闰年”例子:LLM似乎是在“扮演”一个推理者。当面对一个新任务(如f2 o f2)时,它会从训练数据中寻找最相似的“剧本”(如f1 o f2),然后完美地复现这个剧本中的推理步骤,但由于剧本和当前任务不匹配,最终得出了错误的答案。这表明,CoT推理反映的是对训练模式的复制,而非对任务逻辑的真正理解。
“打补丁”能解决问题吗?
研究者们接着探索了一个问题:如果给模型看一点点新任务的例子(即进行监督式微调,SFT),情况会如何?
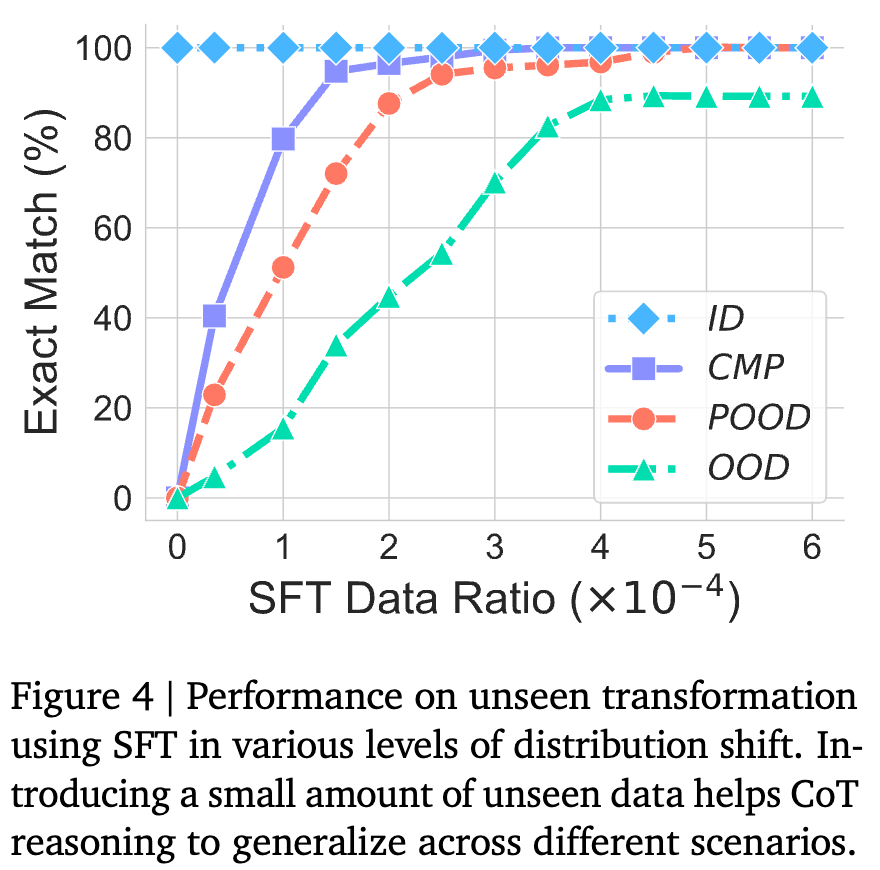
结果显示,只需极少量(例如,比例仅为 1.5e-4)的“新考题”样本,就能让模型的性能迅速提升。 这说明,LLM非常擅长从数据中快速学习新模式。然而,这也从侧面证明了它的脆弱性:它的能力范围被其见过的模式严格限定。这种“打补丁”式的学习方式,与其说是实现了真正的泛化,不如说是不断地扩大其“分布内”的舒适区。
2. 元素泛化(Element Generalization)
这里考察的是,当推理规则(变换)不变时,模型能否处理它从未见过的输入数据(元素)?
实验设置:
同样设置了ID、CMP和OOD三种场景。
-
ID: 测试元素与训练元素使用相同的字母。 -
CMP: 测试元素由训练时见过的字母构成新的组合。 -
OOD: 测试元素包含训练时从未见过的字母。
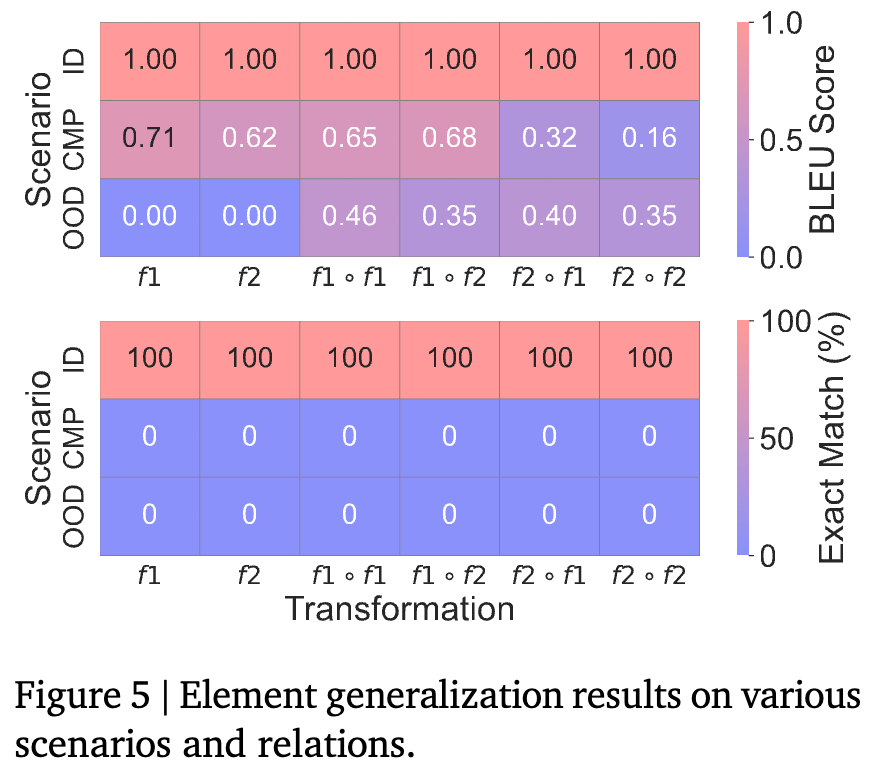
实验结果与发现:
结果与变换泛化非常相似。性能同样随着分布差异的增加而急剧下降。 特别是在OOD场景下,当模型遇到包含新字母的元素时,其性能直接崩溃为零。这表明模型甚至无法处理最基本的输入泛化。附录中的失败案例显示,当面对新元素时,模型甚至无法生成任何有意义的回复。
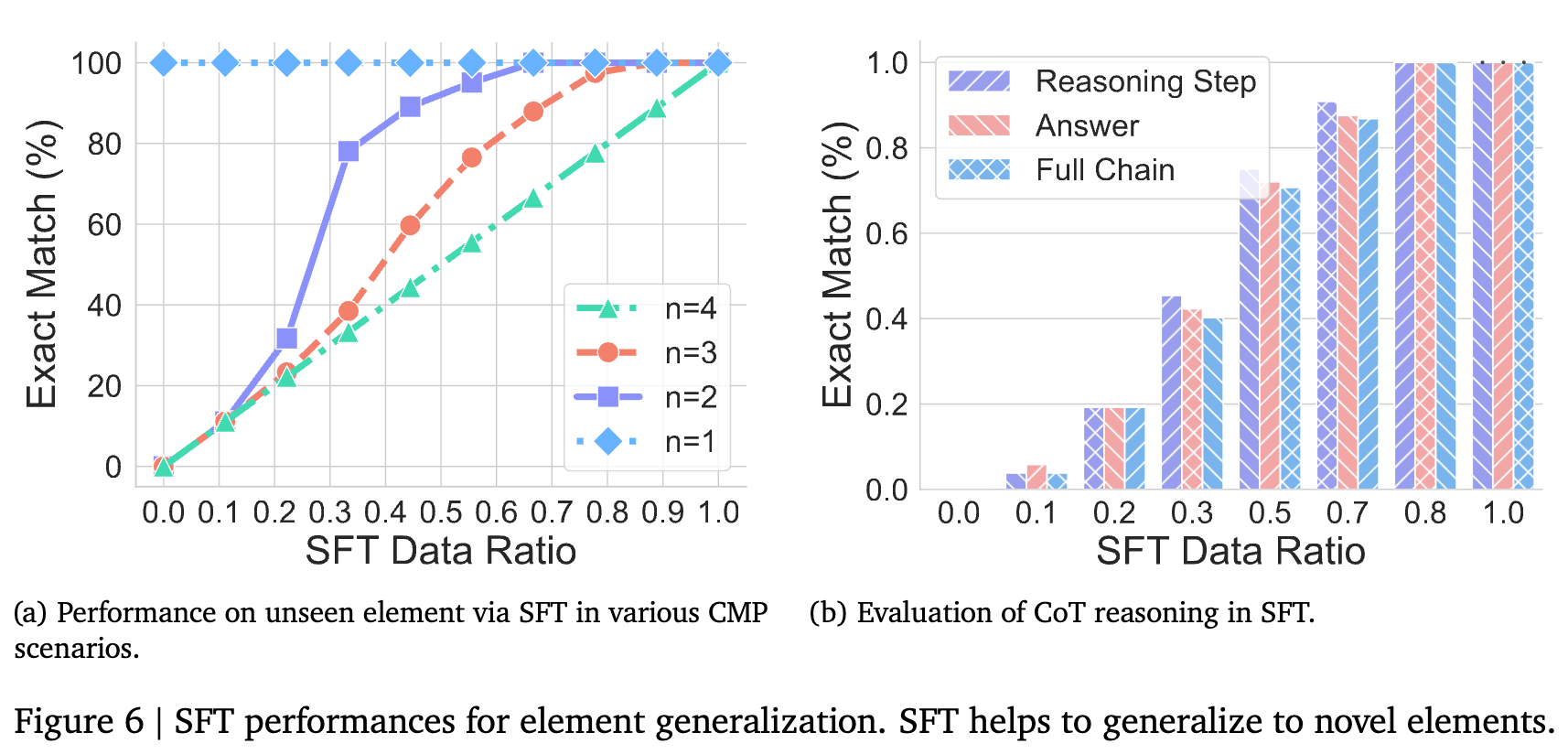
同样的,通过SFT“打补丁”可以快速提升模型在处理新元素上的性能。一个有趣的观察是(见Figure 6b),在微调过程中,模型学会正确答案的速度,要快于它学会正确推理步骤的速度。这再次暗示了答案和推理过程之间的某种脱节,进一步削弱了CoT是忠实推理过程的观点。
维度二:长度泛化 —— 当推理链条变长或变短
在现实世界中,问题的复杂度各不相同,所需要的推理步骤(长度)也千差万别。一个强大的推理模型应该能够灵活应对不同长度的推理任务。长度泛化主要从两个方面考察:输入文本长度和推理步骤长度。
1. 文本长度泛化(Text Length Generalization)
实验设置:
研究者固定在一种推理任务上,仅在输入元素长度为4(例如ABCD)的数据上训练模型。然后,在长度从2到6不等的元素上进行测试。
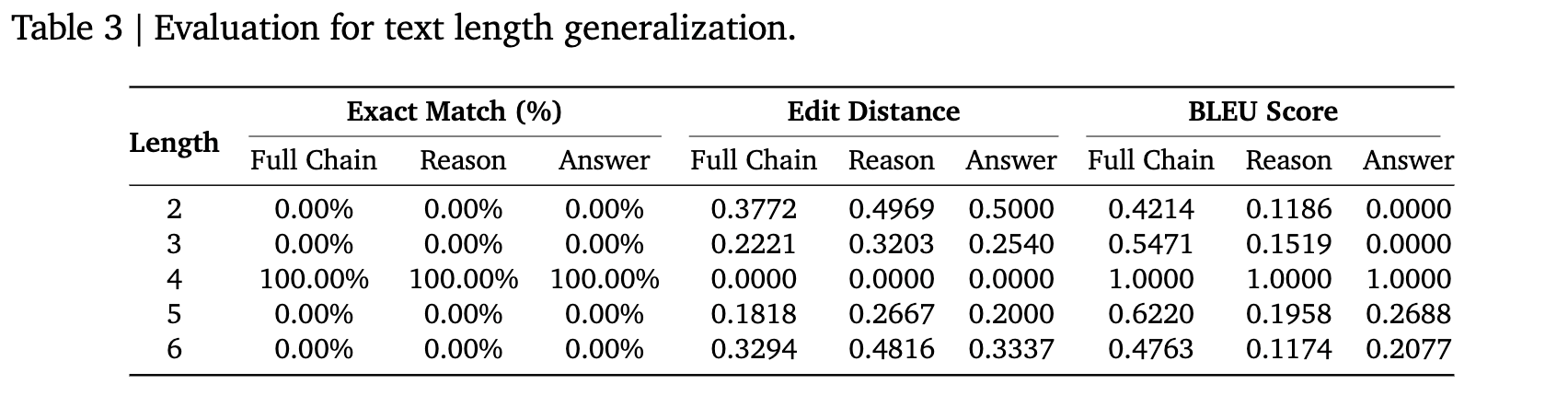
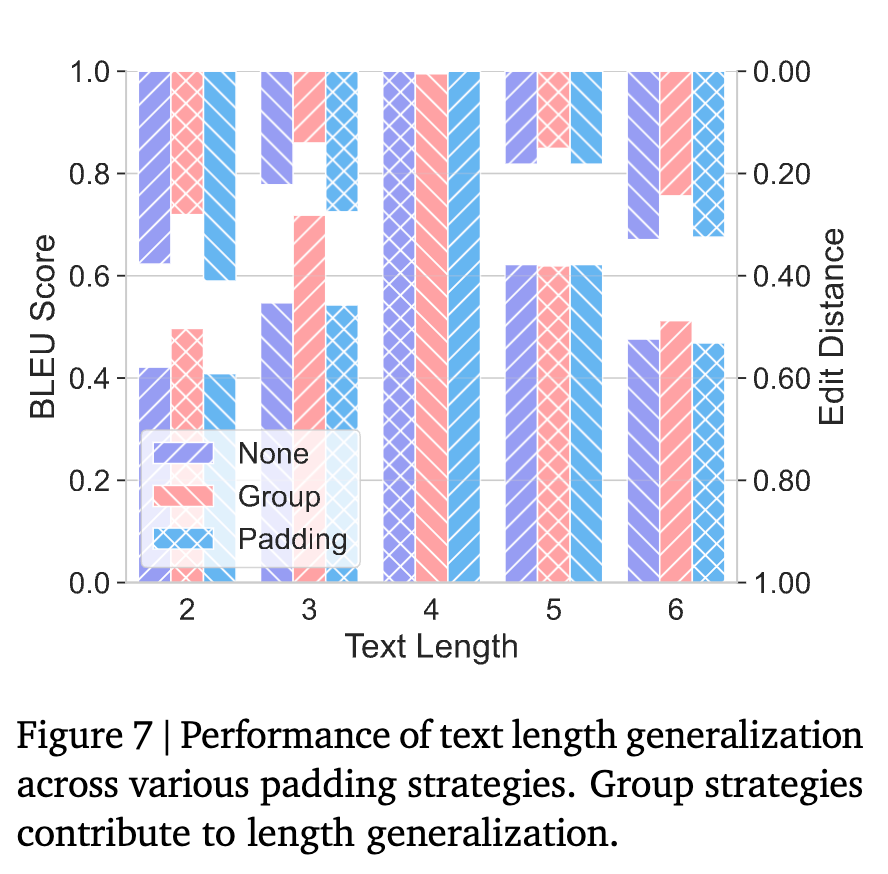
实验结果与发现:
如上表所示,模型仅在训练长度(l=4)上表现完美。对于任何其他长度的输入,即便只相差1个字符(如l=3或l=5),模型的准确率也直接降为0。 BLEU分数也显示,随着长度差异的增加,生成文本的质量显著下降。
这表明LLM对输入的表面统计特性(如长度)极其敏感。附录中的案例(D.1.4)揭示了一个有趣的现象:当面对一个更短的提示时,模型会试图在推理链中“画蛇添足”地增加一些无意义的符号,以使其输出的总长度与训练数据中的长度保持一致。这是一种非常机械的模式复制行为。
研究者还测试了不同的填充(padding)策略,发现简单的填充策略帮助不大,但将填充替换为有意义文本的“分组”(Group)策略能有效提升长度泛化能力,因为它降低了训练和测试数据在长度上的分布差异。
2. 推理步骤泛化(Reasoning Step Generalization)
实验设置:
这次,研究者固定在推理步骤为2步(例如f1 o f2)的数据上训练模型,然后在需要1步或3步推理的任务上进行测试。
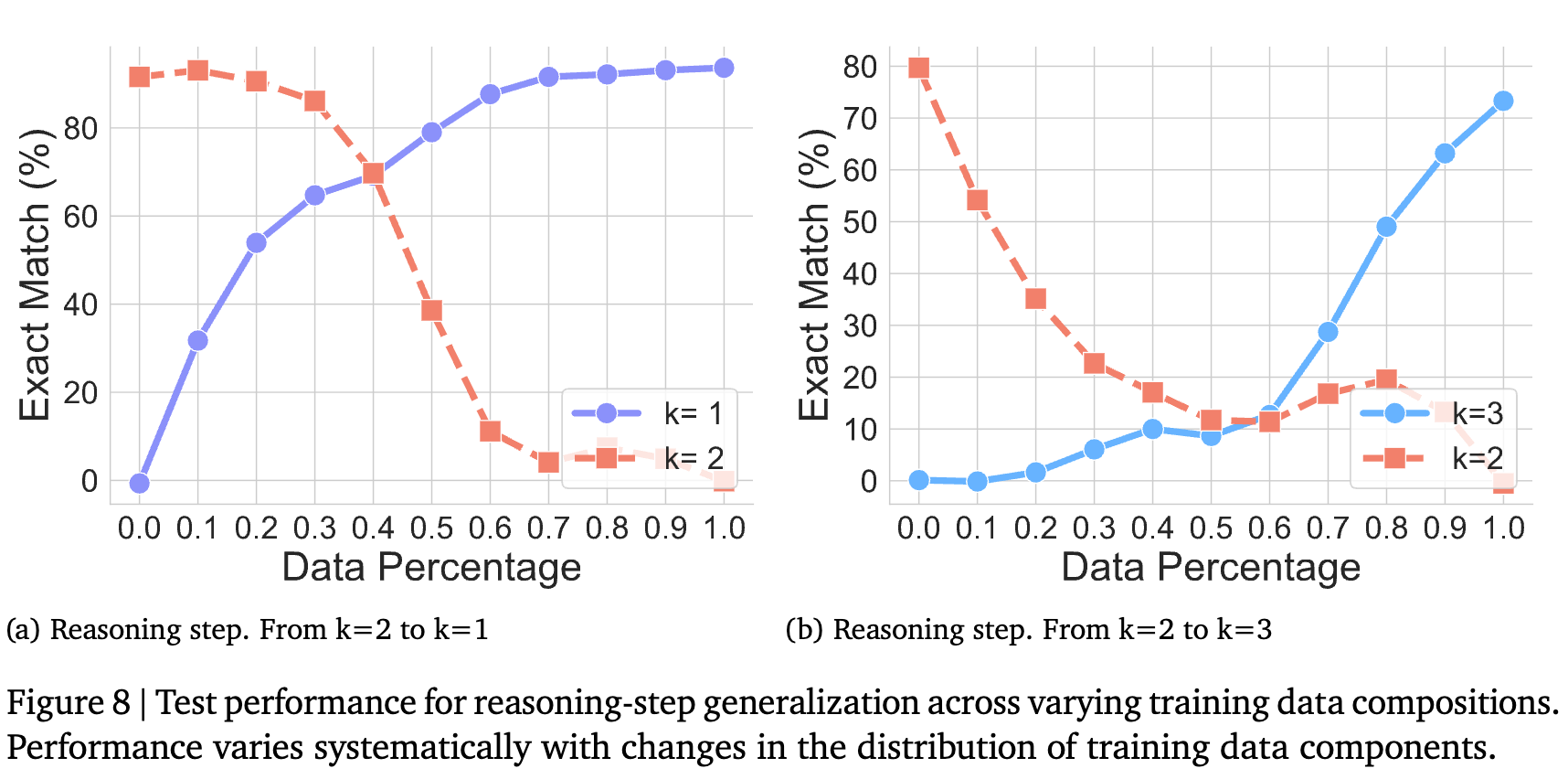
实验结果与发现:
结果再次印证了之前的结论:CoT推理无法泛化到不同长度的推理链上。 无论是从2步泛化到1步,还是从2步泛化到3步,模型都彻底失败了。
图中还展示了另一个实验:研究者将训练数据逐步从原始任务(2步)替换为目标任务(1步或3步),同时保持总数据量不变。可以观察到,随着目标任务数据比例的增加,模型在目标任务上的性能线性提升,而在原始任务上的性能则相应下降。这清晰地表明,模型的性能完全由其训练数据的分布构成所决定,不存在超越数据分布的“顿悟”或“泛化”。
维度三:格式泛化 —— 当“考题”换了一种问法
格式泛化考察的是CoT推理对输入提示词的表面形式变化的鲁棒性。一个真正理解任务的模型,不应该因为问题的措辞、标点符号或无关词语的改变而受到影响。
实验设置:
研究者通过四种方式对原始的、格式正确的提示词进行“加噪”:
-
插入(Insertion):在每个原始词元前插入一个随机的噪声词元。 -
删除(Deletion):随机删除一部分原始词元。 -
修改(Modification):将原始词元替换为噪声词元。 -
混合(Hybrid):结合以上多种方式。
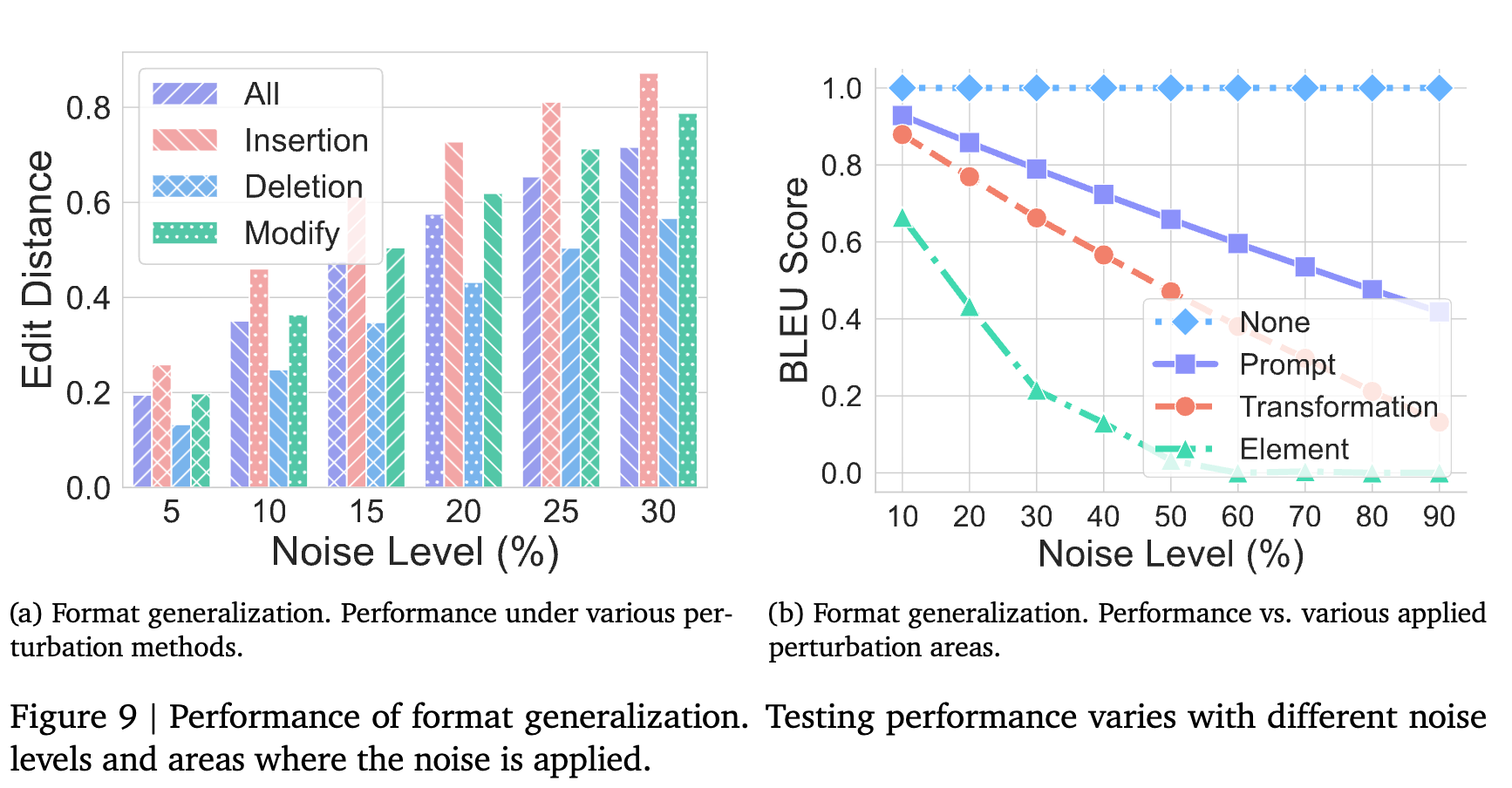
实验结果与发现:
-
CoT对格式变化非常敏感。 如图(a)所示,任何形式的噪声(即使是5%的噪声水平)都会导致性能显著下降。其中,插入噪声的影响最大,而删除噪声的影响相对较小。 -
并非所有部分都同等重要。 如图(b)所示,研究者将噪声分别应用于提示的不同部分:元素本身(Element)、变换指令(Transformation)和提示模板(Prompt,如 <answer>等)。结果发现,对“元素”和“变换指令”这两个核心语义部分的干扰,对性能的打击是毁灭性的。而对其他模板部分的修改,则几乎不影响结果。
这一发现具有重要的现实意义。它表明LLM的推理严重依赖于对输入中特定、僵硬模板的识别。它并没有形成一个灵活、抽象的任务表示,而是将推理能力与输入的特定表述“绑定”在了一起。
最终验证:温度和模型大小会改变结论吗?
为了确保上述发现的普适性,研究者还检验了它们是否在不同的采样温度(Temperature)和模型大小(Model Size)下依然成立。
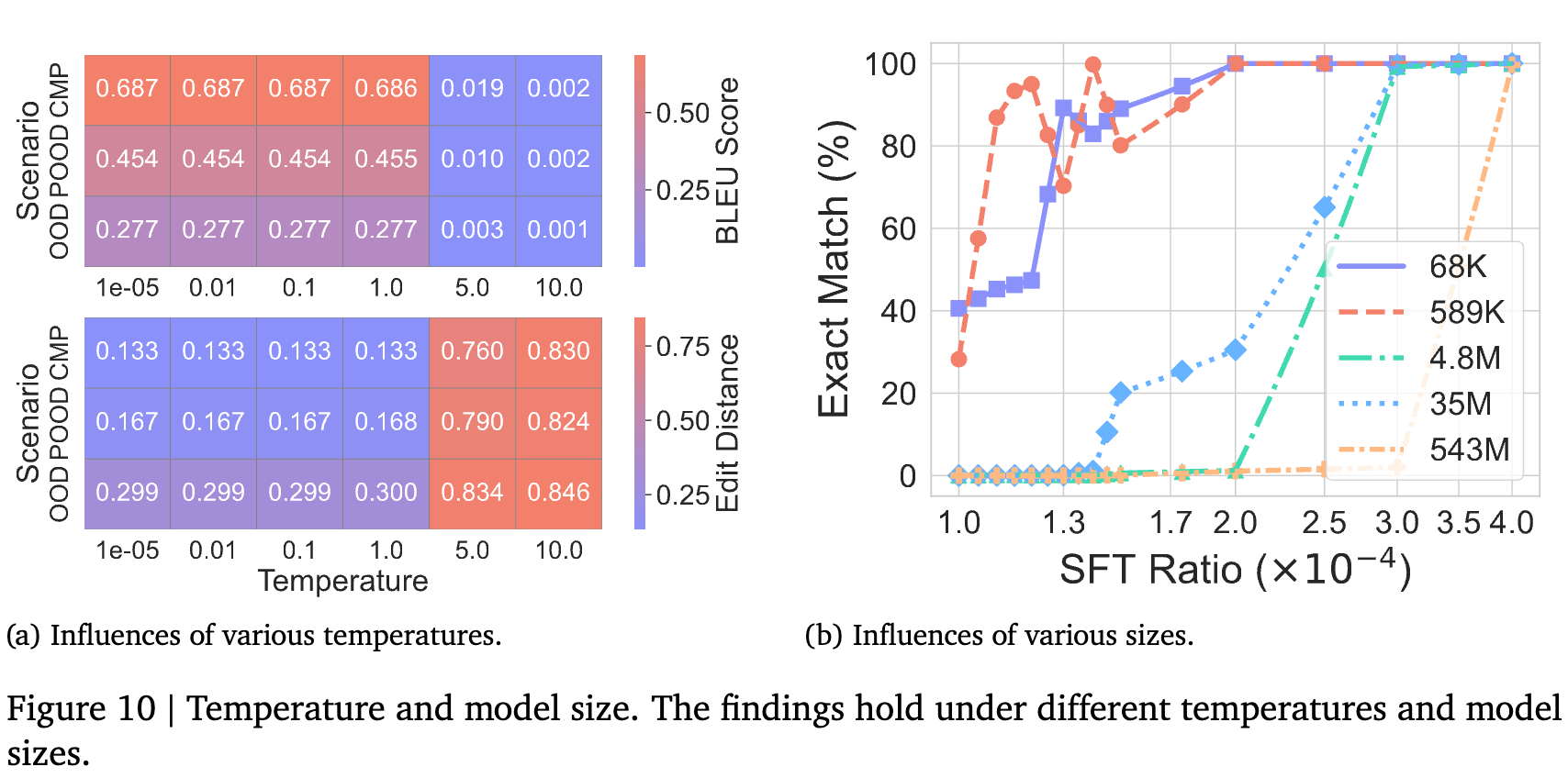
实验结果与发现:
-
温度:在一系列合理的温度值范围内(从1e-5到1.0),CoT的性能表现出高度的一致性。只有在温度过高(>5.0)导致输出完全随机时,性能才会崩溃。 -
模型大小:研究者测试了从68K到543M不同参数量的模型。结果显示,所有规模的模型都表现出与默认模型相似的泛化行为和性能曲线。
点评
论文中使用的模型(从68K到543M参数)与当今的前沿模型(如GPT-4、Claude 3等,参数量可能在万亿级别)之间存在着数个数量级的差距。我们已经知道,模型在跨越某些巨大的规模阈值后,会涌现出之前完全没有的能力。因此,将在小型模型上观察到的“绝对脆弱性”直接外推到超巨型模型上,需要更加谨慎。
前沿LLM的预训练数据是整个互联网的映像,其多样性和复杂性远超DataAlchemy。一种可能性是,这种海量、异构的数据分布本身就包含了足够多的“模式变体”,使得模型学到的“模式匹配”能力变得异常鲁棒和灵活,以至于在宏观上表现得近似于真正的泛化推理。DataAlchemy的纯净环境,可能恰恰过滤掉了这种复杂性带来的“鲁棒性增强”效应。
现实世界中的推理还包括常识推理、类比推理、知识整合、创造性思考等。LLM在这些领域表现出的能力,可能无法被DataAlchemy这种简单的符号任务所完全代表。论文的结论在“LLM无法进行可靠的算法执行”这一点上非常有说服力,但它是否能等同于“LLM无法进行所有类型的有效推理”,仍有待商榷。
往期文章:




