当今的大语言模型(LLM)在各类任务上展现了惊人的能力,但提升其逻辑推理能力,尤其是面对复杂问题时的深度推理,仍然是前沿研究的核心挑战。一种被称为“基于可验证奖励的强化学习”(Reinforcement Learning with Verifiable Rewards, RLVR) 的技术范式应运而生,它通过为模型的正确输出提供明确奖励,在数学、编程等领域取得了显著成功。 然而,RLVR的成功严重依赖于一个“验证器(Verifier)”——一个能够判断答案是否正确的裁判。在数学和代码领域,我们可以轻易地编写规则来验证答案(例如,代码能否通过单元测试,数学题答案是否与标准答案一致)。但当我们将视野扩展到历史、哲学、经济学等通用领域时,答案往往是开放的、自由形式的自然语言,为其构建一个精确的验证器变得极其困难,甚至是不可能的。
这种对领域特定验证器的重度依赖,成为了限制LLM推理能力向更广阔领域泛化的“阿喀琉斯之踵”。为了打破这一枷锁,来自清华大学、新加坡国立大学等机构的研究者们提出了一个简洁而强大的无验证器框架——RLPR(Reinforcement Learning with Reference Probability Reward)。

-
论文标题:Reinforcement Learning with Reference Probability Reward
-
论文链接:https://arxiv.org/abs/2506.18254
RLPR的核心洞见在于:一个LLM生成正确答案的“自信程度”(即内在概率),直接反映了它对引出该答案的推理过程质量的自我评估。 基于此,RLPR巧妙地将LLM自身的内在概率作为奖励信号,彻底摆脱了对外部验证器的依赖,成功将RLVR的强大能力从特定领域推广到通用领域。 实验表明,RLPR不仅在Gemma、Llama、Qwen等多种模型上实现了推理能力的持续提升,甚至超越了那些依赖强大外部验证器模型的先进方法。
本文将作为一篇深度解析,为您详细剖析这篇于2025年6月发布的重磅论文,深入探讨RLPR的动机、核心方法、实验设计及其深远影响。我们将一同见证,AI研究者们是如何通过一个精妙的构想,解决扩展LLM推理能力的核心瓶颈。
1. 引言:RLVR的辉煌与困境
1.1 RLVR:用“对错”信号驱动的推理进化
在提升LLM的推理能力方面,研究者们借鉴了强化学习(RL)的思想。想象一下训练一个孩子解数学题,当他做对一道题时,你给他一颗糖作为奖励;做错了,则没有奖励。久而久之,他会学会如何更准确地解题。
RLVR(Reinforcement Learning with Verifiable Rewards)正是基于这一直观的理念。 在这个框架中,LLM针对一个问题(Prompt),生成一段推理过程(Chain-of-Thought)和最终答案。然后,一个被称为“验证器”的外部模块会检查这个答案的正确性。如果答案正确,模型会得到一个正向奖励(通常是+1);如果错误,则奖励为0。 通过最大化期望奖励,模型被激励去探索和学习能够稳定产生正确答案的推理路径。
这种方法在数学问题求解(如MATH数据集)和代码生成(如HumanEval数据集)等任务上取得了巨大成功,催生了像DeepSeekMath、Qwen2.5-Math等一系列强大的模型。其成功的原因在于,这些领域拥有一个共同的特性:答案的可验证性。我们可以编写精确的规则或程序(即验证器)来自动、客观地判断答案的对错。
1.2 验证器瓶颈:通往通用推理之路的鸿沟
RLVR的成功,恰恰也暴露了其最大的软肋——对验证器的强依赖。 当我们试图将这一范式应用到更广泛的通用领域时,问题就出现了:
-
复杂性与成本高昂:对于“一战爆发的主要原因是什么?”或“请分析苏格拉底的哲学思想”这类问题,答案是复杂的、多方面的、以自由形式的自然语言呈现。为这类问题设计一个能覆盖所有正确表述、排除所有错误理解的基于规则的验证器,其工作量是“无法承受的启发式工程”(prohibitive heuristic engineering)。 -
可扩展性受限:每进入一个新的领域,就需要重新设计一套验证器,这极大地限制了RLVR方法的可扩展性。 -
模型验证器的局限:一个看似可行的替代方案是训练另一个强大的LLM来充当“模型验证器”(model-based verifier)。然而,这引入了新的问题:首先,训练一个高质量的模型验证器本身就需要大量、高质量的人工标注数据,这同样成本高昂且耗时;其次,它使得整个训练框架变得复杂,增加了计算开销;最后,模型验证器本身也可能存在偏见或能力上限,导致奖励信号不准确。
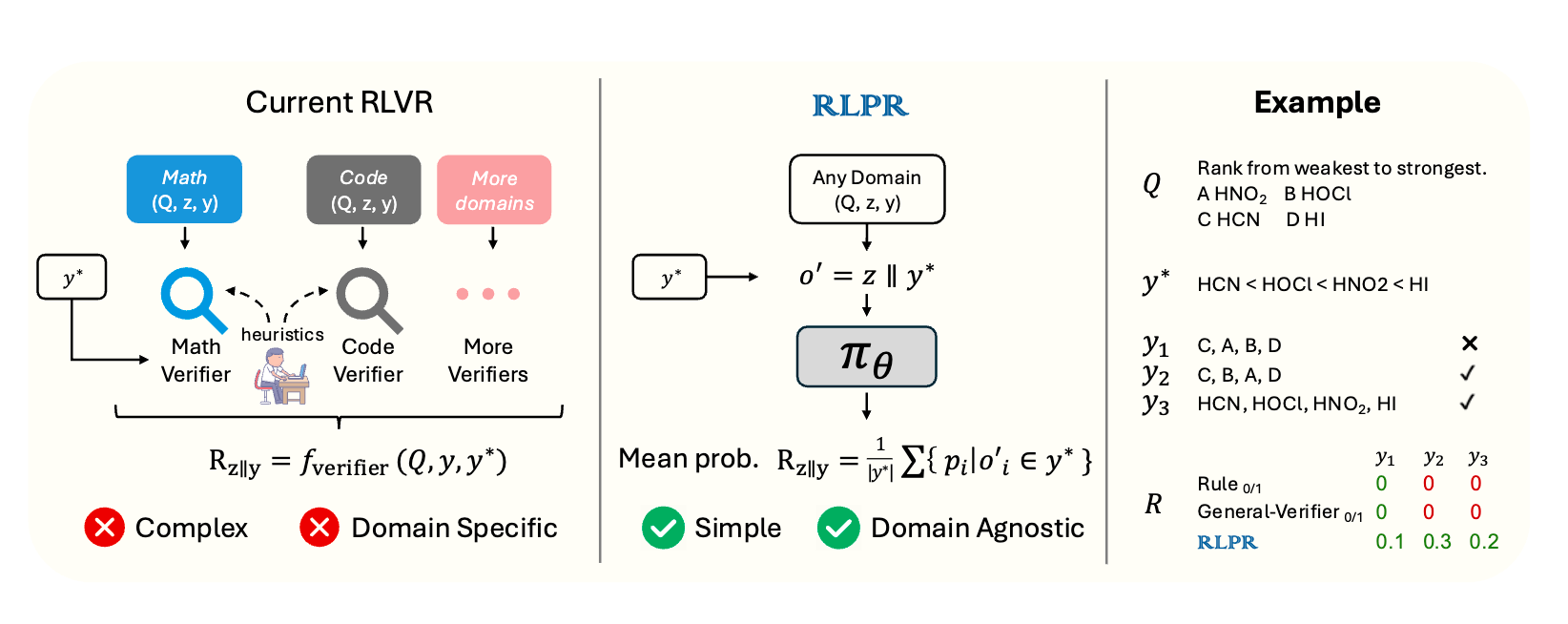
如图1所示,现有的RLVR方法(图左侧)严重依赖于为数学、代码等特定领域定制的验证器,这使得它难以扩展到更多通用领域。
这个“验证器瓶颈”严重阻碍了我们利用强化学习来全面提升LLM在所有知识领域推理能力的步伐。整个领域迫切需要一种能够摆脱验证器束缚的新方法。
2. RLPR框架:从模型自身寻找奖励信号
面对“验证器瓶颈”,RLPR的作者们提出了一个颠覆性的想法:我们真的需要一个外部裁判吗?能不能让模型自己来评判自己? 这正是RLPR(Reinforcement Learning with Reference Probability Reward)框架的核心。
2.1 核心思想:将“自信程度”量化为奖励
RLPR的基本洞见是,LLM在生成文本时,其内部会对每一个可能的词元(token)计算一个概率。一个训练有素的LLM,在经过一段合理、正确的推理后,会以更高的概率生成标准答案中的词元。反之,如果推理过程有误,它生成正确答案的“信心”就会下降。
因此,LLM生成标准答案的内在概率,可以被视为模型对推理质量的一种内隐的、自发的评估。 RLPR正是要捕捉并利用这个内生的信号作为强化学习的奖励,从而彻底绕开外部验证器。如图1(图右侧)所示,RLPR用一个基于模型自身概率的简单奖励计算,替代了RLVR中复杂的、领域特定的验证器模块,实现了“领域无关”(Domain Agnostic)的训练。
为了实现这一思想,RLPR引入了三项关键的技术创新:概率奖励(PR)、奖励去偏(Debiasing) 和 标准差过滤(Standard Deviation Filtering)。
2.2 关键创新一:概率奖励(Probability Reward, PR)的精妙设计
首先,我们需要定义如何从模型的输出概率中计算出奖励值。
传统的RLVR优化目标可以表示为:
其中,是输入问题,是LLM策略模型,是生成的推理过程,是生成的答案,是标准答案,而就是那个麻烦的外部验证器。
RLPR的目标是替换掉。它的具体做法如下:
-
构建新序列:对于一个输入,模型首先生成一个完整的响应,包含推理和答案。然后,RLPR将生成的答案替换为数据集中的标准答案,构建出一个新的、混合的序列(其中表示拼接)。 -
计算概率:将这个新序列喂给模型,计算模型生成该序列中每一个词元的概率。 -
聚合奖励:将属于标准答案部分的所有词元的概率,通过一个聚合函数,计算出一个单一的标量奖励值。
那么,聚合函数应该如何选择呢?一个直观的选择是序列似然度(sequence likelihood),即把所有词元的概率乘起来:。但作者发现,这种方法存在严重问题:它对低概率词元极为敏感,方差极大。
举个例子,假设标准答案是3个词元,两种不同的推理过程分别得到两组概率序列:A=(0.01, 0.7, 0.9)和B=(0.05, 0.7, 0.9)。这两组概率的差异主要在第一个词元上,绝对差异很小。但它们的乘积差异巨大(A为0.0063,B为0.0315,相差5倍),这会导致奖励信号非常不稳定。
为了解决这个问题,RLPR采用了一种更稳健的方式:平均概率(mean probabilities)。
使用平均概率作为奖励,对微小的概率变化不那么敏感,产生的奖励信号更加稳定、鲁棒,并且实验证明与最终答案的质量有更好的相关性。
2.3 关键创新二:巧妙的奖励去偏(Reward Debiasing)
仅仅使用PR作为奖励还不够。作者敏锐地意识到,这个概率奖励不仅受到推理过程质量的影响,还可能受到其他“无关”因素的干扰,比如问题本身的难度、标准答案的文本复杂度(例如,常见词更多的答案本身就更容易获得高概率)等。
我们可以将原始奖励的贡献者分解为两部分:
其中,是我们真正关心的、由推理过程带来的贡献,而则是由问题、标准答案等其他因素带来的“偏见”。如果直接使用进行优化,模型可能会学会利用这些偏见,而不是真正提升推理能力。
为了消除这种偏见,RLPR设计了一个非常巧妙的去偏(Debiasing)步骤:
-
计算基准分:对于同一个问题,RLPR会计算一个没有中间推理过程、直接生成标准答案的概率,得到一个“基准分”。这个可以看作是捕捉了偏见项。 -
计算去偏奖励:真正的奖励,是原始奖励与基准分的差值。
这个差值,直观地衡量了“在加入了推理过程之后,模型生成正确答案的信心的提升量”。这才是对推理质量最纯粹、最直接的度量。最后使用clip函数将奖励值限制在[0, 1]区间内,保证了训练的稳定性。
最终,RLPR的优化目标(梯度估计器)变为:
通过这个精巧的设计,RLPR确保了模型是在为“好的推理”而学习,而非利用数据中的统计偏见。
2.4 关键创新三:自适应课程学习(Standard Deviation Filtering)
在训练过程中,并非所有的问题都具有同等的学习价值。有些问题太简单,模型总是能以很高的奖励轻松解决;有些问题太困难,模型在当前阶段总是得到很低的奖励。这两种情况都无法提供有效的梯度信号来帮助模型学习,反而会浪费计算资源。
传统的做法是设定一个固定的准确率门槛来过滤样本,但这在RLPR的连续奖励设定下难以实施。RLPR再次展现了其设计的巧妙性:它通过分析奖励的标准差(Standard Deviation)来动态地筛选训练样本。
-
识别无效样本:对于一个给定的问题,模型会生成多个不同的推理和答案(例如,采样8个响应)。如果这8个响应的奖励值都非常接近(即标准差很低),这说明这个问题要么太简单(所有响应奖励都很高),要么太难(所有响应奖励都很低)。无论是哪种情况,它对当前的模型来说学习价值都不大。 -
动态过滤:RLPR会过滤掉这些奖励标准差低于某个阈值的样本。 -
自适应阈值:更进一步,这个阈值不是固定的。RLPR使用过去奖励标准差的指数移动平均值(EMA)来动态更新。这意味着随着模型能力的提升,过滤标准也会自适应地调整,始终保持训练集对模型具有一定的挑战性。
这个标准差过滤机制,本质上是一种自适应的课程学习(Adaptive Curriculum Learning)。它确保模型在训练的每个阶段都专注于那些“最值得学习”的问题,从而极大地提升了训练的稳定性和最终的性能。
3. 实验验证:RLPR的全方位性能展示
理论的优雅最终需要实验的支撑。RLPR的作者们进行了一系列详尽的实验,从多个维度验证了其框架的有效性。
3.1 实验设置
-
基础模型:实验涵盖了当前主流的多个开源模型家族,包括 Qwen2.5 (7B)、Llama3.1 (8B) 和 Gemma2 (2B),以保证结论的普适性。 -
训练数据:使用了Ma等人(2025)发布的WebInstruct数据集中的一个子集。为了专注于通用领域推理,作者们特意移除了数学相关的提示,并使用GPT-4.1对数据进行筛选,最终保留了约7.7万条高质量的、有挑战性的通用领域推理问题。 -
评估基准:评估覆盖了7个广泛认可的基准测试,分为两大类: -
通用推理领域:MMLU-Pro、GPQA、TheoremQA、WebInstruct。这些基准涵盖了从研究生水平的科学问题到多学科语言理解的各种复杂推理任务。 -
数学推理领域:MATH-500、Minerva、AIME24。用于测试模型在训练后,其数学能力是否也得到了泛化提升。
-
3.2 主要结果:全面超越,效果显著
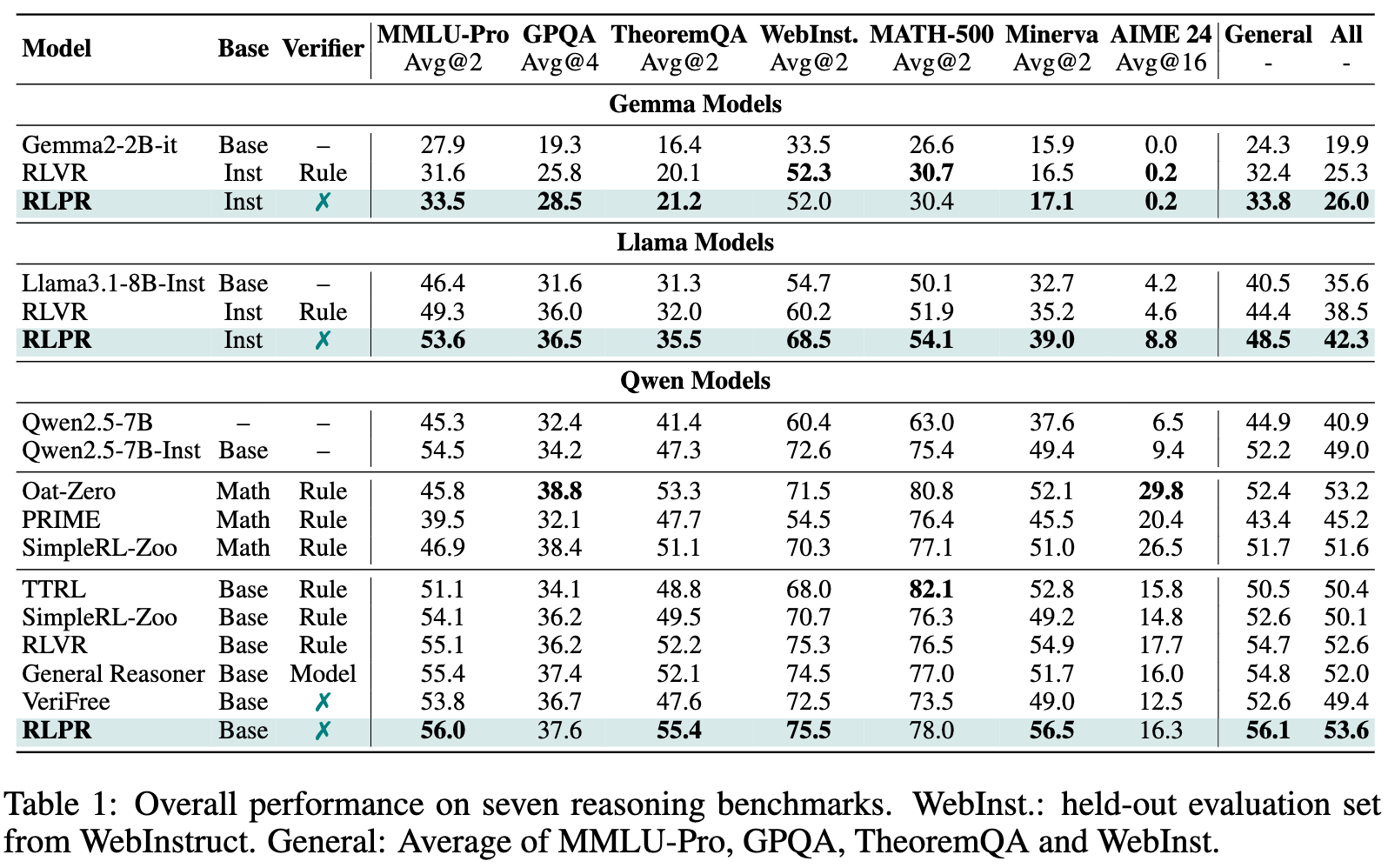
表1展示了RLPR与多种基线方法在7个基准上的详细对比结果。从中我们可以得出几个核心结论:
-
RLPR显著提升通用领域推理能力:相较于基础的指令微调模型(-Inst),RLPR在没有任何外部验证器的情况下,仅在Qwen2.5-7B上,就在四个通用领域基准的平均分上提升了24.9%。这证明了其核心方法的巨大成功。
-
RLPR全面超越传统RLVR:在Qwen、Llama和Gemma三个模型家族中,RLPR的性能都稳定地超过了使用基于规则验证器的传统RLVR方法。例如,在Llama模型上,RLPR在通用领域的平均分比RLVR高出3.9个点,展示了其方法的优越性。
-
RLPR展现出强大的泛化能力:尽管训练数据中不包含数学问题,但经过RLPR训练后,模型在Minerva等多个数学基准上的性能也得到了显著提升。这说明RLPR学到的并不仅仅是特定领域的知识,而是一种更底层的、可泛化的推理能力。
-
RLPR甚至优于依赖模型验证器的方法:实验中的一个重要基线是General Reasoner,它使用了一个专门训练的、拥有15亿参数的LLM作为验证器。令人惊讶的是,简洁的RLPR框架在七个基准上的平均分比这个复杂的系统还要高出1.6个点。这充分说明,利用模型内在概率作为奖励,比依赖一个外部、有监督训练的验证器模型更加有效和高效。
-
RLPR击败同期的无验证器方法:与同期的另一个无验证器工作VeriFree相比,RLPR也展现了巨大的性能优势,在TheoremQA上高出7.6分,在Minerva上高出7.5分。
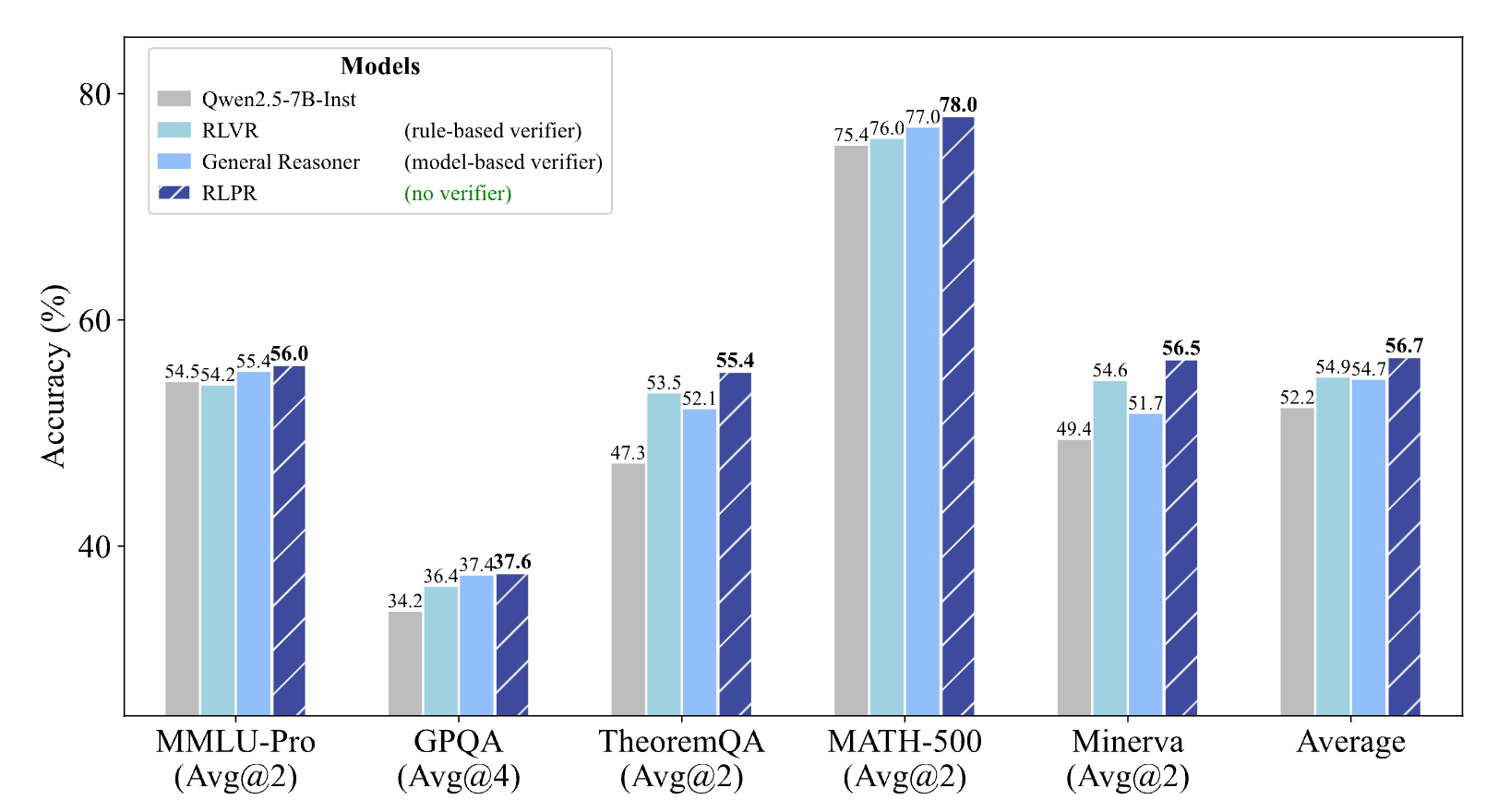
上图直观地展示了RLPR(深蓝色条)在各大基准测试中相较于其他方法(包括使用规则验证器的RLVR和使用模型验证器的General Reasoner)的性能优势。
3.3 奖励质量分析:PR为何优于传统验证器?
RLPR的成功根植于其高质量的奖励信号。为了证明这一点,作者们进行了一项奖励质量分析实验。他们让不同的奖励机制(规则验证器、模型验证器、PR等)去评价一系列模型生成的好坏,并以人类的判断作为黄金标准,计算ROC-AUC分数。AUC越高,代表奖励信号与人类判断越一致,即奖励质量越高。
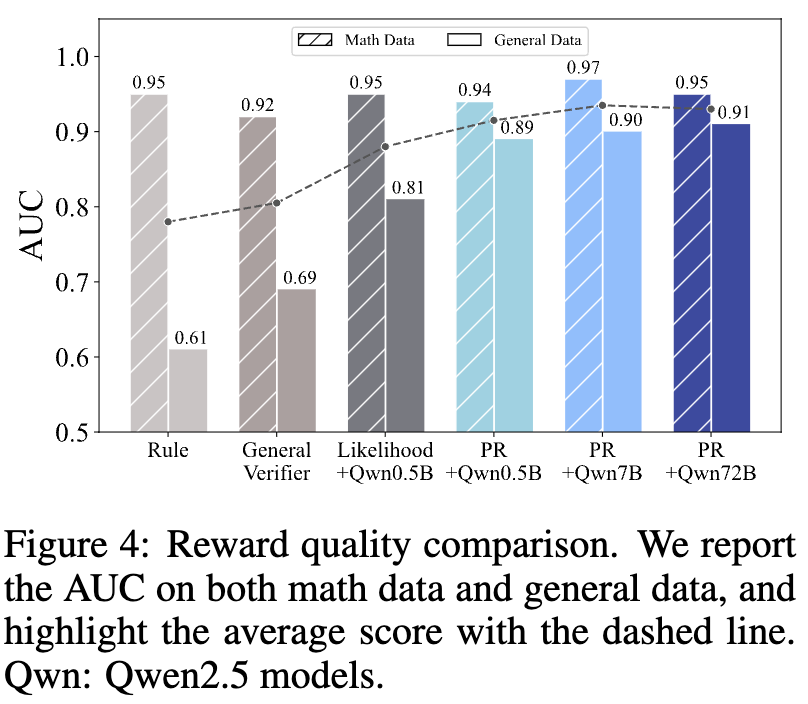
图4的结果令人信服:
-
在通用的WebInstruct数据集上,基于规则的验证器表现很差(AUC仅为0.61),因为它无法理解自然语言的复杂性和多样性,常常将正确的答案误判为错误。 -
模型验证器(General-Verifier)有所改善(AUC为0.69),但仍不理想。分析发现,它在理解复杂响应和解析输出格式方面存在困难。 -
而RLPR提出的概率奖励(PR)表现最佳(AUC高达0.81),远远优于前两者。这证明了PR能够更准确地区分正确与错误的推理,为模型提供高质量的学习信号。 -
更有趣的是,即使是规模小得多的Qwen2.5-0.5B模型,其PR奖励的质量也超过了专门训练的1.5B模型验证器,凸显了PR方法的效率和潜力。
3.4 消融研究:探究RLPR各组件的贡献
为了验证RLPR框架中每个设计选择的必要性,作者进行了一系列消融实验(Ablation Study)。
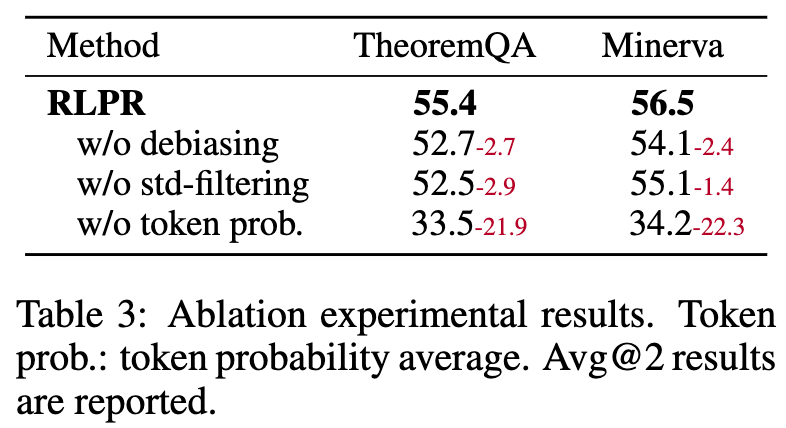
表3的结果清晰地表明:
-
若移除奖励去偏(w/o debiasing),模型在TheoremQA和Minerva上的性能分别下降2.7和2.4个点。这证明了消除问题和答案本身带来的偏见至关重要。 -
若移除标准差过滤(w/o std-filtering),性能同样出现显著下滑(分别下降2.9和1.4个点)。这说明自适应的课程学习机制对于稳定训练和提升最终性能是不可或缺的。 -
若使用序列似然度而非平均概率作为奖励(w/o token prob.),性能会发生“灾难性”的崩溃,直接下降超过20个点。这强有力地印证了平均概率作为奖励信号的稳定性和鲁棒性。
3.5 扩展应用:在可验证领域的锦上添花
RLPR的设计初衷是为了解决通用领域没有验证器的问题。那么,在一个已经存在可靠验证器(如数学领域)的场景下,RLPR还能带来价值吗?
作者们做了一个有趣的实验:他们将基于规则的验证器奖励与RLPR的概率奖励(PR)结合起来,共同作为奖励信号。
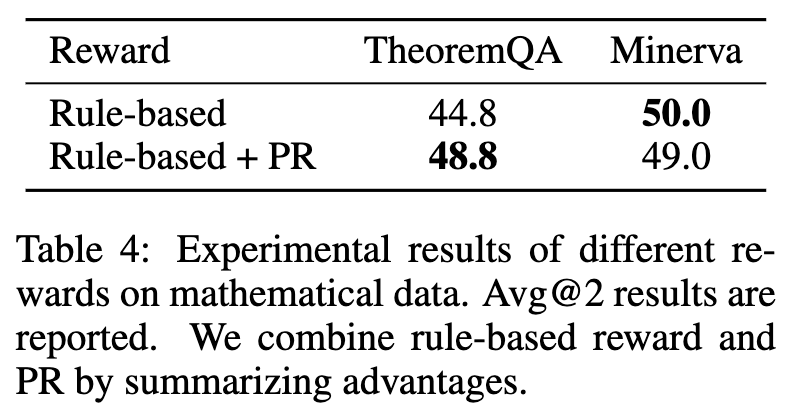
表4的结果显示,Rule-based + PR的组合,其性能优于单独使用Rule-based奖励。这揭示了一个深刻的洞见:
传统的规则验证器只能提供一个二元的、粗糙的奖励信号(对/错)。而PR提供的是一个连续的、细粒度的奖励信号。例如,对于一个答案是“200”的数学题,模型的两个错误输出分别是“199”和“1”。规则验证器会认为两者都是错的,奖励都为0。但直觉上,“199”是一个比“1”好得多的错误答案。PR恰恰能够捕捉到这种细微的差别,为“接近正确”的推理提供更高的奖励,从而帮助模型更有效地学习。
这表明,即使在可验证领域,RLPR的概率奖励依然可以作为一种有力的补充,提供更丰富、更细腻的监督信号。
5. 点评
古德哈特定律指出:“当一个度量变成一个目标时,它就不再是一个好的度量。” 在这里,r - r'(推理带来的概率提升)成为了优化的目标。模型有没有可能学会“欺骗”这个度量?例如,模型可能会学会在推理部分z中生成一些非常“空洞”、“安全”但能统计上最大化y*概率的文本,而不是进行真正深刻的逻辑推理。虽然目前的实验没有显示这个问题,但随着模型变得更强大,这种“钻空子”的风险是存在的。
往期文章:




