大模型强化学习微调不稳定的一个关键来源:训练-推理不匹配(training-inference mismatch)。为了最大化训练效率,框架通常会采用两种不同的计算引擎:一种是为快速推理(rollout)高度优化的引擎,另一种是为梯度计算设计的训练引擎。尽管这两种引擎在数学原理上是等价的,但由于浮点数精度误差和硬件层面的具体优化差异,它们会产生数值上不完全相同的输出。近期的一系列研究已经指出,这种看似微不足道的不匹配,会在优化过程中引入显著的问题,是导致训练不稳定的核心因素之一。
现有的解决方案大多试图通过算法层面的“补丁”来弥补这一差异,其中最主流的方法是基于重要性采样(Importance Sampling, IS)。例如,有工作提出使用令牌级别(token-level)的重要性采样比率来修正梯度,虽然能在一定程度上延长训练过程,但后续研究表明其梯度存在偏差,无法从根本上稳定训练。作为改进,序列级别(sequence-level)的重要性采样被提出,这种方法虽然无偏,但其固有的高方差问题拖慢了收敛速度。更重要的是,这些算法层面的修正方案普遍存在两个基本问题:
-
计算效率低下:为了计算重要性采样比率,它们都需要一次额外的模型前向传播,这会带来大约 25% 的额外训练开销。 -
部署差距(deployment gap)持续存在:这些方法在训练阶段修正了不匹配问题,但最终得到的模型参数仍然是针对训练引擎的概率分布优化的。这意味着,当模型被部署到推理引擎上时,其性能并非最优,从而导致了实际应用中的性能损失。
来自 Sea AI Lab 和新加坡国立大学的论文《Defeating the Training-Inference Mismatch via FP16》回归到了问题的最底层,不再寻求复杂的算法修复,而是探究了这一数值不匹配的根源:浮点数精度。作者发现,当前混合精度训练的主流标准 BFloat16 (BF16) ,正是导致这一问题的“罪魁祸首”。BF16 拥有宽广的动态范围,这对于模型预训练的稳定性至关重要,但其较低的精度(即较少的尾数位)使其对舍入误差高度敏感。这些微小的误差在自回归生成过程中不断累积,最终导致训练和推理策略的概率分布发生显著偏离。

-
论文标题:Defeating the Training-Inference Mismatch via FP16 -
论文链接:https://arxiv.org/pdf/2510.26788
该论文的核心发现与解决方案可以说非常简洁:在 RL 微调阶段,只需将浮点数格式从 BF16 切换回 FP16,即可在很大程度上消除训练-推理不匹配。这一改变:
-
实现简单,现代深度学习框架仅需修改数行代码即可支持。 -
无需对模型架构或学习算法本身进行任何修改。 -
能够带来更稳定的优化、更快的收敛速度和更强的最终性能。
基于 verl 的完整代码见文末。
1. 背景
为了深刻理解为何浮点数精度会成为 RL 微调稳定性的关键,我们首先需要从数学层面剖析训练-推理不匹配所引发的两个核心问题:有偏梯度(Biased Gradient) 和 部署差距(Deployment Gap)。
在现代用于 LLM 微调的 RL 框架中,系统效率的优化催生了推理引擎和训练引擎的分离。推理策略(inference policy)我们记为 ,它通常运行在为速度优化的环境中(例如 vLLM);训练策略(training policy)我们记为 ,它运行在支持反向传播的训练环境中(例如 PyTorch FSDP)。尽管在理想情况下,对于同一组模型参数 ,两者应该是数学等价的(即 ),但由于前文提到的数值差异,它们在实践中会产生偏差。这个偏差带来了两大问题。
1.1. 有偏梯度
在策略优化中,我们的目标是最大化一个目标函数 ,通常是给定提示(prompt) 后,生成的响应(response) 所获得的奖励(reward) 的期望:
其中, 从提示分布 中采样, 根据训练策略 生成。该目标函数的梯度可以通过 REINFORCE 估计器计算得出:
然而,在实践中,为了加速样本生成(rollout),响应 通常是由推理策略 采样的,而不是训练策略 。如果直接忽略这种不匹配,即将从 采样的数据直接用于计算基于 的梯度,那么梯度估计就会变得有偏(biased):
这种有偏的梯度会误导模型的优化方向,是导致训练不稳定的直接原因之一。
1.2. 部署差距
另一个更加隐蔽但影响深远的问题是部署差距。我们在训练循环中优化的是训练策略 ,但最终用于评估和实际部署的却是推理策略 。由于 和 之间存在差异,为训练引擎 优化的参数 对于推理引擎 而言,不一定是最佳的。这可以用以下不等式来描述:
这种部署差距会导致模型在真实应用场景中的性能下降,并且现有的算法补丁本质上无法弥合这一差距,因为它们的设计目标是修正梯度,而非消除 和 的底层差异。
1.3. 通过重要性采样修正有偏梯度
要修正由采样策略和目标策略不一致引入的偏差,一个原则性的方法是使用重要性采样(Importance Sampling, IS)。通过引入一个概率比率(重要性权重)来重新加权梯度计算,可以得到一个无偏的梯度估计器。对于给定的提示 ,修正后的策略梯度如下:
其中, 是用于采样的参数,在同策略(on-policy)设定下 。 是优势函数(advantage),其中 是一个基线(baseline),用于减小梯度的方差。
虽然理论上无偏,但这个估计器在 LLM 的应用中存在严重的高方差问题。因为响应序列 可能很长,导致概率比率 变得极大或极小,从而使得梯度估计的方差爆炸。为了缓解这个问题,作者们提出了一些通过引入少量偏差来大幅降低方差的技巧,例如:
-
截断重要性采样 (Truncated Importance Sampling, TIS) :将重要性权重限制在一个上限 以内。
-
掩码重要性采样 (Masked Importance Sampling, MIS) :只有当重要性权重小于阈值 时,才应用该样本的梯度。
其中 是指示函数。这些方法通过控制重要性权重的幅度来稳定训练。
1.4. 现有框架中的实践
值得注意的是,许多广泛使用的 RL 框架(如 VeRL)是以 GRPO 算法为核心的,它们并未直接实现上述标准的 IS 梯度估计器,而是将 TIS 或 MIS 作为对 GRPO 梯度的“补丁”来应用。标准的 GRPO 梯度(论文中使用的是其变体 Dr.GRPO)计算方式如下,它本身并未修正训练-推理不匹配:
其中 是令牌级别的概率比率, 是优势函数。基于 GRPO,Yao et al. [2025] 引入了令牌级别的 TIS 修正:
其中 是用于修正不匹配的令牌级概率比率。随后,Liu et al. [2025a] 提出了序列级别的 MIS 变体:
其中 是序列级的概率比率。这些基于 GRPO 的修正方法都需要一次额外的前向传播来计算 ,从而带来了前文所述的约 25% 的计算开销。
无论是算法层面还是工程层面的尝试,都未能从根本上解决问题,这凸显了寻找一个更基础、更普适的解决方案的必要性。
2. 重新审视 FP16 精度
论文的作者们在调查训练-推理不匹配问题的过程中,将目光从复杂的算法或工程修复移开,转向了一个更基础的因素:数值精度。他们发现,仅仅是将训练精度从当前占主导地位的 BF16 格式切换到早期的 FP16 格式,就能够显著缓解策略不匹配,并带来 RL 算法性能的提升。本节将详细阐述这两种浮点数格式的差异,并解释为何这一看似简单的改变会产生如此大的影响。
2.1. FP16 vs. BF16:精度与范围的权衡
浮点数格式通过将其比特预算分配给两个主要部分来表示实数:指数位(exponent bits) 和 尾数位(mantissa bits,也称小数位)。指数位决定了数值的动态范围(可以表示多大或多小的数),而尾数位决定了精度(在给定范围内,数值可以被区分得多精细)。FP16 和 BF16 都使用 16 个比特,但它们的分配方式不同,导致了它们在范围和精度之间做出了截然不同的权衡。

-
FP16 (IEEE 754 half-precision) :FP16 将 5 个比特分配给指数,10 个比特分配给尾数。相对较多的尾数位赋予了 FP16 更高的数值精度,使其能够准确表示邻近数值之间的微小差异。然而,其有限的 5 位指数严重限制了动态范围,使得 FP16 容易出现上溢(overflow)(数值超过可表示的最大值)和下溢(underflow)(数值四舍五入到零)的问题。在训练中使用 FP16 通常需要额外的技术(如损失缩放)来保持稳定。
-
BF16 (bfloat16) :由 Google 引入的 BF16 将 8 个比特分配给指数——这与 32 位 FP32 格式的指数位数相同——而只将 7 个比特分配给尾数。这种设计提供了与 FP32 相当的宽广动态范围,使得 BF16 对上溢和下溢具有很强的鲁棒性,但这是以牺牲精度为代价的。其在低精度下的数值稳健性是其在大型深度学习系统中被广泛采用的关键原因。
我们可以通过表格中的 “Next Representable > 1” (大于1的下一个可表示数)来具体感受两者的精度差异。对于 FP16,这个值是 ;而对于 BF16,这个值是 。这表明 FP16 能够表示比 BF16 更密集的数值,或者说,FP16 的精度是 BF16 的 倍。
2.2. 为何 BF16 成为现代 LLM 训练的主流?
尽管 FP16 出现得更早,并且有成熟的稳定化技术,BF16 却后来居上,成为了现代 LLM 预训练的事实标准。其崛起的主要原因在于 易用性。
FP16 的主要挑战——梯度下溢——可以通过一种名为损失缩放(loss scaling)的技术有效解决。其过程很简单:
-
在反向传播前,将损失(loss)乘以一个大的缩放因子 。 -
这会使得所有梯度都相应地乘以 ,将原本可能因过小而落入 FP16 表示范围之外的梯度值“推”回到可表示的范围内,从而保留了梯度信息。 -
在更新权重之前,将梯度除以 以恢复其原始大小。
现代框架已经实现了动态损失缩放(dynamic loss scaling),可以自动调整 的值。然而,这个过程,尤其是在分布式训练中,增加了系统的复杂性。因为它需要在优化器步骤之前进行一次全局同步,以检查是否有梯度溢出(出现无穷大值),并确保所有工作进程(worker)使用相同的缩放因子。
BF16 的出现改变了这一局面。由于其动态范围与 FP32 相同,BF16 对上溢和下溢不敏感,可以作为 FP32 的“直接替代品(drop-in replacement)”,省去了繁琐的损失缩放配置。这种对溢出和下溢的“免疫力”使得 LLM 训练过程显著简化和稳定,因此 BF16 迅速在 Google TPU 和后来的 NVIDIA GPU(从 Ampere 架构开始)上普及开来。
2.3. 为何 FP16 是 RL 微调的关键?
论文的核心论点是:BF16 在预训练阶段的优势(宽动态范围),在 RL 微调阶段反而成为了其劣势(低精度)的根源。
现代 RL 框架为训练和推理使用不同的引擎或优化的 CUDA 核。即使两个引擎都配置为使用 BF16,它们在实现上的微小差异(例如,不同的并行化策略、算子融合方式)也会导致不同的舍入误差。在 BF16 这样低精度的格式下,这些微小的误差会变得更加显著。
当这些单步的、微小的数值差异在自回归采样的长序列中累积时,训练策略 和推理策略 的概率分布就会发生显著的偏离(diverge)。这种偏离正是我们之前讨论的有偏梯度和部署差距的直接来源。
这恰恰是切换回 FP16 能够提供根本性解决方案的原因。凭借其 10 个尾数位,FP16 提供了比 BF16 高 8 倍的精度。这种更高的保真度意味着训练和推理引擎的输出更有可能在数值上保持一致。增加的精度就像一个“缓冲垫”,吸收了两个引擎之间微小的实现差异,防止了舍入误差的累积和最终的策略偏离。
对于 RL 微调而言,模型权重和激活值的动态范围在预训练阶段已经基本确定。因此,BF16 的极端动态范围变得不那么关键,而它所牺牲的精度则成为了主要的瓶颈。通过切换回 FP16,我们实际上是在用非必要的动态范围换取至关重要的精度,从而在不引入任何复杂算法或工程变通方案的情况下,有效地弥合了训练和推理之间的不一致。
3. 实验
为了验证“FP16 能够通过提升数值精度来解决训练-推理不匹配问题”这一核心假设,论文进行了一系列详尽的实验。这些实验从离线分析开始,逐步深入到专门设计的“健全性测试”以及与现有算法的对比,最后扩展到更广泛的泛化场景。
3.1. 离线分析:量化不匹配的程度
在进行 RL 微调实验之前,作者首先进行了一项离线分析,以直观地评估和量化不同数值精度下的训练-推理不匹配程度。
首先,他们使用 DeepSeek-R1-Distill-Qwen-1.5B 模型,在 BF16、FP16 和 FP32 三种精度下,对 AMC 和 AIME 两个基准测试集进行推理,并评估其性能。
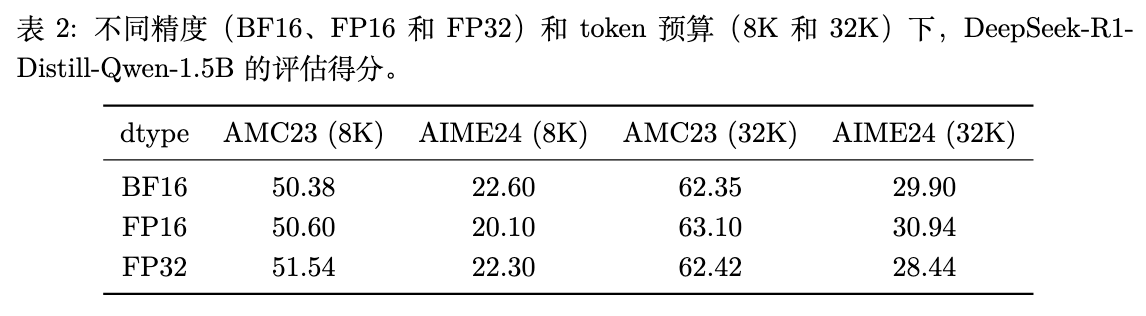
从表 2 可以看出,单纯提高推理时的精度(从 BF16 到 FP16 或 FP32)并不会带来模型性能的显著提升,各项得分基本持平。这个结果排除了“FP16 性能更好仅仅是因为其推理精度更高”这一可能性,并将问题的焦点引向了训练过程中由于 不匹配 造成的动态问题。
接下来是这项工作的关键图表之一,它直观地展示了不匹配的严重程度。作者使用相同的模型权重,分别在 BF16 和 FP16 设置下,通过推理引擎()生成响应,然后通过训练引擎()评估这些响应的对数概率。
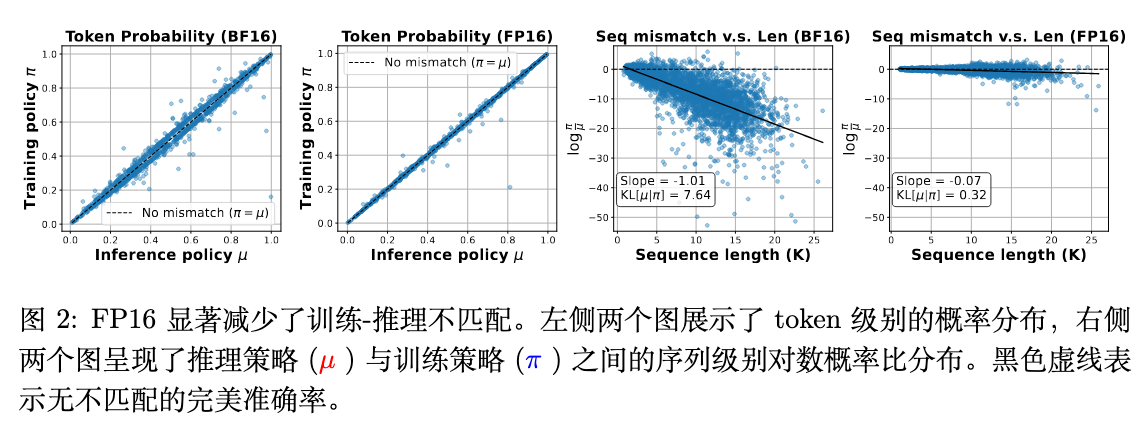
图 2 包含了两个关键信息:
-
左侧两图(token 概率对比):这两个散点图的横轴是推理策略 计算的令牌概率,纵轴是训练策略 计算的概率。黑色的对角虚线代表 的理想情况(无不匹配)。可以清晰地看到,在 BF16 设置下,数据点散布在对角线周围,存在明显的偏差。而在 FP16 设置下,数据点紧密地聚集在对角线上,表明 和 的计算结果高度一致,令牌级别的不匹配被显著减小。
-
右侧两图(序列不匹配 vs. 序列长度):这两个图展示了序列级别的重要性采样权重(以对数形式 表示)如何随生成序列的长度变化。这个权重是衡量整个序列不匹配程度的无偏估计。在 BF16 设置下,我们观察到一个明显的负斜率(Slope = -1.01),这表明随着序列变长,不匹配呈指数级增长。这是因为每一步的舍入误差都在累积。相比之下,在 FP16 设置下,这条线几乎是平的(Slope = -0.07),不匹配程度基本保持在一个非常低的水平,不随序列长度增加而恶化。数据显示,FP16 带来的不匹配比 BF16 小了大约 24 倍。
这一离线分析为论文的核心论点提供了强有力的初步证据:BF16 的低精度确实是导致训练和推理策略之间出现严重、且随序列长度累积的数值偏差的根源,而 FP16 的高精度可以有效地抑制这种偏差。
3.2. RL 算法的“健全性测试”
为了严格地评估 RL 算法的可靠性和鲁棒性,作者设计了一种新颖的 “健全性测试”(Sanity Test)。标准基准测试通常混合了过于简单和模型无法解决的问题,前者浪费计算资源,后者则难以区分是算法缺陷还是模型能力不足。
健全性测试旨在通过构建一个“可完善” (perfectible) 的数据集来消除这种模糊性。在这个数据集上,所有问题对于初始模型来说都是“已知可解但并非琐碎”的。一个设计良好的、可靠的 RL 算法,理论上应该能够在这个数据集上达到接近 100% 的训练准确率。
-
数据集构建:他们从未经微调的 DeepSeek-R1-Distill-Qwen-1.5B 模型出发,针对 MATH 数据集中的每个问题生成 40 个响应。然后,他们只保留那些初始模型准确率在 20% 到 80% 之间的问题,最终得到了一个包含 1460 个问题的目标数据集。 -
评判标准:如果一个 RL 算法在该数据集上的训练准确率能够收敛到某个高阈值(例如 95%)以上,则认为它通过了健全性测试。未能通过测试的算法则被认为在设计上存在不可靠或根本性的缺陷。
这个测试为评估不同算法和设置提供了一个清晰、公平且高效的平台。
3.3. 与现有算法修正的对比
作者在健全性测试的设定下,跨越两个不同的 RL 框架(VeRL 和 Oat)进行了实验,以对比“简单切换到 FP16”与“在 BF16 上应用复杂算法修正”的效果。
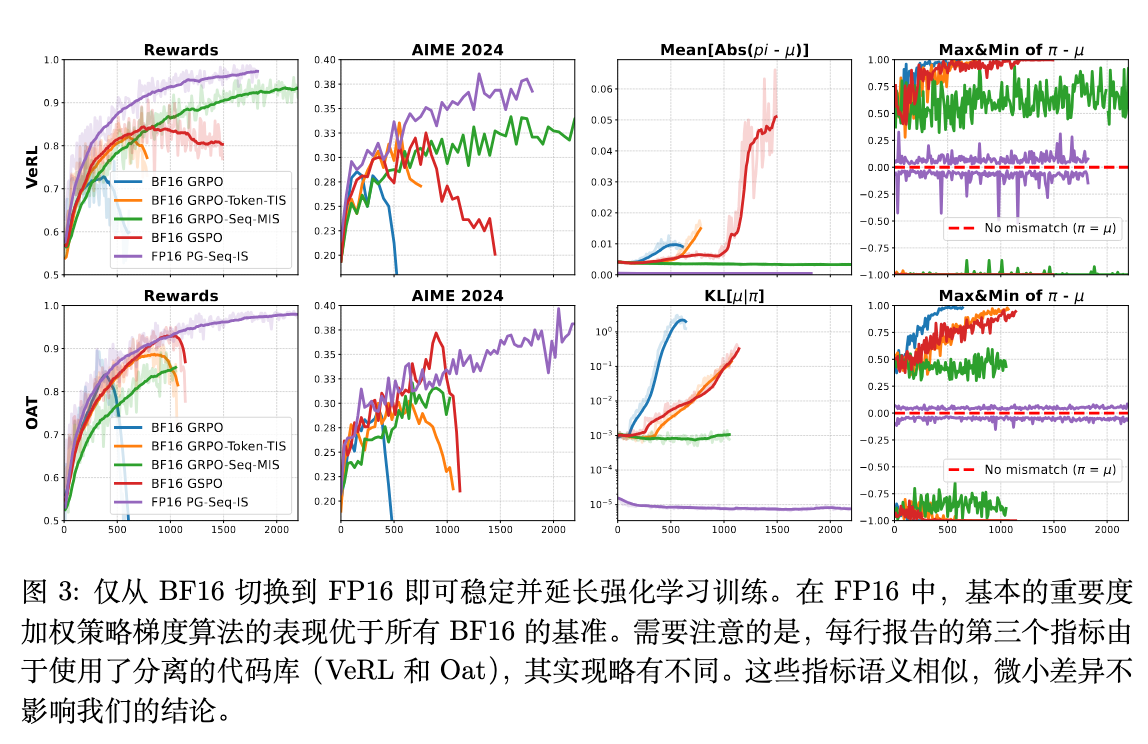
图 3 的结果揭示了深刻的差异:
-
BF16 精度下的表现:
-
Vanilla GRPO(基线):在两个框架中都早早崩溃,性能在达到一个较低的峰值(VeRL 中 73%,Oat 中 84%)后迅速下降。 -
GRPO + Token-TIS:这种修正方法能稍微延长训练,但最终仍然失败,在达到 82% (VeRL) 和 88% (Oat) 的准确率后崩溃。 -
GRPO + Seq-MIS:在所有 BF16 算法修正中,只有这个方法保持了训练的稳定而没有崩溃。然而,这种稳定性是有代价的:由于其序列级别重要性比率的高方差(如图 2 所示),它的收敛速度非常缓慢。更重要的是,即使在训练峰值,它也表现出显著的部署差距,其在 AIME 2024 验证集上的得分远低于 FP16 方法。 -
GSPO:也表现出不稳定的训练行为。
-
-
FP16 精度下的表现:
-
与上述所有复杂的 BF16 算法形成鲜明对比,一个在 FP16 上运行的、最基础的重要性采样策略梯度算法(PG-Seq-IS),表现出了压倒性的优势。它的训练过程稳定、收敛速度快,并且在奖励和验证集得分上都达到了更高的水平,在健全性测试中轻松达到了接近 100% 的准确率。
-
-
不匹配作为预警信号:图 3 中的
Mean[Abs(π - μ)]和Max&Min of π - μ等指标图表揭示了一个有趣的现象。对于那些最终崩溃的 BF16 算法,在崩溃前夕,训练-推理不匹配指标都出现了急剧增长。这表明不匹配程度可以作为训练即将崩溃的早期预警信号。相反,所有稳定训练的算法(包括 FP16 方法和 BF16 的 Seq-MIS)都保持了有界的不匹配。而 FP16 的不匹配水平远低于任何 BF16 方法。
这个实验有力地证明,在精度层面解决不匹配问题(切换到 FP16),比在算法层面应用不稳定或低效的修正,是一种更直接、更有效的解决方案。
3.4. 在 FP16 下重新审视 RL 算法
既然 FP16 能够显著降低不匹配,那么在 FP16 环境下,那些为处理不匹配而设计的复杂 RL 算法是否还有存在的必要?作者对此进行了进一步的探索。
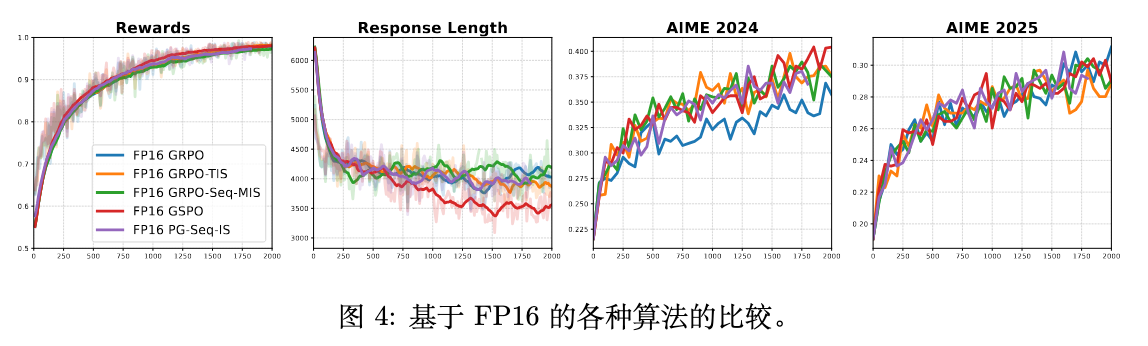
如图 4 所示,当所有算法都在 FP16 精度下进行训练时,它们之间的性能差异变得微乎其微。无论是 GRPO、TIS、MIS 还是最简单的 PG-IS,它们的奖励曲线和验证集得分都高度重合。
这一结果的解释是:FP16 将优化问题有效地转化为了一个近似于同策略(on-policy)的设置。由于训练和推理策略之间的偏差被大幅缩小,那些为修正偏差而设计的复杂机制(如截断、掩码等)失去了用武之地,因而无法提供额外的增益。在这个近乎理想的优化环境中,最简单的无偏策略梯度方法已经足够好。
3.5. 精度组合的消融实验
为了进一步隔离训练精度和推理精度的影响,作者进行了一项消融研究,测试了不同的精度组合。
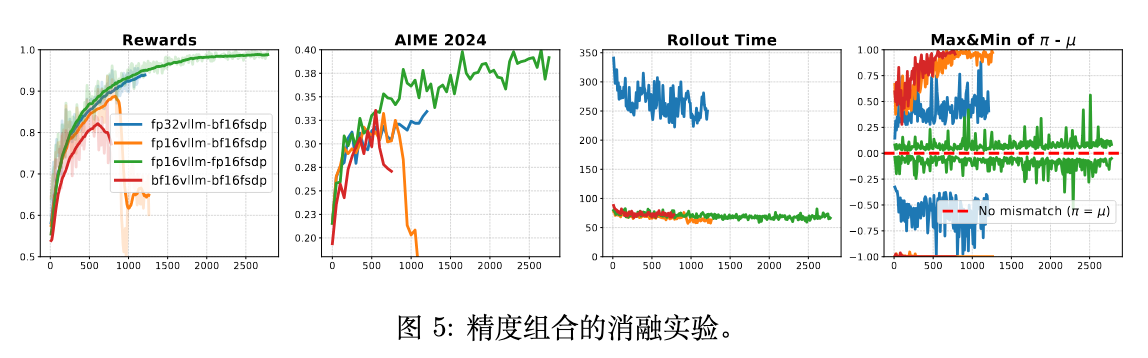
这项实验的结果非常清晰:
-
当训练精度为 BF16 时:提高推理精度(使用 FP16 或 FP32)确实能够延长训练稳定并提升性能。特别是当与 FP32 推理配对时,训练过程完全稳定,没有崩溃。这进一步证实了不匹配是问题的核心。然而,这种稳定性的代价是巨大的:FP32 推理的速度比 FP16 或 BF16 慢了近三倍,使得这种组合在实际大规模实验中不具备可行性。 -
当训练精度为 FP16 时:将训练和推理都设置为 FP16 的组合取得了最佳结果。它不仅产生了最低的训练-推理不匹配,还带来了最稳定的训练动态。它在完美可解数据集上成功达到了近 100% 的训练准确率,并且没有任何速度损失,展现了在稳定性和效率上的双重优势。
4. 泛化性验证
为了证明“使用 FP16 稳定 RL 微调”这一发现的普适性,而不仅仅是在特定实验设置下的偶然现象,论文将验证范围扩展到了更多样化的场景,包括混合专家(MoE)模型、低秩自适应(LoRA)微调、大规模稠密模型以及不同的模型家族。这些实验结果统一展示在论文的图 1 和图 6 中。
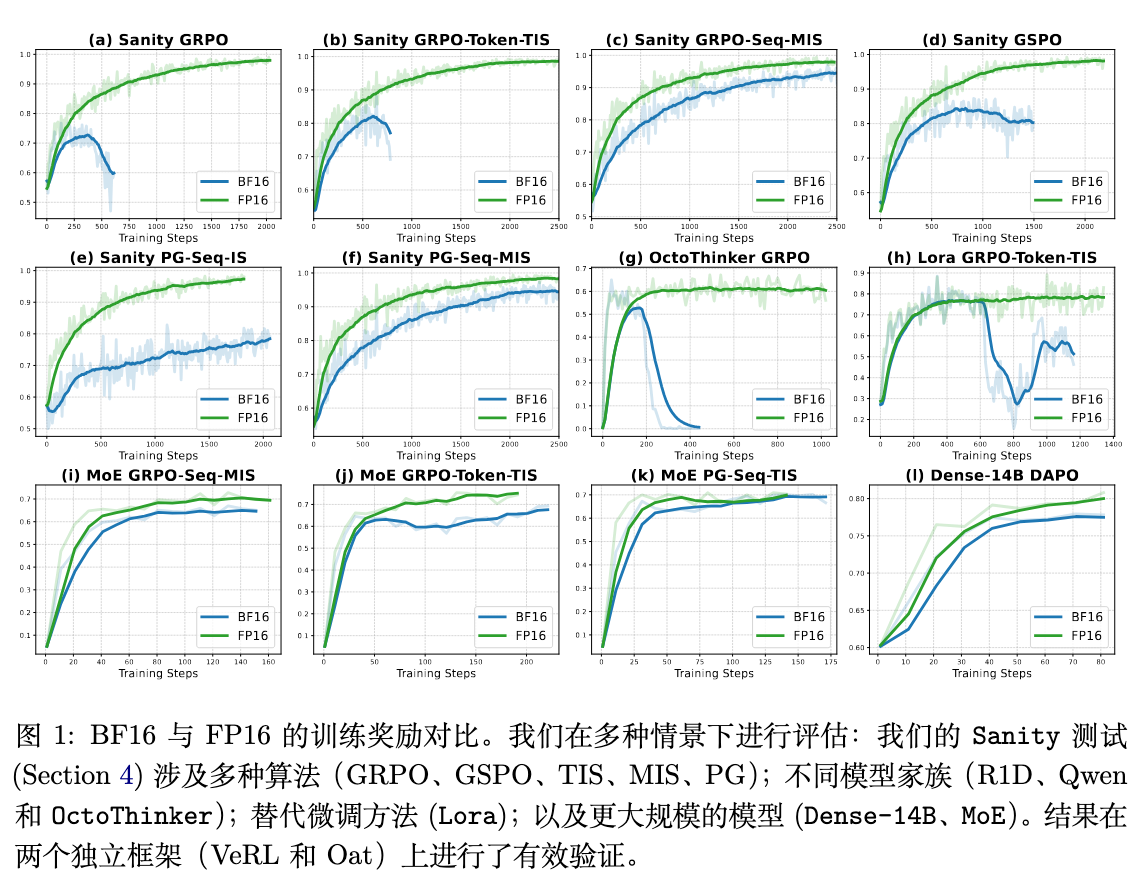
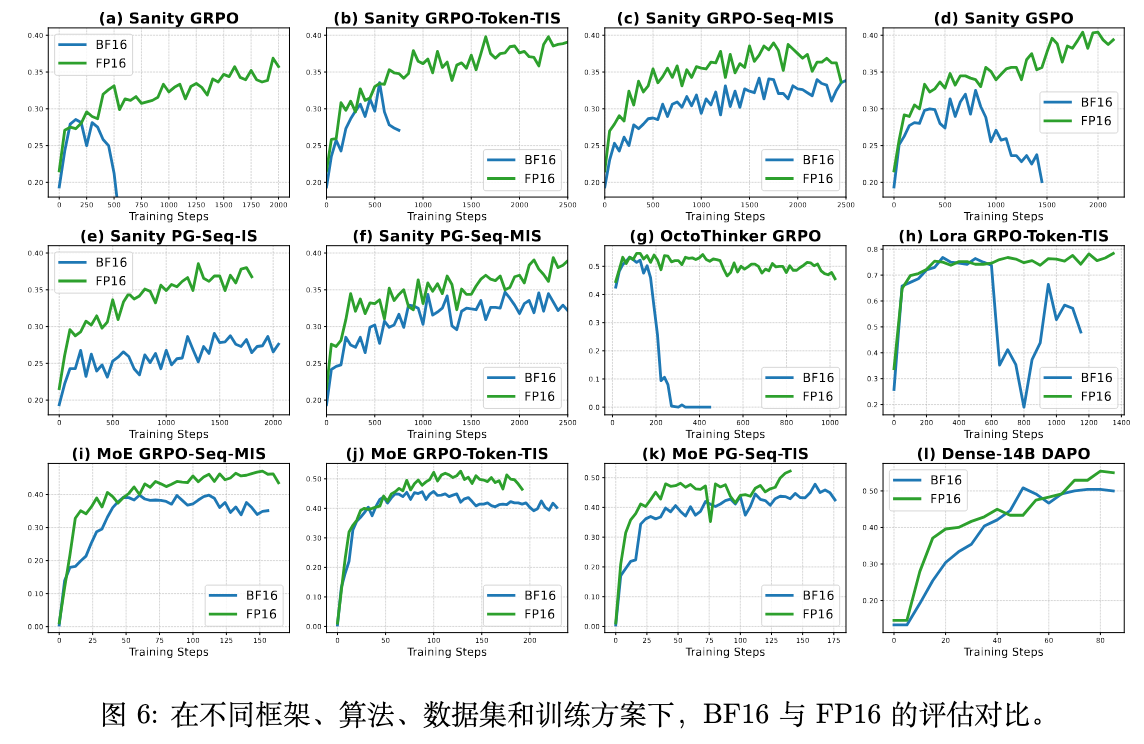
4.1. 混合专家(MoE)模型 RL
MoE 模型的 RL 训练以其不稳定性而闻名,通常需要复杂的稳定化策略。MoE 模型的训练和推理通常涉及不同的并行化策略和对精度敏感的操作(如 top-k 专家选择),这进一步加剧了训练-推理不匹配问题。
作者在 Qwen3-30B-A3B-Base 这一 MoE 模型上进行了实验。如图 1 中的 (i), (j), (k) 所示,在三种不同的 RL 算法(GRPO-Seq-MIS, GRPO-Token-TIS, PG-Seq-TIS)下,FP16 的表现都一致地优于 BF16。FP16 带来了更稳定的训练过程和持续更高的训练奖励。这表明,对于本身就更易出现不匹配问题的 MoE 模型,采用 FP16 是一种有效的缓解手段。
4.2. 低秩自适应(LoRA) RL
由于其高效性和与全参数微调相当的性能,LoRA 近期在 LLM RL 领域重新受到青睐。为了检验精度对 LoRA-based RL 的影响,作者使用 GRPO-Token-TIS 算法在标准 MATH 数据集上训练了 Qwen2.5-Math-1.5B 模型。
如图 1 (h) 所示,结果非常显著。基于 BF16 的 LoRA 训练在大约 600 步后就崩溃了,而 FP16 则自始至终保持了稳定的训练。这说明精度问题在参数高效的微调方法中同样存在,并且 FP16 同样是解决方案。
4.3. 大规模稠密模型上的 RL
现代 LLM 的一个趋势是模型规模的不断增大。为了验证结论是否适用于更大规模的模型,作者在 Qwen3-14B-Base 这一大型稠密模型上进行了实验。
如图 1 (l) 所示,使用 FP16 的训练奖励增长速度远快于 BF16。对应的评估结果(图 6 (l))也显示 FP16 在 AIME 2024 验证集上取得了更高的准确率。这些结果表明,使用 FP16 替代 BF16 同样能够有效缓解大规模模型中的训练-推理不匹配问题,并有潜力用于扩展更大模型的 RL 训练。
4.4. 其他模型家族上的 RL
为了确保结论不局限于 Qwen 系列模型,作者还将实验扩展到了其他模型家族。他们使用 GRPO 算法训练了 OctoThinker-3B 模型,这是一个基于 Llama3.2-3B 并针对推理数据进行过中间训练的模型。
如图 1 (g) 所示,同样的模式再次出现。BF16 的训练在约 150 步后由于数值不匹配而变得不稳定并最终崩溃,而 FP16 则继续平稳地进行训练。这加强了“FP16 优于 BF16”这一结论的普适性,表明它与具体的模型架构无关。
5. 讨论与结论
这篇论文的工作为 RL 微调领域长期存在的不稳定性问题提供了一个基础层面但影响深远的解释和解决方案。
5.1. 重新思考 RL 微调中的精度权衡
数值精度是 LLM 训练技术栈中的一个基础性选择,然而长期以来,这个选择一直由 BF16 主导,无论是预训练还是后训练阶段,人们看重的都是其宽广的动态范围和易用性。然而,本文的研究结果表明,对于 RL 微调这个特定的阶段,这一默认选择值得我们进行仔细的重新审视。
在 RL 微调阶段,训练-推理不匹配成为了不稳定性的一个关键来源,而 BF16 的低精度恰恰加剧了这个问题。论文证明,通过简单地将 BF16 的宽动态范围换成 FP16 的高精度,就可以实现显著更稳定的 RL 训练、更快的收敛和更优的最终性能。
当然,这并不意味着 FP16 是一个放之四海而皆准的最优解。对极致效率的追求可能会催生出更低精度的格式(如 FP8)。同时,在极大模型上使用 FP16 可能会因其有限的动态范围而带来新的工程挑战(如管理潜在的溢出)。但论文的工作启发我们,FP16 是一个强大的、并且在 RL 微调场景下通常更合适的选择。
5.2. BF16 精度下的偏见-方差权衡
论文在第 4.2 节的实验结果揭示了在 BF16 精度下,不同 RL 算法之间存在一个偏见-方差权衡(bias-variance tradeoff)。
-
低方差但高偏见的方法(如 GRPO, Token-level TIS, GSPO)初期收敛快,但由于其对策略不匹配的修正不准确(有偏),最终会变得不稳定并崩溃。 -
低偏见但高方差的方法(如 PG-Seq-IS, GRPO-Seq-MIS)能更准确地修正策略不匹配,因此实现了稳定性,但代价是其重要性采样权重的高方差拖慢了收敛。
然而,在 FP16 精度下,这种权衡变得不再那么关键。通过从根本上减少训练-推理不匹配,FP16 自然地同时降低了由不匹配引入的偏见和重要性采样修正的方差。这种内在的稳定性增强,使得即便是最朴素的策略梯度估计器也能高效地收敛。这创造了一种新的训练动态,其中所有被测试的算法都表现良好,稳定性和收敛速度之间的紧张关系得到了有效化解。
5.3. 结论
这项工作论证了 RL 微调中一个主要的稳定性瓶颈——训练-推理不匹配——其根本原因在于数值精度问题。现有的算法修复方案往往复杂且低效,而本文的研究表明,简单地将浮点数格式从标准的 BF16 切换到高精度的 FP16,就可以在很大程度上消除这种不匹配。
这个单一、高效的改变带来了更稳定的训练、更快的收敛和更优的性能,证明了在精度层面解决问题是一种更有效的策略。我们由此得出结论:FP16 应该被重新考虑,作为 LLM 进行鲁棒 RL 微调的一个基础性选项。
完整代码:
diff --git a/verl/trainer/config/actor/actor.yaml b/verl/trainer/config/actor/actor.yaml
index d5402d87..fc6b949e 100644
--- a/verl/trainer/config/actor/actor.yaml
+++ b/verl/trainer/config/actor/actor.yaml
@@ -8,6 +8,8 @@
# fsdp, fsdp2 or megatron. must be set.
strategy: ???
+dtype: float16
+
# Split each sample into sub-batches of this size for PPO
ppo_mini_batch_size: 256
diff --git a/verl/trainer/config/rollout/rollout.yaml b/verl/trainer/config/rollout/rollout.yaml
index fc3af80d..00f19ef0 100644
--- a/verl/trainer/config/rollout/rollout.yaml
+++ b/verl/trainer/config/rollout/rollout.yaml
@@ -23,7 +23,7 @@ response_length: ${oc.select:data.max_response_length,512}
# for vllm rollout
# Rollout model parameters type. Align with actor model's FSDP/Megatron type.
-dtype: bfloat16
+dtype: float16
# Fraction of GPU memory used by vLLM/SGLang for KV cache.
gpu_memory_utilization: 0.5
diff --git a/verl/workers/actor/dp_actor.py b/verl/workers/actor/dp_actor.py
index d5cea362..a24cff53 100644
--- a/verl/workers/actor/dp_actor.py
+++ b/verl/workers/actor/dp_actor.py
@@ -76,6 +76,12 @@ class DataParallelPPOActor(BasePPOActor):
else entropy_from_logits
)
self.device_name = get_device_name()
+ assert self.config.dtype in ["float16", "float32", "bfloat16"]
+ if self.config.dtype == "float16":
+ from torch.distributed.fsdp.sharded_grad_scaler import ShardedGradScaler
+ self.scaler = ShardedGradScaler(growth_interval=400)
+ else:
+ self.scaler = None
def _forward_micro_batch(
self, micro_batch, temperature, calculate_entropy=False
@@ -97,7 +103,9 @@ class DataParallelPPOActor(BasePPOActor):
[inputs[key] for inputs in micro_batch["multi_modal_inputs"]], dim=0
)
- with torch.autocast(device_type=self.device_name, dtype=torch.bfloat16):
+ from verl.utils.torch_dtypes import PrecisionType
+ torch_dtype = PrecisionType.to_dtype(self.config.dtype)
+ with torch.autocast(device_type=self.device_name, dtype=torch_dtype):
input_ids = micro_batch["input_ids"]
batch_size, seqlen = input_ids.shape
attention_mask = micro_batch["attention_mask"]
@@ -272,6 +280,8 @@ class DataParallelPPOActor(BasePPOActor):
def _optimizer_step(self):
assert self.config.grad_clip is not None
+ if self.scaler is not None:
+ self.scaler.unscale_(self.actor_optimizer)
if isinstance(self.actor_module, FSDP):
grad_norm = self.actor_module.clip_grad_norm_(max_norm=self.config.grad_clip)
elif isinstance(self.actor_module, FSDPModule):
@@ -279,12 +289,17 @@ class DataParallelPPOActor(BasePPOActor):
else:
grad_norm = torch.nn.utils.clip_grad_norm_(self.actor_module.parameters(), max_norm=self.config.grad_clip)
- # if grad_norm is not finite, skip the update
- if not torch.isfinite(grad_norm):
- print(f"WARN: rank {torch.distributed.get_rank()} grad_norm is not finite: {grad_norm}")
- self.actor_optimizer.zero_grad()
+ if self.scaler is not None:
+ self.scaler.step(self.actor_optimizer)
+ self.scaler.update()
else:
- self.actor_optimizer.step()
+ # if grad_norm is not finite, skip the update
+ if not torch.isfinite(grad_norm):
+ print(f"WARN: rank {torch.distributed.get_rank()} grad_norm is not finite: {grad_norm}")
+ self.actor_optimizer.zero_grad()
+ else:
+ self.actor_optimizer.step()
+
return grad_norm
@GPUMemoryLogger(role="dp actor", logger=logger)
@@ -467,7 +482,10 @@ class DataParallelPPOActor(BasePPOActor):
loss = policy_loss * (response_mask.shape[0] / self.config.ppo_mini_batch_size)
else:
loss = policy_loss / self.gradient_accumulation
- loss.backward()
+ if self.scaler is not None:
+ self.scaler.scale(loss).backward()
+ else:
+ loss.backward()
micro_batch_metrics.update(
{
diff --git a/verl/workers/fsdp_workers.py b/verl/workers/fsdp_workers.py
index 4141d986..99513218 100644
--- a/verl/workers/fsdp_workers.py
+++ b/verl/workers/fsdp_workers.py
@@ -243,9 +243,10 @@ class ActorRolloutRefWorker(Worker, DistProfilerExtension):
else:
self.tokenizer.chat_template = self.config.model.custom_chat_template
+ vllm_dtype = PrecisionType.to_dtype(self.config.rollout.dtype)
torch_dtype = fsdp_config.get("model_dtype", None)
if torch_dtype is None:
- torch_dtype = torch.float32 if self._is_actor else torch.bfloat16
+ torch_dtype = torch.float32 if self._is_actor else vllm_dtype
else:
torch_dtype = PrecisionType.to_dtype(torch_dtype)
@@ -340,7 +341,7 @@ class ActorRolloutRefWorker(Worker, DistProfilerExtension):
reduce_dtype = PrecisionType.to_dtype(mixed_precision_config.get("reduce_dtype", "fp32"))
buffer_dtype = PrecisionType.to_dtype(mixed_precision_config.get("buffer_dtype", "fp32"))
else:
- param_dtype = torch.bfloat16
+ param_dtype = PrecisionType.to_dtype(self.config.actor.get("dtype", "float16"))
reduce_dtype = torch.float32
buffer_dtype = torch.float32
往期文章:




