腾讯提出单流策略优化（SPO）：告别组同步瓶颈，回归RL本质

当前，流行的范式是所谓的 group-based 方法，其代表是组相对策略优化（Group Relative Policy Optimization, GRPO）。这类方法的核心思想是，针对同一个输入提示（prompt），生成一个包含多个（例如8个或16个）候选响应的“组”。通过比较组成员的表现，可以“即时”（on-the-fly）地构建一个基线（baseline），用于计算每个响应的相对优势（advantage），从而降低策略梯度的方差，稳定训练过程。这种方法在许多推理任务上推动了最佳性能的提升。

然而，在实践中却存在两个缺陷：

1. 退化组（Degenerate Groups）与计算浪费：一个常见且棘手的情况是，对于某个特定的提示，模型生成的组内所有响应可能获得完全相同的结果——要么全部正确，要么全部错误。在这种情况下，所有响应的奖励值都一样，导致计算出的相对优势全部为零。零优势意味着零学习信号，梯度更新无法进行。这批为了构建基线而付出的生成和评估计算，就此被完全浪费。随着模型能力的提升或对于特定难度区间的提示，这种情况的发生频率会变得很高，造成了严重的计算资源浪费。
2. 同步屏障（Synchronization Barrier）与可扩展性瓶颈：在分布式训练环境中， group-based 方法要求必须等待组内所有成员都完成生成和评估后，才能进行下一步的梯度计算。这个过程形成了一个严格的“同步屏障”。这个问题的严重性在处理复杂智能体（agentic）任务时被急剧放大。这类任务往往涉及多轮工具调用或长程推理，导致不同响应的生成时间（latency）差异巨大。一个耗时超长的“拖后腿”样本（straggler）会迫使整个组的所有计算资源进入闲置等待状态，极大地拖慢了训练吞吐率，严重制约了模型训练的可扩展性。

来自腾讯的论文《Single-stream Policy Optimization》中，为这个问题提供了一个清晰且有力的回答。他们提出的单流策略优化（Single-stream Policy Optimization, SPO），主张回归到经典强化学习的“单流”（single-stream）范式，即每个训练样本就是一个独立的（提示，响应）对。SPO 并非对过往方法的简单回归，而是通过引入一套精心设计的协同组件，在单流框架下解决了高方差这一核心挑战，从而构建了一个更高效、更具可扩展性的 LLM 策略优化框架。

• 论文标题：Single-stream Policy Optimization
• 论文链接：https://arxiv.org/pdf/2509.13232

SPO 的核心思想是通过三个关键设计来取代 group-based 方法中的即时基线：

• 一个持久化的、KL-自适应的价值追踪器，用于提供稳定、低方差的基线估计。
• 一个全局的、跨批次的优势归一化方案，以避免小样本统计带来的不稳定性。
• 一个基于不确定性的优先提示采样机制，以实现自适应的课程学习。

1. 背景

为了更好地理解 SPO 的创新之处，我们首先简要回顾一下其所基于和意图改进的基础概念。

1.1 策略梯度与REINFORCE算法

强化学习的目标是优化一个策略 ，使其在给定提示 时生成的响应 能够最大化期望奖励 。该目标函数定义为：

其中， 是提示的分布， 是对响应 的奖励函数。根据策略梯度定理，该目标的梯度为：

REINFORCE 算法直接使用蒙特卡洛采样来估计这个梯度，并据此更新策略参数 。然而，这个梯度估计量的方差通常非常大，因为奖励 本身可能在很大范围内波动。高方差的梯度会导致训练过程不稳定，收敛缓慢。

1.2 基线与优势函数

为了降低方差，一个标准的技术是引入一个与动作 无关的基线 ，并从奖励中减去它。这不会改变梯度的期望（因为 ），但可以减小其方差。修改后的梯度估计为：

其中，项 被称为优势函数（Advantage Function）。理论上，能够最小化方差的最优基线是策略的真实价值函数 。然而，真实价值函数是未知的，必须对其进行估计。

1.3 组相对策略优化（GRPO）

GRPO 提供了一种简单直接的价值函数估计方法。它为每个提示 生成一个包含 个响应 的组，然后使用这个组的平均奖励作为基线：

对于组内的某个样本 ，其原始优势就是 。进一步，GRPO 会在组内对这些优势进行归一化（通常是减去均值并除以标准差），以获得最终用于策略更新的信号。

虽然 GRPO 在实践中有效，但它正是前文所述的两个根本性缺陷的根源。它的基线估计完全依赖于一个非常小的样本集（一个组），这使得基线本身方差很大，并且当组内奖励一致时，优势信号完全消失。同时，对组的依赖性也带来了无法避免的同步开销。

2. SPO

SPO 的设计哲学是：用一个持久化的、跨时间步的低方差价值估计，取代一个临时的、组内的、高方差的价值估计。它通过三个协同工作的组件实现了这一点。

2.1 KL-自适应价值追踪器

SPO 的核心是一个为每个提示 维护的价值追踪器（value tracker），它旨在提供对当前策略 下的成功概率 的一个稳定估计，我们记为 。

在 LLM 推理任务中，奖励通常是二元的（例如，答案正确为1，错误为0）。对于这种伯努利过程，使用 Beta 分布 来建模成功概率是一个自然且优雅的选择，因为 Beta 分布是伯努利分布的共轭先验。

具体来说，SPO 为每个提示 维护一个 Beta 分布 。这里的 和 可以被直观地理解为该提示历史上“伪”成功和“伪”失败的次数。价值的估计值就是这个 Beta 分布的后验均值：

策略 在训练过程中是不断变化的，因此价值函数 也是非平稳的。一个好的价值追踪器必须能够适应策略的变化，即当策略改变时，它应该更多地依赖新的观测，并逐渐“遗忘”旧的、可能已不再相关的历史信息。

SPO 通过一个KL-自适应的遗忘机制来实现这一点。在每次观测到一个新的奖励 后，它不是直接更新 和 ，而是先将旧的参数 乘以一个折扣因子 ，然后再加入新的观测：

这里的折扣因子 是关键。它由当前策略 与上一次处理提示 时的策略 之间的 KL 散度 决定：

是一个超参数，表示当 KL 散度达到该值时，历史信息的“半衰期”。这个设计的精妙之处在于：

• 如果策略针对提示 的更新很小（），那么 ，追踪器会保留大部分历史信息，保持估计的稳定性。
• 如果策略发生了剧烈变化（ 很大），那么 会变小，追踪器会快速“遗忘”过去，从而更快地适应新策略下的价值函数。

这个贝叶斯更新过程，等价于一个学习率自适应的指数移动平均（EMA）：

其中，学习率 会同时根据策略变化（通过 ）和统计置信度（通过有效样本量 ）进行自适应调整。

2.2 全局优势估计与策略优化

拥有了稳定的价值估计 后，优势的计算变得非常直接。对于在第 次迭代中由策略 生成的样本 ，其原始优势为：

这里使用上一步的价值估计 是一个重要的细节。因为 不依赖于当前步骤生成的动作 ，这保证了基线与动作的无关性，从而确保了策略梯度的无偏性。

接下来是 SPO 的第二个关键设计：全局优势归一化。GRPO 在一个小的组内计算均值和标准差来归一化优势，这些统计量本身就存在很大的噪声。SPO 则在整个训练批次（batch） 的所有样本上计算优势的均值 和标准差 ，然后进行归一化：

由于一个训练批次通常包含数千个样本，远大于一个组的大小 ，因此 和 是稳定得多的统计量，这使得归一化后的优势信号质量更高，训练动态更稳定。

最后，将这个归一化的优势 应用于响应序列 中的每一个 token，并使用标准的 PPO-Clip 损失函数来更新策略网络。

2.3 优先提示采样

为了进一步提升数据效率，SPO 引入了一套课程学习（curriculum learning）策略，即优先提示采样（Prioritized Prompt Sampling）。其核心思想是，在每个训练迭代开始时，不从数据集中均匀采样提示，而是优先选择那些对当前模型来说“学习潜力”最大的提示。

SPO 使用以下权重 来对提示 进行采样：

这个公式的构成非常直观：

• 第一项 正是对应于成功概率为 的伯努利试验的标准差。这个值在 时达到最大，在 接近 0 或 1 时趋于零。这意味着，SPO 会优先采样那些模型最不确定能否成功的提示。这些提示既不是模型已经完全掌握的（），也不是目前看来毫无希望的（），它们恰好位于模型能力的前沿，提供了最丰富的学习信号。
• 第二项 是一个小的探索奖励，确保即使是那些被认为已经掌握或太难的提示，也始终有被采样的机会，防止课程学习陷入局部最优。

2.4 算法流程总结

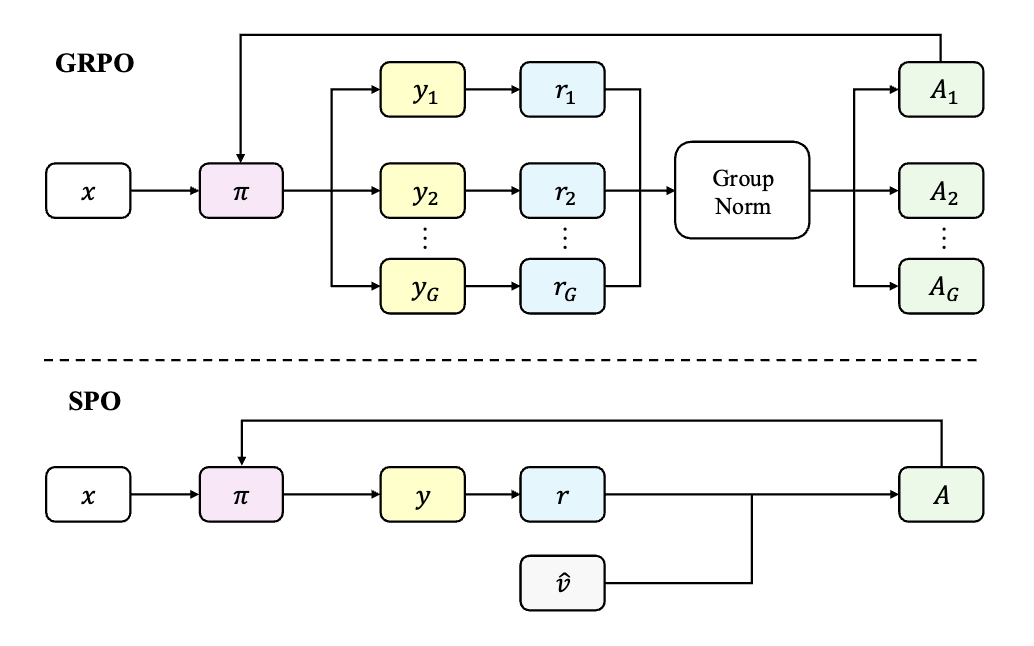
SPO 的完整训练流程可以总结如下（对应论文中的 Algorithm 1）：

1. 对于每次迭代 i = 1, 2, ..., T：
2. 计算采样权重：根据当前的价值追踪器 ，为数据集中的每个提示 计算采样权重 。
3. 采样提示：根据权重 从数据集中采样一个批次的提示 。
4. 生成与评估：对于 中的每个提示 ，使用当前策略 生成一个单一的响应 ，并获得奖励 。
5. 计算优势：计算原始优势 。
6. 更新价值追踪器：使用新的观测 来更新提示 的价值追踪器 。
7. 全局归一化：在整个批次 上，对所有优势进行归一化。
8. 策略更新：使用归一化后的优势，通过 PPO-Clip 等策略梯度算法更新策略参数，从 得到 。

通过这个流程，SPO 实现了一个无组（group-free）、异步友好、数据高效的策略优化循环。

3. 实验

为了验证 SPO 的有效性，研究者们使用 Qwen3-8B 模型，在涵盖 AIME、BRUMO、HMMT 等五个具有挑战性的数学竞赛基准上，将其与强大的基线方法 GRPO 进行了全面的比较。

3.1 性能对比：更优异的推理能力

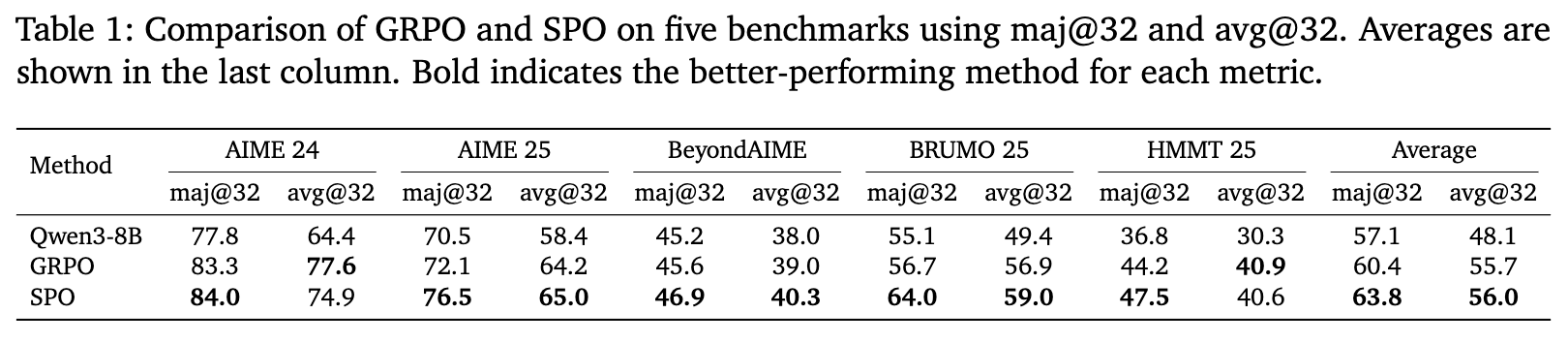
实验结果（如上表所示）清晰地表明，SPO 在各项指标上都优于 GRPO。在平均 maj@32（32个样本中多数投票的准确率）这一核心指标上，SPO 取得了 63.8% 的成绩，相比 GRPO 的 60.4% 有 +3.4 个百分点的显著提升。这种优势在所有五个基准测试中都保持一致，尤其在 BRUMO 25 数据集上，SPO 的提升高达 +7.3 个百分点。这些基准与训练数据的重叠度低，证明了 SPO 带来的提升是泛化能力的真实增长，而非对训练集的过拟合。

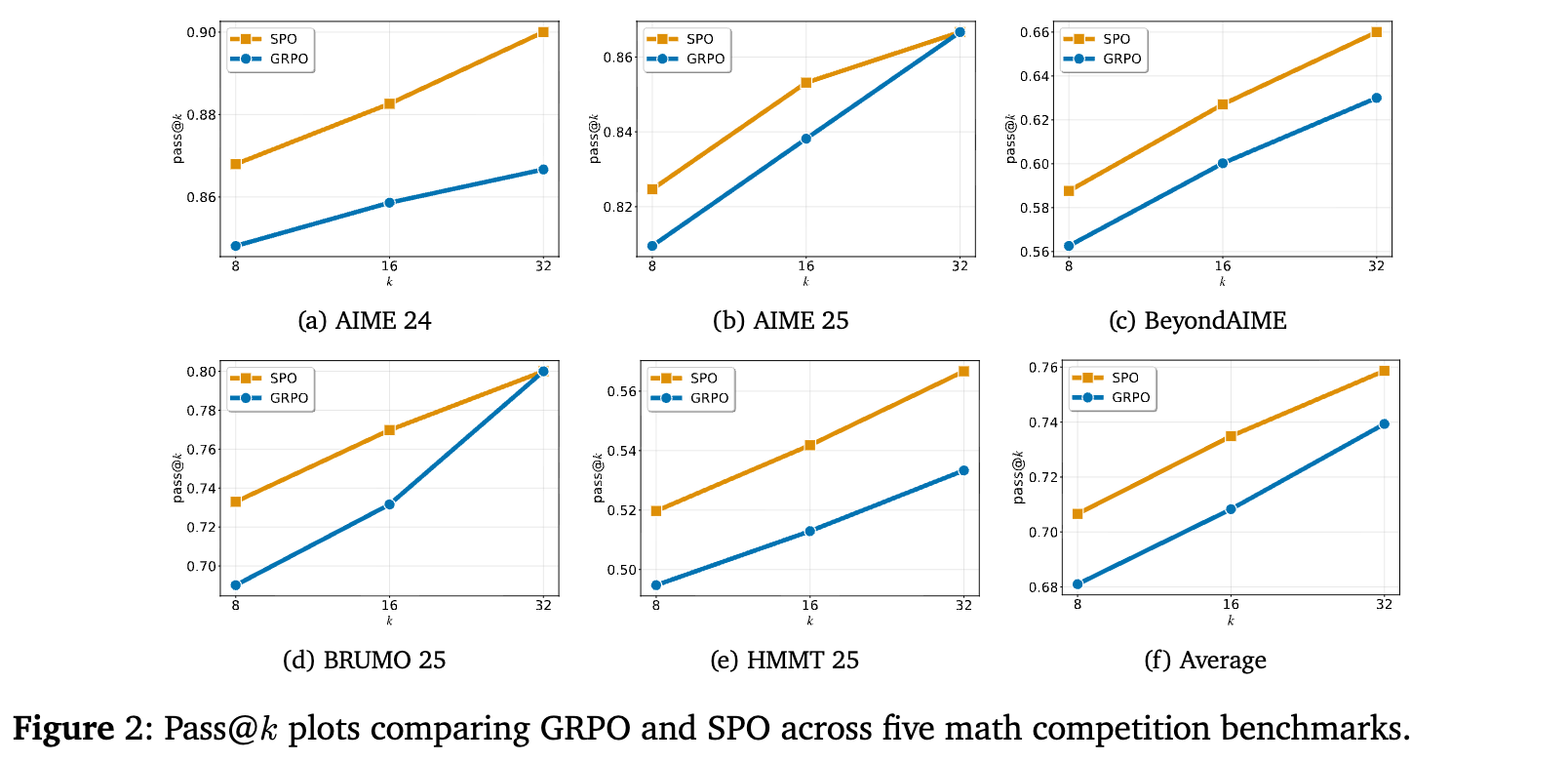
从 pass@k（在 k 次尝试中至少成功一次的概率）曲线上看，SPO 的曲线（蓝色）在所有 k 值上都稳定地高于 GRPO（橙色），进一步证实了 SPO 学习到的策略具有更强的解决问题的能力。

3.2 信号效率与稳定性分析

性能的提升源于架构的优越性。论文通过两个方面的分析，直观地展示了 SPO 在学习信号上的优势。

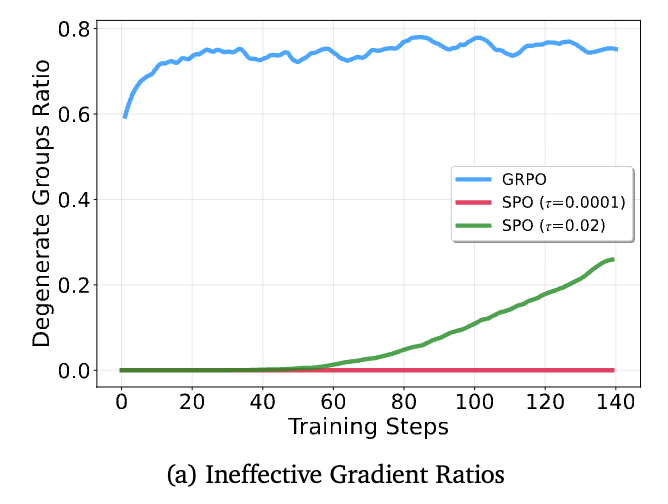
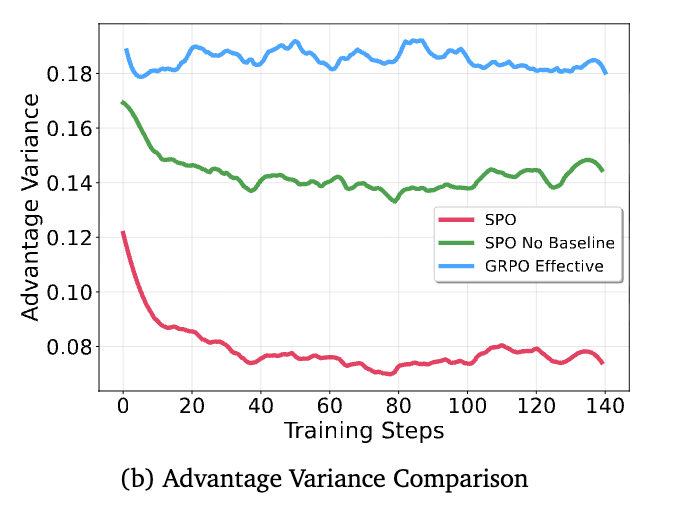
• 信号效率：上图左侧展示了无效学习样本的比例。对于 GRPO（蓝线），“退化组”的比例随着训练从 60% 上升到超过 80%，这意味着大部分计算资源都被浪费在了无法产生有效梯度的样本上。而对于 SPO（红/绿线），研究者追踪了优势绝对值接近于零的样本比例。这个比例随着训练而上升，但这不是浪费，而是模型学习成功的标志——价值追踪器 对奖励的预测越来越准，导致残差（即优势）自然减小。这些样本依然会产生有效的、定义良好的梯度，并对学习做出贡献。

• 信号稳定性：上图右侧比较了不同方法的优势方差。作为参考，“SPO No Baseline”（绿线）代表了不使用任何基线（即原始 REINFORCE）时的高方差情况。GRPO（蓝线，仅在非退化组上计算）的优势信号方差巨大且极不稳定，甚至超过了无基线的情况。这表明 GRPO 的即时基线非常嘈杂。相比之下，SPO 的优势信号（红线）方差显著降低了近50%，且在整个训练过程中保持稳定，证明了其持久化价值追踪器的有效性。

3.3 智能体训练模拟：可扩展性的证明

为了量化“同步屏障”带来的影响，研究者们进行了一项模拟实验，对比了 group方法和 SPO 的无组方法在收集一个训练批次数据时的耗时。

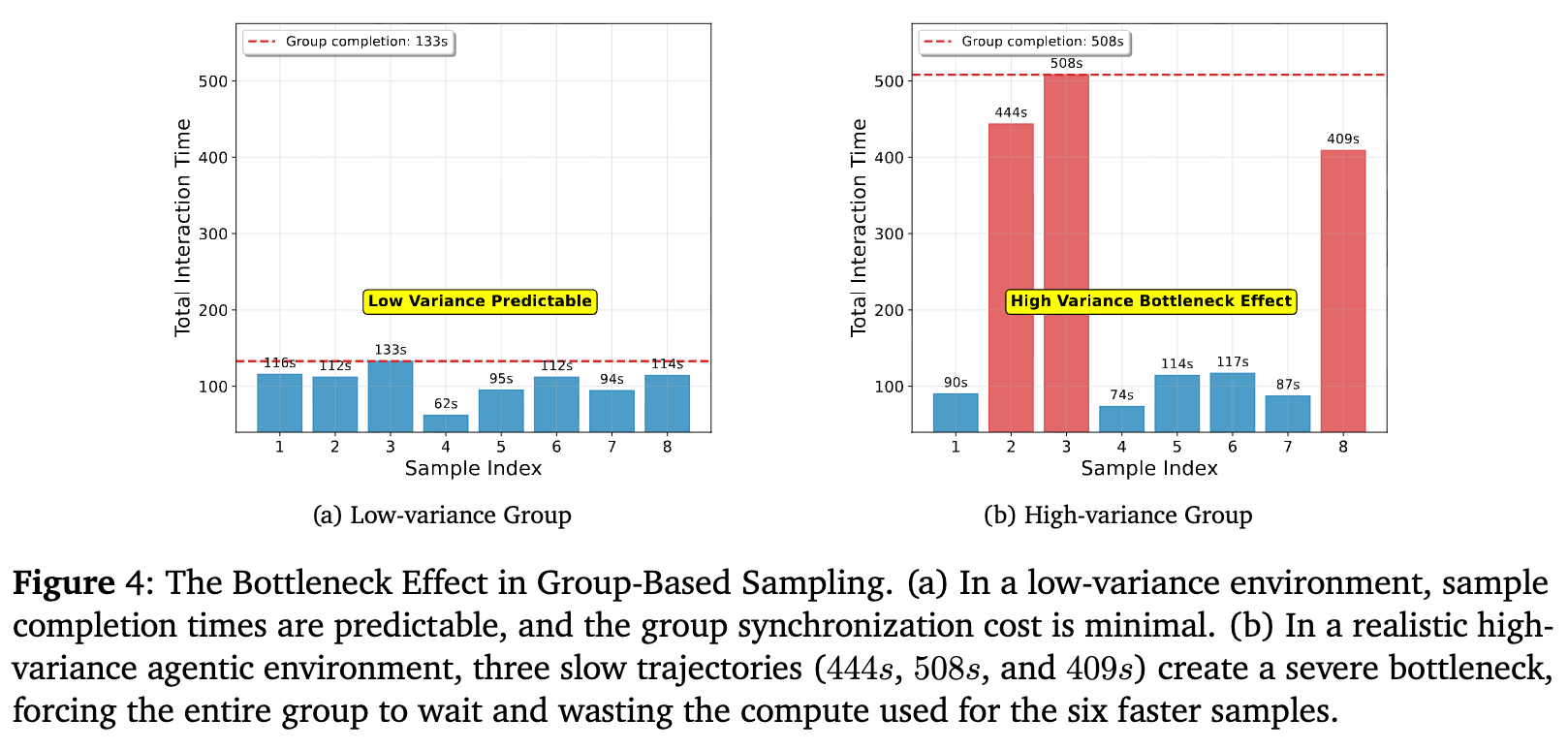
在一个模拟的、具有长尾延迟的真实智能体环境中， group-based方法（如上图右）的效率受到严重影响。尽管大多数样本在 133 秒内完成，但组必须等待最慢的成员（耗时508秒）完成，导致大量计算资源闲置。

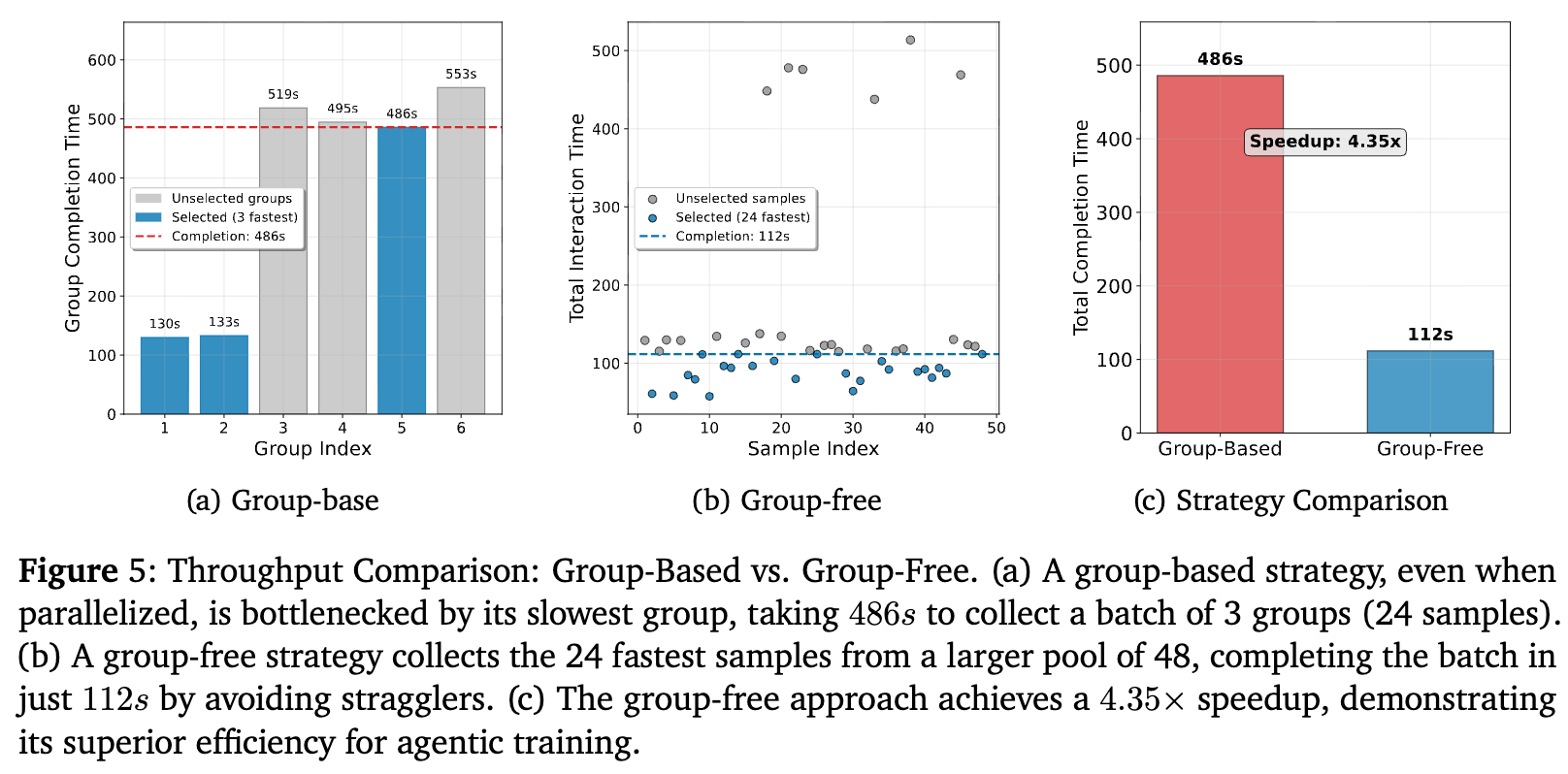
将此扩展到收集一个包含24个样本的训练批次：

• group-based 方法：即使并行运行多个组并选择最先完成的，也仍然受限于所选组内最慢的样本，最终耗时 486 秒。
• SPO（无组方法）：只需异步地启动足够多的独立任务，然后收集最先完成的 24 个即可。这个过程自然地过滤掉了“拖后腿”的慢样本，仅耗时 112 秒。

结果显示，在这种真实的智能体训练场景下，SPO 的无组架构带来了高达 4.35倍的训练吞吐量提升。这是一个对于可扩展性至关重要的实践优势。

4. 消融研究与深度讨论

为了验证 SPO 各个设计组件的必要性，论文还进行了一系列详尽的消融研究。

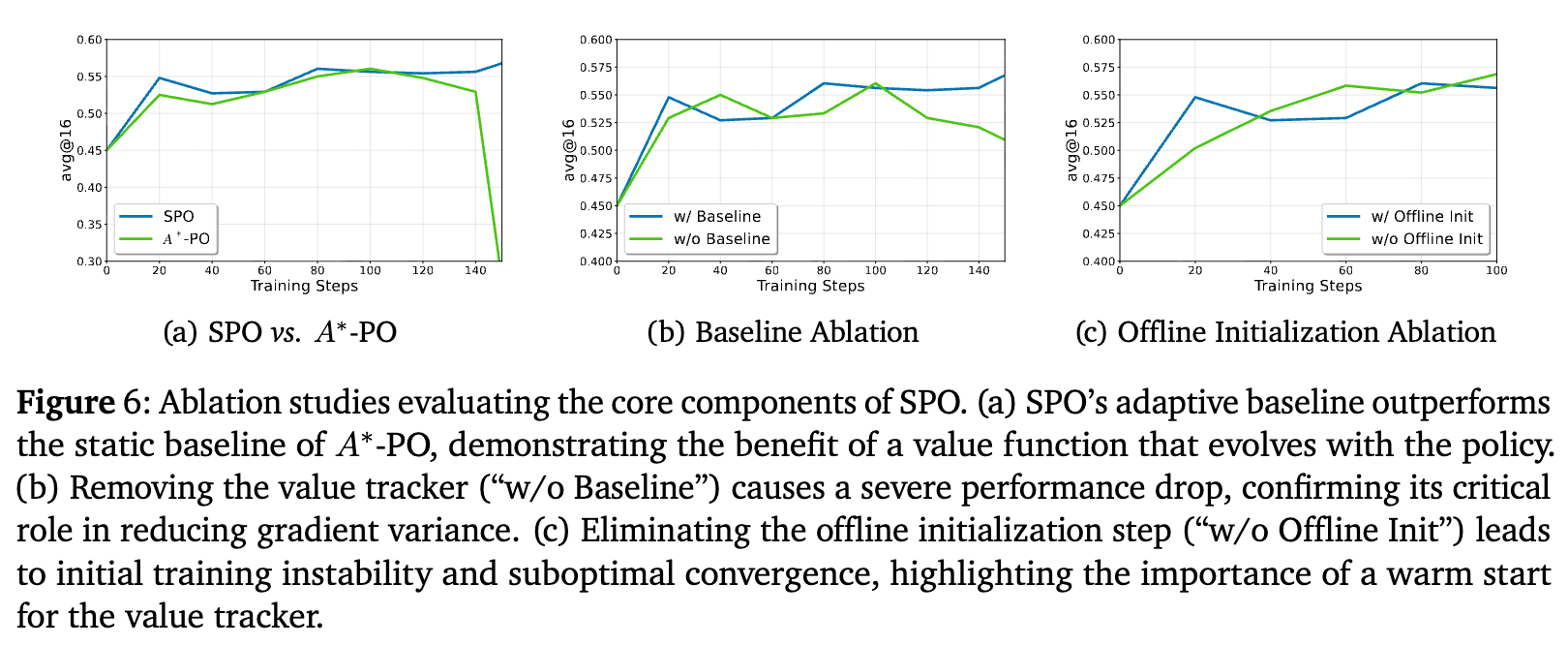
1. SPO vs. A*-PO：A*-PO 是另一种单流方法，但它使用一个固定的、离线预计算的最优价值函数作为基线。实验表明（图a），SPO 的自适应基线性能优于 A*-PO 的静态基线，证明了在策略不断演化的场景下，让基线与策略同步更新是至关重要的。
2. 基线消融：移除 SPO 的价值追踪器，让算法仅依赖全局归一化的原始奖励（图b）。结果显示性能出现断崖式下跌，这强有力地证明了价值追踪器是 SPO 成功的最关键组件，它承担了方差缩减的核心任务。
3. 离线初始化消融：SPO 的价值追踪器需要一个“热启动”阶段，即用少量样本进行离线初始化。移除这个步骤（图c）会导致训练初期剧烈波动，且最终收敛性能也较差。这说明一个好的初始价值估计对于保证训练的稳定和高效至关重要。

4.1 对动态采样的再思考

为了解决“退化组”问题，GRPO 的一些变种（如DAPO）采用了动态采样（dynamic sampling）策略，即持续生成样本，直到组内至少包含一个成功和一个失败的样本。论文在附录中指出，这种“大力出奇迹”的方法计算成本极高。

例如，对于一个成功率为 的提示，为了获得一个非退化组，期望需要生成的样本数量为 。相比之下，SPO 只需要生成 1 个样本，并通过其课程学习机制主动地去降采样这类效率低下的提示。这使得 SPO 在计算效率上具有根本性的优势。

4.2 优势方差的量化分析

论文附录进一步提供了一个简化的量化模型，来比较 GRPO 和 SPO 的梯度方差。方差比可以近似表示为三个效应的乘积：

• 基线噪声：SPO 的基线基于 个历史样本，而 GRPO 仅基于 个。由于 ，SPO 的基线噪声远低于 GRPO。
• 信息损失： 是产生退化组的概率。对于困难（）或简单（）的提示，这个概率很高，导致 GRPO 的方差急剧膨胀。SPO 没有这个问题。
• 归一化噪声：SPO 在大批次 上进行归一化，其引入的噪声 。GRPO 在小组 上的归一化则会引入不可忽略的噪声 。

这个分析从理论上解释了 SPO 在降低方差方面的系统性优势。

往期文章：

• 北大 & 字节 Seed 提出 DACE：难度感知下的确定性引导探索

• 美团 LongCat-Flash-Thinking Technical Report 深度解读

• “移除”还是“回归”？深入探讨 GRPO 中 KL Loss

• 腾讯 AI Lab 推出 EVOL-RL：无监督进化，多数主导选择，新颖性促进变异

• EMNLP 2025 TeleAI 推出 T2R-bench：为表格报告生成任务定义新评估范式

• 无需思维链，LLM如何“凭空”算出答案？探究末位Token的计算机制

• Meta AI 新作 Compute as Teacher: 将 rollouts 转化为高质量的无参考监督

• f-散度直击 GRPO 的传统 Reverse KL：用 Mass-Covering 解决多样性坍塌

• Meta AI 新研究：基于结果的探索，共同提升pass@1和pass@k，缓解大模型推理中的多样性坍塌

• 字节 Seed 提出 REER：由 Query 和 Answer 逆向得到 CoT，专注于开放式任务

• HuggingFace 月度 Top 1 论文：Gensyn AI 提出 SAPO——通过集体经验共享实现高效的语言模型后训练

• 字节 Seed 推出 EMPG：面向长程 LLM Agents 的熵调控策略梯度

• 腾讯 AI Lab 推出 Parallel-R1：引入并行思考进一步释放 LLM 潜力

• 百川提出 DCPO：应用动态自适应裁剪、平滑优势标准化，性能超越 DAPO

• Meta AI 新作 Distilled Pretraining：预训练阶段知识蒸馏会损害ICL能力

• 抛弃Self-Consistency的“答案投票”，用PiCSAR“双重置信度”作为BoN标准

• Meta Superintelligence Labs 首篇论文：重新定义 RAG

• Qwen提出LPPO框架，通过PG-Sampling和LP-Weighting解决数据稀缺与训练效率瓶颈

• DeepSeek V3.1 翻车了！字节 Seed 提出 Inverse IFEval 判断大型语言模型能否听懂“逆向指令”？

• 全网最详细解读 OpenAI 最新论文：为什么大模型会存在“幻觉”？

• 深度解析 Baichuan-M2：解决临床决策实用性难题，推出基于大规模验证器系统扩展医疗能力

• LLM Post-Training 统一视角：清华 & 微信AI 提出统一 Policy Gradient 估计器

• 字节Seed & 复旦提出ThinkDial：首个复现GPT-oss可控推理

• LLM训练新思路：快手RLEP巧用经验回放，实现效率与性能双突破

• PPO、DPO、GRPO及其变体（Dr. GRPO、GSPO、GMPO、LitePPO）策略优化算法综述

• 你没看错，腾讯开始用大模型来玩《王者荣耀》了！

• EMNLP2025 CRAFT：RL引入对比学习，增加LLM训练稳定性，刷新推理上限

• 字节Seed提出AdaCoT：将自适应CoT建模为帕累托优化问题

• 上交 & 上海 AILAB 提出 Memory Decoder：一种用于大语言模型的免微调即插即用记忆模块

• 港科大提出DARS：在RLVR中进行深度广度协同，实现Pass@1与Pass@K性能同步提升

• InternVL3.5 Post-Training 技术解析

• Meta提出StepWiser：引入思维块奖励，基准得分超传统方法20%

• 微软 & UCLA 新作：超越 Pass@1，通过自博弈和变分问题合成，持续提升大模型推理能力

• 大模型SFT数据配比的一些实践启示

• 上交 & 腾讯提出 PSFT：借鉴PPO，为SFT引入近端约束，告别泛化能力差与“熵坍塌”

• 字节Seed&南大提出DuPO：基于广义对偶的自监督大模型优化算法

• 蚂蚁浙大提出基于“评分细则”（Rubric）的奖励机制，仅靠5000+样本，让30B轻松击败671B DeepSeek V3

• MIT：UFT 统一监督微调（SFT）和强化微调（RFT）

• Meta AI&UCSD 提出DeepConf：将GPT-OSS-120B AIME 2025准确率提升至99.9%

• “天下没有免费的午餐”：反思LLM推理中的内在反馈

• GEPA：反思式Prompt进化，效果超过RL

• Qwen团队提出CHORD训练流程：动态融合 SFT 与 RL

• 深挖RLVR探索机制：SFT专攻Pass@k，RL强化Pass@1

• 人大&百度提出ReasonRank：让LLM学会在排序中“思考”

• 深度解析 Seed Diffusion：来自字节跳动的高速推理扩散语言模型

• HuggingFace榜一论文：大模型强化学习中的熵机制

• 字节Seed：Pass@k作为reward可以有效平衡探索与利用

• 深入探讨RL4LLM：解决低概率词元的“过度主导”问题

• 浙大Posterior-GRPO：结合PRM和ORM来优化大模型

• 微软新作GFPO：治疗DeepSeek R1的“话痨”，冗长响应减少80%

• 周志华团队新作：通过IRL挖掘LLM内生奖励，首次理论证明RL对LLM有效性

• FlashRL：引入截断重要性采样，解决Rollout训练不匹配，RL加速可达1.75×

• 超越二元奖励：训练语言模型审视自身的不确定性

• RLVR的一些Tricks到底哪些有用？

• 重磅开源！GLM-4.5 ARC 技术报告深度解读

• Diffusion：真正的王牌不是“快”，而是“超级数据学习者”

• 腾讯 AI Lab提出R-Zero「实现零数据自进化」

• CompassVerifier 深度解析：为大模型打造统一、鲁棒的“裁判”与“奖励”系统

• 一行代码，解锁SFT泛化能力：深度解读DFT如何完胜传统微调

• 告别验证器依赖：RLPR如何将大模型推理能力泛化到通用领域

• ACL2025｜“拉不住的弹簧”：为什么大型语言模型会“抵抗”对齐？

• 大模型3D可视化

• GRPO等于高级版Rejection Sampling？强化学习祛魅时刻：负样本“披沙拣金”才是关键！

• Skywork MindLink 深度解析：如何让 Qwen3 继续进化

• 在数据受限场景下，Diffusion优于自回归模型

• RL+SFT 优势首融合，动态引导模型高效训练

• 阿里通义千问放大招，告别训练崩溃！新算法 GSPO 碾压 GRPO，Qwen3 模型性能暴涨的幕后功臣