我们能否在不引入昂贵的过程监督（process supervision）的前提下，为模型提供更细粒度的学习信号？是否存在一种源自模型内部的、能够反映其推理状态的“内在信号”，可以用来指导其学习过程？

来自北京大学和字节跳动的研究者发表了论文《Know When to Explore: Difficulty-Aware Certainty as a Guide for LLM Reinforcement Learning》，提出了一种名为“难度感知下的确定性引导探索（Difficulty-Aware Certainty-guided Exploration, DACE）”的新型强化学习算法。该方法的核心思想是，利用 LLM 在生成过程中表现出的“自我确定性（self-certainty）”这一内在信号，并结合模型对当前任务难度的实时评估，来动态地、自适应地调整其在“探索（exploration）”与“利用（exploitation）”之间的平衡。DACE 不再依赖于单一、固定的学习目标，而是让模型学会“随机应变”：在它认为困难的任务上，鼓励其进行更大胆、更多样化的探索；在它已经熟练掌握的任务上，则引导其进行更精确、更高效的利用。

  • 论文标题：Know When to Explore: Difficulty-Aware Certainty as a Guide for LLM Reinforcement Learning
  • 论文链接：https://arxiv.org/pdf/2509.00125

1. 背景

在深入 DACE 算法之前，我们有必要更具体地理解 RLVR 中稀疏、二元奖励所带来的具体挑战。论文中的一个实例（图1）直观地揭示了这个问题。

自我确定性为相同奖励结果的响应提供了有意义的训练信号
自我确定性为相同奖励结果的响应提供了有意义的训练信号

该图展示了 Qwen2.5-7B 模型在处理两个来自美国数学竞赛（AMC）的 benchmark 问题时的不同表现。

场景一：对于困难问题（模型成功率低）

  • 问题：求解第四个“平方三角数”的各位数字之和。
  • 模型表现：模型两次尝试均未得到正确答案（18），因此外部奖励同为0。
  • 响应分析：

    1. 低确定性响应：模型提出了一种基于数论（佩尔方程）的解法。虽然最终结果错误，但这个推理方向本身具有探索价值，代表了一种有潜力的、更高级的解题思路。
    2. 高确定性响应：模型提出了一个暴力破解的方法，并附带了一段无效的、不可执行的代码。这种思路相对简单，且实现有误，探索价值较低。
  • 学习困境：在一个标准的 RLVR 框架下，这两个错误的响应会被同等对待，模型无法得知第一种尝试尽管失败，但其探索方向是值得鼓励的。理想的训练信号应该引导模型在遇到此类难题时，降低其对“直观”但错误的方法的信心，转而探索更多样、更根本的解决路径。

场景二：对于简单问题（模型成功率高）

  • 问题：在一个正四面体中，计算一个特定角度的余弦值相关的数值。
  • 模型表现：模型两次尝试均得到了正确答案（4），因此外部奖励同为1。
  • 响应分析：

    1. 低确定性响应：模型提供了一个非常冗长的、教程式的解答，甚至包含了一个用于验证的 Python 脚本。虽然正确，但效率不高。
    2. 高确定性响应：模型给出了一个简洁、优雅的纯数学证明，展现了对问题更深刻的理解。
  • 学习困境：标准的 RLVR 无法区分这两种正确解法的优劣。模型不会因为提供了更优雅、更高效的解法而获得更高的奖励。理想的训练信号应该鼓励模型在已经掌握的问题上，优化其解题路径，追求更高效、更精炼的表达。

这两个场景共同揭示了二元奖励的局限性：它缺乏对“过程”的洞察。学习过程因此变得低效，因为模型无法从失败中汲取有价值的教训，也无法在成功的基础上追求卓越。

而论文作者敏锐地观察到，在这些响应中，存在一个与解法质量隐秘相关的内在信号——模型的自我确定性（self-certainty），即模型对其生成内容的置信度。对于难题，低确定性的响应反而可能包含着有价值的探索；对于简单题，高确定性的响应则往往对应着更优的解法。

这引出了论文的核心研究问题：我们能否利用像“自我确定性”这样的内在信号，根据模型对任务难度的实时评估，来动态地指导其探索与利用的权衡？

2. 探索与利用的权衡取决于任务难度

为了验证“最优学习策略依赖于任务难度”这一核心直觉，并为后续算法设计提供理论依据，研究者们构建了一个简化的“玩具”强化学习环境。这个环境虽然简单，却清晰地揭示了固定学习策略的局限性。

2.1 玩具学习环境的构建

在这个环境中：

  • 智能体（Agent）的策略被建模为一个一维高斯分布 。

    • 均值 代表智能体认为的最优动作（action）的取值。
    • 标准差 代表智能体策略的确定性。 越小，表示策略的确定性越高，倾向于“利用”（exploitation），即在 附近进行高概率采样； 越大，表示策略的确定性越低，倾向于“探索”（exploration），即在更广泛的范围内采样。
  • 奖励函数（Reward Function）由两个高斯分布混合而成，通过调整这两个分布的形状（特别是标准差 ），可以模拟不同难度的任务。

    • 困难任务：奖励函数形态“稀疏”，即奖励峰值所在区域狭窄。智能体需要大范围探索才能找到奖励。
    • 简单任务：奖励函数形态“密集”，即奖励峰值所在区域宽广。智能体只需少量探索即可轻松发现奖励。

2.2 固定的确定性学习目标

研究者将策略的确定性（以对数标准差 来量化）直接引入学习目标函数中：

其中，超参数 控制了对确定性的奖惩，代表了一种固定的学习策略：

  • 强制探索（Forced Exploration, ）：目标函数会奖励更大的 （即更低确定性）。策略被持续鼓励进行探索，类似于最大熵强化学习（Maximum Entropy RL）。
  • 强制利用（Forced Exploitation, ）：目标函数会惩罚更大的 （即奖励更小 ，更高确定性）。策略被鼓励快速收敛，利用已知的奖励信息。
  • 标准强化学习（Standard RL, ）：不对确定性进行显式控制，只最大化期望奖励。

2.3 实验观察：最优策略随难度而变

通过在这个玩具环境中进行实验，研究者得出了清晰且关键的结论。

定性分析（Qualitative Analysis）

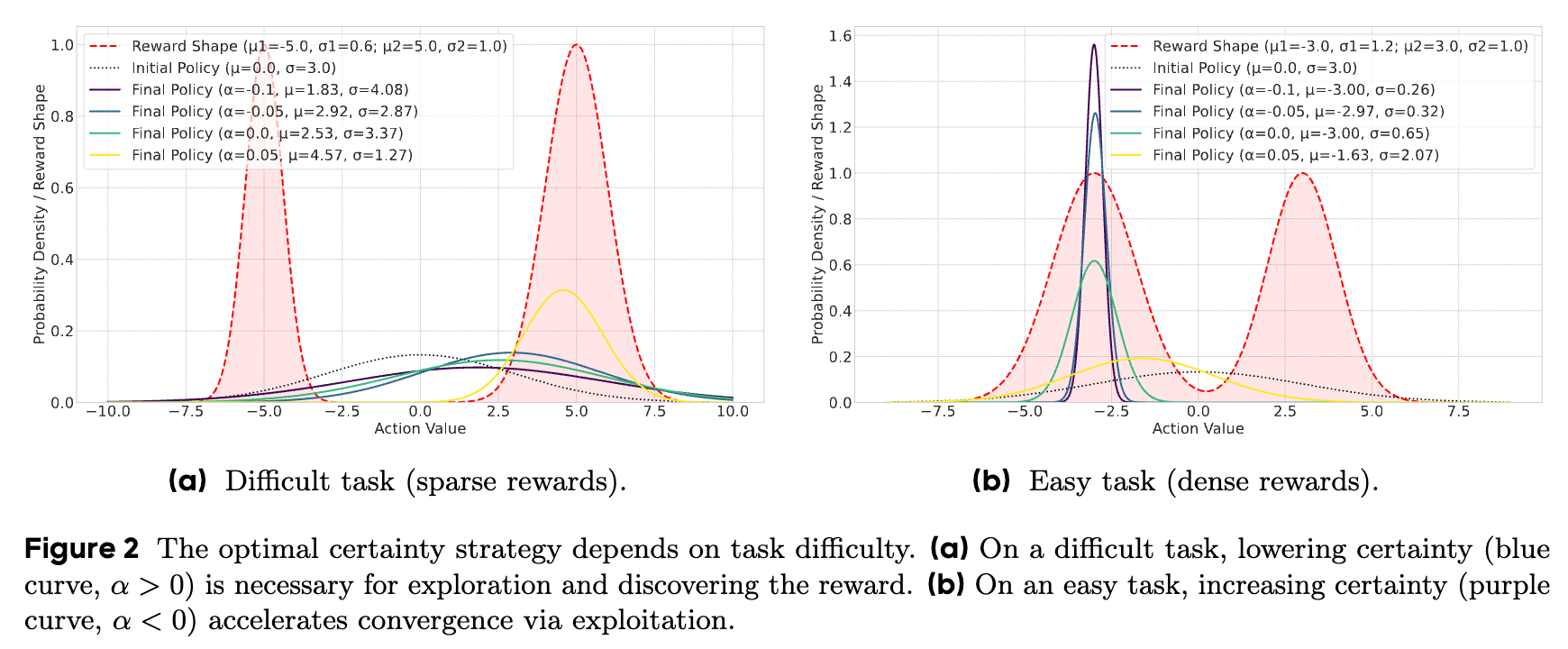
最佳确定性策略取决于任务难度
最佳确定性策略取决于任务难度
  • 在困难任务中（图2a，奖励稀疏）：

    • 采用“强制探索”策略（蓝色曲线, ）的智能体表现最好。通过维持较大的 ，它成功地探索了更广阔的动作空间，最终发现了远离初始点的奖励峰值。
    • 相反，“强制利用”策略（紫色曲线, ）由于过早地收缩了探索范围，完全错过了奖励区域，导致学习失败。
  • 在简单任务中（图2b，奖励密集）：

    • 采用“强制利用”策略（紫色曲线, ）的智能体收敛速度最快，效率最高。因为它能够迅速锁定并利用那个显而易见的奖励区域。
    • “强制探索”策略（蓝色曲线, ）虽然也能找到奖励，但由于其持续的探索行为，收敛得更慢，效率较低。

定量分析（Quantitative Analysis）

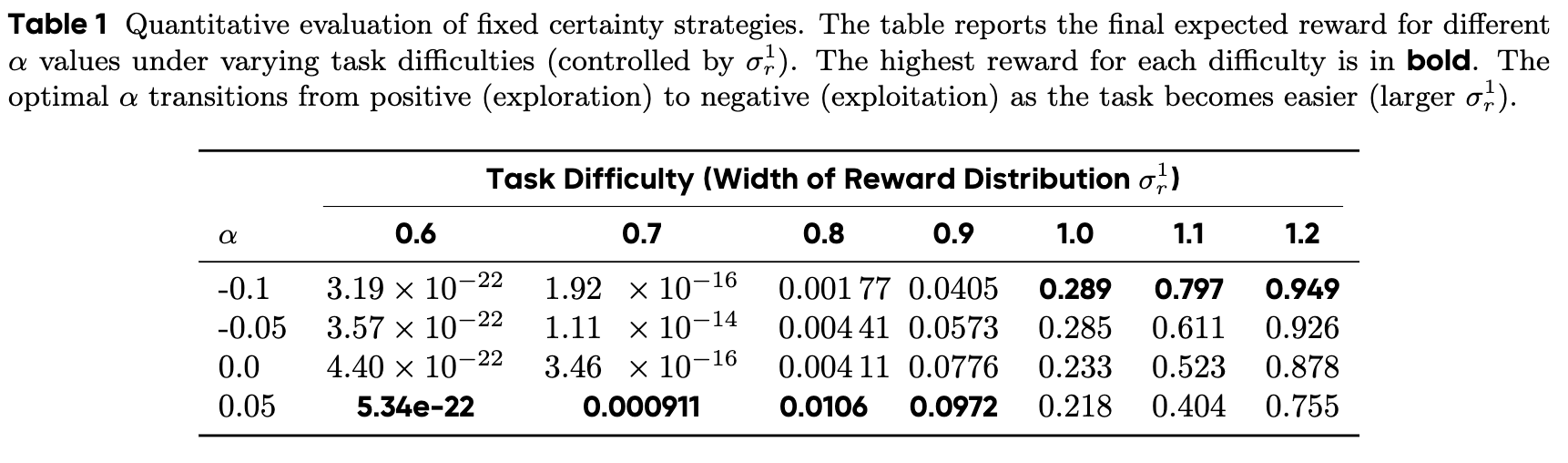
固定确定性策略的量化评估
固定确定性策略的量化评估

表格数据进一步证实了定性观察。研究者通过改变奖励函数的一个峰值的宽度 来控制任务难度（ 越小，任务越难）。

  • 当任务困难时（），最优的 值为正（），表明探索策略获得了最高的最终奖励。
  • 当任务变简单时（），最优的 值变为负（），表明利用策略成为主导。

这个玩具实验的结果强有力地证明了：不存在一个在所有场景下都最优的固定学习策略。 智能体应该采取的策略——是探索还是利用——严重依赖于当前任务的难度。这为设计一个能够根据任务难度自适应调整策略的算法——DACE——奠定了坚实的理论基础。

3. DACE

基于上述洞察，DACE (Difficulty-Aware Certainty-guided Exploration) 算法应运而生。它是一个旨在动态平衡探索与利用的强化学习算法。DACE 的设计精髓在于，它将“评估任务难度”和“调整自身行为”这两个步骤内化到了学习循环中，形成了一个闭环的自适应系统。该系统由三个核心组件构成：难度评估器、确定性杠杆、以及连接两者的自适应内在奖励机制。

3.1 难度感知：如何定义和衡量“难”？

DACE 的第一个核心思想是，任务的“难度”不是一个绝对的、静态的属性，而是相对于智能体（即LLM）当前能力的相对概念。一个对当前模型来说极具挑战的问题，在模型经过充分训练后可能会变得轻而易举。

因此，DACE 使用一个在线的、策略相关的指标来衡量难度：模型在特定问题 上的预期失败率。

具体而言，对于当前策略 和问题 ，其难度值 被定义为：

其中， 是一个二元验证器（返回1代表正确，0代表错误）， 是指示函数。在实践中，这个期望值通过从当前策略中采样 个响应 ，并计算其成功率的均值来近似：

这个定义非常直观：模型在某个问题上犯错的频率越高，这个问题对它来说就越“难”。一个较高的 值表明模型正在该问题上挣扎。

3.2 确定性杠杆：如何控制模型的“行为”？

DACE 的第二个核心组件是量化并控制模型行为的手段。借鉴自玩具实验中的标准差 ，DACE 将自回归 LLM 的策略“确定性”定义为生成序列的负平均对数概率。

对于一个由策略 针对输入 生成的序列 ，其确定性 定义为：

这个指标同样很直观：

  • 最大化确定性：相当于最小化生成序列的负对数概率（即最大化其概率）。这会鼓励模型选择概率最高的词元（token），使其行为更具决定性、更保守，这是一种“利用”行为。
  • 最小化确定性：相当于最大化生成序列的负对数概率。这会鼓励模型尝试选择概率较低的词元，使其行为更多样化、更具探索性，这是一种“探索”行为。

因此，这个确定性指标 成为了 DACE 调节模型探索或利用倾向的“杠杆”。

3.3 连接机制：自适应内在奖励

DACE 的精髓在于其第三个组件：一个将“难度评估”与“确定性杠杆”动态连接起来的自适应内在奖励（Adaptive Intrinsic Reward）机制。

DACE 设计了一个内在奖励 ，它直接作用于确定性杠杆，其奖惩的“方向”由一个自适应系数 决定：

而这个关键的自适应系数 的符号，则由当前问题的难度 与一个预设的“难度阈值” 的比较结果来决定：

其中， 是一个正的缩放因子， 是符号函数。

这个设计巧妙地实现了期望的自适应行为：

  • 对于困难任务（） ：

    • 为负，因此 为负。
    • 学习目标变为最大化 ，这等价于最小化确定性 。
    • 结果：DACE 鼓励模型在它感到挣扎的问题上进行探索，尝试更多样化的解决方案。
  • 对于简单任务（） ：

    • 为正或零，因此 为正。
    • 学习目标变为最大化 ，即最大化确定性 。
    • 结果：DACE 鼓励模型在它已经掌握的问题上进行利用，优化和提炼其已有的成功策略。

3.4 完整的 DACE 目标函数与实现

最终，DACE 的完整学习目标是将这个自适应的内在奖励与环境提供的标准外部奖励 （例如，答案准确率）结合起来：

研究者选择使用组级别拒绝策略优化（Group-wise Rejection Policy Optimization, GRPO）来优化这个目标。这个选择具有高度的协同效应：GRPO 在进行策略更新时，本身就需要为每个输入 采样 个响应。这 个样本可以被直接、无额外成本地用于计算 DACE 所需的难度值 。这使得 DACE 的实现不仅思想优雅，而且在计算上非常高效。

4. 实验

为了验证 DACE 的有效性，研究者在一系列具有挑战性的数学推理 benchmark 上进行了广泛的实验。实验设计严谨，结果令人信服。

4.1 实验设置

  • 基础模型：Qwen2.5-7B，一个强大的开源语言模型。
  • 训练框架：VeRL 框架。
  • 训练数据：混合了 DAPO 和 MATH 数据集的去重版本。
  • 评估基准：四个广泛使用的数学推理数据集：AIME25, AIME24, AMC23, 和 MATH-500。这些数据集覆盖了从高中到奥林匹克竞赛水平的数学难题，是评估模型深度推理能力的黄金标准。
  • 对比基线：

    • GRPO：一个强大的 RLVR 基线方法。
    • 多种先进方法：包括 Ent-Adv, Clip-Cov, KL-Cov, 和 FR3E，这些方法分别从不同角度（如鼓励长推理、控制更新协方差、探索高熵词元等）来尝试改进 LLM 的强化学习。

4.2 主要结果分析

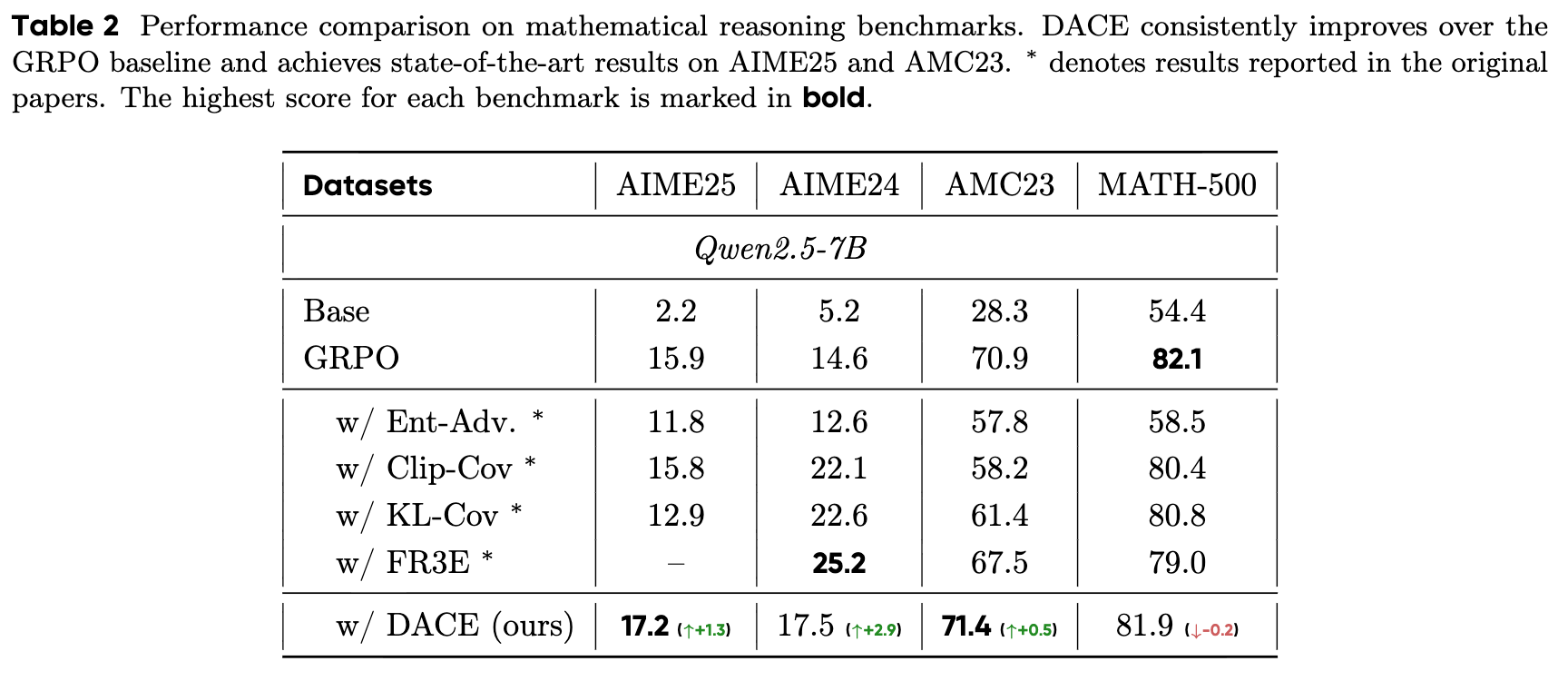
数学推理基准上的性能比较
数学推理基准上的性能比较

实验结果（表2）清晰地展示了 DACE 的优势：

  1. 在最具挑战性的基准上性能领先：DACE 在 AIME25、AIME24 和 AMC23 这三个竞赛级别的基准上，均显著优于强大的 GRPO 基线。具体来说，它在 AIME25 上提升了1.3个绝对点，在 AIME24 上提升了2.9个绝对点，在 AMC23 上提升了0.5个绝对点。这些提升在高难度数学推理任务中是很有意义的。
  2. 成为多个基准的最佳方法：在所有对比的方法中，DACE 在 AIME25 和 AMC23 上取得了最高分。虽然 FR3E 在 AIME24 上表现更优，但 DACE 仍然大幅超越了 GRPO 和其他技术。
  3. 对任务难度的敏感性：在相对简单一些的 MATH-500 数据集上，DACE 的性能与 GRPO 基本持平（仅相差0.2点）。这表明 DACE 的动态策略——在难题上探索，在简单题上利用——对于那些真正需要深度和多样化探索的复杂问题（如AIME）尤其有效。

4.3 拓展性分析：测试时计算资源扩展的影响

一个好的推理模型不仅应该在固定评估设置下表现出色，其性能还应该随着测试时给予更多计算资源（例如，生成更多样本并选取最优）而持续提升。研究者通过 pass@k 指标（即生成k个样本中至少有一个正确的概率）来评估这种拓展性。

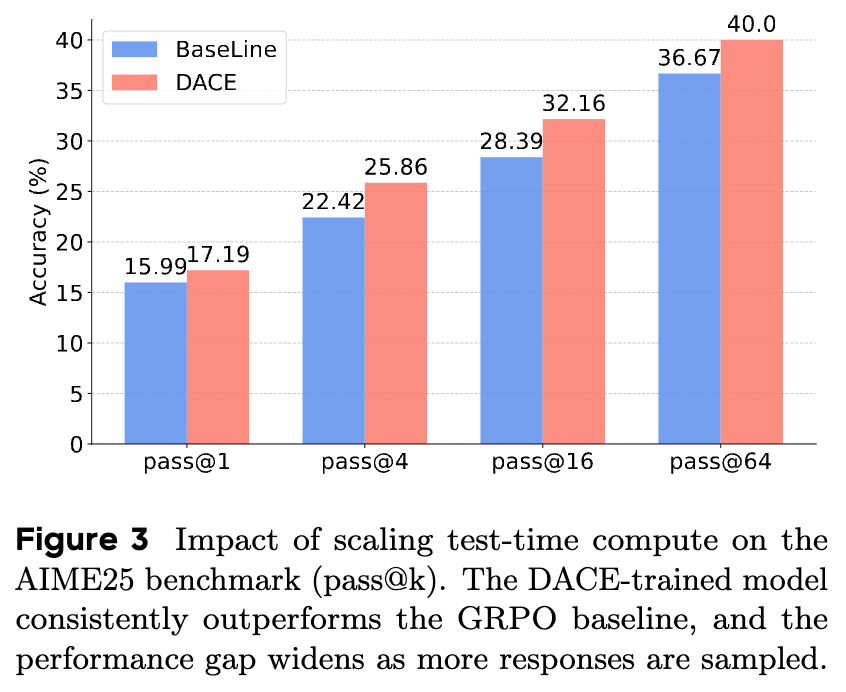
扩展测试时计算对 AIME25 基准的影响 (pass@k)
扩展测试时计算对 AIME25 基准的影响 (pass@k)

如图3所示，在 AIME25 基准上：

  • 持续的性能优势：DACE 训练的模型在所有 k 值（从1到64）上都稳定地优于 GRPO 基线。
  • 差距随采样数增加而扩大：更值得注意的是，随着 k 值的增加，DACE 相对于 GRPO 的性能优势在不断扩大。在 mean@16 时领先1.2个点，而在 mean@128 时领先优势扩大到3.3个点。

这个结果强有力地验证了 DACE 的核心假设。通过在训练时鼓励对难题进行探索，DACE 使得模型能够发现更广泛、更多样的正确解题路径。因此，当测试时有更多采样机会时，这些被发现的多样化路径有更高的概率被激活，从而带来更大的性能提升。同时，通过鼓励对简单问题进行利用，模型保持了在低采样数（如 pass@1）下的高精度，实现了探索与精确性的兼顾。

4.4 训练动态分析：DACE 如何影响学习过程？

为了揭示 DACE 性能优势背后的机制，研究者深入分析了模型的训练过程动态。

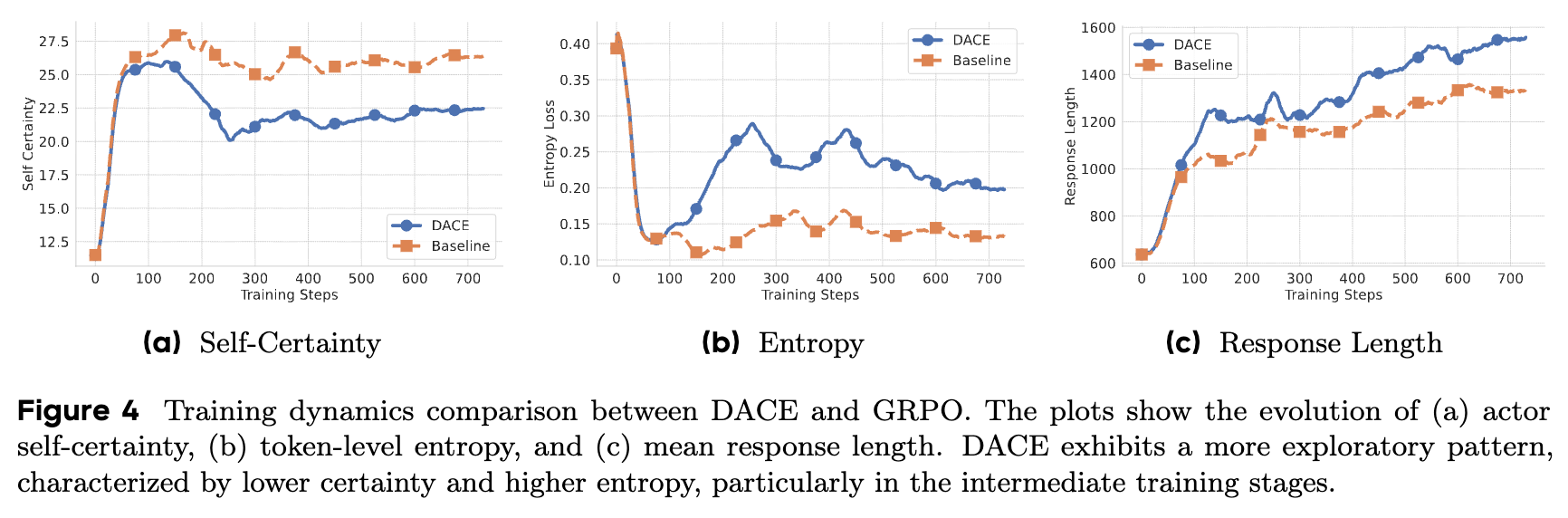
DACE 和 GRPO 的训练动态对比
DACE 和 GRPO 的训练动态对比

通过比较 DACE 和 GRPO 训练过程中的几个关键指标（图4），可以发现：

  • 更低的自我确定性：DACE 训练的模型（蓝色曲线）始终表现出比 GRPO 模型（橙色曲线）更低的自我确定性。
  • 更高的词元级熵：相应地，DACE 模型的词元级熵也持续更高。
  • 更长的响应：DACE 模型的平均响应长度也略长。

这些指标共同描绘了一幅清晰的图景：DACE 的自适应奖励机制成功地在训练过程中注入了更多的探索性行为。特别是在训练的中期阶段，两个模型之间的差异最为显著，这表明 DACE 在关键的学习阶段有效地引导模型跳出局部最优，去探索更广阔的推理空间。正是这种在训练中期的关键探索，为模型发现更鲁棒、更多样的推理策略奠定了基础，最终转化为测试时的性能优势。

4. 消融研究：难度阈值 的关键作用

为了进一步理解 DACE 的核心机制，研究者对其中最重要的超参数——难度阈值 ——进行了深入的消融研究。这个阈值决定了模型将一个问题划分为“困难”（需要探索）还是“简单”（需要利用）的界线。

实验设置是对 进行网格搜索，其取值范围从 0.0 到 1.0。这两个端点分别代表了两种固定的、非自适应的策略：

  • ：所有问题的 都不会小于0，因此模型总是认为问题是“简单”的。这相当于一种纯粹的利用（pure exploitation）策略，总是奖励高确定性。
  • ：所有问题的 都不会大于1，因此模型总是认为问题是“困难”的。这相当于一种纯粹的探索（pure exploration）策略，总是惩罚高确定性（即鼓励熵最大化）。

5.1 阈值对训练动态的影响

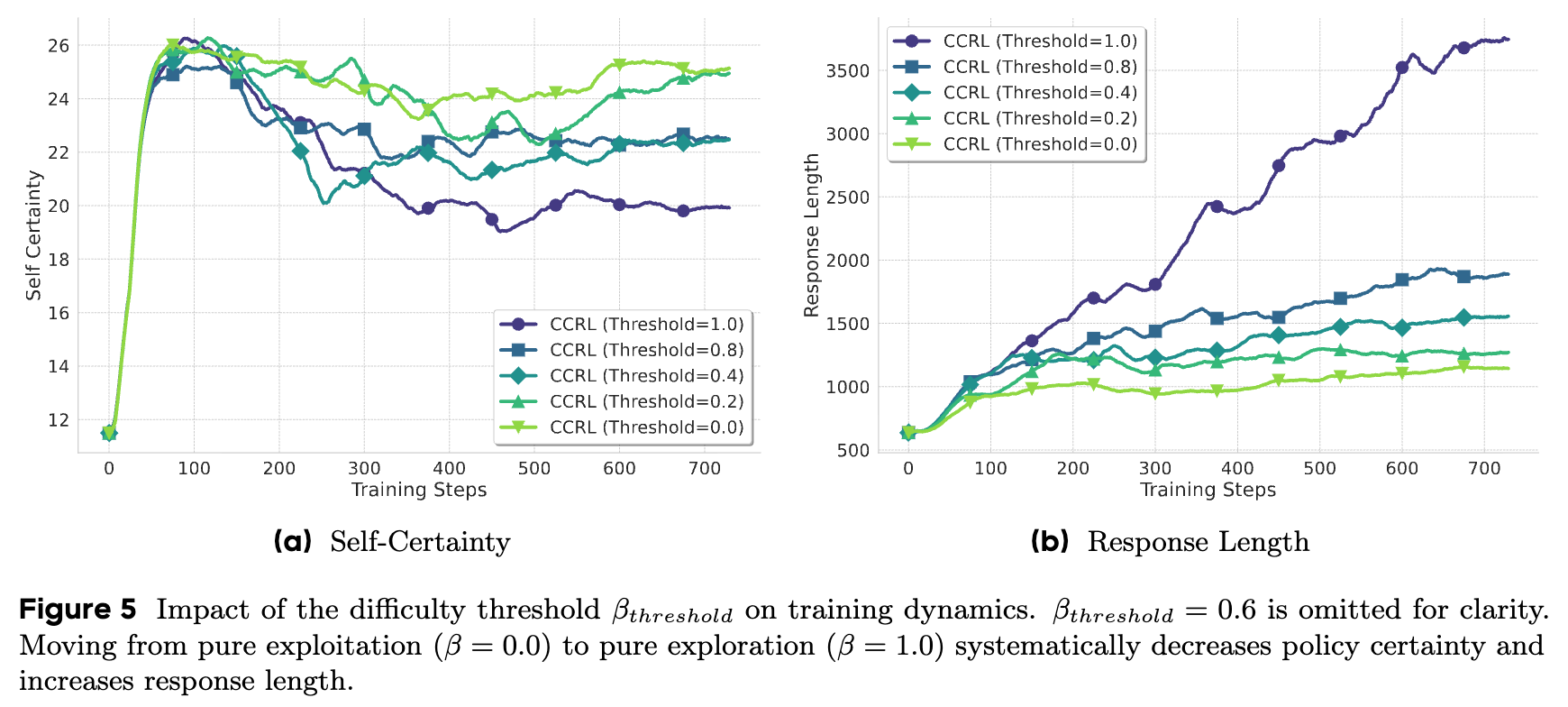
难度阈值 $ \beta_{\text{threshold}} $ 对训练动态的影响
难度阈值 对训练动态的影响

如图5所示，随着 从0.0增加到1.0：

  • 模型的自我确定性系统性地降低。
  • 模型的响应长度系统性地增加。

这个趋势完全符合预期。更高的阈值意味着更多的问题被归类为“困难”，从而触发了更多的探索性、惩罚确定性的奖励。值得注意的是，纯探索策略（）产生的响应长度是其他设置的3倍以上，这揭示了持续探索的一个已知陷阱：可能导致低效、冗余的推理，难以收敛。

5.2 阈值对最终性能的影响

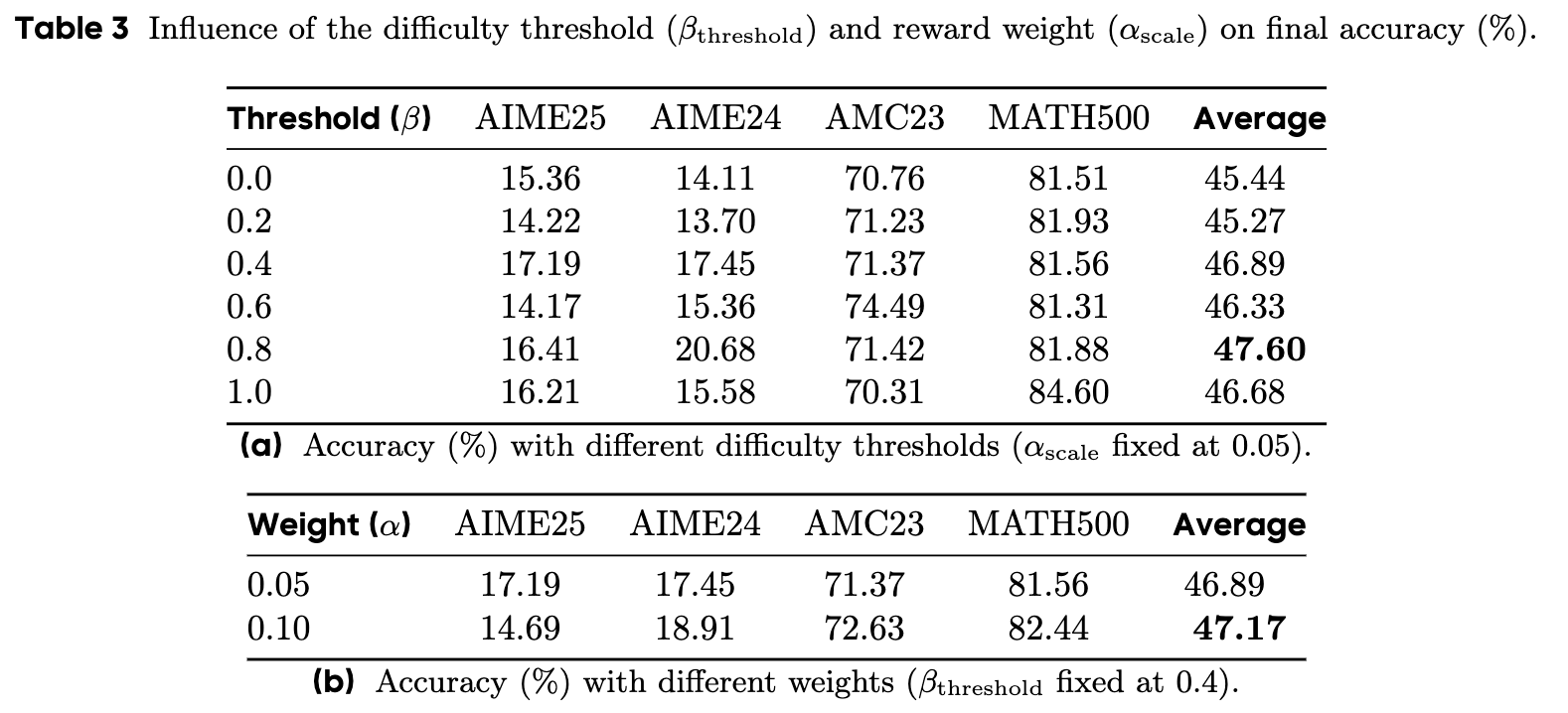
难度阈值 ($ \beta_{\text{threshold}} \alpha_{\text{scale}} $) 对最终准确率的影响
难度阈值 () 和奖励权重 () 对最终准确率的影响

最终准确率的数据（表3a）是整个研究的点睛之笔。它清晰地表明：

  • 固定策略是次优的：纯利用策略（）的平均准确率较低。这表明模型如果只专注于利用已知知识，很容易陷入局部最优，无法发现更优的解题路径。纯探索策略（）同样表现不佳，且带来了巨大的计算成本（过长的响应）。
  • 动态平衡是关键：最佳性能出现在中间的阈值设置上，例如 取得了47.60%的最高平均准确率。

这个结果无可辩驳地证实了 DACE 的核心论点：算法的力量不在于强制模型采取某一种单一行为（探索或利用），而在于赋予其根据任务难度动态切换这两种行为的能力。

往期文章：