LLM 在各种任务上表现出的优秀能力，与其内部工作机制的不透明性形成了鲜明对比。理论上，Transformer架构中的因果自注意力和多层感知器（MLP）的组合，允许每个Token基于所有在它之前的Token来访问和计算信息。 但在实践中，这种理论上的可能性究竟在多大程度上被模型所利用？来自加州大学圣克鲁兹分校、乔治梅森大学和Datadog AI研究部门的学者们，在近期提交的论文《All for One: LLMs Solve Mental Math at the Last Token With Information Transferred From Other Tokens》中，对这一问题进行了深入的探索。

  • 论文标题：All for One: LLMs Solve Mental Math at the Last Token With Information Transferred From Other Tokens
  • 论文链接：https://www.arxiv.org/pdf/2509.09650

该研究聚焦于“mental math”任务——即模型直接通过下一个Token预测来完成数学计算，而无需显式的思维链（Chain-of-Thought）推理。 通过一系列精巧的实验设计，研究者们揭示了一种被称为 All-for-One（AF1）的计算子图。在这个子图中，有意义的计算发生得非常晚，并且几乎全部集中在序列的最后一个Token上。这一发现不仅挑战了我们对于LLM计算过程的直观理解，也为我们提供了新的工具和视角，以解剖这些复杂模型的内部运作。

1. 背景

当我们向一个LLM输入一个算术表达式，例如 42 + 20 – 15，模型能够迅速给出正确答案。这个过程看起来像是“心算”。但这个“心”究竟是什么？是模型将计算过程分布在多个Token上，逐步求解（例如，先算 42+20，再用其结果减去15）？还是采用了某种我们尚未理解的、更直接的计算模式？

这篇论文的作者们提出了几个核心问题，旨在揭开这层神秘的面纱：

  1. 信息交流的即时性：虽然每个Token在每一层都有能力访问所有之前的Token，但这种访问是从一开始（即第0层）就充分进行的吗？还是存在一个“等待”或“预处理”的阶段？
  2. 计算的分布性：是不是所有的Token都需要参与实际的计算过程？或者说，仅仅最后一个Token（负责预测最终结果的那个Token）的计算就足够了？
  3. 信息传输的持续性：如果计算主要由最后一个Token完成，那么它是否需要在所有层级持续不断地从其他Token获取信息？还是说，只需要一个短暂的、集中的信息传输阶段就足够了？

为了回答这些问题，研究者们设计了一套实验流程，通过逐步限制模型的计算和信息流，来寻找“最小计算结构”。

2. CAMA & ABP

作者为此提出了两种创新的方法：上下文感知平均消融（Context-Aware Mean Ablation, CAMA） 和 基于注意力的窥探（Attention-Based Peeking, ABP）。

2.1 上下文感知平均消融 (CAMA)

在模型的初始层，每个Token可能在执行两种不同类型的计算：

  • 任务通用计算 (Task-General Computation) ：这种计算不依赖于输入的具体数值，而是对任务本身的结构进行理解。例如，在处理算术任务时，模型需要识别出哪些是数字Token，哪些是运算符Token，并理解它们构成的算术结构。
  • 输入特定计算 (Input-Specific Computation) ：这种计算直接处理输入中的具体数值，例如执行加法或减法。

CAMA 的核心目标，就是抑制输入特定的计算，同时保留任务通用的计算。它通过一种精巧的“平均化”技巧来实现这一点。

具体来说，在模型的前 层，对于输入序列 中的第 个Token ，CAMA会用其在给定上下文分布下的期望表示来替换其真实的激活值。其公式如下：

这里：

  • 是替换后的第 个Token在第 层的激活值。
  • 是一个条件概率分布，表示在第 个位置的Token固定为 的情况下，所有可能的输入序列 的分布。
  • 是模型 在处理另一个输入序列 时，计算出的第 个Token在第 层的激活值。
  • 表示求期望。

通过这种方式，替换后的激活值 抹去了来自当前输入序列 中其他Token（）的特定信息，因为它是在所有可能的“背景”序列上取平均得到的。然而，它仍然保留了与Token 本身以及任务整体结构相关的通用信息。这使得研究者可以测试模型在多大程度上可以在没有Token间特定信息交换的情况下，仅凭通用计算就能正常工作。

与其他消融方法（如直接复制输入嵌入或用随机Token表示替代）相比，CAMA的优势在于它产生的表示仍然是“分布内”的，不会因为引入异常的激活值而破坏模型的后续处理流程，从而能够更真实地探测模型的“等待”阶段。

2.2 基于注意力的窥探 (ABP)

在通过CAMA确定了模型的“等待”阶段后，研究者需要一个工具来精确控制后续层中的信息流动。为此，他们提出了ABP。

ABP通过直接修改注意力掩码（attention mask）来实现。在标准的自注意力机制中，一个Token可以关注所有在它之前的Token。而ABP允许研究者为每个“查询”（Query）Token 指定一个它可以“窥探”的“键”（Key）Token的子集 。对于任何不在这个子集中的Key Token，其在注意力矩阵中对应的权重将被设置为负无穷，从而在Softmax之后其注意力得分变为零。

在本文的研究中，ABP主要被用于实现两种特定的信息流模式：

  • 完全窥探 (Full-peeking) ：允许一个Token关注所有之前的Token，即恢复标准的因果自注意力。
  • 自我窥探 (Self-peeking) ：只允许一个Token关注它自身（以及一个特殊的BOS Token，因为研究发现对BOS的关注至关重要）。

通过组合使用CAMA和ABP，研究者可以构建出一种高度受限的计算通路：先用CAMA让所有Token在初始层“各自为政”，进行任务通用计算；然后在中间的少数几层，通过ABP选择性地打开信息阀门，比如只允许最后一个Token对所有其他Token进行“完全窥探”，而其他Token只能“自我窥探”；最后在剩余的层中，关闭所有跨Token的信息阀门，让最后一个Token独立完成最终的计算。

3. AF1

通过上述两大工具，研究者在Llama-3-8B模型上，针对 A + B + C 这样的三操作数算术任务，发现了一个令人惊讶的稀疏而高效的计算子图——AF1子图。这个子图的计算过程可以清晰地划分为三个阶段。

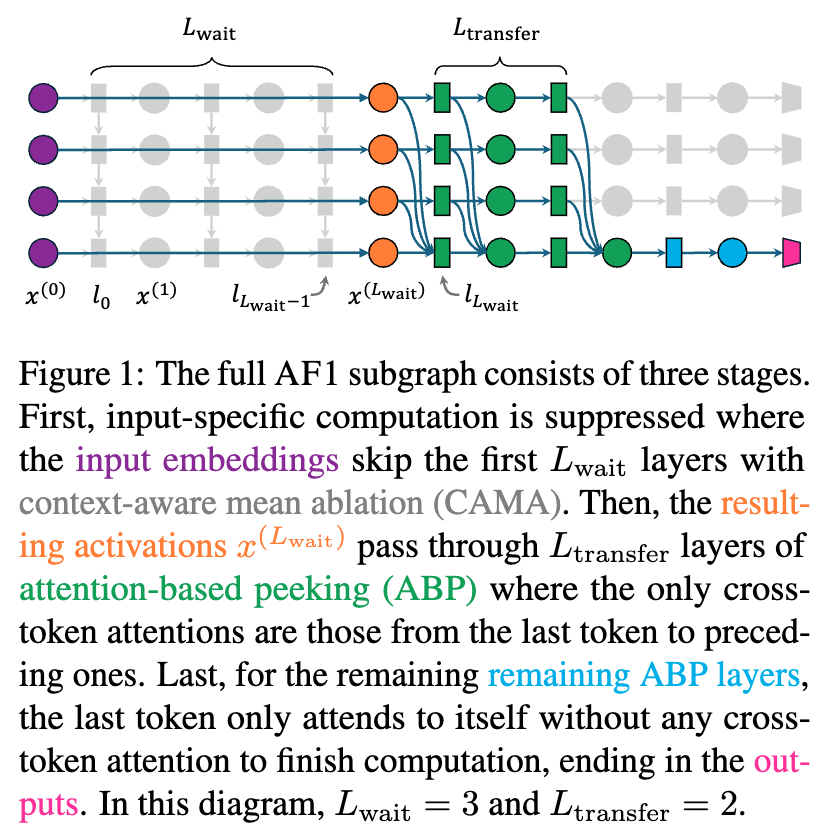
AF1子图的三阶段示意图
AF1子图的三阶段示意图

阶段一：等待期 (Waiting Phase)

  • 层数：从第0层到第 层。
  • 机制：应用CAMA。
  • 过程：在这个阶段，所有的Token都无法访问来自其他Token的输入特定信息。它们各自独立地进行任务通用计算。例如，数字Token 42 的表示会被处理，以提取其数值含义；运算符Token + 的表示会被处理，以理解其操作功能。但模型并不会去计算 42 + 20。
  • 发现：实验表明，在Llama-3-8B上，这个等待期可以长达15层（），模型性能几乎没有损失。但一旦超过这个阈值（），性能就会急剧下降。这说明，在第14层之前，跨Token的特定信息交互对于解决任务并非必要，但从第15层开始，信息交互变得至关重要。

阶段二：信息传输期 (Information Transfer Phase)

  • 层数：从第 层到第 层。
  • 机制：应用ABP。
  • 过程：在这个阶段，信息流被严格控制。只有最后一个Token（例如，在 A + B + C = 这个序列中，就是 = Token）被允许执行“完全窥探”，即它可以关注并收集来自所有前面Token（A, B, C, +, +）的信息。而所有其他的非末位Token则只能进行“自我窥探”，它们只能将自己的信息传递出去，而不能接收来自其他Token的新信息。
  • 发现：令人惊讶的是，这个信息传输期可以非常短暂。实验发现，对于Llama-3-8B，仅仅需要2层（，即第15和16层）就足以让最后一个Token收集到完成计算所需的全部信息，并恢复几乎全部的性能。这表明信息传输是以一种“爆发式”而非“持续性”的方式进行的。

阶段三：最终计算期 (Final Computation Phase)

  • 层数：从第 层到最后一层。
  • 机制：应用ABP。
  • 过程：在这个阶段，所有的信息阀门都被关闭。包括最后一个Token在内的所有Token都只能进行“自我窥探”。此时，最后一个Token已经整合了来自所有操作数和运算符的信息，它将在后续的MLP层中独立地、在自己的“残差流” (residual stream) 中完成所有的计算，最终在模型的输出层预测出正确答案。

这个三阶段的AF1子图模型，描绘了一幅与直觉大相径庭的计算图景：LLM并非通过在不同Token之间逐步传递中间结果来完成多步算术，而是将所有原始信息集中到最后一个Token，然后由这个Token“一锤定音”。

4. 实验

研究者通过一系列详尽的实验，验证了AF1子图的存在、有效性及其泛化能力。

4.1 AF1子图的性能与泛化性

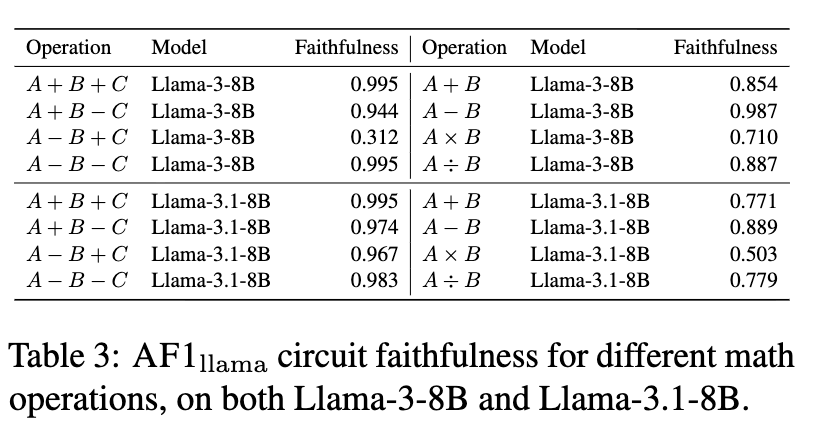
AF1子图在不同数学任务和模型上的忠实度
AF1子图在不同数学任务和模型上的忠实度

研究者在Llama-3-8B和Llama-3.1-8B上，针对8种不同的两操作数和三操作数算术任务，测试了同一个AF1子图（）的性能。这里的性能由“忠实度”（Faithfulness）来衡量，即子图在那些完整模型能够正确解决的问题上的准确率。

结果显示，尽管AF1子图的连接被极大地稀疏化了，但它在绝大多数任务上都表现出了很高的忠实度。例如，在Llama-3-8B的 A+B+C 任务上，忠实度高达0.995。这有力地证明了AF1子图是模型执行这些任务的充分且必要的计算结构。

一个有趣的例外是Llama-3-8B在 A-B+C 任务上的表现。完整模型的准确率本身就很低（低于0.3），AF1子图的忠实度也相应较低。然而，当换成原始准确率更高的Llama-3.1-8B时，AF1子图的忠实度也相应地恢复到了高水平。这表明AF1子图的性能瓶颈在于模型本身解决问题的逻辑，而非子图结构的限制。

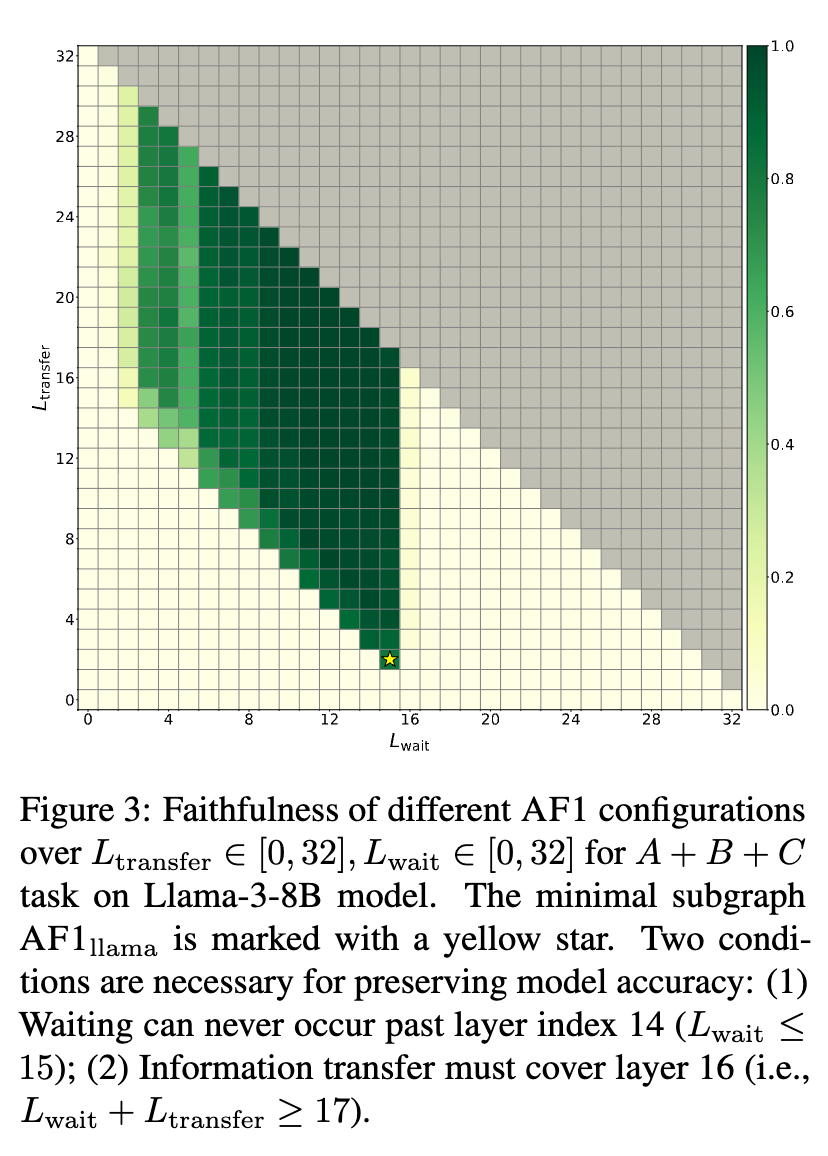
不同L_wait和L_transfer组合下的性能网格图
不同L_wait和L_transfer组合下的性能网格图

为了更系统地探索参数的影响，研究者绘制了不同 和 组合下模型性能的网格图。结果清晰地显示出两个关键边界条件：

  1. 等待必须在第14层或之前结束 ()。
  2. 信息传输必须覆盖到至少第16层 ()。

这两个条件共同定义了一个有效的AF1子图存在的“可行域”。

4.2 信息传输层的必要性

为了进一步证明信息传输层（在Llama-3-8B中是第15和16层）的关键作用，研究者进行了一项“敲除”实验。他们使用完整的模型，但在每一层中，都单独地移除从最后一个Token到其他所有非BOS Token的注意力连接。

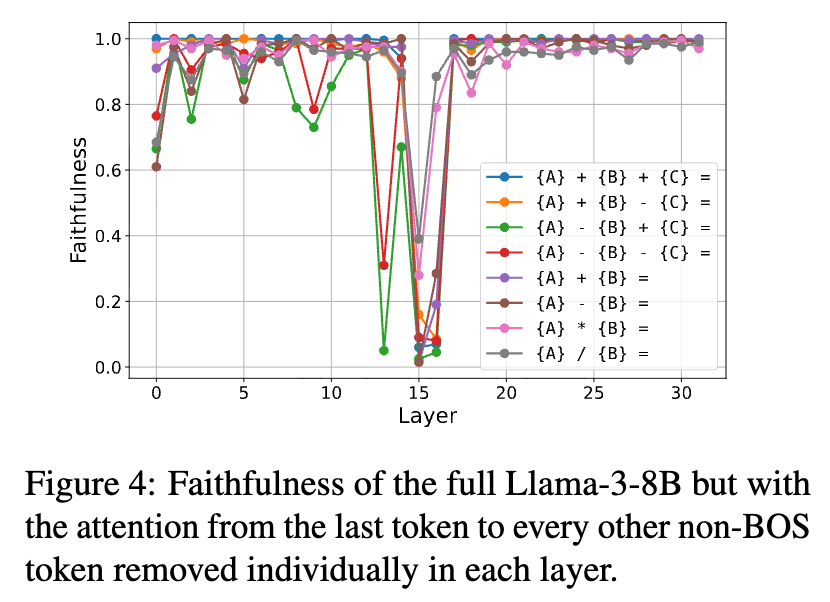
移除单层末位Token注意力后的性能变化
移除单层末位Token注意力后的性能变化

结果显示，当移除第15层的这些注意力连接时，几乎所有任务的性能都出现了断崖式下跌。移除第16层的连接也对大部分任务造成了显著影响。这与AF1子图的发现高度一致，再次确认了这两个特定层在信息从其他Token向最后一个Token汇集过程中的核心枢纽地位。

4.3 深入到注意力头

一个Transformer层由多个注意力头组成。在确定了关键层之后，研究者进一步探究了在这两层（共64个头）中，哪些具体的头是执行信息传输任务的主力。他们采用了一种迭代剪枝的方法：从包含所有64个头的AF1子图开始，在每一步移除对当前模型性能影响最小的那个头，直到所有头都被移除。

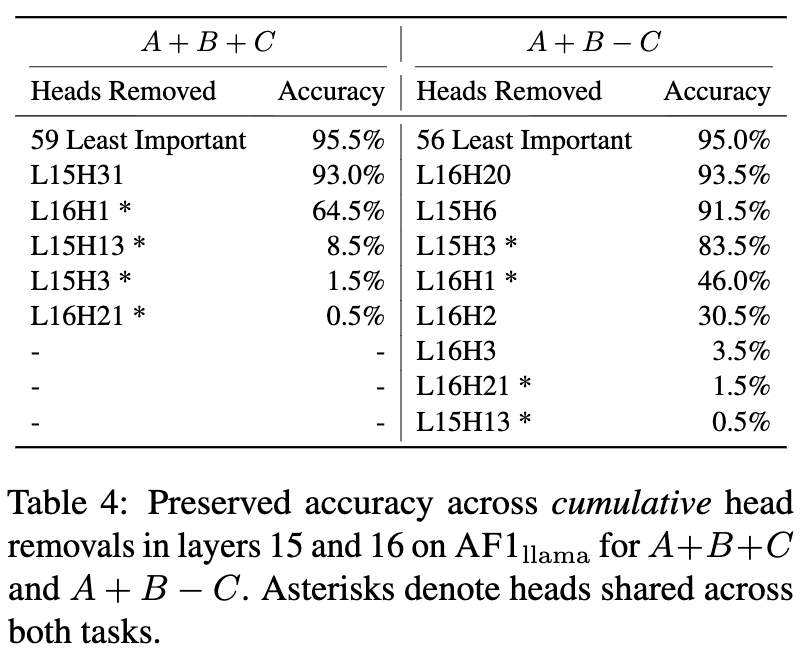
关键注意力头移除过程中的性能保留情况
关键注意力头移除过程中的性能保留情况

结果表明，真正重要的头数量很少。在 A+B+C 任务中，即便移除了64个头中的59个，模型依然能保持95.5%的准确率。这说明计算是高度稀疏的，仅由少数几个关键的注意力头负责。

更有趣的是，研究者发现了一些在多个任务中都扮演关键角色的“共享头”（用星号标记）。通过对这些关键头的注意力模式进行可视化，他们发现这些头确实在执行信息传递的功能：它们精确地从最后一个Token（Query）关注到代表各个操作数（Key）的Token。

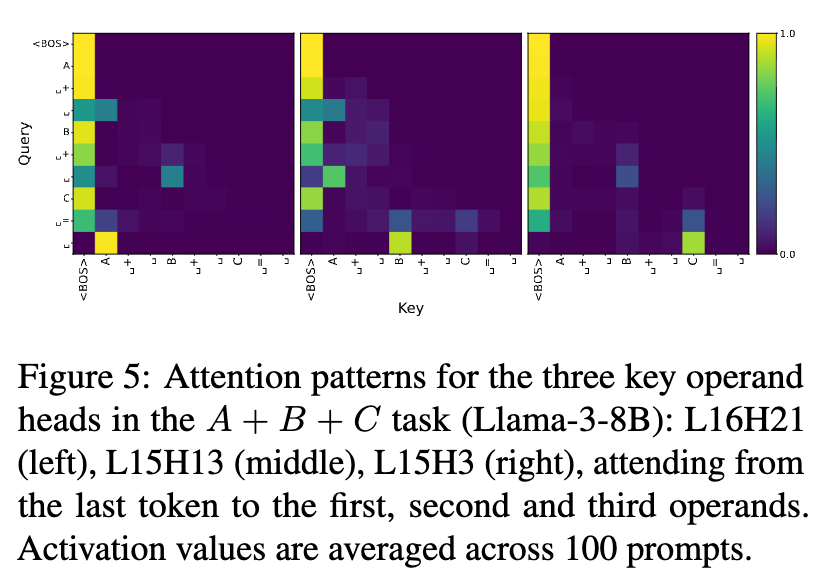
关键操作数头的注意力模式
关键操作数头的注意力模式

例如，在 A+B+C 任务中，头L16H21主要关注第一个操作数，L15H13关注第二个，而L15H3关注第三个。这种清晰的模式为“信息在特定层、通过特定头、汇集到最后一个Token”这一假说提供了直接的视觉证据。

4.4 内部表示分析：AF1是“真通路”还是“旁门左道”？

一个关键的问题是：AF1子图是否捕获了模型原生的、主要的计算通路？还是说，它只是在模型被“残疾化”之后，找到的一条备用的、“取巧”的计算捷径？

为了回答这个问题，研究者使用了Logit Lens技术。该技术通过将模型每一层的残差流投影到词汇表空间，来“窥探”模型在不同计算阶段对下一个Token的预测。他们比较了完整Llama-3-8B模型和AF1子图的Logit Lens输出。

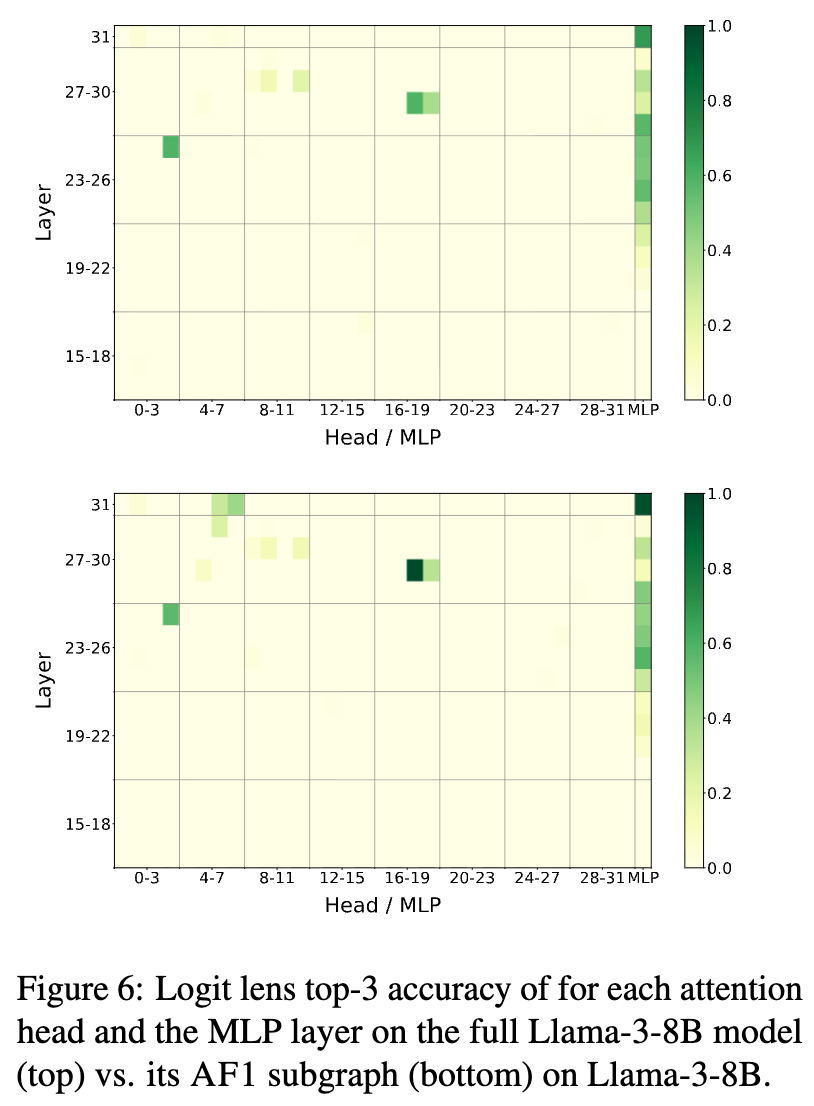
完整模型与AF1子图的Logit Lens准确率对比
完整模型与AF1子图的Logit Lens准确率对比

结果显示，两者的Logit Lens热图高度相似。在这两种情况下，正确的答案都在大约第24层左右开始清晰地“浮现”出来，并且最终都达到了很高的预测准确率。这种内部表征的高度一致性表明，AF1子图并没有另辟蹊径，而是成功地捕获了完整模型中用于算术计算的核心机制。

4.5 任务泛化性：从符号到自然语言

AF1子图是否只能处理 A+B= 这样的符号化输入？研究者测试了其在更自然的语言输入上的表现，例如：

  • 语言描述：“The sum of A and B is”
  • 问答形式：“What is the sum of A and B? Answer:”
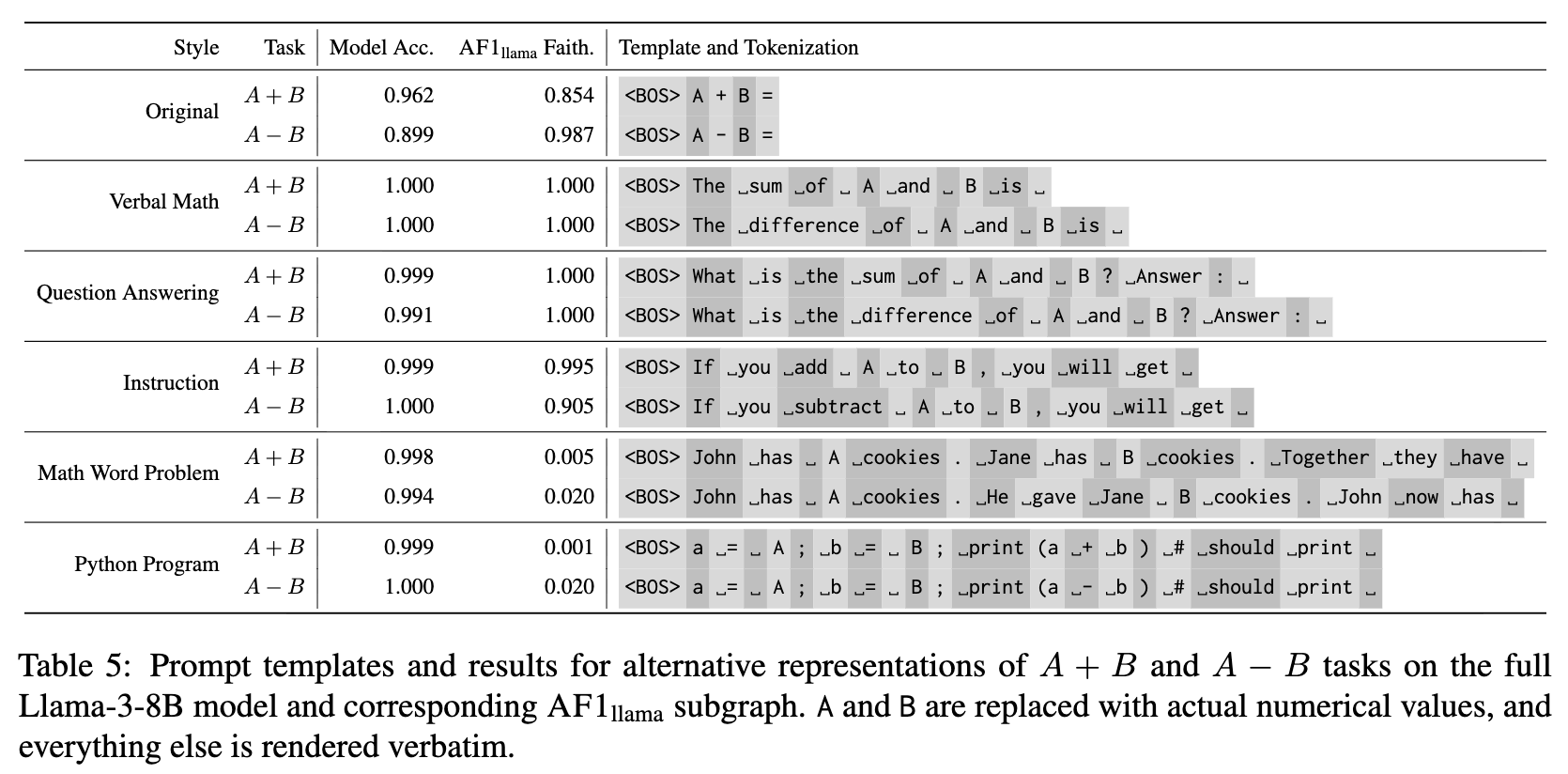
AF1子图在不同输入形式下的表现
AF1子图在不同输入形式下的表现

结果显示，对于这些不含复杂语义的、直接的算术任务，AF1子图依然能保持相当高的准确率。然而，一旦任务需要更深层次的语义理解，例如数学应用题（“John has A cookies, Jane has B cookies...”）或Python代码（a = A; b = B; print(a + b)），AF1子图的性能就完全崩溃了。

这说明，AF1子图捕获的是一个纯粹的、底层的算术计算回路。而理解自然语言、解析应用题逻辑等更高级的能力，则需要模型中其他组件的参与。这为我们解耦LLM的不同能力模块（例如，语义理解模块 vs. 算术计算模块）提供了新的思路。

4.6 模型泛化性：Pythia和GPT-J的表现

最后，为了检验这一发现是否具有跨模型的普适性，研究者在Pythia-6.9B和GPT-J-6B这两个较早期的模型上也进行了类似的实验。

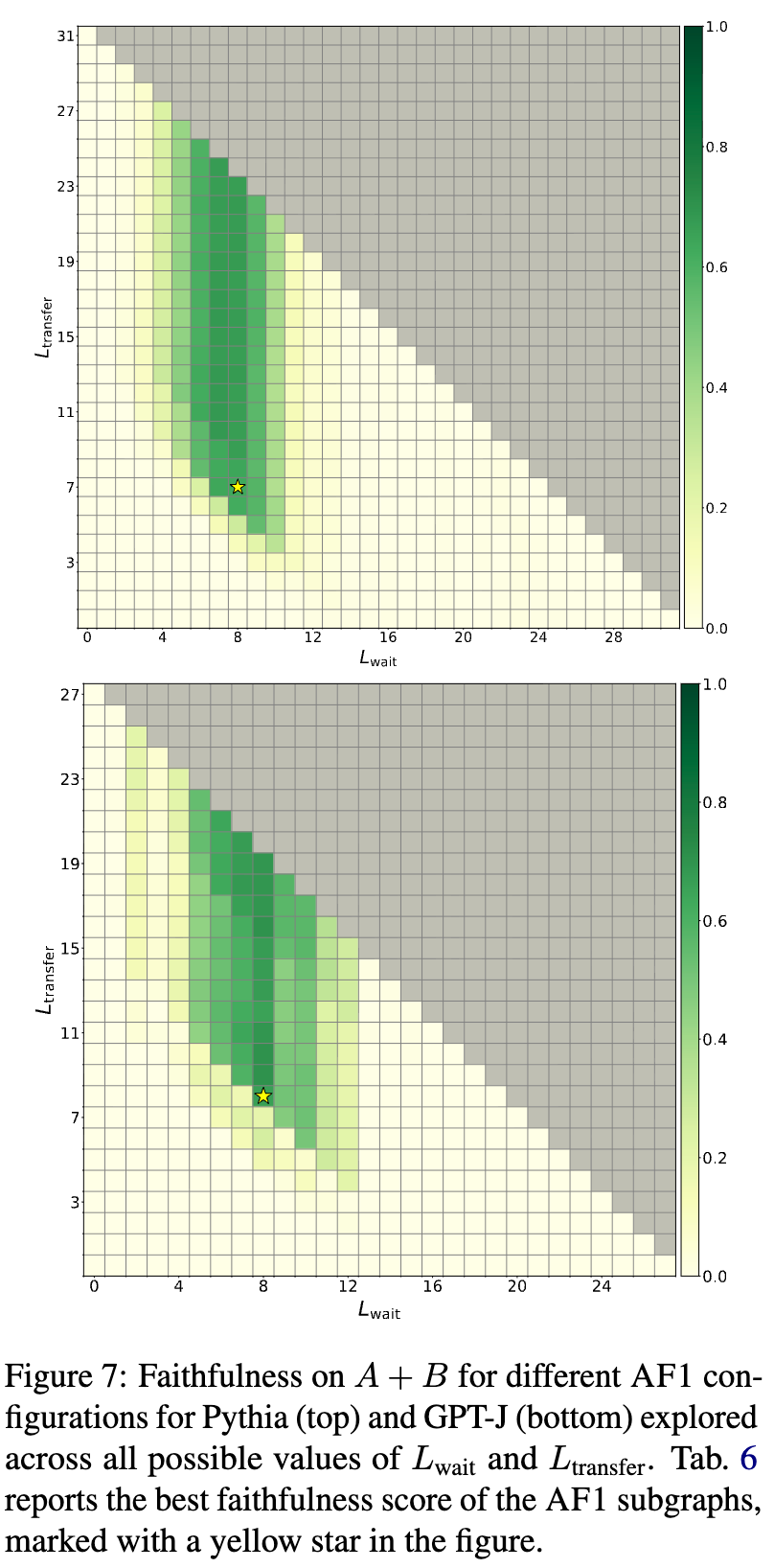
Pythia和GPT-J的性能网格图
Pythia和GPT-J的性能网格图

结果发现，这两个模型中也存在类似的AF1子图结构，但其参数有所不同。具体表现为：

  1. 边界更模糊：性能从高到低的过渡不像Llama-3那样清晰。
  2. 等待期更短： 的最大值约为11，远小于Llama-3的15。这表明关键的信息传输发生得更早。
  3. 传输期更长：它们需要更长的 （例如7-8层）来恢复性能，说明其信息传输的效率低于Llama模型。

尽管存在这些差异，但核心的“等待-传输-计算”三阶段模式是共通的。这表明“众归于一”可能是一种在不同Transformer模型中都存在的、用于解决此类计算任务的通用策略。

5. 总结

  • 计算的非组合性 (Lack of Compositionality) ：对于 A+B+C 这样的任务，一个直观的假设是模型会采用组合性的方式，先计算 A+B，将结果存储在某个中间Token（如B）的表示中，然后再与 C 进行计算。但AF1子图的发现与此相悖。模型似乎并没有利用Token位置来进行中间结果的存储和逐步计算，而是选择了一种更直接的、全局信息汇集的方式。

  • 计算与通信的分离：研究结果揭示了一种“先计算，后通信”的模式。在漫长的等待期，Token主要进行独立的内部计算（任务通用计算）；然后在短暂的传输期，它们进行密集的通信；最后，被选中的“计算Token”（最后一个Token）再次进入独立的计算状态。这可能暗示了模型在处理信息时，其残差流的大部分“带宽”被用于计算而非通信。

  • 训练目标的可能影响：为什么计算会如此集中于最后一个Token？研究者推测，这可能与模型的训练目标——预测下一个Token——密切相关。因为只有最后一个Token的最终表示被直接用于预测结果并接收梯度信号，模型可能会“走捷径”，将所有与预测直接相关的计算都集中到这个位置，而不是费力地去构建一个分布式的、组合式的计算过程。

作者坦诚地指出了当前研究的局限性，并展望了未来的研究方向。

  • Tokenization的依赖：本研究依赖于一个“合作的”Tokenizer，它能将每个数字（例如0-999）表示为单个Token。对于那些会将数字拆分为多个digit Token的模型（如Qwen, Gemma），当前的CAMA和ABP方法需要被扩展才能适用。
  • 任务范围的局限：研究主要集中在定义清晰的算术任务上。AF1子图在需要深度语义理解的任务上失效，这表明需要进一步探索那些负责高级能力的附加组件，以及它们是如何与AF1这样的计算核心协同工作的。

往期文章：