昨天解读了 OLMo3 的技术报告，其中的 DPO 部分用到了 名为 Delta Learning 的方法。提出这个方法的论文《The Delta Learning Hypothesis: Preference Tuning on Weak Data can Yield Strong Gains》恰好中了 COLM 2025，今天我们就来解读一下。

• 论文标题：The Delta Learning Hypothesis: Preference Tuning on Weak Data can Yield Strong Gains
• 论文链接：https://arxiv.org/pdf/2507.06187

TL;DR

该研究提出并验证了“Delta Learning（差分学习）”假设：在偏好微调（Preference Tuning）阶段，语言模型可以从成对数据的相对质量差异（Delta）中学习，即便这些数据的绝对质量远低于模型本身的能力。

研究表明，使用小型、弱模型（如 Qwen 2.5 3B 和 1.5B）生成的偏好对进行直接偏好优化（DPO），可以训练出性能匹配最先进开源模型（如 Tülu 3 8B）的强模型，而后者通常依赖于 GPT-4o 等强监督信号。理论分析进一步在逻辑回归框架下证明，只要两个弱教师模型之间存在性能差距，高维空间中的学生模型就有很大概率通过学习这种相对差异而实现超越教师的性能提升。

1. 引言

在当前大语言模型（LLM）的后训练（Post-training）范式中，一个普遍的共识是“强数据造就强模型”。无论是预训练数据的清洗，还是微调阶段的拒绝采样（Rejection Sampling），亦或是基于人类反馈的强化学习（RLHF），通常都假设监督信号的质量应当优于或至少匹配当前模型的能力。具体到偏好微调（如 DPO、RLHF），通常的做法是利用人类专家或更强的模型（如 GPT-4）来标注数据的优劣，或者从强模型生成的多个输出中筛选最佳结果作为“胜者（Chosen）”。

这种范式隐含了一个限制：模型的能力上限似乎被监督信号的强度所锁定。如果获取强监督信号成本过高（例如需要博士级别的专业知识），或者任务本身超越了当前人类或强模型的能力（例如未解的科学难题），模型的进一步提升将面临瓶颈。

本文探讨的核心问题是：如果只有弱监督信号，模型能否实现超越？

作者通过一系列实证研究和理论推导，展示了一个反直觉的现象：由弱模型生成的成对偏好数据（其中“胜者”和“败者”的绝对质量均低于待训练模型），依然可以驱动强模型的性能提升。这种现象被称为“Delta Learning”。

2. Delta Learning 假设

为了解释弱数据微调带来的增益，论文正式提出了 Delta Learning 假设。

2.1 核心定义

假设 是我们希望改进的目标模型， 表示对于输入提示词 的响应 的效用（Utility）或质量。这里的 可以代表人类偏好，也可以是某个客观的优化目标函数。

Delta Learning 假设认为，存在自然的偏好对 ，满足 ，且具备以下两个关键条件：

1. 低绝对效用（Low Absolute Utility）：
   胜者响应 的效用 并不高于模型 当前的能力水平。这意味着，如果直接在 上进行监督微调（SFT），会因为数据质量低而损害模型性能或导致性能停滞。

   
   

2. 外推增益（Extrapolated Gain）：
   尽管绝对质量较低，但 与 之间的相对质量差异（Delta）指明了改进的方向。在这些配对数据上进行偏好微调（如 DPO），能够推动模型 的性能超越 ，实现外推式增长。

   
   

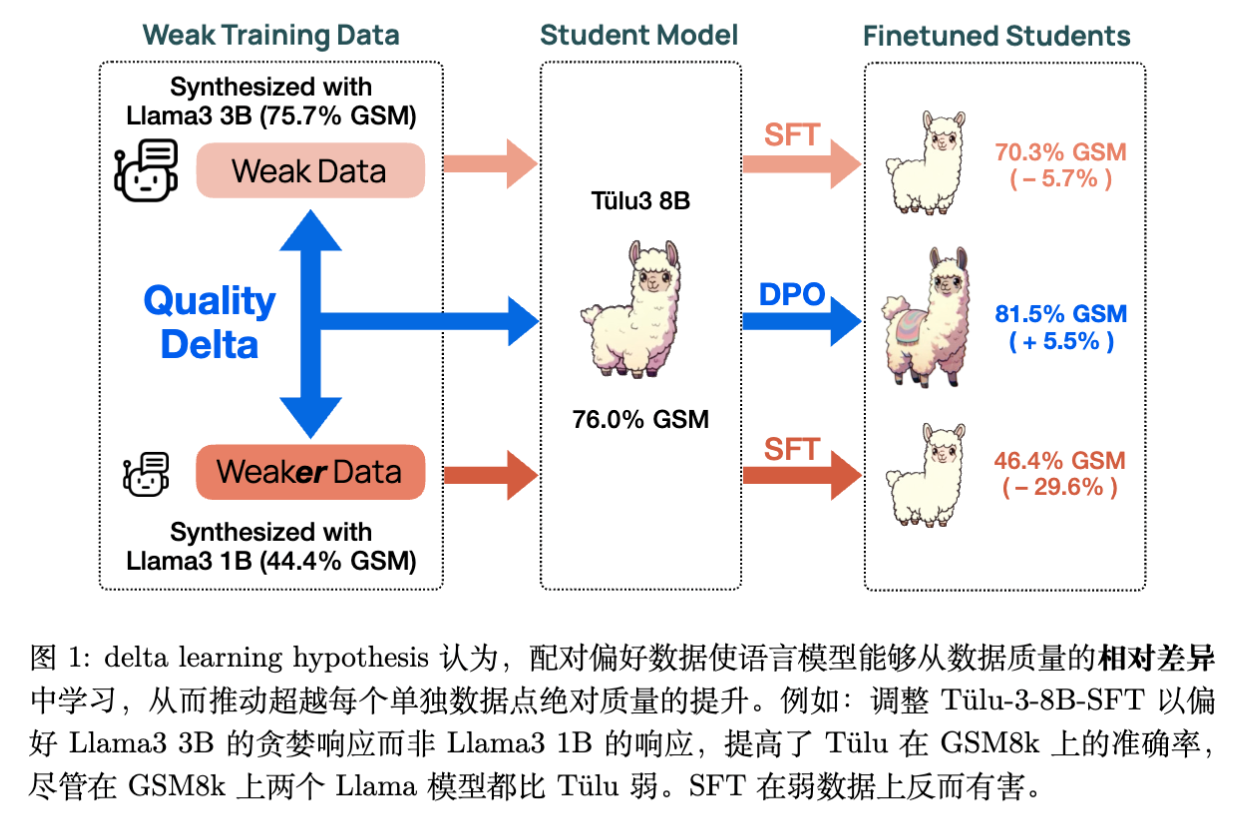
即使训练数据的绝对位置（质量）位于目标模型之下，只要两点构成的向量（Delta）方向正确，模型就能沿着该方向梯度更新，从而攀升至更高的质量平面。

3. 弱数据上的 SFT 与 DPO

论文首先通过一个案例研究（Case Study）初步验证了这一现象。

3.1 实验设置

• 数据集： 基于 UltraFeedback 数据集构建了一个过滤版本，称为 UltraFeedback-Weak。

  • 过滤标准： 移除了所有来自 LMSYS Chatbot Arena ELO 分数接近或高于 Llama-3.2-3B-Instruct 的模型的响应。
  • 结果： 数据集中的胜者响应 均来自较弱的模型（如 Alpaca-7B, Vicuna-33B 等），其绝对质量理论上低于待训练的 Llama 3 模型。
• 待训练模型： Llama-3.2-3B-Instruct 和 Llama-3.1-8B-Instruct。
• 训练方法：

  1. SFT： 仅在胜者响应 上进行监督微调。
  2. DPO： 在偏好对 上进行直接偏好优化。
• 评估指标： 包含 MMLU, MATH, GSM8k, IFEval 等 8 个标准基准。

3.2 实验结果

实验结果呈现出显著的对比（见上表）：

• SFT 的负面效应： 直接在弱模型的“胜者”响应上进行 SFT 导致了模型性能的全面下降。例如，Llama-3.1-8B-Instruct 在经过 SFT 后，MMLU 分数从 71.8 降至 65.7，GSM8k 从 83.7 降至 77.9。这符合“垃圾进，垃圾出”的传统直觉，即强模型模仿弱数据会导致能力退化。
• DPO 的正面效应： 尽管使用完全相同的弱数据集，DPO 训练却带来了性能提升。Llama-3.1-8B-Instruct 的 MMLU 提升至 72.0，GSM8k 提升至 83.9。

这一结果表明，数据的绝对质量并非提升模型的必要条件。偏好微调机制能够利用成对数据中的对比信号（Contrastive Signal），即使在数据整体较弱的情况下也能提取出改进方向。

4. 受控实验验证

为了更严谨地验证假设，排除数据分布的干扰，作者设计了两个受控实验，分别针对“风格（Stylistic）”和“语义（Semantic）”维度的 Delta 进行测试。

4.1 风格 Delta：加粗章节标题的数量

这是一个类似于“玩具模型（Toy Setting）”的实验，旨在验证模型是否能通过学习 Delta 实现简单的数值外推。

• 效用函数 定义： 响应 中包含的 Markdown 加粗章节标题（例如 Section Header）的数量。数量越多，效用越高。
• 数据构建： 构造偏好对 ，其中 包含 个加粗标题， 包含 个。设定 ，即包含更多标题的为胜者。
• 基线能力： Llama-3.2-3B-Instruct 在未训练前，平均每个响应生成约 5.9 个加粗标题。
• 弱数据构造： 强制生成的胜者响应 仅包含 3 个标题，败者响应 仅包含 2 个标题。注意，这里的 ，即胜者数据的绝对质量低于模型基线。

实验结果：

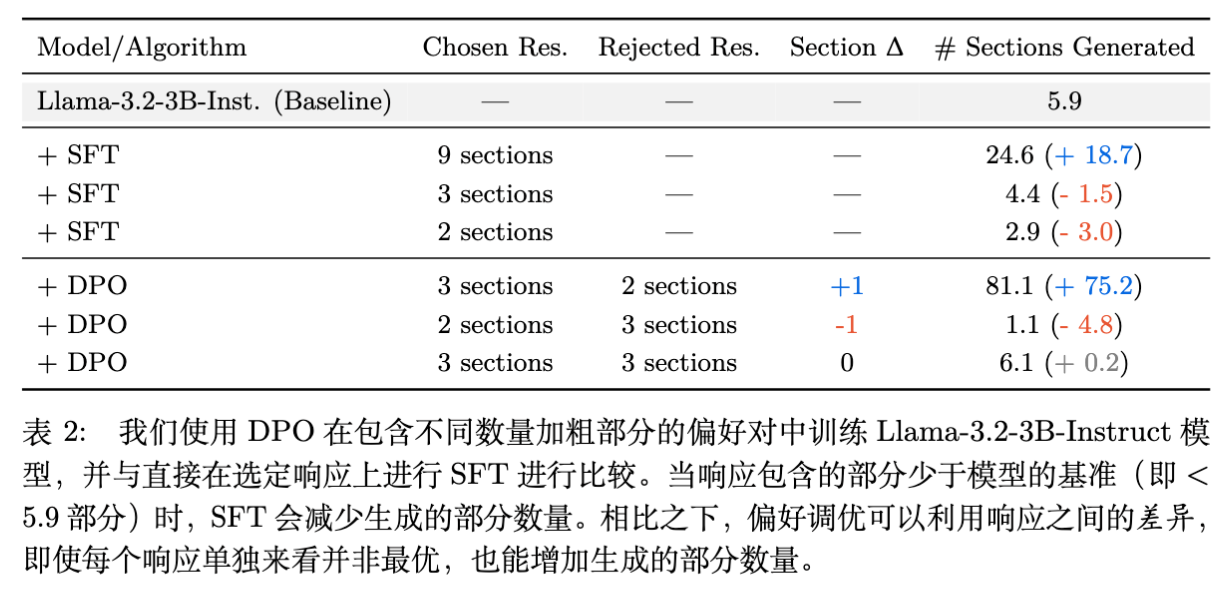
• SFT 失败： 在包含 3 个标题的数据上 SFT，模型生成的标题数降至 4.4，能力退化。
• Delta Learning 成功： 在 (3 vs 2) 的偏好对上进行 DPO，模型生成的标题数激增至 81.1。

这一结果强有力地证明了 外推（Extrapolation） 能力。模型并没有简单地学习“生成 3 个标题”，而是学习了“比另一个响应生成更多标题”这一关系（即梯度方向），并沿着该方向过度泛化（Over-generalization），最终生成了远超训练数据甚至基线模型的标题数量。

4.2 语义 Delta：弱模型作为负例

该实验旨在验证语义层面的质量提升。

• 设置： 待训练模型为 （Llama-3.1-8B）。
• 胜者 ： 由 自身通过贪婪解码（Greedy Decoding）生成。根据定义， 等于模型当前能力上限，理论上 SFT 不应带来提升。
• 败者 ： 由更弱的模型 （Llama-3.2-3B）生成。
• 假设： 尽管 无法看到比自己更好的数据，但通过学习“优于弱模型 ”这一 Delta，应当能获得提升。

实验结果：

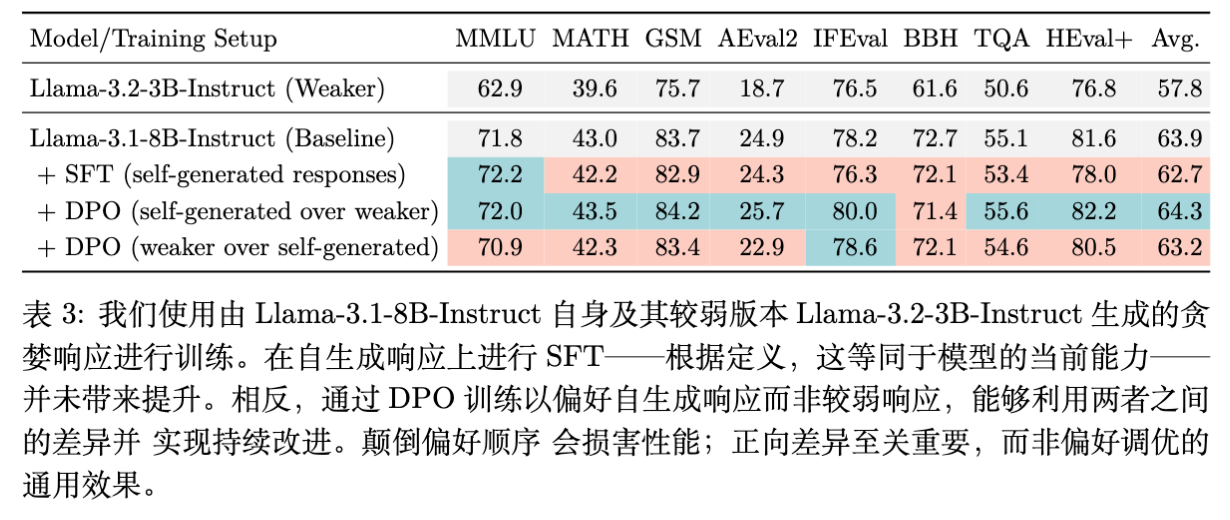
• SFT (Self-generated)： 在自身生成的贪婪解码数据上 SFT，平均分下降了 1.2 分。这可能是由于过拟合导致的探索性降低。
• DPO (Self > Weak)： 训练模型偏好自身输出优于弱模型输出，平均分提升了 0.4 分，且在 GSM8k 等任务上有一致增益。
• 反向控制 (Weak > Self)： 强行训练模型偏好弱模型输出，导致性能显著下降。这证明了提升并非来自 DPO 算法本身的正则化效应，而是来自正确的 Delta 方向。

5. 低成本复现 SOTA 后训练

验证了假设后，作者将目光转向实际应用场景：能否使用纯粹的弱模型流程，复现最先进（SOTA）的开源模型后训练效果？

5.1 对标基线：Tülu 3 Recipe

Tülu 3 是艾伦人工智能研究所（AI2）推出的 SOTA 开源模型系列。其标准的 8B 模型偏好微调流程（Tülu-3-8B-DPO）极其昂贵且依赖强监督：

1. 提示词： 271k 条多样化提示词。
2. 响应生成： 使用多个强模型（Llama-3.1-70B, Qwen-2.5-72B 等）生成响应。
3. 偏好标注： 使用 GPT-4o 对响应进行评分，选出最高分作为 ，较低分作为 。
4. 基座模型： Tülu-3-8B-SFT。

该流程的成本主要在于：(1) 运行 70B+ 模型进行推理的计算成本；(2) 调用 GPT-4o API 的标注成本（估算约 10,000 美元）。

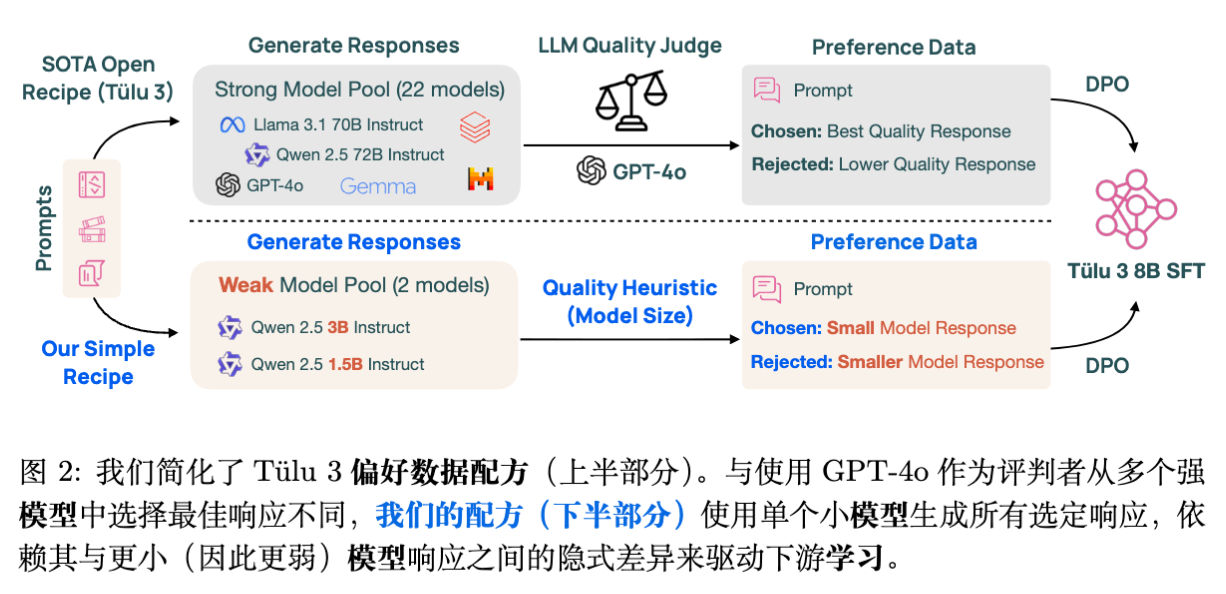
5.2 简化的 Delta Learning Recipe

作者提出了一种极简的替代方案，完全移除了任何强于 3B 参数的模型的使用：

1. 胜者生成（Chosen Generation）： 仅使用 Qwen-2.5-3B-Instruct 生成所有 。注意，该模型在多数基准上弱于待训练的 Tülu-3-8B-SFT。
2. 偏好配对（Forming Pairs）： 使用 模型大小（Model Size） 作为质量的代理（Proxy）。

   • 胜者：Qwen-2.5-3B-Instruct
   • 败者：Qwen-2.5-1.5B-Instruct
   • 不再使用 GPT-4o 打分。 简单地假设 3B 模型的输出优于 1.5B 模型的输出。
3. 基座模型： 同样的 Tülu-3-8B-SFT。

这一流程将数据生成阶段的 FLOPs 降低了一个数量级（约原流程的 6%），并完全消除了 GPT-4o 的标注成本。

5.3 实验结果：以弱胜强

作者在包含 11 个基准的评估套件上对比了两种流程训练出的模型。

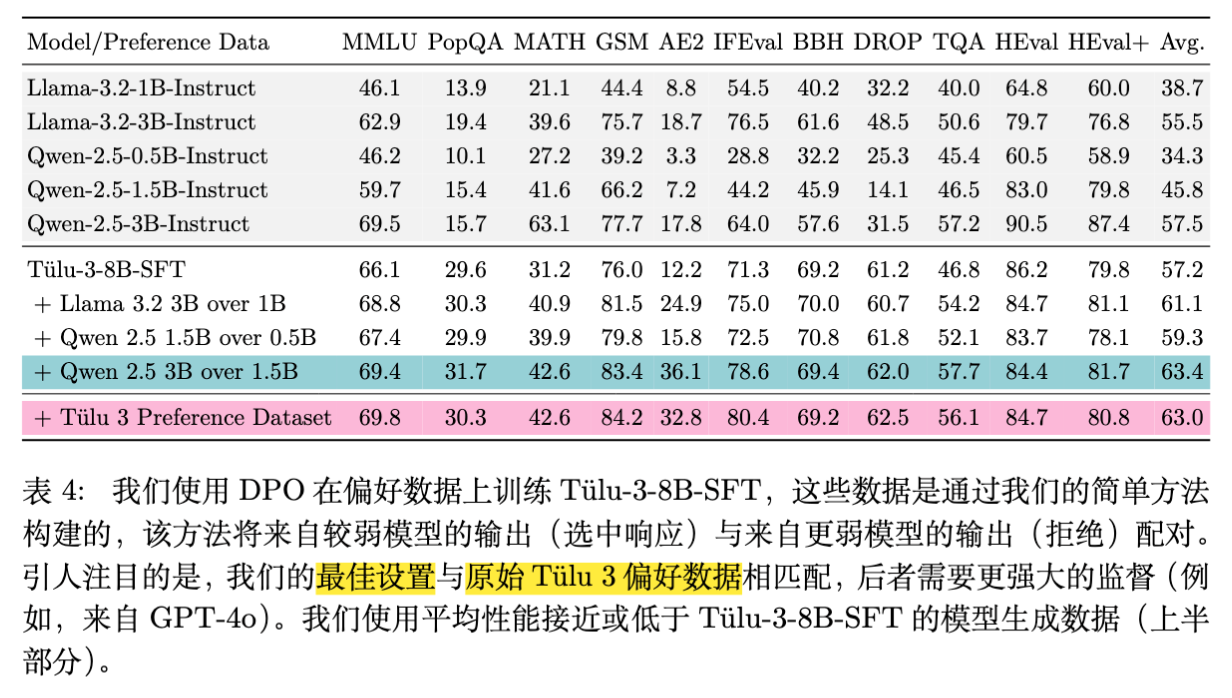
核心发现：

• 性能匹配： 使用 Qwen-2.5-3B (胜) / 1.5B (败) 生成的数据训练的模型，平均分为 63.4。而使用 GPT-4o 筛选强模型数据训练的官方 Tülu-3-8B-DPO 平均分为 63.0。
• 弱数据带来的提升： 即便胜者数据（Qwen 3B）在 GSM8k 上仅有 77.7% 的准确率（低于基座模型的 76.0%），训练后的模型在 GSM8k 上达到了 83.4% 。
• 跨家族泛化： 基座模型是 Llama 架构（Tülu 3 基于 Llama 3.1），而偏好数据来自 Qwen 家族。这表明 Delta Signal 具有跨模型结构的通用性。

这一结果令人震惊：一个 8B 的模型，通过学习“3B 模型比 1.5B 模型好在哪里”，最终性能超越了 3B 模型，甚至达到了利用 GPT-4o 监督的水平。

6. 深入分析与消融实验

为了理解这一现象的边界，作者进行了多维度的分析。

6.1 Delta 幅度与性能的关系

作者构建了 21 个偏好数据集，遍历了 Qwen 2.5 Instruct 家族所有可能的模型对组合（从 0.5B 到 72B）。

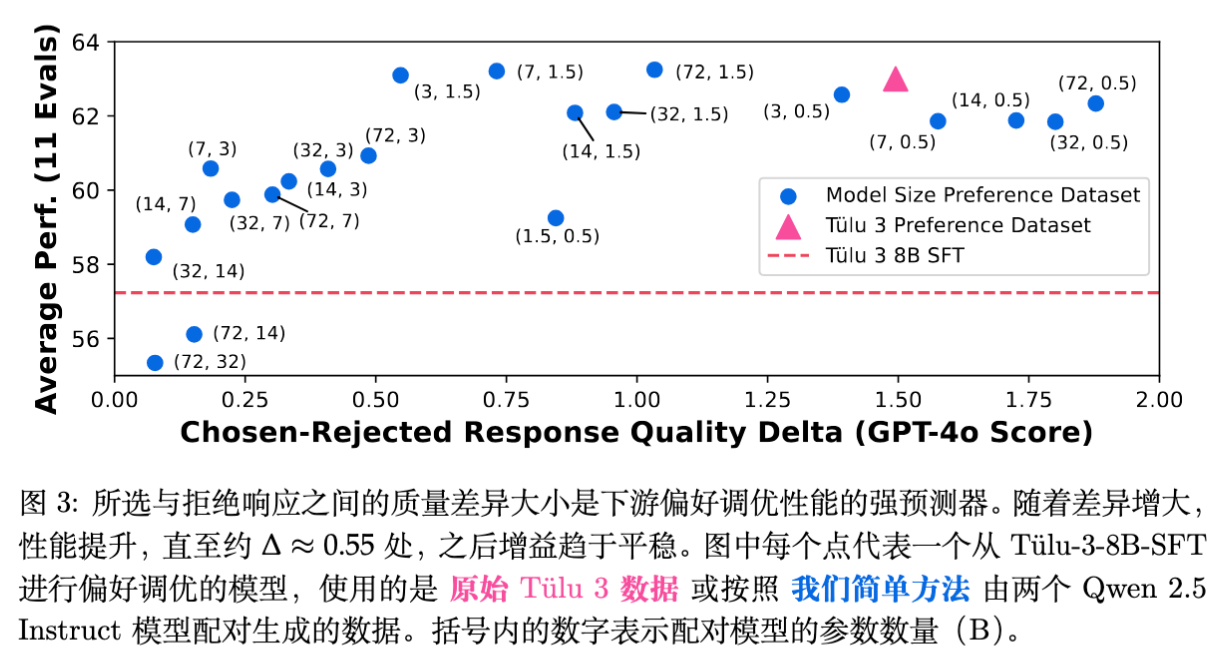
观察：

1. 正相关与饱和： 下游任务的性能与 Delta 的大小（通过 GPT-4o 评分差值衡量）呈强正相关。
2. 阈值效应： 当 Delta 达到约 0.55 分（5分制）时，收益趋于饱和。Tülu 3 的原始数据和作者的最佳配置（3B vs 1.5B）都处于这一饱和区。
3. 负 Delta 的危害： 如果 Delta 为负（即 实际上比 差），训练会损害模型性能。

6.2 胜者绝对质量的影响

作者对比了 SFT 和 DPO 对胜者绝对质量的敏感度。

• SFT： 只有当胜者数据的质量 显著高于 基座模型时，SFT 才能带来正收益。对于弱于基座的数据，SFT 会导致性能急剧下降。
• DPO： 即使胜者数据质量远低于基座模型（例如 Qwen 1.5B），DPO 依然能带来正收益，前提是存在一个更弱的败者构成 Delta。随着胜者质量的提升，收益会增加，但很快进入边际递减阶段。

6.3 偏好标注方法的消融

作者验证了使用“模型大小”作为启发式标签的有效性。

• 将 Qwen 3B vs 1.5B 的数据重新用 GPT-4o 进行打分和筛选。
• 结果发现，模型大小启发式标签与 GPT-4o 的偏好一致性高达 80.5% 。
• 使用模型大小标签训练的模型性能与使用 GPT-4o 标签训练的模型相当（甚至在某些指标上略优）。

6.4 安全性评估

在 XSTest, HarmBench 等安全性基准上，Delta Learning 训练出的模型并未表现出明显的安全性退化，与强监督模型表现相当。这表明弱数据微调并未以牺牲安全性为代价。

7. 理论分析：逻辑回归中的 Delta Learning

为了在数学层面解释 Delta Learning 的机制，作者在二分类逻辑回归（Logistic Regression）的设定下进行了理论推导。

7.1 问题设定

• 数据分布： 输入 是 维各向同性高斯分布。
• 真实标签： 由单位向量 决定， 。
• 学生模型： 参数 ，性能由其与 的余弦相似度 决定。
• 教师模型： 两个弱教师 (Chosen) 和 (Rejected)，其性能分别为 和 。
• 假设： ，即教师 优于教师 。但两者可能都弱于学生，即 。
• 伪标签生成： , 。

7.2 损失函数与梯度

使用朴素的偏好损失函数（简化版的 SimPO/DPO）：

其中 。

对于单个样本，梯度大致为 。在总体期望下（利用 Stein 引理），梯度更新方向包含两部分：

这表明，期望更新方向沿着差分向量 。

7.3 定理 6.1：学习成功的条件

作者证明，在高维空间中，只要满足一定条件，沿着 更新就能提高学生模型与 的对齐度。

条件 C1：

这个公式可以解读为信号与噪声的博弈：

• 第一项（信号）： 是教师之间的性能 Delta。该项总是正的，代表有用的学习信号。
• 第二项（噪声）： 涉及教师错误与学生当前错误在正交于 空间上的投影。

核心洞察：
在高维空间（ 很大）中，随机采样的两个向量在特定子空间上的投影往往是近似正交的。因此，噪声项（第二项）在高维下会趋近于零。这意味着，教师模型具体的错误模式（Error Pattern）与学生模型的错误模式大概率是不重叠的（Orthogonal）。

因此，只要 （存在 Delta），信号项就会主导更新方向，使得学生模型 逐步向 靠近，即使 已经远大于 。

图 5 展示了这一几何直觉：虽然 和 偏离 的角度很大（绝对质量低），但它们的差分向量 恰好指出了通向 的正确旋转方向。

7.4 推论 6.2

作者进一步证明，如果教师模型是在给定性能约束下随机采样的，那么随着维度 的增加，条件 C1 成立的概率趋近于 1。具体来说，只要维度 超过某个阈值 ，Delta Learning 就能以高概率保证学生模型的提升。

这也解释了为什么在语言模型这样极高维的参数空间中，Delta Learning 表现得如此稳健。

8. 讨论与相关工作

8.1 与 Weak-to-Strong Generalization 的联系

OpenAI 的 Burns 等人此前提出了“弱至强泛化（Weak-to-Strong Generalization）”，通过设计辅助损失函数让强模型从弱模型的标签中学习。本文的 Delta Learning 可以看作是该方向的一个特例或延伸，但机制不同：

• OpenAI 的工作主要关注预测一致性或辅助置信度损失。
• 本文强调利用成对数据的差分（Preference Pairs），通过 DPO 天然的对比学习机制来实现泛化。
• 本文方法的优势在于不需要修改训练目标函数，直接复用现有的 RLHF/DPO 基础设施即可。

8.2 为什么 SFT 会失败？

SFT 的本质是最大化似然估计（MLE），即模仿训练数据的分布。当训练数据 的质量 低于模型当前分布的平均质量时，SFT 实际上是在强迫模型“降智”以拟合数据。
相反，DPO 优化的是策略的相对概率比值（Log-odds ratio），关注的是 相对于 的优势。只要 在某些特征维度上优于 ，且该方向与真实改进方向一致，DPO 就能提取出正向的梯度信号。

8.3 局限性与未来工作

尽管结果令人振奋，作者也坦诚了研究的局限性：

1. 评估范围： 主要集中在通用的问答和推理任务（Tülu 3 suite），未涉及多语言、代码生成或特定的长文本写作任务。
2. 模型规模： 实证研究主要在 8B 模型上进行，尚未在 70B 或更大规模的模型上验证（尽管理论推导暗示高维空间更有利）。
3. Delta 的本质： 目前主要依赖“模型大小”作为质量差异的代理。未来需要更细致地探究到底什么样的语义 Delta（例如逻辑性、详细程度、格式规范）对学习最有效。

9. 结论

《The Delta Learning Hypothesis》一文通过严谨的实验和理论分析，挑战了后训练阶段必须依赖强监督数据的传统观念。其核心贡献在于：

1. 发现了 Delta Learning 现象： 证明了相对质量差异（Delta）比绝对质量对偏好学习更重要。
2. 提出了低成本 Recipe： 仅使用 Qwen 2.5 3B/1.5B 生成的数据，就能训练出匹敌 GPT-4o 监督效果的 8B 模型。这极大地降低了开源社区复现 SOTA 模型的门槛。
3. 建立了理论基础： 通过高维空间下的逻辑回归分析，从数学上解释了为何弱教师可以教出强学生。

对于我们而言，这意味着在数据合成（Synthetic Data）和数据管线（Data Pipeline）的设计中，我们不应只盯着数据的绝对质量（例如一味追求 GPT-4 生成），而可以多地关注如何构造具有明确、正向 Delta 的数据对。

附录：技术细节补充

为了满足读者对复现细节的需求，以下整理了论文附录中的关键参数。

A. 训练超参数 (Appendix G)

• 优化器: AdamW ().
• 学习率调度: Cosine Annealing (Warmup ratio 0.03).
• DPO 设置:

  • Batch Size: 32 (global).
  • Epochs: 1.
  • Learning Rate: 搜索范围 . 最佳配置通常在 左右。
  • (KL 惩罚系数): 搜索 。通常取 10。
  • Loss: 使用 Length-normalized DPO loss。
• SFT 设置:

  • Batch Size: 256.
  • Epochs: 1-2.
  • Learning Rate: .

B. 数据集构建细节

• Weak Preference Data: 针对 Tülu 3 的 271k prompt。
• 去重: 由于 Tülu 3 原始数据包含重复 prompt（用于不同模型采样），作者进行了去重，最终保留约 264k 对样本。
• Token 长度: 所有的弱模型（Qwen 3B/1.5B）生成的响应平均长度（约 770 tokens）显著长于 Tülu 3 原始的高质量响应（约 440 tokens）。这表明弱模型可能存在啰嗦或重复的问题，但 Delta Learning 依然有效。

C. 理论证明中的关键步骤 (Appendix F)

证明的核心在于处理随机梯度下降（SGD）中的噪声项。

1. Stein's Lemma 的应用：
   为了计算 ，利用 Stein 引理将其转化为 。由于 是高斯的，这一步可以将非连续的指示函数转化为与参数 相关的平滑项。

2. Martingale Concentration：
   为了证明 SGD 在有限步数内收敛到期望方向，作者定义了误差向量 ，这是一个鞅差序列（Martingale Difference Sequence）。利用 Vector Bernstein-Freedman 不等式，可以以高概率界定累积误差的范数 。

3. 高维正交性：
   利用球面集中（Sphere Concentration）界，证明两个随机向量在第三个向量的正交补空间上的投影的内积 会随着维度 的增加而以 的速度衰减。这是证明噪声项在高维下可忽略的关键。

往期文章：

• AllenAI OLMo 3 技术报告深度解析

• HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题