HuggingFace 高分论文：首个达到 IPhO 金牌水平的开源模型是如何炼成的？

• 论文标题：P1: Mastering Physics Olympiads with Reinforcement Learning
• 论文链接：https://arxiv.org/abs/2511.13612

TL;DR

上海人工智能实验室 P1 团队近期发布了技术报告《P1: Mastering Physics Olympiads with Reinforcement Learning》，介绍了一系列名为 P1 的开源物理推理模型。该工作的主要贡献在于通过基于强化学习（RL）的后训练（Post-training），显著提升了大型语言模型在物理奥林匹克竞赛级别的解题能力。其中，P1-235B-A22B 模型在 2025 年国际物理奥林匹克竞赛（IPhO 2025）中取得了金牌级别的表现，是首个达到此水平的开源模型。该研究提出了一套包含高质量数据集构建、多阶段自适应 RL 训练以及推理时多智能体协同（Agentic Framework）的完整技术方案，并验证了该方法在数学和代码任务上的泛化能力。

1. 引言

随着大型语言模型（LLM）的快速发展，人工智能的能力边界正在从单纯的符号操作和知识检索，向更具挑战性的科学级推理（Science-grade Reasoning）拓展。这一转变要求模型输出不仅要符合语言逻辑或评分标准，更必须通过物理现实和自然法则的严格检验。物理学作为现代科学的基石，要求模型具备概念理解、系统分解以及基于物理定律的精确多步推理能力，是检验 AI 科学推理能力的试金石。

奥林匹克级别的物理竞赛（如 IPhO）因其问题的高度抽象性、数学复杂性以及对创造性洞察力的要求，成为了评估 LLM 科学推理能力的标准化测试平台。P1 团队视竞技性解题为通向机器科学发现（Machine Scientific Discovery）的关键里程碑。

本报告详细介绍了 P1 模型家族的研发过程。该系列模型完全通过强化学习后训练在基座模型之上构建。作者并未止步于单一模型的训练，还引入了推理时的扩展策略（Test-time Scaling），通过名为 PhysicsMinions 的智能体框架，使模型具备自我反思和验证的能力。

2. 物理数据集构建

高质量、特定领域的数据是后训练的基础。P1 团队构建了一个包含 5,065 个奥林匹克级别物理问题的文本数据集。

2.1 数据来源与构成

数据集主要来源于两个方面：

1. 物理奥林匹克竞赛试题：包含截至 2023 年的 10 项主要物理奥林匹克赛事（如 APhO, IPhO 等），涵盖从地区级到国际级的不同难度，占数据总量的 81%（4,126 题）。
2. 竞赛教材：选取了 10 本权威竞赛教材，提供了系统化的例题和习题，占数据总量的 19%（939 题）。

这些数据覆盖了力学、电磁学、热学、光学和现代物理等 5 个主要领域及 25 个子领域。

2.2 数据处理流水线

为了适应强化学习对数据质量的高要求，特别是为了支持规则验证（Rule-based Verification），数据构建过程采用了多阶段流水线：

1. PDF 转 Markdown：利用 OCR 工具处理原始 PDF 文件。
2. 题目与解析解析：针对教材和竞赛题的不同结构设计提取策略。特别是对于奥赛题目，专家手动重构了题目结构，将共享背景信息与具体子问题分离，以保持逻辑完整性。
3. 答案标注（核心环节）：这是支持 RLVR（Reinforcement Learning with Verifiable Rewards）的关键。模型自动提取答案并将其分解为结构化列表。重要的是，数值、单位和变量被分离到明确的字段中，以便进行标准化的规则评分。
4. 语言归一化：非英语源题（如 CPhO）被翻译为英语，保持语料库的单语言一致性。

2.3 质量控制

为确保数据的正确性，研究实施了严格的质检流程：

• OCR 修正：人工校验复杂排版或低质量扫描件。
• 答案交叉验证：使用三个模型（Gemini-2.5-Flash, Claude-3.7-Sonnet, GPT-4o）独立提取答案，仅保留至少两个模型达成一致的条目。
• 数据过滤：移除需要绘图或答案无法验证（如证明题、解释题）的样本。
• 专家审查：进行最终的一致性审计和人工修正。

最终产生的数据集遵循“问题-解析-答案”的结构化模式，并附带了详细的元数据（如物理领域、来源），支持细粒度的训练和分析。

3. 强化学习后训练

P1 模型的核心训练方法是基于强化学习的后训练。作者并未依赖监督微调（SFT），而是直接在基座模型上应用 RL，通过结果导向的奖励信号优化模型的推理路径。

3.1 问题形式化

物理奥赛解题过程被形式化为马尔可夫决策过程（MDP）：

• ：状态空间，包含问题陈述和已生成的推理步骤。
• ：动作空间，即模型的词表。
• ：状态转移函数，由模型生成下一个 token 决定。
• ：奖励函数，评估最终解题轨迹的正确性和质量。

学习目标是最大化期望回报：

3.2 优化算法：GSPO

研究采用了分组序列策略优化（Group Sequence Policy Optimization, GSPO）算法。GSPO 将优化粒度从 token 级别提升到序列级别，并利用长度归一化的序列似然重要性比率（Importance Ratios）。

重要性比率定义为：

其中 是序列长度，引入 项是为了通过长度归一化来减少方差。

优势函数（Advantage Function）在组内计算：

其中 是组的大小。通过减去组内的平均奖励，GSPO 有效降低了梯度估计的方差。

最终的目标函数为：

3.3 奖励设计与验证器

奖励函数

采用基于答案正确性的二元奖励机制（Correct-or-Not）。针对包含多个子问题的物理题，采用类似代码评测的测试用例（Test-case）风格的奖励聚合：

其中 是子问题数量， 是第 个子问题的正确性指标（0 或 1）。

为了便于答案提取，系统提示词（System Prompt）强制模型使用 \boxed{} 格式输出最终答案。

验证器设计

由于物理答案常涉及符号表达式而非单纯数值，简单的字符串匹配无法满足要求。研究采用了混合验证策略：

1. 基于规则的验证器（Rule-based Verifier）：用于训练阶段。结合 SymPy 和 math-verify 启发式规则，进行代数表达式的等价性测试（如交换律、因式分解、化简）。这种方法准确率高（Precision），不易被模型“欺骗”。
2. 基于模型的验证器（Model-based Verifier）：仅用于验证/评估阶段。使用 Qwen3-30B-A3B-Instruct 模型判断提取的预测值与标准答案是否一致。

3.4 技术实现细节

3.4.1 自适应可学习性调整

为了确保持续的性能增长并避免训练停滞，作者设计了动态调整机制，以维持训练过程中的“可学习性”（Learnability）。

预先通过率过滤
在训练前，使用 Qwen3-30B 模型进行采样（pass@88），根据通过率过滤任务：

• 过滤 pass=0 或 pass=1 的任务：防止因组内样本结果全同导致优势函数为 0（奖励稀疏）。
• 过滤 pass > 0.7 的任务：防止因任务过简单导致策略迅速坍缩到低熵解，避免过早收敛。

自适应探索空间扩展
随着模型能力的提升，固定的探索配置可能限制进一步学习。研究在训练的不同阶段逐步扩展探索空间：

1. 组大小（Group Size）扩展：增加采样组的大小 （从 16 增加到 32）。更大的 增加了在困难问题中采样到高回报轨迹的概率，从而提供有效的学习信号。
2. 生成窗口（Generation Window）扩展：逐步增加最大输出长度（从 48k 增加到 80k token）。这允许模型探索更长、更完整的推理链，减少因截断导致的错误。

3.4.2 训练稳定性机制：截断重要性采样 (TIS)

现代 RL 框架通常使用不同的推理引擎（如 vLLM/SGLang）进行数据采样（Rollout），使用训练框架（如 Megatron）进行参数更新。这导致采样策略 和训练策略 之间存在数值精度和实现上的微小差异，即：

这种偏差会导致梯度估计有偏，引发训练不稳定。

为了解决这一“训练-推理失配”问题，研究采用了截断重要性采样（Truncated Importance Sampling, TIS）：

通过引入截断超参数 ，限制重要性权重的上限，在修正分布偏移的同时防止过大的权重破坏训练稳定性。

3.4.3 训练动态

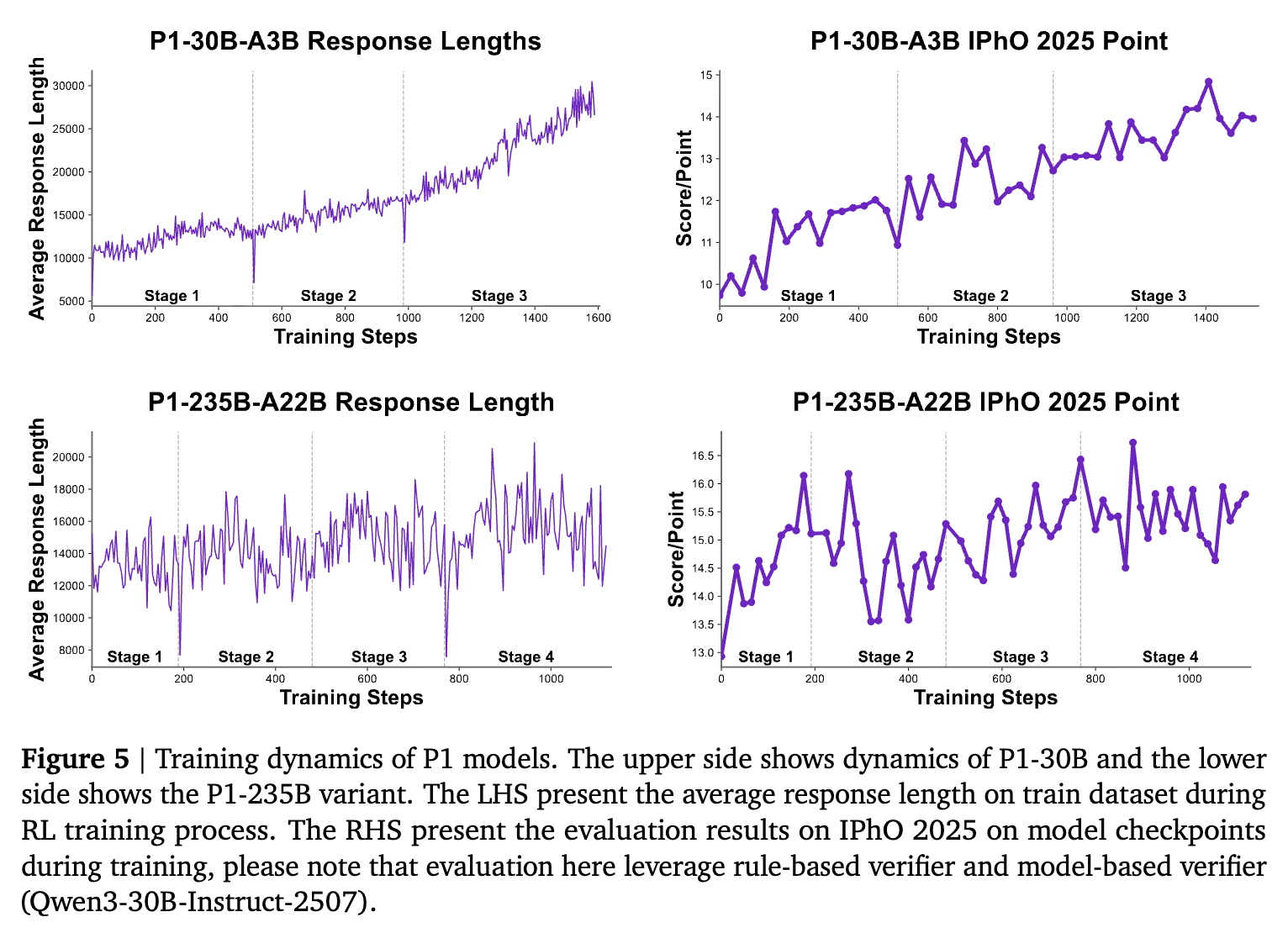
图表显示，随着训练阶段的推进，P1 模型的平均响应长度逐渐增加，表明模型正在学习更深层次的推理。同时，IPhO 2025 的验证分数呈现稳步上升趋势。

训练阶段配置表：

注：P1-235B 在更长的上下文窗口和更多阶段下进行了训练。所有阶段均仅使用基于规则的验证器。

4. 推理时扩展：PhysicsMinions 框架

除了训练时的 Scaling，P1 还结合了名为 PhysicsMinions 的多智能体框架进行测试时扩展（Test-time Scaling）。这是一个针对复杂物理推理设计的协同进化系统，包含三个模块：

1. Visual Studio ：处理包含图表的多模态输入，提取结构化信息（由于 P1 是纯文本模型，此模块主要由多模态模型辅助或处理文本输入）。
2. Logic Studio ：

   • Solver：生成初始解。
   • Introspector：在提交前对解进行自我完善。
   • 此处均由 P1 模型实例化。
3. Review Studio ：进行双重验证。

   • Physics-Verifier：检查物理一致性（如量纲、常数）。
   • General-Verifier：检查逻辑、推理和计算细节。
   • 若验证失败，返回详细的 Bug 报告给 Logic Studio 进行修正。

协同进化机制：系统设定了一个超参数 CV（Consecutive Verifications）。只有当解连续通过 CV 次验证（默认为 2 次）才被接受；如果连续失败 CV 次，则由 Solver 重新生成候选解。这一机制模拟了人类物理学家“推理-批判-修正”的思考过程。

5. 实验与评估

5.1 实验设置

测试数据集：HiPhO
为了评估模型在最新奥赛题目上的表现，团队构建了 HiPhO 基准，涵盖了 2024-2025 年的 13 项主要高中物理奥林匹克竞赛（如 IPhO, APhO, EuPhO 等）。

对比模型
共对比了 33 个模型，包括闭源模型（GPT-5, o3, GPT-4o, Claude-3.7 等）和开源模型（Qwen2.5, DeepSeek-V3, DeepSeek-R1 等）。

评估指标
使用“考试得分”（Exam Score）而非简单的准确率，即按照官方评分标准对每个步骤和最终答案进行打分，能够给予正确中间步骤部分分数，更符合竞赛实际情况。

5.2 物理奥赛评估结果

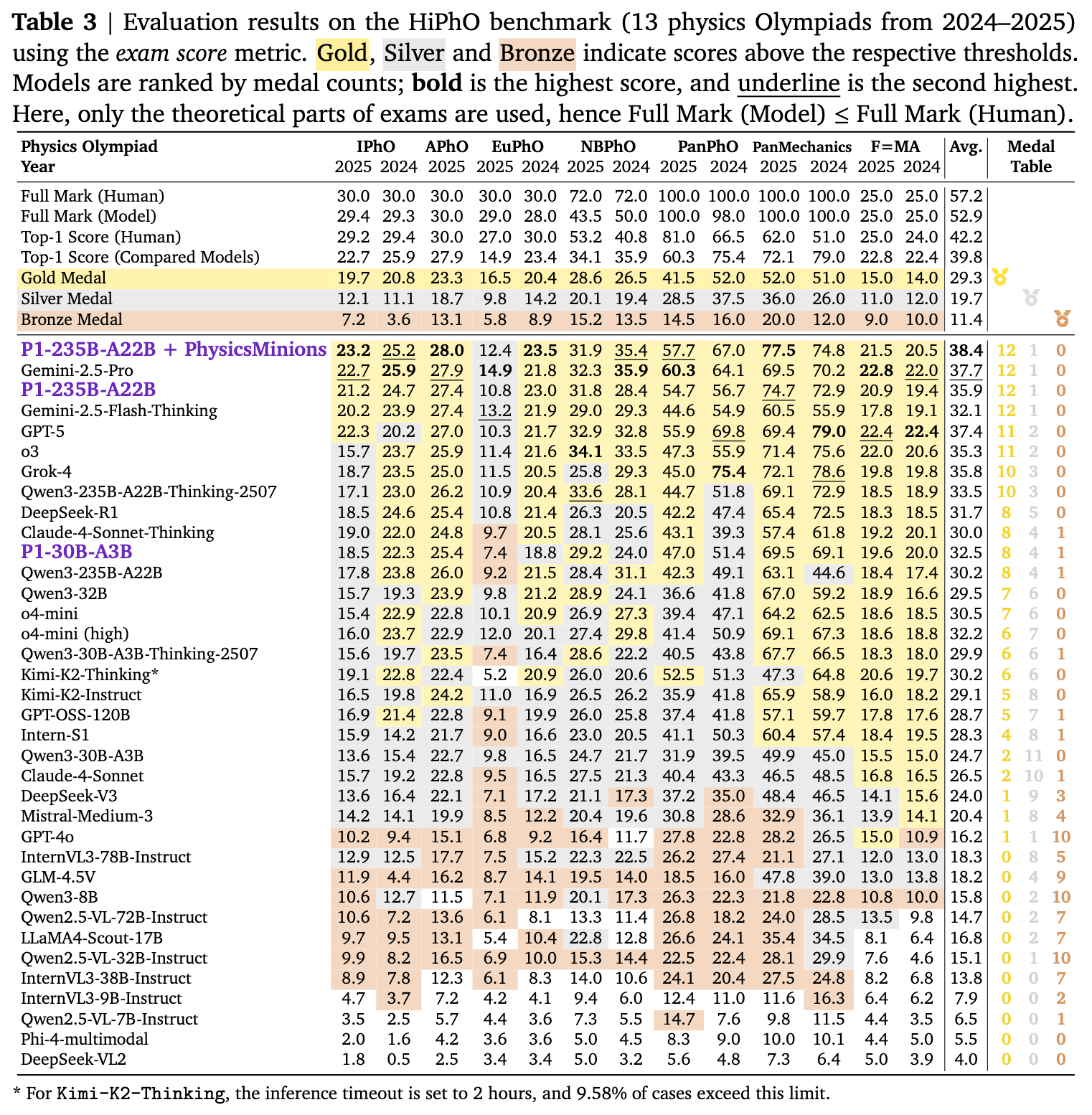
主要发现：

1. P1-235B-A22B 的顶尖表现：

   • 该模型在 HiPhO 基准上的平均得分（35.9）超越了 GPT-4o (16.2)、Claude-3.5-Sonnet 等模型，仅次于 Gemini-2.5-Pro (37.7) 和 GPT-5 (37.4)。
   • IPhO 2025 金牌水平：在 IPhO 2025 理论考试中得分 21.2/30，超过金牌线（约 19.7 分），是目前唯一达到 IPhO 金牌水平的开源模型。
   • 在奖牌榜上，P1-235B 获得了 12 枚金牌和 1 枚银牌。

2. P1-30B-A3B 的高性价比：

   • 作为轻量级模型，其获得了 8 金 4 银 1 铜，排名开源模型第三，仅次于自身的 235B 版本和 DeepSeek-R1，优于 Qwen3-32B 和原始基座模型。

3. PhysicsMinions 的增益：

   • 结合 PhysicsMinions 后，P1-235B 的平均得分从 35.9 提升至 38.4，在所有对比模型（包括闭源）中位列 第一。
   • 在 IPhO 2025 上的得分提升至 23.2，刷新了现有记录。

4. CPhO 2025 案例：

   • 在中国物理奥林匹克（CPhO 2025）这一公认的高难度赛事中，P1-235B 获得了 227/320 分，远超人类金牌选手的最高分（199 分），展示了在长难推理任务上的超人表现。

6. 讨论与分析

6.1 泛化能力

一个关键问题是：针对物理领域的后训练是否会牺牲模型的通用能力？或者物理推理能力是否能迁移？

研究在 MATH, STEM 和代码基准（AIME24/25, GPQA, LiveCodeBench 等）上对比了 P1 模型与其基座模型。

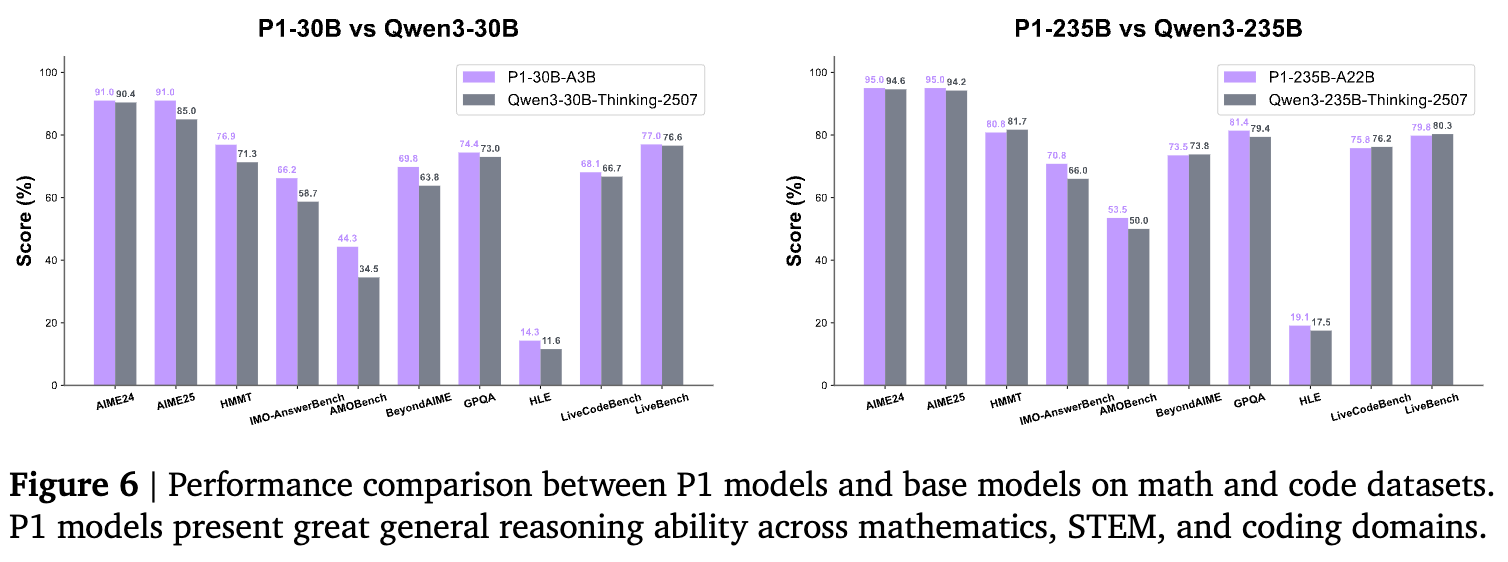
结果显示，P1 模型在这些通用推理任务上全面超越了基座模型。P1-235B 在 AIME、GPQA 和 IMO-AnswerBench 上的表现均优于 Qwen3-235B-Thinking。这表明：

1. 物理训练强化的长链条推理、符号操作和系统分解能力具有跨领域的迁移性。
2. 领域特定的深度后训练可以作为通用推理能力的放大器。

6.2 基于规则 vs 基于模型

报告深入讨论了为何在训练阶段仅使用基于规则的验证器。

尽管基于模型的验证器（Model-based Verifier）理论上能提供更高的召回率（Recall），覆盖规则难以判定的正确答案，但在 RL 训练中直接引入它存在巨大风险：

1. Reward Hacking（奖励劫持）：策略模型（Policy）容易利用验证模型（Verifier）的漏洞，生成冗长或特定风格的“伪解答”来骗取高分。
2. 假阳性（False Positive）的危害：在 RL 中，将错误答案误判为正确的危害远大于漏判正确答案。错误的奖励信号会迅速导致策略退化。

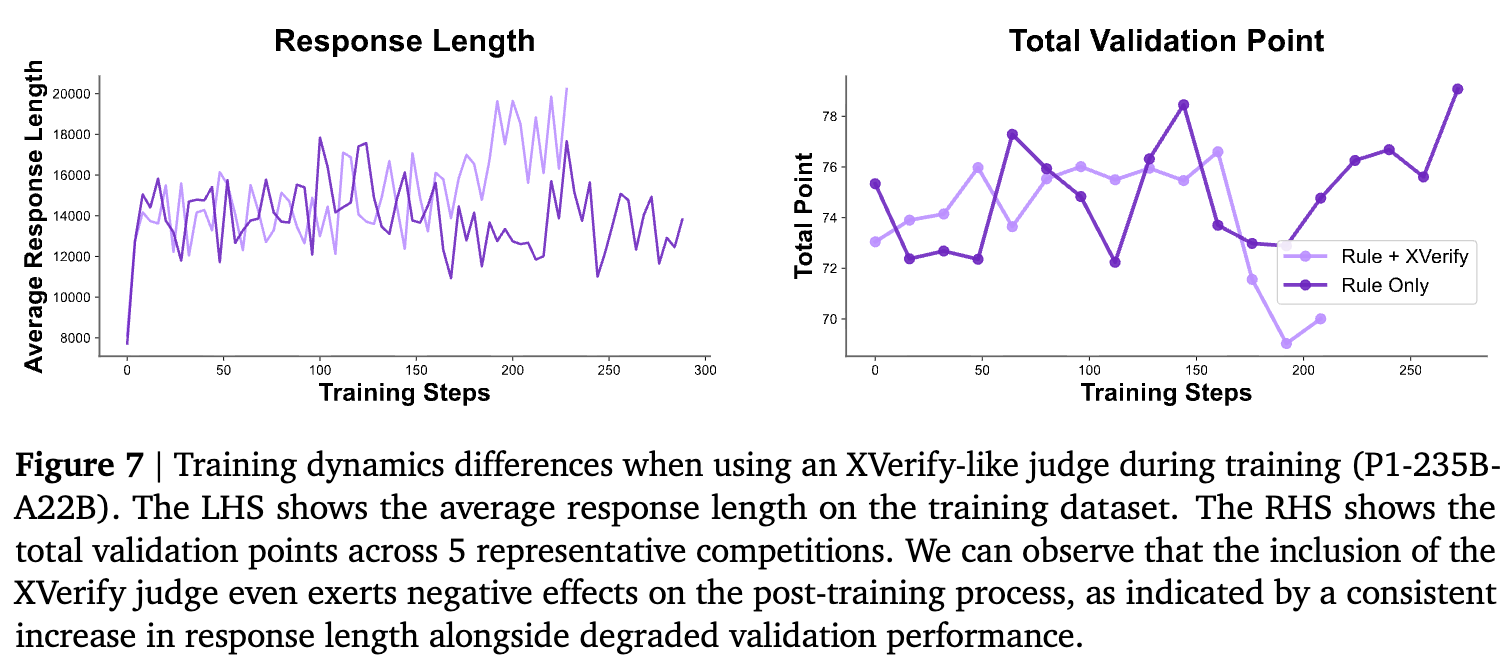
实验表明，引入基于模型的验证器后，模型的响应长度爆炸性增长（试图通过长度欺骗验证器），但实际验证分数却在下降。这强调了在 RL 训练中，验证器的精确率（Precision）优于召回率。只有当模型验证器极其稳健时，才能安全地接入训练循环。

7. 结论

P1 技术报告展示了开源社区在科学推理领域的重大进展。通过精心构建的物理奥赛数据集、针对性的多阶段强化学习策略以及推理时的智能体框架，P1-235B-A22B 成功达到了国际物理奥赛金牌水平。

该工作不仅提供了一个强大的物理推理模型，更重要的是验证了一条路径：通过高质量的领域数据和基于规则的强化学习（RLVR），可以显著激发大模型的深度推理潜力，并且这种能力能够正向迁移到数学和编程等其他领域。

P1 的经验强调了数据质量、奖励函数设计的严谨性以及训练稳定性技术（如 TIS）在后训练阶段的重要性。

往期文章：

• Meta 提出 SoCE 策略，仅靠模型权重融合实现 SOTA

• 陈丹琦团队新作 Retaining by Doing：揭示 RL 比 SFT 为什么更能缓解灾难性遗忘

• 微软提出 GAD：通过生成对抗蒸馏方法实现 On-Policy 蒸馏 GPT-5

• LightReasoner：利用小模型引导大模型推理的对比学习框架

• WeiBo AI 推出 1.5B 小模型，成本实现 SOTA 级推理

• Meta FAIR 推出 HERO：LLM 强化中集成稀疏与密集奖励

• 专挑模型的“软肋”下手：阿里 MIWV 如何实现用1%数据超越全量微调？

• Meta AI 推出 RIFL：基于准则的强化学习来提升 LLM 指令遵循能力

• NeurIPS 2025 满分论文：LLM 强化学习的上限已被基座锁死了

• EMNLP 2025 主会论文解读：Towards Automated Error Discovery

• Meta AI 最新研究：大模型强化学习的几何优化偏置

• Meta AI：Scaling Agent Learning via Experience Synthesis

• 西湖大学提出 SimKO ：一种简单的 Pass@K 策略优化方法

• Google Research 重磅研究：一种用于持续学习的新型机器学习范式 - Nested Learning

• 蚂蚁大模型 Ling 2.0 技术报告

• 腾讯 WeChat AI 提出 Continuous Autoregressive Language Models

• 清华 & 智谱推出 CROPI 框架：通过 Off-Policy Influence 来提升 RLVR 的数据效率

• NVIDIA 提出 CoDeC：通过 In-Context Learning 来区分模型“记忆”还是“泛化”

• Sea AI Lab 新研究：FP16 可以解决 RL 中的训推不一致

• 浙大 & 阿里提出 RAVR：当 LLM 被“剧透”答案后，它的推理能力会发生什么变化？

• 通义 DeepResearch 技术报告解读

• 字节 Seed 重磅新作：Scaling Latent Reasoning via Looped Language Models

• NeurIPS 2025 高分论文 DisCO：利用判别式约束优化增强推理 LLM

• On-Policy Distillation 解读

• Google DeepMind：从开源模型中提取 SFT 和 RL 训练数据

• 南大 NeurIPS 2025：关于 LLM 内部概率与自洽性的理论研究

• LoongRL：面向长上下文推理的强化学习

• RL Grokking：解决 pass@K=0 难题的新思路

• 重新思考 RLVR 中的基线设计：用分位数替代均值，让大模型强化学习更加稳定

• SFT 是通用能力的“杀手”还是“背锅侠”？亚马逊新作揭示其“灾难性遗忘”的真相

• 腾讯优图提出免训练GRPO，在上下文空间中实现策略优化

• 告别“炼丹”，拥抱“工程”：Meta AI 万字长文详解大模型强化学习的 Scaling Law

• Google DeepMind 为提示词优化提供理论保证，文末附优化实践启示

• Sanjeev Arora 团队新作 STAT：破解 SFT 饱和瓶颈，通过“技能驱动”让模型性能再提升7.5%

• Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题