我们对如何有效规模化(scale)RL 的理解却远远没有跟上步伐。与已经建立起成熟、可预测的规模化法则(Scaling Laws)的预训练阶段不同,LLM 的 RL 训练领域至今仍缺乏一套系统的、科学的方法论。目前,该领域的进展主要由少数几个关于新算法的独立研究或特定模型的训练报告驱动。这些研究通常提供针对特定场景的“特设”解决方案,但未能回答一个更根本的问题:我们应该如何开发能够随计算资源投入而稳定提升性能的 RL 方法?
这种方法论的缺失,使得 RL 实践更像一门依赖直觉和经验的“炼丹术”,而非一门严谨的“科学”。研究者们面临着海量的设计选择(如损失函数、数据课程、算法细节等),却没有任何可靠的方法来“先验地”判断哪种选择在更大规模上更具潜力。这不仅导致了大量的计算资源浪费在低效的试错上,也无形中提高了学术界和中小型研究团队参与前沿 RL 研究的门槛。
来自 Meta 的论文《The Art of Scaling Reinforcement Learning Compute for LLMs》,正是为了填补这一关键空白。这项工作通过超过 40 万 GPU 小时的超大规模系统性实验,首次为分析和预测 LLM 中的 RL 规模化行为,定义了一个有原则的框架。 他们提出,使用 Sigmoid 函数(S 型曲线)而非传统的幂律(Power Law)来拟合 RL 训练中的“计算-性能”曲线,并基于此框架,提炼出一套名为 ScaleRL 的最佳实践方案。该研究证明,通过 ScaleRL,我们可以在单次 RL 运行中,成功地将性能可预测地扩展至十万 GPU 小时级别。

-
论文标题:The Art of Scaling Reinforcement Learning Compute for LLMs -
论文链接:https://arxiv.org/pdf/2510.13786
1. 理论框架
在预训练领域,研究人员通常使用幂律(power-law)来拟合损失与计算量之间的关系。然而,在 RL 领域,我们更关心的是一些有界的性能指标,例如任务的“通过率”(Pass rate)。这类指标在达到某个上限后会趋于饱和。直接套用无界的幂律函数显然是不合适的。
为此,作者们借鉴了其他领域研究有界指标的思路,提出使用一个类似 S 型(sigmoidal)的饱和曲线来建模 RL 性能(以预期奖励 表示)与训练计算量 之间的关系。其具体形式如下:
这个公式是整个研究的基础。让我们来详细拆解其中每个参数的含义:
-
:表示在投入计算量为 时的预期奖励或性能(例如,验证集上的平均通过率)。 -
:表示训练开始前()的初始性能。 -
:表示渐进性能(Asymptotic Performance)。这是模型在该 RL 方法下,当计算资源趋于无穷时,能够达到的理论性能上限。这个参数至关重要,它决定了一个 RL 方案的“天花板”有多高。 -
:表示中点计算量(Midpoint Compute)。它定义了性能曲线达到总增益()一半时所需的计算量。 越小,意味着算法达到其中等性能水平的速度越快。 -
:表示缩放指数(Scaling Exponent)。这个参数控制了曲线的陡峭程度。 越大,曲线在 附近爬升得越快,代表着计算效率越高。
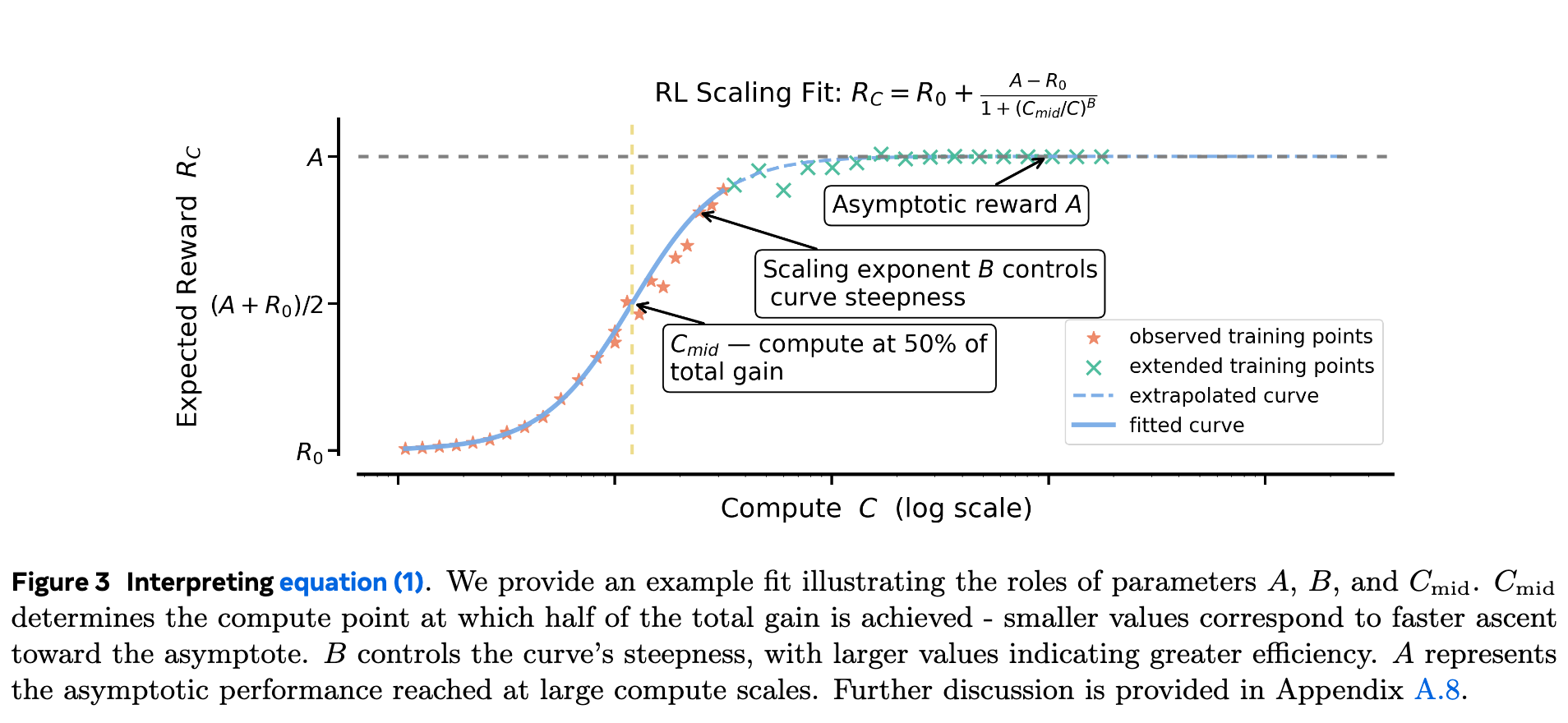
上图直观地展示了这三个核心参数 , , 的作用。 决定了曲线最终能达到的高度; 决定了曲线在横轴上的位置; 决定了曲线的“坡度”。
通过这个框架,我们可以将一个复杂的 RL 训练过程抽象为这三个关键参数。这带来了几个好处:
-
量化评估:我们可以用 来评估一个 RL 算法的潜力,用 和 来评估其计算效率。 -
外推预测:通过在较小计算预算下(例如,训练过程的前半段)拟合这条曲线,我们可以外推(extrapolate)预测在更大计算预算下模型的性能表现。这为在有限资源下评估算法的可扩展性提供了一种强大的工具。 -
指导算法设计:在比较不同的设计选择时,我们有了一个明确的目标:优先选择那些能够提升性能天花板 的方法,其次再优化计算效率(即增大 或减小 )。
作者强调,为了获得稳定且有意义的拟合结果,他们通常会忽略训练最开始的阶段(约 1.5k GPU 小时),因为这个阶段的动态可能不稳定,与后续的平稳扩展阶段不符。这与预训练缩放定律研究中忽略初始“loss spike”阶段的做法类似。
2. ScaleRL
为了找到一个可预测且性能优越的 RL 方案,作者们在一个 8B 参数规模的稠密模型上,进行了一场耗资超过 400,000 GPU 小时的全面实证研究。他们系统地评估了一系列在现代 LLM 的 RL 训练中常见的“设计选择”。本节将详细介绍这些实验,它们共同构成了最终的 ScaleRL 方案。
2.1 基础设置
-
任务与数据集:实验主要在可验证的数学推理任务上进行。训练集使用 Polaris-53K 数据集,这是一个包含数学问题的集合。模型需要生成包含思考过程(enclosed with <think>and</think>tokens)和最终答案的轨迹。 -
基础 RL 算法:作者选择了一个类似于 GRPO (Group Relative Policy Optimization) 的算法作为起点,但移除了 KL 正则化项。同时,他们加入了 DAPO (Decoupled clip and Dynamic sampling Policy Optimization) 中使用的非对称裁剪(asymmetric clipping),以防止熵坍塌。 -
架构:实验采用生成器-训练器分离(generator-trainer split)的架构。大部分 GPU 作为生成器,负责使用优化的推理核心进行高速的轨迹生成(rollout);一小部分 GPU 作为训练器,负责运行训练后端(如 FSDP)并更新模型参数。
2.2 异步 RL 设置
在分布式训练中,如何处理策略的“离线程度”(off-policy)是一个核心问题。作者比较了两种主流的异步 RL 方法:
-
PPO-off-policy-k:这是 Qwen3 和 ProRL 等工作中使用的默认方法。生成器使用旧策略 生成一批完整的轨迹,然后训练器在这批数据上进行 次梯度更新。这种方法的缺点是,训练器处理的数据可能已经“过时”了。 -
PipelineRL-k:这是 Magistral 等工作采用的较新方法。生成器以流式(streaming)的方式持续产生轨迹。一旦训练器完成一次策略更新,新的参数会立即被推送给生成器。生成器会用新权重继续生成未完成的轨迹(但使用旧的 KV 缓存)。这种方法的反馈循环更紧密。
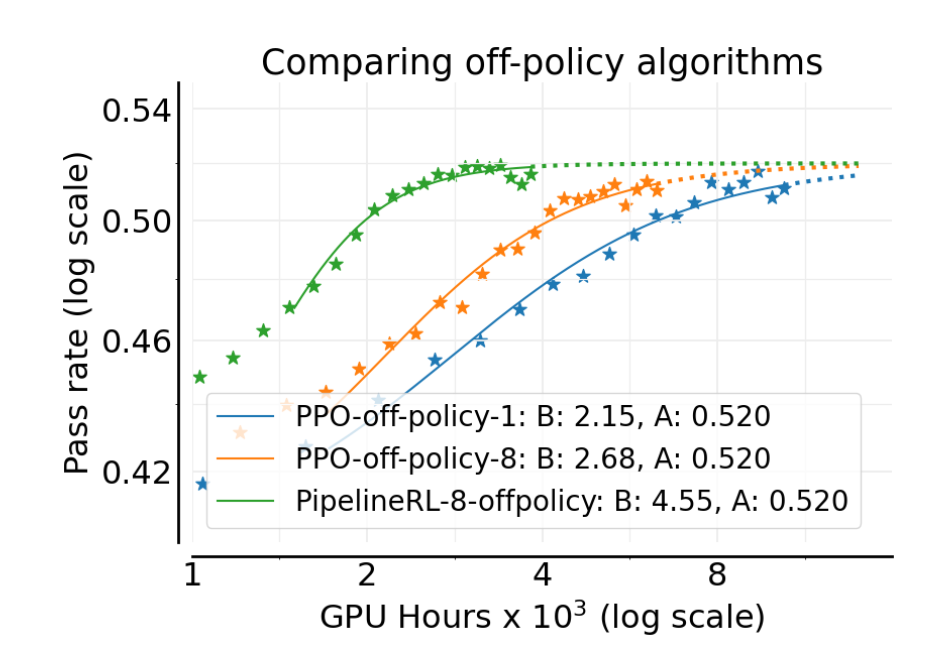
实验结果(上图)显示,虽然两种方法最终能达到的渐进性能 相近(均为 0.520),但 PipelineRL 的计算效率(由参数 体现)显著更高( vs )。这意味着 PipelineRL 能够更快地达到性能上限。其原因是 PipelineRL 减少了训练过程中的闲置时间,使得策略始终保持较小的“离线”程度。作者还进一步探索了 PipelineRL 的最大离线步数 ,发现 是一个最佳选择(图 4b)。因此,PipelineRL-8 成为了后续实验的基准。
2.3 关键算法选择
在确定了使用 PipelineRL-8 作为异步框架后,作者进一步研究了六个关键的算法设计维度。
2.3.1 损失函数
作者比较了三种主流的策略优化损失函数:
-
DAPO:基于 GRPO,使用非对称裁剪的 token 级别重要性采样(IS)比率。 -
GSPO (Group Sequence Policy Optimization) :将 IS 比率从 token 级别提升到序列级别。 -
CISPO (Clipped Importance Sampling Policy Optimization) :结合了截断重要性采样(truncated IS)和朴素策略梯度(vanilla policy gradient)。
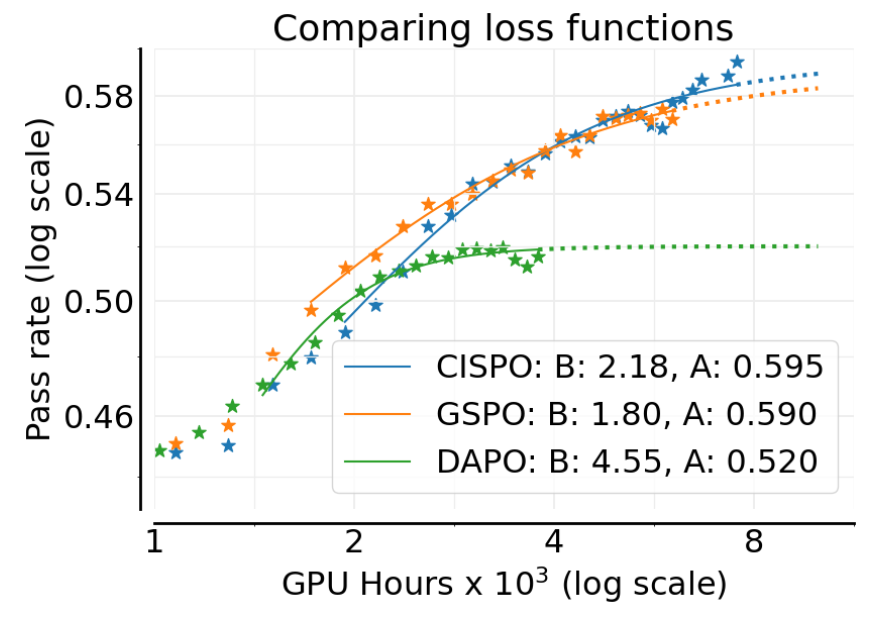
结果(上图)显示,GSPO 和 CISPO 的性能天花板 显著优于 DAPO( vs )。CISPO 在训练后期表现略好于 GSPO,因此被选为最佳损失函数。这是一个关键发现,表明损失函数的选择可以直接影响模型的最终性能上限。
2.3.2 LLM logits 的 FP32 精度
生成器(用于推理)和训练器(用于训练)通常使用不同的计算核心,这会导致它们计算出的 token 概率存在微小的数值差异。RL 训练对这种不一致性很敏感,因为它直接影响 IS 比率的计算。MiniMax 的工作发现,这种不匹配在模型的语言模型头(LM head)部分尤其明显。
为了解决这个问题,作者测试了在生成器和训练器的 LM head 部分都强制使用 FP32 精度进行计算的效果。
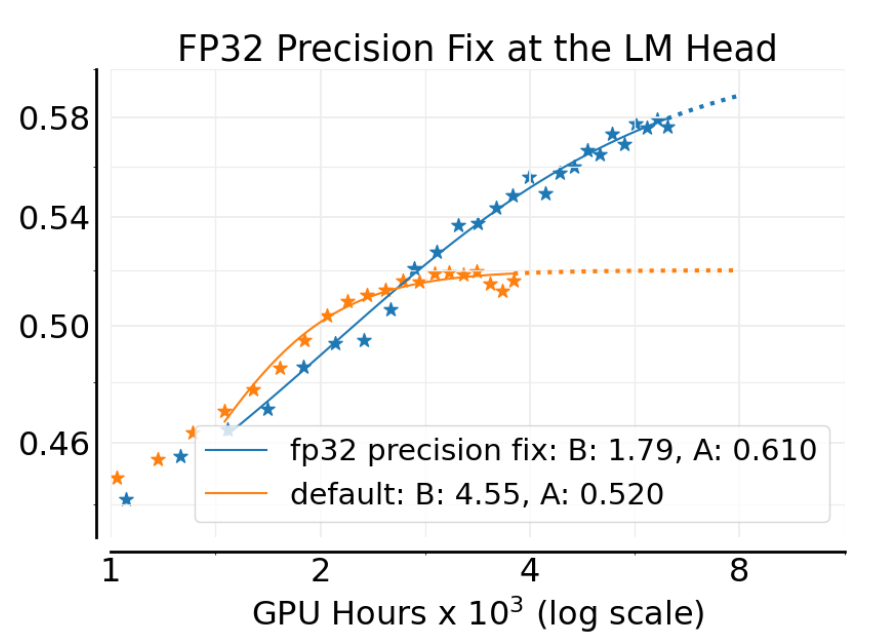
实验结果(上图)可以看出,仅仅是这样一个看似微小的改动,就将渐进性能 从 0.52 大幅提升到了 0.61。这表明,确保计算一致性对于 RL 训练的稳定性和性能至关重要。
2.3.3 损失聚合
在计算批次损失时,有多种聚合方式:
-
样本平均 (Sample average) :每个 rollout 轨迹对总损失的贡献相等(GRPO 方式)。 -
提示平均 (Prompt average) :每个提示(prompt)对总损失的贡献相等,无论它生成了多少个 rollout(DAPO 方式)。 -
Token 平均 (Token average) :批次中所有的 token 对损失的贡献都相等。
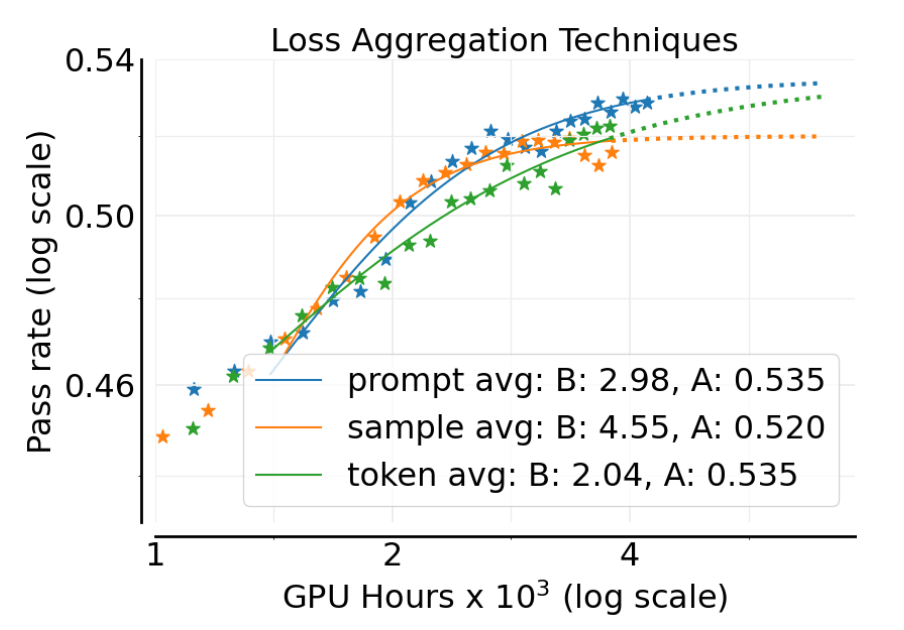
附录中的图 14a 显示,提示平均(prompt-average)取得了最高的渐进性能 。因此,ScaleRL 采用了这种聚合策略。
2.3.4 优势归一化
优势函数(advantage)的归一化是稳定 RL 训练的关键步骤。作者比较了三种方式:
-
提示级别 (Prompt level) :在同一个提示生成的所有 rollout 中计算均值和标准差进行归一化(GRPO 方式)。 -
批次级别 (Batch level) :在整个批次的所有 rollout 中进行归一化。 -
不归一化 (No normalization) :只减去均值,不除以标准差。
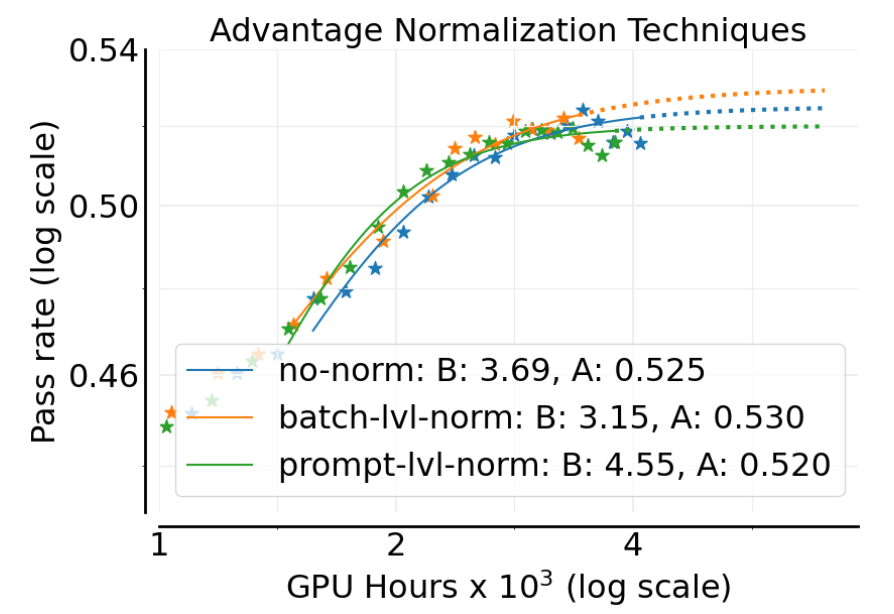
附录中的图 14b 显示,这三种方法的性能非常接近。作者最终选择了批次级别归一化,因为它在理论上更合理且表现略好。
2.3.5 零方差过滤
在一个批次中,有些提示对应的所有生成轨迹可能得到完全相同的奖励(例如,全部正确或全部错误)。这些“零方差”的提示对应的优势函数为零,因此不会产生任何策略梯度。默认的基线算法会将这些样本包含在损失计算中。
作者测试了另一种策略:在计算损失时,过滤掉这些零方差的提示。
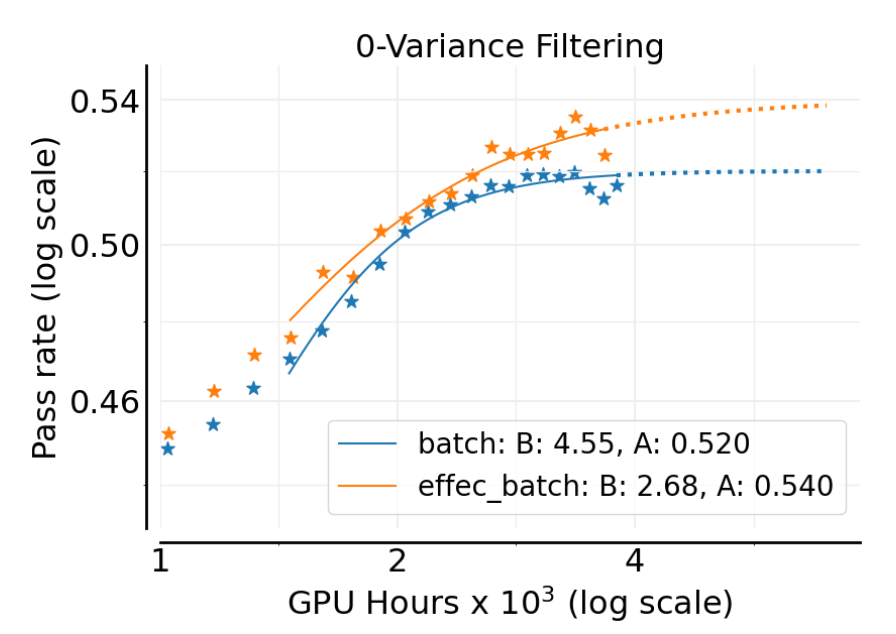
结果(上图)显示,过滤掉零方差样本可以提升渐进性能 (从 0.520 提升到 0.540)。这表明,将计算集中在能够提供有效梯度信号的样本上是更有益的。
2.3.6 自适应提示过滤
数据课程(data curriculum)是提升 RL 训练效率的常用策略。作者实现了一种简单的变体,称为“无正向重采样”(No-Positive-Resampling)。其核心思想是:一旦某个提示的通过率高到一定程度(例如,超过 90%),就认为模型已经“学会”了它,并将其从后续的训练周期中永久移除。
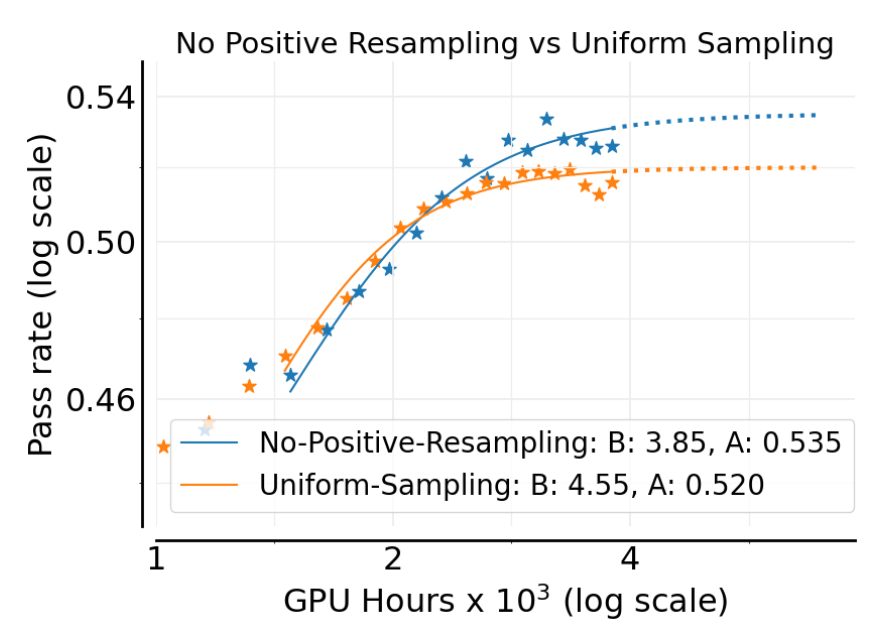
实验结果(上图)表明,这种简单的数据课程策略能够提升可扩展性和渐进奖励 A(从 0.520 提升到 0.535)。这符合直觉:我们应该让模型专注于学习那些尚未掌握的难题。
2.4 ScaleRL 方案与留一法验证
通过上述一系列细致的消融研究,作者将所有表现最佳的设计选择组合在一起,形成了一个统一的、可扩展的 RL 方案,并将其命名为 ScaleRL。
ScaleRL 的核心组件包括:
-
异步框架: PipelineRL with 8 steps off-policyness. -
长度控制: 基于中断的长度控制(Interruption-based length control)。 -
数值精度: 在 logits 计算中使用 FP32 精度。 -
损失函数: CISPO (Truncated importance-sampling REINFORCE loss)。 -
损失聚合: 提示级别(Prompt-level)的损失聚合。 -
优势归一化: 批次级别(Batch-level)的优势归一化。 -
数据过滤: 零方差过滤(Zero-variance filtering)和无正向重采样(No-positive resampling)。
为了验证这些组件在组合后是否仍然保持最优,并且评估每个组件的独立贡献,作者进行了一系列严格的留一法(Leave-One-Out, LOO)消融实验。他们从完整的 ScaleRL 方案开始,每次只将其中一个组件还原为其“基线”对应项(例如,将 CISPO 换回 DAPO,或将 PipelineRL 换回 PPO-off-policy-8),然后将每个变体都训练到 16k GPU 小时。
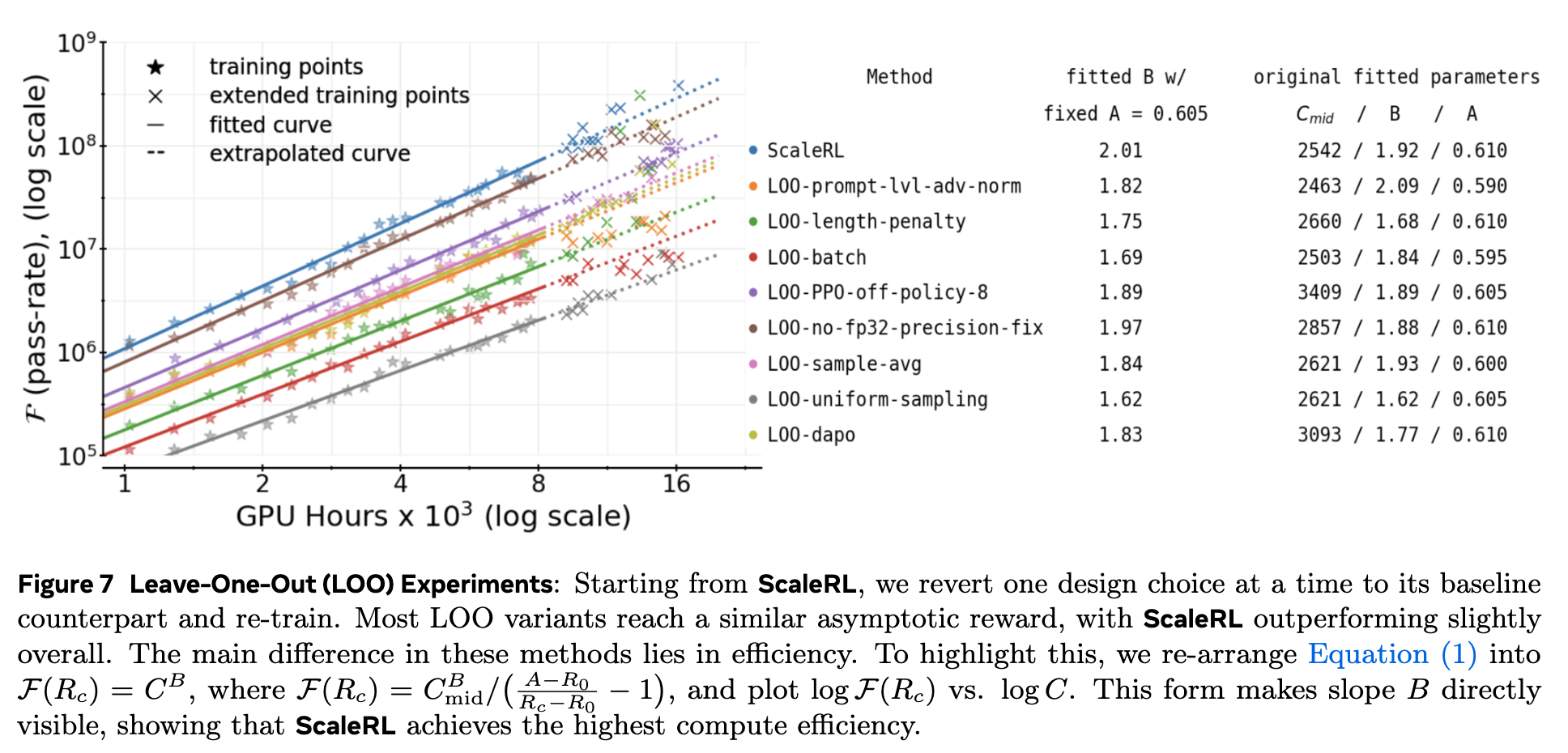
上图展示了 LOO 实验的结果。为了更清晰地比较不同方法之间的计算效率,作者对 S 型曲线公式 (1) 进行了变换,将其转化为一个对数坐标下的线性关系,使得斜率直接对应于缩放指数 。变换过程如下:
定义 ,则有 。两边取对数,得到:
这是一个斜率为 1 的关系。如果我们定义一个新的函数 ,则有 (在 接近 时)。两边取对数:
在论文的图 7 中,作者使用了这个变换,使得 成为斜率。由于大多数 LOO 变体的渐进性能 非常接近,作者将所有运行的 固定为一个平均值(0.605),然后重新拟合曲线,从而可以公平地比较它们的斜率 。
LOO 实验的关键结论:
-
ScaleRL 效率最高:在所有配置中,完整的 ScaleRL 方案(图中的蓝色圆点)具有最大的斜率(),表明其计算效率是最高的。 -
每个组件都有贡献:任何一个组件被还原后,效率(斜率 )都会下降。这证明了每个设计选择都对最终的整体性能做出了积极贡献。例如,移除 FP32 精度修正(L00-no-fp32-precision-fix)或使用 DAPO 损失(L00-dapo)都会导致效率明显降低。 -
组件的冗余性与鲁棒性:一个有趣的问题是,既然在 LOO 实验中,像 FP32 精度修正和 CISPO 损失的移除对最终渐进性能 的影响不大(见图 7 右侧表格),我们是否可以安全地去掉它们?作者认为答案是否定的。他们指出,即使某个组件在特定组合下看起来“冗余”,但它可能在其他模型或设置下提供关键的稳定性或鲁棒性。例如,FP32 修正对于缓解基于 GRPO/DAPO 损失的数值不稳定性至关重要。CISPO 相比于 DAPO,对重要性采样裁剪的超参数不那么敏感(详见附录 A.17),这大大降低了调参的难度。因此,ScaleRL 保留这些组件是为了确保方案的通用性和鲁棒性。
3. 可预测的 scaling
这项工作的核心主张之一是 RL 缩放的可预测性。作者通过多个实验证明,他们提出的 S 型曲线框架能够利用早期训练数据,准确地预测未来更大计算规模下的性能。
3.1 独立运行的方差与误差范围
RL 训练以其高方差而闻名。为了量化这种随机性对拟合参数的影响,作者独立地训练了 3 次完整的 ScaleRL 运行。
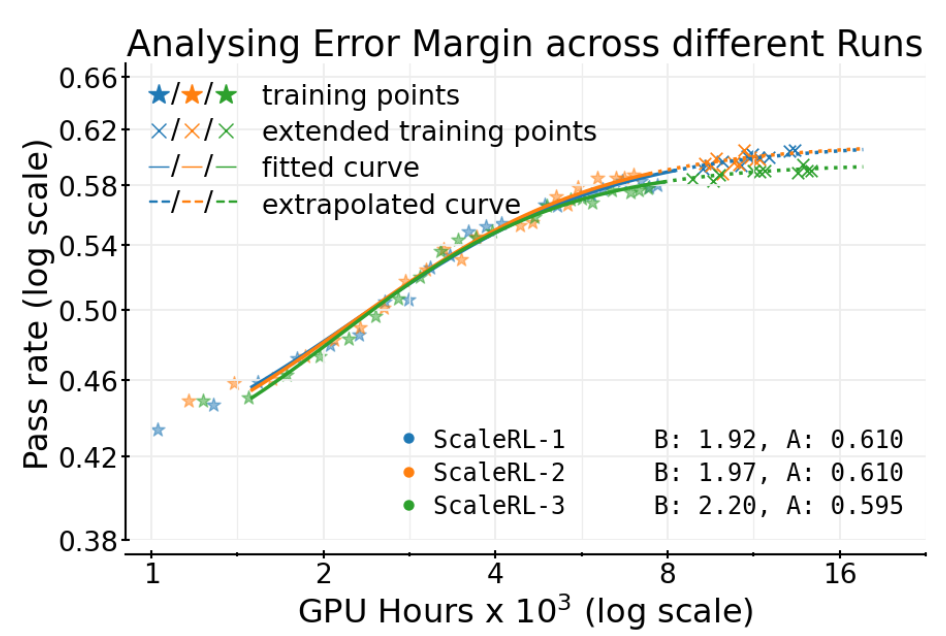
结果(上图)显示,三次运行的轨迹非常相似。拟合得到的渐进性能 分别为 0.610、0.610 和 0.595。这表明,对于 ScaleRL 这样一个稳定的方案,其性能天花板的估计误差大约在 的范围内。这个经验误差范围为后续判断不同算法之间的性能差异是否“显著”提供了一个基准。
3.2 外推预测的验证
最引人注目的验证来自一次长达 100,000 GPU 小时的单次运行。作者在一个 8B 稠密模型上运行 ScaleRL,并在训练进行到 50k GPU 小时的时候,利用当时的数据点拟合 S 型曲线。然后,他们将这条曲线外推至 100k GPU 小时,来预测接下来的训练轨迹。
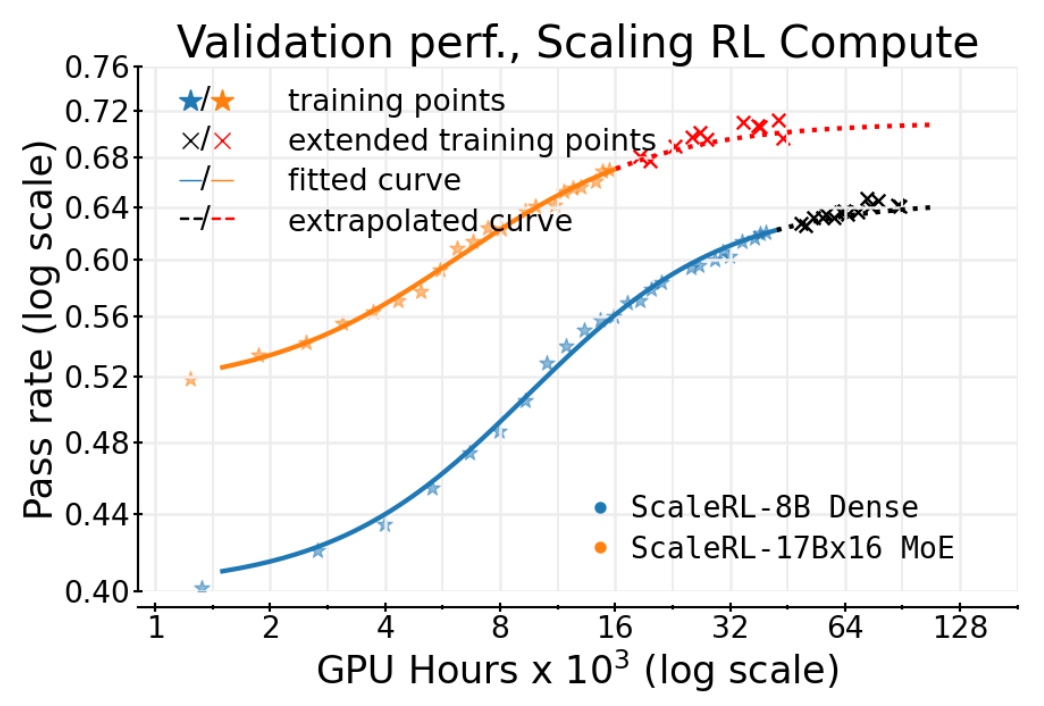
结果如上图所示,外推出的曲线(虚线和 x 标记)与后续实际的训练数据点(* 标记)高度吻合。这强有力地证明了该框架的预测能力。同样地,在一个更大的 17B×16 MoE 模型上,从 16k GPU 小时数据外推到 45k GPU 小时的预测也同样精准。
这一发现意义重大。它意味着研究人员可以在计算预算有限的情况下,通过较小规模的实验来评估不同 RL 方案的“缩放潜力”。一个在早期拟合出更高渐进性能 的算法,即使其初期表现(由 和 决定)不是最好的,也更有可能在未来的大规模训练中胜出。这正是作者在论文中提到的“拥抱苦涩教训(Embracing the Bitter Lesson)”:早期性能的领先者不一定是最终的赢家。
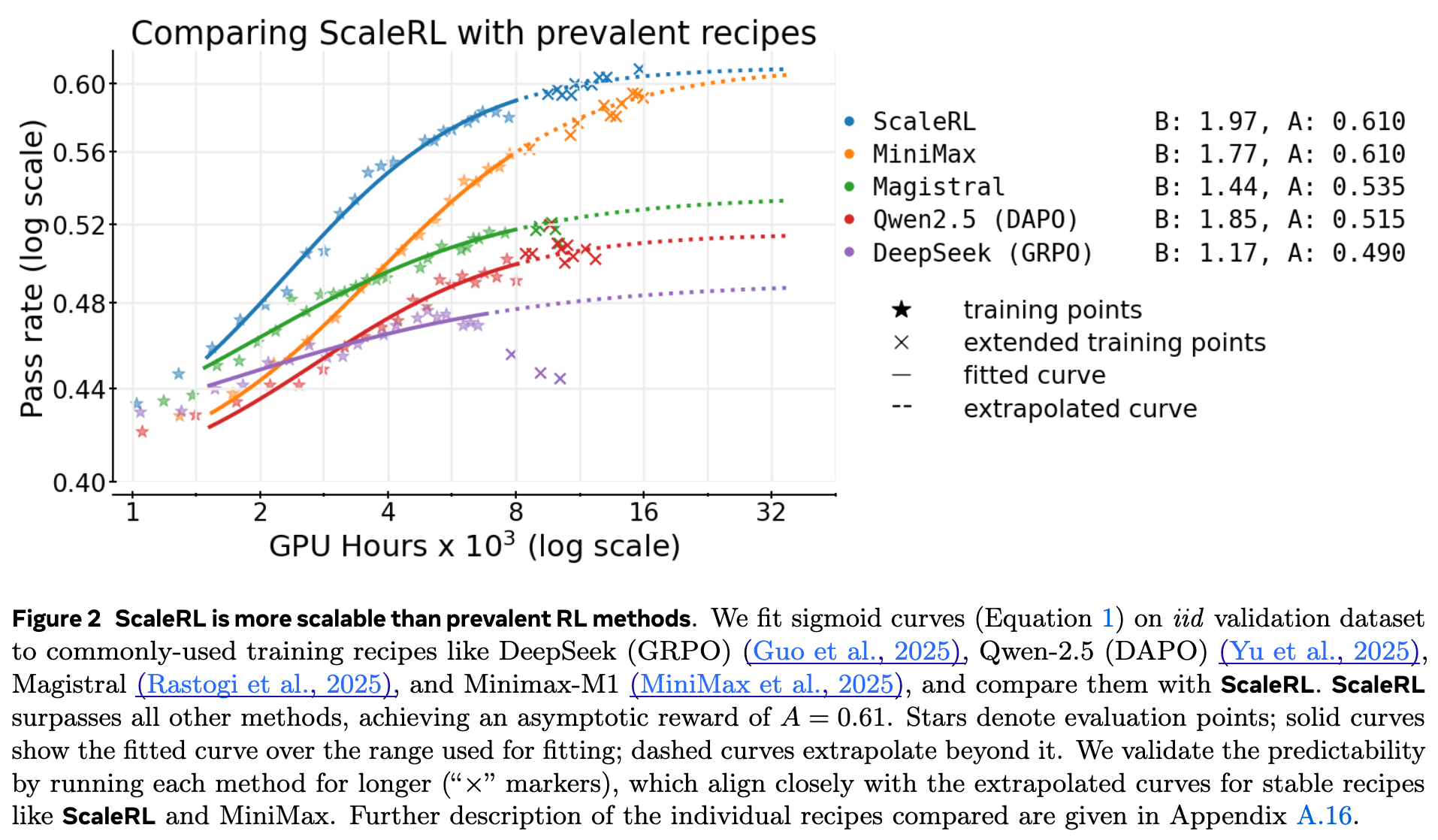
上图清晰地展示了这一点。在早期(例如,低于 4k GPU 小时),Magistral 和 Qwen2.5 (DAPO) 的性能似乎优于 ScaleRL。然而,它们的性能天花板 较低(分别为 0.535 和 0.515),导致它们很早就进入了平台期。相比之下,ScaleRL 和 MiniMax 拥有更高的 (均为 0.610),虽然初期爬升稍慢,但最终达到了远超前者的性能水平。这个框架使得我们能够从早期就识别出像 ScaleRL 这样更有潜力的候选者。
4. 跨越不同 RL 计算轴的可预测性
一个真正通用的缩放框架,其可预测性不仅应体现在增加 GPU 小时上,还应体现在改变其他关键的“计算轴”上。作者在第 5 节中系统地研究了 ScaleRL 在四个不同扩展维度上的表现,并在所有维度上都观察到了清晰、可预测的 S 型曲线行为。
4.1 模型规模
将 ScaleRL 应用于一个更大的 17B×16 MoE 模型(Scout)上,不仅训练过程保持了稳定和可预测,而且其性能也远超 8B 模型。从图 1 可以看出,MoE 模型的渐进性能 明显更高。值得注意的是,MoE 模型仅用了 8B 模型 1/6 的 RL 训练计算量,就达到了后者的性能水平。这表明,增加模型规模是提升 RL 性能上限的有效途径。
4.2 生成长度(上下文预算)
作者比较了使用 14k tokens 生成长度和 32k tokens 生成长度的 ScaleRL 训练。
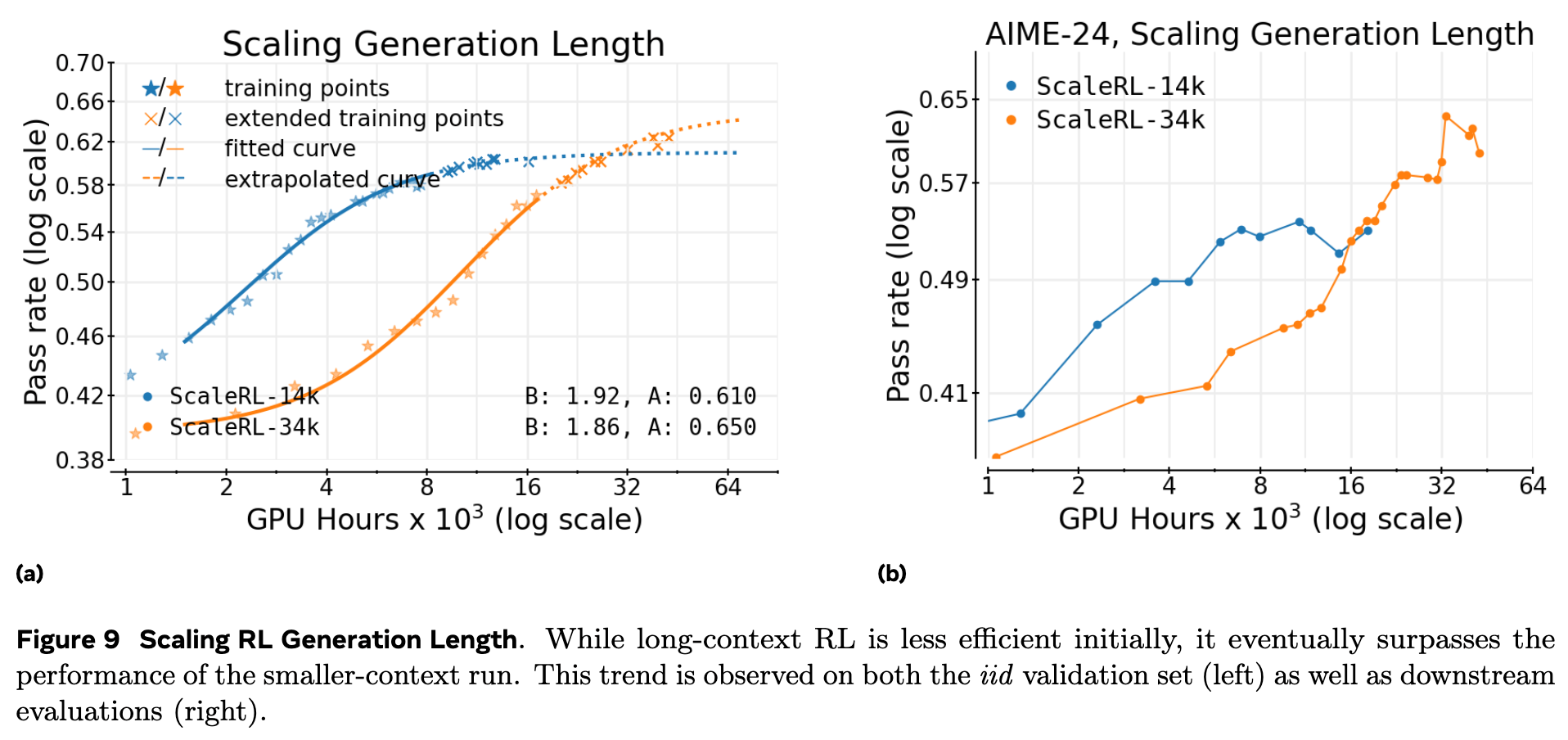
结果(上图)显示,增加生成长度(从 14k 到 32k)会降低初期的计算效率( 值更低,曲线更平缓),但显著提升了最终的性能天花板 (从 0.610 提升到 0.650)。这验证了长上下文 RL 是一个能够“提高天花板”的手段,而非简单的效率权衡。从下游任务(AIME-24)的性能来看,更长的上下文最终也带来了更好的泛化表现。
4.3 全局批量大小
批量大小是另一个关键的超参数。作者比较了 512、768 和 2048 三种不同的批次大小。
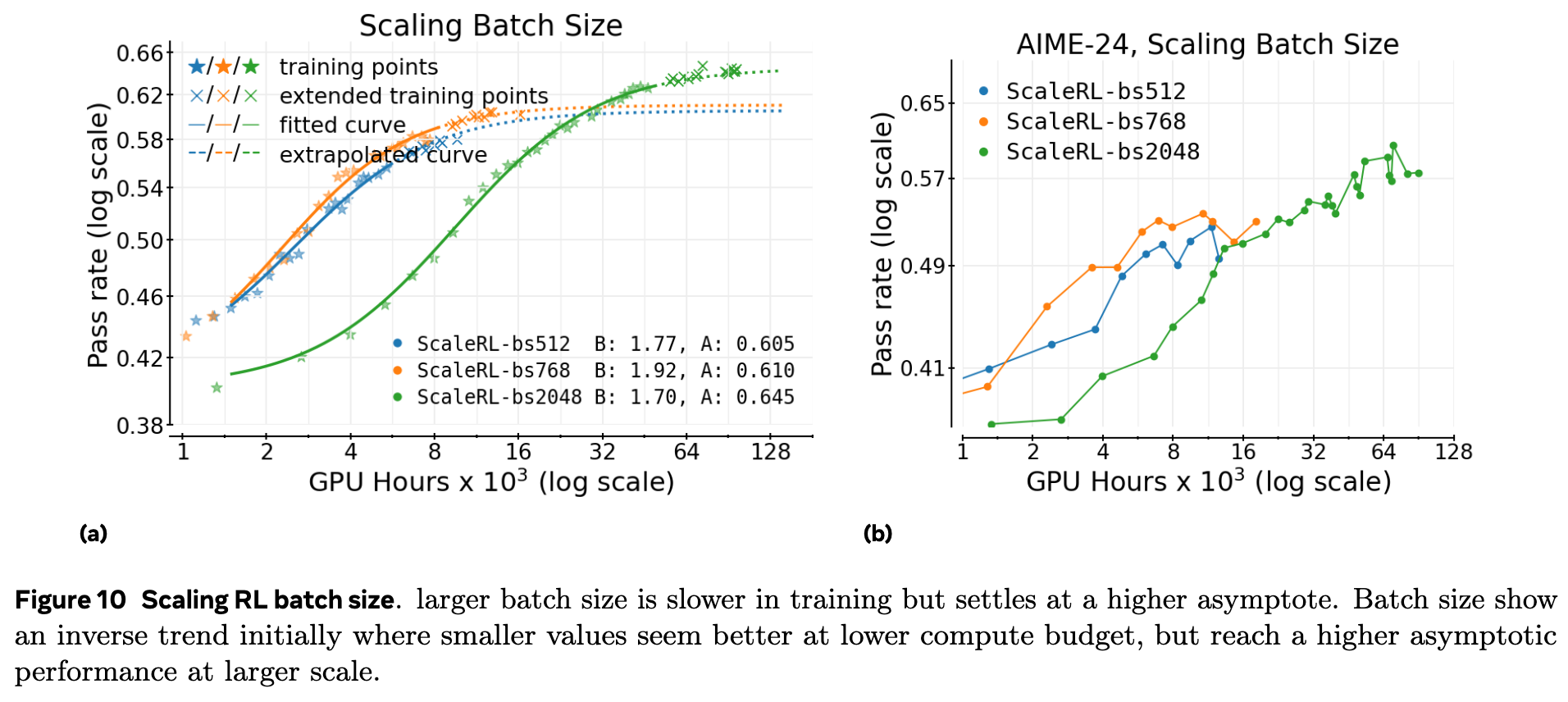
结果(上图)显示,更大的批量大小能够达到更高的渐进性能 。在训练初期,较小的批次(如 512)可能表现更好,但它们会更早地饱和。而最大的批次(2048)虽然初期学习较慢,但最终达到了最高的性能。在他们最大规模的数学模型训练中(图 1),将批次大小增加到 2048 不仅稳定了训练,而且也得到了一个能够从 50k GPU 小时成功外推到 100k 的拟合曲线。
4.4 多任务学习 (Multi-task RL)
为了测试 ScaleRL 在单一领域之外的泛化能力,作者在一个混合了数学(math)和代码(code)任务的数据集上进行了多任务 RL 训练。
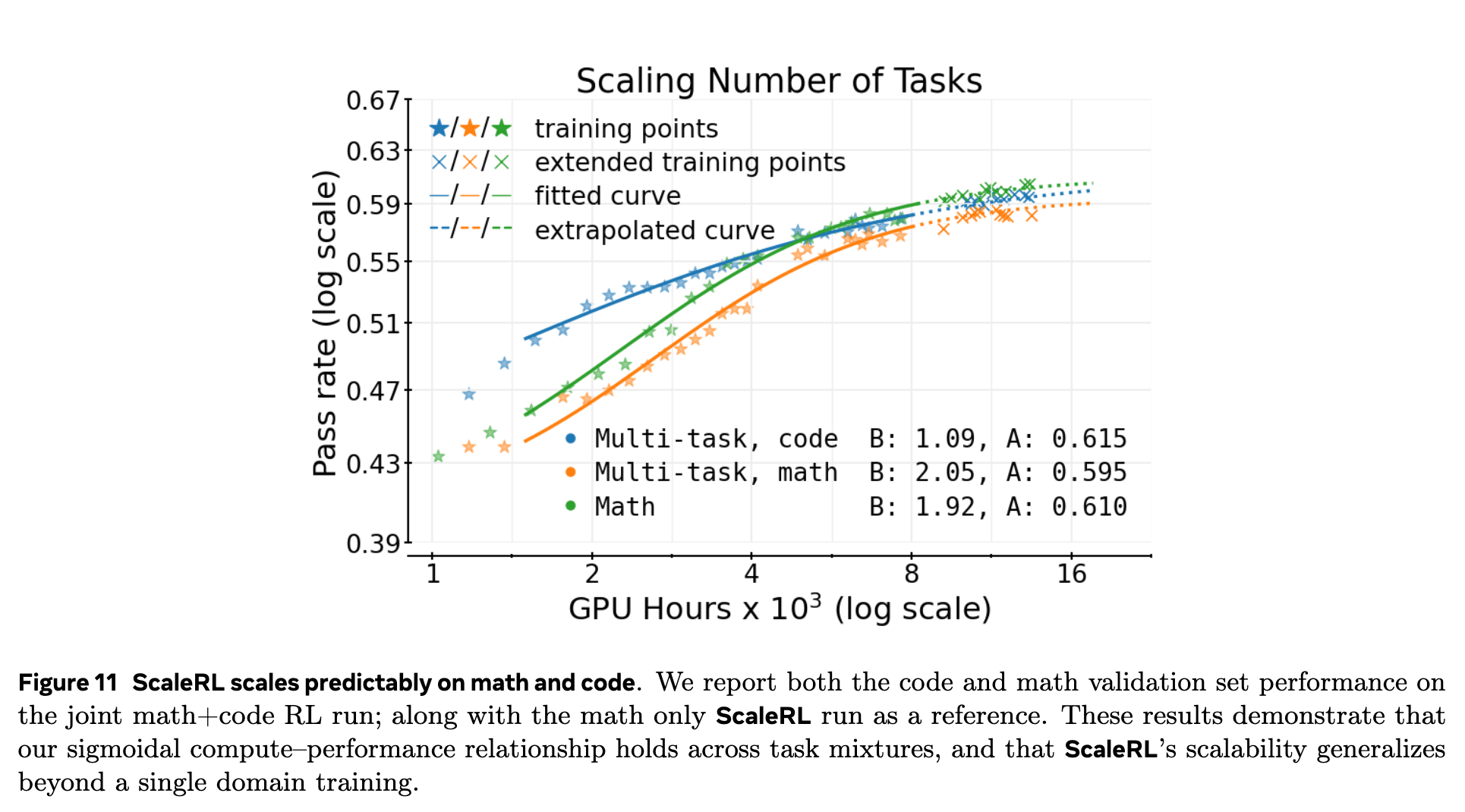
结果(上图)显示,即使在多任务环境下,性能与计算的关系依然遵循清晰的 S 型曲线。数学和代码任务的性能曲线平行发展,验证了该缩放框架在跨任务场景下的有效性。
5. 附录解读
这篇论文的附录提供了大量宝贵的细节信息,对于希望复现或深入理解这项工作的研究者来说是必读的。本节将对附录中的关键内容进行解读。
A.4 & A.7: 为什么是 S 型曲线?拟合的鲁棒性如何?
附录 A.4 详细阐述了为什么选择 S 型曲线而不是预训练中常用的幂律。原因有三:
-
有界指标:RL 中的奖励/通过率是 [0, 1] 之间的有界指标,S 型曲线天然适合建模这种饱和现象。 -
数据稀疏性:RL 训练的评估点远少于预训练,幂律拟合需要丢弃更多的早期数据点,这在数据稀疏时是不可行的。 -
经验鲁棒性:作者发现,S 型曲线的拟合结果对拟合区间的选择远不比幂律敏感。例如,在 100k GPU 小时的实验中,幂律拟合在 1.5k-50k 区间上预测的 (完全错误),而在 30k-60k 区间上才能得到正确的结果。但我们的目标正是从低计算区域预测高计算区域,因此幂律在此场景下失效。S 型拟合则在所有区间上都给出了稳健的预测 ()。
附录 A.7 进一步探讨了拟合的鲁棒性。作者指出,对于像 ScaleRL 这样稳定的方案,无论是否包含最初的 1.5k GPU 小时,或者改变拟合区间的终点,得到的参数值都在经验误差范围内。这再次证明了该框架的可靠性。
A.8: S 型曲线参数的直观理解
附录 A.8 通过一系列控制变量的示意图,帮助读者更直观地理解参数 的作用。
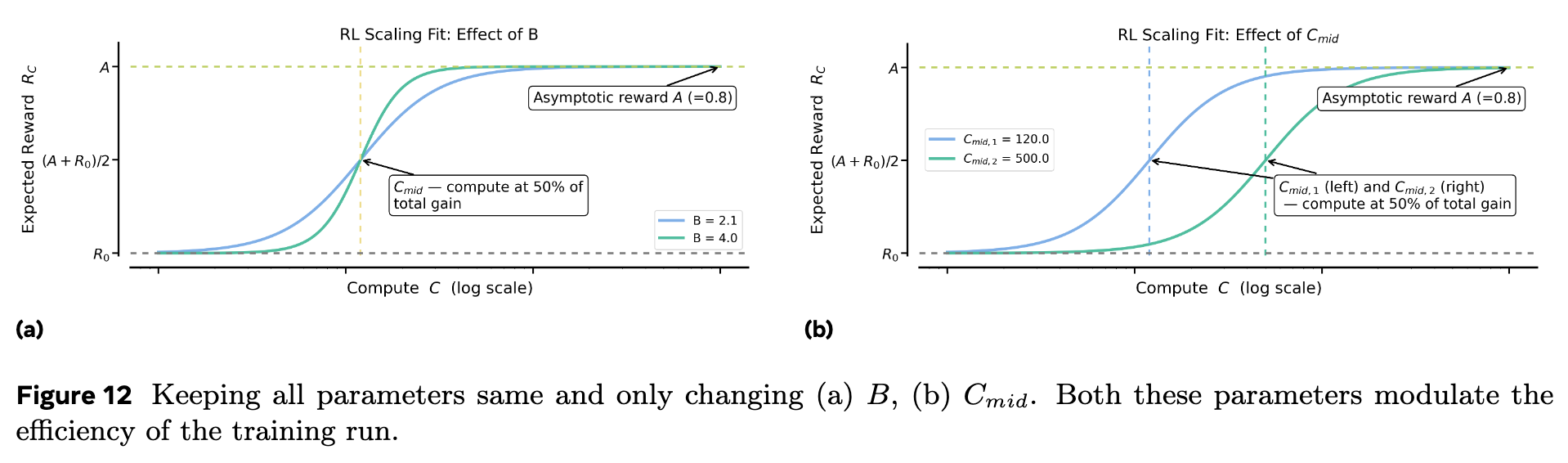
上图展示了 和 主要调节效率。 越大,曲线越陡峭; 越小,曲线越早开始爬升。
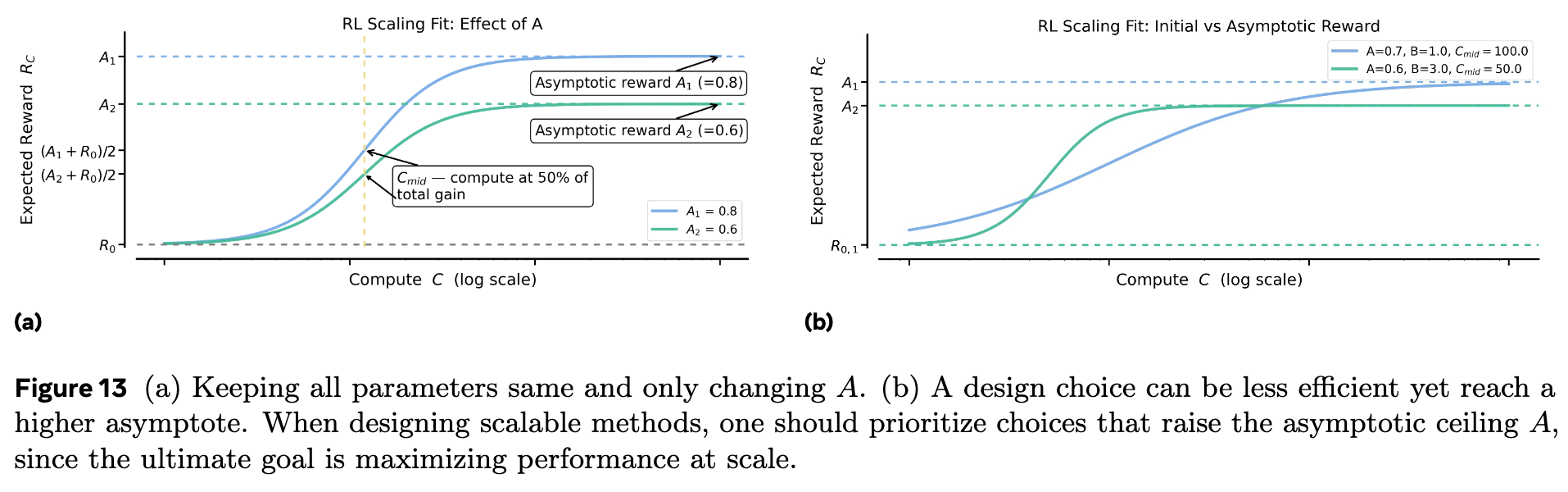
上图 a 展示了 控制性能上限。上图 b 则形象地描绘了“拥抱苦涩教训”的情景:一个方案(绿色曲线)初期效率高( 大, 小),但天花板 低;另一个方案(蓝色曲线)初期效率低,但天花板 高,最终实现了超越。在设计可扩展的 RL 方法时,应优先选择提升 的策略。
A.15: 训练不稳定性与截断
附录 A.15 讨论了一个非常实际的工程问题:训练不稳定性。作者发现,训练不稳定的一个重要预警信号是截断率(truncation rate)的上升。当模型生成的轨迹超过最大长度限制而被强制截断时,就会发生截断。过高的截断率(例如,10-15%)通常预示着性能即将下降或崩溃。
ScaleRL 通过其组件设计,表现出很强的稳定性。在 8B 模型上,其截断率大部分时间低于 5%。在更大的 Scout (MoE) 模型上,截断率稳定在 2% 以下。这可能得益于大模型更强的指令遵循能力,能够更好地响应中断信号(如 </think>)。
A.16 & A.17: 主流方法比较与损失函数的超参数鲁棒性
附录 A.16 详细描述了图 2 中与其他主流 RL 方案(DeepSeek, Qwen2.5, Magistral, MiniMax)进行比较时的具体设置。一个关键细节是,为了公平,对于像 Qwen2.5 (DAPO) 和 MiniMax 这类需要丢弃零方差样本的算法,作者为它们设置了更大的初始批次,以确保有效批次大小不小于 ScaleRL。这说明图 2 的比较是相当公允的。
附录 A.17 深入探讨了不同损失函数对裁剪超参数 的敏感性,这是一个极其重要的实践洞见。
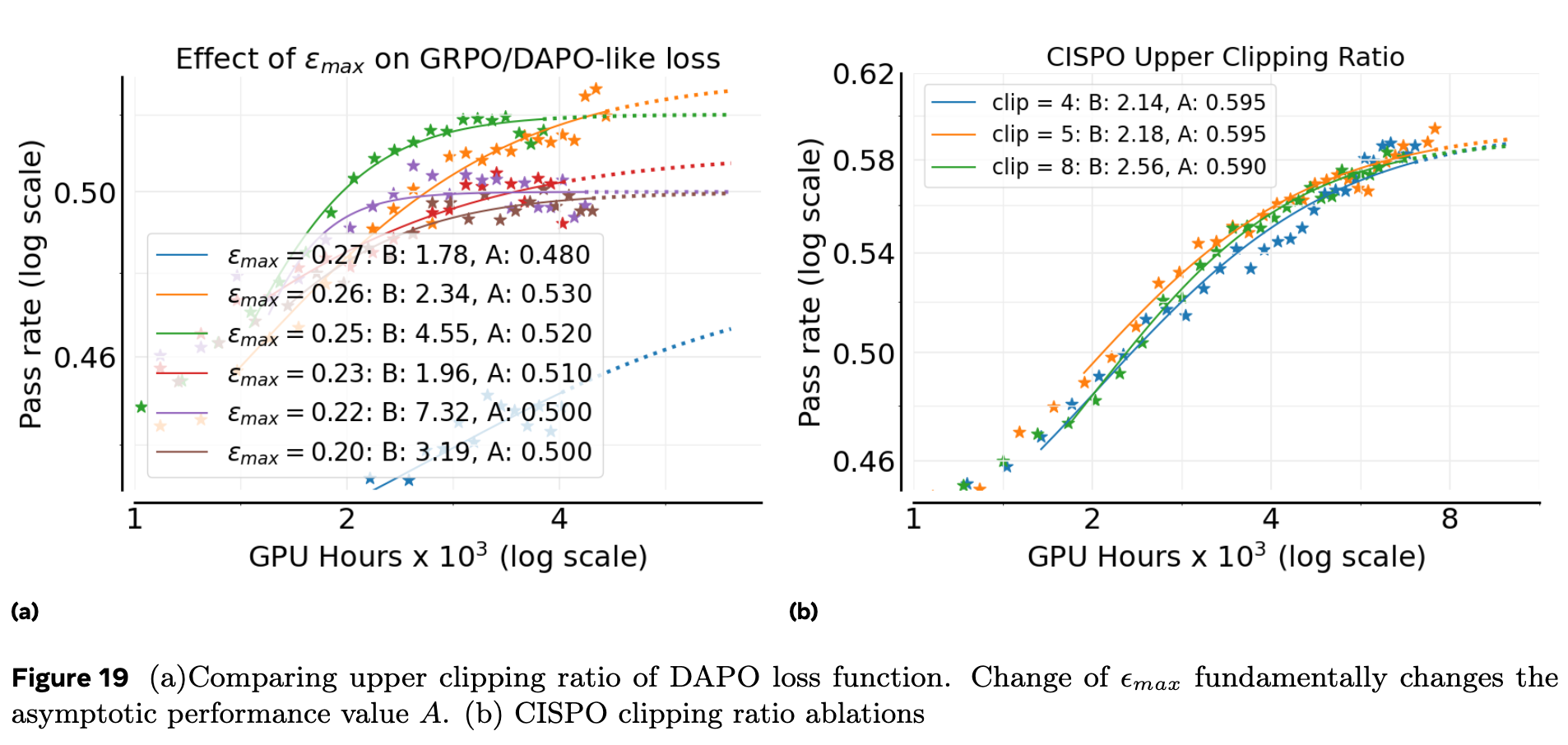
上图 a 显示,对于 DAPO 风格的损失, 的取值极大地影响了最终的渐进性能 A。 从 0.20 变化到 0.26,性能天花板 先升后降。这是一个“致命”的特性,意味着为了达到最佳性能,研究者需要对这个超参数进行精细的调整,试错成本很高。
相比之下,上图 b 显示 CISPO 对其上裁剪边界的选择非常不敏感。在一个很宽的范围内改变裁剪值,性能曲线几乎没有变化。GSPO 也表现出类似的鲁棒性(一旦找到了正确的数量级)。这种对超参数的鲁棒性使得 CISPO 成为大规模训练中一个更安全、更可靠的默认选项。这充分解释了为什么 ScaleRL 即使在 LOO 实验中 reverting to DAPO 性能下降不大的情况下,依然坚持选择 CISPO——因为它带来了宝贵的鲁棒性。
往期文章:




