对于大型语言模型(LLM)的研究者和实践者而言,提示工程(Prompt Engineering)已成为与模型交互、引导其生成特定高质量输出的核心技术。无论是通过手动迭代、自动化搜索,还是基于梯度的连续空间优化,我们总能找到在训练数据上表现优异的提示。然而,一个根本性的问题始终存在:这些在有限数据上优化出的提示,其泛化能力(generalization)如何保证?尤其是在我们通常只有少量标注样本的“低数据”(low-data)场景下,模型为何不会对这些样本过拟合,从而在未见数据上表现不佳?
这个关于泛化的问题,对于将优化后的提示部署到实际应用中至关重要。近期的理论工作,例如 Akinwande 等人(2023)的研究,为这个问题提供了一些解释。他们创新性地将 PAC-Bayes 理论应用于离散的提示空间,而非模型的权重空间,并在数据丰富的场景下(data-rich scenarios)推导出了非空泛(non-vacuous)的泛化界。所谓“非空泛”,指的是理论上界定的误差上限具有实际意义(例如,小于100%),而不是一个平凡的、无法提供任何信息的数值。然而,他们的理论在数据稀疏的场景下便会失效,其泛化界也重新变为空泛。这与实践经验相悖:在实际应用中,即便只有几十或几百个样本,精心设计的提示依然表现出良好的泛化性。
理论与实践之间的这一差距表明,现有的泛化理论可能遗漏了某些关键因素。来自 Google DeepMind 的论文《Prompts Generalize with Low Data: Non-vacuous Generalization Bounds for Optimizing Prompts with More Informative Priors》中,提供了新的视角。他们认为,LLM 广泛成功泛化的关键,在于更精细地利用了模型自身蕴含的先验知识。具体而言,他们聚焦于一个核心指标——困惑度(perplexity)。困惑度衡量了模型对一个文本序列的“自然”程度的预估。一个更“自然”、更符合模型内部语言知识的提示,其困惑度更低。该论文的核心假设是:这种由困惑度体现的、依赖于数据或分布的先验信息,能够有效地引导优化过程,使其倾向于选择那些本质上更可能泛化的提示。

-
论文标题:Prompts Generalize with Low Data: Non-vacuous Generalization Bounds for Optimizing Prompts with More Informative Priors -
论文链接:https://arxiv.org/pdf/2510.08413
基于这一见解,研究者们推导出了新颖的泛化界。这些泛化界通过引入更有信息量的先验(more informative priors),即使在数据稀疏的场景下也能保持非空泛。他们从理论上分析了困惑度正则化(perplexity regularization)如何通过限制对提示空间的探索,从而收紧泛化界。同时,通过在文本分类任务上的实证研究,他们不仅验证了理论界的有效性,也展示了利用困惑度正则化来优化提示,确实能够带来实际的泛化性能提升。
1. 背景
在深入探讨论文的核心贡献之前,我们首先需要理解其所基于的理论背景和试图解决的问题的上下文。这包括提示优化的基本概念、现有泛化理论的局限性,以及作为本文理论基石的 PAC-Bayes 框架。
1.1 提示优化与泛化
大型语言模型通过“提示”——即为模型提供的一段输入文本序列——来引导其执行特定任务。提示优化(Prompt Optimization)指从一个巨大且离散的潜在提示空间 中,搜索出一个最优的“硬提示”(hard prompt) ,使得该提示在经过一个给定的 LLM 处理后,能在特定任务上最小化某个损失函数。
优化的方法多种多样,从早期的人工调整(manual tuning),到后来发展的自动化技术,如基于贪心或进化算法的离散空间搜索,以及选择最优的少样本示例(few-shot exemplars)。这些方法的共同目标是在一个有限的训练数据集 上找到一个提示 ,使其经验风险 尽可能小。
然而,真正的挑战在于泛化。我们希望 在未见过的、来自同一数据分布的测试数据上同样表现良好。也就是说,它的真实风险(或称群体风险) 需要与经验风险 足够接近。当训练数据量 很小时,即在数据稀疏的场景下,这个问题尤为突出。因为此时的经验风险 可能只是对真实风险的一个噪声很大的估计,模型很容易找到一个仅在训练集上表现优异但缺乏泛化能力的提示,这种现象称为过拟合(overfitting)。
1.2 现有的泛化界
泛化界(Generalization bounds)为学习模型在未见数据上的预期性能提供了数学上严格的保证。它通常将可观测的、在训练集上的经验风险与不可观测的、真实的群体风险联系起来。然而,为现代深度神经网络,特别是 LLM,推导有意义的泛化界是出了名的困难。
经典的学习理论工具,如 VC 维(VC-dimension)或 Rademacher 复杂度(Rademacher complexity),在应用于 LLM 时常常会失效。这些复杂度度量通常与模型的参数数量有关。由于 LLM 拥有数以十亿计的参数,即所谓的过参数化(overparameterization),这些经典理论计算出的泛化界往往是空泛的(vacuous)。一个空泛的界指的是它给出的误差上限是平凡的,例如,在一个二分类任务中,预测的误差上限大于 100%。这样的界没有任何实际指导意义。
当我们把目光从模型权重转向提示空间时,问题依然存在。提示空间 虽然是离散的,但其规模极其巨大。对于一个词汇表大小为 、提示长度为 的模型,提示空间的大小为 。例如,一个拥有 词汇量、上下文长度为 的模型,其潜在的提示空间规模是天文数字。在这种情况下,即便是应用 PAC-Bayes 理论,如果使用一个无信息量的先验(uninformative prior),得到的泛化界也很容易因为巨大的假设空间而变为空泛,尤其是在训练样本 较小的时候。此外,诸如负对数似然(Negative Log-Likelihood, NLL)这样的无界损失函数也给标准分析带来了复杂性,尽管对于很多下游分类任务,我们可以使用有界的 0-1 损失,从而简化了这一方面的问题。
1.3 PAC-Bayes 框架
PAC-Bayes 框架是推导泛化界的一套强大方法。它结合了 PAC(Probably Approximately Correct)学习理论和贝叶斯推理的思想。其核心是比较一个先验分布(prior)和一个后验分布(posterior)。
在一个假设空间 (在本文中,即为提示空间 )上,我们首先定义一个先验分布 。这个分布独立于训练数据,反映了我们对“好的假设”(好的提示)的初始信念。然后,在看到了训练数据 之后,我们得到一个后验分布 ,这个分布通常会集中在那些在训练数据上表现良好的假设上。
一个典型的 PAC-Bayes 泛化界表明,对于任意的 ,至少以 的概率(这个概率是针对训练数据 的随机抽样而言),以下不等式成立:
我们来逐项解析这个不等式:
-
是后验分布 下的期望群体风险。 -
是后验分布 下的期望经验风险。 -
是后验 和先验 之间的Kullback-Leibler (KL) 散度。这个KL散度项是 PAC-Bayes 界的核心。它惩罚那些远离先验的后验分布。如果后验 相对于先验 是“可压缩的”,即 KL 散度很小,那么泛化差距( 和 之间的差异)就小。因此,KL 散度项可以被看作是一种正则化项。 -
是一个复杂度项,依赖于置信度 和样本量 。对于有限的假设空间 ,它可能是 ;在更一般的情况下,它可能是 。
传统上,先验 是数据独立的。然而,PAC-Bayes 理论的一个强大之处在于它也允许使用数据依赖的先验(data-dependent priors)。在这种情况下,我们可以使用一部分数据 来选择或调整先验 ,只要在后续的分析中妥善处理这种依赖性(例如,确保用于评估经验风险 的数据 与 相互独立,或者将这种依赖性的影响计入复杂度项 中)。一个精心选择的数据依赖先验如果能有效捕捉数据的特定结构,就有可能得到比数据无关先验更紧的泛化界。这正是本文方法论的关键所在。
1.4 相关工作
Akinwande 等人(2023)的工作是理解提示优化泛化能力的一个重要进展。他们将 PAC-Bayes 界应用于离散的提示空间,并使用另一个 LLM 来定义提示的先验分布 。对于一个选定的最优提示 (可以看作一个狄拉克 分布的后验 ),其 KL 散度项简化为 。在数据丰富的场景下(例如,在 ImageNet 上使用 CLIP 提示进行零样本分类),他们获得的泛化界非常紧,与真实的测试误差仅相差几个百分点。
然而,他们的方法有两个关键局限:
-
它依赖于一个可靠的经验风险估计 ,这需要大量的训练数据。 -
它使用了一个固定的、数据无关的 LLM 先验。在数据稀疏的情况下,一个过拟合的、非典型的提示 可能具有非常低的先验概率 ,导致 KL 散度项非常大,从而使泛化界变为空泛。
这就提出了一个开放性问题:为什么在数据稀疏的场景下提示依然能够泛化?
另一项相关的经验性工作来自 Gonen 等人(2022),他们发现一个提示的任务相关困惑度(在给定无标签任务输入的情况下的平均负对数似然)与其下游任务性能之间存在负相关关系。也就是说,困惑度更低、对于 LLM 来说更“自然”的提示,往往表现得更好。这启发了本文的核心思想:困惑度可以作为一个有价值的启发式指标,来指导我们构建更有信息量的先验。
此外,Zollo 等人(2024)提出了提示风险控制(Prompt Risk Control, PRC),这是另一种数据依赖的性能保证方法。PRC 使用一个验证集 ,通过无分布不确定性量化(Distribution-Free Uncertainty Quantification, DFUQ)技术,为预先指定的风险度量(如平均损失)提供高概率的上限。与 PAC-Bayes 不同,PRC 的目标是控制损失分布的特定统计量,而本文的目标是利用数据衍生的信息来收紧 PAC-Bayes 先验本身,从而界定泛化误差。
2. 数据依赖、基于困惑度的 PAC-Bayes 界
为了解决现有泛化界在低数据场景下的局限性,论文作者们从数据依赖的泛化界研究中汲取灵感,并将其与困惑度的概念相结合,提出了新的理论框架。
2.1 动机
在数据稀疏的情况下,我们必须利用预训练 LLM 内部编码的大量先验知识。困惑度,作为语言建模中的一个标准度量,提供了一个自然的途径来访问这些知识。Gonen 等人(2022)的经验性发现——低困惑度提示通常性能更好——暗示了困惑度捕捉了提示的某种内在质量,这种质量与模型有效处理和执行指令的能力相关,且独立于具体的任务标签。
这引出了本文的核心假设:一个基于困惑度构建的、数据依赖的先验 ,能够更有效地约束那些泛化性能好的提示的 项。具体来说,如果一个先验 能够给那些低困惑度的(也就是更“自然”的)提示赋予更高的概率,那么即使在训练样本 很小的情况下,我们也能得到非空泛的泛化界。而如果这个先验 本身是基于部分数据(例如,无标签的任务数据,或一小部分留出的有标签数据)来选择或调整的,它就成了一个数据依赖的先验。本文的目标就是将这一直觉形式化,并推导出相应的泛化界。
2.2 泛化界的推导
让我们回顾一下标准的 PAC-Bayes 界。设 为假设空间, 为 上的先验分布, 是从数据分布 中抽取的 个样本。对于任意 ,以至少 的概率,对于任意后验分布 ,以下不等式成立:
其中,损失函数 对于固定的 是有界的。在本文的实验部分,作者们还使用了另一个版本的 PAC-Bayes 界,即 Tolstikhin and Seldin (2013) 界。这个界的一个优点是,当训练误差为零时,其泛化差距的阶为 ,而非 。其形式如下:
在提示优化的背景下, 是所有可能提示的集合。即使我们用一个 LLM 的对数似然来定义先验,当 时,对于之前 Akinwande 等人的方法,由于 KL 散度项过大,这些界仍然是空泛的。
关键思想:为了获得更紧的界,我们不应使用一个宽泛的、无信息的先验,而应构建一个经过优化的、数据依赖的先验。这个先验能够利用 LLM 的“压缩能力”,显著减小我们实际需要搜索的假设空间。
本文采将假设空间 设为所有离散提示的集合。我们定义一个由 LLM 产生的、以某个“先验提示”(prior prompt) 为条件的先验分布 。然后,我们可以通过在一个数据子集 上进行优化,来构造一个数据依赖的先验提示 。这个 的目标是,使得最终由任务优化出的提示构成的后验分布 与由 导出的先验 之间的 KL 散度最小化。
基于这个设定,作者们推导出了以下定理:
定理 1 (数据依赖的 PAC-Bayes 提示界)
设 是一个大小为 的独立同分布样本集, 是 的一个大小为 的均匀子集。假设底层的损失函数 对于任意提示 和数据点 都是 -subgaussian 的。那么,对于任意 -可测的先验 和任意 -可测的后验 ,以下不等式在期望上成立:
(其中 )
进一步,给定一个在 上由 LLM 优化得到的先验提示 ,以及一个由 个在 上优化得到的任务提示构成的离散后验 ,那么以高恒定概率,对于至少一个 ,以下不等式成立:
其中, 度量了在给定先验提示 的条件下,某个 LLM 生成任务提示 的概率(这与 的困惑度直接相关)。
推导与理解:
-
第一个不等式是 Negrea 等人(2019)工作中数据依赖互信息界的一个应用。这里的关键是训练集被分为了两部分: (大小为 ) 用于确定先验,而 (大小为 ) 用于评估泛化误差。 -
第二个不等式是该理论在提示优化场景下的具体化。我们来详细看一下 KL 散度项是如何推导的。 -
我们的先验 是由先验提示 条件化的 LLM 分布,即 。 -
我们的后验 是在 个优化后的提示 上的一个均匀分布,即对于 ,。 -
KL 散度的定义为 。代入我们的 和 :
-
-
将这个 KL 散度表达式代入第一个不等式,并通过马尔可夫不等式(Markov's inequality),我们就可以得到对某个特定提示 的高概率界。
这个结果的直观解释是:泛化界的大小现在与后验提示 在由先验提示 导出的先验分布下的对数似然(或困惑度)有关。如果优化的任务提示 对于 LLM 来说是“自然的”(即 很大, 很小),那么 KL 散度项就会很小,从而得到一个更紧的泛化界。
通过使用一个随机后验(即 ),理论上我们可以通过 项来进一步收紧界。然而在实践中,作者们发现,即使采用最简单的设定,即 (后验是一个狄拉克 分布,集中在单个最优提示上),仅仅通过利用数据依赖性来构建一个好的先验提示 ,就足以推导出非空泛的界。
3. 实验与结果
为了验证上述理论的实际效用,研究者们设计了一系列实验,旨在评估使用更有信息量的先验提示对 PAC-Bayes 泛化界以及实际泛化性能的影响。
3.1 实验设置
-
任务与数据集:实验选用了一个真实的文本分类任务:仇恨言论检测。数据集为 ETHOS Hate Speech dataset,这是一个公开可用的数据集,包含了从各种在线来源收集的评论,并标注了它们是否构成仇恨言论(二元 "Yes/No" 标签)。这是一个典型的、可能需要通过少量样本进行提示微调的任务场景。 -
模型:实验中使用的 LLM 是 Gemini 2.0 Flash。 -
优化算法:为了系统性地搜索提示空间,实验采用了 Automated Prompt Optimization (APO) 算法。APO 是一种通过迭代编辑来优化提示的方法,它基于先前预测的结果来生成和评估新的候选提示。一个关键的设定是,APO 的优化目标并非传统的经验准确率,而是本文前面推导出的理论泛化上界。具体来说,在每一步,算法都会计算当前候选提示的泛化上界,并致力于最小化这个上界。实验中,他们最小化了一个 90% 置信度的误差上界。
3.2 先验的设定
实验的核心在于探索不同类型的先验提示 如何影响泛化界。他们测试了三种先验:
-
空先验 (empty prior) :这是一个空字符串 ""。这代表了最基础、无信息的先验,类似于 Akinwande 等人工作中的设定。 -
信息性先验 (informative prior) :这是一个人工撰写的、为任务提供上下文的提示。具体内容为: "We are trying to find classification labels for hate speech detection. <empty line> The text of the prompt is as follows: <empty line>"。这个先验为 LLM 提供了关于任务元信息,旨在引导模型生成更相关的任务提示。 -
优化后的先验 (optimized prior) :这是一个完全数据依赖的先验。它是通过在一次前期的、基于准确率的 APO 运行中,收集多个表现良好的任务提示,然后再次运行 APO 来找到一个能够最大化这些任务提示的联合对数似然的“元提示”(meta-prompt)。这个过程完全自动化,旨在学习一个能够生成“好”提示的先验。这个优化后的先验内容较长,详细内容可以在论文附录中找到,其大意是要求模型创建一个基于决策树的、用于仇恨言论分类的评分标准。
3.3 结果分析
实验结果汇总在下表中。
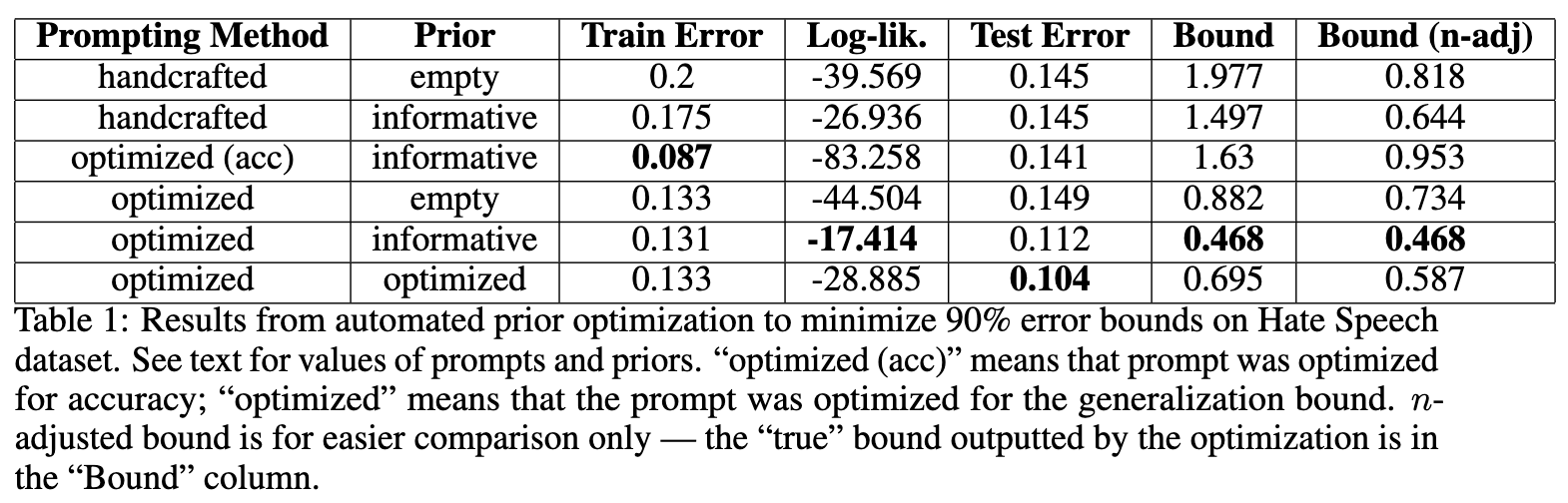
表中的关键列解释如下:
-
Prompting Method:handcrafted指手动设计的提示;optimized (acc)指以准确率为目标优化的提示;optimized指以泛化界为目标优化的提示。 -
Prior:使用的先验类型。 -
Train Error:在训练集上的错误率。 -
Log-lik.:任务提示在给定先验下的对数似然,即 。 -
Test Error:在测试集上的真实错误率。 -
Bound:由优化过程直接输出的理论泛化误差上界。 -
Bound (n-adj):为了公平比较,将所有实验的样本量 统一调整为最大值(160)后重新计算的泛化界。这是因为 APO 这种 bandit-style 算法可能会给更优的提示分配更多样本进行测试,导致 的不同。
从这张表中,我们可以得出几个核心观察:
观察 1:更有信息量的先验带来了更紧的界。
观察 Bound (n-adj) 这一列。使用空先验时,无论是手工提示还是优化提示,其泛化界分别为 0.818 和 0.734。而当使用信息性先验或优化后的数据依赖先验时,通过优化泛化界得到的提示,其界可以收紧到 0.468 和 0.587。一个小于 0.5 的泛化界虽然离真实的测试误差(约 0.11)还有距离,但在深度学习领域,尤其是在低数据场景下,这已经是一个非常有意义的非空泛结果。它表明理论界是有效的。这与 Akinwande 等人在拥有约 10k 样本的 CIFAR-10 数据集上获得的结果形成对比,本文仅使用了 150-300 个样本就获得了非平凡的结果,突显了在提示优化过程中利用精心设计的先验的价值。
观察 2:优化泛化界能够提升实际测试性能。
比较 Test Error 列。直接以准确率为优化目标的提示(optimized (acc) 行)测试误差为 0.141。而以泛化界为优化目标的几行,特别是使用信息性先验和优化后先验的提示,其测试误差分别达到了 0.112 和 0.104。使用数据依赖先验并以泛化界为目标的提示,取得了所有方法中最低的测试误差。尽管作者指出由于置信区间重叠,我们应谨慎得出过强的结论,但这无疑是一个积极的信号。它表明,泛化界中固有的困惑度正则化项(通过 体现)可能扮演了一个有益的角色,帮助模型避免在少量数据上过拟合,从而提升了鲁棒性和泛化能力。即使理论界本身还不够紧到可以被独立用于风险控制,优化这个界的过程本身就是有价值的。
观察 3:与先前工作的对比。
与 Akinwande 等人工作最接近的对照组是 (handcrafted, empty) 和 (optimized, empty) 这两行。与他们的“空先验”方法相比,本文提出的使用信息性先验和数据依赖先验的方法在理论界和实际性能上都展现了优势。这表明,在他们工作的基础上,通过引入更有结构的先验,可以进一步收紧泛化界并提升性能。作者也坦诚,本文得到的界比 Akinwande 等人的工作要松散,这主要是因为:
-
数据量级差异:本文使用了数量级更少的数据(O(100) vs O(10000))。 -
优化算法精度差异:本文使用的 APO 算法将 LLM 视为黑箱进行提示级别的优化,而 Akinwande 等人的工作使用了更精细的、逐个 token 的贪心采样来直接优化界本身。
尽管存在这些差异,实验结果仍然有力地证明了本文所提方法的潜力:在数据稀缺的环境下,利用信息更丰富的先验是通往有意义泛化保证的关键路径。
下面是实验中使用的一些具体提示词,可以帮助我们更直观地理解:
-
Handcrafted: "Does this input contain hate speech?" -
Optimized (for bound, using empty prior): “ Is this message hateful or discriminatory?” -
Optimized (for bound, using data-dependent prior): “Does this statement contain hate speech? (Yes/No)”
4. 实践启示
4.1. 追求提示的“自然度”(低困惑度)
这是论文最核心、最直接的启示。
-
是什么:一个提示的“自然度”或“困惑度”(Perplexity),衡量的是语言模型认为这个提示有多“正常”或“可能”。一个低困惑度的提示,是符合模型内部语言规律、语法结构清晰、语义连贯的提示。反之,一个高困惑度的提示可能看起来像随机的词语拼接,或者使用了非常规的、黑客式的语法(即使它在几个样本上碰巧有效)。
-
为什么重要:论文的理论和实验都表明,低困惑度的提示更可能泛化。在少量样本上通过“暴力破解”找到的、看起来很奇怪却有效的提示(“对抗性提示”或“过拟合提示”),很可能在遇到未见过的真实数据时表现不佳。它们只是利用了训练样本的偶然特性,而不是教会模型一个通用的规则。
4.2 善用“元提示”(Meta-Prompts)来提供上下文
论文中的“信息性先验”(Informative Prior)和“优化后的先验”(Optimized Prior)在实践中可以理解为“元提示”。
-
是什么:元提示是在你的核心任务提示之前的一段描述性文本。它不直接指导模型完成最终任务,而是为模型理解和评估你的核心任务提示提供上下文。
-
为什么重要:元提示能够有效地将模型的注意力“锚定”在一个更相关的语义空间内,从而降低后续核心提示的相对困惑度,收紧泛化界。它相当于告诉模型:“接下来我要给你一个用于XX任务的提示,请从这个角度来理解它。”
4.3 将“泛化界”作为你的优化目标,而不仅是“经验准确率”
这是论文中最具前瞻性的实践建议,它改变了我们衡量“好提示”的标准。
-
是什么:传统的提示优化目标是最大化在验证集上的准确率 。论文提出的新目标是最小化泛化误差上界,其简化形式可以理解为优化一个组合目标:。其中, 是提示 在验证集上的误差,而 可以看作是提示的复杂度或“非自然度”(比如,用 来代理)。 是一个平衡权重。
-
为什么重要:直接优化这个组合目标,本质上是在进行正则化。它会惩罚那些虽然在验证集上误差低、但本身很复杂或“不自然”的提示。这种正则化有助于防止模型对验证集中的少数样本过拟合,从而选出泛化能力更强的提示。论文的实验结果也证明了这一点:以泛化界为目标的优化,最终在测试集上取得了比直接优化准确率更好的性能。
-
实践指南:
-
在 A/B 测试中引入正则项:当你对比两个提示 和 时,不要只看谁的准确率高。计算一个综合得分,例如: Score(p) = Accuracy(p) - 0.1 * (-log_likelihood(p))。选择得分最高的那个。 -
对于自动化提示优化工具:如果工具允许自定义损失函数,可以尝试将对数似然项整合进去,作为对模型鲁棒性和泛化能力的直接优化。
-
4.4 从“好提示”中学习,构建数据驱动的“元提示”
论文中“优化后的先验”是通过一个全自动的过程找到的,但我们可以手动应用这个思想。
-
是什么:当你在一个任务上通过实验找到了多个表现不错的提示后,不要只保留最好的那一个。这些“好提示”本身就是宝贵的数据。
-
为什么重要:这些“好提示”的共性,揭示了能够有效引导模型解决此类任务的语言模式。将这些模式提炼出来,可以形成一个强大的、数据驱动的元提示,用于指导后续更精细的提示工程。
5. 总结
对提示词工程师而言,这篇论文最大的启示是:优秀的提示工程不仅仅是与模型进行“指令-响应”的博弈,更是与模型进行一场关于“语言和世界知识”的对话。 一个好的提示,应该能无缝地融入模型已有的知识体系,以一种“低能耗”(低KL散度/低困惑度)的方式引导模型到达我们想要的目的地。
因此,我们的工作重点应该从“找到能用的提示”转向“找到能泛化的、鲁棒的、可解释的提示”,而衡量标准,也应从单一的准确率,扩展到准确率和“自然度”的平衡。
往期文章:




