上海 AI lab 提出 SIREN：重新思考 RLVR 中的熵正则

我们知道 RLVR 存在 熵坍缩与过早收敛的问题。具体来说，当模型的策略（policy）在探索过程中偶然生成一个正确答案并获得正奖励后，策略梯度会迅速强化这条“成功路径”上的每个决策，导致模型后续的输出高度集中于这条或几条相似的路径上。策略的熵（entropy）衡量其输出不确定性或多样性的指标急剧下降。模型在训练的早期阶段就变得过于“自信”和确定性，停止了对解题空间的探索。这不仅降低了训练效率，更重要的是，它将模型的最终性能限制在了一个次优的局部最优点，难以发现更鲁棒、更泛化或更简洁的解法。

一个直观的解决方案是从传统强化学习中借鉴熵正则化（entropy regularization）。其核心思想是在优化目标中加入一个熵的奖励项，以鼓励策略保持一定的随机性，从而持续探索。然而，这种“朴素”的熵正则化方法在大型推理模型（LRMs）的场景下，效果并不理想，甚至会带来新的问题。我们的分析揭示了其失败的根源在于 LRMs 的两个内在特性：

1. 巨大的动作空间（Vast Action Space）：LRMs 的词汇表示一个拥有数万甚至数十万个“动作”（token）的离散动作空间。在如此巨大的空间里，即便是微小的熵正则化系数，也可能导致概率质量从少数有意义的 token 弥散到大量无意义的 token 上，引发“熵爆炸”（entropy explosion）。这种探索是无效且破坏性的，它会严重损害生成内容的语义连贯性。
2. 长轨迹的自回归生成（Long Trajectories in Autoregressive Generation）：推理任务通常需要生成包含数百甚至数千 token 的长序列。在自回归的生成过程中，早期 token 的不确定性会像滚雪球一样被累积和放大。一个位置上的高熵会引发后续位置的连锁反应，最终导致整个轨迹的熵失控，生成结果变差。

这两个因素共同导致朴素熵正则化在 LRMs 上表现出对超参数的高度敏感性：一个小的系数收效甚微，无法阻止熵坍缩；一个大的系数则会直接触发熵爆炸。这就引出了一个核心的研究问题：我们如何在 RLVR 框架下，为大型推理模型设计一种能够有效且可控地促进探索，同时避免熵爆炸的正则化机制？

来自上海人工智能实验室的论文《Rethinking Entropy Regularization in Large Reasoning Models》为解决这一难题提供了新的视角。他们提出的 SIREN (SelectIve entRopy rEgularizatioN) 方法，其核心思想是，探索不应是盲目和全局的，而应是有选择性的 (selective) 。SIREN 不再将整个词汇表和生成轨迹上的所有位置同等对待，将熵正则化应用在那些最值得探索的“动作”和“状态”上。

• 论文标题：Rethinking Entropy Regularization in Large Reasoning Models
• 论文链接：https://arxiv.org/pdf/2509.25133

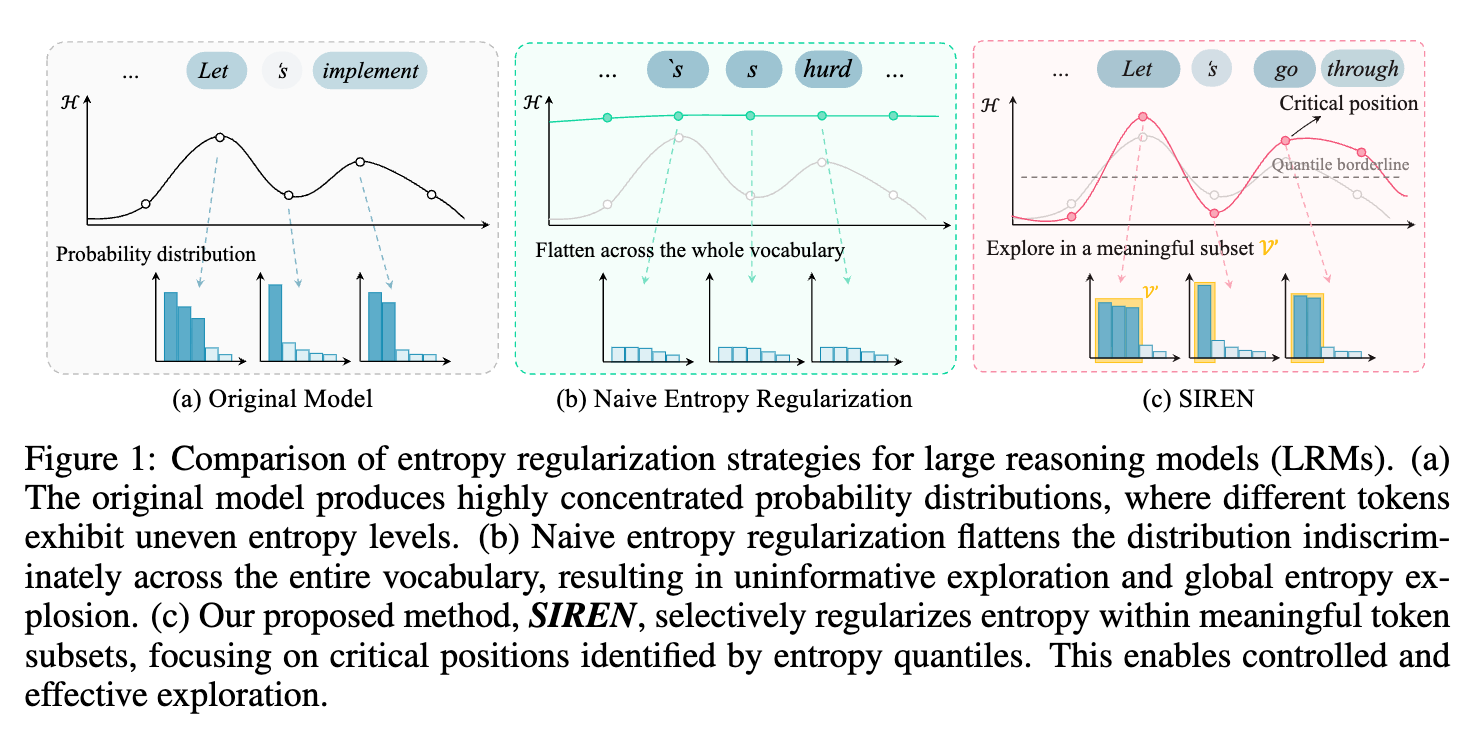
具体而言，SIREN 包含三个关键部分：

1. Top-p 掩码：在动作空间层面，将探索范围限制在由高概率 token 构成的“策略核”（policy nucleus）内部，避免在无意义的 token 上浪费探索预算。
2. 峰值熵掩码：在轨迹层面，识别出那些对推理路径起关键引导作用的“逻辑节点” token（这些 token 通常表现出更高的熵），并只对它们施加正则化，避免在无关紧要的“填充” token 上引入噪声。
3. 自锚定正则化：将正则化目标从单纯的“最大化熵”转变为将熵“维持在初始水平附近”，通过一个均方误差损失项将策略熵锚定在预训练模型自身的、未经 RL 微调的初始熵水平。这个初始熵代表了模型内在的、尚未被奖励信号“污染”的知识多样性，是一个天然且优质的探索起点。

通过这三个部分，SIREN 在促进探索和维持生成质量之间取得了平衡，有效解决了 RLVR 中的过早收敛问题。

1. 背景

为了深入理解传统熵正则化在 LRMs 场景下的具体失效模式，论文首先进行了一项详细的预备实验。他们使用一个较高的熵系数（0.005）在 Qwen2.5-Math-7B 模型上进行 RLVR 训练，并观察在训练过程中出现的“熵爆炸”现象。

在强化学习中，给定一个查询 ，策略 在第 个 token 位置的熵 定义为：

其中 代表整个词汇表。朴素熵正则化的训练目标是在原始的策略优化目标 （例如 PPO 的目标函数）基础上，加上一个由系数 加权的熵奖励项：

其中 代表一条完整的生成轨迹。这个目标旨在最大化累积熵，从而鼓励策略探索。

研究者选取了一个来自 AIME24 数据集的代表性问题，对比了模型在 RL 训练前和熵爆炸后的行为。

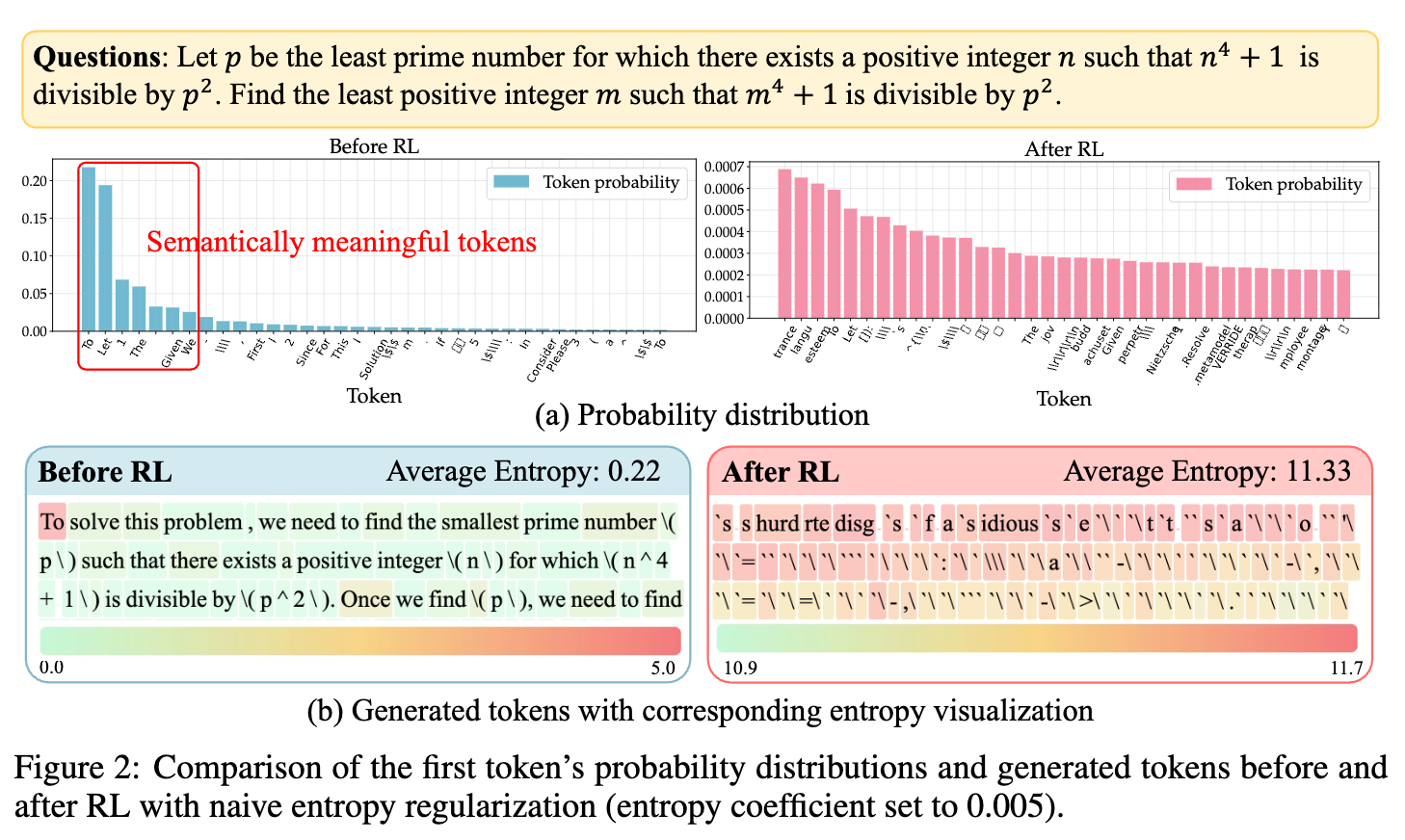
如图 2(a) 所示，分析聚焦于模型为第一个 token 生成的概率分布：

• RL 之前 (Before RL) ：模型的原始策略表现出高度的确定性。绝大部分概率质量都集中在少数几个语义上合理的 token 上（如 “To”, “solve”, “this”, “problem” 等，图中红框所示）。这些 token 构成了有意义回答的合理开端。大部分其他 token 的概率趋近于零。此时，该位置的平均熵非常低（0.22）。
• RL 之后 (After RL) ：在经历了熵爆炸后，概率分布变得极其平坦。之前概率很高的有意义 token，其概率被大幅稀释。与此同时，大量语义上风马牛不相及的、甚至是乱码的 token（如 “`s”, “hurd”, “rte”, “disg” 等）的概率被提升到与有意义 token 相近的水平。这验证了我们的假设：在巨大的词汇空间中，最大化熵的目标会不成比例地奖励那些将概率均匀散布的行为，因为这种行为能最快地提升熵值。此时，该位置的平均熵飙升至 11.33，接近在整个词汇表上均匀分布时的理论最大值。

进一步，如图 2(b) 所示，分析扩展到整个生成轨迹：

• RL 之前：模型生成了连贯、有逻辑的解题步骤，整个轨迹的平均 token 级熵保持在较低水平。
• RL 之后：模型的输出退化为一串毫无意义的乱码。通过热力图可视化每个 token 的熵值可以发现，轨迹中的几乎每一个位置都呈现出极高的熵。这揭示了熵爆炸的“连锁反应”：自回归生成过程将初始位置的熵（不确定性）不断传递和放大，最终导致整个序列的崩溃。

与此形成鲜明对比的是，在原始模型中，token 熵在轨迹上是动态变化的。研究者观察到，少数 token（如 “To”, “Once”, “Then” 等）表现出相对较高的熵。这些 token 往往扮演着引导推理方向、开启新逻辑步骤的关键角色。而大多数主要起填充句子作用的 token，则表现出低得多的熵。

这两点观察构成了 SIREN 方法的基础：

1. 策略核 (Policy Nucleus) 的提出：既然有效的探索只应发生在语义有意义的 token 子集上，那么我们可以借鉴 Top-p 采样的思想，定义一个“策略核”——即那些占据了绝大部分概率质量的顶层 token 集合。探索应该被严格限制在这个“核”的内部。
2. 关键 token 的识别：既然轨迹中只有少数 token 对推理至关重要，且这些 token 天然具有更高的熵，那么我们可以利用 token 级别的熵作为信号，识别出这些关键 token，并选择性地只对它们施加正则化。

2. SIREN

基于以上分析，SIREN (SelectIve entRopy rEgularizatioN) 被设计为一个包含两步熵掩码和自锚定正则化的新框架。它建立在 Dr.GRPO 算法之上。

2.1 基础 RL 框架：Dr.GRPO

论文的实现基于 GRPO (Group Relative Policy Optimization, Shao et al., 2024) 及其变体 Dr.GRPO (Liu et al., 2025)。

• GRPO：作为 PPO 的一种变体，GRPO 将整个生成序列视为一个整体动作。对于每个查询 ，它会从旧策略 采样一批（Group）共 个输出 。每个输出 会得到一个二元奖励 。然后，它计算一个组内归一化的优势（advantage）：

这个优势函数使得奖励信号在批次内部相对化，有助于稳定训练。其最终的 PPO-Clip 目标函数为：

其中 是重要性采样权重。

• Dr.GRPO：Dr.GRPO 是 GRPO 的一个简化版本，它在计算优势时去掉了分母中的标准差项：

实验表明，Dr.GRPO 在获得更高准确率的同时，能生成更短的响应，因此论文选择它作为基础框架。

2.2 两步选择性熵掩码

这是 SIREN 的核心。它包含一个作用于动作空间（词汇表）的 Top-p 掩码和一个作用于状态空间（轨迹）的峰值熵掩码。

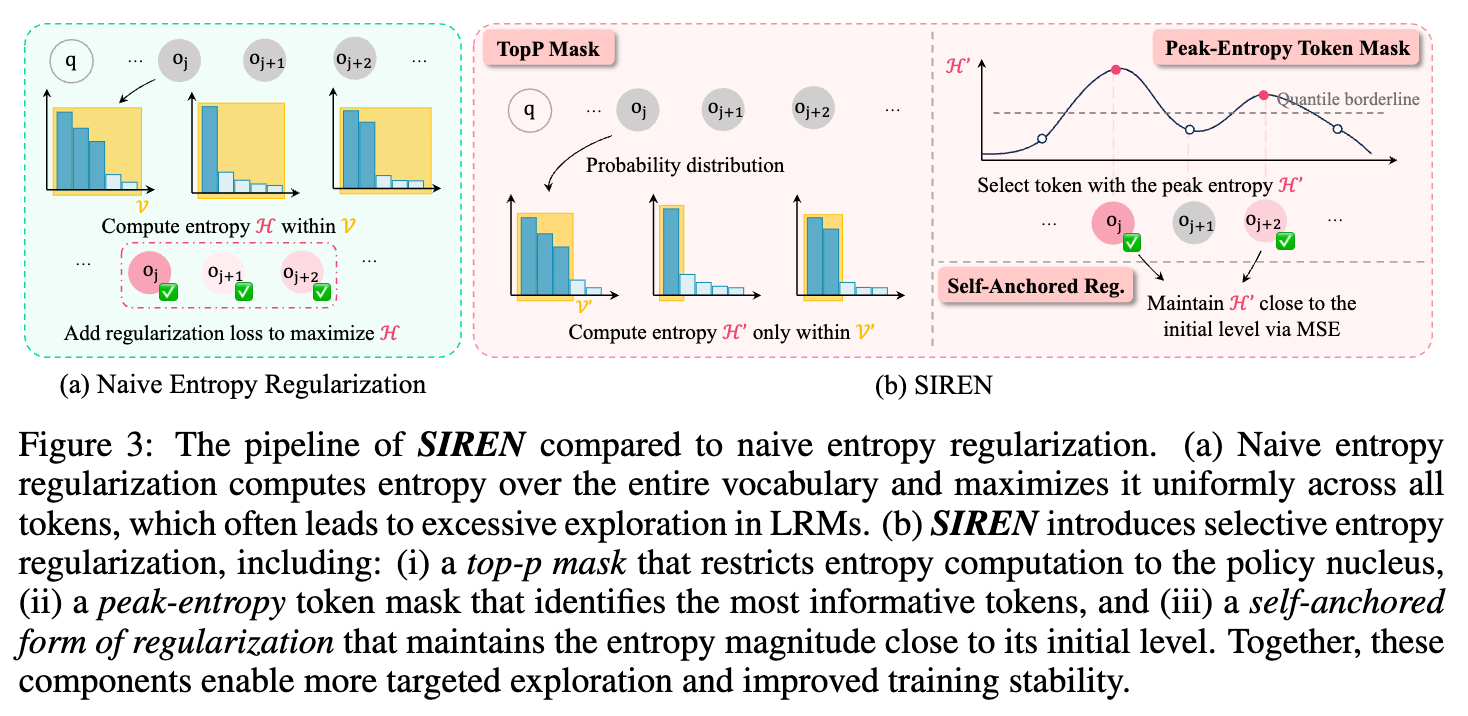
2.2.1 Top-p 掩码 (Top-p Mask within a Token)

为了解决在整个词汇表上进行探索导致的熵爆炸问题，SIREN 引入 Top-p 掩码，将熵的计算和正则化严格限制在“策略核” 内部。

1. 定义策略核：对于第 个 token 位置，策略核 被定义为满足累积概率大于等于 的最小 token 集合：

2. 构建 Top-p 掩码与重计算熵：Top-p 掩码 是一个指示函数，当 时为 1，否则为 0。利用这个掩码，可以得到一个在策略核内重新归一化的概率分布 ：

然后，新的熵 仅基于这个截断且归一化的分布 进行计算：

通过这种方式，熵正则化的梯度将只会反向传播到策略核内的 token，而不会影响到核外的低概率 token，从而避免了向无意义 token 的概率弥散。

2.2.2 峰值熵掩码 (Peak-Entropy Mask for a Trajectory)

为了解决在长轨迹中不加区分地对所有位置进行正则化导致的熵累积和连锁反应问题，SIREN 引入峰值熵掩码，仅对轨迹中的“关键” token 进行正则化。

1. 识别关键 token：基于之前的观察——关键逻辑 token 天然具有更高的熵——SIREN 使用上一部计算出的、在策略核内得到的熵 作为信号。具体来说，对于一个批次中的第 条轨迹 ，它首先计算出这条轨迹上所有 token 的熵的 -分位数 ：

2. 构建峰值熵掩码：峰值熵掩码 是一个指示函数，它只保留那些熵值高于或等于该分位数的 token：

这意味着，只有轨迹中熵最高的 比例的 token 会被选中，参与后续的正则化损失计算。

2.3 自锚定正则化 (Self-Anchored Regularization)

传统的熵正则化目标是最大化熵，这在 LRMs 中容易走向极端。SIREN 提出了一种新的正则化目标，旨在将策略的熵维持在一个“恰当”的水平。

1. 聚合批次熵：首先，通过结合上述两个掩码，计算出一个批次（batch）内的平均有效熵 。这个值只考虑了被两个掩码同时选中的 token 的熵：

其中 是批次中的轨迹数量。
2. 定义自锚定损失：新的正则化损失被定义为聚合熵 与一个熵锚点 之间的均方误差（MSE）：

3. 设置锚点：这里的关键在于锚点 的选择。SIREN 并未将其设为一个需要手动调整的超参数，而是采用了“自锚定”的策略：在训练开始时（第 0 步），用预训练模型计算一次初始的聚合熵，并将这个值固定为整个训练过程中的锚点 。
   这么做的动机是，预训练模型本身蕴含了从海量数据中学到的丰富多样的语言和推理模式，其初始的策略熵反映了这种内在的不确定性。这个状态是一个理想的、对探索友好的起点。自锚定正则化的目标就是让模型在接受 RL 奖励信号进行“剥削”（exploit）的同时，不要离这个探索友好的初始状态太远，从而在探索和剥削之间维持动态平衡。
   最终，SIREN 的训练目标变为：

注意，这里是减去 ，因为优化器会最小化这个目标，相当于最小化 ，从而驱动 逼近 。

3. 实验

3.1 实验设置

• 模型：实验主要在 Qwen2.5-Math-7B 上进行，并扩展到更小的 Qwen2.5-Math-1.5B 和社区流行的 Llama3.1-8B 模型以验证泛化性。
• 数据集：训练集使用 OpenR1-Math-46k-8192。评估则在五个广泛使用的数学推理基准上进行：AIME24, AIME25, AMC22, MATH500, OlympiadBench。
• 评估指标：

  • maj@k (majority voting @ k)：从 个采样回答中，选出出现次数最多的答案，并验证其正确性。这个指标同时衡量了模型的探索能力（能否在 次尝试中找到正确答案）和内在置信度（能否稳定地收敛到正确答案）。
  • avg@k：计算 个采样回答的平均得分。这个指标反映了模型的整体性能。
• 基线方法：

  1. Dr.GRPO：不带任何熵正则化的基础模型。
  2. Naive Entropy Regularization：使用传统熵最大化目标。
  3. Clip-Cov / KL-Cov ：通过裁剪或 KL 惩罚来间接控制高协方差 token 的熵。
  4. Entropy Adv. ：将熵作为启发式信号来调整优势函数。
  5. RL on forking tokens ：只对高熵的“分叉” token 应用策略梯度更新。

3.2 主要结果

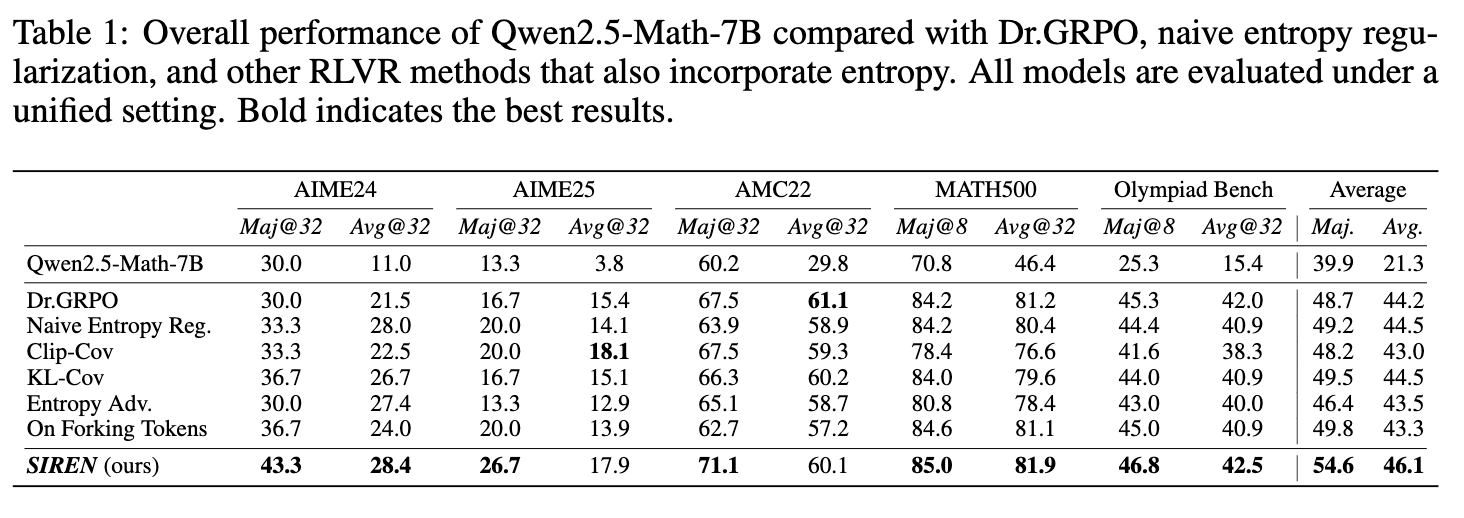
如表 1 所示，在 Qwen2.5-Math-7B 模型上，SIREN 在所有五个基准测试中都取得了最优或具有竞争力的结果。

• 平均性能：SIREN 的平均 maj@k 达到了 54.6，比表现最好的基线方法（RL on forking tokens, 49.8）高出 4.8 个点。平均 avg@k 达到了 46.1，同样是所有方法中最高的。
• 高难度基准：在最具挑战性的 AIME24 和 AIME25 数据集上，SIREN 的优势尤为明显。例如，在 AIME24 上，其 maj@32 分数为 43.3，相比 Dr.GRPO 的 30.0 有着巨大的提升，也显著优于其他所有熵相关方法。这表明 SIREN 的受控探索机制在高难度、需要深度推理的任务中尤为有效。

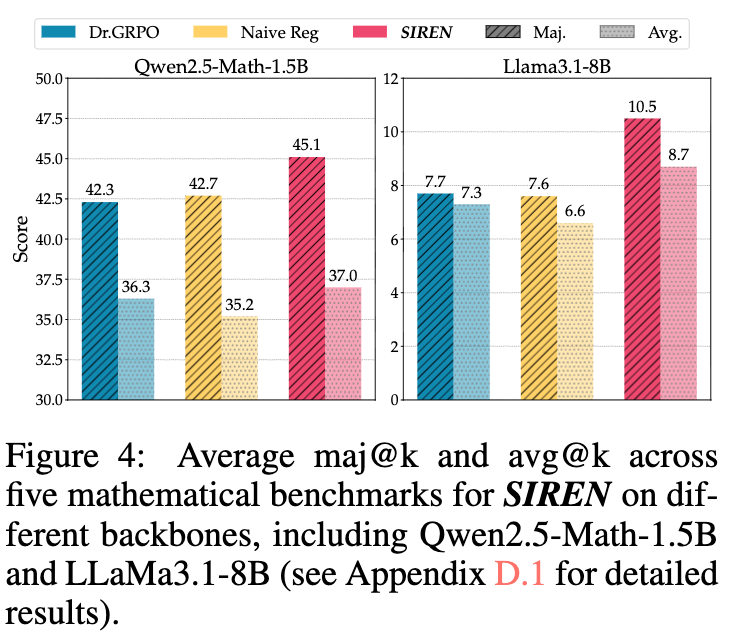
为了验证方法的泛化性，研究者将 SIREN 应用于不同规模和架构的模型。如图 4 所示，无论是在较小的 Qwen2.5-Math-1.5B 还是在 Llama3.1-8B 上，SIREN 都稳定地超越了 Dr.GRPO 和朴素熵正则化基线。在 Qwen2.5-Math-1.5B 上，SIREN 带来了 +2.4 的 maj@k 提升；在 Llama3.1-8B 上，带来了 +2.8 的 maj@k 提升。这证明了 SIREN 的有效性并不局限于特定的模型。

3.3 深入分析

3.3.1 Pass@k 分析

Pass@k 指标衡量在 次采样中至少有一次答对的概率，它被广泛认为是模型推理能力上限和探索范围的指标。

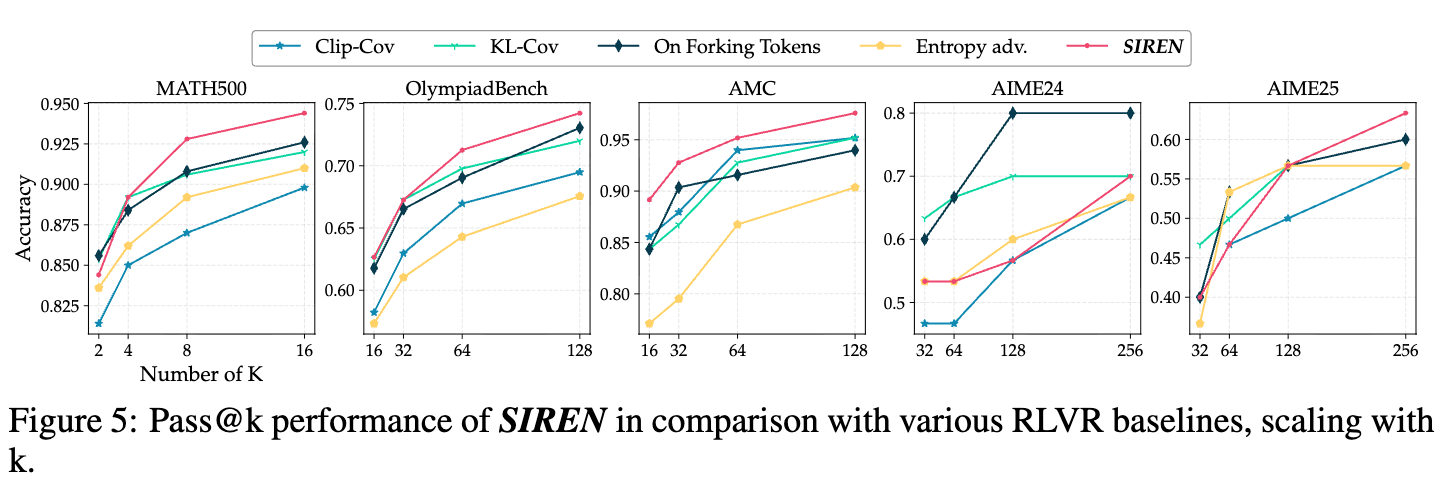
如图 5 所示，随着采样次数 的增加，所有方法的 pass@k 都会提升。然而，SIREN 的曲线在大多数基准（尤其是 MATH500, AMC, OlympiadBench）上都处于领先位置，并且其优势随着 的增大而更加明显。这说明 SIREN 生成的响应集合具有更高的多样性，其探索的“网”撒得更广，更有可能覆盖到正确的解题路径。

3.3.2 困惑度 (Perplexity) 分析

困惑度（Perplexity, PPL）可以用来衡量模型对一个给定响应的预测难度。在这里，研究者使用原始的预训练模型来计算由不同 RL 算法微调后的模型所生成的响应的 PPL。如果 PPL 较高，说明这些响应对于原始模型来说更“意外”、更多样，表明 RL 过程没有导致响应模式的坍缩。

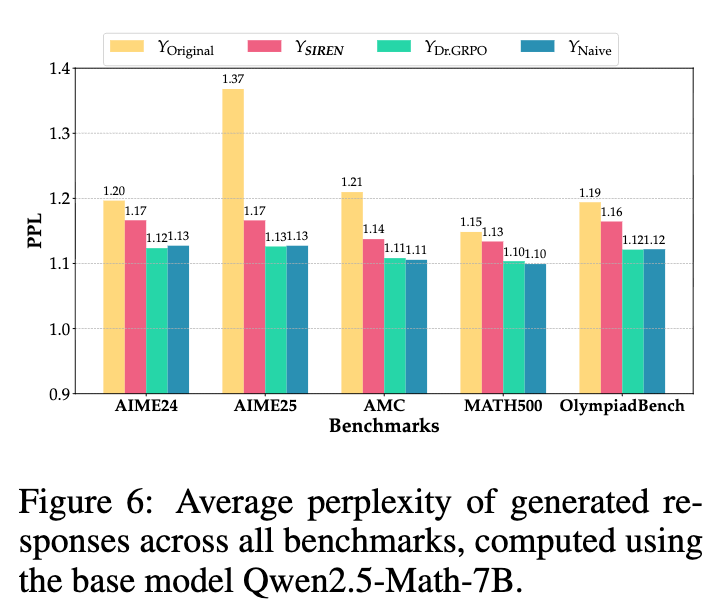
如图 6 所示，相比于 Dr.GRPO 和朴素熵正则化等基线 RL 方法，SIREN 生成的响应始终具有更高的 PPL。这从另一个角度印证了 SIREN 能够有效缓解过早收敛，鼓励模型产生更广泛、更多样的输出。

3.3.3 训练动态分析

为了直观展示 SIREN 如何实现“受控探索”，研究者绘制了模型在训练过程中的熵和验证集 pass@16 性能随步数变化的曲线。

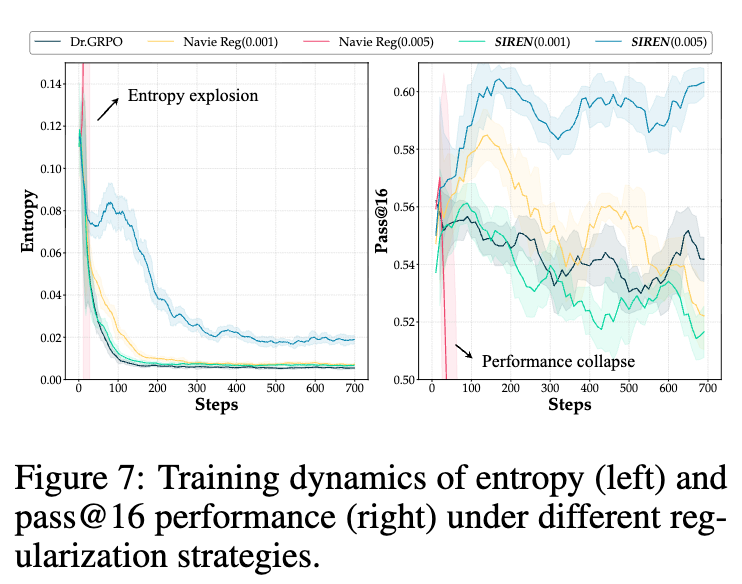
图 7 揭示了不同策略的本质区别：

• Dr.GRPO 和 Naive Reg (0.001) ：它们的熵在训练开始后迅速下降并维持在极低水平，这正是“熵坍缩”。与之对应，它们的验证性能 pass@16 在早期达到一个平台期后便停滞不前甚至下降。这体现了“过早收敛”。
• Naive Reg (0.005) ：它的熵在训练开始的瞬间就急剧飙升，发生了“熵爆炸”。与之对应，其验证性能直接崩溃。这体现了“无效探索”。
• SIREN (0.005) ：SIREN 的行为则截然不同。在训练的早期和中期（大约 0-400 步），它将熵维持在一个显著高于其他基线方法的稳定水平。这种持续的、高水平的熵代表了“持续探索”。重要的是，这种探索是有效的，因为它被稳定地转化为验证性能的持续提升，其 pass@16 曲线一路上扬，最终收敛到一个更高的水平。在训练后期，熵才开始逐渐下降，表明模型在充分探索后开始收敛。

这个对比清晰地证明了 SIREN 的核心优势：它不是简单地最大化或最小化熵，而是将其动态地维持在一个对探索有益的“甜点区”，从而实现了有效探索与性能提升的良性循环。

3.4 消融实验

为了验证 SIREN 各个组件的必要性，研究者进行了一系列消融实验。

如表 2 所示，移除 SIREN 的任何一个组件都会导致性能下降：

• 移除自锚定正则化 (w/o Self-Anchored Reg.) ：这是性能下降最严重的一项，maj@k 下降了 10.3 个点，avg@k 下降了 15.5 个点。这凸显了自锚定机制在稳定训练、防止熵爆炸方面的关键作用。没有它，即便使用很小的熵系数（0.0001），模型依然会遭受熵爆炸。
• 移除 Top-p 掩码 (w/o TopP Mask) 或 峰值熵掩码 (w/o Peak-Entropy Mask) ：移除任何一个掩码都会导致性能下降，说明仅靠单层级的过滤是不够的。动作空间和轨迹层面的协同选择对于精准探索缺一不可。
• 仅使用自锚定正则化 (w/ only Self-Anchored Reg.) ：这个实验将自锚定机制应用于朴素熵正则化。结果显示，性能相比朴素方法有所提升，但仍显著低于完整的 SIREN。这证明了自锚定本身是一个有效的稳定器，但要达到最佳性能，仍需与两步掩码机制相结合，实现探索的“精准制导”。

4. 结论与思考

这篇工作深入剖析了在大型推理模型（LRMs）的强化学习（RLVR）中，朴素熵正则化因巨大的动作空间和长轨迹的自回归特性而失效的根本原因。为解决这一问题，论文提出了 SIREN，一个创新的选择性熵正则化框架。

SIREN 的核心贡献在于其“选择性”和“自锚定”的思想：

1. 选择性：通过 Top-p 掩码和峰值熵掩码，SIREN 实现了对探索范围在动作和状态两个维度上的精准控制，将探索资源集中于最有可能产生回报的区域，避免了盲目、破坏性的全局熵增。
2. 自锚定：通过将正则化目标从“最大化熵”转变为“锚定于初始熵”，SIREN 为训练过程提供了一个动态、数据驱动的稳定锚点，巧妙地解决了熵正则化超参数难以调整的问题，在防止熵坍缩和熵爆炸之间找到了一个稳定的平衡点。

大量的实验和深入分析一致证明，SIREN 不仅在多个数学推理基准上取得了领先的性能，并且其设计思想具有良好的泛化性。更重要的是，通过对训练动态的细致观察，该工作清晰地揭示了 SIREN 是如何实现“受控且有效”的探索，从而克服了 RLVR 中普遍存在的过早收敛难题。

对于大型模型研究社区而言，这项工作带来的启示是深刻的：

• 探索需要被“精细化管理”：对于 LRMs 这样的复杂系统，简单粗暴的全局正则化策略往往是无效的。未来的研究需要更多地考虑模型的内在结构（如概率分布的稀疏性）和任务的特性（如推理轨迹中的关键节点），设计出更加精细化的探索与正则化机制。
• 利用模型自身的先验：将预训练模型的初始状态（如初始熵）作为正则化的目标或锚点，是一个非常值得借鉴的思路。它利用了模型在预训练阶段学到的丰富先验知识，为后续的微调过程提供了一个稳定且有意义的参照系。
• RL for LLM 的稳定性是关键：这篇工作再次证明，解决强化学习在应用于大型语言模型时的训练不稳定性问题，是释放其全部潜力的关键。SIREN 提供了一个强有力的范例。

未来的工作可以在 SIREN 的基础上进一步探索，例如将掩码的选择机制从启发式（如熵分位数）变为可学习的模块。

往期文章：

-Meta AI 提出 RECAP：真正的稳健推理源于纠正错误，而非模仿正确

• ExGRPO：超越在线策略，让大模型从“经验”中高效学习推理

• 苹果提出 RL4HS：用强化学习来进行幻觉范围检测

• NVIDIA 大规模实证研究揭示：推理数据前置到预训练阶段的必要性

• Meta AI 揭示 SFT 陷阱：盲目追求高分，可能会损害模型在 RL 阶段的潜力

• 腾讯混元提出 RLPT ：在预训练数据上进行 RL，进一步 scaling LLM 推理边界

• GRPO 就是 DPO ? 2-GRPO 媲美 16-GRPO，训练时间缩短 70%

• DeepSearch：将 MCTS 嵌入到 RLVR，解决信用分配难题

• 腾讯混元提出TFPI：效率性能双重提升，解决 RLVR 中长上下文训练难题

• Meta AI：将 LLMs 定义为改进算子，定义效率与效果的新边界

• 腾讯 AI LAB 提出 MoE-CL：用 MoE 和 GAN 来解决 LLM 的持续学习问题

• DeepSeek-V3.2-Exp 论文详细解读

• Meta AI 提出基于 RL 的连续 CoT 训练新范式

• 陈丹琦团队新作：通过RLMT（模型奖励思考的强化学习）将推理能力泛化到开放式任务

• 腾讯提出单流策略优化（SPO）：告别组同步瓶颈，回归RL本质

• 北大 & 字节 Seed 提出 DACE：难度感知下的确定性引导探索

• 美团 LongCat-Flash-Thinking Technical Report 深度解读

• “移除”还是“回归”？深入探讨 GRPO 中 KL Loss

• 腾讯 AI Lab 推出 EVOL-RL：无监督进化，多数主导选择，新颖性促进变异

• EMNLP 2025 TeleAI 推出 T2R-bench：为表格报告生成任务定义新评估范式

• 无需思维链，LLM如何“凭空”算出答案？探究末位Token的计算机制

• Meta AI 新作 Compute as Teacher: 将 rollouts 转化为高质量的无参考监督

• f-散度直击 GRPO 的传统 Reverse KL：用 Mass-Covering 解决多样性坍塌

• Meta AI 新研究：基于结果的探索，共同提升pass@1和pass@k，缓解大模型推理中的多样性坍塌

• 字节 Seed 提出 REER：由 Query 和 Answer 逆向得到 CoT，专注于开放式任务

• HuggingFace 月度 Top 1 论文：Gensyn AI 提出 SAPO——通过集体经验共享实现高效的语言模型后训练

• 字节 Seed 推出 EMPG：面向长程 LLM Agents 的熵调控策略梯度

• 腾讯 AI Lab 推出 Parallel-R1：引入并行思考进一步释放 LLM 潜力

• 百川提出 DCPO：应用动态自适应裁剪、平滑优势标准化，性能超越 DAPO

• Meta AI 新作 Distilled Pretraining：预训练阶段知识蒸馏会损害ICL能力

• 抛弃Self-Consistency的“答案投票”，用PiCSAR“双重置信度”作为BoN标准

• Meta Superintelligence Labs 首篇论文：重新定义 RAG

• Qwen提出LPPO框架，通过PG-Sampling和LP-Weighting解决数据稀缺与训练效率瓶颈

• DeepSeek V3.1 翻车了！字节 Seed 提出 Inverse IFEval 判断大型语言模型能否听懂“逆向指令”？

• 全网最详细解读 OpenAI 最新论文：为什么大模型会存在“幻觉”？

• 深度解析 Baichuan-M2：解决临床决策实用性难题，推出基于大规模验证器系统扩展医疗能力

• LLM Post-Training 统一视角：清华 & 微信AI 提出统一 Policy Gradient 估计器

• 字节Seed & 复旦提出ThinkDial：首个复现GPT-oss可控推理

• LLM训练新思路：快手RLEP巧用经验回放，实现效率与性能双突破

• PPO、DPO、GRPO及其变体（Dr. GRPO、GSPO、GMPO、LitePPO）策略优化算法综述

• 你没看错，腾讯开始用大模型来玩《王者荣耀》了！

• EMNLP2025 CRAFT：RL引入对比学习，增加LLM训练稳定性，刷新推理上限

• 字节Seed提出AdaCoT：将自适应CoT建模为帕累托优化问题

• 上交 & 上海 AILAB 提出 Memory Decoder：一种用于大语言模型的免微调即插即用记忆模块

• 港科大提出DARS：在RLVR中进行深度广度协同，实现Pass@1与Pass@K性能同步提升

• InternVL3.5 Post-Training 技术解析

• Meta提出StepWiser：引入思维块奖励，基准得分超传统方法20%

• 微软 & UCLA 新作：超越 Pass@1，通过自博弈和变分问题合成，持续提升大模型推理能力

• 大模型SFT数据配比的一些实践启示

• 上交 & 腾讯提出 PSFT：借鉴PPO，为SFT引入近端约束，告别泛化能力差与“熵坍塌”

• 字节Seed&南大提出DuPO：基于广义对偶的自监督大模型优化算法

• 蚂蚁浙大提出基于“评分细则”（Rubric）的奖励机制，仅靠5000+样本，让30B轻松击败671B DeepSeek V3

• MIT：UFT 统一监督微调（SFT）和强化微调（RFT）

• Meta AI&UCSD 提出DeepConf：将GPT-OSS-120B AIME 2025准确率提升至99.9%

• “天下没有免费的午餐”：反思LLM推理中的内在反馈

• GEPA：反思式Prompt进化，效果超过RL

• Qwen团队提出CHORD训练流程：动态融合 SFT 与 RL

• 深挖RLVR探索机制：SFT专攻Pass@k，RL强化Pass@1

• 人大&百度提出ReasonRank：让LLM学会在排序中“思考”

• 深度解析 Seed Diffusion：来自字节跳动的高速推理扩散语言模型

• HuggingFace榜一论文：大模型强化学习中的熵机制

• 字节Seed：Pass@k作为reward可以有效平衡探索与利用

• 深入探讨RL4LLM：解决低概率词元的“过度主导”问题

• 浙大Posterior-GRPO：结合PRM和ORM来优化大模型

• 微软新作GFPO：治疗DeepSeek R1的“话痨”，冗长响应减少80%

• 周志华团队新作：通过IRL挖掘LLM内生奖励，首次理论证明RL对LLM有效性

• FlashRL：引入截断重要性采样，解决Rollout训练不匹配，RL加速可达1.75×

• 超越二元奖励：训练语言模型审视自身的不确定性

• RLVR的一些Tricks到底哪些有用？

• 重磅开源！GLM-4.5 ARC 技术报告深度解读

• Diffusion：真正的王牌不是“快”，而是“超级数据学习者”

• 腾讯 AI Lab提出R-Zero「实现零数据自进化」

• CompassVerifier 深度解析：为大模型打造统一、鲁棒的“裁判”与“奖励”系统

• 一行代码，解锁SFT泛化能力：深度解读DFT如何完胜传统微调

• 告别验证器依赖：RLPR如何将大模型推理能力泛化到通用领域

• ACL2025｜“拉不住的弹簧”：为什么大型语言模型会“抵抗”对齐？

• 大模型3D可视化

• GRPO等于高级版Rejection Sampling？强化学习祛魅时刻：负样本“披沙拣金”才是关键！

• Skywork MindLink 深度解析：如何让 Qwen3 继续进化

• 在数据受限场景下，Diffusion优于自回归模型

• RL+SFT 优势首融合，动态引导模型高效训练

• 阿里通义千问放大招，告别训练崩溃！新算法 GSPO 碾压 GRPO，Qwen3 模型性能暴涨的幕后功臣